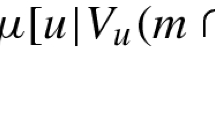Anticipated stochastic choice

Abstract

The purpose of this study is to characterize stochastic choice influenced by the objective or subjective positions of alternatives in a menu. The main theorem axiomatizes the anticipated stochastic choice (ASC) representation, wherein the decision maker maximizes the expected utility by the cognitive control of a probability measure over mental states that trigger the ex post choice of alternatives. A key prerequisite for this axiomatization is that the randomization between menus is identified with their perfectly correlated mixture, which includes only mixtures of specific alternative pairs. The essential uniqueness of an ASC representation defines an index of rationality that is relevant to a preference for commitment. Special cases of ASC include exact utility maximization, uncontrolled stochastic choice, trembling hands, and choice with limited attention. Furthermore, ASC accommodates potentially stochastic choice anomalies such as the attraction effect, cyclical choice, and position effects.

Appendix

1.1 Proof of Theorem 1

For the sufficiency part of Theorem 1 (a regular ASC representation implies the axioms), we only present proofs for Axioms 2, 7b, and 7c, because the sufficiency for the other axioms is straightforward.

To confirm that Axiom 2 holds, we note that the affineness of u implies that $\int _{\mathcal {A}} u(\phi (x, s)) dP(x) = \lambda _1 u(\phi (x_1, s)) + \cdots + \lambda _m u(\phi (x_m, s))$ for all finite random menus $P = (\lambda _1, x_1; \ldots ; \lambda _m, x_m)$ that generate menu $x_i$ with probability $\lambda _i$ for $i = 1, \ldots , m$, and all $s \in S$. Then, Axiom 2b follows from regularity conditions (a) and (b), and considering $P = (\lambda , x; 1-\lambda , x)$ also implies Axiom 2a.

On the other hand, Axioms 7b and 7c are implied by the regularity conditions of $\phi$. First, Axiom 7b is proved by induction. Let $x^*_1 = \{\beta ^1_1\}$ for an arbitrary $\beta ^1_1 \in {\varDelta }(Z)$. Next, fix $n \ge 1$ and assume that $x^*_i$ satisfies the implication of Axiom 7b for $i = 1, \ldots , n$. The construction of $\phi$ implies, for any given $x^*_{n+1} \in {\mathcal {A}}$ such that $|x^*_{n+1}| = n+1$, that $\lambda x^*_n \oplus (1-\lambda ) x^*_{n+1} \sim \cup ^{n+1}_{i=1} \{\lambda \phi (x^*_n, s_i) +(1-\lambda )\phi (x^*_{n+1}, s_i)\}$ for all $\lambda \in [0, 1]$. By defining $\beta ^{n+1}_i \equiv \phi (x^*_{n+1}, s_i)$ for $i = 1, \ldots , n+1$, regularity conditions (a) and (b) imply that $x^*_{n+1} = \{\beta ^{n+1}_1, \ldots , \beta ^{n+1}_{n+1}\}$ and $\lambda x^*_n \oplus (1-\lambda ) x^*_{n+1} \sim \cup ^{n+1}_{i=1} \{\lambda \beta ^n_{\min \{i, n\}} + (1-\lambda ) \beta ^{n+1}_i\}$ for all $\lambda \in [0, 1]$. Because the same argument holds for all $n \ge 1$, we obtain Axiom 7b. Second, regularity condition (c) implies that, for all $x \in {\mathcal {A}}, 1 \le k \le |x|$, and ${\bar{\beta }} \in {\varDelta }(Z)$, there exists $x' \in {\mathcal {A}}$ such that $|x'| = |x|, \phi (x', s_i) \sim \phi (x, s_i)$ for all $i \ne k$, and $\phi (x', s_k) \sim {\bar{\beta }}$, which implies Axiom 7c.

Below, we prove the necessity part of the theorem. The first lemma indicates that Axiom 2 derives a bijection between menus of identical cardinality that describes the DM’s perception of random menus.

Lemma 1

Axiom 2 implies the following axiom:

Axiom $2^{*}$ For all $x, y \in {\mathcal {A}}$ such that $|x| = |y|$, there exists a bijection $\tau : x \rightarrow y$ such that $\lambda x \oplus (1-\lambda ) y \sim \{\lambda \alpha + (1-\lambda ) \tau (\alpha ): \alpha \in x \}$ for all $\lambda \in [0, 1]$.

Proof

Axiom 2b (specifically, Definition 1a) implies that, for given $x, y \in {\mathcal {A}}$ such that $|x| = |y|$, there exists $C \subseteq x \times y$ such that $\lambda x \oplus (1-\lambda ) y \sim \{\lambda \alpha + (1-\lambda ) \beta : (\alpha , \beta ) \in C \}$ for all $\lambda \in [0, 1]$. By construction, we also have $\lambda ' y \oplus (1-\lambda ') x \sim \{\lambda ' \beta + (1-\lambda ') \alpha : (\alpha , \beta ) \in C \}$ for all $\lambda ' \in [0, 1]$. From Axiom 2b (Definition 1b), it follows that

$$\begin{aligned} \lambda '' x \oplus (1-\lambda '') x \sim \{\lambda '' \alpha + (1-\lambda '') \alpha ': (\alpha , \beta ) \in C \ \text {and} \ (\alpha ', \beta ) \in C\} \end{aligned}$$

(4)

for all $\lambda '' \in [0, 1]$. Axiom 2a implies that there exists some C such that the right-hand side of (4) is equivalent to x.

Now, assume that for all C satisfying (4), there is no bijection $\tau : x \rightarrow y$, such that $\beta = \tau (\alpha )$ if and only if $(\alpha , \beta ) \in C$. This implies that (i) there exists ${\tilde{\alpha }} \in x$ such that $({\tilde{\alpha }}, \beta ) \not \in C$ for all $\beta \in y$, (ii) there exist distinct ${\tilde{\alpha }}, {\hat{\alpha }} \in x$ such that $({\tilde{\alpha }}, \beta ), ({\hat{\alpha }}, \beta ) \in C$ for some $\beta \in y$, or (iii) there exist distinct ${\tilde{\beta }}, {\hat{\beta }} \in y$ such that $(\alpha , {\tilde{\beta }}), (\alpha , {\hat{\beta }}) \in C$ for some $\alpha \in x$. In case (i), we assume without loss of generality that there is no $C' \subseteq x \times y$ such that $C' \supsetneq C$ satisfies (4) in replacing C. Then, the right-hand side of (4) cannot be indifferent to x for all $\lambda '' \in [0, 1]$ because it never includes ${\tilde{\alpha }}$. In case (ii), we assume without loss of generality that there is no $C' \subseteq x \times y$ such that $C' \subsetneq C$ satisfies (4) in replacing C. Then, the right-hand side of (4) cannot be indifferent to x for all $\lambda '' \in [0, 1]$, because it includes $\lambda {\tilde{\alpha }} + (1-\lambda ) {\hat{\alpha }}$. Finally, case (iii) is equivalent to case (ii) after exchanging the roles of x and y. Accordingly, all the cases contradict Axiom 2a.

The above discussion holds for all such menus x and y, and thus, we obtain the desired result. $\square$

Next, we construct the sets of mental states and a regular choice function.

Lemma 2

There exist $S_n = \{s_1, \ldots , s_n\}, S = \cup ^\infty _{n=1} \{S_n\}$, and a regular $\phi$ such that

$$\begin{aligned} \lambda x \oplus (1-\lambda ) y \sim \cup _{s \in S_{\max \{|x|, |y|\}}} \{\lambda \phi (x, s) + (1-\lambda ) \phi (y, s)\} \end{aligned}$$

(5)

for all $x, y \in {\mathcal {A}}$ and $\lambda \in [0, 1]$.

Proof

We prove the lemma by induction. First, define $S_1 = \{s_1\}$ and $\phi (x, s_1) = \beta$ for all $x = \{\beta \} \in {\mathcal {A}}_1$. These definitions, combined with Lemma 1, imply regularity condition (a) and (5) for all singleton menus x and y.

Next, set $n \ge 1$ and assume that $S_n$ and $\phi$ satisfy regularity condition (a) and (5) for all $x, y \in \mathcal{A}_n$. Axiom 7b implies that, for menus $x^*_n = \{\beta ^n_1, \ldots , \beta ^n_n\}$ and $x^*_{n+1} = \{\beta ^{n+1}_1, \ldots , \beta ^{n+1}_{n+1}\}$ defined in the axiom, $\lambda x^*_n \oplus (1-\lambda ) x^*_{n+1} \sim \cup ^{n+1}_{i=1}\{\lambda \beta ^n_{\min \{i, n\}} + (1-\lambda ) \beta ^{n+1}_i\}$ for all $\lambda \in [0, 1]$. Accordingly, by defining $S_{n+1} \equiv S_n \cup \{s_{n+1}\}, \phi (x^*_n, s_i) \equiv \beta ^n_{\min \{i, n\}}$, and $\phi (x^*_{n+1}, s_i) \equiv \beta ^{n+1}_i$ for $i = 1, \ldots , n+1$, we obtain $\lambda x^*_n \oplus (1-\lambda ) x^*_{n+1} \sim \cup _{s \in S_{n+1}}\{\lambda \phi (x^*_n, s) + (1-\lambda ) \phi (x^*_{n+1}, s)\}$ for all $\lambda \in [0, 1]$ and $\phi (x^*_n, s_{n+1}) = \phi (x^*_n, s_n)$.

Now, iteratively applying Axiom 2b (i.e., $\succsim$ having consistent perceptions of random menus) to the above argument implies that, for all $m \le n+1, \lambda x^*_m \oplus (1-\lambda ) x^*_{n+1} \sim \cup _{s \in S_{n+1}} \{\lambda \phi (x^*_m, s) + (1-\lambda ) \phi (x^*_{n+1}, s)\}$ for all $\lambda \in [0, 1]$ and $\phi (x^*_m, s_i) = \phi (x^*_m, s_m)$ for $i = m+1, \ldots , n+1$. Moreover, Lemma 1 implies that, for all $x, y \in {\mathcal {A}}$ such that $|x| = m$ and $|y| = n+1$, there exist bijections ${\hat{\tau }}: x^*_m \rightarrow x$ and ${\tilde{\tau }}: x^*_{n+1} \rightarrow y$ such that $\lambda ' x^*_m \oplus (1-\lambda ') x \sim \{\lambda ' \beta ^m_i + (1-\lambda ') {\hat{\tau }} (\beta ^m_i): i = 1, \ldots , m \}$ for all $\lambda ' \in [0, 1]$ and $\lambda '' x^*_{n+1} \oplus (1-\lambda '') y \sim \{\lambda '' \beta ^{n+1}_i + (1-\lambda '') {\tilde{\tau }} (\beta ^{n+1}_i): i = 1, \ldots , n+1 \}$ for all $\lambda '' \in [0, 1]$. Accordingly, by defining $\phi (x, s_i) = {\hat{\tau }}(\beta ^m_{\min \{i, m\}})$ and $\phi (y, s_i) = {\tilde{\tau }}(\beta ^{n+1}_i)$ for $i = 1, \ldots , n+1$, Axiom 2b implies that $\lambda x \oplus (1-\lambda ) y \sim \cup _{s \in S_{n+1}} \{\lambda \phi (x, s) + (1-\lambda ) \phi (y, s)\}$ for all $\lambda \in [0, 1]$, and $\phi (x, s_i) = \phi (x, s_m)$ for $i = m+1, \ldots , n+1$. This implies (5) for all $x, y \in {\mathcal {A}}_{n+1}$. The construction of $\phi (y, \cdot )$ also gives regularity condition (a) for all $y \in {\mathcal {A}}_{n+1}$. Moreover, because the above argument implies that $\phi (x, s_{n'}) = \phi (x, s_{|x|})$ for all $x \in {\mathcal {A}}$ and $n' \in {\mathbb {N}}$ such that $n' \ge |x|$, regularity condition (b) is obtained.

Finally, by the construction of $\phi$, Axiom 7c implies that, for all $1 \le k \le n, {\bar{\beta }} \in {\varDelta }(Z)$, and $x = \{\beta _1, \ldots , \beta _n\}$ such that $\phi (x, s_i) = \beta _i$ for $i = 1, \ldots , n$, there exists $x' = \{\beta '_1, \ldots , \beta '_n\}$ such that $\phi (x', s_i) = \beta '_i$ for $i = 1, \ldots , n, \beta '_i \sim \beta _i$ for all $i \ne k$, and $\beta '_k \sim {\bar{\beta }}$. Regularity condition (c) is obtained by iteratively applying the argument for $k = 1, \ldots , n$. $\square$

The iterative application of (5) in Lemma 2 implies that a finite random menu $P = (\lambda _1, x_1; \ldots ; \lambda _m, x_m)$ is indifferent to a finite nonrandom menu $\Psi (P) \equiv \cup _{s \in S_{{\bar{n}}(P)}} \{ \lambda _1 \phi (x_1, s)+ \cdots +\lambda _m \phi (x_m, s)\}$. Thus, we focus on the preference over finite menus, rather than that over random menus.

Next, we show that there is an affine function u (i.e., $u(\lambda \beta + (1-\lambda ) \gamma ) = \lambda u(\beta ) + (1-\lambda ) u(\gamma )$ for all $\lambda \in [0, 1]$ and $\beta , \gamma \in {\varDelta }(Z)$) representing the commitment ranking.

Lemma 3

There is an affine function u that represents $\succsim$ on ${\varDelta }(Z)$; that is, for all $\beta , \beta ' \in {\varDelta }(Z), u(\beta ) \ge u(\beta ')$ whenever $\{\beta \} \succsim \{\beta '\}$. Furthermore, u is unique up to a positive affine transformation.

Proof

The conclusion is straightforward from Axioms 1, 3, and 4. Note that the independence axiom for alternatives follows from singleton independence. $\square$

The following lemma indicates that there is a functional J representing the restriction of $\succsim$ on ${\mathcal {A}}$.

Lemma 4

Let u be an affine function derived from Lemma 3. Then, there is a functional $J: {\mathcal {A}} \rightarrow \mathfrak {R}$ such that

• (a) for all $x, y \in {\mathcal {A}}, x \succsim y$ if and only if $J(x) \ge J(y)$, and

• (b) for all $\beta \in {\varDelta }(Z)$ and $x = \{\beta \}, J(x) = u(\beta )$.

Proof

For singleton menus, J is uniquely defined by (b). To define J for all menus, fix ${\bar{\beta }}$ and ${\underline{\beta }}$ such that $\{{\bar{\beta }}\} \succsim x \succsim \{{\underline{\beta }}\}$ for all $x \in {\mathcal {A}}$. It follows from Axiom 3 and Lemma 1 that there exists a unique $\lambda \in [0, 1]$ such that $x \sim \lambda \{{\bar{\beta }}\} \oplus (1-\lambda ) \{{\underline{\beta }}\} \sim \{\lambda {\bar{\beta }} + (1-\lambda ) {\underline{\beta }}\}$. Thus, by defining $J(x) = J(\{\lambda {\bar{\beta }} + (1-\lambda ) {\underline{\beta }}\}), J$ also satisfies (a). $\square$

Now, fix the cardinality n of the menus and the function u such that $u(\beta ) > 1$ and $u(\beta ') < -1$ for some $\beta , \beta ' \in {\varDelta }(Z)$ (which is allowed by Axiom 7a). We denote by B the linear space of all functions $a: S_n \rightarrow \mathfrak {R}$ endowed with state-wise scalar multiplication and addition; that is, for all $a, b \in B$ and $\lambda \in \mathfrak {R}, \lambda a$ and $a + b$ are defined by $(\lambda a)(s) = \lambda (a(s))$ and $(a + b)(s) = a (s) + b (s)$ for all $s \in S_n$, respectively. Because $S_n$ is finite, B is equivalent to the linear subspace of simple functions, which we denote by $B_0$. We also define $K = u({\varDelta }(Z))$ and denote by $B_0(K)$ the set of simple functions that have range K. For all $\xi \in \mathfrak {R}$, we denote by $\xi ^* \in B$ a constant function such that $\xi ^*(s) = \xi$ for all $s \in S_n$. Now, define $\phi ^x_n(\cdot ) \equiv \phi (x, \cdot )$ on $S_n$. From regularity condition (c) of $\phi$, which we proved in Lemma 2, it follows that the set of functions $u \circ \phi ^x_n$ with x ranging over $\mathcal{A}_n$ is equivalent to $B_0(K)$, i.e., $\{u \circ \phi ^x_n : x \in {\mathcal {A}}_n \} = B_0(K)$.

Let ${\tilde{u}}: {\mathcal {A}}_n \rightarrow K^{S_n}$ be such that ${\tilde{u}}(x) = u \circ \phi ^x_n$ for all $x \in {\mathcal {A}}_n$. The following lemmas, which are counterparts of Gilboa and Schmeidler’s (1989) lemmas, characterize the functional I on B derived from the axioms. Note that, unlike Gilboa and Schmeidler’s argument, I is sublinear instead of superlinear and is denoted by the maximum of integrals rather than the minimum.

Lemma 5

There is a functional $I: B \rightarrow \mathfrak {R}$ such that

• (a) for all $x \in {\mathcal {A}}$ such that $|x| = n, I({\tilde{u}}(x)) = J(x)$,

• (b) I is monotonic, that is, $a \ge b$ implies $I(a) \ge I(b)$ for all $a, b \in B$,

• (c) I is sublinear (subadditive and homogeneous of degree one), and

• (d) I is C-independent, that is, $I(a+\xi ^*) = I(a)+I(\xi ^*)$ for all $a \in B$ and $\xi \in \mathfrak {R}$.

Proof

We define I on $B_0(K)$ by condition (a). This also implies that $I({\tilde{u}}(\{\beta \})) = J(\{\beta \}) = u(\beta )$ for all $\beta \in {\varDelta }(Z)$, and thus, $I(1^*) = 1$. The monotonicity (b) of I follows from Lemma 2 and Axiom 6. We indicate that I satisfies (c) and (d).

First, we show $I(\lambda a) = \lambda I(a)$ for all $\lambda \in (0, 1]$ and $a, \lambda a \in B_0(K)$. Let $y \in {\mathcal {A}}$ be such that $|y| = n$ and $a = {\tilde{u}}(y)$, and $\beta \in {\varDelta }(Z)$ be such that ${\tilde{u}}(\{\beta \}) = 0^*$. (The existence of such y is guaranteed by regularity condition (c) of $\phi$.) Now, let $x = \cup _{s \in S_n} \{\lambda \phi (y, s) + (1-\lambda ) \beta \}$. Lemma 2 implies $x \sim \lambda y \oplus (1-\lambda ) \{\beta \}$, and thus, we have $J(x) = I({\tilde{u}}(x)) = I(\lambda a + (1-\lambda ) {\tilde{u}}(\{\beta \})) = I(\lambda a)$. Next, let $\beta '$ be such that $\{\beta '\} \sim y$. Then, by Axiom 4 and Lemma 1, $x \sim \lambda y \oplus (1-\lambda ) \{\beta \} \sim \lambda \{\beta '\} \oplus (1-\lambda ) \{\beta \} \sim \{\lambda \beta ' + (1-\lambda ) \beta \}$. That is, $J(x) = J(\{\lambda \beta ' + (1-\lambda ) \beta \}) = \lambda J(\{\beta '\}) + (1-\lambda ) J(\{\beta \}) = \lambda I({\tilde{u}}(y)) + (1-\lambda ) I({\tilde{u}}(\{\beta \})) = \lambda I(a)$. Accordingly, we obtain $I(\lambda a) = \lambda I(a)$. Now, define $I(a) = \frac{1}{\lambda }I(\lambda a)$ for all $\lambda > 0$ and $\lambda a \in B_0(K)$. By the positive homogeneity of I on $B_0(K)$ that we have shown, I(a) is homogeneous of degree one for all $a \in B$.

Second, we show that I is C-independent. By homogeneity, it suffices to show that $I(\frac{1}{2} a + \frac{1}{2} \xi ^*) = \frac{1}{2} I(a) + \frac{1}{2} I(\xi ^*)$ for all $a, \xi ^* \in B_0(K)$. Let $x \in {\mathcal {A}}$ be such that $|x| = n$ and $a = {\tilde{u}}(x), \beta ' \in {\varDelta }(Z)$ be such that $\{\beta '\} \sim x$, and $\beta \in {\varDelta }(Z)$ be such that ${\tilde{u}}(\{\beta \}) = \xi ^*$. By Lemma 2 and Axiom 4, $\cup _{s \in S_n} \{\frac{1}{2} \phi (x, s) + \frac{1}{2} \beta \} \sim \frac{1}{2}x \oplus \frac{1}{2}\{\beta \} \sim \frac{1}{2}\{\beta '\} \oplus \frac{1}{2}\{\beta \} \sim \{\frac{1}{2}\beta ' + \frac{1}{2}\beta \}$, which implies that $I(\frac{1}{2}a+\frac{1}{2}\xi ^*) = J(\{\frac{1}{2} \beta ' +\frac{1}{2} \beta \}) = \frac{1}{2}J(\{\beta '\}) + \frac{1}{2} J(\{\beta \}) = \frac{1}{2}J(x) + \frac{1}{2} J(\{\beta \}) = \frac{1}{2}I(a) + \frac{1}{2} I(\xi ^*)$.

Finally, we show that I is subadditive. By homogeneity, it suffices to show that $I(\frac{1}{2}a + \frac{1}{2}b) \le \frac{1}{2}I(a) + \frac{1}{2}I(b)$ for all $a, b \in B_0(K)$. Let $x, y \in {\mathcal {A}}$ be such that $|x| = |y| = n, a = {\tilde{u}}(x)$, and $b = {\tilde{u}}(y)$. Suppose $I(a) = I(b)$, that is, $x \sim y$. Then, it follows from Axiom 5 and Lemma 2 that $x \succsim \frac{1}{2}x \oplus \frac{1}{2}y \sim \cup _{s \in S_n} \{\frac{1}{2} \phi (x, s) + \frac{1}{2} \phi (y, s)\}$, implying that $I(a) = \frac{1}{2}I(a)+\frac{1}{2}I(b) \ge I(\frac{1}{2}a+\frac{1}{2}b)$. Next, suppose that $I(a) > I(b)$. Define $\xi = I(a) - I(b)$ and $c = b + \xi ^*$. Note that $I(c) = I(b + \xi ^*) = I(b) + \xi = I(a)$ (the second equality follows from C-independence). Accordingly, we obtain

$$\begin{aligned} I\left( \frac{1}{2}a+\frac{1}{2}b\right) + \frac{1}{2} \xi = I\left( \frac{1}{2}a+\frac{1}{2}c\right) \le \frac{1}{2}I(a)+\frac{1}{2}I(c) = \frac{1}{2}I(a)+\frac{1}{2}I(b)+ \frac{1}{2}\xi , \end{aligned}$$

which completes the proof. The first and third equalities follow from C-independence, while the second inequality follows from $I(a) = I(c)$. $\square$

Lemma 6

Let I be a monotonic, sublinear, and C-independent functional on B with $I(1^*) = 1$. Then, there is a closed and convex set $\mathcal{M}_n$ of finitely additive probability measures over $S_n$ such that $I(b) = \max _{\mu \in {\mathcal {M}}_n}\int _{S_n} b d\mu$ for all $b \in B$. Furthermore, ${\mathcal {M}}_n$ is unique.

Proof

Fix $b \in B$ such that $I(b) > 0$. We first show that there is a (finitely additive) probability measure $\mu _b$ over $S_n$ such that $I(b) = \int _{S_n} b d\mu _b$ and $I(a) \ge \int _{S_n} a d\mu _b$ for all $a \in B$. Define

$$\begin{aligned} D_1 = \text {co}(\{a \in B : a \ge 1^*\} \cup \{a \in B : a \ge b/I(b)\}) \end{aligned}$$

(where $\text {co}(\cdot )$ denotes the convex hull of the set $(\cdot )$) and

$$\begin{aligned} D_2 = \{a \in B : I(a) < 1\}. \end{aligned}$$

Let $d_1 = \lambda a + (1-\lambda ) a'$, where $a \ge 1^*, a' \ge b/I(b)$, and $\lambda \in [0, 1]$. Then, it follows from monotonicity, homogeneity, and C-independence that $I(d_1) \ge \lambda + (1-\lambda )I(a') \ge 1$, which implies that $D_1 \cap D_2 = \emptyset$. Furthermore, both $D_1$ and $D_2$ have inner points and are convex (the convexity of $D_2$ follows from the sublinearity of I). Thus, by a separating hyperplane theorem (e.g., Aliprantis and Border 2006), there is a linear functional $F_b$ and $\lambda \in \mathfrak {R}$ such that

$$\begin{aligned} F_b(d_1) \ge \lambda \ge F_b(d_2) \end{aligned}$$

(6)

for all $d_1 \in D_1$ and $d_2 \in D_2$. Because we clearly have $\lambda > 0$ (otherwise $F_b$ must be identically zero), we set $\lambda = 1$ without loss of generality.

Then, (6) implies that $F_b(1^*) \ge 1$. In addition, because $1^*$ is a limit point of $D_2$, the inverse inequality also holds, and we can conclude that $F_b(1^*) = 1$. Furthermore, $F_b$ is nonnegative because, for all nonempty $E \subseteq S_n$ and the indicator function $1_E$ of E, we have $1^*-1_E \in D_2$ and $F_b(1_E) + F_b(1^*-1_E) = F_b(1^*) = 1$, which implies that $F_b(1_E) \ge 0$.

Accordingly, because $F_b$ is a nonnegative linear functional, the Riesz representation theorem (e.g., Aliprantis and Border 2006) implies that there is a finitely additive probability measure $\mu _b$ such that $F_b(a) = \int _{S_n} a \hbox {d} \mu _b$ for all $a \in B$. We show that

$F_b(a) \le I(a)$ for all $a \in B$ and $F_b(b) = I(b)$. First, assume that $I(a) > 0$. Because $a/I(a)-(1/m)^* \in D_2$ for all $m \in {\mathbb {N}}$ and $F_b(a)$ is continuous with respect to a, we have $F_b(a) \le I(a)$ from (6). A similar implication for $I(a) \le 0$ follows from C-independence (set $\xi \in \mathfrak {R}$ such that $I(a+\xi ^*) > 0$). Second, we focus on the special case $a = b$. Note that $b/I(b) \in D_1$, and so it follows from (6) that $F_b(b) \ge I(b)$. Because the previous argument indicates that the inverse inequality also holds, we have $F_b(b) = I(b)$.

Now, let ${\mathcal {M}}_n \equiv \overline{\text {co}(\{\mu _b : b \in B, I(b) > 0 \})}$, for $\mu _b$ defined above. It follows from the previous paragraph that $I(a) \ge \max _{\mu \in \mathcal {M}_n}\int _{S_n} a \hbox {d}\mu$ for all $a \in B$. It has also been shown that, for all $a \in B$ such that $I(a) > 0$, there is a probability measure $\mu _a \in {\mathcal {M}}_n$ such that $I(a) =\int _ {S_n} a \hbox {d}\mu _{a}$, which implies that $I(a) \le \max _ {\mu \in {\mathcal {M}}_n} \int _ {S_n} a \text{ d } \mu$. Applying C-independence, a similar argument also holds for $I(a) \le 0$.

Finally, we show the uniqueness of ${\mathcal {M}}_n$. Suppose that there are distinct sets ${\mathcal {M}}_n$ and ${\mathcal {M}}'_n$ satisfying the statements of this lemma; that is, $I({\tilde{u}}(x)) = \max _{\mu \in {\mathcal {M}} _n} \int _{S_n} u(\phi (x, s)) \text{ d }\mu (s)$ and $I'({\tilde{u}}(x)) = \max _{\mu \in {\mathcal {M}}'_n} \int _{S_n} u (\phi (x, s)) \hbox {d}\mu (s)$ both represent $\succsim$ for all $x \in {\mathcal {A}}$ such that $|x| = n$. Choose ${\tilde{\mu }} \in {\mathcal {M}}_n\setminus {\mathcal {M}}'_n$ (if such ${\tilde{\mu }}$ does not exist, choose ${\tilde{\mu }} \in \mathcal{M}'_n\setminus {\mathcal {M}}_n$ instead and proceed accordingly). Then, because ${\mathcal {M}}'_n$ is convex, the separating hyperplane theorem indicates that there exists $a \in B$ such that $\int _{S_n} a \hbox {d}{\tilde{\mu }} > \max _{\mu \in {\mathcal {M}}'_n} \int _{S_n} a \hbox {d} \mu$. It follows from regularity condition (c) that there exists $y \in \mathcal{A}$ such that $|y| = n$ and $a(\cdot ) = u \circ \phi (y, \cdot )$, implying $I({\tilde{u}}(y)) > I'({\tilde{u}}(y))$, which is a contradiction. $\square$

We now conclude the proof of Theorem 1. Because Lemmas 5 and 6 hold for an arbitrary $n \in {\mathbb {N}}$, Lemmas 1– 6 imply that, by defining $S = \{s_1, s_2, \ldots \}, {\mathcal {M}} = \cup _{i=n}^{\infty } {\mathcal {M}}_n$, and a regular $\phi$, we obtain an ASC representation for all $x \in {\mathcal {A}}$. The essential uniqueness follows from the construction of $S, {\mathcal {M}}$, and $\phi$.

In particular, the uniqueness of $\phi$ with respect to the relevant mental states is shown as follows. Suppose that there exist regular $\phi$ and $\phi '$ representing the preference, and $x, y \in \mathcal{A}$ such that $\phi (x, {\tilde{s}}) = \phi '(x, {\tilde{s}})$ and $\phi (y, {\tilde{s}}) \ne \phi '(y, {\tilde{s}})$ for some relevant ${\tilde{s}} \in S$. Without loss of generality, we assume $|x| = |y|$. By construction, $\lambda y \oplus (1-\lambda ) x \sim \cup _{s \in S_{|y|}} \{\lambda \phi (y, s) + (1-\lambda ) \phi (x, s)\}$ and $\lambda ' x \oplus (1-\lambda ') y \sim \cup _{s' \in S_{|y|}} \{\lambda ' \phi '(x, s') + (1-\lambda ') \phi '(y, s')\}$ for all $\lambda , \lambda ' \in [0, 1]$, and so Axiom 2b implies that $\lambda '' y \oplus (1-\lambda '') y \sim \{\lambda '' \phi (y, s) + (1-\lambda '') \phi '(y, s'): \phi (x, s) = \phi '(x, s') \ \text {for some} \ s, s' \in S_{|y|}\} \equiv z_{\lambda ''}$ for all $\lambda '' \in [0, 1]$. However, because $z_{\lambda ''}$ includes $\lambda '' \phi (y, {\tilde{s}}) + (1-\lambda '') \phi '(y, {\tilde{s}}), \phi (y, {\tilde{s}}) \ne \phi '(y, {\tilde{s}})$, and ${\tilde{s}}$ is relevant, we conclude without loss of generality that $z_{\lambda ''}$ is not indifferent to y for all $\lambda '' \in [0, 1]$, contradicting Axiom 2a.

Finally, the desired representation for all random menus P follows from the affineness of u. $\square$

1.2 Proof of Theorem 2

The sufficiency (${\mathcal {M}}_n = {\varDelta }(S_n)$ implies monotonicity) is straightforward. We show the necessity. First, we prove the following lemma.

Lemma 7

Suppose that $\succsim$ admits a regular ASC representation $(u, \phi , S, {\mathcal {M}})$ and satisfies monotonicity. Let $x \in {\mathcal {A}}, {\hat{\beta }} \in x$, and ${\hat{s}} \in S_{|x|}$ be such that ${\hat{\beta }} \succ \beta$ for all $\beta \in x, \beta \ne {\hat{\beta }}$, and $\phi (x, {\hat{s}}) = {\hat{\beta }}$. Then, there exists $\mu \in {\mathcal {M}}_{|x|}$ such that $\mu ({\hat{s}}) = 1$.

Proof

Let $x \in {\mathcal {A}}, {\hat{\beta }} \in x$, and ${\hat{s}} \in S_{|x|}$ be such that ${\hat{\beta }} \succ \beta$ for all $\beta \in x, \beta \ne {\hat{\beta }}$, and $\phi (x, {\hat{s}}) = {\hat{\beta }}$. Suppose that $\mu ({\hat{s}}) < 1$ for all $\mu \in {\mathcal {M}}_{|x|}$. Then, we have $u({\hat{\beta }}) > V(x) = \max _{\mu \in \mathcal{M}_{|x|}}\int _{S_{|x|}} u(\phi (x, s))d\mu (s)$, or $\{{\hat{\beta }}\} \succ x$, which contradicts the monotonicity. $\square$

Because Lemma 7 applies to all such x and ${\hat{\beta }}$, there exists $\mu \in {\mathcal {M}}_n$ such that $\mu (s) = 1$ for any given $n \in {\mathbb {N}}$ and $s \in S_n$. Furthermore, because ${\mathcal {M}}_n$ is closed and convex, ${\mathcal {M}}_n \supseteq \overline{\text {co}(\{\mu \in {\varDelta }(S_n): \mu (s) = 1 \text { for some} { \ } s \in S_n\})} = {\varDelta }(S_n)$. ${\mathcal {M}}_n \subseteq {\varDelta }(S_n)$ is straightforward, which concludes the proof. $\square$

1.3 Proof of Theorem 3

The sufficiency (${\mathcal {M}}^1 \supseteq {\mathcal {M}}^2$ implies that ${\succsim }_2$ exhibits a greater preference for commitment to a singleton menu than $\succsim _1$) is straightforward.

Conversely, we show that $\succsim _2$ with a greater preference for commitment to a singleton menu than $\succsim _1$ implies ${\mathcal {M}}^1 \supseteq {\mathcal {M}}^2$. Assume that there exists $n \in {\mathbb {N}}$ such that $\mu ' \in {\mathcal {M}}^2_n \setminus {\mathcal {M}}^1_n$, where ${\mathcal {M}}^i_n \in {\mathcal {M}}^i$ for $i = 1$ and 2 denote the sets of probability measures over $S_n$ in each ASC representation. Because ${\mathcal {M}}^1_n$ is convex, the separating hyperplane theorem implies that there exists $a: S_n \rightarrow \mathfrak {R}$ such that $\max _{\mu \in {\mathcal {M}}^1_n} \int _{S_n} a \hbox {d}\mu < \int _{S_n} a \hbox {d}\mu '$, and so it follows from regularity condition (c) that there exists some $x \in {\mathcal {A}}$ such that $|x| = n$ and $a(\cdot ) = u \circ \phi (x, \cdot )$. Without loss of generality, we also assume that $\beta \in x$ exists such that $u(\beta ) = \int _{S_n} u (\phi (x, s)) \hbox {d}\mu '(s) < \max _{\mu \in {\mathcal {M}}^2_n} \int _{S_n} u(\phi (x, s)) \hbox {d}\mu (s)$. Then,

$$\begin{aligned} \max _{\mu \in {\mathcal {M}}^1_n} \int _{S_n} u(\phi (x, s)) \hbox {d}\mu (s)< & {} \int _{S_n} u(\phi (x, s)) \hbox {d}\mu '(s) \\= & {} u(\beta ) < \max _{\mu \in \mathcal{M}^2_n} \int _{S_n} u(\phi (x, s)) \hbox {d}\mu (s), \end{aligned}$$

implying that $\{\beta \} \succ _1 x$ and $x \succ _2 \{\beta \}$, which is a contradiction. $\square$

1.4 Proof of Observation 2

Showing that Axiom 2’ implies Axiom 2” is straightforward. Conversely, let $x, y \in {\mathcal {A}}$ be such that $|x| \le |y|$. Axiom 2”b (specifically, Definition 1a) implies that there exist a nonempty $C_0 \subseteq x \times y$ and $({\tilde{\alpha }}, {\tilde{\beta }}) \in C_0$ such that $\lambda _0 x \oplus (1-\lambda _0) y \sim \{\lambda _0 \alpha + (1-\lambda _0) \beta : (\alpha , \beta ) \in C_0\}$ for all $\lambda _0 \in [0, 1]$. Next, Axiom 2”a implies that for $C_1 \equiv x \times x$ and all $\lambda _1 \in [0, 1], \lambda _1 x \oplus (1-\lambda _1) x \sim \{\lambda _1 \alpha + (1-\lambda _1) \alpha ': (\alpha , \alpha ') \in C_1\}$, which gives $(\alpha , {\tilde{\alpha }}) \in C_1$ for all $\alpha \in x$. Axiom 2”a also implies that for $C_2 \equiv y \times y$ and all $\lambda _2 \in [0, 1], \lambda _2 y \oplus (1-\lambda _2) y \sim \{\lambda _2 \beta ' + (1-\lambda _2) \beta : (\beta ', \beta ) \in C_2\}$, which obtains $({\tilde{\beta }}, \beta ) \in C_2$ for all $\beta \in y$. The iterative application of Axiom 2”b (specifically, Definition 1b) implies that for $C = \{(\alpha , \beta ): (\alpha , {\tilde{\alpha }}) \in C_1, ({\tilde{\beta }}, \beta ) \in C_2\} = x \times y$ and all $\lambda \in [0, 1], \lambda x \oplus (1-\lambda ) y \sim \{\lambda \alpha + (1-\lambda ) \beta : (\alpha , \beta ) \in C\} = \lambda x + (1-\lambda ) y$, which concludes the proof. $\square$