Abstract
Based on first-principles calculations and the Wannier-function-based tight-binding method, we investigate the topological electronic properties of designed noncentrosymmetric transition metal monochalcogenide superlattices AX/BX (A, B = Cr, Mo, W, A ≠ B; X = Se, Te). Here, we mainly consider time-reversal symmetry (TRS) MoTe/WTe and MoSe/WSe and TRS broken CrTe/WTe and CrTe/MoTe, which are the Weyl and magnetic Weyl semimetals, respectively. The considered systems are nodal line semimetals with nodal lines on three mirror planes of the Brillouin zone of hexagonal lattice in the absence of spin–orbit coupling (SOC). When considering the SOC, each nodal line opens a gap except for some pairs of Weyl points (WPs) on the kz ≠ 0 planes and the number of WPs is material-dependent. We identify the termination-dependent Fermi arc connection patterns on the (001) and (00 ) surfaces for four Weyl semimetal superlattices AX/BX. These results provide a theoretical basis to realize the possible applications of these superlattice materials in future topological electronic devices.
) surfaces for four Weyl semimetal superlattices AX/BX. These results provide a theoretical basis to realize the possible applications of these superlattice materials in future topological electronic devices.
Export citation and abstract BibTeX RIS
1. Introduction
Topological semimetals [1] have become the frontier field of condensed matter physics since the discovery of the integer quantum Hall effect in the two-dimensional electron gas in the 1980s [2, 3] and important progress have been made [4–9]. Topological semimetals can be classified into topological Weyl semimetals (WSM) [5, 6], topological Dirac semimetals (DSMs) [8, 9] and multifold fermion semimetals [10, 11]. Particularly, WSM has been studied extensively due to unique Weyl fermion and exotic topologically nontrivial surface states.
A WSM can be realized by breaking either the inversion symmetry (IS) or the time-reversal-symmetry (TRS) or both of a DSM, in these cases, the original four-fold degenerate Dirac point splits into two two-fold degenerate Weyl Points (WPs) with opposite chirality [12, 13]. The IS broken WSM includes the famous type-I TaAs family [14, 15] with twelve 12 pairs of WPs, transition metal dichalcogenide type-II MoTe2 [16, 17] and WTe2 [18] and monochalcogenides MX [19]. The TRS WSM with definite magnetic structure called magnetic WSM has also obtained great progress since strongly correlated iridates with all-in-all-out magnetic structure was proposed as the first magnetic WSM [20]. However, it has not been identified experimentally thanks to complicated magnetic domain structure [21]. Xu et al [22] proposed ferromagnetic spinel compound HgCr2Se4, which has a Curie temperature around 106 K and a pair of (double) WPs at the Fermi energy (EF) and recently had been demonstrated experimentally [23]. Wang et al [24] and Chang et al [25] predicted a family of cubic magnetic WSM Co-based Heusler materials and found that the WPs are protected by the C2,110 for XCo2Z (X = IVB or VB; Z = IVA or IIIA) or C4z for Co2TiX (X = Si, Ge, Sn) rotational symmetry. Recently, the magnetic WSM Co3Sn3S2 [26] and Co2MnGa [27] have been identified experimentally by observing the nontrivial surface-dependent Fermi arc connection pattern. However, there is almost no research about magnetic WSM superlattices.
Since the WPs in WSM do not need the protection of other crystal symmetry except translation symmetry, the WSM is difficult to identify by symmetry index method [28–31]. As a result, the realized WSM materials are still sparse compares to TRS- and non-translation-symmetry-dependent topological materials such as topological insulator [32], topological crystalline insulator [33], symmetry-enforced multifold degeneracy semimetal [34]. To date, it is still challenging work to obtain an ideal WSM by the effective route. Constructing a superlattice utilizing two different materials is a possible way to realize the modulation of electronic states. Recently, our previous research demonstrated a WSM superlattice W2XY (X, Y = S, Se, Te, X ≠ Y) [35] containing simultaneously type-I and type-II WPs can be realized by hybriding layered transition metal monochalcogenides (TMMs). The interesting results lead us to study further the superlattice systems which hybridize with the magnetic elements Cr and metal elements Mo/W to find possible novel (magnetic) topological states.
In this work, we designed artificially superlattices AX/BX (A, B = Cr, Mo, W, A ≠ B; X = Se, Te) from noncentrosymmetric TMM compounds AX(A = Cr, Mo, W; X = Se, Te). We calculated the energy bands and analyzed the topological properties including the distribution of the WPs and the connection pattern of surface Fermi arcs through first-principles and Wannier-function-based tight-binding (WFTB) method in the absence/presence of spin–orbit coupling (SOC). Our calculations reveal that all of the superlattices are nodal line semimetals when ignoring SOC. Notably, based on the AX structure, we here replace the Mo/W with the same family magnetic element Cr which has magnetic moment due to unpaired 3d electrons. As a consequence, we achieve magnetic WSM superlattices of CrTe/WTe and CrTe/MoTe which have broken TRS, in addition to non-magnetic WSMs MoTe/WTe and MoSe/WSe. Magnetic WSM CrTe/WTe and CrTe/MoTe show the distinct distribution of WPs compared with non-magnetic WSMs MoTe/WTe and MoSe/WSe. Additionally, CrSe/WSe and CrSe/MoSe have comparatively weaker SOC among six superlattices and resulting in the lack of bands crossing when concluding SOC, then making them complementary metals with zero WP. We mainly present the results of both MoTe/WTe and CrTe/WTe as respective representatives of nonmagnetic and magnetic WSMs in the main text. Some calculation results for MoSe/WSe, CrSe/WSe, CrTe/MoTe and CrSe/MoSe are provided in the supplemental material (available online at stacks.iop.org/JPhysD/55/335304/mmedia).
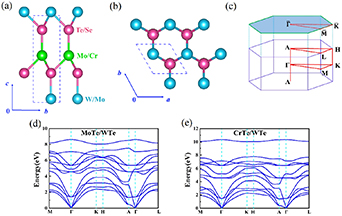
2. Superlattice models and computation methods
We design artificially superlattices AX/BX (A, B = Cr, Mo, W, A ≠ B; X = Se, Te) by replacing one of an atom layer with the same family B atom layer in the prototype TMM AX (A = Cr, Mo, W; X = Se, Te). There are totally six superlattices mentioned above, four of them CrTe/WTe, CrSe/WSe, CrTe/MoTe and CrSe/MoSe including the magnetic element Cr. Both lattice constants and atom positions are fully relaxed for six superlattice structures and optimized lattice parameters are shown in table 1. Their atomic structures crystalize in the space group P3m1 (NO. 156) and Brillouin zone (BZ) are presented in figures 1(a)–(c). The corresponding point group of P3m1 is isomorphic to C3v , which is generated by the threefold rotation C3z and a plane mirror reflection Mxz including the z-axis. We use the projector augmented wave method [36] as implemented in the Vienna Ab initio Simulation Package [37] within the generalized gradient approximation in the Perdew–Burke–Ernzerhof parameterization for the exchange-correlation functional and density-functional theory (DFT) [38, 39] to obtain electronic structures. An energy cutoff was set to 500 eV for a plane wave basis, a force convergence criterion of 10−3 eV Å−1 and a Monkhorst-Pack mesh of 12 × 12 × 6 were used in the calculations. The SOC effect was included self-consistently and the van der Waals correction between two monolayers was considered. To verify the dynamic stability of systems, we carried out, by obtaining their harmonic interatomic force constants and dynamical matrices, the calculations of phonon spectra based on 6 × 6 × 1 supercell using the PHONOPY code [40]. The phonon spectra for superlattice MoTe/WTe and CrTe/WTe are presented in figures 1(d) and (e) and the dispersion without virtual frequency shows that both systems are stable dynamically. The phonon spectra of MoSe/WSe, CrSe/WSe, CrTe/MoTe and CrSe/MoSe are given in figure 1S in supplemental material. The values after fully relaxed the magnetic moment of CrTe/WTe and CrTe/MoTe are 0.269 μB and 0.361 μB, respectively. In order to systematically calculate the topological properties under SOC, we constructed the tight-binding Hamiltonian for each structure by projecting the extended Bloch states into the localized Wannier orbitals by utilizing WANNIER90 package [41]. We focused on the W/Cr/Mo-d and Se/Te-p orbitals to construct Wannier functions and reproduce accurately the DFT-based bands in the energy window −1.5 ∼ 1.5 eV. All calculations of the surface states were conducted by iterative Green's function method [42], which is composed of the spectral weight near the surface of a half-infinite system.
Figure 1. A side view (a) and a top view (b) of superlattice structure. Blue dash rectangle and rhombus indicate a primitive cell. (c) The bulk and (001) surface BZ of the hexagonal lattice. (d), (e) Phonon bands of MoTe/WTe and CrTe/WTe.
Download figure:
Standard image High-resolution imageTable 1. Optimized lattice parameters with DFT-D3 vdW correction, positions, energies and chirality of the irreducible WPs for MoTe/WTe, MoSe/WSe, CrTe/WTe and CrTe/MoTe. Distance of nearest WPs for MoTe/WTe and MoSe/WSe, distance of irreducible WPs for CrTe/WTe and CrTe/MoTe.
| Systems | a = b (Å) | c (Å) | kx (1 Å−1) | ky (1 Å−1) | kz (1 Å−1) | Energy (meV) | Chirality | Distance (1 Å−1) |
|---|---|---|---|---|---|---|---|---|
| MoTe/WTe | 3.250 | 9.145 | 0.082 | 0.180 | −0.263 | −60 | −1 | dmin = 0.038 |
| 0.115 | 0.161 | 0.264 | −59 | +1 | dmax = 0.163 | |||
| MoSe/WSe | 3.086 | 8.571 | 0.080 | 0.176 | −0.286 | −61 | −1 | dmin = 0.038 |
| 0.112 | 0.157 | 0.287 | −61 | +1 | dmax = 0.161 | |||
| 0.082 | 0.221 | −0.223 | −100 | +1 | dmin = 0.078 | |||
| 0.149 | 0.181 | 0.226 | −100 | −1 | dmax = 0.165 | |||
| CrTe/WTe | 3.230 | 8.864 | −0.156 | 0.201 | 0.119 | −86 | −1 | d = 0.066 |
| −0.096 | 0.235 | −0.118 | −85 | +1 | ||||
| 0.085 | 0.257 | −0.149 | −33 | −1 | d = 0.112 | |||
| 0.185 | 0.206 | 0.136 | −34 | +1 | ||||
| CrTe/MoTe | 3.246 | 8.848 | −0.005 | −0.003 | −0.218 | 54 | +1 | d = 0.008 |
| 0.003 | −0.004 | 0.219 | 54 | −1 | ||||
| 0.576 | 0.074 | −0.055 | −180 | +1 | d = 0.147 | |||
| 0.577 | −0.073 | 0.053 | −179 | −1 |
3. Results and discussion
We mainly discuss the four superlattices (MoTe/WTe, MoSe/WSe, CrTe/WTe and CrTe/MoTe) in the following text. The bands of MoTe/WTe and CrTe/WTe without and with SOC along the high symmetry lines are depicted in figure 2. The bands of MoSe/WSe, CrSe/WSe, CrTe/MoTe and CrSe/MoSe are presented in figure 2S in supplemental material. In the absence of SOC, we find the crossing points of bands between the conduction band and valence band near the EF along the Γ-M and Γ-L lines (figure 2(a)), which are the part of node lines that on the Γ-A-L-M mirror plane shown in figure 3(a). Consequently, four superlattice systems are all nodal semimetals with six nodal lines on the three equivalent mirror planes those are related by C3z symmetry. When considering the SOC, each nodal line opens a gap with the exception of some discrete touching points near the proximity of mirror planes. These touching points can be verified to be WPs by calculating their topological charge/chirality (see table 1) based on WFTB Hamiltonian. The specific number of WPs is material-dependent and the relevant properties of WPs are listed in table 1. Additionally, fourfold-degenerate bands along high-symmetry line Γ-A split into four twofold-degenerate bands due to the SOC (figures 2(b) and (e)), which are different from the monochalcogenides MoTe and WTe [19] and similar to W2XY [35] and Mo2XY [43].
Figure 2. The bulk bands with/without SOC for MoTe/WTe (a), (b) and CrTe/WTe (d), (e), respectively. Blue solid lines and red dash lines represent DFT- and WFTB- bands in (a), (b), (d) and (e). The orbital-resolved bands with SOC for MoTe/WTe (c) and CrTe/WTe (f). The W/Mo/Cr-d and Te/Se-p orbitals are the main orbital components near the EF.
Download figure:
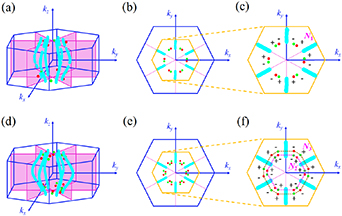
Standard image High-resolution imageFigure 3. Nodal lines without SOC (cyan dotted lines) and WPs with SOC (red and green points) of MoTe/WTe (a)–(c) and MoSe/WSe (d)–(f). (b) and (e) are a top view, (c) and (f) are enlarged portion of the area in (b) and (e), respectively. The symbol '+' and '−' represents the kz > 0 and kz < 0 respectively. The green/red dots denote the positive/negative chirality. These notations are the same below. Especially, the magenta and dark yellow dash loops in (f) represent different energies E 1MoSe/WSe = −63 meV and E 2MoSe/WSe = −99 meV.
Download figure:
Standard image High-resolution imageAccording to the orbital-resolved bands as shown in figures 2(c) and (f), we consider the W/Cr/Mo-d and Se/Te-p orbitals as initial projection orbitals to obtain Wannier-based tight-binding Hamiltonian. As shown in figures 2(a), (b), (d) and (e), the DFT- and WFTB-bands are highly consistent near the EF. In MoTe/WTe, we found six pairs of twofold degenerate WPs between conduction and valence band which are manifested in figure 3(a). All six pairs of WPs have the same energy EMoTe/WTe = −60 meV that appears nearly in the kz = ±0.39 × 2π/c planes. All WPs of MoTe/WTe are positioned symmetrically with respect to the kz = 0 plane. Both MoTe/WTe and MoSe/WSe exhibit the TRS, three-fold rotational C3z and mirror Mxz symmetries as shown clearly in figures 3(c) and (f). Consequently, utilizing symmetry analysis, we obtain two (MoTe/WTe) or four (MoSe/WSe) irreducible WPs as listed in table 1.
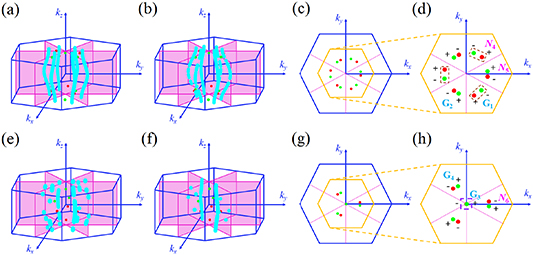
For both CrTe/WTe and CrTe/MoTe, they lack TRS compared with MoTe/WTe due to containing magnetic element Cr. We also verified their nodal lines for each spin polarized band (figures 4(a)–(f)). When considering SOC, the nodal lines split into some pairs of discrete node points (WPs), hence CrTe/WTe and CrTe/MoTe transform into magnetic WSM with six and four pairs of WPs, respectively. According to the rotational C3z and mirror Mxz symmetries, the WPs for CrTe/WTe and CrTe/MoTe can be reduced to four irreducible WPs as shown in figures 4(d) and (h), the coordinates of four WPs are presented in table 1. In CrTe/WTe, the six pairs of WPs in energy can be divided into two groups: G1(−34 meV, kz = ±0.20 × 2π/c) and G2(−86 meV, kz = ±0.16 × 2π/c), the G1 group was denoted by brown dash box in figure 4(d). The distance between a pair of WPs in the G1 group is larger than that of a pair of WPs in the G2 group. As a consequence, the length of Fermi arcs arising from G1 is longer than that of G2, which is identified in the following calculations. In CrTe/MoTe, the four pairs of WPs in energy can be grouped into G3(54 mev, kz = ±0.31 × 2π/c) and G4(−179 meV, kz = ± 0.07 × 2π/c). Note that the energies of most of WPs are below the EF , hence, these WPs can be observed by conventional angle-resolved photoemission spectroscopy technique [44]. In addition, for CrSe/WSe and CrSe/MoSe, they have no WP between conduction and valence band due to the weaker SOC, making them compensatory metals (see figure 2S).
Figure 4. The nodal lines and WPs for CrTe/WTe (a)–(d) and CrTe/MoTe (e)–(h) with spin-up (a), (e) and spin-down (b), (f) nodal lines (cyan). (c) and (g) are top view, (d) and (h) are enlarged portion of the area in (c) and (g), respectively. Especially, for CrTe/WTe, WPs in brown dash rectangle (G1) have energy −34 meV, other WPs (G2) have energy −86 meV, for MoTe/CrTe in (d) WPs in purple dash rectangle (G3) have energy 54 meV, other WPs (G4) have energy −179 meV in (h).
Download figure:
Standard image High-resolution imageIn order to elucidate the type of WSM, we calculate the two-dimensional dispersions around the selected WP N1 (figure 3(c)) and WP N6 (figure 4(h)) as depicted in figure 5. According to the open constant energy contour and band dispersions with tilted cones around the WPs, we have identified that all materials under consideration fall into Type-II WSMs [45]. More band dispersions and Wannier charge center calculations are presented in figures 5S and 6S in the supplementary material.
Figure 5. Band dispersions around WP (a) N1(MoTe/WTe) and WP (b) N6(CrTe/MoTe). The WP N1 and WP N6 are labeled in figures 3(c) and 4(h), respectively.
Download figure:
Standard image High-resolution imageA WSM is expected to manifest Fermi arc states on its surface which are fantastic discontinuous or disjoint segments of a two-dimensional Fermi contour. The Fermi arcs are terminated onto the projections of the WPs with opposite handedness on the surface. We calculate the surface states for both (001) and (00 ) by iterative Green's function method based on WFTB Hamiltonian for four superlattices. Unlike complex surface states and Fermi arcs connection patterns of TaAs family [45], the superlattices under consideration have relatively concise surface states. The connection patterns generally depend on the surface chemical potential and the energies of WPs which results in different connection patterns on the (001) and (00
) by iterative Green's function method based on WFTB Hamiltonian for four superlattices. Unlike complex surface states and Fermi arcs connection patterns of TaAs family [45], the superlattices under consideration have relatively concise surface states. The connection patterns generally depend on the surface chemical potential and the energies of WPs which results in different connection patterns on the (001) and (00 ) surfaces with respective W (Cr) and Te (Te) surface terminations for MoTe/WTe (CrTe/WTe).
) surfaces with respective W (Cr) and Te (Te) surface terminations for MoTe/WTe (CrTe/WTe).
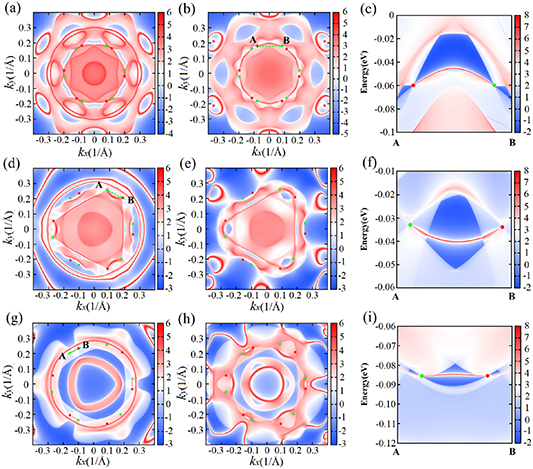
For MoTe/WTe and CrTe/WTe, the surface spectra on (001) and (00 ) surfaces are plotted in figures 6(a), (b) and (d)–(e) (MoTe/WTe), (g), (h) (CrTe/WTe). For MoTe/WTe, it is clear that there are two types of connection patterns: pattern I and pattern II connecting two short- and long-distance WPs as shown in figures 6(a) and (b), respectively. The short-/long- distances are dmin = 0.038 1/Å and dmax = 0.163 1/Å as listed in table 1. Notably, the twelve Fermi arcs connecting two neighboring WPs can be achieved simultaneously because twelve WPs have nearly the same energy (∼−59 meV). The Fermi arcs on the (00
) surfaces are plotted in figures 6(a), (b) and (d)–(e) (MoTe/WTe), (g), (h) (CrTe/WTe). For MoTe/WTe, it is clear that there are two types of connection patterns: pattern I and pattern II connecting two short- and long-distance WPs as shown in figures 6(a) and (b), respectively. The short-/long- distances are dmin = 0.038 1/Å and dmax = 0.163 1/Å as listed in table 1. Notably, the twelve Fermi arcs connecting two neighboring WPs can be achieved simultaneously because twelve WPs have nearly the same energy (∼−59 meV). The Fermi arcs on the (00 ) surface are clearly visible as displayed in figure 6(b), which implies to be easily observed experimentally. Comparatively, the Fermi arcs on the (001) surface are mostly embedded in the surface projections of the bulk continuum bands as demonstrated in figure 6(a). The surface bands along with green dash line AB (figure 6(b)) reveal clearly a Fermi arc connecting a pair of long-distance WPs with opposite chirality as depicted in figure 6(c). The energies of WPs in surface bands are around −59 meV which is consistent with previous calculations given in table 1. Note that there are other large amounts of arc-like or loop-like structures in surface spectra that possibly originated from the crossing points of interbands of conduction and valence bands [25–27].
) surface are clearly visible as displayed in figure 6(b), which implies to be easily observed experimentally. Comparatively, the Fermi arcs on the (001) surface are mostly embedded in the surface projections of the bulk continuum bands as demonstrated in figure 6(a). The surface bands along with green dash line AB (figure 6(b)) reveal clearly a Fermi arc connecting a pair of long-distance WPs with opposite chirality as depicted in figure 6(c). The energies of WPs in surface bands are around −59 meV which is consistent with previous calculations given in table 1. Note that there are other large amounts of arc-like or loop-like structures in surface spectra that possibly originated from the crossing points of interbands of conduction and valence bands [25–27].
Figure 6. Surface states and Fermi arcs for MoTe/WTe (a)–(c) and CrTe/WTe (d)–(i). Spectral functions (a), (d) and (g) are (001) surface, (b), (f) and (h) are (00 ) surface, surface dispersions (c), (f) and (i) along green dash lines AB show in (b), (d) and (h), respectively. Energy for (a)–(c) is −59 meV, (d)–(f) is −34 meV, (g)–(i) is −86 meV. The red and green points represent the projection of WPs with positive and negative chirality.
) surface, surface dispersions (c), (f) and (i) along green dash lines AB show in (b), (d) and (h), respectively. Energy for (a)–(c) is −59 meV, (d)–(f) is −34 meV, (g)–(i) is −86 meV. The red and green points represent the projection of WPs with positive and negative chirality.
Download figure:
Standard image High-resolution imageFor CrTe/WTe, surface spectral structures demonstrate the reduced symmetry compared with those of MoTe/WTe, awing to broken TRS arising from magnetic element Cr as illustrated in figures 6(d), (e) and (g), (h). Similar to MoTe/WTe, surface spectra for CrTe/WTe exhibit surface-dependent connection patterns and arc-/loop-like structures for two of group WPs G1 and G2. For G1 WPs with energy −34 meV, the Fermi arcs on (001) and (00 ) surface display opposite curvature of bending. However, the surface Fermi arcs on (001) surface termination are accessible easily, compared with those of the (00
) surface display opposite curvature of bending. However, the surface Fermi arcs on (001) surface termination are accessible easily, compared with those of the (00 ) surface, due to less surface projections of bulk bands as shown in figure 6(f). For G2 with energy around −86 meV, the surface spectra show the Fermi arcs stemming from another six WPs for both (001) and (00
) surface, due to less surface projections of bulk bands as shown in figure 6(f). For G2 with energy around −86 meV, the surface spectra show the Fermi arcs stemming from another six WPs for both (001) and (00 ) terminations. One of Fermi arcs along the green dash line (figure 6(g)) through a pair of WPs display a higher flatness as plotted in figure 6(i).
) terminations. One of Fermi arcs along the green dash line (figure 6(g)) through a pair of WPs display a higher flatness as plotted in figure 6(i).
4. Conclusion
In summary, we designed six artificially noncentrosymmetric layer WSM superlattices by stacking alternatively the monochalcogenides AX (A = Cr, Mo, W; X = Se, Te). In these superlattices, CrSe/WSe and CrSe/MoSe have weaker SOC leading to complementary metals, we mainly focus on MoTe/WTe, MoSe/WSe, CrTe/WTe and CrTe/MoTe, identify four superlattices' topological electronic properties by adopting first-principles calculations and the WFTB method. Considering the SOC effect, each of six nodal lines without SOC opens partially a gap and leads to some pairs of WPs. MoTe/WTe possesses six pairs of WPs with the same energy, whereas MoSe/WSe has twelve pairs of WPs with different energies. CrTe/WTe and CrTe/MoTe containing the magnetic element Cr are magnetic WSM with broken TRS, which only remain rotational C3z and mirror Mxz symmetries and show more reduced symmetry surface states. Fermi arcs length and the maximum distance between a pair of WPs of all considered systems are on the order of magnitude of 0.10 Å−1, which makes them be observed easily by ARPES. The connectivity pattern of the surface Fermi arcs in the superlattices may lead to exotic electronic transport behaviors and we expect a verification in future experiments.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant No. 11204261), Natural Science Foundation of Hunan Province (Grant No. 2018JJ2381), a Key Project of Education Department of Hunan Province (Grant No. 19A471), Hunan Provincial Innovation Foundation for Postgraduate (Grant No. CX20210615), and Postgraduate Scientific Research Innovation Project of Hunan Province (Grant No. XDCX2021B127).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).