Abstract
The exciton binding energy, mechanical properties, and lattice thermal conductivity of monolayer BiI3 are investigated on the basis of first principle calculation. The excitation energy of monolayer BiI3 is predicted to be 1.02 eV, which is larger than that of bulk BiI3 (0.224 eV). This condition is due to the reduced dielectric screening in systems. The monolayer can withstand biaxial tensile strain up to 30% with ideal tensile strength of 2.60 GPa. Compared with graphene and MoS2, BiI3 possesses superior flexibility and ductility due to its large Poisson's ratio and smaller Young's modulus by two orders of magnitude. The predicted lattice thermal conductivity kL of monolayer BiI3 is 0.247 W m−1 K−1 at room temperature, which is lower than most reported values for other 2D materials. Such ultralow kL results from the scattering between acoustic and optical phonon modes, heavy atomic mass, and relatively weak chemical bond.
Export citation and abstract BibTeX RIS
1. Introduction
As a typical layered metal halide, bulk bismuth tri-iodide (BiI3) crystallizes in a rhombohedral structure that belongs to the trigonal crystal system with the space group of R3 (No. 148) [1]. Figure 1(a) shows its conventional cell in hexagonal representation. Bulk BiI3 has a layered structure, and the layers stack in an ABC order with weak van der Waals interaction [2]. Similar to graphite, the strong intralayer ionic Bi–I bonds and the weak interlayer van der Waals interactions indicate that monolayer BiI3 is likely to be mechanically exfoliated from its bulk counterpart. The theoretical cleavage energy was estimated to be from 0.25 J m−2 to 0.43 J m−2 [3, 4], which is comparable to the experimentally estimated cleavage energy of graphite (0.37 J m−2) [5]. This condition indicates that exfoliating BiI3 monolayer from its bulk BiI3 is experimentally feasible. Heidary et al [6] and Mu et al [7] experimentally obtained few-layered BiI3 sheets via liquid phase exfoliation and molecular beam epitaxy method, respectively. With these encouraging studies, we believe that the experimental realization of high-quality monolayer BiI3 will be achieved in the future. Theoretical predictions and experimental observations revealed that monolayer and few-layered BiI3 are potential candidates for future solar energy conversion applications [3, 4, 8, 9], ultrasensitive photoresponsive optoelectronic devices [10, 11], flexible visible light photodetectors [12], and thermoelectric devices [13].
Figure 1. (a) Top and side views of (a) layered structure of BiI3 compounds in hexagonal crystal structure, (b) BiI3 monolayer striped from its bulk layered structure. (c) Representation of the rectangular unit cell of BiI3 monolayer. Large and small balls correspond to Bi and I atoms, respectively. x and y directions correspond to the zigzag and armchair directions, respectively.
Download figure:
Standard image High-resolution imageAlthough the stability, structural, electronic, optical properties, and the intrinsic defects of monolayer BiI3, and its potential applications in photonics and photovoltaic solar cells were systematically explored [8, 14, 15], other foundational physical properties, such as exciton binding energy (Eb), mechanical properties, and lattice thermal conductivity (kL), are still unavailable. Fully understanding these intrinsic natures of materials holds great interest in theoretical exploration and is beneficial to synthesize, tune, and utilize them in practice. Exciton states as a bound state of electron–hole pair are of practical importance for applications, including solar energy conversion and optical detection. Strain engineering is experimentally viewed as an effective means to generate unanticipated novel functions in 2D materials [3, 4]. Therefore, knowing the ability to withstand the largest tensile strain and whether the material is free-standing or not is important. In this study, we used first principle calculations to investigate the Eb of bulk and monolayer BiI3, intrinsic mechanical responses to tensile strain applied to monolayer BiI3, and the kL at room temperature in monolayer BiI3.
2. Computational methodology
Our first principle calculations were conducted on the Vienna Ab initio Simulation Package (VASP) [16] by using generalized gradient approximation in the Perdew–Burke–Ernzerhof (PBE) form [17] for the exchange-correlation. The electron–ion interactions were mapped by using the plane wave basis projector augmented wave method with an energy cutoff of 500 eV for the wave functions. The criteria for total energy and stress components were less than 10−5 eV and 0.01 eV Å−1, respectively. A large vacuum space greater than 12 Å was left along the z direction to shield interactions between the adjacent atomic layers. The k-point meshes in Monkhorst–Pack scheme [18] were adopted for sampling Brillouin zone integration. To verify the validation of electronic band structures, we conducted more reliable calculations with the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional [19] and spin–orbit coupling (SOC).
GW calculations in single-shot approximation (G0W0) [20, 21] were conducted to obtain the quasiparticle energies and to study the excitonic effects. The optical properties were investigated by solving the Bethe–Salpeter equation (BSE) [22] on top of the G0W0 calculations. Eight highest valence bands and eight lowest conduction bands were used in the BSE calculations. The Brillouin zone was sampled with a 12 × 12 × 1 Γ-centered k-point mesh. The quasiparticle band structures were extracted by using the maximally localized Wannier functions [23]. In BSE calculations, we increased the cell length Lz up to 30 Å in the z direction, which is the largest we can computationally afford.
The phonon spectra are extracted from the harmonic interatomic force constants obtained using Phonopy [24]. κL is obtained by solving the linearized phonon Boltzmann transport equation (BTE) with single-mode relaxation time approximation (RTA) on the Phono3py [25] software package. For κL calculation, a 3 × 3 × 1 supercell is chosen with a 3 × 3 × 1 k-mesh for evaluating the second-order force constants, and a 2 × 2 × 1 supercell is used with a 3 × 3 × 1 k-mesh for calculating the third-order force constants. The convergence criterion for total energies is less than 10−8 eV in the calculation of atomic forces.
3. Results and discussion
3.1. Exciton binding energy
The appropriate choice of computational methods is vital to accurately describe the band gap characteristics and optical properties of BiI3 monolayer. To this end, we first calculated the relevant properties of bulk BiI3. The corresponding analyses are provided in the supporting information (supplemental material (https://stacks.iop.org/JPCM/34/055302/mmedia)). Calculations without considering SOC reproduced a sound Eb for bulk BiI3, thereby giving us some confidence in using this approach for the BiI3 monolayer. Therefore, we calculated the physical properties without including the SOC effect in the following sections. The calculated electronic band gaps of monolayer BiI3 within the PBE + SOC, PBE, and HSE06 + SOC schemes are 1.635, 2.580, and 2.214 eV respectively, with conduction band minimum (CBM) at Γ point and valence band minimum at the midway of the Γ → K direction, as presented in figure S3, which is perfectly consistent with references [3, 4].
As mentioned previously, we investigated the Eb in the framework of the G0W0 + BSE scheme with the Tamm–Dancoff approximation, which accounts for the many-body electron interactions and the electron–hole interactions. For a 2D system, a subtlety arises from the calculated dielectric constant, which includes the contributions from the layer of material and the layer of vacuum with ε0 (permittivity of vacuum). The size of the vacuum layer should approach to ∞ in principle to eliminate the influence [26]. The inset in figure 2 shows Eb as a function of Lz , indicating that Lz of 30 Å provides a relatively well-converged test result. Figure 2 shows the imaginary part of dielectric constant ε2 obtained from DFT + G0W0 + BSE scheme and the G0W0 band structures of BiI3 monolayer with Lz = 30 Å. The minimum direct band gap occurs at Γ point with a value of 4.196 eV; this value is slightly smaller than the direct excitation at M point (4.272 eV). In figure 2(a), the first peak is observed at the photon energy of 3.176 eV, which corresponds to the optical gap. Eb is calculated by taking the difference between the minimum direct G0W0 band gap and the G0W0 + BSE optical gap.
Figure 2. (a) Calculated imaginary part of dielectric constant for monolayer BiI3 as a function of photon energy using G0W0 + BSE scheme. xx (yy) and zz correspond to the in-plane and out-of-plane dielectric constants, respectively. (b) G0W0 band structures for monolayer BiI3. Inset presents Eb versus the length of z axial.
Download figure:
Standard image High-resolution imageThe obtained Eb is 1.02 eV, which is larger than that of bulk (0.224 eV). This condition is due to the reduced dielectric screening in 2D materials. This result is fairly consistent with the theoretical modification  [27] for 2D materials. The large Eb observed in monolayer BiI3 is comparable with the reported value of 500–1100 meV in the monolayers of molybdenum and tungsten dichalcogenides [28, 29]. This finding indicates that the strongly bound exciton is fairly stable and has an excellent resistance to the thermal disturbance and external electric field [30, 31]. At the same time, a large Eb may indicate a defining role in the optoelectronic processes in this strongly quantum-confined material after photoexcitations [32].
[27] for 2D materials. The large Eb observed in monolayer BiI3 is comparable with the reported value of 500–1100 meV in the monolayers of molybdenum and tungsten dichalcogenides [28, 29]. This finding indicates that the strongly bound exciton is fairly stable and has an excellent resistance to the thermal disturbance and external electric field [30, 31]. At the same time, a large Eb may indicate a defining role in the optoelectronic processes in this strongly quantum-confined material after photoexcitations [32].
Therefore, the material exhibits great potential for the development of new excitonic lasers [33]. Theoretical calculations revealed that the CBM states mainly originate from the Bi-6pz orbitals, and the valence band states near the Fermi level is dominated by I-5p states with a large admixture of Bi-6s states [3, 4], as shown in the insets of figure 3. This scenario in monolayer BiI3 is extremely similar to in its bulk counterpart, indicating that the exciton transitions s → p can be attributed to the transitions in the Bi metal ion [34].
Figure 3. (a) Strain–energy and (b) strain–stress relationships for monolayer BiI3. The monolayer can sustain stress up to 4.09 and 3.09 GPa in the x and y directions, respectively. The critical strains are 37% and 34% in the x and y directions, respectively. Insets show the projected band structures of (left) I-5p and (right) Bi-6p and 6s states.
Download figure:
Standard image High-resolution image3.2. Mechanical property
To obtain preliminary insight into the mechanical property, we calculated the elastic constants and ideal tensile strength of monolayer BiI3 from the strain–energy and stress–strain relationship. The monolayer BiI3 is a hexagonal structure, where the independent linear elastic constants reduce to two components of C11 and C12, and the mechanical stability criteria are given as C11 > C12 and C66 = (C11 − C12)/2 > 0 [35]. The elastic constants can be deduced from the strain–energy relation as follows:
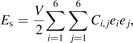
where V is the volume of the undistorted crystal, ei
is an element of strain tensor e = (e1, e2, e3, e4, e5, e6), Ci,j
are elastic constants [36, 37]. For the unstained structure, C11 = C22 = 7.216 N m−1, and C12 = C21 = 2.196 N m−1; thus, they satisfy the Born–Huang criteria [35], indicating that the monolayer is mechanically stabile. The Young's modulus (Y) and Poisson's ratio (ν) can be calculated from equations:  , and ν = C12/C11. The obtained Y and ν are 6.547 N m−1 and 0.304, respectively. The Cij
values of graphene, monolayer MoS2, and BiI3 monolayer with strain ε at 5% are tabulated in table 1. Such small Y and large ν demonstrate that BiI3 is more flexible and ductile than grapheme (330–348 N m−1) [37, 39] and MoS2 (122–126 N m−1) [39, 40], implying that it is unlikely to be free-standing. Therefore, a suitable substrate is highly desirable to experimentally support the 2D film. Hexagonal BN is a suitable choice for the epitaxial growth for BiI3 monolayer due to its low cost, resistance to high temperature and strong acid corrosion, extremely stable chemical properties, ultrawide band gap [41]. The lattice parameters of h-BN were determined to be a = b = 2.50 Å and c = 7.44 Å in our calculation, therefore, in-plane parameters are very close to the experimental value of 2.504 Å [42]. The lattice parameters of BiI3 monolayer were determined to be a = b = 7.80 Å which means a small mismatch of 1.9% = [7.80 − (7.50 + 7.80)/2]/[(7.50 + 7.80)/2] with the lattice parameter of 2.50 Å of h-BN.
, and ν = C12/C11. The obtained Y and ν are 6.547 N m−1 and 0.304, respectively. The Cij
values of graphene, monolayer MoS2, and BiI3 monolayer with strain ε at 5% are tabulated in table 1. Such small Y and large ν demonstrate that BiI3 is more flexible and ductile than grapheme (330–348 N m−1) [37, 39] and MoS2 (122–126 N m−1) [39, 40], implying that it is unlikely to be free-standing. Therefore, a suitable substrate is highly desirable to experimentally support the 2D film. Hexagonal BN is a suitable choice for the epitaxial growth for BiI3 monolayer due to its low cost, resistance to high temperature and strong acid corrosion, extremely stable chemical properties, ultrawide band gap [41]. The lattice parameters of h-BN were determined to be a = b = 2.50 Å and c = 7.44 Å in our calculation, therefore, in-plane parameters are very close to the experimental value of 2.504 Å [42]. The lattice parameters of BiI3 monolayer were determined to be a = b = 7.80 Å which means a small mismatch of 1.9% = [7.80 − (7.50 + 7.80)/2]/[(7.50 + 7.80)/2] with the lattice parameter of 2.50 Å of h-BN.
Table 1. Calculated elastic constants Cij (N m−1), Young's modulus Y (N m−1), and Poisson's ratio ν, critical strain εc, ideal strength σi (GPa), and lattice thermal conductivity ƘL (W m−1 K−1).
| C11 | C12 | Y | ν | εc | σi | ƘL | |
|---|---|---|---|---|---|---|---|
| Graphene [37] | 354 | 60 | 348.1 | 0.169 | |||
| Graphene [39] | 330 | 0.19 | 20% | 96 | |||
| MoS2 [39] | 122 | 0.26 | 22% | 26 | |||
| MoS2 [40] | 130 | 32 | 126.2 | 0.246 | |||
| MoS2 | 134.3 | 33.0 | 126.5 | 0.245 | 31.24 | ||
| MoS2 [43] | 33.6 | ||||||
| BiI3 (ε = 0%) | 7.216 | 2.196 | 6.547 | 0.304 | 30% | 2.6 | 0.247 |
| BiI3 (ε = 5%) | 6.340 | 2.972 | 4.947 | 0.469 | 0.206 |
To explore the flexibility and ideal tensile strengths, we investigated the mechanical responses to tensile strain. The strain is defined as ɛ = (a − a0)/a0, where a0 and a denote the lattice parameters of relaxed and strained systems. Primitive unit cell and rectangular cell (figure 1(c)) were adopted to calculate the responses to the biaxial and uniaxial strains, respectively. When a uniaxial strain was applied in x/y direction, the lattice constant in the y/x direction and internal atomic coordinates were fully relaxed by using the minimum energy method [38]. Under a biaxial strain, the internal atomic coordinates fully relaxed with the given lattice unchanged. The in-plane stress must be rescaled by Lz /d0 because the unit cell includes the vacuum space along the z direction [38, 39]. Here, d0 is the effective layer thickness of BiI3 monolayer. Following the approach descripted in reference [38], we take the interlayer spacing 7.68 Å of bulk BiI3 as d0 for the monolayer.
When the strain is less than 4% along the x or y direction, we can observe the near degeneracy of energy and stress responses, as shown in figure 3. This condition implies that the monolayer BiI3 is characterized by an isotropic elastic behavior in linear elastic regime, which is consistent with the theory for 2D system with hexagonal symmetry [37]. With the increase in ε, the calculated energy and stress curves are nonlinear and exhibit difference between the x and y directions. The critical strains along the x and y directions are 37% and 34%, respectively, and the corresponding stresses are 4.09 and 3.09 GPa, respectively. The biaxial stress–strain curve reaches its maximum of 2.60 GPa when the strain reaches up to 30%, which is larger than the previously reported (13%) [3]. The discrepancy stems from the relaxation for the strained structure being done or not. The maximum value of stress at critical strain is referred to as the ideal strength, which is the ultimate stress that a material can bear. The biaxial critical strain and ideal strengths are summarized in table 1. One can see that the monolayer BiI3 is more flexible and ductile than graphene and MoS2 by comparison.
Determining whether the monolayer BiI3 remains stable before approaching the critical strain is necessary because elastic instability or dynamical instability may intrude prior to the maximum stress on the strain path. We calculated the phonon dispersions of the monolayers at various biaxial strains. Figure 4 shows that the BiI3 monolayer is still dynamically stable at ε = 7%. It becomes dynamically instable when the tensile strain rises up to 8% because imaginary frequencies are identified at the M point. Since the system with strain of 7% is dynamically stable, the system at the strain of 5% is dynamically stable. The elastic constants C11 = C22 = 7.216 N m−1 and C12 = C21 = 2.196 N m−1 at ε = 5% also indicate the elastic stability. Interestingly, the Poisson's ratio (ν = 0.469) approaches the limiting value (0.5). Therefore, tensile strain sharply softens the material and highly controls the band gap and electronic structure of single layer BiI3 [3, 4].
Figure 4. Phonon band structures of monolayer BiI3 with strains ε at (a) 0%, (b) 7%, and (c) 8%. Distinct imaginary frequencies appear at M point at strain of 8%.
Download figure:
Standard image High-resolution image3.3. Lattice thermal conductivity
We solve the linearized phonon BTE with RTA [25] to obtain the macroscopic thermal conductivity tensor k L which can be calculated as a sum of contributions from individual phonon modes λ according to [44]:
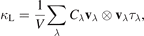
where V is the volume of the unit cell. Suffix λ ≡ q, j represents the mode index, which enumerates phonon wave vector q and branch j. Cλ , vλ , and τλ are the specific heat, group velocity, and phonon lifetime, respectively. The thermal conductivity tensor k L give the cumulative lattice thermal conductivity of six elements, kxx , kyy , kzz , kyz , kxz , kxy . The total lattice thermal conductivity kL can be calculated by kL = (kxx + kyy )/2 for 2D materials [45]. Figure 5 shows the temperature-dependent kL of monolayers. At strains ε = 0% and 5%, the calculated kL values at 300 K is 0.247 and 0.206 W m−1 K−1, respectively, which is smaller than that of MoS2 monolayer (31.2 W m−1 K−1) by two orders of magnitude and is extremely lower than that of graphene (3080–5150 W m−1 K−1) [46]. The iterative method as performed in ShengBTE code [47] gives rise to a value of 0.398 W m−1 K−1, as shown in figure S2.
Figure 5. Lattice thermal conductivities of monolayer BiI3 in plane and out of plane without and with strain (ε = 5%) as a function of temperature. Green lines are 1/T fitting of temperature dependent kL. The inset shows kλ as a function of the frequency at 300 K.
Download figure:
Standard image High-resolution imageTo explore the origin of ultralow kL, we examined the phonon dispersion. Figure 6 shows the phonon dispersion spectra along high-symmetry directions in the Brillouin zone. Twenty-four phonon branches, including three acoustical branches and 21 optical branches, are found due to eight atoms in the primitive cell. In the small region of long wavelength limit (λ → ∞), the transverse acoustic (TA) and longitudinal acoustic (LA) phonon modes are linear, whereas the out-of-plane acoustic (ZA) phonon mode is parabolic. In pristine semiconductors and insulators, phonons rather than electrons take the main responsibility for heat transport, where the low-frequency acoustic phonon branches are the dominant contributors to kL. This condition is consistent with the inset in figure 5. No phonon frequency gap is found between acoustic and optical phonon branches. Therefore, acoustical and optical branches in the range of 0.49 THz to 0.82 THz involve the resistive Umklapp scattering through the channel of acoustic + acoustic → optical [48]. The fitting lines of kL are inversely proportional to the temperature at high temperature, further verifying that the anharmonic phonon–phonon interaction is a key to the thermal resistivity at high temperature.
Figure 6. (a) Phonon group velocities vλ of phonon modes along high symmetry directions and (b) dependences of lifetimes τλ on frequency at 300 K. The color background represents the magnitude of group velocity vλ .
Download figure:
Standard image High-resolution imageTo explain the reason for the low kL, we analyzed the phonon group velocity vλ and phonon lifetime τλ . Phonon vλ can be determined from
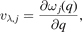
where ω, j, and
q
represent the frequency, phonon branch index, and the wave vector, respectively. Figure 6(a) shows the vλ
distributions for each acoustic phonon mode in the Brillouin zone. The calculated vλ
for LA and TA phonons close to the Γ point ranges from 1.34 to 1.78 km s−1, which are on the same magnitude as that (6.61 and 3.90 km s−1) of MoS2 monolayer, but they are smaller than that of graphene (21–22 km s−1) [43, 49, 50]. Although large vλ
is observed around 2.5 and 3.6 THz for the high-lying optic modes, the corresponding phonon lifetime τλ
is smaller than of the acoustic branches by two orders of magnitude. Thus, the acoustic branch is responsible for thermal transport. Their small group velocity lowers the thermal conductivity. Such low vλ
originates from the weak interaction between Bi and I atoms and their heavy atomic mass. At the long wavelength limit, the group velocity vλ
reaches the speed of sound,  [51], in a crystal. Here, ρ and M are the mass density and mass in a unit cell, respectively, and Y is intimately associated with the bond strength. Thus, the larger the atomic number and the smaller the Young's modulus, the lower the phonon thermal conductivity.
[51], in a crystal. Here, ρ and M are the mass density and mass in a unit cell, respectively, and Y is intimately associated with the bond strength. Thus, the larger the atomic number and the smaller the Young's modulus, the lower the phonon thermal conductivity.
Another underlying cause for the ultralow thermal conductivity is the short τλ given that kL is directly proportional to τλ . In the RTA, the τλ are calculated as the inverse of the phonon linewidths Γλ : τλ = 1/(2Γλ ) [25]. Figure 6(b) shows that the average τλ is less than 200 ps, which is approximately two orders of magnitude lower than that of MoS2 monolayer [52]. Such short τλ results in a low kL. The scattering between acoustic and optical phonon modes is the main reason for the extremely short phonon relaxation time.
As mentioned previously, the strained monolayer within a strain of less than 7% is a thermodynamically stable structure. Therefore, determining the effect of strain on kL is important. The corresponding kL is illustrated in figure 5(a) when the biaxial strain of 5% is applied. The estimated kL value is 0.206 W m−1 K−1 at 5% strain and 300 K. Compared with the unstrained case, the strain at 5% slightly lowers kL. The value is lower than that (0.30 W m−1 K−1) of penta-germanene with the lowest kL in 2D crystal materials [53] and most other 2D materials [54]. The low kL results from the short length of Bi–I bonds (3.118 Å → 3.144 Å). Similar to the electronic band gap, kL can be effectively regulated and controlled by applying external strain, which can result in a wider and more flexible range of application.
4. Summary
In this study, we theoretically investigated the excitonic effects in the framework of the BSE, the mechanical properties, and the kL of monolayer BiI3 obtained by resolving the BTE with RTA. We first predicted the strongly bound exciton with a large Eb of 1.02 eV in this monolayer, which is four times than that of its bulk (0.224 eV). This condition is attributable to the reduced dielectric screening in low-dimensional materials. BiI3 demonstrates superior flexibility and ductility because its large ν approaches 0.5, and its Y is two orders of magnitude smaller than graphene and monolayer MoS2. The ideal tensile strength is found to be 2.60 GPa with a critical biaxial tensile strain of 30%. When the strain is less than 8%, the monolayer is still mechanically and dynamically stable. The predicted kL of monolayer BiI3 is 0.247 and 0.206 W m−1 K−1 at room temperature under 0% and 5% strains, respectively, which is lower than most reported values for other 2D materials. Such ultralow kL can be attributed to the Umklapp scattering, heavy atomic mass, and relatively weak chemical bond.
Acknowledgments
This work was supported by the Scientific Research Fund of Hunan Provincial Education Department (Nos. 20A106, 18A351, 20B129, 19C0487) and Hunan Provincial Natural Science Foundation under Grant No. 2021JJ30179.
Data availability statement
The data generated and/or analysed during the current study are not publicly available for legal/ethical reasons but are available from the corresponding author on reasonable request.
Conflict of interest
There are no conflicts to declare.







