Abstract
We investigated magnetic field effect on the topological properties of transition metal dichalcogenide Dirac semimetals (DSMs) PdTe2/PtTe2/PtSe2 based on Wannier-function-based tight-binding (WFTB) model obtained from first-principles calculations. The DSMs PdTe2/PtTe2/PtSe2 undergo a transition from DSMs into Weyl semimetals with four pairs of Weyl points (WPs) in the entire Brillouin zone by splitting Dirac points under external magnetic field B. The positions and energies of WPs vary linearly with the strength of the B field under the c-axis magnetic field B. Under the a- and b-axis B field, however, the positions of magnetic-field-inducing WPs deviate slightly from the c axis, and their kz coordinates and energies change in a parabolic-like curve with the increasing B field. However, the system opens an axial gap on the A–Γ axis, and the gap changes with the direction of the B field when the out of c-axis B field is applied. When we further apply the magnetic field in the ac, bc, and ab planes, the results are more diverse compared to the axial magnetic field. Under the ac and bc plane B field, the kz and energies of WPs within angle θ = [0°, 90°] and θ = [90°, 180°] are mirror symmetrically distributed. The distribution of WPs shows broken rotational symmetry under the ab plane B field due to the difference of non-diagonal part of Hamiltonian. Our theoretical findings can provide a useful guideline for the applications of DSM materials under external magnetic field in the future topological electronic devices.
Export citation and abstract BibTeX RIS
1. Introduction
Since the discovery of two-dimensional quantum spin Hall effect in 2006 [1], the development of topological electronic materials (TEMs) has entered a new stage. Various novel TEMs have been discovered one after another, such as topological insulator [2], Weyl semimetal (WSM) [3], triple-point fermion semimetals [4], Dirac semimetal (DSM) [5–8], manifold fermion semimetal [9], topological node line semimetal [10, 11], etc. Recently, TEM has been further extended to high-order topological materials [12, 13] and non-Hermitian topological states of matter [14], which show very rich physical significance and tremendous application potential. The DSM can be further classified into magnetic and non-magnetic DSM according to whether they break time reversal symmetry (TRS). Nonmagnetic or TRS invariant DSM can be obtained through both symmetry-enforced and band inversion routes [11, 15]. Symmetry-enforced DSM only exists in crystal with nonsymmorphic space group symmetry and has four-dimensional irreducible (co)representations [15]. And the Dirac points (DPs) must be located at high-symmetry momenta on the boundary of Brillouin zone (BZ). Recent studies showed that there are 69 nonsymmorphic space groups host symmetry-enforced DPs [11]. Band inversion-induced DSM possesses crossing points of inverted band, which are protected by rotational and mirror symmetries and formed on high symmetry lines (HSLs) [11, 15], such as Na3Bi [5], Cd3As2 [16].
When a system has TRS and inversion symmetry (IS), each band at each k point is double degeneracy, which is a manifestation of Kramers theorem. Due to orbital hybridization, crystal field effect, and spin–orbit coupling (SOC), the degeneracy band generally will be split and then be possibly reversed [17]. The inverted bands must have crossing nodes under symmetry protection. The little groups of non-high symmetry points (HSPs) or lines in the BZ possess lower-dimensional irreducible representation and then non-degenerate bands there. While the group representation of HSPs and lines in the BZ exit possibly higher dimension and results in a higher degree of degeneracy of bands. Discrete crystal rotational symmetry will cause double degenerate inverted bands intersecting on the rotation axis to form band-inverted DPs [11]. The stability of the four-fold degenerate point formed by the above band-inverted mechanism is relatively weak, because the Dirac node can be split by adjusting the parameters (removing band inversion) or breaking the crystal symmetry [7, 11, 16]. Therefore, band inversion-induced DSM as a parent compound can be transformed into other novel states. The three-dimensional Dirac fermions in a DSM are composed of two overlapped Weyl fermions, which can be separated in momentum space if TRS or IS was broken [16, 18, 19].
In our work, we constructed a Wannier-function-based tight-binding (WFTB) model for band inversion-induced DSM PdTe2/PtTe2/PtSe2 with magnetic field B applied along various directions. Atom-centered localized Wannier functions (WFs) are generated based on the calculations of ab initio electronic structure by selecting appropriate initial atomic orbitals. We then constructed a WFTB model by separately adding SOC Hamiltonian and Zeeman energy based on atomic-like Wannier orbitals. Landau levels or Peierls phases are not considered in our WFTB model. Since three systems PdTe2/PtTe2/PtSe2 have the same symmetry and similar band structure near the Fermi level (EF), we mainly focus on PdTe2. However, the analysis and main conclusions are also applicable to the other two systems (PtTe2 and PtSe2). Some calculations for PtTe2 and PtSe2 are provided in the supplementary material (see supplementary material (https://stacks.iop.org/JPCM/34/085802/mmedia)).
2. Method and models
Bulk PdTe2, PtTe2 and PtSe2 crystallize in the trigonal CdI2-type crystal structure with space group  (No. 164) and the corresponding point group is D3d
. The crystal structure and the first BZ with HSLs and HSPs are shown in figures 1(a)–(c), respectively. The generators of the D3d
include C3z
, C2x
, and σd1, therefore the bulk crystal has twelve symmetry operators. The DPs of PdTe2/PtTe2/PtSe2 are protected by IS, TRS, and C3v
symmetries [8].
(No. 164) and the corresponding point group is D3d
. The crystal structure and the first BZ with HSLs and HSPs are shown in figures 1(a)–(c), respectively. The generators of the D3d
include C3z
, C2x
, and σd1, therefore the bulk crystal has twelve symmetry operators. The DPs of PdTe2/PtTe2/PtSe2 are protected by IS, TRS, and C3v
symmetries [8].
Figure 1. The crystal structures of PdTe2/PtTe2/PtSe2 in the space group  under (a) side view; (b) top view. The dash blue rectangle and rhombus indicate primitive cell. (c) The HSPs and HSLs in the bulk BZ.
under (a) side view; (b) top view. The dash blue rectangle and rhombus indicate primitive cell. (c) The HSPs and HSLs in the bulk BZ.
Download figure:
Standard image High-resolution imageThe initial positions of atoms and lattice parameters are fully optimized through adopting conjugate gradient method. The obtained lattice constants are given in table 1. We first calculated the electronic structure of PdTe2/PtTe2/PtSe2 without SOC and magnetic field by using the density functional theory (DFT) code VASP [20, 21]. With the DFT calculated bands and initial atomic orbitals, we generated WFs by Wannier90 code [22]. The overlap and projection matrixes are computed at each DFT-sampled k point. In order to maintain the features of atomic orbitals, maximal localization is not applied in the calculations of Wannierization. We checked that the generated WFs are close to atomic-like orbitals. Then we constructed a SOC-free WFTB model from the WFs and added SOC Hamiltonian to the WFTB model such that the model-calculated bands near the EF agree with the DFT bands. Lastly, we considered Zeeman energy in the WFTB model to study the magnetic field effect on the bands, especially the bands near the DPs.
Table 1. The calculated lattice parameters, the energies and kz positions of Dirac nodes for PdTe2, PtTe2 and PtSe2.
| Systems | a = b (Å) | c (Å) | ED (eV) | ZD (2π/c) |
|---|---|---|---|---|
| PdTe2 | 4.107 | 5.217 | −0.534 | ±0.402 |
| PtTe2 | 4.086 | 5.259 | −0.758 | ±0.381 |
| PtSe2 | 3.774 | 5.317 | −1.049 | ±0.294 |
In the DFT calculations, we adopted the Perdew–Burke–Ernzerhof generalized gradient approximation [23] for the exchange correlation functional with and without SOC. We used projector augmented wave pseudopotentials [24] with an energy cutoff of 500 eV and a 16 × 16 × 8 Monkhorst-Pack k-point mesh. In order to construct the SOC-free WFTB model, we start with an initial set of 12 projected atomic orbitals comprised of s, dz2, dx2–y2, dxy , dyz , and dxz orbitals centered at the one Pd/Pt sites and px , py , and pz orbitals centered at the two Te/Se sites in the primitive unit cell. We need to include both Pd/Pt-s/d orbitals and Te/Se-p orbitals in the WFTB model due to their large contributions to the bands near the EF indicated by our DFT calculations (figure 2(c)).
Figure 2. (a) The comparison between the VASP- (blue) and WFTB-calculated (pink) bands for PdTe2 without SOC. (b) Likewise with SOC included. Red circles highlight two DPs at A–Γ path. (c) The orbit-resolved bands with SOC for PdTe2. The Pd-s/d and Te-p orbitals are major orbital components near the EF. The green horizontal line indicates the EF. No B field is included here.
Download figure:
Standard image High-resolution imageWe constructed the SOC-free WFTB model by using the generated WFs, | R + s β ⟩, centered at R + s β , where R is Bravais lattice vector and s β denote the sites of orbital β (β = 1, ..., 12). The SOC-free Hamiltonian matrix H0 [25] reads
where |ψk ⟩ are Bloch orbitals and can be expanded by WFs basis. Here tαβ ( R − 0) is a hopping energy between orbital α at site s α in the home cell at R = 0 and orbital β at site s β in the unit cell located at R . We added SOC term to the SOC-free Hamiltonian H0. The order of the basis in the SOC/Zeeman term is (pz ↑, px ↑, py ↑) and (s↑, dz2↑, dxz ↑, dyz ↑, dx2–y2↑, dxy ↑) for respective Te/Se-p and Pd/Pt-s/d orbitals. Considering the spin degrees of freedom, the number of WFs basis is now 24. The SOC Hamiltonian is HSOC = λ L · σ , where λ is the SOC strength parameter, L is the orbital angular momentum, and σ represents Pauli spin matrix. By fitting with the VASP-calculated bands, we found the fitted SOC parameters for PdTe2/PtTe2/PtSe2 listed in table 2. The magnetic field induced Zeeman term is HZee = gμB SB , where g is Lande factor, μB is Bohr magneton and S is the spin angular momentum. Taking Te atom as an example, the SOC matrix and Zeeman matrix of Te atom are respectively
Here, the 3 × 3 matrices  and
and  (superscript + denotes Hermitian conjugate) are non-diagonal
(superscript + denotes Hermitian conjugate) are non-diagonal
where a+ = gμB
B sin θ e−iφ
, a− = gμB
B sin θ eiφ
, az
= gμB
B cos θ, the 3 × 3 matrices  and
and  are diagonal, the (θ, φ) represents the azimuth angle in the spherical coordinates. When the magnetic field B is applied in different directions, the
are diagonal, the (θ, φ) represents the azimuth angle in the spherical coordinates. When the magnetic field B is applied in different directions, the  matrix will change periodically with the azimuth angle. Considered the total number of orbitals in three systems is 24, and the Zeeman matrix is
matrix will change periodically with the azimuth angle. Considered the total number of orbitals in three systems is 24, and the Zeeman matrix is
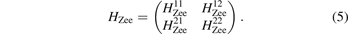
When the matrix  is direct sum of the Zeeman matrix of three atoms and results in a 12 × 12 matrix. The diagonal matrix
is direct sum of the Zeeman matrix of three atoms and results in a 12 × 12 matrix. The diagonal matrix  is the spin up/down part of all atoms and
is the spin up/down part of all atoms and  , the non-diagonal matrix
, the non-diagonal matrix  is the up-down spin coupling part of all atoms and
is the up-down spin coupling part of all atoms and  . When an external magnetic field is applied, the matrix
. When an external magnetic field is applied, the matrix  also changes periodically, similar to the matrix
also changes periodically, similar to the matrix  , and hence leads to distinct evolution of positions and energies of magnetic-induced WPs.
, and hence leads to distinct evolution of positions and energies of magnetic-induced WPs.
Table 2. Topological charge χ, kz coordinates and energies with respect to the EF of two WPs in the kz > 0 half BZ, the SOC parameter λ, where Wnα is the αth WP arising from band n, note that gμB B = 10 meV.
| Wnα | χ | kz (2π/c) | Energy (eV) | λ (eV) | |
|---|---|---|---|---|---|
| PdTe2 | W16a | +1 | 0.405 | −0.547 | λPd = 0.15 |
| W16b | −1 | 0.398 | −0.521 | λTe = 0.65 | |
| PtTe2 | W16a | +1 | 0.384 | −0.773 | λPt = 0.45 |
| W16b | −1 | 0.378 | −0.747 | λTe = 0.70 | |
| PtSe2 | W16a | +1 | 0.298 | −1.061 | λPt = 0.60 |
| W16b | −1 | 0.290 | −1.034 | λSe = 0.40 |
The total Hamiltonian for the WFTB model is H = H0 + HSOC + HZee. We presented the results under magnetic field gμB B = 10 meV in the following calculations, unless specified otherwise. And the strength of B that we considered here is experimentally achievable [16]. Furthermore, our findings would not qualitatively change with the field strength if the magnetic field is not extremely high. We choose a larger B field, because the split of each DP is more obvious and easier to analyze.
3. Results and discussion
We check whether our WFTB model is correct by comparing the WFTB band with the first-principles electronic bands. In the absence of magnetic field, the WFTB and VASP-calculated bands for PdTe2 are in high agreement near the EF in the absence/presence of SOC as shown in figures 2(a) and (b). The positions and energies of DPs for three considered systems are listed in table 1, which are consistent with the previous calculations [6, 8]. The bands for PtTe2 and PtSe2 are presented in the supplementary material. In the vicinity of the DPs, the bands are mainly composed of Te-p orbitals and a small proportion of Pd-s/d orbitals as shown in figure 2(c).
We apply a uniform magnetic field along the C3z rotation axis, and find each DP was split into four separate WPs along the c axis as illustrated in figure 3(c). The result of magnetic field effects on the rotation axis was also discussed in previous studies [16, 18, 19]. Figures 3(b) and (c) show the development of the four WPs along the c axis in the half BZ under the + B field. The positive/negative sign means the direction of B along with the ±z axis, labeled by + B /− B . The number of field-induced WPs does not change and nor do their chiralities (topological charge χ) within magnetic field strength [0, 10] meV. The chirality of the WPs is identified by calculating Wannier charge center of the Bloch bands which was obtained from our generated total WFTB model H, which was realized by using WannierTools code [26]. The IS partner of the four WPs (W15, W16a /W16b , W17) in the kz > 0 BZ is located in the kz < 0 BZ as shown in figure 3(d). We only analyzed two WPs W16a /W16b near the A–Γ line formed between the 16th (blue conduction band) and 17th band (green valence band) shown in figures 3(b) and (c).
Figure 3. WFTB-calculated bands of PdTe2 along A–Γ direction when
B
field is parallel to the
c
axis with (a) gμB
B = 0 meV, (b) gμB
B = 5 meV, and (c) gμB
B = 10 meV. The red and blue arrow/circle mark four WPs on the A–Γ line. (d) The positions and energies of eight WPs at A–Γ–A line under magnetic field gμB
B = 10 meV. Square/triangle represents W15/W17 WP, W15 WP is the crossing point between 15th and 16th band, W17 WP is the crossing point between 17th and 18th band, the circle represents W16a
/W16b
. Red and blue color correspond to WPs with topological charge χ of −1 and +1 in (d). (e) The  and E16a
/E16b
of two WPs change with the magnetic field.
and E16a
/E16b
of two WPs change with the magnetic field.
Download figure:
Standard image High-resolution imageThe kz
positions  and energies E16a
/E16a
of two WPs are listed in table 2 for three considered systems. The
and energies E16a
/E16a
of two WPs are listed in table 2 for three considered systems. The  and E16a
/E16a
change linearly with the +
B
varies ranging from 0 meV to 10 meV as shown in figure 3(e) and so do when
B
is from −10 meV to 0 meV. Hence, the
and E16a
/E16a
change linearly with the +
B
varies ranging from 0 meV to 10 meV as shown in figure 3(e) and so do when
B
is from −10 meV to 0 meV. Hence, the  and E16a
/E16a
demonstrate a direction symmetrical variation under the +B and −B. The symmetrical change of WPs can be understood by the Zeeman matrix (4) and (5). Firstly, we note the H0 + HSOC is unchanged and the HZee is the only changing term under magnetic field
B
. Secondly, when the θ = 0° (+
B
) or θ = 180° (−
B
), the non-diagonal part
and E16a
/E16a
demonstrate a direction symmetrical variation under the +B and −B. The symmetrical change of WPs can be understood by the Zeeman matrix (4) and (5). Firstly, we note the H0 + HSOC is unchanged and the HZee is the only changing term under magnetic field
B
. Secondly, when the θ = 0° (+
B
) or θ = 180° (−
B
), the non-diagonal part  and
and  disappear and the Zeeman matrix HZee only includes the
disappear and the Zeeman matrix HZee only includes the  and
and  diagonal part. Thirdly, the +
B
and −
B
will change entirely a sign on HZee due to the az
factor in the diagonal part, for example,
diagonal part. Thirdly, the +
B
and −
B
will change entirely a sign on HZee due to the az
factor in the diagonal part, for example,  and
and  . As a result, the total Hamiltonian will change from H+
B
= H0 + HSOC + HZee to H−
B
= H0 + HSOC − HZee. However, it is noteworthy that both H+
B
and H−
B
have the same eigenvalue, resulting in the same two WPs as identified in our calculations. As the strength of magnetic field increases, the kz
coordinate
. As a result, the total Hamiltonian will change from H+
B
= H0 + HSOC + HZee to H−
B
= H0 + HSOC − HZee. However, it is noteworthy that both H+
B
and H−
B
have the same eigenvalue, resulting in the same two WPs as identified in our calculations. As the strength of magnetic field increases, the kz
coordinate  is moving away from (close to) the Γ point, the energy E16a
(E16b
) is moving away from (close to) the EF.
is moving away from (close to) the Γ point, the energy E16a
(E16b
) is moving away from (close to) the EF.
Figures 4(a) and (b) show WFTB-calculated energies and the kz
of W16a
/W16b
nodes when the
B
field along the
a
axis. The energies of two WPs change in a parabolic-like shape as
B
field changes from −10 meV to 10 meV as shown in figure 4(a). Interestingly, the energies E16a
/E16b
of both WPs close gradually to the EF (=0) with the increasing
B
field, regardless of the
B
field direction, which is different from the behavior of E16a
/E16b
when
B
field along z-axis as shown in figure 3(f). Additionally, it is noted that the energy E16a
is slightly lower (higher) than the E16b
when
B
field along with +
a
(−
a
) axis. This variation reflects roughly a distinct splitting of bands under the reversed magnetic field. In order to understand the different behavior of energies and coordinates of W16a
/W16b
, we here consider a simple atomic extreme 'bands' case under magnetic field. In the absence of SOC, the degenerate spin-up and spin-down bands are split due to the Zeeman effect and form crossing points cp1 and cp2 when applying a +
B
magnetic field as shown in figure 4(e). However, both cp1 and cp2 exchange their positions and energies when reversing the direction of magnetic field (i.e. −
B
) as shown in figure 4(f). When further adding SOC, although spin-up and spin-down bands will mix, mixed bands generally possess non-equal percentage spin bands. As a consequence, the above similar exchange of mixed bands will take place and then exchange positions of two crossing points, leading to finally opposite 'positions' for both W16a
and W16b
under +
B
and −
B
field in figures 4(a) and (b). The positions of both WPs demonstrate similar parabolic variation and the dependence of magnetic field direction shown in figure 4(b). When in
a
-axis magnetic field, the kz
of W16a
/W16b
moves toward the Γ as the magnetic field increases. The energies and kz
coordinates of both W16a
/W16b
under
b
-axis magnetic field are presented in figures 4(c) and (d). The results are similar qualitatively in addition to the larger differences between  /E16a
and
/E16a
and  /E16b
compare with those of the corresponding values under
a
-axis magnetic field. In addition, the positions of both W16a
/W16b
slightly deviate from the kz
-axis under both
a
- and
b
-axes magnetic field and other materials have similar results [18].
/E16b
compare with those of the corresponding values under
a
-axis magnetic field. In addition, the positions of both W16a
/W16b
slightly deviate from the kz
-axis under both
a
- and
b
-axes magnetic field and other materials have similar results [18].
Figure 4. WFTB-calculated energies and coordinates of WP W16a /W16b when B field changes from −10 meV to 10 meV along the a axis (a) and (b) and b axis (c) and (d). The red square and blue dot correspond to WP with topological charge χ of +1 (W16a ) and −1 (W16b ). The schematic of splitting of bands under − B field (e) and + B field (f), and demonstrate the movement of W16a /W16b WPs under magnetic field gμB B = 10 meV. The dotted and solid lines represent bands in the absence and presence of a magnetic field, respectively. The pink arrow represents the DP before the magnetic field is applied.
Download figure:
Standard image High-resolution imageWe also investigated the band's evolution when a
B
field is applied in ac/bc/ab plane for three considered systems. Here, we only focus on the PdTe2 and the results for PtTe2 and PtSe2 are given in supplementary material. When the
B
field is rotated from (θ, φ) = (0°, 0°) to (θ, φ) = (180°, 0°) with angle step 5°, we also identified two pairs of WPs that are close to the kz
-axis between the 16th and 17th band and the distribution of magnetic-induced WPs is discussed in reference [18]. The evolution of kz
and energy of W16a
/W16b
with kz
> 0 as a function of angle φ are shown in figures 5(a) and (b). The W16a
/W16b
with larger/smaller kz
is further/closer to the point Γ at each angle. The kz
of WPs shows both mirror symmetries over [0°, 180°] and center IS over [0°, 360°]. The chirality of W16a
/W16b
WPs changes from +1/−1 (θ = [0°, 90°]) to −1/+1 (θ = [90°, 180°]). The two WPs merge when the θ is 90°. These symmetries can be rational by the Zeeman term. The angle θ is only variable for ac plane
B
field and have cos θ/sin θ factor in the diagonal part  ,
,  and non-diagonal part
and non-diagonal part  ,
,  of HZee, which leads to a periodical change of H as angle θ. Consequently, the kz
of WPs within θ = [0°, 90°] is mirror-symmetric to that of WPs within θ = [90°, 180°] due to the symmetry of sine/cosine function. The kz
of WPs within θ = [0°, 90°] decrease as the increasing θ. The kz
of W16a
/W16b
in unit 1 Å−1 are 0.487/0.480 for PdTe2, 0.459/0.452 for PtTe2, 0.352/0.343 for PtSe2 at θ = 0° and 0.484/0.484 for PdTe2, 0.456/0.456 for PtTe2 and 0.347/0.347 for PtSe2 at θ = 90°. The energies E16a
/E16b
show a similar variation tendency as angle θ as depicted in figure 5(b).
of HZee, which leads to a periodical change of H as angle θ. Consequently, the kz
of WPs within θ = [0°, 90°] is mirror-symmetric to that of WPs within θ = [90°, 180°] due to the symmetry of sine/cosine function. The kz
of WPs within θ = [0°, 90°] decrease as the increasing θ. The kz
of W16a
/W16b
in unit 1 Å−1 are 0.487/0.480 for PdTe2, 0.459/0.452 for PtTe2, 0.352/0.343 for PtSe2 at θ = 0° and 0.484/0.484 for PdTe2, 0.456/0.456 for PtTe2 and 0.347/0.347 for PtSe2 at θ = 90°. The energies E16a
/E16b
show a similar variation tendency as angle θ as depicted in figure 5(b).
Figure 5. The kz and energies of W16a /W16b WPs under the (a) and (b) ac plane B field; (c) and (d) bc plane B field and (e) and (f) ab plane B field. Here, square/circle represents W16a /W16b and blue/red color represents topological charge +1/−1 of WP.
Download figure:
Standard image High-resolution imageWhen the
B
field is rotated from (θ, φ) = (0°, 90°) to (θ, φ) = (180°, 90°) in the bc plane, the kz
and energy evolution of W16a
/W16b
as a function of angle θ is shown in figures 5(c) and (d). The symmetrical evolution of the positions and energies of W16a
/W16b
as well as the change in chirality is similar to
a
-axis magnetic field. These symmetries are reasonable according to the analysis of Zeeman terms. The angle θ is only variable for bc plane
B
field and has a cos θ/i sin θ factor in the diagonal/non-diagonal part  and
and  /non-diagonal part
/non-diagonal part  and
and  of HZee, which leads to a periodical change of H as angle θ. The kz
of W16a
/W16b
in unit 1 Å−1 are 0.488/0.480 for PdTe2, 0.459/0.452 for PtTe2, 0.352/0.343 for PtSe2 at θ = 0° and 0.484/0.483 for PdTe2, 0.456/0.456 for PtTe2 and 0.348/0.347 for PtSe2 at θ = 90°.
of HZee, which leads to a periodical change of H as angle θ. The kz
of W16a
/W16b
in unit 1 Å−1 are 0.488/0.480 for PdTe2, 0.459/0.452 for PtTe2, 0.352/0.343 for PtSe2 at θ = 0° and 0.484/0.483 for PdTe2, 0.456/0.456 for PtTe2 and 0.348/0.347 for PtSe2 at θ = 90°.
The kz and E16a /E16 of WPs are presented in figures 5(e) and (f) when the B field varies in the ab plane, i.e. θ = 90°, 0° ⩽ φ < 360°. The distribution of kz and energies demonstrates a broken rotational symmetry which can be understood by the analysis of Hamiltonian. Specifically, the distribution of both kz and E16a /E16 is approximate left-right mirror symmetrical between [0°, 90°] and [180°, 90°] and strict up-down mirror symmetrical between [0°, 180°] and [360°, 180°]. Firstly, the variable φ dominates the change of non-diagonal term of HZee including the sine/cosine factor. For example, the non-diagonal part contains a+ and a− in the equation (4). Secondly, the characteristic variation of sine function causes approximate rational symmetries of the kz and E16a /E16b among four quadrants, though sine function shows a strict symmetry for φ and 180° − φ. Specifically, the φ and 180° − φ show an approximate symmetry because the HSOC + HZee is different at φ and 180° − φ, which in turn leads to slight different eigenvalues. However, the φ and 360° − φ show a strict symmetry because the HSOC + HZee is same at φ and 360° − φ, which then leads to the same eigenvalues, and strict 'mirror' symmetry of WPs when φ lies between [0°, 180°] and [180°, 360°].
Additionally, when the B field is along the direction other than the c axis, the 16th and 17th bands have an on-axis bandgap on the A–Γ line and similar studies arediscussed in reference [18], and the bandgap is the largest under the bc plane B field. Notably, the crossing points are possible near the kz axis. Figure 6(a) shows typical WFTB-calculated bands for the B field at (θ, φ) = (45°, 90°), and the bands indicate a gap between the 16th band (blue) and 17th band (green) on the A–Γ line. The gap as a function of θ is given in figure 6(b) and the θ and 180° − θ shows an approximate mirror symmetry. The gaps are zero for both θ = 0° and 180°, which implies the existence of nodes and agrees with the result of z-axis B field. The maximal gaps appear at around θ ≈ 50° and 130°.
Figure 6. (a) WFTB-calculated bands for the B field in the bc plane at (θ, φ) = (45°, 90°) along A–Γ path, (b) the axial gap evolution between the 16th (blue) band and the 17th (green) band in (a) when B field is rotated from (θ, φ) = (0°, 90°) to (θ, φ) = (180°, 90°), note that gμB B = 10 meV.
Download figure:
Standard image High-resolution image4. Conclusions
In summary, we have developed a WFTB model for the topological DSM PdTe2/PtTe2/PtSe2, which reproduces the DFT-calculated bands well. Based on the WFTB model, we investigate the magnetic effect on topological properties of the considered systems under magnetic field B along various directions in three-dimensional space. The magnetic field-induced the phase transition of DSM-WSM and the topological properties of the resulting WSM are discussed systematically. The DSM PdTe2/PtTe2/PtSe2 would transit into WSM with four pairs of Weyl points in the entire BZ under the axial-oriented magnetic field. Under the c -axis B field, each DP on the c axis will be split into four WPs, and their positions are still located on the c axis. The position and energy evolution of four splitting WPs vary linearly with the strength of magnetic field. Under the a - and b -axes magnetic field, however, the positions of the splitting WP deviate slightly from c axis, and their coordinates and energies change in parabolic-like curves with the increasing magnetic field. The symmetrical characterization of WPs' distribution under an inverted magnetic field can be rationalized by analyzing the Zeeman term in the WFTB model. When we further apply a magnetic field in the three typical planes (ac, bc, and ab), the results are more diverse compared to the axial magnetic field. When the B field is applied in the ac and bc plane, the systems also turn into WSM with four pairs of WPs. The kz and energies of WPs within θ = [0°, 90°] and θ = [90°, 180°] is symmetrical. Under the ab plane magnetic field, the distribution of kz and energies show broken rotational symmetry over angle φ = [0, 360°] due to the variation of non-diagonal part of Hamiltonian. Additionally, when the B field is along the direction other than the c axis, the system opens a gap on the A–Γ path, and the gap changes with the direction of a magnetic field. When the magnetic field intensity is increased to 0.1 eV, these results are still reliable and the corresponding calculations are provided in the supplementary material (see supplementary material). These results are useful for improving the understanding of the magnetic field-induced effect of other DSMs. Furthermore, our findings are meaningful for the possible applications of DSMs in the topological electronic devices under external magnetic field.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant No. 11204261), Natural Science Foundation of Hunan Province (Grant No. 2018JJ2381), Postgraduate Scientific Research Innovation Project of Hunan Province (Grant No. XDCX2021B127), a Key Project of Education Department of Hunan Province (Grant No. 19A471), and Postgraduate Scientific Research Innovation Project of Hunan Province (Grant No. CX20210615).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Conflict of interest
There are no conflicts to declare.







