Nesting-induced local electronic patterns around a single As (Te, Se) vacancy in iron-based superconductors

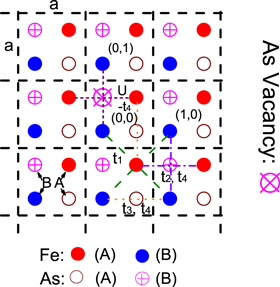
The mechanism of high temperature superconductivity has been one of the great challenges in the condensed matter physics community since the discovery of the cuprates in 1986 [1]. A series of high T_c cuprate superconductors commonly possesses layered crystal structures consisting of the conducting CuO₂ planes separated by the other elements and oxygen layers. The ligand O ions in the CuO₂ planes just locate on the Cu–Cu bonds and are believed to play an important role in forming superconductivity. The surface effects of the cuprates can be neglected due to the positions of the O ions. However, it is difficult to evaluate the impact of the O ions on the electronic states in the CuO₂ planes due to the lattice distortion or in-plane disorders. Fortunately, new family of high T_c superconductors, i.e. iron-based superconductors, was found in 2008 [2–7]. The iron-based superconductors also have a layer crystal structure and each unit cell contains two Fe ions (A and B) and two As (Te, Se) ions (A and B) (see figure 1). The high temperature superconductivity is originated in the electron pairing in the Fe–Fe plane by doping electrons or holes. The ligand As (Te, Se) ions A and B are located just below and above the center of each face of the Fe square lattice, respectively, rather than in the conducting plane. Such a crystal structure provides us an excellent platform for exploring the ligand effects on the electronic states, which can easily distinguish from the disorders in the conducting plane. Obviously, the impacts of As (Te, Se) ions A and B in the surface layer of the iron-based superconductors on the local density of states (LDOS) are inequivalent due to their different environments. It is known that the experimental results observed by both angle resolved photoemission spectroscopy (ARPES) and scanning tunneling microscopy (STM) contain unavoidably this kind of surface effect.

Zoom In Zoom Out Reset image size

In order to figure out the origin of high temperature superconductivity in iron-based superconductors, we first understand the role of the ligand As (Te, Se) ions. Recently, Li and Yin investigated the As vacancies on the surface of optimally electron-doped BaFe_2−xCo_xAs₂ by performing STM observations and found a pair of LDOS peaks within superconducting energy gap [8, 9]. In [10, 11], the dI/dV curves were measured around the Se vacancies in monolayer and crystalline FeSe superconductors. In this work, motivated by the interesting STM experiments, we study the influence of a single As (Te, Se) vacancy on the LDOS in the Fe–Fe plane by employing a two-orbit four-band tight binding model [12], which takes the asymmetric effect of the ligand As (Te, Se) ions in the surface Fe–As (Te, Se) layer into account. Such an empirical model can fit excellently the energy band structure of iron-based superconductors and its evolution with electron or hole doping measured by ARPES experiments [13–22]. This model also explained successful a series of STM experiments in iron-based superconductors, e.g. in-gap impurity bound states [12, 23], the negative energy resonance peak in the vortex core [24, 25], the 90° domain walls and anti-phase domain walls [26–29], the zero energy bound state induced by the interstitial excess Fe ions [30–32], etc, and especially repeated the phase diagram observed by nuclear magnetic resonance and neutron scattering experiments [33–35].

The Hamiltonian describing a single As (Te, Se) vacancy located at point $\left(0,\tfrac{1}{2}\right)$ in Fe sublattice B or $\left(-\tfrac{1}{2},0\right)$ in Fe sublattice A (see figure 1) can be written as H = H₀ + H_BCS + H_V, where H₀ is the two-orbit four-band tight binding model proposed in [12], H_BCS is the mean field BCS pairing Hamiltonian in the Fe–Fe plane, ${H}_{V}=U{\sum }_{\alpha ,\sigma }[{c}_{A,\alpha ,(0,0),\sigma }^{+}{c}_{A,\alpha ,(-\mathrm{1,0}),\sigma }+{c}_{B,\alpha ,(0,1),\sigma }^{+}{c}_{B,\alpha ,(\mathrm{0,0}),\sigma }+{\rm{h}}.{\rm{c}}.]$ $+\,W{\sum }_{\alpha ,\sigma }[{c}_{A,\alpha ,(0,0),\sigma }^{+}{c}_{A,1-\alpha ,(-\mathrm{1,0}),\sigma }$ $+\,{c}_{B,\alpha ,(0,1),\sigma }^{+}\times {c}_{B,1-\alpha ,(\mathrm{0,0}),\sigma }+{\rm{h}}.{\rm{c}}.]$, α = 0 and 1 represent the degenerate orbitals d_xz and d_yz, respectively, ${c}_{A(B),\alpha ,(i,j),\sigma }^{+}$ (c_{A(B), α, (i, j), σ}) creates (destroys) an α electron with spin $\sigma (=\uparrow$ or $\downarrow$) in the unit cell (i, j) of the Fe sublattice A (B), and U (W) is the local hopping correction between the same (different) orbitals due to the As (Te, Se) vacancy. Because a vacancy cannot mix d_xz orbital and d_yz orbital, we always have W = −t₄.

After introducing first the Fourier transformations ${c}_{A(B),\alpha ,(i,j),\sigma }=\tfrac{1}{\sqrt{N}}{\sum }_{k}{c}_{A(B),\alpha ,{\bf{k}},\sigma }{{\rm{e}}}^{{\rm{i}}({k}_{x}{x}_{i}+{k}_{y}{y}_{j})}$ with N the number of unit cells and the canonical transformations for ${c}_{A,\alpha ,{\bf{k}},\sigma }$ and ${c}_{B,\alpha ,{\bf{k}},\sigma }$, and then taking the Bogoliubov transformations for new fermion operators, we can solve exactly the Hamiltonian H for a single ligand vacancy in iron-based superconductors by using the T-matrix approach [12, 31, 36]. The analytic formulas for the Green's functions in momentum space have been derived. The LDOS on the Fe sites at different bias voltages and the Fourier component of LDOS (FCLDOS) can be obtained through the Green's functions. Here we have calculated a square Fe lattice with N = 500 × 500 unit cells, which is enough to ensure the accuracy of theoretical results. We have also employed the energy band parameters: t₁ = −0.5 eV, t₂ = −0.2 eV, t₃ = 1.0 eV, and t₄ = −0.02 eV, which are same with the previous works [12, 25, 28, 29, 31, 32, 35]. We note that the electron-doped BaFe_2−xCo_xAs₂ has a superconducting energy gap Δ₀ = 5.8 meV observed by the STM experiments [10, 11, 37]. After a lots of numerical calculations, we found that when U > 0.12 eV or U < −0.22 eV, the LDOS is negative at some bias voltages, which is unphysical. In other words, An As (Te, Se) vacancy can produce a local hopping modification in the interval [−0.22, 0.12] eV. This manifests that the ligand ions play an important role in forming high temperature superconductivity in iron-based superconductors.

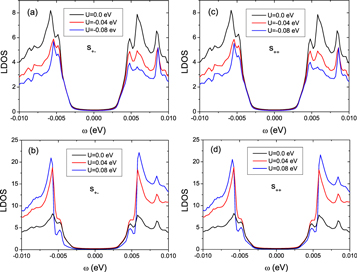
We plot the LDOS on the point (0,0) or (0,1) in the Fe sublattice B as a function of the bias voltage ω under different U and the optimal electron doping (15%) for the s₊₋ pairing symmetry ${{\rm{\Delta }}}_{{uv}{\bf{k}}}=\tfrac{1}{2}{{\rm{\Delta }}}_{0}({\rm{\cos }}{k}_{x}+{\rm{\cos }}{k}_{y})$ in figures 2(a) and (b) and the s₊₊ pairing symmetry ${{\rm{\Delta }}}_{{uv}{\bf{k}}}=\tfrac{1}{2}{{\rm{\Delta }}}_{0}| {\rm{\cos }}{k}_{x}+{\rm{\cos }}{k}_{y}|$ in figures 2(c) and (d), respectively. Here, u = 0 (1) represents the Fermi surfaces around M (Γ) point while v = 0 (1) denotes the outer (inner) Fermi surfaces around M or (Γ) point [12]. Obviously, the curves of the LDOS for the s₊₋ pairing symmetry coincide completely with those for the s₊₊ pairing symmetry when all the other parameters are fixed. Two resonance peaks exhibit in the LDOS at ω = ±4.8 meV and their locations do not move with increasing U. These results agree well the recent STM observations [10, 11]. However, even if U = 0, two resonance peaks still stand there. This means that the hybridization among Fe d and As (Te, Se) p orbitals cannot be neglected. When U < 0, with decreasing U, the superconducting coherence peaks and the resonance peaks are suppressed, and their heights at positive bias voltages become lower than those at negative bias voltages. It is quite obvious that the resonance peak is higher than the coherence peak at the positive energy side for enough small U (see figure 2(a)). If U > 0, with increasing U, the superconducting coherence peaks grow up, but the resonance peaks first become higher, then become lower. However, the coherence peaks and the resonance peaks are symmetric with respect to the bias voltage in figure 2(b). We note that the in-gap resonance peaks is irrelative to the phase of the superconducting order parameter, similar to those induced by interstitial excess Fe impurities in iron-based superconductor Fe(Te, Se) [30–32].Therefore, very different from nonmagnetic impurities on the Fe sites [12], such a ligand vacancy cannot be used to distinguish the s₊₋ and s₊₊ pairing symmetries.

Zoom In Zoom Out Reset image size

Figure 3 shows the LDOS images at different U and ω under optimal electron doping for the s₊₋ pairing symmetry in the Fe sublattice B with 31 × 31 sites due to quasiparticle interference. The As (Te, Se) vacancy is located at the point $\left(0,\tfrac{1}{2}\right)$. Because up As (Te, Se) and down As (Te, Se) are inequivalent in the surface layer, all the LDOS images have a C₂ symmetry. Obviously, the LDOS on the points (0, 0) and (0, 1) has a maximum (minimum) value for U > 0 (<0). Hence we can judge that the As (Te, Se) vacancy is attractive or repulsive according to the extreme value of the LDOS on the nearest neighboring Fe sites around it. When U = −30.0 meV, the LDOS has 0^◦ modulation at ω = 2.0 meV in figure 3(a). With increasing ω, both 0° and 45° stripes show up in figure 3(b). If U = 30.0 meV, the real space LDOS also possesses energy-dependent modulations along both 0° and 45° directions at ω = 2.0 and 4.8 meV (see figures 3(c) and (d)).

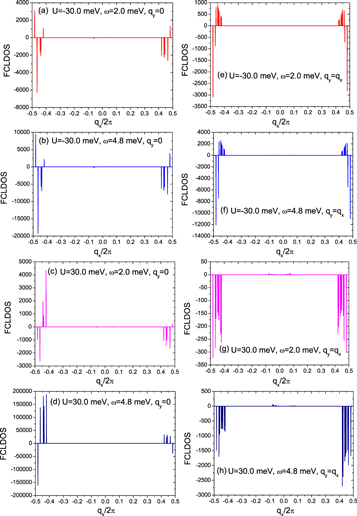
Zoom In Zoom Out Reset image size

To understand the origin of the LDOS modulations produced by quasiparticle interference and the modulation periods, we have obtained the FCLDOS at different U and ω. Figures 4(a)–(d) and (e)–(h) exhibit the modulation wave vectors and their intensities along 0° and 45° directions, respectively, corresponding to the real space LDOS images in figure 3. It is very interesting that all the modulation wave vectors are independent of U and ω. Therefore, the energy-dependent charge modulations are due to the variations of the FCLDOS intensities at the modulation wave vectors with energy. Comparing carefully figures 4(e)–(h) with figures 4(a)–(d), we can see clearly that the modulation wave vectors along 0° direction are nothing but the x components of those along 45° direction. The magnitudes of the modulation wave vectors along 45° direction mainly distribute in the range of $0.84\sqrt{2}\pi \sim 0.97\sqrt{2}\pi$. Because the single vacancy is not located at the center of the Fe sublattice B, the modulation wave vectors have fine structures with double lines, which are never reported. Obviously, this quasiparticle interference phenomenon is different from that in the cuprate superconductors, where the charge modulation wave vectors shift with the bias voltage, and their change trends along 0° (antinodal) and 45° (nodal) directions are just opposite with increasing energy [38–40].

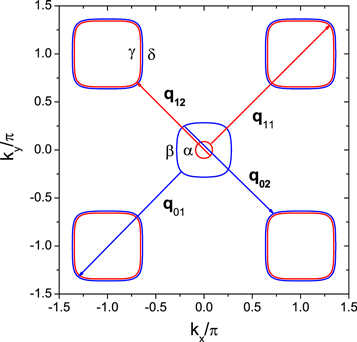
Zoom In Zoom Out Reset image size

Now we determine the modulation wave vectors in the LDOS images. Figure 5 depicts two hole Fermi surfaces (i.e. α band with u = v = 1 and β band with u = 1 and v = 0) around Γ point and two electron Fermi surfaces (i.e. γ band with u = 0 and v = 1 and δ band with u = v = 0) around M point of iron-based superconductors at optimal electron doping [12]. According to the analytic expression of the Green's function or the LDOS, we found that the interband transition is only allowed for those bands with the same index v. In figure 5, q_0τ (q_1τ) (τ = 1 and 2) represent the allowed nesting vectors connecting to two outer (inner) Fermi surfaces around Γ and M points, and $| {{\bf{q}}}_{11}| \gt | {{\bf{q}}}_{01}| \gt | {{\bf{q}}}_{02}| \gt | {{\bf{q}}}_{12}|$. We analyze in detail the numerical values of the modulation wave vectors in figure 4 and the nesting vectors in figure 5, and conclude firmly that the nesting vectors q_vτ and their vector differences q_v1 − q_v2 are nothing but the modulation wave vectors in the LDOS images.

Zoom In Zoom Out Reset image size

In summary, we have explored the impact of a single As (Te, Se) vacancy on the electronic states in iron-based superconductors. The ligand vacancy can induce two robust resonance peaks in the superconducting energy gap at the fixed symmetric positions about zero energy, which are consistent with the STM experiments. The resonance peaks are independent of the phase of the superconducting order parameter in the bulk, similar to zero energy bound state produced by the interstitial Fe ions. Because a magnetic field that is not too strong changes predominately the phase of the superconducting order parameter, we predict that these two bound states keep unchanged with increasing magnetic field strength, which could be detected by STM experiments. The energy-dependent LDOS images possess 0° and 45° stripes with multiple periods. The modulation wave vectors come from the nesting vectors of the Fermi surfaces, which are independent of the local hoping correction and the bias voltage. The quasiparticle interference patterns induced by As (Te, Se) vacancies are undoubtedly originated in the nesting effect in iron-based superconductors.

Acknowledgments