Abstract
We study the effectiveness of quantum error correction against coherent noise. Coherent errors (for example, unitary noise) can interfere constructively, so that in some cases the average infidelity of a quantum circuit subjected to coherent errors may increase quadratically with the circuit size; in contrast, when errors are incoherent (for example, depolarizing noise), the average infidelity increases at worst linearly with circuit size. We consider the performance of quantum stabilizer codes against a noise model in which a unitary rotation is applied to each qubit, where the axes and angles of rotation are nearly the same for all qubits. In particular, we show that for the toric code subject to such independent coherent noise, and for minimal-weight decoding, the logical channel after error correction becomes increasingly incoherent as the length of the code increases, provided the noise strength decays inversely with the code distance. A similar conclusion holds for weakly correlated coherent noise. Our methods can also be used for analyzing the performance of other codes and fault-tolerant protocols against coherent noise. However, our result does not show that the coherence of the logical channel is suppressed in the more physically relevant case where the noise strength is held constant as the code block grows, and we recount the difficulties that prevented us from extending the result to that case. Nevertheless our work supports the idea that fault-tolerant quantum computing schemes will work effectively against coherent noise, providing encouraging news for quantum hardware builders who worry about the damaging effects of control errors and coherent interactions with the environment.
Export citation and abstract BibTeX RIS
1. Introduction
Although there is no rigorous proof, much evidence supports the widely held belief that an ideal noiseless quantum computer would be able to solve problems that are intractable for classical digital computers. But in the real world, quantum computers are noisy. We therefore expect that quantum error correction will be needed to overcome the noise and reliably operate a large-scale quantum computer that can solve hard problems. Fortunately, the accuracy threshold theorem for quantum computation establishes that quantum computing is scalable, assuming that the noise is neither too strong nor too strongly correlated [1–5].
Until we try it on a real device, though, we will not know for sure whether realistic noise is sufficiently benign for quantum error correction to work effectively. A general noise channel acting on n qubits is extremely complex when n is large, so it will not be practical to fully characterize the noise in a complex quantum device using any feasible experimental protocol. A commonly used metric for the performance of single-qubit and two-qubit quantum gates is the 'average infidelity' r = 1 − F, where F is the fidelity of the output from the gate relative to the output of an ideal gate, averaged uniformly over all possible input states. This quantity r has the great virtue that it can be feasibly measured using randomized benchmarking [6, 7], but as a characterization of the noise strength it has shortcomings. Assuming an uncorrelated noise model, threshold theorems guarantee scalability if a different metric, the diamond distance D◊, is less than a critical value. Here D◊ denotes the deviation of the noisy gate from the ideal gate as measured by the diamond norm. For an incoherent noise channel like a Pauli channel, the diamond distance D◊ is equal to the average infidelity r; in contrast, for a highly coherent channel, D◊ scales like the square root of r. If we know only r, and have no information about the coherence of the noise, we cannot estimate D◊ accurately, and therefore cannot easily make sound predictions about how effectively any error-correcting code will combat the noise [8–10]. The situation is even worse for correlated noise models.
Our purpose in this paper is to study further how well quantum error correction performs against coherent noise models. To make our analysis manageable, we will make some simplifying assumptions. For one, we will not actually consider quantum computation, but instead will focus on the easier task of operating a quantum memory. We envision encoding a quantum state in the memory using a quantum code; after the encoding step the memory is subjected to noise, and then the quantum state is decoded. As a further simplification, we will assume that the encoding and decoding are noiseless. Therefore, the performance of the code against the noise is captured by a logical channel, the result of composing the encoding channel, noise channel, and decoding channel.
We will be interested in what happens to a quantum state which is stored in the memory for a long time, and undergoes many rounds of error correction—that is, we want to characterize the effect of applying the logical channel many times in succession. For this purpose, we will need to understand the coherence properties of the logical channel. If the logical channel is incoherent, then the diamond distance of the decoded state from the ideal state grows linearly with the number of channel repetitions, while for a highly coherent logical channel, it can grow quadratically. Our main conclusion is that, even if the physical noise acting on the quantum memory is highly coherent, the coherence of the logical channel becomes strongly suppressed as the block length of the quantum error-correcting code increases, assuming that the noise is sufficiently weak and sufficiently weakly correlated.
Although we can analyze the logical channel only in a simplified setting, and only for particular code families, we believe that the lessons learned apply more broadly. We expect, for example, that randomized benchmarking applied to logical gates will accurately characterize logical noise even when the physical noise is highly coherent, at least for large code blocks. This also suggests that for concatenated coding schemes, in which the 'physical' qubits of a higher-level code are themselves the logical qubits of a lower-level code, the average infidelity of the lower-level code should be a good predictor for the performance of the higher-level code.
Our main conclusion is not unanticipated [4], as the suppression of coherence in the logical channel has an intuitive explanation. To decode, one measures the error syndrome, and then applies a recovery operation conditioned on the syndrome. For a large code, many different syndromes are possible, and only the errors which are projected onto the same syndrome value can interfere constructively, while errors projected onto different syndrome values add stochastically. The stochastic average over many syndrome sectors suppresses coherence, leaving only small residual coherent effects arising from summing coherently over errors which are projected onto a given syndrome sector. That said, carefully analyzing the residual coherence in the logical channel involves daunting combinatorics. It turns out that further cancellations occur, resulting in even stronger suppression of logical coherence than might be naively expected.
This discussion about averaging over all syndrome sectors highlights an important issue. We will consider the logical channel obtained by averaging over error syndromes, and then study the coherence of the resulting channel. One could make a case for an alternative procedure: define a metric that characterizes coherence, evaluate that metric for the logical channel conditioned on each syndrome, and then average the value of the metric over syndromes by weighting each syndrome with its probability. To argue in favor of this alternative procedure one might note that the experimentalist who executes the error correction protocol could know the syndrome she measures in each run of the protocol, and might be interested in the properties of the logical channel conditioned on that knowledge [11]. Our view is that properties of logical channels conditioned on the syndrome are potentially of interest for near-term experiments using relatively small codes, particularly because it might be feasible to postselect by retaining favorable syndromes and rejecting unfavorable ones. In future experiments using larger codes, though, syndrome histories will be quite complex, and it will be impractical to make useful inferences about the logical channel conditioned on syndrome information. For long computations using large codes, properties of the logical channel averaged over syndromes will most likely provide more usable guidance regarding the features of the protected quantum computation.
We should also note that methods have been proposed to suppress the coherence of physical noise. One such method is randomized compiling, which, under certain assumptions, can transform any single-qubit noise channel into an incoherent depolarizing channel [12]. The assumptions include a Markovian noise model and gate independence of the noise for the 'easy' gates in the scheme. These assumptions may hold to a good approximation for some realistic cases, but they will not hold exactly. We may then ask how the residual coherence is affected by error correction, an issue that can be addressed using the methods in this paper. Other schemes for mitigating coherent noise have been proposed in [13–16]. These papers focus on the strength of the logical noise, whereas we study the character of the logical noise channel, specifically its degree of coherence.
Here we investigate the coherence of the logical channel in the case where the physical noise is fully coherent unitary noise. This problem has been previously studied [17–19], and we discuss this related work in section 1.3 below. Our work improves on these past results in that we consider a family of codes with an accuracy threshold (toric codes without boundaries) and prove bounds on the logical coherence which apply in the limit of a large code block. By specializing to a particular code family, we also find better bounds on the logical coherence for finite code length. Other authors have obtained numerical results for sufficiently small codes in the case where all physical qubits are rotated about a fixed axis [20–22], including analyses of logical channels conditioned on particular error syndromes [11]. We focus instead on investigating asymptotic properties for large codes, using analytic methods. Some asymptotic statements about the performance of concatenated codes were proven in [23].
In our analysis we make extensive use of the chi-matrix formalism for describing quantum channels. The chi matrix arises when the action of a channel on an input density operator is expanded in terms of Pauli operators (tensor products of 2 × 2 Pauli matrices) acting on the density operator from the left and from the right. A channel can be expressed as the sum of an 'incoherent part' in which the Pauli operators on left and right are equal, and a 'coherent part' in which the Pauli operators on left and right are distinct. Our main task will be to infer, in the case of stabilizer codes, how the logical chi matrix which describes the logical channel after error correction is related to the physical chi matrix which describes the noise acting on physical qubits.
Specifically, we study the logical channel for the toric code on an L × L lattice where L is large, and where error correction is carried out using minimal-weight decoding. We estimate the coherent component of the logical chi matrix up to order L + 2ζ in the rotation angle θ, where ζ is any L-independent constant, and relate this coherent component to the incoherent component of the logical channel. Our main theorem states that the strength of the coherent part of the logical channel is bounded above by strength of the incoherent part times a factor of 1/θ. (Here θ is the rotation angle applied to each of the physical qubits—our result also holds for rotation angles and axes that vary somewhat from qubit to qubit.) From this statement, we may infer that when the logical channel is applied m times in succession, the average infidelity grows linearly with m. (There is a small contribution to the infidelity that grows quadratically with m, but this contribution is highly suppressed by a factor that scales as L−L.) Stated differently, our result says that after m applications of the logical channel, the accumulated distance from the identity channel, as measured by the diamond norm, grows linearly with m, apart from a correction which is negligible for large L. We emphasize that to reach this conclusion we assumed that the rotation angle θ scales with the block size as 1/L. Therefore, unfortunately, we are not able to make a definitive statement about the coherence of the logical channel in the more physically relevant case where L becomes large with θ fixed; the combinatoric task required exceeded our ability.
A related conclusion holds for a broad class of correlated noise models. We provide a detailed analysis of correlated noise for the simpler case of the quantum repetition code, under the assumption that the noise Hamiltonian commutes with the Pauli operator X acting on each qubit, so that the repetition code provides effective protection against the noise model. In a model in which the rotations acting on pairs of qubits are strongly correlated, we find as expected that the correlations significantly enhance the probability of an uncorrectable logical error. However, the correlations enhance the coherent and incoherent parts of the logical chi matrix by comparable factors. Therefore, our conclusion that the coherence of the logical channel is heavily suppressed in the limit of large code length continues to apply despite the strong pairwise correlations in the noise.
1.1. Summary of the paper
The rest of this paper is organized as follows. In section 1.2 we present an overview of the proof of our main theorem, and in section 1.3 we compare our results to related work by previous authors. Section 2 is a self-contained review of quantum channels, emphasizing metrics for characterizing coherence and relations among them. In particular, we prove a relationship between the chi matrix and the Pauli transfer matrix which had not been previously discussed to our knowledge. In section 3 we compute the logical channel for the repetition code assuming independent unitary noise, finding that the coherence of the logical channel becomes strongly suppressed as the code length increases. Then in section 4 we analyze the repetition code again, this time using the chi-matrix formalism; we find that this analysis can be extended more easily to other stabilizer codes and other noise models. We consider the performance of the repetition code against two-body correlated noise in section 5, again concluding that the logical noise becomes incoherent in the limit of large code length.
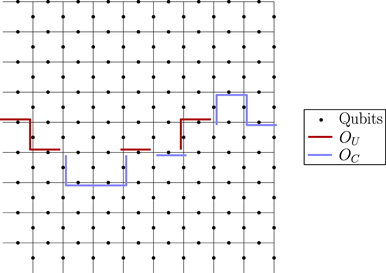
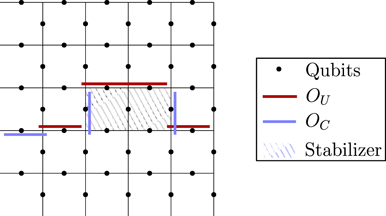
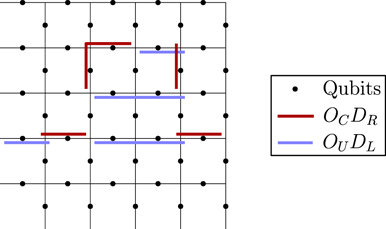
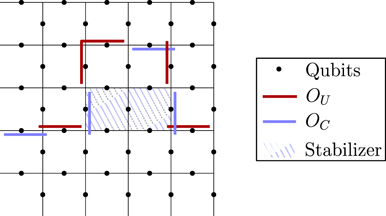
The heart of the paper is section 6, where we build on lessons learned from the analysis of the repetition code to prove our main result, which asserts that, for an independent unitary noise model, the coherence of the logical channel is strongly suppressed by the toric code when the code block is large, assuming that the noise strength scales like 1/L. The proof mainly consists of a combinatoric analysis which allows us to estimate the coherent and incoherent components of the logical chi matrix. We have divided the proof into a series of lemmas; figure 1 indicates how these lemmas fit together to build our main theorem, and section 1.2 provides further guidance concerning the structure of the proof. Furthermore, our analysis of two-body correlated noise in the repetition code can be extended to the toric code assuming the noise is sufficiently weak for error correction to succeed with high probability; we therefore conclude that the coherence of the logical channel is highly suppressed even in the case of strongly correlated two-body noise.
Figure 1. How the different parts of this paper fit together to build our main result, theorem 3 in section 6.13. See section 1.2 for further details.
Download figure:
Standard image High-resolution imageSection 7 contains our conclusions. There we recount some of the obstacles that prevented us from extending our main theorem to the more physically relevant case where the noise strength is a constant independent of L.
1.2. Overview of the proof of theorem 3
Here we provide some additional guidance regarding how the different parts of this paper fit together to build our main result, theorem 3 in section 6.13. The structure of our argument is also summarized in figure 1.
As already noted, we study the logical channel acting on the code's protected qubits by deriving the chi matrix of this logical channel from the chi matrix of the noise channel acting on the physical qubits. To interpret the meaning of the logical chi matrix, we find it convenient to relate the chi matrix to another formalism for describing quantum channels—the Pauli transfer matrix. We explain some properties of the Pauli transfer matrix N of a channel 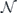 in section 2, relating N to the diamond distance
in section 2, relating N to the diamond distance 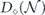 in equation (51) and to the average infidelity rm of the m-times repeated channel
in equation (51) and to the average infidelity rm of the m-times repeated channel 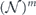 in equations (41) and (44). Using lemma 1, these expressions for the diamond distance and the average infidelity in terms of the Pauli transfer matrix can be restated in terms of the chi matrix.
in equations (41) and (44). Using lemma 1, these expressions for the diamond distance and the average infidelity in terms of the Pauli transfer matrix can be restated in terms of the chi matrix.
In section 3 we study the performance of the quantum repetition code against coherent noise, and prove theorem 1 using explicit computation of the logical channel combined with results derived in section 2. This result shows that the logical channel is highly incoherent when the code block is large. An alternative proof of theorem 1, making essential use of the chi matrix, is presented in section 4, where we develop the key tools needed for the proof of theorem 3. We also prove lemma 2, which is used to show that, for independent unitary noise acting on the physical qubits, the coherence of the logical channel for the repetition code is maximized when all qubits are rotated by the same angle. A similar idea can be adapted for analyzing the coherence of the logical channel for the toric code.
In section 5, we extend the analysis of the repetition code to the case of two-body correlated coherent noise, culminating in the proof of theorem 2, showing that the coherence of the logical channel is heavily suppressed in this case as well. The proof is a computation of the logical channel for this case, achieved by a detailed combinatoric analysis. As expected, the noise correlations enhance the probability of a decoding error, but it turns out that both the coherent and incoherent parts of the logical channel are enhanced, so that the relationship between the two is not changed much compared to the case of uncorrelated coherent noise. The same reasoning used to prove theorem 2 can also be applied to the toric code to show that, in that case as well, two-body correlations in the noise do not enhance the coherence of the logical channel.
Our analysis of the performance of the toric code against coherent noise, culminating in the proof of theorem 3, is in section 6. To prove the theorem we compute first the coherent part of the logical channel, and then the incoherent part, after which we can make an inference about how the two are related. For this purpose, upper bounds on the logical noise strength would not suffice. Instead, we compute both the coherent and incoherent part of the logical channel up to an error which we show is small if the physical noise is sufficiently weak.
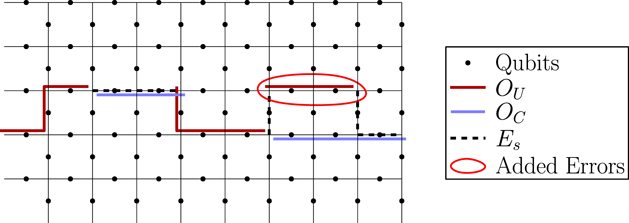
Our arguments in section 6 make use of observations, discussed in section 4, which apply to any stabilizer code. We may assign a 'standard error' Es to each error syndrome s, and define a decoder which returns the damaged state to the code space by applying 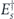 when the syndrome is measured to be s. This Es is a Pauli operator acting on the code block. Furthermore, each logical Pauli operator
when the syndrome is measured to be s. This Es is a Pauli operator acting on the code block. Furthermore, each logical Pauli operator 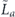 acting on the code may by convention be associated with a particular standard physical Pauli operator La—the choice of La is not unique, and therefore must be fixed by convention, because we have the freedom to multiply La by an element of the code's stabilizer group without changing its logical action. Once the standard error for each syndrome, and the physical Pauli operator corresponding to each logical Pauli operator, are determined, any physical Pauli operator acting on the code block has a unique decomposition of the form (up to a phase factor) σ(s, a, x) = EsLaGx, where Es is a standard error, La is a standard logical Pauli operator, and Gx is an element of the code stabilizer.
acting on the code may by convention be associated with a particular standard physical Pauli operator La—the choice of La is not unique, and therefore must be fixed by convention, because we have the freedom to multiply La by an element of the code's stabilizer group without changing its logical action. Once the standard error for each syndrome, and the physical Pauli operator corresponding to each logical Pauli operator, are determined, any physical Pauli operator acting on the code block has a unique decomposition of the form (up to a phase factor) σ(s, a, x) = EsLaGx, where Es is a standard error, La is a standard logical Pauli operator, and Gx is an element of the code stabilizer.
In the chi matrix formalism, the result 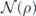 of applying noisy channel
of applying noisy channel 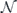 to density operator ρ is expanded as a sum of terms of the form σ(s, a, x) ρ σ(s',a',x')†. As explained in section 4.2, if ρ is a logical density operator, then a term of this form is annihilated by the error recovery operation for s ≠ s', and for s = s' is mapped to
to density operator ρ is expanded as a sum of terms of the form σ(s, a, x) ρ σ(s',a',x')†. As explained in section 4.2, if ρ is a logical density operator, then a term of this form is annihilated by the error recovery operation for s ≠ s', and for s = s' is mapped to 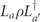 , up to a phase. (That phase is important, and we will need to keep track of it carefully.) Recovery is successful if La and La' are both logical identity operators. The terms in the logical channel with La = La' are said to be incoherent, and the terms with La ≠ La' are said to be coherent.
, up to a phase. (That phase is important, and we will need to keep track of it carefully.) Recovery is successful if La and La' are both logical identity operators. The terms in the logical channel with La = La' are said to be incoherent, and the terms with La ≠ La' are said to be coherent.
The key point is that we have a conceptually simple algorithm for computing the chi matrix for the logical channel, and for identifying its coherent and incoherent parts. To find the coefficient of 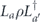 in the logical channel, we just need to sum up the coefficients of all terms in the physical chi matrix of the form σ(s, a, x) ρ σ(s,a',x')†, being mindful of phase factors, for all possible values of s, x, x'. Unfortunately, in general this algorithm is too complex to carry out in practice, but under suitable conditions we can estimate logical chi matrix with sufficient accuracy for our purposes.
in the logical channel, we just need to sum up the coefficients of all terms in the physical chi matrix of the form σ(s, a, x) ρ σ(s,a',x')†, being mindful of phase factors, for all possible values of s, x, x'. Unfortunately, in general this algorithm is too complex to carry out in practice, but under suitable conditions we can estimate logical chi matrix with sufficient accuracy for our purposes.
For the case of the toric code, we can begin by noting some helpful simplifications. We choose standard errors defined by minimal-weight decoding. Because of the code's CSS structure, we can analyze the logical X and logical Z errors separately, and in fact a single analysis applies to errors of both types. We do not need to worry about logical Y errors or about logical errors acting nontrivially on more than one of the code's logical qubits (lemma 14 in appendix 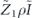 term and the incoherent term
term and the incoherent term 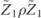 , where
, where 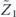 denotes the logical Z operator acting on one of the code's two encoded qubits. In the proof of theorem 3, we estimate both quantities using a series of approximations, and verify that these approximations are trustworthy when the physical noise is sufficiently weak.
denotes the logical Z operator acting on one of the code's two encoded qubits. In the proof of theorem 3, we estimate both quantities using a series of approximations, and verify that these approximations are trustworthy when the physical noise is sufficiently weak.
First consider the coherent part of the logical chi matrix. We need to sum up all the terms in the physical chi matrix which contribute to 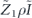 after the action of the decoding map. Each such term has the form
after the action of the decoding map. Each such term has the form 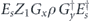 , where Es denotes a standard correctable Pauli error, Gx and Gy are Pauli operators in the code stabilizer, and Z1 is the standard physical Pauli operator whose logical action matches
, where Es denotes a standard correctable Pauli error, Gx and Gy are Pauli operators in the code stabilizer, and Z1 is the standard physical Pauli operator whose logical action matches 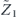 . For the purpose of our computation, we may assume that all the Pauli operators are of the Z type—that is, each applies Z to a subset of the qubits and applies I to the complementary set. For the purpose of enumerating all such contributions, it is convenient to note that the product
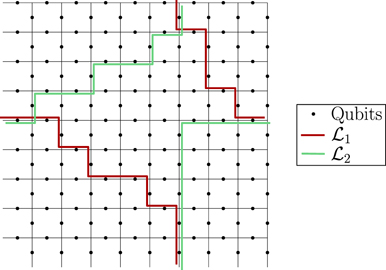
. For the purpose of our computation, we may assume that all the Pauli operators are of the Z type—that is, each applies Z to a subset of the qubits and applies I to the complementary set. For the purpose of enumerating all such contributions, it is convenient to note that the product 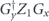 of the Pauli operators acting on the density operator from the right and from the left is a logical operator, one commuting with the code stabilizer. This logical operator can be decomposed into a connected path that winds once around on the periodically identified square lattice—what we call a 'logical string'—and a collection of homologically trivial closed loops on the lattice—what we call the 'disconnected part' of the logical Pauli operator.
of the Pauli operators acting on the density operator from the right and from the left is a logical operator, one commuting with the code stabilizer. This logical operator can be decomposed into a connected path that winds once around on the periodically identified square lattice—what we call a 'logical string'—and a collection of homologically trivial closed loops on the lattice—what we call the 'disconnected part' of the logical Pauli operator.
We can therefore enumerate all the contributions to 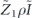 by this procedure: (1) consider all possible logical strings. (2) For each logical string, consider all possible 'partitions' of that string into an uncorrectable error acting from the left and a correctable error acting from the right. (3) For each logical string and partition, consider all possible choices for the disconnected part. We compute
by this procedure: (1) consider all possible logical strings. (2) For each logical string, consider all possible 'partitions' of that string into an uncorrectable error acting from the left and a correctable error acting from the right. (3) For each logical string and partition, consider all possible choices for the disconnected part. We compute 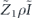 by summing all these contributions. Though we cannot perform this sum exactly, we can approximate the sum and estimate the resulting errors.
by summing all these contributions. Though we cannot perform this sum exactly, we can approximate the sum and estimate the resulting errors.
It is for the purpose of approximating this sum that we need the assumption that the rotation angle θ scales like 1/L, where L is the linear system size. Under this assumption, we show that we make a small error by truncating the sum to include only relatively short logical strings (lemma 3 in section 6.5) which have a typical shape (lemmas 9 and 10 in appendix
For a fixed connected logical string and partition of that string, we need to sum over disconnected closed loops and partitions of those loops. Performing this sum is almost equivalent to adding up all possible error patterns weighted by their probabilities, which trivially sums to unity. The only complication is that, for some closed loops that closely approach the logical string, and for some special partitions, the additional loop can flip how the error is decoded. It turns out, though, that we make only a small error by ignoring this effect (lemma 11 in appendix
With all the above simplifications in hand, we can estimate the coherent part of the logical chi matrix. In particular, the sum over partitions for a fixed logical string can be evaluated much as in the proof of theorem 1 for the repetition code. It then remains to estimate the incoherent part and compare the two.
In the incoherent part, 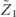 acts from both the left and the right; therefore, there are two logical strings to keep track of, one on each side. These two logical strings have segments in common, determined by the intersection of the string with the standard error, but are free to fluctuate independently away from those segments (figure 10 of section 6.8). To approximate the sum over contributions from these logical strings to the incoherent part of the logical chi matrix, we may truncate the sum as in the computation of the coherent part, limiting our attention to relatively short strings with a typical shape (lemma 5 in section 6.8 and lemma 6 in section 6.9), and ignoring complications arising from the disconnected part of the error (lemma 12 in appendix
acts from both the left and the right; therefore, there are two logical strings to keep track of, one on each side. These two logical strings have segments in common, determined by the intersection of the string with the standard error, but are free to fluctuate independently away from those segments (figure 10 of section 6.8). To approximate the sum over contributions from these logical strings to the incoherent part of the logical chi matrix, we may truncate the sum as in the computation of the coherent part, limiting our attention to relatively short strings with a typical shape (lemma 5 in section 6.8 and lemma 6 in section 6.9), and ignoring complications arising from the disconnected part of the error (lemma 12 in appendix
As for the repetition code, we can justify considering unitary noise such that all physical qubits are rotated by the same angle—rotating different qubits by different angles only makes the logical channel less coherent (lemma 8 in section 6.11). For such a coherent noise model with uniform rotation angles, we compare the coherent and incoherent parts of the logical chi matrix, proving theorem 3 (section 6.13). Using the findings from section 2, these results can be translated into statements about the diamond distance of the logical channel and about the average infidelity of the m-times repeated logical channel. We also observe (section 6.12), that our analysis of the performance of the repetition code against two-body correlated coherent noise (theorem 2) is applicable with few modifications to the toric code as well.
Our conclusion that the coherence of the logical channel is heavily suppressed applies in the limit of large code size L, and under the assumption that the physical qubits are rotated by an angle θ scaling like 1/L. In Section 7 we discuss the difficulties that have prevented us from extending the result to larger values of θ.
1.3. Related work
The performance of stabilizer codes against fully coherent unitary noise has been previously studied in [17–19]. Huang, Doherty, and Flammia [18] derived an inequality which relates the diamond distance D◊ of the logical channel from the identity to the rotation angle θ for independent unitary noise, finding
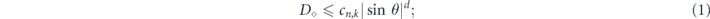
here d is the code distance, n is the code length, and k is the number of encoded qubits. Their result applies to any stabilizer code, but cn,k grows exponentially with n (it is bounded above by 23n+k+1), so their result is not very informative for large codes. In contrast, we derive a bound relating the coherent and incoherent components of the logical channel which does not involve any exponentially large factors. We achieve this improved result by specializing to the toric code, and by assuming sin θ < 1/L. Furthermore, to obtain equation (1) the authors of [18] bounded a sum of contributions to the logical channel using the triangle inequality, hence obtaining a bound that would apply even if all the terms in the sum had a common phase. Instead, we sum the contributions with the appropriate phases; the resulting cancellations among terms yield a much smaller result than we would have obtained by merely invoking the triangle inequality. We are able to carry out this more detailed analysis because our assumption sin θ < 1/L allows us to restrict our attention to short logical strings, for which approximating the sum becomes a manageable task.
Beale, Wallman, Guttiérrez, Brown, and Laflamme [19] also studied the performance of stabilizer codes against independent unitary noise, and they concluded that the coherence of the logical channel is suppressed. For a fixed code length, they study the limit of small rotation angle θ. If the logical channel is expanded in powers of θ, then for sufficiently small θ the leading term in this expansion dominates, and they draw their conclusions by analyzing this leading term. In effect, they (like us) investigate the case in which the noise strength deceases as the code length increases, but their assumption about the noise strength is much stronger than ours. We (unlike them) include all corrections to the logical channel higher order in θ that are needed to accurately approximate the logical channels for sin θ < 1/L, albeit only for the special case of the toric code.
Bravyi, Engelbrecht, König, and Peard [21] have studied the performance of the toric code against independent unitary noise numerically, using a clever mapping from qubits to Majorana fermions, for code distance up to d = 37, and they found that the coherence of the logical channel becomes negligible as the code length increases, provided that the rotation angle θ is smaller than a nonzero constant threshold value θ0. Their numerical method applies to a noise model in which all qubits are rotated about the Z axis, which according to our analysis is the worst case that maximizes the coherence of the logical channel. The numerical results support a value of θ0 greater than 0.25 and less than 0.32, while for the largest code sizes they consider our analytic results apply only for θ less than about 0.027. They characterize the coherence of the logical channel by sampling from the distribution governing the logical rotation angle θlogical conditioned on the measured error syndrome, finding that this distribution becomes strongly peaked around θlogical = 0 for large code length when θphysical is smaller than θ0. They also consider, as we do, the logical channel averaged over syndromes, and show that the 'twirled' logical channel has an error probability close to the error probability of the untwirled logical channel for large code length, a further indication of suppressed logical coherence. Their numerical findings appear to be at least notionally consistent with our analytic results, though it is difficult to make a quantitative comparison because our formulas are accurate only for asymptotically large L and for L sin θ sufficiently small compared to 1.
2. Channel parameters
2.1. Pauli transfer matrix
We will use the Pauli transfer matrix representation to describe channels acting on n qubits. For this purpose we expand the density operator ρ in the Pauli operator basis {σi}:
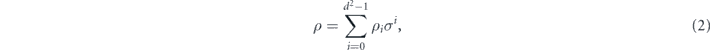
where
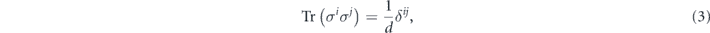
and σ0 = (id)/d. Here d = 2n is the Hilbert-space dimension, and id denotes the d × d identity matrix. Note that Tr(ρ) = ρ0. A linear map  acting on density operators defines a d2 × d2 matrix (the Pauli transfer matrix associated with
acting on density operators defines a d2 × d2 matrix (the Pauli transfer matrix associated with  ) according to
) according to
This matrix is real if 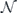 maps Hermitian operators to Hermitian operators. If the map
maps Hermitian operators to Hermitian operators. If the map  is trace preserving, then ∑iN0iρi = ρ0; hence N0i = δ0i. If the map
is trace preserving, then ∑iN0iρi = ρ0; hence N0i = δ0i. If the map  is unital (that is,
is unital (that is,  ), then ∑iNijδj0 = δi0; hence Ni0 = δi0. Thus the matrix representing the map
), then ∑iNijδj0 = δi0; hence Ni0 = δi0. Thus the matrix representing the map  may be expressed as
may be expressed as
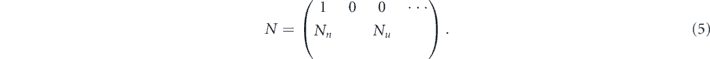
We say that the (d2 − 1) × (d2 − 1) matrix Nu is the unital part of 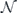 and that the length-(d2 − 1) vector Nn is its nonunital part. Altogether the trace-preserving map
and that the length-(d2 − 1) vector Nn is its nonunital part. Altogether the trace-preserving map 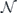 is specified by d2(d2 − 1) parameters.
is specified by d2(d2 − 1) parameters.
For a unitary map  , we have Nn = 0 and (for i ≠ 0)
, we have Nn = 0 and (for i ≠ 0)
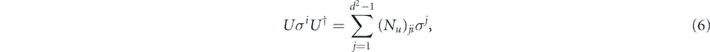
where
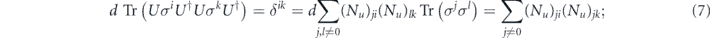
hence Nu is an orthogonal matrix.
The matrix representing  is diagonal if and only if the map is a convex sum of Pauli operators
is diagonal if and only if the map is a convex sum of Pauli operators
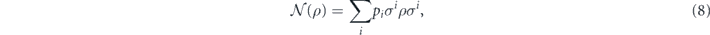
in which case the diagonal entries are
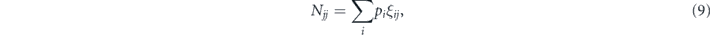
where σiσj = ξijσjσi; that is, ξij is the sign ±1 determined by whether the Pauli operators σi and σj commute or anticommute.
2.2. Average infidelity
The fidelity F of a channel 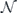 acting on a pure state |ψ⟩ is defined by
acting on a pure state |ψ⟩ is defined by
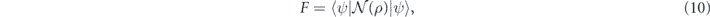
and 1 − F is called the infidelity. The average infidelity r of 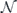 is
is
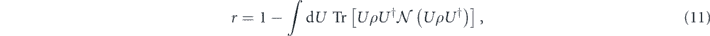
where the integral is with respect to the normalized invariant Haar measure on the unitary group, and ρ is any pure state. Equivalently, r is the infidelity of the averaged channel
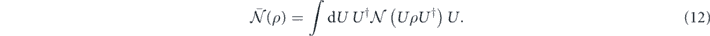
We may just as well define r as the infidelity of 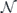 averaged over a unitary two-design. Hence r can be measured in randomized benchmarking experiments, in which U is chosen by sampling uniformly from the Clifford group, which is a unitary two-design.
averaged over a unitary two-design. Hence r can be measured in randomized benchmarking experiments, in which U is chosen by sampling uniformly from the Clifford group, which is a unitary two-design.
The d × d unitary matrix U defines an orthogonal (d2 − 1) × (d2 − 1) matrix Nu = O according to
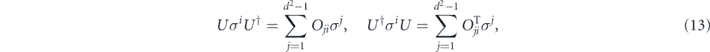
where OT denotes the transpose of O; therefore
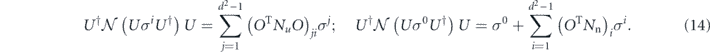
The uniform average of U over the unitary group becomes a uniform average of O over the orthogonal group. The nonunital part of 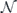 averages to zero, and the average of the unital part can be evaluated using
averages to zero, and the average of the unital part can be evaluated using
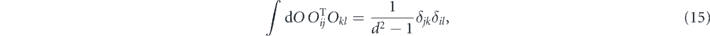
which yields
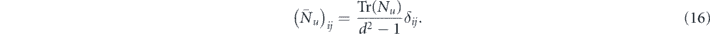
Hence, the averaged channel is a completely depolarizing Pauli channel of the form
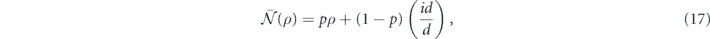
where
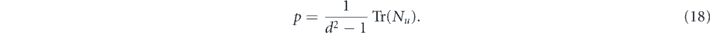
Note that if this averaged channel is applied m times in succession, we obtain
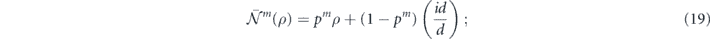
thus p is called the benchmarking parameter because it determines the rate of exponential decay of fidelity in benchmarking experiments. The average infidelity r is given by
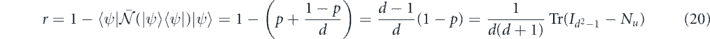
for any pure state |ψ⟩. Here 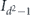 denotes the (d2 − 1) × (d2 − 1) identity matrix. Because N00 = 1, we may also express the infidelity as
denotes the (d2 − 1) × (d2 − 1) identity matrix. Because N00 = 1, we may also express the infidelity as
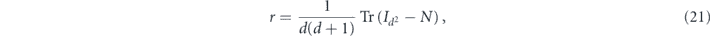
where 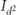 denotes the d2 × d2 identity.
denotes the d2 × d2 identity.
2.3. Examples
2.3.1. Depolarizing channel
We have seen that if 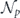 is the depolarizing channel with benchmarking parameter p, then
is the depolarizing channel with benchmarking parameter p, then 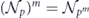 . Using the relation
. Using the relation 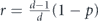 , we can express the infidelity rm of
, we can express the infidelity rm of 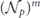 in terms of the infidelity r of
in terms of the infidelity r of 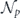 , finding
, finding
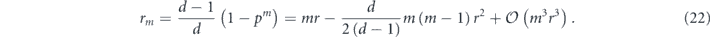
If mr is small, the infidelity accumulates linearly with m, the number of times the channel is applied. A similar remark applies to more general Pauli channels.
We say that a channel with this property is incoherent. The interpretation is that (up to a constant factor), the infidelity r may be regarded as a probability of error. If the channel is applied m times, where mr is small, any one of the m instances of the channel could be faulty, so that the total probability of error is mr + higher-order terms.
2.3.2. Qubit rotation
In contrast, consider the case of a unitary rotation of a single qubit about the X-axis
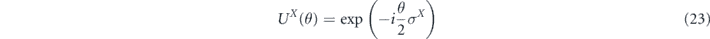
which rotates the Bloch sphere by θ. For this channel the Pauli transfer matrix is
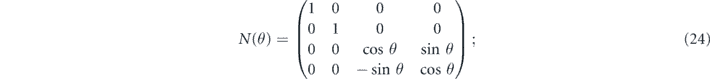
therefore, the infidelity is
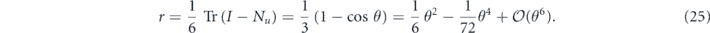
Applying this channel m times, we obtain N(θ)m = N(mθ), a rotation by an angle m times larger. Therefore,
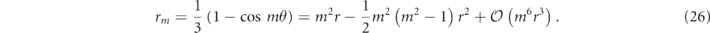
Here, for m2r small, the infidelity accumulates quadratically with m; it is the rotation angle, rather than the error probability, that increases linearly. We say that a channel like this one, for which the infidelity increases faster than linearly with m, is coherent.
2.3.3. Rotation/dephasing channels
The distinction between a coherent and incoherent channel is not always clearcut, and we will need measures that quantify the degree of coherence. As an example, consider the case where a qubit either dephases in the X-basis (with probability qD) or is rotated by angle θ about the X-axis (with probability qR):
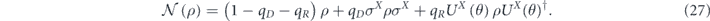
The Pauli transfer matrix is
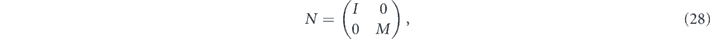
where I is the 2 × 2 identity, and M is the 2 × 2 matrix
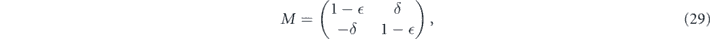
with
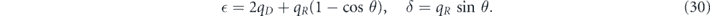
The infidelity is
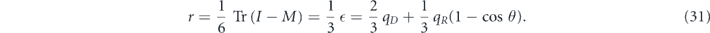
The eigenvalues of M are
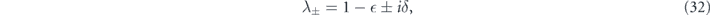
and therefore the infidelity of 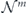 is
is
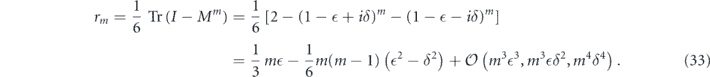
Here the degree of coherence depends on the relative value of  and δ. In the case of a unitary rotation, we have
and δ. In the case of a unitary rotation, we have 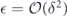 , which means that the term growing quadratically with m can dominate. On the other hand, for
, which means that the term growing quadratically with m can dominate. On the other hand, for  ⩾ δ, there is no quadratically growing term at all.
⩾ δ, there is no quadratically growing term at all.
A generalization of this channel will be useful in section 3. Instead of a single rotation by θ occurring with probability qR, we may consider an ensemble of possible rotations, where a rotation by θa occurs with probability qa. In that case rm is still given by equation (33), but now
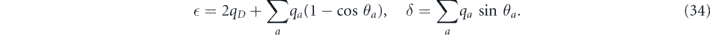
2.4. Unitarity and the coherence angle
We have seen that Nu is an orthogonal matrix if (and only if) the channel 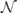 is unitary. Hence a deviation from orthogonality of Nu indicates a deviation from unitarity of
is unitary. Hence a deviation from orthogonality of Nu indicates a deviation from unitarity of 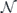 . With that in mind, following [10] we define the unitarity
. With that in mind, following [10] we define the unitarity 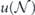 of the channel
of the channel 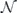 as
as

which is 1 for unitary channels and strictly less than 1 for nonunitary channels. For a fixed value of the infidelity r, the unitarity achieves its minimum for the depolarizing channel [24], where
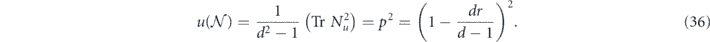
The unitarity u and the benchmarking parameter p together provide a useful characterization of the coherence of a channel. We will be primarily interested in the case where the infidelity r is small, so that the diagonal elements {Nii} of the Pauli transfer matrix are close to one, and it makes sense to expand in the small quantity 1 − Nii. Writing
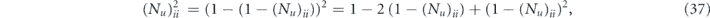
we see that
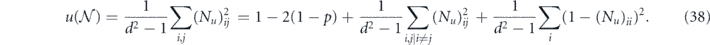
Expanding the square root of u, we find
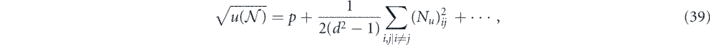
where the ellipsis indicates terms that are fourth order in the off-diagonal entries 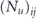 and terms that are quadratic order in
and terms that are quadratic order in 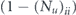 .
.
The coherence angle Θ is defined as
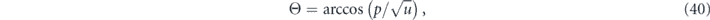
which for p and u close to one, can be expressed as
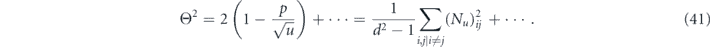
Apart from a normalization factor, and neglecting the higher-order terms, Θ2 is the sum of squares of all off-diagonal terms in Nu. It quantifies the coherence in the channel.
For the qubit rotation channel in equation (24), the coherence angle is related to the rotation angle θ by
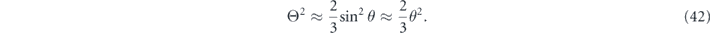
For the dephasing/rotation qubit channel in equation (29), our truncated power series expansion used to derive equation (41) is justified if  is negligible compared to δ, in which case we find
is negligible compared to δ, in which case we find
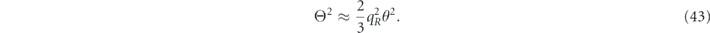
For the depolarizing channel, u = p2 and hence Θ = 0.
In [25], Carignan-Dugas et al derived a bound on rm, the infidelity when a unital channel  is applied m times in succession, in terms of the infidelity r and coherence angle Θ of
is applied m times in succession, in terms of the infidelity r and coherence angle Θ of  :
:
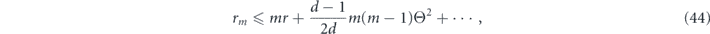
where the ellipsis indicates terms higher order in r and Θ2. In this sense (for unital channels), the coherence angle controls the quadratic growth of rm as a function of m, when r and Θ2 are small.
2.5. Diamond distance
In some versions of the quantum accuracy threshold theorem, the strength of Markovian noise is characterized by the deviation of a noisy gate from the corresponding ideal gate in the diamond norm [26]. This diamond norm deviation is useful for quantifying the damage inflicted when the noisy gate acts on qubits which are entangled with other qubits in a quantum computer. The diamond norm 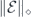 of a linear map
of a linear map  is defined as the L1 norm of the extended map
is defined as the L1 norm of the extended map  :
:
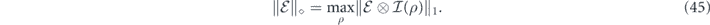
If  acts on Hilbert space
acts on Hilbert space 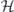 with dimension d, then
with dimension d, then 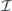 denotes the identity acting on another Hilbert space
denotes the identity acting on another Hilbert space 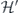 with dimension d; the maximum is over all density operators on
with dimension d; the maximum is over all density operators on  . A measure of noise strength for a noisy channel
. A measure of noise strength for a noisy channel 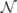 is the diamond distance of
is the diamond distance of  from the identity channel,
from the identity channel,
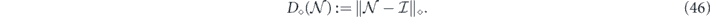
If  is applied m times in succession, we have
is applied m times in succession, we have
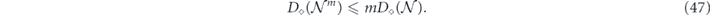
Upper and lower bounds on the diamond distance can be expressed in terms of the benchmarking parameter 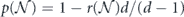 and the unitarity
and the unitarity 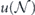 [9]:
[9]:
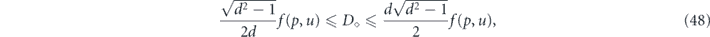
where
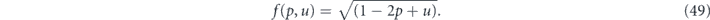
For the depolarizing channel, we have u = p2 and f = 1 − p = rd/(d − 1); the diamond distance scales linearly with the infidelity r. But for a unitary channel, we have u = 1 and 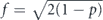 ; then the diamond distance scales like
; then the diamond distance scales like 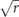 .
.
From equation (38), we see that
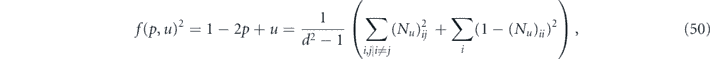
which together with equation (48) provides upper and lower bounds on the diamond distance written in terms of Pauli transfer matrix elements:
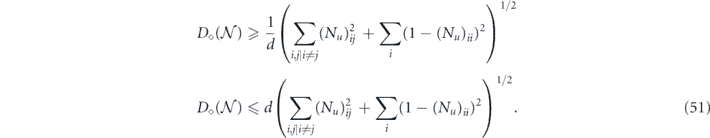
We will be mostly interested in the upper bound on the diamond distance for a logical channel with a fixed number of encoded qubits; therefore, the unfavorable scaling of the upper bound with the dimension d need not cause us great concern.
2.6. Coherence in the chi-matrix representation
The Pauli transfer matrix representation is useful for proving the preceding relationships between channel components, the growth of average infidelity, and the dependence of the diamond distance from identity on the average infidelity. When we analyze error correction, we will make use of a different representation of the noise channel. Any channel 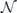 has an expansion in terms of Pauli operators. Consider a completely positive map
has an expansion in terms of Pauli operators. Consider a completely positive map 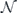 with Kraus operators {Kα} and expand each Kα as
with Kraus operators {Kα} and expand each Kα as
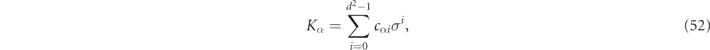
where all Pauli operators {σi} are chosen to be Hermitian, and the {cαi} are complex numbers. Then
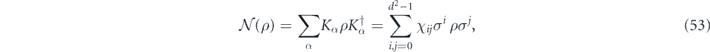
where
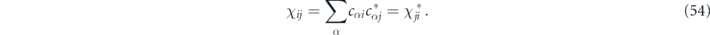
This is called the chi-matrix representation of the channel. The map 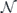 is trace preserving if
is trace preserving if
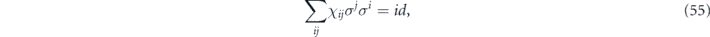
and unital if
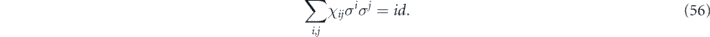
Note that σiσkσj = ±σk if and only if i = j; therefore, in the Pauli transfer matrix language, the terms in equation (53) with i = j contribute to the diagonal entries in Nab, while the terms with i ≠ j contribute to the off-diagonal entries.
To be more concrete, consider the single-qubit rotation about the X-axis 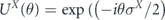 , for which
, for which
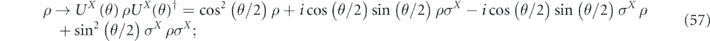
hence
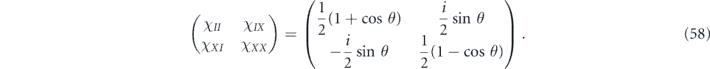
More generally, for the channel with Pauli transfer matrix
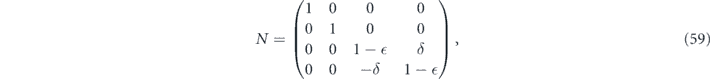
as in equation (29), we have
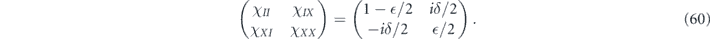
There is a simple general relationship between the off-diagonal entries of the Pauli transfer matrix Nab and the chi matrix χij, namely
Lemma 1. The off-diagonal elements of the Pauli transfer matrix Nab and the chi matrix χij are related by
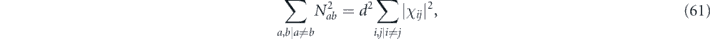
where d = 2n is the Hilbert space dimension.
Because of this identity, we may quantify the coherence of a channel using the off-diagonal entries in either Nab or χij. The case d = 2 is explained explicitly in appendix
Proof. To prove the claim, note that, for any Hermitian Pauli operators σi, σj, σa, we have
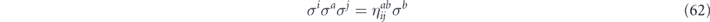
for some Hermitian Pauli operator σb and some phase  . By taking Hermitian adjoints of both sides, we also have
. By taking Hermitian adjoints of both sides, we also have
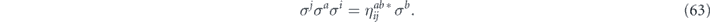
The phase is 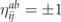 if σiσaσj is Hermitian, and it is
if σiσaσj is Hermitian, and it is 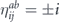 if σiσaσj is anti-Hermitian. Furthermore, for each fixed i ≠ j, as σa ranges over the d2 Hermitian Pauli operators, σiσaσj is Hermitian for d2/2 choices of σa, and anti-Hermitian for the remaining d2/2 choices. (If σi and σj commute, then σiσaσj is Hermitian if and only if σa commutes with σjσi. If σi and σj anticommute, then σiσaσj is Hermitian if and only if σa anticommutes with σjσi.) Note that b ≠ a if i ≠ j.
if σiσaσj is anti-Hermitian. Furthermore, for each fixed i ≠ j, as σa ranges over the d2 Hermitian Pauli operators, σiσaσj is Hermitian for d2/2 choices of σa, and anti-Hermitian for the remaining d2/2 choices. (If σi and σj commute, then σiσaσj is Hermitian if and only if σa commutes with σjσi. If σi and σj anticommute, then σiσaσj is Hermitian if and only if σa anticommutes with σjσi.) Note that b ≠ a if i ≠ j.
The entries in the Pauli transfer matrix are (for a ≠ b).
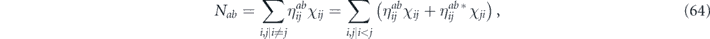
where the sum is restricted to {i, j} such that σiσaσj ∝ σb. The summand is 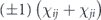 if σiσaσj is Hermitian, and it is
if σiσaσj is Hermitian, and it is 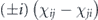 if σiσaσj is anti-Hermitian. Suppose now that, for fixed i, j, we collect all the terms in
if σiσaσj is anti-Hermitian. Suppose now that, for fixed i, j, we collect all the terms in 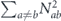 which are quadratic in {χij, χji}. Because σiσaσj is Hermitian for half the choices of σa and anti-Hermitian for half the choices, we have
which are quadratic in {χij, χji}. Because σiσaσj is Hermitian for half the choices of σa and anti-Hermitian for half the choices, we have
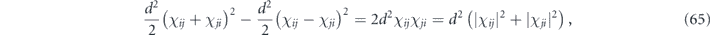
where we have used 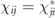 , which is required by complete positivity.
, which is required by complete positivity.
To complete the proof of the claim, we must verify that all the multilinear terms of the form χijχkl (where {i, j} and {k, l} are disjoint) cancel in the sum 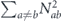 . Such a cross term of the form
. Such a cross term of the form
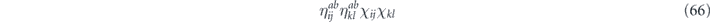
arises in 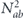 when we have
when we have
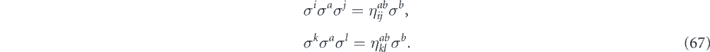
We will consider all such terms with i, j, k, l fixed, as we vary σa and σb over the possible Hermitian Pauli operators. Multiplying both sides on the left by Hermitian Pauli operator σc, we obtain
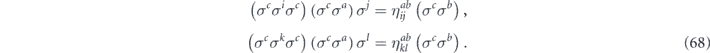
Given a standard sign choice for the d2 Hermitian Pauli operators, we may write
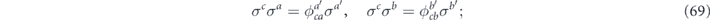
here e.g. 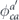 is a phase, which is ±1 if σa and σc commute and ±i if σa and σc anticommute. We also have
is a phase, which is ±1 if σa and σc commute and ±i if σa and σc anticommute. We also have
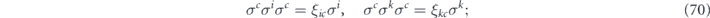
here ξic = ±1 is a sign indicating whether σc and σi commute or anticommute. Therefore
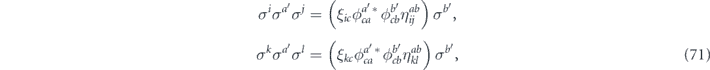
and the corresponding cross term arising from  is
is
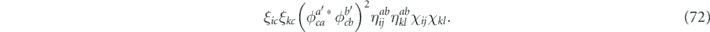
Now suppose that either σc commutes with both σa and σb or anticommutes with both; in either case 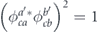 . As we vary σc over the d2/2 Pauli operators with this property, the sign ξicξkc has the value +1 for the d2/4 choices of σc such that σc commutes with both σi and σk or anticommutes with both, while ξicξkc has the value −1 for the d2/4 choices of σc such that σc commutes with one of σi and σk and anticommutes with the other. Therefore, as we vary a' and b' over these d2/2 possible choices for σc, with i, j, k, l fixed, the cross terms cancel.
. As we vary σc over the d2/2 Pauli operators with this property, the sign ξicξkc has the value +1 for the d2/4 choices of σc such that σc commutes with both σi and σk or anticommutes with both, while ξicξkc has the value −1 for the d2/4 choices of σc such that σc commutes with one of σi and σk and anticommutes with the other. Therefore, as we vary a' and b' over these d2/2 possible choices for σc, with i, j, k, l fixed, the cross terms cancel.
Alternatively, suppose that σc commutes with one of σa and σb and anticommutes with the other; then 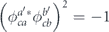 . Again, as we vary a' and b' over the d2/2 possible choices for σc, with i, j, k, l fixed, ξicξkc = +1 for half of the terms and ξicξkc = −1 for the other half; therefore, the cross terms cancel. This completes the proof. □
. Again, as we vary a' and b' over the d2/2 possible choices for σc, with i, j, k, l fixed, ξicξkc = +1 for half of the terms and ξicξkc = −1 for the other half; therefore, the cross terms cancel. This completes the proof. □
3. Logical channel for the repetition code
From now on we will use the streamlined notation for single-qubit Pauli operators:
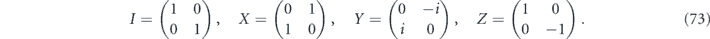
Consider the repetition code, which protects one logical qubit against bit flip (X) errors, but provides no protection against phase (Z) errors. Let us analyze how well this code protects against coherent errors, in which each physical qubit in the code block rotates about the X-axis. Similar calculations were carried out in [17, 18]. Understanding this example will prepare us for an analysis of more general stabilizer codes.
To be as concrete as possible, we will start with the simplest interesting case, the three-qubit repetition code spanned by |000⟩ and |111⟩. Our goal is to determine the logical channel that results when rotation errors applied to the physical qubits are followed by error correction. We will assume for now that the same rotation is applied to each of the three qubits; this will be generalized later.
Suppose that each physical qubit is subjected to the unitary rotation
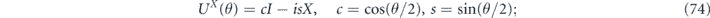
thus the product unitary map applied to the three physical qubits is
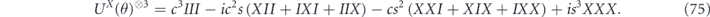
To perform error correction we measure the operators ZZI and IZZ to obtain two syndrome bits. If the syndrome is trivial (both measurements yield +1), no further action is required. If the syndrome is nontrivial, X is applied to one of the three qubits, returning the state to the code space. Thus the terms in the expansion in equation (75) with weight 0 or 1 (where the weight is the number of X's) are error corrected to the logical operator Ī = III, while terms with weight 2 or 3 are error corrected to the logical operator 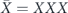 . We conclude that the logical channel
. We conclude that the logical channel 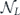 is a convex combination of two unitary transformations,
is a convex combination of two unitary transformations,
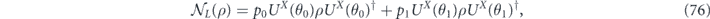
where
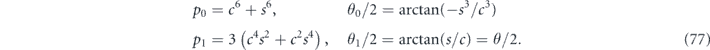
A logical rotation by θ0 is applied when the syndrome is trivial (weight 0), and a logical rotation by θ1 is applied when the syndrome is nontrivial (weight 1).
The logical channel has the form specified in equation (29), where
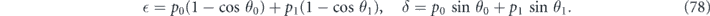
These expressions for  and δ can be simplified using trigonometric identities. In terms of s/c = t = tan θ/2, we have
and δ can be simplified using trigonometric identities. In terms of s/c = t = tan θ/2, we have
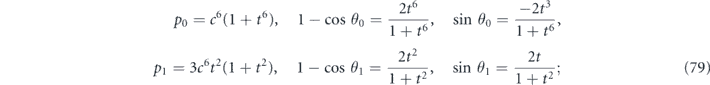
therefore we find
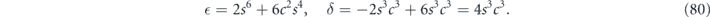
Expanding to leading order for small θ, we have
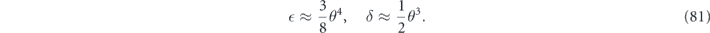
Here, because  is higher order in θ than δ, equation (41) applies, and therefore the coherence angle is
is higher order in θ than δ, equation (41) applies, and therefore the coherence angle is
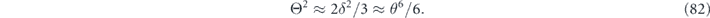
From equation (33), we see that if this logical channel 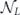 is applied m times, the infidelity becomes
is applied m times, the infidelity becomes
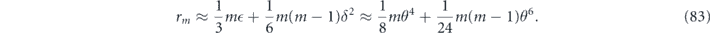
Note that the term quadratic in m actually matches the upper bound in equation (44). Equation (83) reveals that the coherence of the logical channel is somewhat suppressed, as it takes a number of repetitions 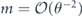 for the quadratically growing contribution to r to 'catch up' with the dominant linear term.
for the quadratically growing contribution to r to 'catch up' with the dominant linear term.
Now let's do a similar analysis for the length-n repetition code (where n is odd), which corrects up to (n − 1)/2 bit-flip errors. In this case the logical channel is a convex combination of (n + 1)/2 unitary rotations,
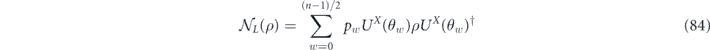
where w ranging from 0 to (n − 1)/2 indicates the weight of a correctable X error occurring in the expansion of 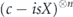 . When the (n−1)-bit syndrome is measured, syndromes pointing to a weight-w error occur with total probability
. When the (n−1)-bit syndrome is measured, syndromes pointing to a weight-w error occur with total probability
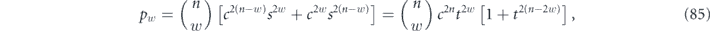
and the logical rotation angle conditioned on a weight-w syndrome is
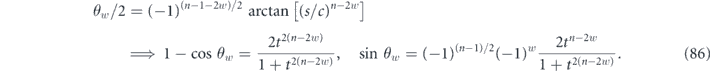
Summing over the weight of the syndrome, we find
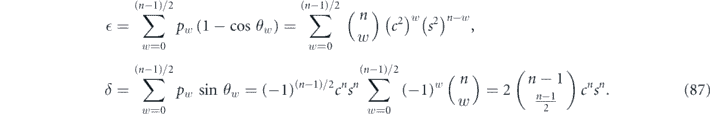
In appendix  . Applying Stirling's approximation to our expression for δ as well, we have proven
. Applying Stirling's approximation to our expression for δ as well, we have proven
Theorem 1. Consider the length-n repetition code which protects against bit flip (X) errors, subject to the independent unitary noise map 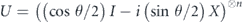 , where sin2 θ/2 < 1/2. Let
, where sin2 θ/2 < 1/2. Let 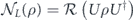 be the logical map, where ρ is a code state and
be the logical map, where ρ is a code state and 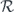 decodes using majority voting. Then
decodes using majority voting. Then 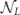 has Pauli transfer matrix N of the form given in equations (28) and (29), with
has Pauli transfer matrix N of the form given in equations (28) and (29), with  and δ given by
and δ given by
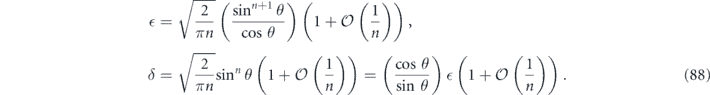
Therefore, using equation (33) and approximations that are well justified (according to theorem 1) when n is large and sin2 θ/2 < 1/2, we can estimate the infidelity when the logical channel is applied m times is succession, finding
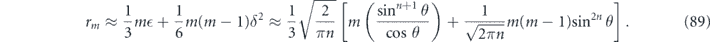
The scaling of the infidelity 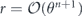 arises because a bit flip error must have weight at least w = (n + 1)/2 to cause a logical error. The scaling
arises because a bit flip error must have weight at least w = (n + 1)/2 to cause a logical error. The scaling 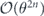 of the term quadratic in m indicates that the coherence of the logical channel is suppressed when θ is small. It takes
of the term quadratic in m indicates that the coherence of the logical channel is suppressed when θ is small. It takes 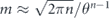 successive applications of the logical channel
successive applications of the logical channel  for the quadratic term in rm to become comparable to the linear term. This suppression arises because larger logical rotations occur with only smaller probability; for example a logical rotation by θ occurs with probability
for the quadratic term in rm to become comparable to the linear term. This suppression arises because larger logical rotations occur with only smaller probability; for example a logical rotation by θ occurs with probability 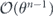 .
.
Keeping only the leading-order terms in equation (87), we obtain
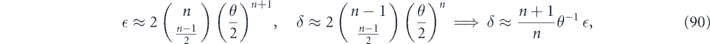
generalizing equation (81). We derived the relationship
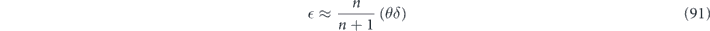
using the identity
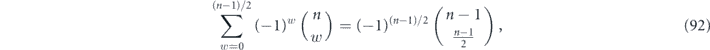
which can be proved by induction. For drawing the conclusion that θδ/ is bounded above by an n-independent constant, the oscillating minus sign in this expression is important—if not for the oscillating sign, the sum would be 2n−1, hence larger than equation (92) by a factor which scales like
is bounded above by an n-independent constant, the oscillating minus sign in this expression is important—if not for the oscillating sign, the sum would be 2n−1, hence larger than equation (92) by a factor which scales like 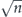 . This would mean that average infidelity rm in equation (33) would have a large quadratic component relative to the linear component as the code length n becomes large. In other words, the logical noise channel would have significant coherence.
. This would mean that average infidelity rm in equation (33) would have a large quadratic component relative to the linear component as the code length n becomes large. In other words, the logical noise channel would have significant coherence.
4. Repetition code revisited
In this section we will compute the logical channel for the repetition code using a different method than in section 3. This new method can be extended more easily to general stabilizer codes.
4.1. Stabilizer formalism
We now briefly review the structure of stabilizer codes, as this will be used in our analysis. Let {gα, α = 1, 2, ..., n − k} denote the n − k stabilizer generators for an [[n, k, d]] stabilizer code. These generators are mutually commuting Hermitian Pauli operators such that 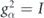 . The syndrome s(σi) of Pauli operator σi is a length-(n − k) binary vector such that
. The syndrome s(σi) of Pauli operator σi is a length-(n − k) binary vector such that 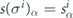 where
where
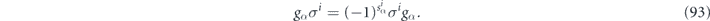
Note that the syndrome of a product of Pauli operators is additive: 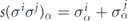 , where the addition is modulo 2.
, where the addition is modulo 2.
The code space is the simultaneous eigenstate with eigenvalue 1 of all the stabilizer generators. If 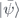 is a pure state in the code space, then
is a pure state in the code space, then
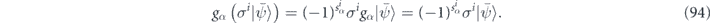
Therefore, the syndrome of σi can be identified by measuring all of the stabilizer generators. Hence we may say that  is the syndrome of the state
is the syndrome of the state 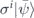 . A Pauli operator that commutes with the stabilizer generators preserves the code space and is said to be logical. We may define a complete set of orthogonal projectors {Πs} on the n-qubit Hilbert space, where Πs projects onto the subspace with syndrome s. Then
. A Pauli operator that commutes with the stabilizer generators preserves the code space and is said to be logical. We may define a complete set of orthogonal projectors {Πs} on the n-qubit Hilbert space, where Πs projects onto the subspace with syndrome s. Then
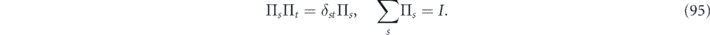
An encoded density operator 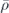 (one supported on the code space) has the property
(one supported on the code space) has the property
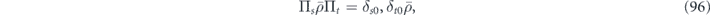
where s = 0 denotes the trivial syndrome.
To construct the error recovery map 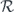 , we first perform an orthogonal measurement to identify the syndrome s. Then for each syndrome s, a particular Pauli operator
, we first perform an orthogonal measurement to identify the syndrome s. Then for each syndrome s, a particular Pauli operator 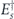 is applied, which returns the measured state to the code space; therefore,
is applied, which returns the measured state to the code space; therefore,
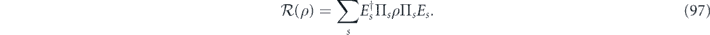
One says that Es is the standard error associated with the syndrome s. In the case of minimal-weight decoding, Es is chosen to be a minimal-weight Pauli operator with syndrome s. By the weight w(σ) of the n-qubit Pauli operator σ, we mean the number of qubits to which a nontrivial Pauli matrix X, Y, or Z is applied, while I is applied to the remaining n − w qubits.
By summing over all values of the syndromes s to construct the error recovery channel, we are averaging over all the possible outcomes of the syndrome measurement, with each syndrome weighted by its probability. We discussed in the introduction how to justify performing this average when computing the logical channel.
4.2. Recovery in the chi-matrix representation
For any such noise channel 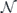 acting on an encoded density operator
acting on an encoded density operator 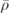 , we would like to find the error corrected map
, we would like to find the error corrected map 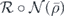 . Using the chi representation of the noise channel, it evidently suffices to compute
. Using the chi representation of the noise channel, it evidently suffices to compute
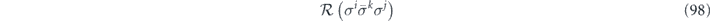
for each pair of physical Pauli operators σi, σj and each logical Pauli operator 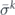 . Because the syndrome is additive, we have
. Because the syndrome is additive, we have
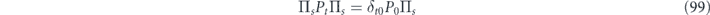
if Pt is any physical Pauli operator with syndrome t, and therefore
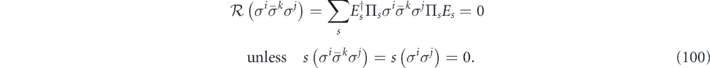
That is, only the terms for which σi and σj have the same syndrome survive when the error recovery map is applied. This property will be crucial in our analysis of the logical channel.
Now let's understand the action of 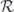 in more detail. An [[n, k, d]] stabilizer code has 4k logical Pauli operators. The physical Pauli operator L representing a logical Pauli operator is not unique, because L and LG act in the same way on the code space, where G is any element of the stabilizer group. But let us by convention choose standard physical operators {La, a = 0, 1, 2, ..., 4k − 1} representing each of the logical Pauli operators. Since we have also assigned a standard error operator Es to each syndrome s, any Hermitian Pauli operator has a unique decomposition of the form
in more detail. An [[n, k, d]] stabilizer code has 4k logical Pauli operators. The physical Pauli operator L representing a logical Pauli operator is not unique, because L and LG act in the same way on the code space, where G is any element of the stabilizer group. But let us by convention choose standard physical operators {La, a = 0, 1, 2, ..., 4k − 1} representing each of the logical Pauli operators. Since we have also assigned a standard error operator Es to each syndrome s, any Hermitian Pauli operator has a unique decomposition of the form
where Gx is an element of the stabilizer group, and ηsax is a phase. Since there are 2n−k stabilizer group elements (up to phases), 2n−k distinct syndromes, and 22k logical Pauli operators, we see that this decomposition accounts for all 4n physical Pauli operators. We conclude that if  is an encoded density operator, then
is an encoded density operator, then
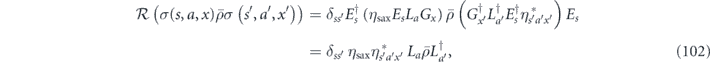
where we have used the property that σ(s', a', x') is Hermitian. In the logical channel, the terms with La = La' are incoherent—they contribute to the on-diagonal elements of the logical Pauli transfer matrix. The terms with La ≠ La' are coherent—they contribute to the off-diagonal elements.
When the noise channel  is weak, the dominant terms in the chi-matrix expansion in equation (53) are those such that σiσj has minimal weight, and we have also seen that the only terms that survive when the recovery map is applied are those such that σiσj is a logical operator (has trivial syndrome). Now let's suppose that the code distance is d and that minimal-weight decoding is performed. This means that we choose Es such that La = I (up to multiplication by an element of the stabilizer) whenever σ(s, a, x) has weight no larger than (d − 1)/2, assuming d is odd.
is weak, the dominant terms in the chi-matrix expansion in equation (53) are those such that σiσj has minimal weight, and we have also seen that the only terms that survive when the recovery map is applied are those such that σiσj is a logical operator (has trivial syndrome). Now let's suppose that the code distance is d and that minimal-weight decoding is performed. This means that we choose Es such that La = I (up to multiplication by an element of the stabilizer) whenever σ(s, a, x) has weight no larger than (d − 1)/2, assuming d is odd.
To get a contribution to the incoherent part of the logical channel, we will need both σi and σj to have weight at least (d + 1)/2, so that the total weight must be at least d + 1. In that case it is possible for both σi and σj to be error corrected to a nontrivial logical operator. But there are also weight-d contributions to the coherent part of the logical channel, arising from the terms in which w(σi) + w(σj) = d, where w(σ) denotes the weight of Pauli operator σ. In that case one of the two Pauli operators has weight less than or equal to (d − 1)/2, hence is error corrected to the identity, while the other has weight greater than or equal to (d + 1)/2, hence is corrected to a nontrivial logical operator L. The resulting term in the logical channel is either  or
or 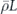 (up to a phase), depending on whether σi or σj has higher weight.
(up to a phase), depending on whether σi or σj has higher weight.
If we choose the standard errors {Es} differently, then the action of the recovery operator may be modified. But it is evident from equation (102) that if we make the replacement Es → Es' = ϕsEsGy, where Gy is an element of the stabilizer and ϕs is a phase, then 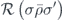 is not changed. In particular, when we perform minimal-weight decoding, there may be more than one minimal-weight Pauli operator with syndrome s, so that the choice of Es is ambiguous. However, as long as any two minimal-weight Pauli operators Es and Es' with syndrome s have the property that
is not changed. In particular, when we perform minimal-weight decoding, there may be more than one minimal-weight Pauli operator with syndrome s, so that the choice of Es is ambiguous. However, as long as any two minimal-weight Pauli operators Es and Es' with syndrome s have the property that 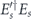 is an element of the code stabilizer, then the logical channel will not depend on how the minimal-weight standard errors are chosen. This will certainly be the case if the code distance is d and the standard errors have weight not larger than (d − 1)/2, since then
is an element of the code stabilizer, then the logical channel will not depend on how the minimal-weight standard errors are chosen. This will certainly be the case if the code distance is d and the standard errors have weight not larger than (d − 1)/2, since then 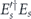 has weight at most d − 1 and cannot be a nontrivial logical operator.
has weight at most d − 1 and cannot be a nontrivial logical operator.
4.3. Analysis of repetition code using the chi-matrix formalism
To illustrate this method, we return to the length-3 repetition code, where the noise channel is as in equation (75). We write out the chi-matrix expansion of 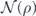 in equation (53), and then apply the recovery operator
in equation (53), and then apply the recovery operator 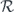 to find the logical channel
to find the logical channel 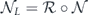 . The task of applying
. The task of applying 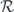 is simplified by the observation that, if the state ρ is supported on the code space, then
is simplified by the observation that, if the state ρ is supported on the code space, then  annihilates all terms in which σiσj is not logical; that is, as indicated in equation (100), σiσj must commute with the stabilizer for the term to survive. We may write
annihilates all terms in which σiσj is not logical; that is, as indicated in equation (100), σiσj must commute with the stabilizer for the term to survive. We may write
where  is the sum of terms such that σiσj is not logical (hence
is the sum of terms such that σiσj is not logical (hence  acting on encoded density operators),
acting on encoded density operators),  is the sum of terms such that σiσj is the logical identity, and
is the sum of terms such that σiσj is the logical identity, and 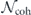 is the sum of terms such that σiσj is a nontrivial logical operator. Then
is the sum of terms such that σiσj is a nontrivial logical operator. Then 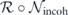 is the incoherent part of
is the incoherent part of 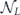 and
and 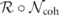 is its coherent part. Explicitly,
is its coherent part. Explicitly,
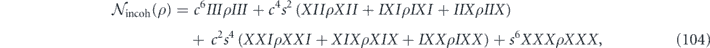
and
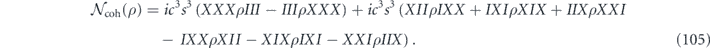
The code has two syndrome bits, given by the measured values of ZZI and IZZ, and for a minimal-weight decoder we choose the standard errors to be

while the nontrivial logical operator is 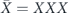 . Each of the Pauli operators in equations (104) and (105) can be expressed as a product of a standard error and a logical operator which is either Ī = III or
. Each of the Pauli operators in equations (104) and (105) can be expressed as a product of a standard error and a logical operator which is either Ī = III or 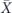 , so the logical map becomes
, so the logical map becomes
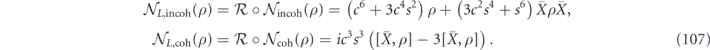
To compare with our previous calculation of the logical channel, we note that
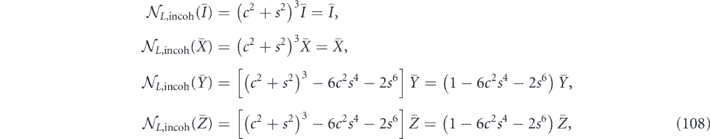
and
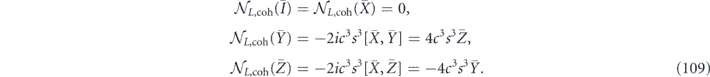
In the notation of equation (29), we have found that the logical channel is parametrized by
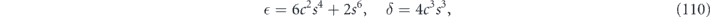
in agreement with the result found in equation (80).
Now consider the length-n repetition code, for n odd, where the noise is the product unitary transformation UX(θ)⊗n. The incoherent part 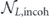 of the logical channel arises from the diagonal terms {σiρσi} in the chi-matrix expansion of
of the logical channel arises from the diagonal terms {σiρσi} in the chi-matrix expansion of 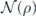 . Here σi can be any one of the 2n Pauli operators contained in
. Here σi can be any one of the 2n Pauli operators contained in 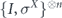 . The code can correct t = (n − 1)/2 σX errors, so σi is error corrected to Ī if its weight w(σi) is t or less, and is error corrected to
. The code can correct t = (n − 1)/2 σX errors, so σi is error corrected to Ī if its weight w(σi) is t or less, and is error corrected to 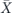 if its weight is t + 1 or more. Therefore, if ρ is an encoded density operator, then
if its weight is t + 1 or more. Therefore, if ρ is an encoded density operator, then
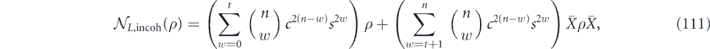
where the binomial coefficient 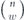 counts the number of weight-w (or weight-(n − w)) operators. Using
counts the number of weight-w (or weight-(n − w)) operators. Using
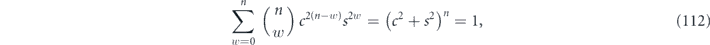
we see that 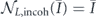 and
and 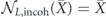 , and furthermore
, and furthermore
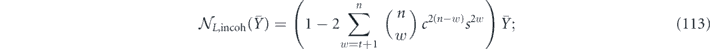
hence
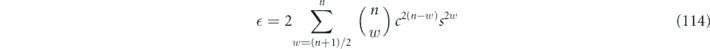
in agreement with equation (87). To leading order in s ≈ θ/2, this becomes
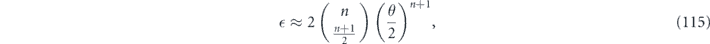
as in equation (90).
The coherent part 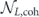 of the logical channel arises from the terms in the Pauli operator expansion of
of the logical channel arises from the terms in the Pauli operator expansion of 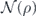 such that
such that 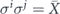 . There are 2n such terms—σi can be any operator among {I,X}⊗n, and σj is then the complementary operator with X and I interchanged. If σi has weight ⩽t, and so is error corrected to Ī, then σj has weight ⩾(t + 1), and so is error corrected to
. There are 2n such terms—σi can be any operator among {I,X}⊗n, and σj is then the complementary operator with X and I interchanged. If σi has weight ⩽t, and so is error corrected to Ī, then σj has weight ⩾(t + 1), and so is error corrected to 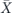 . We obtain
. We obtain
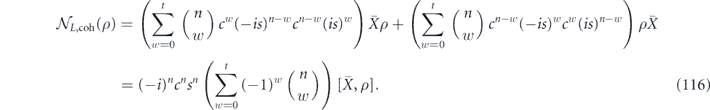
Therefore,
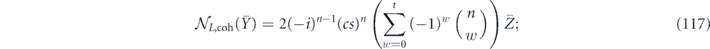
hence

in agreement with equation (90).
4.4. Inhomogeneous X-axis rotations
Now let's consider the logical channel obtained by decoding the length-n repetition code, in the case where the rotation angle varies from qubit to qubit. That is, the unitary noise channel is
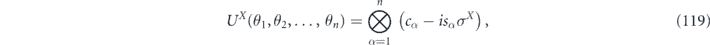
where cα = cos θα/2 and sα = sin θα/2. As in our previous derivation for the case where all angles are equal, we can calculate the incoherent and coherent parts of the logical channel by expanding this tensor product and isolating the terms in  of the form σiρσj where σiσj is either a trivial logical operator (for the incoherent part) or a nontrivial logical operator (for the coherent part). The only difference from the previous calculation is that, while previously all terms in the expansion of UX with the same weight occurred with equal amplitudes, now operators of the same weight may have different amplitudes.
of the form σiρσj where σiσj is either a trivial logical operator (for the incoherent part) or a nontrivial logical operator (for the coherent part). The only difference from the previous calculation is that, while previously all terms in the expansion of UX with the same weight occurred with equal amplitudes, now operators of the same weight may have different amplitudes.
Still, the derivation goes through in much the same way as before. Let S denote a subset of the n qubits, let |S| denote the size of S, and let 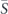 denote the subset complementary to S. Extending our previous argument to the case of unequal angles yields
denote the subset complementary to S. Extending our previous argument to the case of unequal angles yields
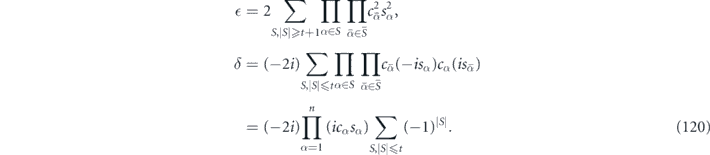
Note that the sum in the expression for δ does not depend on the angles. To leading order in the small {sα}, we find
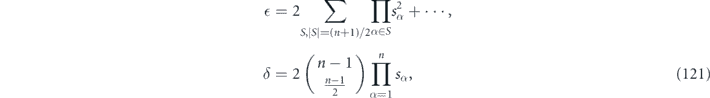
where we have used the identity
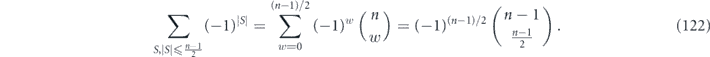
As before we find 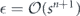 and
and 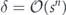 . Furthermore, the expression for δ is very simple—the same as our previous formula, but with sn replaced by ∏αsα.
. Furthermore, the expression for δ is very simple—the same as our previous formula, but with sn replaced by ∏αsα.
The formula for  depends in a more complicated way on the set of angles {θα}. But we can show that for fixed δ,
depends in a more complicated way on the set of angles {θα}. But we can show that for fixed δ,  is minimized when all the sα are equal. Therefore, we have a lower bound on
is minimized when all the sα are equal. Therefore, we have a lower bound on  , namely
, namely
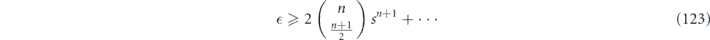
where the ellipsis indicates terms higher order in s, and we have defined
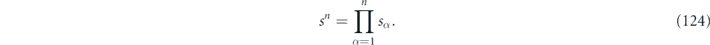
Correspondingly, using
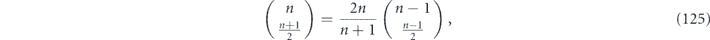
we have the upper bound on δ:
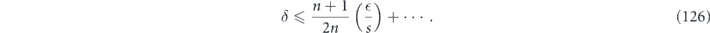
Therefore, for inhomogeneous as well as homogeneous rotations, we conclude that the coherent part of the logical channel is suppressed. In fact, the case where all rotation angles are equal is the worst case, where equation (126) is saturated.
Now let's prove that  is minimized (for fixed δ), when all {sα} are equal.
is minimized (for fixed δ), when all {sα} are equal.
Lemma 2. Consider minimizing the function
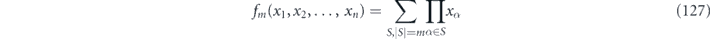
subject to the constraint 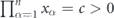 , where all xα are nonnegative. Here S denotes a subset of the n variables, and |S| is the size of S. The minimum occurs for x1 = x2 = ⋯ = xn = c1/n.
, where all xα are nonnegative. Here S denotes a subset of the n variables, and |S| is the size of S. The minimum occurs for x1 = x2 = ⋯ = xn = c1/n.
Proof. Note that fm is a symmetric function, invariant under permutations of its n arguments, and can be decomposed as
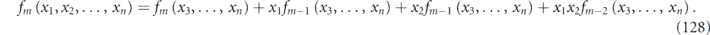
Using the constraint we write
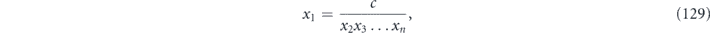
and regard fm as a function of the n − 1 independent variables x2, x3, ..., xn; then
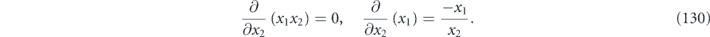
Therefore, setting the gradient of fm equal to zero, we find
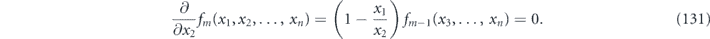
The constraint requires that all xα are positive; therefore fm−1(x3, ..., xn) is positive and we find that x1 = x2. From the symmetry of fm, we conclude that x1 = xα = c1/n for α = 2, 3, ..., n, when fm is stationary. This is the unique stationary point of fm(x1, x2, ..., xn) when all xα are positive; furthermore fm is smooth and bounded below. Therefore it must be the minimum of fm. □
5. Correlated unitary noise
Now let's consider unitary noise acting on n qubits which does not factorize into a product of single-qubit unitaries. Since we still wish to consider noise that can be corrected by the repetition code, assume that the n-qubit unitary U has an expansion in terms of X-type Pauli operators:
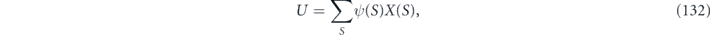
where S denotes a subset of the n qubits and X(S) = ⊗α∈SXα is the X-type operator supported on S. (Xα means X acting on the αth qubit, and it is implicit that I acts on qubit α for α ∉ S.) Unitarity of U implies
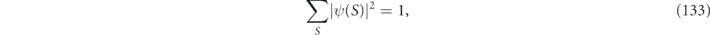
and
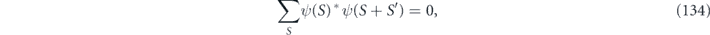
where S' is a nonempty set and S + S' = S ∪ S'\S ∩ S' is the disjoint union of S and S'. To make the analysis of the noise more tractable, let's also suppose the noise is invariant under permutations of the n qubits. In that case ψ(S) = ψ(|S|); that is, the amplitude ψ depends only on the weight w = |S| of the error operator X(S). A tensor product of n identical unitary X rotations,  , is the special case where
, is the special case where
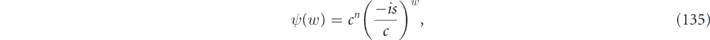
an exponential function of the weight w.
The symmetric unitary transformation may also be expressed as U = e−iH where H is a symmetric n-qubit Hamiltonian of the form
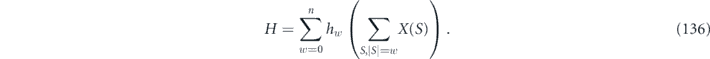
We are assuming that there is no geometric locality constraint on the interactions among the qubits—the strength of a weight-w term in the Hamiltonian depends only on the weight, not on which set S of w qubits are interacting. Since hw is the coefficient of a sum of 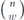 terms, it is implicit that hw decays as a function of w. It is natural to assume that
terms, it is implicit that hw decays as a function of w. It is natural to assume that  , as only in that case do we expect (for hw sufficiently small) the probability of a logical error to drop rapidly as n gets large. For example, if
, as only in that case do we expect (for hw sufficiently small) the probability of a logical error to drop rapidly as n gets large. For example, if  , then each qubit has
, then each qubit has 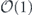 coupling strength with n − 1 other qubits, so the strength of the noise acting on each qubit grows linearly in n, and error correction fails for n sufficiently large. We will elaborate on this point in the discussion below of two-body correlated noise. In a more realistic noise model, the higher-weight terms in the Hamiltonian would have
coupling strength with n − 1 other qubits, so the strength of the noise acting on each qubit grows linearly in n, and error correction fails for n sufficiently large. We will elaborate on this point in the discussion below of two-body correlated noise. In a more realistic noise model, the higher-weight terms in the Hamiltonian would have 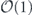 strength (independent of system size), but would decay sufficiently rapidly as the qubits separate that the effective single-qubit noise strength is also
strength (independent of system size), but would decay sufficiently rapidly as the qubits separate that the effective single-qubit noise strength is also 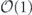 [27, 28].
[27, 28].
The structure of the noise correlations is determined by how hw falls off as the weight w increases. In particular, if 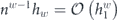 , then ψ(w) in equation (132) is a sum of
, then ψ(w) in equation (132) is a sum of 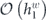 terms; in that case the parameters of the logical channel will be
terms; in that case the parameters of the logical channel will be 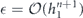 and
and 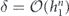 , so the coherent and incoherent parts of the logical channel qualitatively resemble what we found for uncorrelated noise. On the other hand, in the extreme case where hn ≠ 0 and hw = 0 for 0 ⩽ w ⩽ n − 1, the code provides no protection against logical errors and there is no suppression of coherence. Instead we find
, so the coherent and incoherent parts of the logical channel qualitatively resemble what we found for uncorrelated noise. On the other hand, in the extreme case where hn ≠ 0 and hw = 0 for 0 ⩽ w ⩽ n − 1, the code provides no protection against logical errors and there is no suppression of coherence. Instead we find 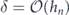 and
and 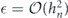 so that
so that 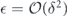 just as in equation (24).
just as in equation (24).
To be concrete, consider the three-qubit repetition code and noise Hamiltonian
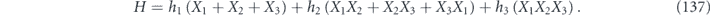
The unitary noise has the expansion
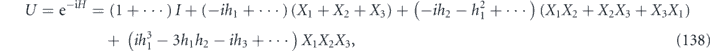
where only the leading terms are shown in the coefficient of each Pauli operator. Repeating the analysis of the logical channel as in section 4.3, but now using this modified unitary noise operator, we find
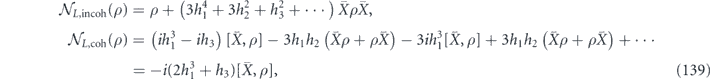
(showing only the leading terms), which yields
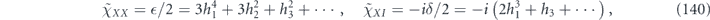
where  denotes the logical chi matrix after error correction. (We do not find any contribution to the coherent part of the logical channel depending only on h2, because the h2 term in the Hamiltonian has even X parity, while the logical operator
denotes the logical chi matrix after error correction. (We do not find any contribution to the coherent part of the logical channel depending only on h2, because the h2 term in the Hamiltonian has even X parity, while the logical operator  has odd parity.) Now whether coherence is suppressed hinges on the strength of the h3 term in the Hamiltonian. In particular, if h3 is large compared to
has odd parity.) Now whether coherence is suppressed hinges on the strength of the h3 term in the Hamiltonian. In particular, if h3 is large compared to 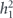 and h2, then highly correlated noise dominates, and coherence of the logical channel is unsuppressed.
and h2, then highly correlated noise dominates, and coherence of the logical channel is unsuppressed.
As another instructive example, consider the length-n repetition code, where the Hamiltonian contains only single-qubit and two-qubit terms. We will compute the coherent and incoherent parts of the logical channel following the same reasoning as in section 4.3. Again, we will need to sum over all the possible values of the syndrome weight, which we will now denote by k. For each value of k, we will find a contribution to the chi matrix for the error-corrected logical channel, with logical operators acting on the encoded density operator ρ from the left and from the right. Each such operator can be obtained in many ways as a product of one-body and two-body terms in the Hamiltonian, and we will have to do some combinatorics to sum up those contributions. By computing the logical chi matrix, and comparing its coherent and incoherent parts, we can prove the following:
Theorem 2. Consider the bit flip code with n qubits, and let the noise model be given by the n-qubit unitary map
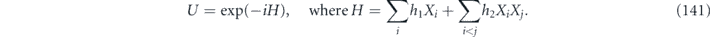
After error correction, the logical noise channel satisfies the following bound relating the coherent and incoherent components:
where  denotes the logical chi matrix. Equation (142) holds for any odd n, and for any h1, but we have made the approximation nh2 ≪ 1, neglecting a multiplicative
denotes the logical chi matrix. Equation (142) holds for any odd n, and for any h1, but we have made the approximation nh2 ≪ 1, neglecting a multiplicative 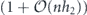 correction on the right-hand side.
correction on the right-hand side.
Theorem 2 implies that, even for this correlated unitary noise model, the coherence of the logical noise channel is heavily suppressed for large n. In fact, the ratio of the coherent to incoherent components of the logical noise channel is similar to what we found for the uncorrelated case, where h1 ≈ θ/2; compare to equation (91).
Proof. The proof of theorem 2 is contained in the next few subsections. We will compute first the coherent component of the logical channel, then the incoherent component, and finally we will compare the two to obtain equation (142).
The unitary operator U = e−iH can be expressed as
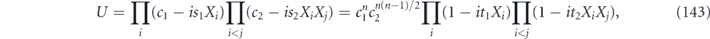
where s1 = sin h1, c1 = cos h1, t1 = tan h1, and likewise for h2. In our computations, we will suppress the prefactor  , which is implicit in all formulas, and we will expand U in a collisionless approximation. That is, we will neglect terms in the expansion in which operators such as Xi and XiXj or XkXi and XiXj act on a qubit in common. The terms we are neglecting are systematically suppressed by powers of nh2 compared to the terms we are keeping. More precisely, these corrections can be absorbed into a multiplicative renormalization of h1 and h2 by a factor
, which is implicit in all formulas, and we will expand U in a collisionless approximation. That is, we will neglect terms in the expansion in which operators such as Xi and XiXj or XkXi and XiXj act on a qubit in common. The terms we are neglecting are systematically suppressed by powers of nh2 compared to the terms we are keeping. More precisely, these corrections can be absorbed into a multiplicative renormalization of h1 and h2 by a factor 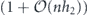 .
.
5.1. Coherent component
Let us look first at the coherent component 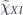 of the logical chi matrix. For each syndrome of weight k, the physical error contributing to this logical component consists of an uncorrectable X error of weight n − k on the left of ρ and a correctable X error of weight k on the right, where k ranges from 0 to (n − 1)/2. The operators on the left and right are supported on disjoint sets of qubits. When we write these operators as products of one-body and two-body terms we will need to count the number of ways of dividing a set of 2p X errors into distinct combinations of p two-body terms. We denote this number by κp where
of the logical chi matrix. For each syndrome of weight k, the physical error contributing to this logical component consists of an uncorrectable X error of weight n − k on the left of ρ and a correctable X error of weight k on the right, where k ranges from 0 to (n − 1)/2. The operators on the left and right are supported on disjoint sets of qubits. When we write these operators as products of one-body and two-body terms we will need to count the number of ways of dividing a set of 2p X errors into distinct combinations of p two-body terms. We denote this number by κp where
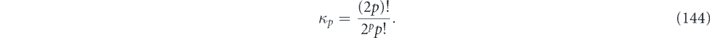
Let us count the terms with kL factors of t2 on the left and kR factors of t2 on the right. In addition, there will be some number w of factors of t1 on the right and n − 2kL − 2kR − w factors of t1 on the left to fill out the coherent term. First we choose the 2kL qubits on the left where the t2 terms act; these qubits can be chosen in 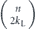 ways. Once these 2kL qubits have been chosen, there are
ways. Once these 2kL qubits have been chosen, there are 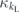 ways to divide up the qubits into pairs where the two-body terms act. Next, we choose the 2kR qubits on the right where the t2 terms act. Because the operators on the left and right are supported on disjoint sets of qubits, these 2kR qubits can be chosen in
ways to divide up the qubits into pairs where the two-body terms act. Next, we choose the 2kR qubits on the right where the t2 terms act. Because the operators on the left and right are supported on disjoint sets of qubits, these 2kR qubits can be chosen in 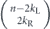 ways. Once these 2kR qubits have been chosen, there are
ways. Once these 2kR qubits have been chosen, there are 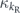 ways to divide up the qubits into pairs where the two-body terms act. Of the remaining n − 2kL − 2kR qubits where no two-body terms act, we choose w qubits on the left where the one-body terms acts; these can be chosen in
ways to divide up the qubits into pairs where the two-body terms act. Of the remaining n − 2kL − 2kR qubits where no two-body terms act, we choose w qubits on the left where the one-body terms acts; these can be chosen in 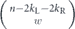 ways. As usual, this contribution to the logical channel has a phase, which is determined by including a factor of −i for each term in the Hamiltonian which acts from the left and a factor of i for each term in the Hamiltonian which acts from the right. By combining all these factors, we find a contribution to
ways. As usual, this contribution to the logical channel has a phase, which is determined by including a factor of −i for each term in the Hamiltonian which acts from the left and a factor of i for each term in the Hamiltonian which acts from the right. By combining all these factors, we find a contribution to 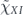
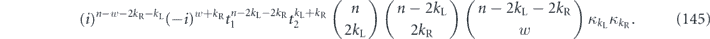
Next we sum over w, taking care to note the w-dependent phase in equation (145). Fortunately, this sum can be evaluated explicitly using an identity satisfied by binomial coefficients, just as we saw in section 3. The sum ranges from w = 0 to w = (n − 1)/2 − kR, so we have
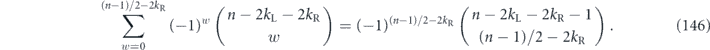
To complete the evaluation of 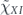 , it remains to sum over kL and kR in
, it remains to sum over kL and kR in
where from equations (145) and (146) we have
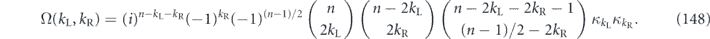
In the sum in equation (147), 2kR can be any nonnegative integer less than or equal to (n − 1)/2, and 2(kR + kL) can be any nonnegative integer less than or equal to n − 1.
Our goal is to compare this coherent component with the incoherent component, which can also be expressed as a sum. Instead of performing an unrestricted sum over kL and kR, we will consider the sum over kL where kL + kR = q is fixed. This collects all the terms in 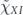 of order
of order 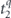 . Then we will follow a similar path to compute the incoherent component
. Then we will follow a similar path to compute the incoherent component  to order
to order 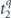 , so that we can compare the coherent and incoherent components in each order.
, so that we can compare the coherent and incoherent components in each order.
Let us isolate the parts of Ω(kL, q − kL) that depend on q only (not on kR), and let us introduce the shorthand m = (n − 1)/2, finding
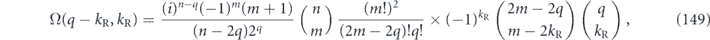
where we have used equation (144). Now we need to sum kR from kR = 0 to kR = q, and then sum q from q = 0 to q = (n − 1)/2.
We observe that, due to the oscillating sign 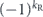 , the sum over kR vanishes when q is odd. This cancellation occurs because if we replace kR by q − kR, the summand remains the same except for a change in phase (−1)q. What's happening is that for each term contributing to
, the sum over kR vanishes when q is odd. This cancellation occurs because if we replace kR by q − kR, the summand remains the same except for a change in phase (−1)q. What's happening is that for each term contributing to 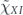 with l factors of it2 on the right and q − l factors of −it2 on the left, there is a corresponding term with q − l factors of it2 on the right and l factors of −it2 on the left. These two terms have equal magnitude but opposite sign, if q is odd. Similar cancellations occur in the computation of the incoherent component
with l factors of it2 on the right and q − l factors of −it2 on the left, there is a corresponding term with q − l factors of it2 on the right and l factors of −it2 on the left. These two terms have equal magnitude but opposite sign, if q is odd. Similar cancellations occur in the computation of the incoherent component 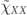 .
.
5.2. Incoherent component
Now we can use similar reasoning to compute the incoherent component 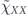 of the logical channel. In this case, though, we will not perform a sum over all syndromes; instead we will keep only the contribution of lowest order in t1 and t2, arising from the syndrome of highest weight. This will suffice for deriving the lower bound in equation (142), because the contributions to
of the logical channel. In this case, though, we will not perform a sum over all syndromes; instead we will keep only the contribution of lowest order in t1 and t2, arising from the syndrome of highest weight. This will suffice for deriving the lower bound in equation (142), because the contributions to 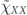 higher order in t1 and t2 are nonnegative. Furthermore, keeping only the lowest-order term is a good approximation when t1 and t2 are sufficiently small.
higher order in t1 and t2 are nonnegative. Furthermore, keeping only the lowest-order term is a good approximation when t1 and t2 are sufficiently small.
For n odd, this leading-order contribution arises from terms with X acting (n + 1)/2 times from both the left and the right. In a term with kL factors of t2 on the left and kR factors of t2 on the right, there will also be (n + 1)/2 − 2kL factors of t1 on the left, and (n + 1)/2 − 2kR factors of t1 on the right. Summing over kL and kR, and arguing as in our discussion of the coherent contribution, we find
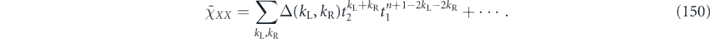
Here
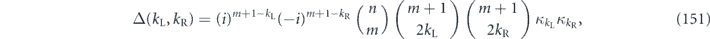
we have defined m = (n − 1)/2, and the ellipsis indicates nonnegative higher-order corrections. We can again introduce q = kL + kR and isolate the portion of Δ(q − kR, kR) that depends only on q:
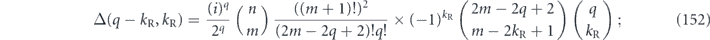
here kR is to be summed from 0 to q, followed by a sum over q from 0 to (n + 1)/2. As for the coherent component, the sum over kR with q fixed vanishes when q is odd, due to the oscillating minus sign 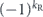 .
.
5.3. Comparing the coherent and incoherent components
Now we are ready to compare 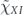 and
and 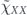 . In both cases there is a sum over kR to perform for each even value of q, and by inspecting (149) and (152) we see that the kR-dependent factors in Ω(q, kR) and Δ(q, kR) are nearly the same; the factor in Δ is obtained from the factor in Ω if we replace m by m + 1. Because this factor grows rapidly with m, we see that the factor in Δ is larger than the factor in Ω for each value of q and kR, but that by itself does not suffice for comparing
. In both cases there is a sum over kR to perform for each even value of q, and by inspecting (149) and (152) we see that the kR-dependent factors in Ω(q, kR) and Δ(q, kR) are nearly the same; the factor in Δ is obtained from the factor in Ω if we replace m by m + 1. Because this factor grows rapidly with m, we see that the factor in Δ is larger than the factor in Ω for each value of q and kR, but that by itself does not suffice for comparing 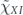 and
and 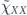 , due to the alternating sign
, due to the alternating sign 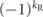 in the sum over kR.
in the sum over kR.
To compare the coherent and incoherent logical noise components properly, we must perform the sum over kR. We will make use of the generalized hypergeometric function 3F2. This function is defined
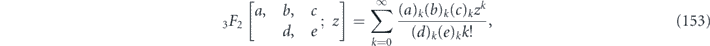
where (a)k denotes the Pochhammer function or the rising factorial
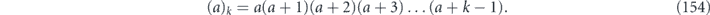
If a is a negative integer, then
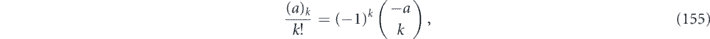
and the sum over k in equation (153) terminates—instead of 0 to ∞, the sum runs from 0 to −a. The same is true if b or c is a negative integer.
Using this definition of 3F2, we can write the sum over kR of Ω or Δ in terms of 3F2. We will have to distinguish the two cases 2q < m and 2q ⩾ m, although we will see at the end that the final expressions will coincide for the two cases. Take the second term in equation (149). Supposing that 2q < m, we can write
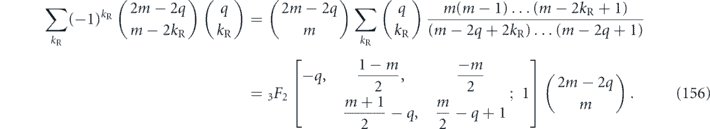
Then we can apply Dixon's identity for the hypergeometric function 3F2. This reads
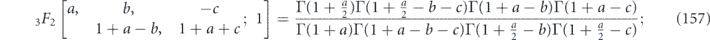
cf equation (2.3.3.5) in [29]. Applying this formula to equation (156), we get
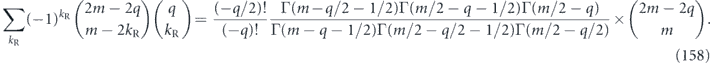
We need to do something about the first factor on the right-hand side (−q/2)!/(−q)! because the gamma function has poles at each negative integer. However, this ratio can still be defined:
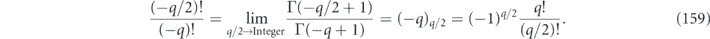
We can substitute this into equation (158) and we find that we can simplify the expression
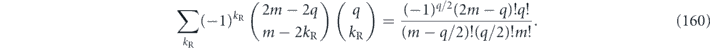
Up until now we have assumed 2q < m. If we instead assume 2q ⩽ m, we find that the intermediate steps look different, but we arrive at the same final answer as in equation (160).
Now we can compute the sum of equation (149) as kR goes from 0 to q using what we found in equation (160). We can also apply our result to perform the sum over kR for equation (152). This gives:
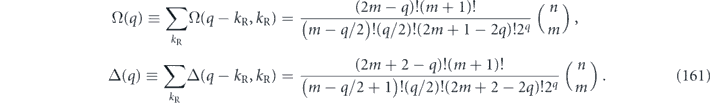
The ratio of these quantities is
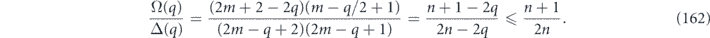
Now we can sum over q; because all terms are nonnegative and the bound holds for every q, we conclude
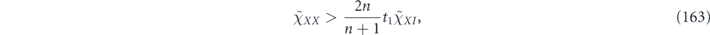
thus proving theorem 2. □
5.4. Summary
By setting q = 0, we can check that the result in equation (161) matches what we found in section 3 for the uncorrelated case. It is also instructive to consider the expansion of 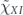 in powers of t2, under the assumption q ≪ m. From equation (161) we see that
in powers of t2, under the assumption q ≪ m. From equation (161) we see that
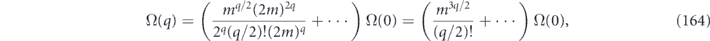
where the ellipsis indicates 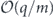 corrections.
corrections.
Restoring the factors of t1 and t2 from equation (147), we see that this expansion in t2 generates a multiplicative correction to  which exponentiates:
which exponentiates:
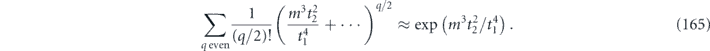
Since the sum over q is dominated by terms with 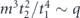 , this exponential series should be a good approximation for
, this exponential series should be a good approximation for 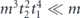 , or
, or 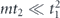 , since in that case neglecting the terms higher order in q/m can be justified. Under this condition, the two-body terms in the Hamiltonian in equation (162) make a small contribution to the total energy, suppressed by
, since in that case neglecting the terms higher order in q/m can be justified. Under this condition, the two-body terms in the Hamiltonian in equation (162) make a small contribution to the total energy, suppressed by 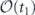 compared to the one-body terms. Recall that we also needed mt2 ≪ 1 to justify the collisionless approximation used in the proof of theorem 2; this condition is subsumed by
compared to the one-body terms. Recall that we also needed mt2 ≪ 1 to justify the collisionless approximation used in the proof of theorem 2; this condition is subsumed by 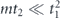 if
if 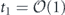 .
.
We see that there is a regime
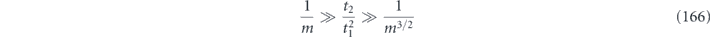
in which our approximations are reliable, yet the multiplicative corrections to  are large. That large corrections occur, even when the two-body terms make a small contribution to the total energy, is not a surprise; we have found as expected that the noise correlations can substantially enhance the probability of a logical error. The important point established by theorem 2 (at least for the simple noise model we have analyzed) is that even when the correlated noise produces large corrections to the logical channel, the corrections occur in both the coherent part and the incoherent part of the channel, so that our conclusion that the coherence is strongly suppressed for large n continues to apply.
are large. That large corrections occur, even when the two-body terms make a small contribution to the total energy, is not a surprise; we have found as expected that the noise correlations can substantially enhance the probability of a logical error. The important point established by theorem 2 (at least for the simple noise model we have analyzed) is that even when the correlated noise produces large corrections to the logical channel, the corrections occur in both the coherent part and the incoherent part of the channel, so that our conclusion that the coherence is strongly suppressed for large n continues to apply.
It is not immediately obvious why the leading power of m in equation (164) should be m3q/2, because higher powers of m occur in Ω(q − kR, kR) and Δ(q − kR, kR) for each fixed kR and q. It turns out that these higher powers of m all cancel when we do the sum over kR. In appendix
6. The toric code against coherent noise
We now analyze the logical channel for the two-dimensional toric code on an L × L square lattice, where L is odd. We will consider uncorrelated unitary noise acting on the 2L2 qubits, and suppose that error correction is performed using minimal-weight decoding. Our goal is to show that, when the noise is sufficiently weak, the coherence of the logical noise channel is highly suppressed for large L.
Our analysis will draw heavily on the tools we developed in our study of the repetition code. Before proceeding further, we will review some notation.
6.1. The toric code
We will consider the 2D toric code, which is defined on a square lattice with qubits placed on edges. We choose a square patch of lattice with side length L and identify opposite edges. (The toric code can be constructed on a lattice with boundaries, but for simplicity we choose periodic boundary conditions.) The stabilizer group for the toric code is generated by the X and Z generators shown in figure 2. The logical operators of the toric code are topologically non-trivial loops that wrap around the torus. Figure 3 shows two logical operators.
Figure 2. In blue is a Z-type stabilizer generator for the toric code. There are Z generators on every plaquette in the lattice. In red is an X-type stabilizer generator. There are X generators at every vertex of the lattice.
Download figure:
Standard image High-resolution imageFigure 3. This figure illustrates two of the logical Pauli operators in the toric code. X and Z logical operators are shown for one of the two encoded qubits. Each logical operator is a topologically non-trivial loop that wraps around the torus. The logical operators for the other encoded qubit are similar but rotated by 90 degrees.
Download figure:
Standard image High-resolution imageThe toric code is parameterized by the linear dimensions of the lattice; when the side length is L, the code distance (the minimum weight of a nontrivial logical operator) is L. We will also sometimes refer to L as the code 'size'. The number of physical qubits in the code block is 2L2, and there are two encoded logical qubits. To analyze the logical channel, we must choose a decoding procedure. Decoding the toric code is a well-studied problem and many good algorithms are known [30–32]. We will choose minimal-weight decoding, in which the applied recovery operation has the lowest possible weight consistent with the measured error syndrome. This recovery operation can be computed efficiently on a classical computer [33], and corrects the error with a success probability that is exponentially close to 1 when L is large and the noise is both sufficiently weak and sufficiently weakly correlated.
6.2. Notation
We will use the chi matrix to describe the physical noise channel 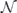 acting on the 2L2 qubits in the code block:
acting on the 2L2 qubits in the code block:
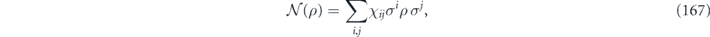
where {σi} is a basis of Pauli operators.
Definition 1. When we speak of a 'noise term', we will mean a component of the chi matrix for the physical noise channel acting on the qubits in the code block. We will find it convenient to use the notation (σiρ σj) for the number χij, the coefficient of σiρ σj in the chi-matrix expansion in equation (167).
We may choose the index that labels a Pauli operator to be (s, a, x ), where σ(s, a, x ) = EsLaGx; here s denotes the error syndrome, Es is the standard error associated with the syndrome s, La is a standard choice for the physical Pauli operator that acts as the logical Pauli operator 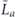 , and Gx is an element of the code stabilizer. To compute the logical chi matrix, we sum over the syndrome s and the stabilizer elements, observing that the standard error Es is removed by the recovery procedure. Hence we find that a term in the logical chi matrix can be expressed in our notation as
, and Gx is an element of the code stabilizer. To compute the logical chi matrix, we sum over the syndrome s and the stabilizer elements, observing that the standard error Es is removed by the recovery procedure. Hence we find that a term in the logical chi matrix can be expressed in our notation as
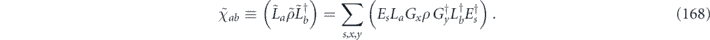
We say that the diagonal components of the logical chi matrix 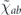 with a = b are 'incoherent' noise terms. and that the off-diagonal terms with a ≠ b are 'coherent'.
with a = b are 'incoherent' noise terms. and that the off-diagonal terms with a ≠ b are 'coherent'.
6.3. Coherent and incoherent logical components
We are going to analyze the coherent and incoherent sums separately at first. Using path counting and assuming the noise is sufficiently weak, we will prove that in both cases the logical chi matrix is dominated by 'short logical strings' (logical Pauli operators of relatively low weight), those with length ⩽L + 2ζ for a constant ζ. Then by summing up the contributions due to these short logical strings, we will derive an inequality relating the coherent and incoherent components of the logical channel.
Our argument will use equation (168), where we have expressed the logical chi matrix as a sum of terms in the physical chi matrix. In the next several sections we will analyze the sums contributing to coherent and incoherent components of 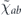 . We will make a series of approximations to simplify the sums by neglecting certain terms. In the end we will demonstrate that the two sums are related by a constant factor.
. We will make a series of approximations to simplify the sums by neglecting certain terms. In the end we will demonstrate that the two sums are related by a constant factor.
6.4. The coherent sum
First, consider the coherent sum. The coherent components of the logical noise channel are sums of terms from the physical noise channel. We want to upper bound the magnitude of these coherent logical components. Before we go any further, we will make some simplifications. For one, we will neglect certain coherent logical noise components. We focus on the components of the logical noise 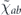 , where exactly one of the operators La and Lb is identity and the other is either an X or a Z error on one of the two encoded qubits. These components of the logical noise channel can be expressed as a sum over physical noise terms:
, where exactly one of the operators La and Lb is identity and the other is either an X or a Z error on one of the two encoded qubits. These components of the logical noise channel can be expressed as a sum over physical noise terms:
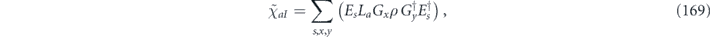
where La is either an X or Z logical error on one of the two encoded qubits of the toric code. In appendix
We will make use of another way of writing the coherent sum. Each coherent term in the form of equation (169) can be unambiguously associated with a logical string. The product of the Pauli operators acting on the left-hand and right-hand sides is the logical operator LaGxGy, which in general consists of a connected logical string wrapping around the code block, accompanied by some number of closed loops. To be concrete, if La is a logical X error, then the logical string contains only physical X errors, the closed loops are either loops of X errors which are disjoint from the logical string, or closed loops of Z errors which may or may not intersect with the logical string or with the closed loops of X errors (the intersections are the Y errors).
Definition 2. For a given noise term  , we can extract a connected logical string by removing the topologically trivial loops from LaGxGy. Call this logical string
, we can extract a connected logical string by removing the topologically trivial loops from LaGxGy. Call this logical string 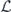 . We define the 'connected part' of the noise term as the restriction to the qubits in
. We define the 'connected part' of the noise term as the restriction to the qubits in  . The connected part of
. The connected part of 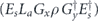 is a noise term given by
is a noise term given by
where the symbol  denotes the restriction of an operator to the support of
denotes the restriction of an operator to the support of  .
.
Definition 3. For a noise term 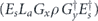 the 'disconnected part' is the part of the noise term not in the connected part. Once again, we can define a continuous logical string
the 'disconnected part' is the part of the noise term not in the connected part. Once again, we can define a continuous logical string 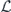 by removing all topologically trivial closed loops from LaGxGy. The disconnected part of
by removing all topologically trivial closed loops from LaGxGy. The disconnected part of 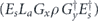 is given by
is given by
where the symbol  denotes the restriction of an operator to the qubits in the complement of the support of
denotes the restriction of an operator to the qubits in the complement of the support of  .
.
Furthermore, we will be able to assume that all of the physical single-qubit errors in the connected part are X- or Z-type. For example, in the case of a logical X-type error, we may neglect terms in which a closed loop of Z errors intersects with the logical string. To justify this assumption, we show in appendix
A coherent term contributing to the logical chi matrix element 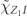 , which includes disconnected errors, is illustrated in figure 4. The disconnected part includes identity on the qubits without errors in addition to the disconnected errors. Z errors acting on the density operator from the left are shown in red, and Z errors acting from the right are shown in blue. Because the errors acting from the left and right have the same syndrome s, the product of the left and right logical operators is logical. The connected logical string crosses the code block near the bottom of the figure. Associated with the syndrome s is the corresponding standard error Es, the Z error of minimal weight with that syndrome. (If the minimal-weight error is not unique, we arbitrarily choose Es to be one of the errors of minimal weight by convention.) To evaluate the logical chi matrix element
, which includes disconnected errors, is illustrated in figure 4. The disconnected part includes identity on the qubits without errors in addition to the disconnected errors. Z errors acting on the density operator from the left are shown in red, and Z errors acting from the right are shown in blue. Because the errors acting from the left and right have the same syndrome s, the product of the left and right logical operators is logical. The connected logical string crosses the code block near the bottom of the figure. Associated with the syndrome s is the corresponding standard error Es, the Z error of minimal weight with that syndrome. (If the minimal-weight error is not unique, we arbitrarily choose Es to be one of the errors of minimal weight by convention.) To evaluate the logical chi matrix element 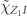 as in equation (168), we need to sum over the syndrome s and the stabilizer elements Gx and Gy. To facilitate estimating the sum, it will be helpful to organize it in an appropriate way.
as in equation (168), we need to sum over the syndrome s and the stabilizer elements Gx and Gy. To facilitate estimating the sum, it will be helpful to organize it in an appropriate way.
Figure 4. In this coherent term, the uncorrectable error OU (acting on the density operator from the left) is in red, while the correctable error OC (acting from the right) is in blue. Only Z errors are shown. The connected logical string consists of the five qubits near the bottom that are split between red and blue. In addition, there are disconnected errors in the form of the closed loop containing two red edges and two blue edges and the pair of cancelling single-qubit errors acting on the left (in red) and right (in blue).
Download figure:
Standard image High-resolution imageTo this end, we introduce the following definition:
Definition 4. For a logical string 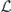 with no topologically trivial closed loops, the word 'partition' denotes a connected noise term (O1ρO2) such that
with no topologically trivial closed loops, the word 'partition' denotes a connected noise term (O1ρO2) such that 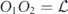 and O1 and O2 are disjoint. In other words, each partition is a way of dividing the single-qubit errors in
and O1 and O2 are disjoint. In other words, each partition is a way of dividing the single-qubit errors in  into two subsets, O1 and O2. By definition O1 and O2 share the same syndrome. Because the code size L is odd, exactly one of O1 and O2 will be corrected to a logical operator with the same action as
into two subsets, O1 and O2. By definition O1 and O2 share the same syndrome. Because the code size L is odd, exactly one of O1 and O2 will be corrected to a logical operator with the same action as  and the other will be corrected to the logical identity.
and the other will be corrected to the logical identity.
For each fixed logical string, the sum over all partitions of the logical string will produce the full set of connected terms derived from that logical string. The sum over partitions, for a fixed logical string, is directly analogous to the sum over syndromes we encountered in our analysis of the repetition code in section 4.3. In the case of the toric code, we compute the coherent part 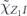 of the logical channel by summing over all possible logical strings, and for each choice of logical string we sum over all partitions of the logical string. In addition, for each chosen logical string, we sum over the possible disconnected pieces, the additional closed loops of Z errors which are disjoint from the logical string.
of the logical channel by summing over all possible logical strings, and for each choice of logical string we sum over all partitions of the logical string. In addition, for each chosen logical string, we sum over the possible disconnected pieces, the additional closed loops of Z errors which are disjoint from the logical string.
Schematically, the coherent component of the logical chi matrix is

This form will allow us to approximate the coherent sum. Assuming that the noise is sufficiently weak, we will prove that we can truncate the sum over logical strings, including only short strings. Furthermore, most of the short logical strings have a particular shape. To complete the argument, we will show that the disconnected sum is approximately the same for each short logical string and for each partition of the logical string.
6.5. Counting of logical strings
We want to find an upper bound on the magnitude of the coherent component of the logical noise channel. We have already put the sum over physical noise terms into a convenient form by factoring out the disconnected piece of each term. Next, we will simplify the sum by restricting the set of connected pieces we need to consider; we will neglect the long logical strings in favor of those strings with length no larger than than L + 2ζ, where ζ is an L-independent constant. To justify this truncation we will require a strong assumption on how the physical noise strength scales with L; namely, the single-qubit rotation angles must scale as 1/L.
In equation (172) we wrote the contribution of a given logical string to the coherent logical noise as a product of a connected and disconnected part as described in definitions 2 and 3. The connected part summed over partitions as defined in definition 4. The sum over partitions contains 2w−1 terms for a weight-w logical string (one containing w lattice edges). Suppose that the unitary rotation 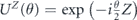 is applied to each physical qubit in the toric code block. We can upper bound the sum using the number of terms times the magnitude of each term. Then the contribution of each logical string is upper bounded by 2w−1(|sin(θ/2)|cos(θ/2))w times the factor from the disconnected part. We will prove in section 6.7 and appendix
is applied to each physical qubit in the toric code block. We can upper bound the sum using the number of terms times the magnitude of each term. Then the contribution of each logical string is upper bounded by 2w−1(|sin(θ/2)|cos(θ/2))w times the factor from the disconnected part. We will prove in section 6.7 and appendix
There is a regime where we can upper bound the number of logical strings as a function of the string's length. Asymptotically, the number cw of self-avoiding random walks with length w was proven in [34] to satisfy
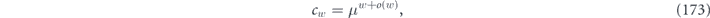
where μ ≈ 2.64 for the 2D square lattice. We can start a walk from a fixed point along one edge of the toric code. Logical strings will be the self-avoiding walks that wrap around the torus and end at the starting point. We can use equation (173) to show that the contribution to the coherent logical noise from logical strings of length ℓ is exponentially decaying with ℓ as long as |θ| < arcsin 1/μ ≈ 0.39. This statement applies only for logical strings with length much greater than the minimum of L, the code distance. We do not have a precise estimate indicating at what length above L the number of logical strings begins to scale like equation (173). This means we do not know at what string length ℓ the contribution will begin to decay exponentially, and therefore we do not know where to truncate the sum if we wish to use equation (173) to bound the terms we are neglecting. In any case, in our subsequent analysis we will truncate the sum over the string length ℓ at L + 2ζ for some constant ζ. In this regime the asymptotic estimate in equation (173) is not helpful and we will not make use of it. Instead, we will assume that |θ| is sufficiently small that we can use the following lemma to bound the terms we neglect.
Lemma 3. Suppose that |sin θ| < 1/L. In equation (172) we wrote 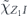 as a sum over logical strings. If we truncate the sum to include only logical strings of length w ⩽ L + 2ζ, then magnitude of the difference between the truncated sum and the complete sum is
as a sum over logical strings. If we truncate the sum to include only logical strings of length w ⩽ L + 2ζ, then magnitude of the difference between the truncated sum and the complete sum is
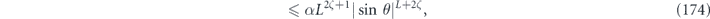
where α = (1 − L|sin θ|)−1.
Proof. We begin by fixing a point along one edge of the code block, which can be chosen in L ways. We will count the number of logical strings that wrap around the torus and pass through that fixed point on the edge. Let ℓ denote the logical string length. At minimum length ℓ = L, there is only one logical string. At length ℓ = L + 2, if the logical string runs left to right across the code, then the string features one step up and one step down. There are L(L − 1) such logical strings. At longer string lengths, there are many steps up and down. We can upper bound the number of such logical strings by supposing we choose any of the L positions to place each of the steps up and steps down. We divide by ((ℓ − L)/2)! to capture the fact that the (ℓ − L)/2 steps up are all identical, and the same for the steps down. This encompasses all possible combinations of steps up and down including cases where the several steps up are placed at the same point creating a step up of more than one. It does not encompass strings that backtrack, but in lemma 9 we show that among strings of length L + 2ζ, those that feature backtracking are suppressed by 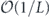 . Also, the number of strings grows most quickly near minimum and eventually approaches the asymptotic value, where the number of strings grows like μL. In the asymptotic regime, the number of strings grows much slower than Lℓ−L. We conclude that
. Also, the number of strings grows most quickly near minimum and eventually approaches the asymptotic value, where the number of strings grows like μL. In the asymptotic regime, the number of strings grows much slower than Lℓ−L. We conclude that
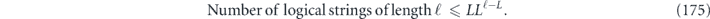
In equation (172) for each logical string in the sum the contribution to the logical noise is a sum over partitions of the connected part times a disconnected part. We will discuss the sum over partitions in detail in section 6.6, but for now it is enough that we know that the sum over partitions contains 2ℓ−1 terms for each connected logical string of length ℓ. These terms have different phases and in general the sum can be complicated. We can obtain a simple bound by multiplying the number of terms by the magnitude of each term, in other words treating all the phases as if they are the same. For each weight w string,
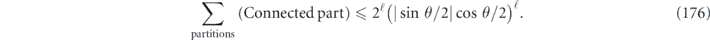
We still have to handle the disconnected piece. In section 6.7 we will argue that the disconnected sum decreases as the length of the logical string increases. Furthermore, the disconnected part equals 1 up to corrections which are small for logical strings with length ⩽L + 2ζ for a constant ζ. This means that we can upper bound the coherent logical noise component 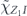 by
by
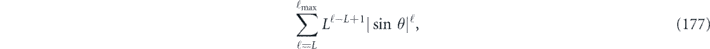
where ℓmax is the longest Z1 logical string supported on the code. If |sin θ| < 1/L, the contribution from logical strings of length ℓ decreases exponentially with ℓ.
If we truncate the sum over logical strings to those with weight w ⩽ L + 2ζ, the error we make is equal to the total contribution of strings with weight w > L + 2ζ. The contribution at weight w is exponentially decreasing with w, so we can bound the sum over the long logical strings using
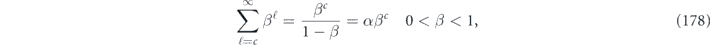
where  . We conclude that the absolute error we make by truncating the series is
. We conclude that the absolute error we make by truncating the series is
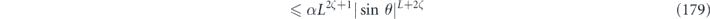
where α = (1 − L|sin θ|)−1. Therefore, the error due to truncation is exponentially small in both L and ζ. □
In lemma 3 we proved an upper bound on the absolute magnitude of the error due to truncation in the coherent sum. However, so far we have not described any lower bound on the terms that we have kept, arising from the logical strings with length ⩽L + 2ζ. Therefore, we have not yet justified that the error we have neglected is small relative to the coherent noise contributions that we kept. However, we will prove in section 6.10 that the incoherent logical noise component is at least 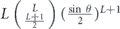 ; compared to this incoherent component the contribution in equation (179) to the coherent component due to strings of length >L + 2ζ is suppressed by a factor (L sin θ)2ζ. This means that the error we make in truncating the sum in lemma 3 is negligible compared to the incoherent component, an observation which will be helpful for showing that the coherence of the logical channel is suppressed. For now, we will restrict our attention to connected logical strings with length ⩽L + 2ζ for a constant ζ. We will refer to these as 'short logical strings'.
; compared to this incoherent component the contribution in equation (179) to the coherent component due to strings of length >L + 2ζ is suppressed by a factor (L sin θ)2ζ. This means that the error we make in truncating the sum in lemma 3 is negligible compared to the incoherent component, an observation which will be helpful for showing that the coherence of the logical channel is suppressed. For now, we will restrict our attention to connected logical strings with length ⩽L + 2ζ for a constant ζ. We will refer to these as 'short logical strings'.
Definition 5. A 'short logical string' is a nontrivial logical Pauli operator with no topologically trivial closed loops and length ⩽L + 2ζ, where L is the code size and ζ is our chosen cutoff constant.
6.6. Sum over partitions
In the previous section we restricted our attention to short logical strings, which have length ⩽L + 2ζ where L is the code size and ζ is a constant. We can go further by characterizing the shape of a logical string, and arguing that logical strings with shape meeting certain criteria give a dominant contribution to the logical channel.
Definition 6. Among short logical strings, we will speak of those with 'typical shape.' This means two things. First, supposing that the logical string in question runs left to right across the code block, then the steps up and down along the string are by one lattice spacing at a time. Furthermore, the string contains no backtracking steps that move from right to left. Second, the individual steps up and down are separated from each other by at least 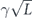 , where γ is a small constant we may choose. This constant γ will appear in the error term in many of our subsequent estimates.
, where γ is a small constant we may choose. This constant γ will appear in the error term in many of our subsequent estimates.
In lemmas 9 and 10 in appendix
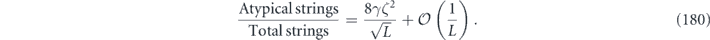
Figure 5 illustrates a string with typical shape for some small γ. Short logical strings with typical shape are simple, which makes our analysis easier, particularly when we discuss the sum over partitions.
Figure 5. Here we have one logical string  of length 15 in an L = 9 toric code. Imagine the code size growing while ζ remains fixed. The likely strings will be those where the steps up and down are widely separated.
of length 15 in an L = 9 toric code. Imagine the code size growing while ζ remains fixed. The likely strings will be those where the steps up and down are widely separated.
Download figure:
Standard image High-resolution imageLet's revisit the sum over partitions for a fixed connected logical string. That is, for a given logical string contributing to 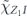 , we wish to enumerate all the ways to divide the Z errors along the string into an uncorrectable error acting on the density operator from the left and a correctable error acting from the right. This sum over partitions of a fixed logical string is analogous to the sum we encountered when we summed over syndromes in our analysis of the repetition code. In the case of the repetition code of length n, there is just one length-n 'logical string' to consider, and summing over syndromes is equivalent to summing over all ways of choosing a (correctable) error acting on the right that has weight at most (n − 1)/2 (where n is odd).
, we wish to enumerate all the ways to divide the Z errors along the string into an uncorrectable error acting on the density operator from the left and a correctable error acting from the right. This sum over partitions of a fixed logical string is analogous to the sum we encountered when we summed over syndromes in our analysis of the repetition code. In the case of the repetition code of length n, there is just one length-n 'logical string' to consider, and summing over syndromes is equivalent to summing over all ways of choosing a (correctable) error acting on the right that has weight at most (n − 1)/2 (where n is odd).
In the toric code, although the sum over partitions is similar to the sum over syndromes in the repetition code, there is a complication.
Definition 7. An 'exceptional term' is a partition of a connected logical string 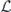 such that the uncorrectable error has lower weight than the correctable error.
such that the uncorrectable error has lower weight than the correctable error.
In some cases, depending on the geometry of the logical string, we will have some number of exceptional terms. These exceptional terms complicate our analysis of the logical channel. Fortunately, because we need only consider contributions to the logical channel arising from short logical strings when the noise is weak enough, we will be able to fully characterize the exceptional terms and show they are negligible.
How exceptional terms can occur is illustrated in figure 6. Here, for the toric code with L = 9, we consider the logical string of length 15 shown in figure 5, and we have chosen a partition such that the uncorrectable error shown in red has weight 7, while the correctable error shown in blue has weight 8. Note that the minimal-weight standard error associated with the error syndrome on the logical string has weight 6—it follows nearly the same path as the correctable error, but achieves a lower weight than the correctable error by taking a 'shortcut' across the blue notch on the logical string. Another example of an exceptional term for this same logical string is shown in figure 7, where this time the weight of the uncorrectable error is 6, and the minimal-weight error has weight 5. Again, the minimal-weight error takes a shortcut, avoiding the excursions up and down followed by the correctable error.
Figure 6. Now we choose a subset of 7 of the errors in the logical string in figure 5. The uncorrectable error OU is in red and the correctable error OC is in blue. All three errors along the 'cap' in the top right appear on the correctable side. For this reason, the correctable error has weight 8, which is higher than the uncorrectable error with weight 7. We call this a weight-7 exceptional term.
Download figure:
Standard image High-resolution imageFigure 7. Again, one possible partition of the logical string in figure 5 is illustrated. The uncorrectable error OU is in red, and the correctable error OC is in blue. The correctable error includes all the errors along both the cap in the top right and the bottommost cap of the logical string. For this reason, the correctable error has weight 9, while the uncorrectable error has weight 6. Therefore, we call this partition a weight-6 exceptional term.
Download figure:
Standard image High-resolution imageFor all these examples, the correctable error contains the qubits along the logical string that make the furthest excursions up and down. This turns out to be a universal rule, at least among the typical short logical strings—for exceptional terms, the uncorrectable error has no support on the outermost steps along the string. In the next lemma we count the number of exceptional terms and find that relative to the total number of partitions of a typical short logical string, these exceptional terms are exponentially unlikely in L.
Lemma 4. Fix a logical string of length ℓ ⩽ L + 2ζ, where ζ is a specified L-independent constant, with a typical shape according to definition 7. This means that if the string runs left to right across the code block, it has steps up and down by one lattice spacing at a time and the steps are separated by at least 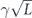 for some constant γ. To keep the fraction of atypical strings small in equation (180), we will choose γ to be a sufficiently small constant. Now consider all the ways of partitioning this typical logical string into a correctable error and an uncorrectable error. Then the fraction of exceptional partitions relative to all partitions of this string is bounded by
for some constant γ. To keep the fraction of atypical strings small in equation (180), we will choose γ to be a sufficiently small constant. Now consider all the ways of partitioning this typical logical string into a correctable error and an uncorrectable error. Then the fraction of exceptional partitions relative to all partitions of this string is bounded by
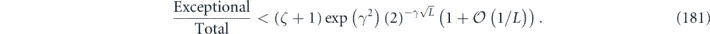
Exceptional terms are exponentially rare for typical short logical strings and large L.
Proof. Take a logical string of length ℓ ⩽ L + 2ζ with typical shape. Each step is separated from the others by at least 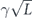 for some γ. Now, consider taking a subset of
for some γ. Now, consider taking a subset of  of the qubits in the logical string. We would expect such a subset to be correctable. If not, this partition is exceptional.
of the qubits in the logical string. We would expect such a subset to be correctable. If not, this partition is exceptional.
Choose a partition of a connected logical string and let OU be the uncorrectable error and OC be the correctable error. OU and OC share a syndrome by definition. Denote that syndrome by s. The decoding algorithm, which in our case is minimal-weight decoding, applies some correction to this syndrome to return it to the code space. Call this correction Es. Es is by definition a correctable error in the code, and therefore, because we are using minimal-weight decoding, Es must have lower weight than OU. The fact that we chose our code size L to be odd ruled out the case where the two might be equal. Now if the partition we are considering happens to be exceptional, this means by definition that OC has higher weight than OU, and we have
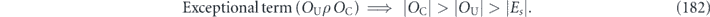
We will use this condition to bound the number of exceptional terms for a given connected logical string.
What does it mean for OC to have higher weight than Es? For connected logical strings of typical shape as in definition 6, this happens only if on some subset or subsets of the logical string, the correctable error OC contains errors on qubits arranged in a 'cap'. By this we mean a configuration of errors where the errors form three edges of a rectangle. The minimal-weight decoder will choose the fourth edge of the rectangle as part of the correction Es. This is illustrated in figures 6 and 7. If the connected logical string has length greater than L, then it has steps up and down if it crosses the code block left to right. In every exceptional term, the correctable error OC will contain the outermost qubits around some of the steps, forming a cap.
Now that we have a simple necessary condition for an exceptional term, we will bound the number of exceptional terms for each short logical string with a typical shape according to definition 6. Start with a logical string of length ℓ. Consider first the partitions into  and
and 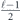 . Of course, those partitions for which the weight-
. Of course, those partitions for which the weight-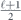 error is correctable will be exceptional. Every exceptional term like this will have the property that the correctable error contains some number of 'caps' where all of the qubits around three sides of a rectangle are part of the correctable error. To bound the number of exceptional terms, we will count the number of partitions with this property.
error is correctable will be exceptional. Every exceptional term like this will have the property that the correctable error contains some number of 'caps' where all of the qubits around three sides of a rectangle are part of the correctable error. To bound the number of exceptional terms, we will count the number of partitions with this property.
Each partition of a weight-ℓ connected logical string into weight-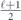 and
and 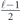 errors is formed by choosing
errors is formed by choosing 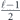 out of the ℓ errors in the logical string. This is what we mean by a partition. We want to count the number of ways of choosing these errors such that the correctable error (of weight
out of the ℓ errors in the logical string. This is what we mean by a partition. We want to count the number of ways of choosing these errors such that the correctable error (of weight 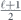 because we are counting exceptional terms) contains all the errors along a 'cap'. This means that the subset of
because we are counting exceptional terms) contains all the errors along a 'cap'. This means that the subset of 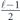 errors contains no errors along one or more of the 'caps'. A typical short logical string running left to right across the code consists of horizontal segments separated by single steps up and down. The outermost of these steps form 'caps'. The number of such 'caps' depends on the particular pattern of steps in the logical string. However, we can bound the number of exceptional terms by counting the number of ways of choosing no qubits along one of the horizontal segments of length
errors contains no errors along one or more of the 'caps'. A typical short logical string running left to right across the code consists of horizontal segments separated by single steps up and down. The outermost of these steps form 'caps'. The number of such 'caps' depends on the particular pattern of steps in the logical string. However, we can bound the number of exceptional terms by counting the number of ways of choosing no qubits along one of the horizontal segments of length 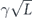 . This is because every 'cap' consists of an outermost horizontal segment combined with the up and down steps on either side. This counting gives
. This is because every 'cap' consists of an outermost horizontal segment combined with the up and down steps on either side. This counting gives
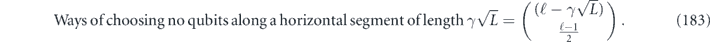
We want the number of ways of choosing no qubits along at least one of the horizontal segments. There are ⩽2ζ steps up and down along the logical string. Therefore, there are ⩽2ζ horizontal segments. We can use a union bound to write
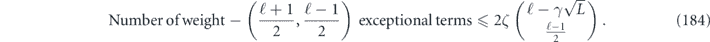
This is relative to the total number of 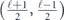 partitions for our logical string of length ℓ, which is
partitions for our logical string of length ℓ, which is
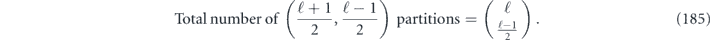
We can expand the ratio of exceptional terms to the total using Stirling's approximation. This gives
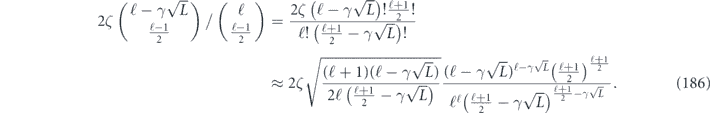
This approximation holds up to corrections  . We can rewrite this as
. We can rewrite this as
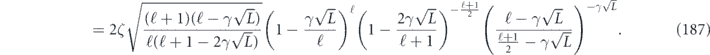
Next we square the 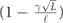 term in order to combine terms:
term in order to combine terms:
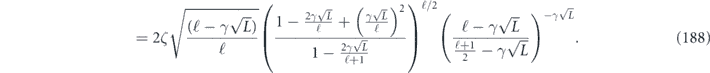
We upper bound the term inside the radical and also the term raised the power ℓ/2:
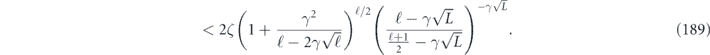
The second of the three terms is exponentially decaying to exp(γ2/2). As long as ℓ ⩾ 4, we can bound it by
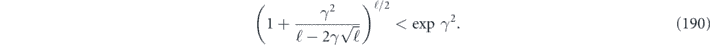
Now, we bound 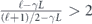 and assemble one term raised to the power L and another to the power (ℓ − L)/2:
and assemble one term raised to the power L and another to the power (ℓ − L)/2:
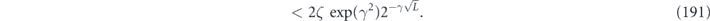
We chose some small value for γ in lemma 10, and then the number of exceptional terms with a weight- logical error on one side and a weight-
logical error on one side and a weight- correctable error on the other is exponentially small in L.
correctable error on the other is exponentially small in L.
For the chosen connected logical string of weight ℓ, we have calculated the fraction of exceptional terms among the partitions into  and
and 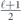 . We will also have exceptional terms among the partitions into other weights, possibly all the way down to partitions into weight
. We will also have exceptional terms among the partitions into other weights, possibly all the way down to partitions into weight 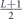 and
and 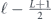 . Above, we applied the condition in equation (182) that for every exceptional term the correctable error must have higher weight than the minimal-weight correction. If we apply this same method to bound the number of exceptional terms among partitions into
. Above, we applied the condition in equation (182) that for every exceptional term the correctable error must have higher weight than the minimal-weight correction. If we apply this same method to bound the number of exceptional terms among partitions into 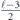 and
and 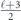 , we find that the correctable error must be at least 4 longer than the minimal-weight correction. This means we want to count the number of configurations where at least two of the 'caps' are contained in the correctable error. This is clearly far fewer than the number of configurations where one 'cap' is contained. Therefore, the ratio of exceptional terms to total partitions is bounded by the ratio we found for partitions into
, we find that the correctable error must be at least 4 longer than the minimal-weight correction. This means we want to count the number of configurations where at least two of the 'caps' are contained in the correctable error. This is clearly far fewer than the number of configurations where one 'cap' is contained. Therefore, the ratio of exceptional terms to total partitions is bounded by the ratio we found for partitions into 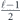 and
and 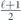 .
.
In the end we see that number of weight-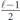 exceptional terms is exponentially small in L for fixed ζ and further that the weight-
exceptional terms is exponentially small in L for fixed ζ and further that the weight-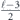 exceptional terms are exponentially small in L relative to the higher-weight exceptional terms, and so on. Then for large L, exceptional terms are negligible. □
exceptional terms are exponentially small in L relative to the higher-weight exceptional terms, and so on. Then for large L, exceptional terms are negligible. □
Lemma 4 allows us to approximate the sum over partitions for a typical, short logical string  . Neglecting exceptional terms, the sum over partitions resembles the calculation of what we called δ in the repetition code in equations (87) and (118). Let
. Neglecting exceptional terms, the sum over partitions resembles the calculation of what we called δ in the repetition code in equations (87) and (118). Let  have length ℓ. Each partition contributes
have length ℓ. Each partition contributes 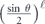 with a phase. The sum over partitions is given by
with a phase. The sum over partitions is given by
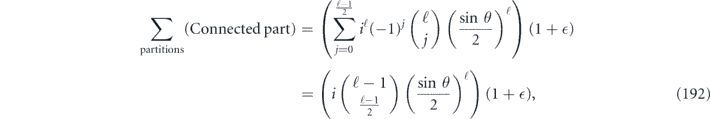
where  is the error from exceptional terms, which is upper bounded
is the error from exceptional terms, which is upper bounded
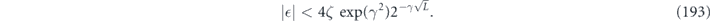
This is two times the expression in equation (191), because each exceptional term contributes to the sum over partitions with the opposite sign relative to a non-exceptional term.
6.7. The disconnected part
In the preceding subsections, we analyzed the coherent component of the logical noise channel, expressed as a sum over many physical noise terms. So far we have only considered the connected logical string associated with each coherent term. In this subsection, we will analyze the disconnected errors in more detail, and describe more rigorously how they affect the evaluation of the coherent terms in the logical channel. In section 6.4 we described how to decompose a contribution to  into a connected piece and some number of disconnected pieces. The left- and right-hand side of each coherent term can be expanded as the product of the errors contained in the connected logical string and the errors outside of it; schematically,
into a connected piece and some number of disconnected pieces. The left- and right-hand side of each coherent term can be expanded as the product of the errors contained in the connected logical string and the errors outside of it; schematically,
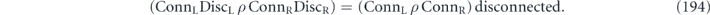
The factor 'disconnected' means the contribution to the coherent term from disconnected components that appeared in equation (172). The product of the two (disjoint) factors ConnL and ConnR yields the connected logical string, with no additional disjoint loops included. The connected factor includes sin θ/2 cos θ/2 for each qubit along the connected logical string. The disconnected factor includes (cos θ/2)2 on every qubit not in the connected logical string in addition to a sum over all possible disconnected errors.
Fix a partition (OUρOC) of a short, typical logical string, and consider dressing it with disconnected errors. We can distinguish two types of added errors: incoherent and coherent. If the disconnected error is DL acting on the density operator from the left, and DR acting from the right, then if a particular qubit is hit by the same error contained in both DL and DR, we say that the disconnected error acting on that qubit is incoherent. If a particular qubit is hit by distinct errors contained in DL and DR, then the error is coherent. The product DLDR of the errors added on right and left must be a non-identity stabilizer operator, i.e. a closed loop or a set of disjoint closed loops. (Here, because we are investigating the encoded Z errors in the logical channel, only the Z-type physical errors are considered.) The two types of added error—incoherent and coherent—are shown in figure 8, where (A) is an incoherent-type added error and (B)–(D) are coherent-type.
Figure 8. Here we have a partition (OUρOC) of a connected logical string adorned in four different ways by added errors. The errors in red are the uncorrectable part, OU, of the partition, while the errors in blue form the correctable part, OC. The four added errors are labelled (A)–(D). In (A), the same error has been added to both OU and OC. In (B) and (D), three errors are added to one side of the partition and one to the other. This produces a minus sign. In (C), two errors are added to each side.
Download figure:
Standard image High-resolution imageLet us first treat the case of incoherent-type added errors, where DL = DR ≡ D. These are the ones with the same disconnected error added to both operators in the partition, for example (A) from figure 8. These terms do not change the phase of the original partition, and they multiply the magnitude by (sin θ/2)2m if m is the weight of the error added on each side. The disconnected part contains cos2 θ/2 on each qubit corresponding to no disconnected errors plus many configurations of disconnected errors. The incoherent-type added errors on each qubit in the disconnected part supply the sin2 θ/2 term to give 1 on the qubits not contained in the connected logical string. This reasoning applies to each incoherent-type added error that does not change how the operators OU and OC are decoded. In other words, if D is the disconnected error we add to OU and OC, we require that DOU is an uncorrectable error.
We must be careful because in some cases the added incoherent-type errors can change how the correctable and uncorrectable errors in the partition are decoded. The added error can 'flip' the uncorrectable error to a correctable one. This means that the noise term that contributes to the logical 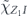 component is not (DOUρDOC) as we would have expected but is instead (DOCρDOU). This term has the opposite sign relative to the expected term. This is only possible when the added error D is located very near the connected logical string and only for special partitions. We prove in lemma 11 in appendix
component is not (DOUρDOC) as we would have expected but is instead (DOCρDOU). This term has the opposite sign relative to the expected term. This is only possible when the added error D is located very near the connected logical string and only for special partitions. We prove in lemma 11 in appendix
What of the coherent-type added errors? Again, fix a partition of a connected logical string. Let OU and OC be the correctable and uncorrectable errors. Now consider choosing a stabilizer operator or a closed loop, ℓ that is disjoint from the connected logical string. Let the length of the loop be |ℓ|. Now choose a subset of p of the qubits in the loop, and let the disconnected error DL act on these p qubits from the left, while the disconnected error DR acts on the remaining |ℓ| − p qubits from the right. Suppose further that the qubits in the loop and the partition are such that the uncorrectable error OU plus the additional error DL remains uncorrectable. This need not always be true; we will consider the case where the OUDL is correctable in a moment.
Supposing that the disconnected error DL does not change the decoding, we can perform a sum over all the ways of choosing the p errors in DL from among the |ℓ| errors in the loop. The number of ways of choosing p errors is given by a binomial coefficient, and the magnitude of each term is suppressed by (sin θ/2)|ℓ| relative to the original partition of the connected logical string without any additional disconnected errors added. The phase of each term depends, as always, on the relative weight of the errors on the right and the left. The disconnected part contributes a phase of (i)p(−i)|ℓ|−p, and ℓ is a closed loop so |ℓ| is even. The sum yields
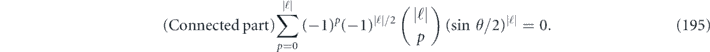
When we sum over all ways of forming disconnected terms out of the original loop ℓ, the sum is 0. This holds for any loop such that the disconnected part does not change how the connected part is decoded.
In the examples we considered in figure 8, the additional disconnected errors did not change how the connected part was decoded. This is the same condition we encountered in the discussion of incoherent-type added errors. In certain cases the error DL that we add to the OU side of the partition can be such that DLOU is a correctable operator. This means the partition is 'flipped' by the disconnected error. We account for this case in lemma 11 and prove that the contribution to the logical noise from these special disconnected terms is negligible for short logical strings.
Using lemma 11, we can neglect the added errors that change how the partition is decoded. Then we can conclude that the net contribution from coherent-type added errors is 0 and the incoherent-type added errors contribute a sin2 θ/2 factor on each qubit not in the connected logical string. This implies that the 'disconnected sum' term in equation (172) is equal to 1 plus a small correction. This implies that
where  is a connected, short, typical logical string, partitions refers to the partitions of
is a connected, short, typical logical string, partitions refers to the partitions of 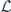 denoted (OUρOC), and
denoted (OUρOC), and 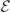 is a noise term. The error term satisfies
is a noise term. The error term satisfies
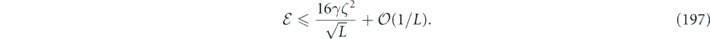
This error term is from lemma 11 and comes from the added errors that change how the partition is decoded. The term 'high weight' in equation (196) is the error from lemma 3 corresponding to the contributions of logical strings with length >L + 2ζ. We have not yet justified that this error is small relative to the short strings. This is because we do not have a lower bound on the short strings. The justification comes from our subsequent discussion of the incoherent logical noise components.
6.8. Incoherent sum
Now that we have simplified the sum for the coherent components of the logical noise channel, factored out the disconnected pieces, and performed the sum over syndromes for the connected pieces, we turn our attention to the incoherent logical noise components. We start by making several of the same simplifications we made in the coherent sum. Of the incoherent logical components 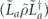 , we neglect all the terms where La is a logical Y operator or acts non-trivially on both encoded qubits. We retain only the terms where La is a logical X or Z on one of the two encoded qubits. The reason is the same as for the coherent sum. The neglected terms are much higher weight, such that the path counting excludes them. Then we have the sum
, we neglect all the terms where La is a logical Y operator or acts non-trivially on both encoded qubits. We retain only the terms where La is a logical X or Z on one of the two encoded qubits. The reason is the same as for the coherent sum. The neglected terms are much higher weight, such that the path counting excludes them. Then we have the sum
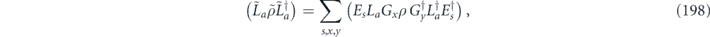
where La is an X or Z logical operator on one of the encoded qubits and identity on the other. Again, we suppose that all the angles are equal to some fixed θ for each single-qubit rotation. We will extend to general rotations in lemma 8.
Again, we will divide each term into connected and disconnected pieces. In this discussion of the incoherent logical noise components, definition 2 must be modified. The noise terms that enter into the incoherent logical noise contain an uncorrectable error on both sides of ρ. We will need to consider two logical strings in our definition.
Definition 8. The 'connected part' of a noise term 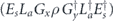 is a noise term defined in the following way: let
is a noise term defined in the following way: let  equal LaGx with all topologically trivial closed loops removed and
equal LaGx with all topologically trivial closed loops removed and  equal LaGy with all trivial closed loops removed. Then let A denote the set of qubits
equal LaGy with all trivial closed loops removed. Then let A denote the set of qubits  where either EsLaGx or EsLaGy, or both, act non-trivially. The connected part of
where either EsLaGx or EsLaGy, or both, act non-trivially. The connected part of 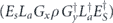 is given by
is given by
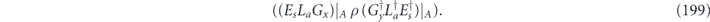
|A denotes the restriction of an operator to the set of qubits A.
If the incoherent term is (OUρOU'), then this definition captures the set of qubits in the support of OU or OU' that lie along the two logical strings formed by OU and Es and OU' and Es pruned of all trivial closed loops. Figure 9 illustrates the connected and disconnected part of a noise term that enters into the incoherent logical noise. The connected part of the noise term in the figure features factors of sin θ/2 cos θ/2 for the qubits that appear in exactly one of OU or OU' and sin2 θ/2 for the qubits that appear in both OU and OU'. We can lower bound the connected part of each incoherent noise term by  . This will be useful later on when we sum over many possible choices for the operators OU and OU'.
. This will be useful later on when we sum over many possible choices for the operators OU and OU'.
Figure 9. A noise terms (OUρOU') is shown with OU in red and OU' in blue. The standard correction Es chosen by the minimal-weight decoder is drawn as a dotted black line. The connected part of this noise term is signified by the orange qubits, while the disconnected part contains the black qubits.
Download figure:
Standard image High-resolution imageDefinition 9. The "disconnected part" of a noise term 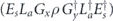 is the restriction of the noise term to the qubits not in the connected part. In definition 8 we constructed the set A, which contained the qubits in the connected part. The disconnected part is given by
is the restriction of the noise term to the qubits not in the connected part. In definition 8 we constructed the set A, which contained the qubits in the connected part. The disconnected part is given by
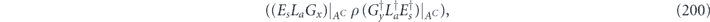
where  denotes the restriction of an operator to the complement of the set A.
denotes the restriction of an operator to the complement of the set A.
For the example in figure 9, the disconnected part features factors of sin θ/2 cos θ/2 for the six qubits along the trivial closed loop near the top of the figure and cos2 θ/2 for the rest of the qubits. For a given connected part, we can imagine adding disconnected errors to form many different noise terms. The connected part contains factors of sin θ/2 cos θ/2 for each qubit that appears in one of the uncorrectable errors and sin2 θ/2 for each qubit that appears in both errors. The disconnected term includes cos2 θ/2 for each qubit not in the connected part plus a sum over all possible coherent and incoherent-type disconnected error. Just as in section 6.7, when the disconnected errors do not change how the connected term is decoded, the incoherent-type errors give cos2 θ/2 + sin2 θ/2 = 1 on qubits not in the connected part. The coherent-type disconnected errors, which form loops split between left and right, sum to zero because of the alternating signs.
Just as in the case of the coherent logical noise components, some disconnected errors will not be allowed because they change how the connected term is decoded. We will set the disconnected part equal to 1 plus an error term that comes from these disallowed disconnected errors. In lemma 12 we justify this by proving that the error term is small. This is analogous to lemma 11, where we prove that the disconnected part of the coherent logical noise components is equal to 1 up to small corrections.
We want to continue to follow a similar argument to the one for the coherent terms. The next step is restricting the set of connected terms we consider. We will break up each error into connected and disconnected pieces and restrict ourselves to noise terms with low-weight connected part, where the total weight of the connected part is bounded by L + 2ζ + 1; here ζ is the same L-independent cutoff as in the coherent sum. Just as for the analysis of the coherent logical noise in section 6.5, we will require θ to scale like 1/L to justify this truncation of the noise terms contributing to the connected part.
Lemma 5. Consider an incoherent logical noise component, say 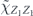 . We write this logical noise component as a sum over physical noise terms (OUρOU'). Then if |sin θ| < 1/L, we can truncate the sum to include only those noise terms where |OU| + |OU'| ⩽ L + 2ζ + 1, where ζ is the same cutoff constant as in lemma 3. In other words,
. We write this logical noise component as a sum over physical noise terms (OUρOU'). Then if |sin θ| < 1/L, we can truncate the sum to include only those noise terms where |OU| + |OU'| ⩽ L + 2ζ + 1, where ζ is the same cutoff constant as in lemma 3. In other words,
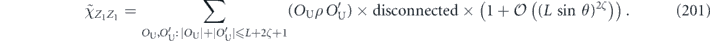
Proof. We split each noise term into connected and disconnected parts. We show in lemma 12 that the disconnected part is decreasing as the weight of the connected part increases. Moreover, the disconnected part is approximately equal to 1 for connected terms with total weight ⩽L + 2ζ + 1. Therefore, we need only consider the connected part as we proceed to truncate the sum and upper bound the error.
Let us denote the connected part of a noise term that enters into the logical 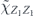 component by (OUρOU'). All such noise terms have the shape drawn in figure 10. The connected part is supported on a series of loops. The loops are joined by the minimal-weight correction. Denote the minimal-weight correction of OU and of OU' by Es. Let w be the weight of OU and w' the weight of OU'. Suppose w ⩽ w'. If not, then swap OU and OU' in what follows. Let
component by (OUρOU'). All such noise terms have the shape drawn in figure 10. The connected part is supported on a series of loops. The loops are joined by the minimal-weight correction. Denote the minimal-weight correction of OU and of OU' by Es. Let w be the weight of OU and w' the weight of OU'. Suppose w ⩽ w'. If not, then swap OU and OU' in what follows. Let  . Then
. Then  is a connected Z1 logical string with length at most 2w − 1. The number of such logical strings is upper bounded by L2w−L using our bound on the number of logical strings in equation (175).
is a connected Z1 logical string with length at most 2w − 1. The number of such logical strings is upper bounded by L2w−L using our bound on the number of logical strings in equation (175).
The number of ways of choosing a weight w operator OU as a subset of 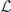 is upper bounded by 22w−2. Now that OU is fixed, the number of ways of choosing the operator OU' is upper bounded by
is upper bounded by 22w−2. Now that OU is fixed, the number of ways of choosing the operator OU' is upper bounded by 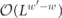 . This is because the lowest-weight operator with the same syndrome and logical action has weight ⩽w. Then OU' consists of this lowest-weight operator combined with a number of additional deviations like we considered to derive equation (175). (Here we are neglecting a factor which is polynomial in w and w'; bounding the exponential dependence on w' − w will suffice for what follows.) All together we have the following upper bound on the number of noise terms with fixed w and w':
. This is because the lowest-weight operator with the same syndrome and logical action has weight ⩽w. Then OU' consists of this lowest-weight operator combined with a number of additional deviations like we considered to derive equation (175). (Here we are neglecting a factor which is polynomial in w and w'; bounding the exponential dependence on w' − w will suffice for what follows.) All together we have the following upper bound on the number of noise terms with fixed w and w':
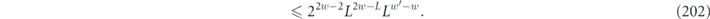
Each of these terms has magnitude at most (sin θ/2)w+w', which is positive because w + w' is even. As in lemma 3 we will truncate the sum and keep only those connected noise terms with w + w' ⩽ L + 2ζ + 1. If we let w + w' = wtotal, for each wtotal there are several combinations of w and w' with the same total. Because w and w' must be >(L + 1)/2, there are less than wtotal − L combinations. We perform a sum over wtotal from L + 2ζ + 1 up to the maximum weight. Therefore, if we let  denote the contribution from the higher weight connected terms to
denote the contribution from the higher weight connected terms to 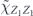 , then
, then  is bounded by
is bounded by
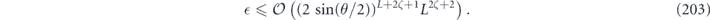
Here we have estimated the sum over wtotal using the same method as in the derivation of equation (179). We will compare this error  to the contribution from the lowest weight noise terms. These terms have w = w' = (L + 1)/2, and contribute at least ξ, where
to the contribution from the lowest weight noise terms. These terms have w = w' = (L + 1)/2, and contribute at least ξ, where
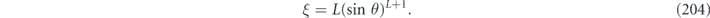
Then the relative error associated with our truncation is given by
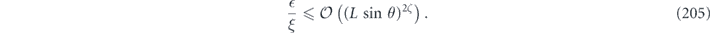
We have neglected a polynomial factor in L in our counting of noise terms. Nevertheless, as long as L|sin θ| < 1, the relative error is exponentially small in ζ, and the higher-weight connected terms are negligible. □
Figure 10. This is a connected incoherent noise term, (OUρOU'). The operator OU is drawn with the solid blue line. The operator OU' is drawn with the dashed blue line. The standard correction Es for the syndrome shared by OU and OU' is drawn with the solid red line. Each connected incoherent term is a configuration of loops where each loop is formed by two segments with shared endpoints, one segment from OU and one from OU'. The operator Es links together the loops like beads on a string, so that OUEs and OU'Es are both continuous logical strings spanning the code.
Download figure:
Standard image High-resolution image6.9. The incoherent sum over strings
The connected part of the incoherent components is not as simply expressed as a sum over strings as the coherent components because each uncorrectable error EsLaGx can generally be completed to many different logical strings by multiplying by different correctable errors. Nevertheless, we can rewrite the sum in a similar way. This will form our primary tool for comparing coherent and incoherent logical noise components. We will write a sum over each logical string with logical action La. For each string, we will sum over different ways of choosing the uncorrectable subset OU. We will restrict the subsets we consider for each logical string in order to control the over-counting factor that we will describe shortly. Then for each operator OU, we will sum over all possible uncorrectable operators OU' with the same syndrome and logical action. Fix a connected logical string  with length ℓ and choose an uncorrectable subset of the logical string OU with weight w. We impose two constraints on OU: first that w ⩾ (ℓ + 1)/2 and second that the complement of OU has the same weight as the minimal-weight correction Es. The complement of OU is
with length ℓ and choose an uncorrectable subset of the logical string OU with weight w. We impose two constraints on OU: first that w ⩾ (ℓ + 1)/2 and second that the complement of OU has the same weight as the minimal-weight correction Es. The complement of OU is 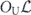 , which we will denote OC. Note that the name OC is chosen in analogy to the way the errors were labelled in the coherent noise terms, but OC is not a part of the incoherent noise term, which is notated (OUρOU'). Now that OU is fixed, choose a second uncorrectable error OU' with the same syndrome and with weight w'. This will produce every incoherent connected term (OUρOU'). However, each uncorrectable error OU will appear many times as a subset of many different logical strings. This is the over-counting we mentioned above.
, which we will denote OC. Note that the name OC is chosen in analogy to the way the errors were labelled in the coherent noise terms, but OC is not a part of the incoherent noise term, which is notated (OUρOU'). Now that OU is fixed, choose a second uncorrectable error OU' with the same syndrome and with weight w'. This will produce every incoherent connected term (OUρOU'). However, each uncorrectable error OU will appear many times as a subset of many different logical strings. This is the over-counting we mentioned above.
Each operator OU can be completed to a logical string in many ways. Because of the constraints we imposed on the subset OU, the complement, which we called OC, must have the same weight as the minimal-weight correction to OU, denoted Es. Let {OC'} be the set of possible complements. Then each possible complement OC' ∈ {OC'} defines a logical string OUOC', which will appear in the sum over strings. For each operator OU in the sum over strings, we need to divide by the number of complements OC' with weight |Es|. Each incoherent logical noise component can be written as a sum over connected logical strings  times a disconnected factor. This form of the sum will allow us to compare with equation (172). We sum over logical strings, and for each logical string we sum over possible choices of OU and OU'. We divide by the over-counting factor for each OU. This gives
times a disconnected factor. This form of the sum will allow us to compare with equation (172). We sum over logical strings, and for each logical string we sum over possible choices of OU and OU'. We divide by the over-counting factor for each OU. This gives
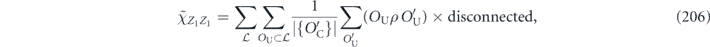
where
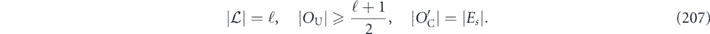
To reiterate, equation (206) expresses an incoherent logical noise component as a sum over connected logical strings. For each string  with weight ℓ, we sum over all uncorrectable subsets OU of weight ⩾(ℓ + 1)/2 such that the complement OC has weight equal to the minimal-weight correction of OU, namely Es. For each OU we must divide by the number of complements OC' with the same syndrome and weight as Es in order to cancel the over-counting. {OC'} is the set of such operators, and |{OC'}| is its cardinality. Finally, we sum over all uncorrectable operators OU' with the same syndrome to produce the complete set of incoherent terms. We will prove the following lemma, which provides a lower bound on the contribution of each logical string to the incoherent logical noise component. We will apply this lemma to lower bound the incoherent logical noise strength in terms of the coherent logical noise strength.
with weight ℓ, we sum over all uncorrectable subsets OU of weight ⩾(ℓ + 1)/2 such that the complement OC has weight equal to the minimal-weight correction of OU, namely Es. For each OU we must divide by the number of complements OC' with the same syndrome and weight as Es in order to cancel the over-counting. {OC'} is the set of such operators, and |{OC'}| is its cardinality. Finally, we sum over all uncorrectable operators OU' with the same syndrome to produce the complete set of incoherent terms. We will prove the following lemma, which provides a lower bound on the contribution of each logical string to the incoherent logical noise component. We will apply this lemma to lower bound the incoherent logical noise strength in terms of the coherent logical noise strength.
Lemma 6. As long as |sin θ| < 1/L, we can apply lemma 5. This means that in equation (206) we can restrict to the case where |OU| + |OU'| ⩽ L + 2ζ + 1. Let us also suppose that |OU| = |OU'|. This assumption will be justified by lemma 7. Then we can pick a connected logical string  with
with 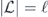 such that ℓ ⩽ L + 2ζ.
such that ℓ ⩽ L + 2ζ. 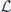 is a Z1 logical string if we are calculating the
is a Z1 logical string if we are calculating the 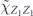 logical noise component. OU is subset of
logical noise component. OU is subset of  such that OU is corrected to a logical Z1 operator and |OU| = (ℓ + 1)/2. OU' is an operator with the same weight, syndrome, and logical action as OU. For each fixed
such that OU is corrected to a logical Z1 operator and |OU| = (ℓ + 1)/2. OU' is an operator with the same weight, syndrome, and logical action as OU. For each fixed  with length ℓ ⩽ L + 2ζ, the following holds:
with length ℓ ⩽ L + 2ζ, the following holds:
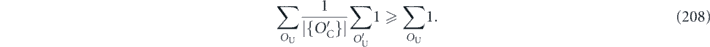
Proof. For each short logical string  with length ℓ, we partition it into an uncorrectable operator OU of weight w = (ℓ + 1)/2 and a correctable operator OC of length |OC| = |Es|. Then we consider the alternative uncorrectable and correctable paths, OU' and OC', with weight w and |Es|, respectively. The logical string
with length ℓ, we partition it into an uncorrectable operator OU of weight w = (ℓ + 1)/2 and a correctable operator OC of length |OC| = |Es|. Then we consider the alternative uncorrectable and correctable paths, OU' and OC', with weight w and |Es|, respectively. The logical string  is short, so we can use lemmas 9 and 10. Say the logical string runs right to left across the code. We observe by studying figure 12 that we have multiple possible strings of the same weight exactly when both a vertical error and some number of adjacent horizontal errors are contained in either the correctable or uncorrectable part.
is short, so we can use lemmas 9 and 10. Say the logical string runs right to left across the code. We observe by studying figure 12 that we have multiple possible strings of the same weight exactly when both a vertical error and some number of adjacent horizontal errors are contained in either the correctable or uncorrectable part.
Suppose that for some partition consisting of an uncorrectable operator 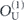 and a correctable operator
and a correctable operator 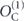 , denote the operators with the same weight, syndrome, and logical action by
, denote the operators with the same weight, syndrome, and logical action by 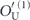 and
and 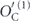 . Suppose
. Suppose 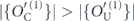 . We construct a new operator
. We construct a new operator 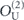 by exchanging all but one of the errors in
by exchanging all but one of the errors in 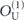 with the errors in
with the errors in  , so that
, so that  is equal
is equal  plus one additional error. This is shown in figure 11, where we have kept the error on the farthest left vertical segment fixed and flipped the rest relative to the term in figure 12. For every OU there are w possible mappings, one for each of the w choices of the single-qubit error that remains fixed. In the same way, every OU is mapped onto by w different mappings acting on w other operators with the same logical action as OU. Then there exists a convention that selects exactly one partner for each OU.
plus one additional error. This is shown in figure 11, where we have kept the error on the farthest left vertical segment fixed and flipped the rest relative to the term in figure 12. For every OU there are w possible mappings, one for each of the w choices of the single-qubit error that remains fixed. In the same way, every OU is mapped onto by w different mappings acting on w other operators with the same logical action as OU. Then there exists a convention that selects exactly one partner for each OU.
We assumed that for the original 
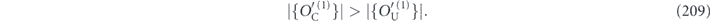
The mapping we described constructs a partner  such that
such that
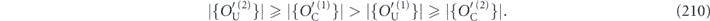
Then for each pair  and
and  , we can lower bound the contribution to the incoherent logical noise using
, we can lower bound the contribution to the incoherent logical noise using
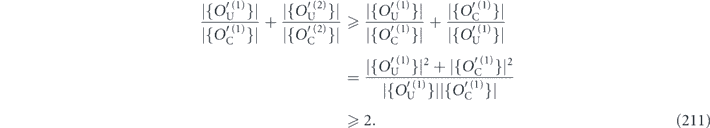
Finally, we apply the lower bound to the entire sum over OU to conclude
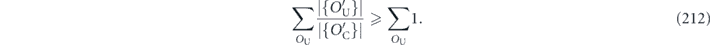
The number of terms in the sum over OU is at most  , where ℓ is the length of the logical string
, where ℓ is the length of the logical string 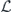 . For typical, short logical strings the binomial coefficient will be the number of terms in the sum over OU up to a small correction. □
. For typical, short logical strings the binomial coefficient will be the number of terms in the sum over OU up to a small correction. □
Figure 11. A partition of a length-13 logical string is shown in a toric code with L = 9. The operator OU is shown in solid red. The operator OC is shown in solid blue. The alternative operators with the same weight, syndrome, and logical action, which we denoted OU' and OC', are drawn with dotted lines. For this partition |{OU'}| = 2 and |{OC'}| = 4.
Download figure:
Standard image High-resolution imageFigure 12. This is a partner of the partition shown in figure 11. It is another partition of the same logical string, and the errors in OU and OC are interchanged except for one qubit. In this case that qubit is the one that lies on the farthest left vertical segment. The error on that qubit is part of OU in both partitions. Once again, the operator OU is in red and the operator OC is in blue. The alternative operators with the same weight, syndrome, and logical action are given by the dashed lines. For this partition |{OU'}| = 12 and |{OC'}| = 2.
Download figure:
Standard image High-resolution image6.10. Noise terms with mismatched weight
We have already shown that we can neglect the high-weight noise terms in the incoherent logical noise components, and we can also write the incoherent logical noise components as a sum over logical strings. Next, we will show that among the low-weight noise terms, we may neglect the terms with different weight errors on each side of ρ. This is crucial to our proof that the coherence of the logical noise is suppressed. We will construct a lower bound on the incoherent logical noise components and an upper bound on the coherent logical noise components. The noise terms with mismatched weight enter with a phase of −1 whenever the difference between the weights on left and right = 2 mod 4. A large contribution from noise terms with mismatched weight could spoil our lower bound on the incoherent logical noise. Fortunately, no such contribution occurs.
Lemma 7. If |sin θ| < 1/L, then the incoherent logical noise component 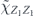 can be written
can be written
The sum over 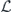 includes all typical, short logical strings with length ℓ such that ℓ ⩽ L + 2ζ. The sum over OU includes uncorrectable subsets of
includes all typical, short logical strings with length ℓ such that ℓ ⩽ L + 2ζ. The sum over OU includes uncorrectable subsets of  with weight (ℓ + 1)/2 such that the complement OC has minimal weight. The sum over OU' has the same syndrome and the same weight as OU. The error term comes from the high-weight terms we neglected in lemma 5.
with weight (ℓ + 1)/2 such that the complement OC has minimal weight. The sum over OU' has the same syndrome and the same weight as OU. The error term comes from the high-weight terms we neglected in lemma 5.
Proof. Using lemma 5, we can truncate the sum over noise terms in the incoherent logical noise component 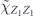 to include only those noise terms with total weight ⩽L + 2ζ + 1. In doing so we make an error that is exponentially small in the cutoff ζ, assuming that the single-qubit angle of rotation θ satisfies |sin θ| < 1/L. We will use equation (206) to express the incoherent logical noise components as a sum over strings. We will begin by reviewing how we construct that form of the sum.
to include only those noise terms with total weight ⩽L + 2ζ + 1. In doing so we make an error that is exponentially small in the cutoff ζ, assuming that the single-qubit angle of rotation θ satisfies |sin θ| < 1/L. We will use equation (206) to express the incoherent logical noise components as a sum over strings. We will begin by reviewing how we construct that form of the sum.
We denote the weight of OU by w and OU' by w'. We upper bound the mismatched-weight terms where w ≠ w' by letting w > w' and multiplying by two. As in equation (206) we can generate the complete set of connected incoherent terms with fixed w and w' by summing over connected logical strings  . Denote the length of the logical string by
. Denote the length of the logical string by 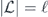 . To produce the incoherent terms with fixed w + w', it will suffice to sum over logical strings with ℓ < w + w'. We already restricted to low-weight terms, so w + w' ⩽ L + 2ζ + 1. For each logical string, we sum over the uncorrectable subsets OU with weight w. We will also require that the complement of OU, which we denoted OC, has minimal weight. This is to control the over-counting of each incoherent term (OUρOU'). Then for each OU, we sum over the operators OU' with weight w' that have the same syndrome and logical action as OU. As discussed in section 6.9, we must also divide by an over-counting factor 1/|{OC}| that is a function of OU and equals one over the number of times OU appears in the sum over
. To produce the incoherent terms with fixed w + w', it will suffice to sum over logical strings with ℓ < w + w'. We already restricted to low-weight terms, so w + w' ⩽ L + 2ζ + 1. For each logical string, we sum over the uncorrectable subsets OU with weight w. We will also require that the complement of OU, which we denoted OC, has minimal weight. This is to control the over-counting of each incoherent term (OUρOU'). Then for each OU, we sum over the operators OU' with weight w' that have the same syndrome and logical action as OU. As discussed in section 6.9, we must also divide by an over-counting factor 1/|{OC}| that is a function of OU and equals one over the number of times OU appears in the sum over 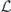 . The contribution to the incoherent logical noise is lower bounded by
. The contribution to the incoherent logical noise is lower bounded by
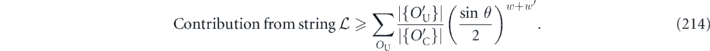
The inequality comes from the cosine factors. If the operators OU and OU' act on the same set of qubits, then we have (sin θ/2)2w with no cosine factors in the connected part. The lower bound corresponds to the case where OU and OU' act on disjoint sets of qubits, and we pick up a cosine factor on each qubit in the connected part. We also have an upper bound:
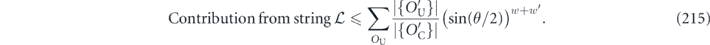
In this bound, we have 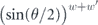 . This corresponds to the case when OU and OU' act on the same qubits, yielding no cosine terms.
. This corresponds to the case when OU and OU' act on the same qubits, yielding no cosine terms.
Consider first the terms with w = w'. These are generated from logical strings of length ℓ ⩽ 2w − 1. Some strings  with length ℓ such that L ⩽ ℓ ⩽ L + 2ζ have typical shape and some do not. We will prove first that the contribution from a given string of atypical shape is no greater than that of a string of typical shape, in fact it will be less. We will conclude that we can safely neglect the contribution from strings of atypical shape (because there are fewer such strings). This is the same simplification we made in our discussion of the coherent logical noise components in section 6.6.
with length ℓ such that L ⩽ ℓ ⩽ L + 2ζ have typical shape and some do not. We will prove first that the contribution from a given string of atypical shape is no greater than that of a string of typical shape, in fact it will be less. We will conclude that we can safely neglect the contribution from strings of atypical shape (because there are fewer such strings). This is the same simplification we made in our discussion of the coherent logical noise components in section 6.6.
We require that OU is an uncorrectable error, so we cannot choose any subset of w qubits in  . We ignore the subsets that correspond to exceptional partitions like we discussed in section 6.6. Now, if we have two connected logical strings of the same length, one with a typical shape and one with an atypical shape, we want to compare the terms with w = w'. The first thing we notice is that exceptional terms are exponentially unlikely for the string with typical shape, while for the atypical string, exceptional terms may be a significant fraction of the total partitions. This tells us that in the sum over OU there are many more terms for the typical string than for the atypical string. We have argued about the number of terms in the sum in equations (214) and (215), but we must also consider the magnitude of each term, which is given by the ratio of |{OU'}| over |{OC'}|.
. We ignore the subsets that correspond to exceptional partitions like we discussed in section 6.6. Now, if we have two connected logical strings of the same length, one with a typical shape and one with an atypical shape, we want to compare the terms with w = w'. The first thing we notice is that exceptional terms are exponentially unlikely for the string with typical shape, while for the atypical string, exceptional terms may be a significant fraction of the total partitions. This tells us that in the sum over OU there are many more terms for the typical string than for the atypical string. We have argued about the number of terms in the sum in equations (214) and (215), but we must also consider the magnitude of each term, which is given by the ratio of |{OU'}| over |{OC'}|.
We must argue that after summing the ratio of {OU'} and {OU'} over OU, the result is less for an atypical string than for a typical string. {OU'} here is the set of uncorrectable operators with the same weight and syndrome as OU and {OC'} is the set of correctable weight-ℓ − w operators with the same syndrome. Suppose the logical string runs left to right across the code. The set {OU'} contains more than one element whenever OU contains a set of contiguous qubits around one or more of the vertical steps in the logical string. This was discussed in detail in section 6.9. |{OU'}| and |{OC'}| are large when either OU or OC contain contiguous sets of qubits around the vertical steps. The typical logical string has at least 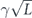 horizontal steps around each of the vertical steps. The atypical string does not. This means that the typical string has more possible sets of qubits around each vertical step that make |{OU'}| or |{OC'}| large. Therefore, |{OU'}| and |{OC'}| will tend to be larger for the typical string. The ratio of |{OU'}| to |{OC'}| is what determines the contribution to the incoherent logical noise. In lemma 6 we showed how we can match up terms such that for each OU satisfying |{OU'}|/|{OC'}| = c, the partner has |{OU'}|/|{OC'}| ⩾ 1/c. If c is large, then
horizontal steps around each of the vertical steps. The atypical string does not. This means that the typical string has more possible sets of qubits around each vertical step that make |{OU'}| or |{OC'}| large. Therefore, |{OU'}| and |{OC'}| will tend to be larger for the typical string. The ratio of |{OU'}| to |{OC'}| is what determines the contribution to the incoherent logical noise. In lemma 6 we showed how we can match up terms such that for each OU satisfying |{OU'}|/|{OC'}| = c, the partner has |{OU'}|/|{OC'}| ⩾ 1/c. If c is large, then 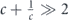 . It follows that because the typical string has more operators OU in the sum and the |{OU'}|/|{OC'}| factors tend to be larger, the contribution to the incoherent logical noise is smaller for an atypical string than the contribution from a typical string. When we combine this fact with the fact that the atypical strings represent an small minority, this means we can neglect the atypical strings among the w = w' terms in the incoherent logical noise. The error is given by lemma 10.
. It follows that because the typical string has more operators OU in the sum and the |{OU'}|/|{OC'}| factors tend to be larger, the contribution to the incoherent logical noise is smaller for an atypical string than the contribution from a typical string. When we combine this fact with the fact that the atypical strings represent an small minority, this means we can neglect the atypical strings among the w = w' terms in the incoherent logical noise. The error is given by lemma 10.
Now, consider the mismatched-weight terms that are the subject of this lemma. Fix w + w' and suppose w > w'. For each 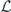 we can construct a number of incoherent terms with mismatched weight depending on the length and shape of
we can construct a number of incoherent terms with mismatched weight depending on the length and shape of  . Let
. Let  . Once again OU is an uncorrectable subset of the logical string
. Once again OU is an uncorrectable subset of the logical string  with weight w. Then for each OU we have the possibility that there may exist an operator OU' with the same syndrome as OU and lower weight. We sum over the set of OU such that for each OU there exists an OU' with weight w'. If we sum over all logical strings of length <w + w', we produce every connected incoherent term with |OU| = w and |OU'| = w'. We will proceed by fixing a logical string and upper bounding the sum over w of the noise terms derived from this logical string with w + w' fixed. In this sum the terms will alternate sign as w increases. The terms with w = w' have a positive sign. As we seek to bound the contribution of these mismatched-weight terms to the incoherent logical noise, there are two things we need to bound. First, we must understand the combinatorics that govern the number of operators OU that permit lower-weight OU'. Second, we must bound the factor |{OU'}|/|{OC'}| for each such OU.
with weight w. Then for each OU we have the possibility that there may exist an operator OU' with the same syndrome as OU and lower weight. We sum over the set of OU such that for each OU there exists an OU' with weight w'. If we sum over all logical strings of length <w + w', we produce every connected incoherent term with |OU| = w and |OU'| = w'. We will proceed by fixing a logical string and upper bounding the sum over w of the noise terms derived from this logical string with w + w' fixed. In this sum the terms will alternate sign as w increases. The terms with w = w' have a positive sign. As we seek to bound the contribution of these mismatched-weight terms to the incoherent logical noise, there are two things we need to bound. First, we must understand the combinatorics that govern the number of operators OU that permit lower-weight OU'. Second, we must bound the factor |{OU'}|/|{OC'}| for each such OU.
Suppose that the logical string 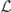 has a typical shape. To be concrete, consider the set of operators OU with weight w = (ℓ + 3)/2. If there exist lower-weight OU', then OU must contain all of the qubits around a 'cap', which is similar condition to the one we discussed in section 6.6. Each cap has width at least
has a typical shape. To be concrete, consider the set of operators OU with weight w = (ℓ + 3)/2. If there exist lower-weight OU', then OU must contain all of the qubits around a 'cap', which is similar condition to the one we discussed in section 6.6. Each cap has width at least 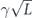 because the string is typical. This means that such OU are exponentially few relative to the total set of uncorrectable OU with weight w. This is the same calculation as in lemma 4. We compare these terms to the terms with |OU| = (ℓ + 1)/2 = |OU'|. There are exponentially more of these terms where |OU| = |OU'|. This means that in equations (214) and (215) the sum over OU contains exponentially more terms when w = w' for a typical logical string. The summand also tends to be less for the w > w' terms. The argument is similar to the one we used earlier when we were discussing the w = w' terms from typical and atypical strings. |{OU'}| is large when OU contains many qubits around several of the different steps up and down along the logical string. In this case the terms with w > w' feature operators OU that contain at least one of the 'caps' along the logical string. This removes at least two of the vertical steps. These steps cannot contribute to |{OU'}|. Then by the argument we used above, the ratio |{OU'}|/|{OC'}| tends to be less for the w > w' terms relative to the w = w'. We chose w = (ℓ + 3)/2, but we could have chosen any w > (ℓ + 1)/2 and any w' < w. We would find that there are
because the string is typical. This means that such OU are exponentially few relative to the total set of uncorrectable OU with weight w. This is the same calculation as in lemma 4. We compare these terms to the terms with |OU| = (ℓ + 1)/2 = |OU'|. There are exponentially more of these terms where |OU| = |OU'|. This means that in equations (214) and (215) the sum over OU contains exponentially more terms when w = w' for a typical logical string. The summand also tends to be less for the w > w' terms. The argument is similar to the one we used earlier when we were discussing the w = w' terms from typical and atypical strings. |{OU'}| is large when OU contains many qubits around several of the different steps up and down along the logical string. In this case the terms with w > w' feature operators OU that contain at least one of the 'caps' along the logical string. This removes at least two of the vertical steps. These steps cannot contribute to |{OU'}|. Then by the argument we used above, the ratio |{OU'}|/|{OC'}| tends to be less for the w > w' terms relative to the w = w'. We chose w = (ℓ + 3)/2, but we could have chosen any w > (ℓ + 1)/2 and any w' < w. We would find that there are 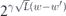 fewer of the mismatched weight terms. We have a factor of
fewer of the mismatched weight terms. We have a factor of 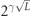 for each cap contained in OU. We conclude that the mismatched-weight terms are negligible for strings of typical shape.
for each cap contained in OU. We conclude that the mismatched-weight terms are negligible for strings of typical shape.
Finally, consider a logical string 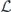 with an atypical shape. Fix w + w'. We already neglected the contribution of atypical strings to the w = w' terms. We seek a bound on the contribution from the terms with w > w' for atypical strings. We will compare two sets of terms for fixed
with an atypical shape. Fix w + w'. We already neglected the contribution of atypical strings to the w = w' terms. We seek a bound on the contribution from the terms with w > w' for atypical strings. We will compare two sets of terms for fixed  with length ℓ. On the one hand, take the terms with w = w1 for some w1 > (ℓ − 1)/2 and w' = w2 < w1. On the other hand, take the terms with w = w1 + 1 and w' = w2 − 1. We will show that the latter set of terms contribute less than the former. This will tell us that the sum over mismatched-weight terms for the fixed string
with length ℓ. On the one hand, take the terms with w = w1 for some w1 > (ℓ − 1)/2 and w' = w2 < w1. On the other hand, take the terms with w = w1 + 1 and w' = w2 − 1. We will show that the latter set of terms contribute less than the former. This will tell us that the sum over mismatched-weight terms for the fixed string  is bounded by the contribution from terms with |OU| = |OU'|.
is bounded by the contribution from terms with |OU| = |OU'|.
When OU' has lower weight than OU, OU must contain all the qubits along a cap. If OU − OU' = 2j, then OU must contain at caps with total height at least j. Because the logical string  has an atypical shape, these caps may have width one or height greater than one. It will not be exponentially unlikely that all qubits around a small cap are contained in OU. For the terms with w = w1 and w' = w2, relative to OU', OU contains all the qubits around w1 − w2 of the caps. These terms will be a fraction of the
has an atypical shape, these caps may have width one or height greater than one. It will not be exponentially unlikely that all qubits around a small cap are contained in OU. For the terms with w = w1 and w' = w2, relative to OU', OU contains all the qubits around w1 − w2 of the caps. These terms will be a fraction of the 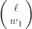 subsets of w1 qubits in the logical string
subsets of w1 qubits in the logical string  . We compare these terms to the ones with w = w1 + 1 and w' = w2 − 1 keeping our logical string
. We compare these terms to the ones with w = w1 + 1 and w' = w2 − 1 keeping our logical string  fixed. These terms include all the qubits around an additional cap. On one of the caps, instead of containing at least one and less than all of the qubits, OU contains all of the qubits around that cap. This stricter condition of OU means that the fraction of the total
fixed. These terms include all the qubits around an additional cap. On one of the caps, instead of containing at least one and less than all of the qubits, OU contains all of the qubits around that cap. This stricter condition of OU means that the fraction of the total 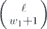 weight w1 subsets of
weight w1 subsets of  that feature an OU' operator with weight w2 − 1 is smaller than the fraction of the total
that feature an OU' operator with weight w2 − 1 is smaller than the fraction of the total 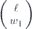 weight w1 subsets of
weight w1 subsets of 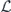 that feature an OU' operator with weight w2. This means that in equations (214) and (215) in the sum over OU for our fixed logical string, the number of possible OU at a given weight w > (ℓ + 1)/2 is given by a binomial coefficient times a function that decreases monotonically as w increases. As for the summand |{OU'}|/|{OU'}|, we apply the same reasoning as above. For each cap contained in OU, there are fewer vertical steps to create many operators OU'. This implies that the summand will tend to be smaller as w increases. The sum over the different values of w has the form
that feature an OU' operator with weight w2. This means that in equations (214) and (215) in the sum over OU for our fixed logical string, the number of possible OU at a given weight w > (ℓ + 1)/2 is given by a binomial coefficient times a function that decreases monotonically as w increases. As for the summand |{OU'}|/|{OU'}|, we apply the same reasoning as above. For each cap contained in OU, there are fewer vertical steps to create many operators OU'. This implies that the summand will tend to be smaller as w increases. The sum over the different values of w has the form
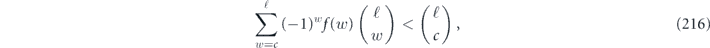
where c ⩾ (l + 1)/2 and f is a monotonically decreasing function. The inequality in equation (216) is proven by pairing the adjacent terms in the sum, positive and negative, to produce small positive contributions bounded by the contributions in the case where f(w) = 1 for all w. It follows that the sum over the mismatched-weight terms derived from the logical string  is positive, and moreover is bounded by the w = w' terms. We already argued that the w = w' terms from atypical strings are negligible relative to those terms from typical strings. Finally, we can lower bound the incoherent logical noise component by neglecting the atypical strings and for the typical strings, neglecting the mismatched-weight terms. This yields equation (213). □
is positive, and moreover is bounded by the w = w' terms. We already argued that the w = w' terms from atypical strings are negligible relative to those terms from typical strings. Finally, we can lower bound the incoherent logical noise component by neglecting the atypical strings and for the typical strings, neglecting the mismatched-weight terms. This yields equation (213). □
We are left with only the incoherent terms that have the same weight of uncorrectable error on each side and the weight is 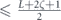 . These terms all have the same phase +1, so the incoherent terms with different weights will add constructively. This gives us lower bounds on the logical incoherent noise strength. Each logical string with length ℓ ⩽ L + 2ζ contributes at least
. These terms all have the same phase +1, so the incoherent terms with different weights will add constructively. This gives us lower bounds on the logical incoherent noise strength. Each logical string with length ℓ ⩽ L + 2ζ contributes at least 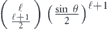 . When ℓ is much larger than the minimum logical string length, L, the number of logical strings is given by equation (173).
. When ℓ is much larger than the minimum logical string length, L, the number of logical strings is given by equation (173).
In particular, the incoherent logical noise components must be larger than the lowest order term. This at last completes the argument begun in section 6.5 about neglecting the contribution to the coherent logical noise from connected logical strings with length >L + 2ζ for a cut-off constant ζ. In lemma 3 we proved that the contribution from long logical strings is upper bounded by αL2ζ+1|sin θ|L+2ζ, where α is (1 − L|sin θ|)−1. This bound is exponentially small in ζ relative to the lowest order incoherent logical noise component, 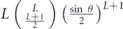 . Our aim is to compare the logical coherent and incoherent noise components, and we have shown that the contribution to the coherent logical noise from long strings is small relative to the incoherent logical noise components. Therefore, we can safely neglect the long connected logical strings. The same applies for the truncation error in lemma 5. The truncation error is negligible relative to the lowest order incoherent terms for large enough ζ.
. Our aim is to compare the logical coherent and incoherent noise components, and we have shown that the contribution to the coherent logical noise from long strings is small relative to the incoherent logical noise components. Therefore, we can safely neglect the long connected logical strings. The same applies for the truncation error in lemma 5. The truncation error is negligible relative to the lowest order incoherent terms for large enough ζ.
6.11. More general rotation angles
In sections 6.4 and 6.8, we simplified the problem by assuming that all qubits are rotated by the same single-qubit unitary rotation. Now we want to extend our result to more general single-qubit rotations. We will allow the magnitude of the rotation angle to vary from qubit to qubit and will also allow different axes of rotation for different qubits. Here we will assume that each rotation axis is contained in the X–Z plane. Physical Y errors are treated in appendix
The idea of the proof is the same as that of lemma 2. We will consider the coherent and incoherent logical noise components as functions of individual qubit rotation angles and prove that the coherent component is maximized relative to the incoherent component when all rotation angles are equal.
Lemma 8. Consider the toric code with qubits subject to single-qubit rotations, where each rotation axis lies in the X–Z plane, and both the rotation axis and angle of rotation may vary from qubit to qubit. The bound on the coherence of the logical noise channel proved in theorem 3 continues to apply if the rotations are sufficiently close to uniform; that is, provided that each rotation axis and angle deviates from a fixed constant value within a bounded region.
Proof. Suppose at first that all rotations are about the Z-axis and denote the rotation angle for the ith qubit by θi. Each logical coherent or incoherent component is a sum of physical noise terms, which are functions of all the angles θi. We will refer to the coherent or incoherent logical noise strength; by this we mean the sum of norms squared of the off-diagonal or diagonal components of the chi matrix for the logical noise channel. We are interested in the coherence of the logical noise channel, that is, the relative magnitude of the coherent and incoherent logical noise strength. Our approach will be to fix the coherent logical noise strength and calculate how the incoherent logical noise strength varies as we change rotation angles while remaining in the submanifold with constant coherent logical noise strength.
We begin at a point where all single-qubit rotation angles are equal. Suppose that this rotation angle is >0. The proof will be similar if the angle is <0. We will perturb away from this point, moving along the submanifold with fixed coherent logical noise strength. These perturbations can be built out of small elementary steps, in which two qubits, i and j, are selected. We require that θi ⩾ θj. Then the elementary step consists of increasing θi by some amount and decreasing θj such that we remain on the submanifold with constant coherent logical noise strength. We will prove that such elementary steps increase the incoherent logical noise strength. Therefore, we will conclude that the coherence of the logical noise is maximized when all single-qubit rotation angles are equal. Our calculation will be limited to configurations of angles not too far from the point where all angles are equal.
In lemmas 3 and 5, we proved that when all the rotation angles are equal and satisfy |sin θ| < 1/L, the logical noise is dominated by the contributions of the low-weight connected terms. We bounded the absolute magnitude of the sum over high-weight connected terms. These high-weight terms were negligible relative to the low-weight connected terms in the incoherent logical noise. If the rotation angles are allowed to differ, so long as all the angles θi satisfy |sin θi| < 1/L, our upper bound on the absolute magnitude of the error from the high-weight terms continues to hold. We require that this error is negligible relative to the low-weight terms we keep in the incoherent logical noise components. This was true when all angles were equal and will continue to be true for a wide range of configurations; only certain edge cases will violate this condition. For instance, one such edge case arises if all the rotation angles are 0 except for the qubits along a long logical string with a shape such that it contains no low-weight uncorrectable subsets.
We previously defined the connected and disconnected parts of a noise term (definitions 2, 3, 8, and 9). As we described in section 6.7 and lemmas 11 and 12, the disconnected part has a value of 1 up to corrections. These corrections are small for low-weight connected terms when all rotation angles are equal. If the angles are different, we can still apply our analysis, so long as the absolute error from the corrections is small relative to the low-weight connected terms in the incoherent logical noise components. This holds in a region around the point where all angles are equal. Hence, in this proof we will compare only the connected terms in the coherent and incoherent logical noise components with the understanding that the error terms we are neglecting are small relative to the low-weight connected terms we have kept.
We can build any general perturbation out of an elementary (non-infinitesimal) perturbation where we increase one rotation angle θi and decrease a second angle, θj, such that the connected contribution to the coherent logical noise strength is unchanged. The perturbation will look different depending on how the two qubits are positioned. If the qubits i and j are adjacent to each other and aligned in the correct direction, they will appear together in many short logical strings. Otherwise, i and j will not appear together in short logical strings. Throughout this section, we will approximate sin θi/2 ≈ θi/2 to simplify the equations. We will incur a relative error of 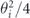 , that will always be small, since we have assumed that |sin θi| < 1/L for every i. Then the contribution to the coherent logical noise strength from the low-weight connected terms as a function of θi and θj is
, that will always be small, since we have assumed that |sin θi| < 1/L for every i. Then the contribution to the coherent logical noise strength from the low-weight connected terms as a function of θi and θj is
The coherent logical noise strength is a sum of norms squared and is therefore positive. This implies that γ0 > 0. Moreover, the sum over partitions has the same phase for every short logical string as in equation (192). This means that each logical string makes a positive contribution to the noise strength. Therefore, γ1 and γ2 are both non-negative. The relative size of γ1 and γ2 depends on how close the two chosen qubits i and j are. When i and j are both along the same horizontal or vertical line, many low-weight logical strings will contain both qubits. These strings contribute to γ2, so that the γ2 term may be comparable to the γ1 term. On the other hand, if qubits i and j are not along a horizontal or vertical line, then none of the minimal-weight logical strings contain both qubits. Also, for any fixed length ℓ ⩽ L + 2ζ, the number of logical strings of length ℓ that contain both qubits i and j is negligible relative to the number of length ℓ logical strings that contain qubit i and not qubit j. In this case the γ2 term is negligible relative to the γ1 term. In either case, we can write down the perturbation that leaves the coherent logical noise strength unchanged. Let θi = ciθ and θj = cjθ for some θ, and then we will solve for cj such that the connected coherent sum is constant. This yields
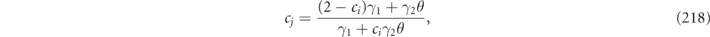
so that when γ2 = 0, we have cj = 2 − ci.
We can expand the incoherent logical noise strength in the same way. The noise terms that enter into the incoherent logical noise have the form (OUρOU'). As we expand in the angles θi and θj, we have cases where the qubits i and j are contained in neither, one of, or both OU and OU':
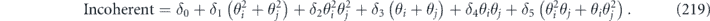
By lemma 5, the contributions of high-weight logical strings to the logical incoherent noise components are negligible. The contributions for each short logical string are positive due to lemma 7. If we fix a short logical string that contains both qubit i and qubit j and require that OU and OU' both contain i and j or one of i and j, then the same proof as in lemma 7 implies that these contributions are positive. Therefore, the coefficients δ1 and δ2 are positive when all rotation angles are equal. We can now substitute the perturbation from equation (218) into each of the terms in equation (219). We compute the perturbed value of the incoherent logical noise strength and subtract the initial value when all the angles of rotation are equal. Let incoherent(a) denote the value of the incoherent term in equation (219) with ci = a. The difference between the perturbed and initial values is
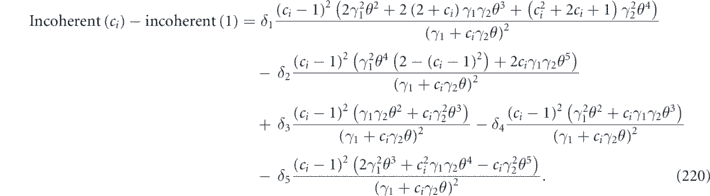
We see that the δ1 term is positive for all ci > 1. We will show that the positive terms are larger than the other terms for all ci > 1. Each term has the same denominator and contains a factor of 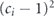 in the numerator. This means immediately that the first derivative with respect to ci vanishes at the point ci = 1. We pull out the shared factors of
in the numerator. This means immediately that the first derivative with respect to ci vanishes at the point ci = 1. We pull out the shared factors of 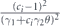 and rearrange terms in equation (220):
and rearrange terms in equation (220):
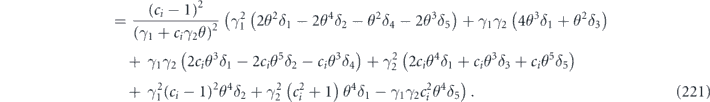
If the conditions,
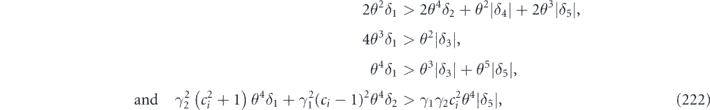
are satisfied, then each line of equation (221) is greater than 0. Recall that γ1, γ2, δ1, and δ2 are non-negative. Each elementary perturbation increases the value of ci. Therefore, if the conditions in equation (222) are satisfied, then each elementary step along the submanifold with constant coherent noise strength increases the incoherent logical noise strength. It remains for us to argue that these conditions are satisfied when the rotation angles are close to equal.
Consider two cases for the relative positions of qubits i and j. In the first case, suppose qubits i and j are positioned so that no short logical strings contain both. Then the strings that contribute to γ2 as well as δ2, δ4, and δ5 are all long. Such strings do not appear in the sum over low-weight connected terms, so γ2 = 0 in equation (221). Therefore, the only condition is the first line of equation (222). In this inequality δ2, δ4 and δ5 are 0, and the condition is satisfied.
In the other case, qubits i and j are in a horizontal or vertical line so that both qubits are contained in several short logical strings. In this case θγ2 is comparable to γ1. Now consider the incoherent contribution from the strings that contain both qubits i and j. For each weight-(2w − 1) logical string containing both qubits i and j, the errors OU are weight-w subsets of the logical string. Nearly half will contain exactly one of qubits i and j and one quarter will contain both qubits i and j. This means that more terms contribute to θ2δ1 and θδ3 than to θ4δ2, θ2δ4, and θ3δ5. In particular, θ2δ1 > 2θ4δ2. For each OU, the set {OU'} contains operators with the same syndrome, logical action and weight. OU' differs from OU only near certain transverse steps along the logical string as we described in section 6.9. For most logical strings, if OU does not contain qubit i, then most of the operators OU' also will not. If OU contains qubit i, most operators OU' will as well. This implies that
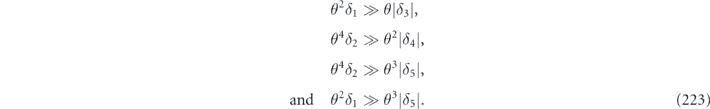
Together with our earlier statement that θ2δ1 > 2θ4δ2, this implies that even when i and j are near to each other, the conditions in equation (222) are satisfied.
We have proven that each of the elementary perturbations starting from uniform angles increases the incoherent logical noise strength. However, we must also consider elementary perturbations that are applied after a different elementary perturbation has taken us away from uniform angles. In that case in equations (217) and (219) we would no longer have exact symmetry between θi and θj. In other words, equation (217) would read
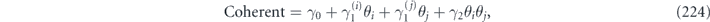
where 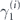 and
and 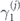 are different coefficients. However, as long as we are not too far from uniform angles,
are different coefficients. However, as long as we are not too far from uniform angles, 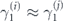 , and the change in the incoherent logical noise strength will be almost the same as in equation (220). We have argued that the conditions in equation (222) are satisfied by a large margin. Therefore, there exists a region around the point with uniform angles where every elementary perturbation on the submanifold with fixed coherent logical noise strength increases the incoherent logical noise strength. We conclude that in a region around the symmetric point where every single-qubit rotation is by the same angle θ, this symmetric point gives the largest coherent logical noise strength relative to the incoherent logical noise strength. This means that the connected contribution to the incoherent logical noise strength has a local minimum at the point with uniform rotations within the submanifold with constant connected contribution to the coherent logical noise strength. This implies that the upper bound on logical coherence we derive in theorem 3 for the case where all angles are equal also upper bounds the logical coherence in a region around the point where all angles are equal.
, and the change in the incoherent logical noise strength will be almost the same as in equation (220). We have argued that the conditions in equation (222) are satisfied by a large margin. Therefore, there exists a region around the point with uniform angles where every elementary perturbation on the submanifold with fixed coherent logical noise strength increases the incoherent logical noise strength. We conclude that in a region around the symmetric point where every single-qubit rotation is by the same angle θ, this symmetric point gives the largest coherent logical noise strength relative to the incoherent logical noise strength. This means that the connected contribution to the incoherent logical noise strength has a local minimum at the point with uniform rotations within the submanifold with constant connected contribution to the coherent logical noise strength. This implies that the upper bound on logical coherence we derive in theorem 3 for the case where all angles are equal also upper bounds the logical coherence in a region around the point where all angles are equal.
Now consider changing the axes of rotation while keeping the total rotation angle the same. Let the noise model be a rotation in the X–Z plane such that the rotation angles are θX and θZ for every qubit. We show that Y rotations on the qubits will produce less coherent logical noise in lemma 13. The X and Z rotations contribute to independent components of the logical noise channel. Then each noise term that enters into the X-type logical noise components depend on at least L powers of θX. Similarly, the Z-type logical noise depends on at least L powers of θZ. Therefore, if the total rotation angle for each qubit, 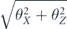 , is fixed, the logical noise strength is greatest when either θX or θZ is 0. Also, because the X and Z-type errors contribute to different logical noise components, we can apply our analysis of coherent and incoherent logical noise components to the two types of errors separately. If both |sin θX| and |sin θZ| are <1/L, then lemmas 3 and 5 imply that the logical coherent and incoherent X and Z noise is dominated by the contributions of short logical strings. With this noise model, we will in general expect logical Y noise, but lemma 14 implies that logical Y-type errors are negligible relative to X- and Z-type errors. The θX rotations contribute to the X1 and X2 logical noise, while the θZ rotations contribute to the Z1 and Z2 logical noise. The bounds we proved for coherent and incoherent logical noise components apply equally well to the X- and Z-type noise separately in this noise model. □
, is fixed, the logical noise strength is greatest when either θX or θZ is 0. Also, because the X and Z-type errors contribute to different logical noise components, we can apply our analysis of coherent and incoherent logical noise components to the two types of errors separately. If both |sin θX| and |sin θZ| are <1/L, then lemmas 3 and 5 imply that the logical coherent and incoherent X and Z noise is dominated by the contributions of short logical strings. With this noise model, we will in general expect logical Y noise, but lemma 14 implies that logical Y-type errors are negligible relative to X- and Z-type errors. The θX rotations contribute to the X1 and X2 logical noise, while the θZ rotations contribute to the Z1 and Z2 logical noise. The bounds we proved for coherent and incoherent logical noise components apply equally well to the X- and Z-type noise separately in this noise model. □
Lemma 8 states that among noise models consisting of single-qubit rotations where each rotation is close to the same, the coherence of the logical channel is greatest for the noise model consisting of Z-axis rotations on every qubit by the same angle. The same does not necessarily hold for noise models consisting of single-qubit rotations with wildly different angles of rotation on each qubit. This is not surprising because if we allow for wildly different rotation angles, we encounter the case where all the rotation angles are 0 except for the qubits along some very long logical string. This kind of high-weight connected term is beyond the scope of the present work, cf lemmas 3 and 5.
6.12. Correlations
We can apply theorem 2 to study the toric code with minimal-weight decoding subject to correlated unitary noise. In the repetition code, we found that adding two-body correlations did not change the relation between coherent and incoherent components of the logical noise when the code size n is large. We can transfer that to the toric code using what we have already proven. Consider a single logical string. We can sum over its partitions. With correlated unitary noise, instead of sin θ/2 cos θ/2 for each qubit in the logical string, we have a sum over the one- and two-body couplings in the Hamiltonian, h1 and h2. The model of correlated noise that we considered in theorem 2 included two-body coupling terms between every pair of qubits in the code. Therefore, the magnitude of each multi-qubit error is a function only of its weight. We found that the coherent and incoherent logical noise in the toric code is dominated by the contributions from short logical strings with typical shape. In theorem 3 we will finish proving a relation between the coherent and incoherent terms that is based on the number of terms and their magnitudes, which we always assumed to be sin θ/2 raised to the weight of the terms. In the correlated case we alter the magnitude of each term, but theorem 2 tells us that string by string we can bound the coherent logical noise contribution in terms of the incoherent logical noise contribution.
6.13. Main theorem
Theorem 3. Consider the L × L toric code without boundaries subject to single-qubit unitary noise acting on each qubit. We chose minimal-weight decoding and assume that syndrome extraction is perfect. Suppose that each qubit is rotated by an angle θ about some axis and that |sin θ| < 1/L. Our conclusion will also hold for angles and axes that differ among the qubits, so long as the deviation is small as discussed in lemma 8. Let Ñ be the logical noise channel produced by encoding into the toric code, acting with single-qubit unitary noise, and then decoding. Denote by  the chi matrix for the logical noise channel Ñ. Then the coherent and incoherent components of the logical channel are related by
the chi matrix for the logical noise channel Ñ. Then the coherent and incoherent components of the logical channel are related by
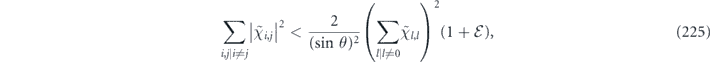
where
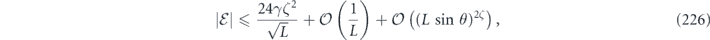
and ζ is an arbitrary L-independent constant. We denote the diamond norm distance of Ñ from the identity channel by D◊(Ñ). It follows that
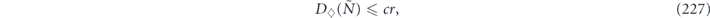
for a constant c given by
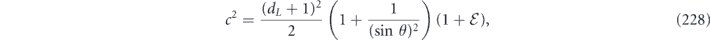
where dL is the dimension of the code space (dL = 4 for the 2D toric code without boundaries). Here r is the average infidelity of the logical noise channel Ñ, and  is the error term bounded in equation (226). (If the logical noise channel Ñ were unitary, then D◊(Ñ) would be proportional to
is the error term bounded in equation (226). (If the logical noise channel Ñ were unitary, then D◊(Ñ) would be proportional to  .) We can also consider the growth of the average infidelity as we apply the logical noise channel many times in succession. Let rm be the average infidelity after m applications of Ñ; then using equation (225), we can write
.) We can also consider the growth of the average infidelity as we apply the logical noise channel many times in succession. Let rm be the average infidelity after m applications of Ñ; then using equation (225), we can write
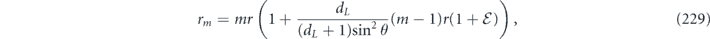
where dL = 4 for the 2D toric code without boundaries,  is the error term that is upper bounded in equation (226), and r is the average infidelity for a single application of the logical noise channel. As long as the physical noise strength is below the fault-tolerant threshold, r will be exponentially small in the code distance L. Therefore, equation (229) states that the term growing quadratically in m is exponentially small in L relative to the term growing linearly with m. In this sense, the coherence of the logical channel is heavily suppressed.
is the error term that is upper bounded in equation (226), and r is the average infidelity for a single application of the logical noise channel. As long as the physical noise strength is below the fault-tolerant threshold, r will be exponentially small in the code distance L. Therefore, equation (229) states that the term growing quadratically in m is exponentially small in L relative to the term growing linearly with m. In this sense, the coherence of the logical channel is heavily suppressed.
Proof. We start with a noise model consisting of Z rotations by angle θ on every qubit in the L × L block of toric code. We seek to approximate the coherent logical noise component 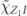 and relate it to the incoherent logical noise component
and relate it to the incoherent logical noise component 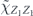 . First, let us calculate the coherent component. We write
. First, let us calculate the coherent component. We write 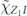 as a sum over strings and partitions with a connected and disconnected part as in equation (172). Applying lemma 3 to the connected part, we neglect high-weight terms, leaving only the logical strings with length ⩽L + 2ζ for a fixed ζ, and making an error which is exponentially small in ζ. For this step, the magnitudes of the sines of the single-qubit rotation angles are required to be below a threshold value 1/L. We apply lemma 11 to argue that the disconnected part is equal to 1 up to a small correction. Lemmas 9 and 10 tell us that we can treat all short logical strings
as a sum over strings and partitions with a connected and disconnected part as in equation (172). Applying lemma 3 to the connected part, we neglect high-weight terms, leaving only the logical strings with length ⩽L + 2ζ for a fixed ζ, and making an error which is exponentially small in ζ. For this step, the magnitudes of the sines of the single-qubit rotation angles are required to be below a threshold value 1/L. We apply lemma 11 to argue that the disconnected part is equal to 1 up to a small correction. Lemmas 9 and 10 tell us that we can treat all short logical strings  as typical and make another small error. Now that we have only short typical logical strings, we apply lemma 4 to perform the sum over partitions. We conclude that
as typical and make another small error. Now that we have only short typical logical strings, we apply lemma 4 to perform the sum over partitions. We conclude that
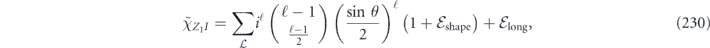
where the sum is over all connected logical Z1 strings  with length ℓ such that ℓ ⩽ L + 2ζ. The error from logical strings with length greater than L + 2ζ is bounded
with length ℓ such that ℓ ⩽ L + 2ζ. The error from logical strings with length greater than L + 2ζ is bounded
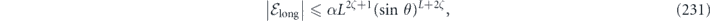
where α = (1 − L sin θ)−1. This error is from lemma 3. The other error term from lemmas 10 and 11 is bounded
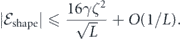
A further error due to neglecting exceptional partitions is subdominant according to lemma 4 and is not shown in equation (230).
Now, we will lower bound the incoherent logical noise component  . Lemma 5 implies that we can neglect the contributions of noise terms (OUρOU') such that |OU| + |OU'| > L + 2ζ + 1. The error we make by truncating the sum is exponentially small in ζ, so long as the rotation angle θ satisfies |θ| < 1/L. The incoherent logical noise component can be put in the form of a sum over logical strings as in equation (206). Using lemma 7, we restrict to the connected terms where the logical string
. Lemma 5 implies that we can neglect the contributions of noise terms (OUρOU') such that |OU| + |OU'| > L + 2ζ + 1. The error we make by truncating the sum is exponentially small in ζ, so long as the rotation angle θ satisfies |θ| < 1/L. The incoherent logical noise component can be put in the form of a sum over logical strings as in equation (206). Using lemma 7, we restrict to the connected terms where the logical string  is short and has typical shape and |OU| = |OU'|. We can also keep only the terms with |OU| = (ℓ + 1)/2, because just as in the repetition code, these higher-weight partitions are suppressed by factors of sin θ2 and the binomial coefficients are decreasing as we consider higher-weight OU. The disconnected part is equal to 1 up to small correction according to lemma 12. Finally, lemma 6 gives a lower bound on the contribution of each logical string to the incoherent logical noise. All together, we have the following lower bound on
is short and has typical shape and |OU| = |OU'|. We can also keep only the terms with |OU| = (ℓ + 1)/2, because just as in the repetition code, these higher-weight partitions are suppressed by factors of sin θ2 and the binomial coefficients are decreasing as we consider higher-weight OU. The disconnected part is equal to 1 up to small correction according to lemma 12. Finally, lemma 6 gives a lower bound on the contribution of each logical string to the incoherent logical noise. All together, we have the following lower bound on 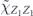 :
:
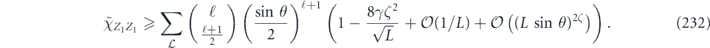
The error terms come from lemmas 10, 5, and 12. A subdominant error term from lemma 4 is suppressed in equation (232).
Putting together equations (230) and (232), we conclude the following about how the coherent and incoherent terms in the logical chi matrix are related:
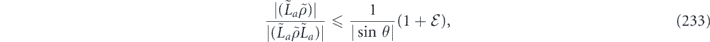
where
We used
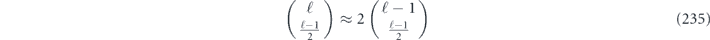
to arrive at equation (233).
We have restricted our attention to the coherent logical component 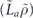 and the corresponding incoherent component
and the corresponding incoherent component 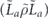 , where
, where  was either X or Z on one of the two encoded qubits. We did this because these are the largest components in the logical noise. This is proven in appendices
was either X or Z on one of the two encoded qubits. We did this because these are the largest components in the logical noise. This is proven in appendices 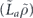 where
where 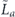 is a logical Y or a non-trivial operator on both encoded qubits. In lemma 15 we prove that we can neglect coherent terms of the form
is a logical Y or a non-trivial operator on both encoded qubits. In lemma 15 we prove that we can neglect coherent terms of the form 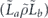 with a ≠ b. Using these results, we can bound the sum of all coherent logical terms relative to the sum of all incoherent logical terms. There are two off-diagonal terms for each diagonal term, e.g.
with a ≠ b. Using these results, we can bound the sum of all coherent logical terms relative to the sum of all incoherent logical terms. There are two off-diagonal terms for each diagonal term, e.g. 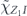 and
and 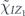 are matched with
are matched with 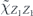 , so we have
, so we have
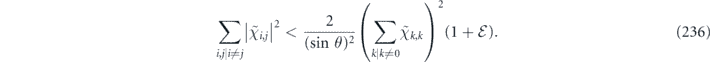
We have proven equation (225). The term on the right-hand side is proportional to the infidelity by equation (K.9). Going back to lemma 1 and equation (44), we can write
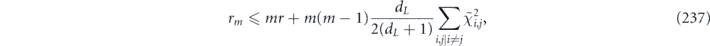
where dL is the dimension of the physical Hilbert space, which is 4 for the toric code without boundaries. We can combine this with equation (236).

Finally, we can use lemma 16 with equation (236) to derive equation (227).
So far we have considered a noise model consisting of the same Z rotation by angle θ on every qubit in the code block. We can use lemmas 8 and 13 to prove that this noise channel produces maximally coherent logical noise in a region around uniform rotations. The single-qubit rotation angles are allowed to differ so long as the deviation is not too great. Therefore, the relation we found between coherent and incoherent logical noise components for the Z rotation noise model bounds the coherence of the logical noise channel for small rotations about any axis, so long as the rotations are close to uniform across the qubits.□
There are some subtleties in the interpretation of theorem 3. We address these in the next subsection, but first we will make a remark about the error bound in equation (226). This error bound is satisfactory for finite code size L; however, we will need make a small modification before the bound is suitable for the L → ∞ limit. This is because the term 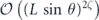 in equation (226) contains a factor polynomial in L. If the single qubit rotation angle θ satisfies |sin θ| ∝ 1/L, then this polynomial factor would make the truncation error large as L → ∞. The polynomial factor comes partly from the fact that the truncation error in equation (230) has a factor of 2L relative to the factor of
in equation (226) contains a factor polynomial in L. If the single qubit rotation angle θ satisfies |sin θ| ∝ 1/L, then this polynomial factor would make the truncation error large as L → ∞. The polynomial factor comes partly from the fact that the truncation error in equation (230) has a factor of 2L relative to the factor of 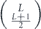 that appears in the lowest-weight incoherent noise terms. The ratio is proportional to
that appears in the lowest-weight incoherent noise terms. The ratio is proportional to  . The other contribution to this polynomial factor comes from the path counting in lemma 5, where we neglected a factor polynomial in w + w' in equation (202). We can cancel the polynomial factor by slightly modifying our truncation procedure. Denote this polynomial factor p(L). Instead of neglecting noise terms with weight >L + 2ζ in the coherent logical noise components, we neglect noise terms with weight >L + 2⌈ζ' log(L)⌉ for a constant ζ'. We perform a similar truncation for the incoherent logical noise components. Then we can choose ζ' large enough that (L sin θ)2ζ'p(L) is decreasing with L. The minimum value for ζ' such that this is decreasing depends on the degree of p(L) and the magnitude of L sin θ. If ζ' is greater than this minimum value, then (L sin θ)2ζ'p(L) is bounded above by a|L sin θ|λζ'log(L), where a is a constant that is determined by the coefficients in the polynomial p(L), and λ is a constant that depends on ζ', the degree of p(L), and the magnitude of L sin θ. Our new truncation rule slightly alters the other error terms in equation (234). The new error term is
. The other contribution to this polynomial factor comes from the path counting in lemma 5, where we neglected a factor polynomial in w + w' in equation (202). We can cancel the polynomial factor by slightly modifying our truncation procedure. Denote this polynomial factor p(L). Instead of neglecting noise terms with weight >L + 2ζ in the coherent logical noise components, we neglect noise terms with weight >L + 2⌈ζ' log(L)⌉ for a constant ζ'. We perform a similar truncation for the incoherent logical noise components. Then we can choose ζ' large enough that (L sin θ)2ζ'p(L) is decreasing with L. The minimum value for ζ' such that this is decreasing depends on the degree of p(L) and the magnitude of L sin θ. If ζ' is greater than this minimum value, then (L sin θ)2ζ'p(L) is bounded above by a|L sin θ|λζ'log(L), where a is a constant that is determined by the coefficients in the polynomial p(L), and λ is a constant that depends on ζ', the degree of p(L), and the magnitude of L sin θ. Our new truncation rule slightly alters the other error terms in equation (234). The new error term is
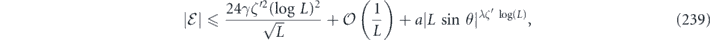
where a, ζ', and λ are constants. a and λ are determined as we described above. We are free to choose ζ', so long as it is greater than a minimum value. Now, if we take the limit L → ∞, we find that the error term in equation (239) remains small. Therefore, we may apply theorem 3 in the limit of L → ∞ with equation (239) replacing equation (226).
6.14. Interpreting bounds on coherence
We have proved a relation between the diagonal and off-diagonal components of the chi matrix of the logical noise channel. The interpretation is a bit subtle, so it is worth commenting on here. We upper bounded the off-diagonal components by 1/|sin θ| times the diagonal components, and we were forced to assume that |sin θ| < 1/L because our analysis only applies to logical strings with length ⩽L + 2ζ where ζ is a constant. With this assumption, the factor of 1/|sin θ| implies that the coherent component of the logical channel may be L times larger than the incoherent component. This might seem to indicate that the coherence of the logical channel is not suppressed for large L, but that is not the best way to think about the comparison.
In equation (229) the term quadratic in m has a coefficient proportional to 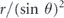 relative to the linear term. But the average infidelity r is exponentially small in L. Thus the coefficient of the quadratic term is really exponentially smaller in L relative to the coefficient of the linear term. In equation (227) the constant c2 is not really a constant, since it scales like L2 if θ scales like 1/L. The point is that if the logical noise channel were fully coherent, i.e. unitary, then c would scale like
relative to the linear term. But the average infidelity r is exponentially small in L. Thus the coefficient of the quadratic term is really exponentially smaller in L relative to the coefficient of the linear term. In equation (227) the constant c2 is not really a constant, since it scales like L2 if θ scales like 1/L. The point is that if the logical noise channel were fully coherent, i.e. unitary, then c would scale like 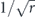 , but we find that
, but we find that 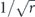 scales like LL/2, which is vastly greater than L2. We conclude that, although the logical noise channel is not exactly incoherent, it is quite close to an incoherent channel as measured by our statements about the growth of average infidelity and the relation between diamond distance and average infidelity.
scales like LL/2, which is vastly greater than L2. We conclude that, although the logical noise channel is not exactly incoherent, it is quite close to an incoherent channel as measured by our statements about the growth of average infidelity and the relation between diamond distance and average infidelity.
We could also consider writing our logical noise channel as a product of a unitary rotation and a Pauli channel. We can solve for the single parameter in each of these two channels. In the limit of low logical noise strength, the angle of rotation of the unitary channel approximately equals one of the off-diagonal chi matrix elements, and the probability of error in the Pauli channel is comparable to one of the diagonal components of the chi matrix. Theorem 3 implies that the logical channel can be written as a product of a unitary channel and a Pauli channel where the angle of rotation of the unitary is larger than the error probability of the Pauli channel by a factor which is approximately 1/|sin θ|, and therefore enhanced by a factor of L if θ scales like 1/L. Again, this might make it seem like the coherence is not suppressed; however, the coherent channel makes a contribution to the average infidelity proportional to the rotation angle squared. This is why we find that the growth of average infidelity becomes nearly linear in m as the code size L increases. As the code block becomes large, the diamond distance for the logical noise channel is much smaller than what one would expect for a coherent channel based on the value of the average infidelity r. This is another way of making the same point as in the previous paragraph.
One might wonder whether a tighter upper bound than theorem 3 can be derived on the strength of the coherent part of the logical channel relative to the incoherent part. In fact, a substantially tighter upper bound is not possible, if we want this bound to hold for arbitrary small rotation angles. For instance, we could choose to set every rotation angle equal to zero except for the qubits along a single length L logical string. For this case, the computation of the logical channel is similar to our computation for the repetition code, where we were able to compute the logical channel quite precisely. Alternatively, for a fixed code size we could choose sufficiently small uniform rotation angles θ such that the lowest-weight terms dominate in the logical noise. In this case the computation of the logical channel is again similar to that of the repetition code. Since the bound we proved for the toric code nearly matches what we found for the repetition code, we know that our result is optimal in this special case. Of course, for some other particular set of single-qubit rotations, the logical noise channel may be less coherent than our upper bound predicts.
7. Conclusions
We have studied characterizations of coherence in quantum channels. One useful method for diagnosing the coherence of a channel  is to consider applying
is to consider applying  times in succession, and to investigate how the average infidelity r of the composite channel
times in succession, and to investigate how the average infidelity r of the composite channel 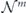 increases with m. For incoherent channels r is linear in m, while for highly coherent channels it can grow quadratically with m. Another useful diagnostic is provided by the relationship between r and
increases with m. For incoherent channels r is linear in m, while for highly coherent channels it can grow quadratically with m. Another useful diagnostic is provided by the relationship between r and 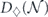 , the distance between
, the distance between 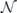 and identity channel as measured by the diamond norm. For incoherent channels this distance scales linearly with r, while for highly coherent channels it scales like
and identity channel as measured by the diamond norm. For incoherent channels this distance scales linearly with r, while for highly coherent channels it scales like 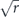 .
.
Using these criteria we have investigated the coherence properties of logical channels. To define a logical channel, we choose a particular quantum error-correcting code and decoding method; then we consider encoding an initial input state, subjecting the physical qubits to a noise model, and finally applying the decoder to obtain the channel's output. Our main conclusion is that, for the code families we examined, even if the physical noise model is highly coherent, the coherence of the logical channel is heavily suppressed in the limit of a large code block.
For the case of the quantum repetition code, we can compute the logical channel precisely, and verify that the logical channel is highly incoherent for large block size. Most of this paper was devoted to the analysis of a more challenging case, the L × L two-dimensional toric code subject to independent unitary noise. Our main conclusion about this case is encompassed by theorem 3. Regrettably, for the case of the toric code we were able to prove that the coherence of the logical channel is suppressed only under an unrealistic assumption: that as the size L of the code block increases, the rotation angle θ applied to each qubit scales like 1/L.
Under this assumption, we can estimate the logical channel well enough for our purposes by expanding it to a constant (L-independent) order in θ, and argue that the higher-order terms we ignore make a contribution that can be safely neglected. A key step in our argument is the observation, backed up by lemmas 9 and 10, that, for L|sin θ| < 1, the logical channel is dominated by logical strings with an easily characterized typical shape. For the logical strings of this typical shape, lemmas 4, 7, 11, and 12 provide a sufficiently accurate estimate of the logical channel to prove theorem 3.
Our main conclusion, that the coherence of the logical coherence is heavily suppressed, applies to unitary physical noise such that each qubit is rotated independently, even if the rotation axis and rotation angle vary from qubit to qubit, as long as the rotations are close to the same and sufficiently small. It also applies for some highly correlated noise models. The result also extends to physical noise channels which are convex combinations of unitary channels, or convex combinations of unitary channels and depolarizing channels. (Depolarizing physical noise is mapped to an incoherent depolarizing logical channel under error correction.)
We emphasize that our result is an asymptotic statement in the limit of large code size L, albeit under the assumption that the noise strength scales like 1/L. For codes of fixed size our results may not be tight; the coherence of logical channels for finite code blocks has been studied elsewhere [11, 17, 21]. Our goal was to study a family of codes with an accuracy threshold instead. When the noise is below threshold, the logical channel approaches the identity as the code block increases in size. In addition, under conditions where theorem 3 applies, the coherent component of the logical channel vanishes much more rapidly than the incoherent component.
It is reasonable to expect that our conclusion—that the logical channel becomes increasingly incoherent as L grows—continues to hold even if we allow L to increase while the rotation angle θ has a fixed constant value. But proving this will be challenging. For one thing, if θ is a constant we cannot accurately estimate the logical channel by expanding to a constant order in θ. Instead, logical strings with length ⩽L(1 + β) need to be included for some constant β. These logical strings are not easy to count. A logical string can be regarded as a self-avoiding walk on the square lattice whose endpoints are a distance L apart, but previously derived upper bounds on the number of self-avoiding walks with specified length [34–36] do not treat the case where the distance between the endpoints differs from the length of the walk by an 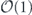 multiplicative factor. And even if we could count the logical strings accurately, we would still need to overcome some additional obstacles to prove that the coherence of the logical channel is suppressed.
multiplicative factor. And even if we could count the logical strings accurately, we would still need to overcome some additional obstacles to prove that the coherence of the logical channel is suppressed.
First, to prove theorem 3, we disposed of the 'exceptional' terms (definition 7), those in which the uncorrectable error on a logical string has lower weight than the correctable error, by arguing that these terms are sufficiently rare as to make a negligible contribution to the coherent part of the logical channel. But for logical strings with length L(1 + β), exceptional terms will be far more common.
Second, when we calculated the contribution to the coherent or incoherent logical noise, we separated the computation into a sum over a connected part and a disconnected part, and argued in lemmas 11 and 12 that the disconnected part contributes a multiplicative factor close to 1. But the proofs of these lemmas required the logical strings to be short, of length L + 2ζ for constant ζ; these proofs do not apply for longer logical strings of length L(1 + β).
Third, and even more dauntingly, our proof of theorem 3 made use of a relationship between the physical noise terms that contribute to the coherent and incoherent logical noise. But as the logical string length increases, the contributions to the coherent and incoherent component of the logical channel become less and less alike. Each contribution to the coherent logical noise is associated with a logical string. In contrast, each contribution to the incoherent logical noise is associated with a pair of logical strings; these strings have segments in common, but they fluctuate relative to one another apart from those shared segments. For short logical strings, these fluctuations are relatively mild, and did not prevent us from relating the incoherent and coherent logical noise, as described in section 6.9. For longer logical strings, the combinatorics become much harder to handle.
Unable to overcome these obstacles ourselves, we settled for proving a weaker result that applies for L|sin θ| < 1 rather than constant θ. Perhaps a more ambitious combinatoric analysis can push the proof through even for constant θ. Or perhaps a completely different approach will be more successful. Conceivably, it is not true that the coherence of the logical channel becomes heavily suppressed for large L and sufficiently small constant θ, though we consider that possibility unlikely.
Further numerical studies of logical coherence may also prove to be instructive. The problem has already been studied numerically [11, 20–22]; however, our methods for organizing the estimate of the logical channel suggest different approaches to numerically simulating the logical channel. Numerics could help to resolve the issues that prevented us from extending theorem 3 to the case where θ is an L-independent constant.
In our analysis of the toric code subject to single-qubit unitary rotations, we used minimal-weight decoding because it can be systematically analyzed. However, we do not expect our conclusion about suppression of logical coherence to be very sensitive to the choice of decoding method. The suppression arises from averaging over many error syndromes, and therefore should occur for other families of stabilizer codes with good decoders. Many of the elements from which we built the proof of theorem 3 can be applied to more general stabilizer codes, including 'logical strings', partitions, exceptional terms, and the decomposition into connected and disconnected parts.
We analyzed the toric code because it has an accuracy threshold, and we aspired to study the coherence of the logical channel for a fixed nonzero value of θ as the linear size L of the code block gets large. That aspiration eluded us, so we settled for investigating the logical coherence in the regime L|sin θ| < 1. In that regime, asymptotic results similar to ours, derived using similar methods, may be applicable to other code families that do not have an accuracy threshold. For example, for the Bacon-Shor code family subjected to depolarizing noise with error probability p, the optimal logical failure probability, computed analytically in [37], is achieved by the code with distance 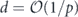 . We anticipate that, for unitary noise, decoding the optimal Bacon-Shor yields a logical channel with strongly suppressed coherence, though we have not done a careful analysis.
. We anticipate that, for unitary noise, decoding the optimal Bacon-Shor yields a logical channel with strongly suppressed coherence, though we have not done a careful analysis.
It has long been suspected that error correction suppresses the coherence of noise. Such suppression had been observed numerically for the toric code [21], but no rigorous argument supporting this conclusion had been previously known for any code family with an accuracy threshold. Our goal in this project was to prove that, for the toric code subject to sufficiently weak independent or weakly correlated unitary noise, the logical channel after decoding is highly incoherent in the limit of a large code block. We fell short of this goal, settling for a proof that coherence is suppressed in the case where the noise strength decreases as the code block grows. Nevertheless, we hope and expect that the tools we have developed will prove to be useful in future studies of quantum error correction.
Acknowledgments
We would like to thank Michael Beverland, Robin Blume-Kohout, Benjamin Brown, Aaron Chew, Andrew Darmawan, Andrew Doherty, Steven Flammia, Daniel Gottesman, Tomas Jochym-O'Connor, Aleksander Kubica, Richard Kueng, David Poulin, and Leonid Pryadko for valuable discussions. We gratefully acknowledge support from ARO-LPS (W911NF-18-1-0103) and NSF (PHY-1733907). The Institute for Quantum Information and Matter is an NSF Physics Frontiers Center.
Appendix A.: Chi matrix and Pauli transfer matrix for qubits
Here we verify lemma 1 for qubits by expressing all non-diagonal terms in Nkl in terms of χij explicitly:
When we collect all the terms in 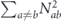 which are quadratic in {χXY, χYX}, we obtain
which are quadratic in {χXY, χYX}, we obtain
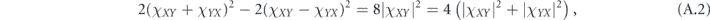
using  , as required by complete positivity. The same applies to the terms involving χIX, χIY, χIZ, χZX, χYZ, and their complex conjugates.
, as required by complete positivity. The same applies to the terms involving χIX, χIY, χIZ, χZX, χYZ, and their complex conjugates.
To prove the claim we must verify that the linear terms cancel. This can be shown using the general argument in lemma 1, but in the qubit case it may be easier to verify the cancellation explicitly. For example, the contributions to Nab involving χIX, χXI, χYZ, χZY are
and we therefore see that the cross terms cancel in 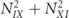 and in
and in 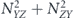 . Similar cancellations occur for all other cross terms.
. Similar cancellations occur for all other cross terms.
Appendix B.: Approximating sums
We wish to evaluate the sum in equation (87):
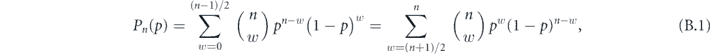
where p = s2 = sin2 θ/2, and (1 − p) = c2 = cos2 θ/2. Note that Pn(p) is the probability of a decoding error for the n-bit repetition code subject to independent noise with bit-flip probability p. It is convenient to redefine the summation index obtaining
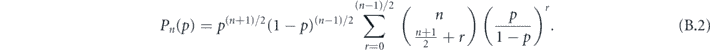
From the Stirling approximation, we have
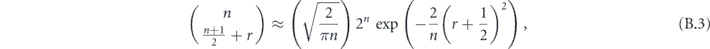
neglecting a multiplicative  correction. Making another
correction. Making another  multiplicative error, we may replace the exponential inside the sum over r by 1, obtaining
multiplicative error, we may replace the exponential inside the sum over r by 1, obtaining
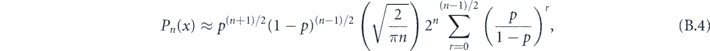
and we also make a negligible error (assuming 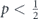 ) by extending the upper limit on the sum to infinity, finding
) by extending the upper limit on the sum to infinity, finding
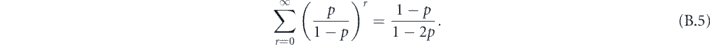
We conclude that
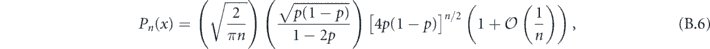
assuming 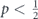 . Using
. Using
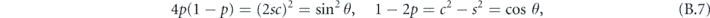
we find
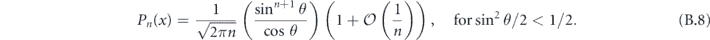
Appendix C.: Correlated noise: leading behavior for large n
Here we will describe an alternative way of understanding equation (164), where the coefficient of  in the logical channel is
in the logical channel is  . This leading behavior results from cancellations of terms higher order in m that occur when we perform the sum over kR in equation (161). What is the explanation for these cancellations?
. This leading behavior results from cancellations of terms higher order in m that occur when we perform the sum over kR in equation (161). What is the explanation for these cancellations?
In section 5 we calculated the coherent and incoherent logical components for the bit-flip code of size n subject to correlated unitary rotations given by a Hamiltonian of the form:
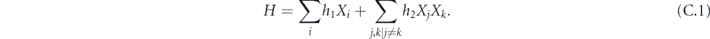
We expressed the logical coherent component  and the logical incoherent component
and the logical incoherent component  in terms of functions Ω and Δ such that
in terms of functions Ω and Δ such that
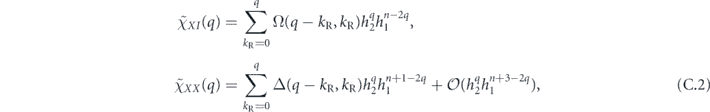
where
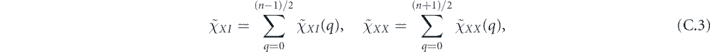
and only even values of q contribute. Here kR is the number of times the Hamiltonian term ih2X X acts on the density operator from the right, and kL = q − kR is the number of times −ih2X X acts from the left.
We were able to compute Ω and Δ by counting the ways of decomposing each physical noise term into combinations of one- and two-body Hamiltonian terms. Repeating equations (149) and (152), we found
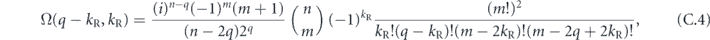
and
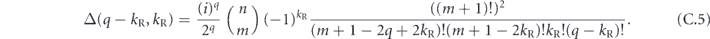
Let's evaluate the sum over kR to leading order in 1/m in both equations (C.4) and (C.5). We focus on the second factor in each equation, which contains all of the kR dependence. In equation (C.4) this factor is
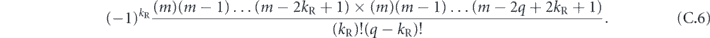
The dominant term for m large is given by
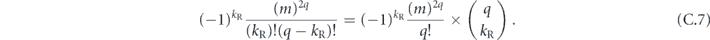
Then when we sum over kR, we have
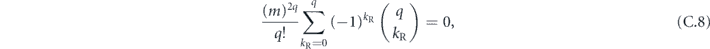
where we have made use of the identity
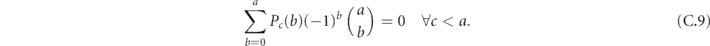
Here Pc(b) denotes any polynomial in b of degree c < a. The situation for Δ is the same except that m is replaced by m + 1. Therefore, the leading term for m large in equations (C.4) and (C.5) vanishes.
Similar cancellations occur for higher-order corrections which are suppressed by powers in 1/m. These corrections are computed by expanding the numerator, equation (C.6), as a 2qth order polynomial in m. For example, the coefficient of m2q−1 is
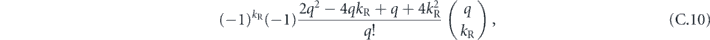
in which the prefactor multiplying  is a second-degree polynomial in kR, so that equation (C.9) implies that the sum over kR vanishes if q > 2. Likewise, the coefficient of m2q−r is a polynomial in kR of degree of 2r, and the sum over kR vanishes if 2r < q. Recalling that only even q contribute, we see that the leading term that survives the summation over kR has r = q/2 and is therefore order m2q−r = m3q/2. We have now seen why terms higher order in m cancel. The term of order m3q/2 can be evaluated using the identity
is a second-degree polynomial in kR, so that equation (C.9) implies that the sum over kR vanishes if q > 2. Likewise, the coefficient of m2q−r is a polynomial in kR of degree of 2r, and the sum over kR vanishes if 2r < q. Recalling that only even q contribute, we see that the leading term that survives the summation over kR has r = q/2 and is therefore order m2q−r = m3q/2. We have now seen why terms higher order in m cancel. The term of order m3q/2 can be evaluated using the identity
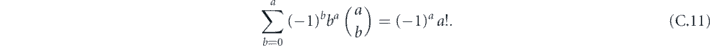
The identities in equations (C.9) and (C.11) can be derived by performing the binomial expansion of (1 + x)a, differentiating repeatedly, and then setting x = −1.
Appendix D.: The shape of the logical string
In this appendix, we prove that among short logical strings nearly all have typical shape as in definition 6.
Lemma 9. In a size L toric code, all but order 1/L of the logical strings running left to right across the code with length ⩽L + 2ζ consist of single steps up and down, so that no vertical segment is longer than one qubit.
Proof. If the size of the code is L and we consider all length L + 2ζ logical strings for fixed ζ, we will count the number of strings that satisfy the condition that each step up or down is only length one. First, we start with a horizontal logical string of length L and then pick ζ sites along it. We have ζ upward steps and ζ downward steps, and we need to fix an ordering. Alternatively, we could think of choosing ζ sites for the upward steps and another ζ sites for the downward steps. In total the number of strings of this type is
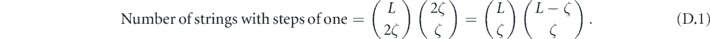
The L dependence in equation (D.1) is
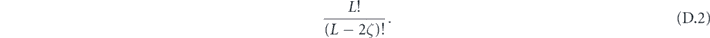
Next, we will count the total number of strings that consist of no backwards steps, that is starting from the left of the code block the strings move only right, up, and down. These strings potentially contain upward and downward steps of more than one. In general, such a string involves q1 distinct steps up with ζ total length and q2 steps down also totaling ζ in length. The number of ways of writing ζ as a sum of q1 terms, not ignoring order, is given by the number of compositions of the integer ζ into q1 terms, which is 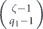 . Each of the q1 steps up and q2 steps down can be placed independently. This gives us
. Each of the q1 steps up and q2 steps down can be placed independently. This gives us 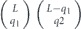 combinations of possible configurations. In total we have
combinations of possible configurations. In total we have
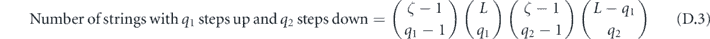
such strings. When q1 = q2 = ζ, we recover the case where each step up or down is by one lattice site. Then we can isolate the L dependence in equation (D.3):
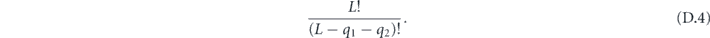
We can compare this to equation (D.2), and we see that there are fewer paths with steps larger than one. The ratio is proportional to
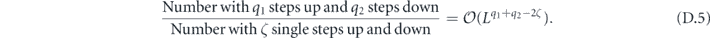
Then if we count the paths with a single step of two and the other steps are all one, there are order 1/L of these relative to the number of paths with single steps up and down.
We must also count the number of logical strings where the string backtracks on itself. There are even fewer of these than the strings with jumps up or down by two. Each string with backtracking can be produced from a string with a jump up or down of at least two lattice spacings. We add some additional cap onto the vertical segment of at least length 2. The number of strings with one instance of backtracking like figure D1 will be proportional to the number of strings of length two shorter that also have at least one step up or down of more than one. For this reason strings like the one in figure D1 are an exponentially smaller minority than the strings with steps up and down of more than one. Then we conclude that nearly all short logical strings spanning the code left to right consist of steps up and down by only one qubit.□
Figure D1. The logical string 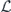 has backtracking. Among short logical strings, those with backtracking are unlikely relative to strings without.
has backtracking. Among short logical strings, those with backtracking are unlikely relative to strings without.
Download figure:
Standard image High-resolution imageLemma 10. For the class of length L + 2ζ strings described in lemma 9 (those with exactly ζ steps up and ζ steps down as they span the code block from left to right), for large L nearly all will have spacings between the steps growing proportional to 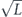 . We choose a small constant γ and define typical strings as those for which all vertical steps are separated by at least
. We choose a small constant γ and define typical strings as those for which all vertical steps are separated by at least 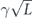 . If we fix the length of logical strings and combine this lemma with lemma 9, we can make the following statement about the fraction of strings of that length that have atypical shape:
. If we fix the length of logical strings and combine this lemma with lemma 9, we can make the following statement about the fraction of strings of that length that have atypical shape:
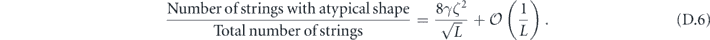
Proof. The total number of strings of the type in lemma 9 is 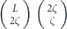 . Now let us compute the number of strings such that each step up or down is separated from others by
. Now let us compute the number of strings such that each step up or down is separated from others by 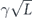 for some constant γ. We can lower bound the number by starting with a length L string running left to right across the code and placing our steps up and down. We suppose that each step we place prohibits placing another step on a further
for some constant γ. We can lower bound the number by starting with a length L string running left to right across the code and placing our steps up and down. We suppose that each step we place prohibits placing another step on a further 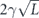 of the sites. This is a lower bound because in the true answer these intervals will sometimes overlap. The lower bound is
of the sites. This is a lower bound because in the true answer these intervals will sometimes overlap. The lower bound is
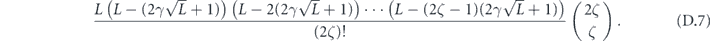
Compared to the total, n − i has been replaced by n − i(2γ + 1) for each i, so that when γ = 0 we recover the total number of strings. In general, the ratio of this limited set to the total for fixed ζ and γ is given by
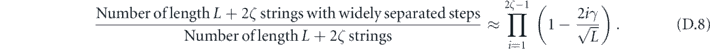
We can lower bound this by
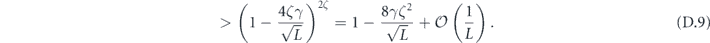
This approaches 1 as L increases, and we see that with high probability a short logical string will have the property that the steps up and down are separated by more than  , as L becomes large. □
, as L becomes large. □
Appendix E.: Disconnected errors
Fix a coherent logical noise component and consider the sum in equation (172). In section 6.7 we argued that the disconnected term is 1 for disconnected errors that do not change how a given connected term is decoded. This allows us to write the sum as
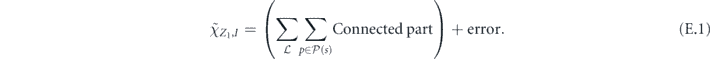
The sum over  includes all typical short connected logical strings.
includes all typical short connected logical strings. 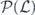 is the set of likely partitions of connected logical string
is the set of likely partitions of connected logical string  . This excludes the partitions we called 'exceptional terms' in definition 7 and lemma 4. '
. This excludes the partitions we called 'exceptional terms' in definition 7 and lemma 4. ' ' contains all the terms we have neglected. This includes the contribution of long logical strings, short logical strings with atypical shape, and exceptional terms. It also includes the terms with disconnected pieces that we did not consider in section 6.7. These are all of the terms where the disconnected errors flip the way the partition is decoded, where we start with a partition and after adding disconnected errors to each side, the error that was originally uncorrectable becomes correctable and vice versa. These terms will not follow the analysis we did in section 6.7. We will describe these terms now and show that they are negligible in the following lemma.
' contains all the terms we have neglected. This includes the contribution of long logical strings, short logical strings with atypical shape, and exceptional terms. It also includes the terms with disconnected pieces that we did not consider in section 6.7. These are all of the terms where the disconnected errors flip the way the partition is decoded, where we start with a partition and after adding disconnected errors to each side, the error that was originally uncorrectable becomes correctable and vice versa. These terms will not follow the analysis we did in section 6.7. We will describe these terms now and show that they are negligible in the following lemma.
Lemma 11. In equation (E.1) the error from the neglected terms 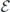 can be expressed
can be expressed
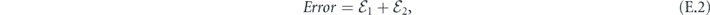
where 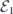 contains the contributions that we have already proven are negligible—long connected logical strings, logical strings with an atypical shape, and exceptional partitions.
contains the contributions that we have already proven are negligible—long connected logical strings, logical strings with an atypical shape, and exceptional partitions.  contains the contributions from terms where the disconnected errors have flipped the way the partition is decoded. These are the terms we neglected in section 6.7. The following is true:
contains the contributions from terms where the disconnected errors have flipped the way the partition is decoded. These are the terms we neglected in section 6.7. The following is true:
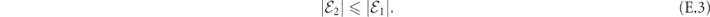
Proof. We start with a typical short connected logical string and take a partition into a correctable operator and an uncorrectable operator, denoted (OUρOC). Now we add disconnected errors, DL and DR to the left and right side of the partition. In some cases the uncorrectable error may become correctable and vice versa. That is, OUDL will be correctable, while OCDR is uncorrectable. For example, the term that contributes to the 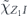 component of the logical noise might be (OCDRρOUDL). Our treatment of the disconnected part in section 6.7 assumed that the added errors did not flip the correctable and uncorrectable sides of the original partition. Now we will justify this assumption by proving that such terms are negligible.
component of the logical noise might be (OCDRρOUDL). Our treatment of the disconnected part in section 6.7 assumed that the added errors did not flip the correctable and uncorrectable sides of the original partition. Now we will justify this assumption by proving that such terms are negligible.
First, we must understand the conditions when an added error will turn the uncorrectable side of a partition into a correctable error. OU is the uncorrectable side of the partition, so the minimal-weight correction to OU is equal to OC up to stabilizers. For OUDL to be correctable, the minimal-weight correction must equal OUDL up to stabilizers and not equal OCDL up to stabilizers. Note that we write DL and not DR because DL and DR have the same syndrome, so as far as the decoder is concerned they are equivalent. This implies
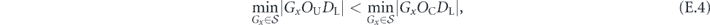
where Gx is an element of  , which denotes the stabilizer group, and |⋅| denotes the weight of a Pauli operator. The weight of the minimal-weight operator equivalent up to stabilizers to OCDL is no greater than the sum of the weights of the minimal-weight operators equivalent up to stabilizers to OC and DL individually. We can continue:
, which denotes the stabilizer group, and |⋅| denotes the weight of a Pauli operator. The weight of the minimal-weight operator equivalent up to stabilizers to OCDL is no greater than the sum of the weights of the minimal-weight operators equivalent up to stabilizers to OC and DL individually. We can continue:
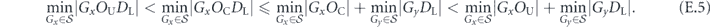
We conclude that the added error must be such that the minimal-weight correction of OUDL is less than the minimal-weight correction of OU plus the minimal-weight correction of DL. This happens when the disconnected error DL lies near OU such that the minimal-weight decoder will tend to form a loop out of parts of DL and OU. This is possible only in cases like the one in figure E1.
The condition in equation (E.5) requires a special combination of disconnected error and original partition. This is possible for both coherent- and incoherent-type disconnected errors as defined in section 6.7. Let us consider incoherent-type disconnected errors first. This is what is illustrated in figure E1. The disconnected error causes the uncorrectable side of the partition to become correctable when DL contains at least two errors in a row adjacent to OU. Based on our condition, we observe that the number of added errors that flip the partition is greatest for the lowest-weight partitions. These terms require the fewest added errors to flip. We also see that the number of these added errors increases with the length of the logical string. A longer string has more adjacent qubits. This implies that the value of the disconnected part is decreasing with string length. This fact was used in lemma 3.
We seek to prove that terms like the one in figure E1 are negligible in the coherent logical noise components. We will do this by mapping each combination of a partition of a connected logical string and a set of disconnected errors such that uncorrectable and correctable errors in the partition are flipped to a partition of a longer connected logical string. There exists a unique stabilizer operator that will multiply the starting partition plus disconnected errors and produce a partition of a longer logical string. This is illustrated in figure E2. Our condition in equation (E.5) says that the minimum stabilizer-equivalent operator to OU is lower weight than OU. The stabilizer operator we need to map figures E1 to E2 is the product of OUDL and its minimal-weight correction. The resulting connected logical string is longer than the original connected logical string, but the total weight of the noise term (connected and disconnected) is smaller. This must be true because we have lowered the weight of the errors in blue (OUDL), and we have not changed the weight of the errors in red (OCDR).
In our previous analysis of the connected part of the coherent logical noise, we neglected logical strings with length >L + 2ζ for a cut-off constant ζ. Then we neglected short logical strings with atypical shape. Finally, we neglected the unlikely partitions of each string, which we called exceptional terms. In this proof we began with a likely partition of a short, typical connected logical string. We added disconnected errors, and in cases like the one in figure E1 where the added errors flipped the partition, we mapped these terms to partitions of a different connected logical string like in figure E2. The final part of our proof is to argue that we can neglect this class of terms, where disconnected errors changed how the connected partition is decoded.
First, we observed above that the weight of the new connected term produced by our mapping is less than the weight of the original term with disconnected errors. This means that the term in figure E1 is suppressed in powers of sin θ/2 relative to the term in figure E2. Second, we will argue that the new connected term is one we have already neglected. Recall how we constructed new connected terms like the one in figure E2. We took a likely partition of a typical, short, connected logical string and added disconnected errors to it in such a way that we flipped how the partition was decoded. The original uncorrectable side became correctable and vice versa. Then we multiplied the correctable error OUDL by a particular stabilizer operator to produce a new term that is a partition of a new connected logical string. We make the following observation. One of two things must be true. One is that the new logical string has an atypical shape, specifically if the logical string runs left to right across the code, the steps up and down in the lattice are separated by less than γL. γ was our chosen constant from lemma 10 that lower bounded the separation between the vertical steps in the logical string. The alternative is that the new connected logical string has a typical shape, but the partition we produce is unlikely. If the stabilizer we multiply by in figure E2 has a width of at least γL, the shape of the new connected logical string may be typical. However, in that case the partition we get for the longer connected logical string has a row of γL qubits all belonging to the blue error. We proved in lemma 4 that partitions with this feature are an exponentially small (in 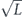 ) fraction of the total partitions. We neglected these partitions in our earlier sum over connected terms. We find that the terms with disconnected errors that flip how the partition is decoded are in one-to-one correspondence with terms we have already neglected and moreover, the magnitudes of the terms with disconnected errors are smaller by a number of powers of sin θ/2. We conclude that such terms contribute less to the logical noise than the terms we have already neglected.
) fraction of the total partitions. We neglected these partitions in our earlier sum over connected terms. We find that the terms with disconnected errors that flip how the partition is decoded are in one-to-one correspondence with terms we have already neglected and moreover, the magnitudes of the terms with disconnected errors are smaller by a number of powers of sin θ/2. We conclude that such terms contribute less to the logical noise than the terms we have already neglected.
So far in this proof, we dealt with incoherent-type added errors. This was for simplicity, so that we had only one picture in mind. The argument for coherent-type added errors is the same. Coherent-type disconnected errors can also flip the correctable and uncorrectable sides of a partition of a connected logical string. We have already stated the condition when this occurs. The disconnected terms on the uncorrectable side DL must contain a contiguous set of errors near a contiguous set of errors in the uncorrectable part of the partition OU.
We bound the contribution of the disconnected coherent-type errors that flip the correctable and uncorrectable sides of the partition in the same way as we did the incoherent-type. We will use a mapping that takes such a term and produces a partition of a longer connected logical string. The mapping multiplies by a suitable stabilizer operator as depicted in figure E4. In this case the new connected term is negligible for the same reasons as in the incoherent-type added error case. The connected logical string produced from the original partition plus the disconnected coherent-type errors either has an atypical shape or the original partition was exponentially unlikely (in 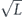 ). We conclude that the contribution of terms with disconnected errors that flip the partition is negligible in the logical noise. □
). We conclude that the contribution of terms with disconnected errors that flip the partition is negligible in the logical noise. □
Figure E1. This figure shows a partition of a connected logical string together with a disconnected error. The disconnected error is incoherent-type, so DL = DR. The uncorrectable error OCDR is in red, while the correctable error OUDL is in blue. The two form a length-5 connected logical string that runs left to right across the code. Without the disconnected errors, OC would be correctable and OU, uncorrectable. Therefore, the added disconnected errors have flipped the original partition.
Download figure:
Standard image High-resolution imageFigure E2. Here is the partition of a connected logical string corresponding to figure E1, with the new uncorrectable error OU in red and the new correctable error OC in blue. This term shares the same syndrome as the one in figure E1. We can always multiply right or left-hand sides by a stabilizer to produce different coherent terms. This term is produced from figure E1 by multiplying the correctable side in blue by the stabilizer operator in gray crosshatching. Notice that the connected logical string is longer, but the total weight of the term is smaller.
Download figure:
Standard image High-resolution imageFigure E3. Here we have a partition of a connected logical string together with a disconnected error. The partition is the same as the one in figures E1 and E2. The disconnected error is now a coherent-type error. The uncorrectable error OCDR is in red, while the correctable error OUDL is in blue. Without the disconnected errors, OC would be correctable and OU, uncorrectable. The added loop of disconnected errors has flipped the original partition.
Download figure:
Standard image High-resolution imageFigure E4. This is the connected string and partition that corresponds to figure E3, with the new uncorrectable error OU in red and the new correctable error OC in blue. We can always multiply right or left-hand sides by a stabilizer to produce different coherent terms. This term is produced from figure E3 by multiplying the correctable side in blue by the stabilizer operator in gray crosshatching. The connected logical string is longer than the one in figure E3, but the total weight of the term is less.
Download figure:
Standard image High-resolution imageAppendix F.: The disconnected part of the incoherent logical noise
In appendix E we proved that for the dominant noise terms in the coherent logical noise components, the disconnected part was equal to 1 up to small corrections. We will now prove the same statement for the dominant noise terms in the incoherent logical noise components.
Lemma 12. In equation (206) we wrote an incoherent logical noise component as a sum over the contributions from individual logical strings. This included a disconnected factor. Here we prove that we can set the disconnected factor equal to 1 and make only a small error. In other words suppose we write
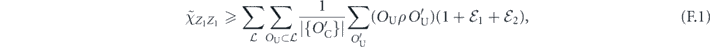
where the sum over  includes all short typical logical strings, OU, |{OC'}|, and OU' are all as described in section 6.9, and
includes all short typical logical strings, OU, |{OC'}|, and OU' are all as described in section 6.9, and  is the error we make by neglecting various connected terms, including high-weight terms and terms with mismatched weight. In lemma 5 we proved that
is the error we make by neglecting various connected terms, including high-weight terms and terms with mismatched weight. In lemma 5 we proved that
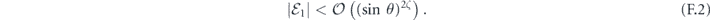
 represents the error we make when we set the disconnected factor equal to 1. Then
represents the error we make when we set the disconnected factor equal to 1. Then
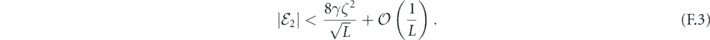
Proof. We can follow the argument from section 6.7 and appendix E. The connected noise terms we considered in those sections had the form (OUρOC). Here we will consider noise terms with the form (OUρOU'). We will imagine arriving at these noise terms in the manner of section 6.9. Namely, we begin with a short logical string with a typical shape. We partition the logical string into OU and OC. Then we choose an operator OU' with the same syndrome as OU. We denoted the set of possible OU' by {OU'}.
Now that we have a connected noise term (OUρOU'), we can think of dressing it with disconnected errors in exactly the same way as we did in the coherent case. In section 6.7 we observed that the added errors that make up the disconnected part can be divided into coherent- and incoherent-type. The coherent-type added errors are when we add different errors to OU and OU'. In this case the errors we add to OU and OU' form a loop (with nonzero area). We saw that as long as the loop was positioned such that the added errors did not change how the connected noise term was decoded, the sum over the possible ways of dividing the errors in the loop between OU and OU' gave zero. We considered incoherent-type added errors where we added the same error to OU and OU'. In this case the contribution was nonzero. As long as the added error did not change how the connected noise term was decoded, the incoherent-type added errors contributed a sin2 θ/2 term on each qubit. Together with the cos2 θ/2 term corresponding to no error on each qubit, this gives 1 for the disconnected part. This applies to the added errors that do not change how the connected part was decoded. Therefore, our approach is to write the disconnected part as 1 plus a correction that comes from the configurations of added errors that change how the connected part is decoded.
In lemma 11 we considered added errors that change how OU is decoded in the coherent logical noise components. For connected noise terms that enter into the incoherent logical noise, the correction to the disconnected part comes from the same source, certain added errors that change how the connected term is decoded. In that case the added errors flipped the correctable and uncorrectable sides of the partition, which gives a phase of −1. In the incoherent case, if OU is made correctable by the added errors, then so is OU', and the resulting term contributes to the identity part of the logical noise. In effect, there are disallowed added errors, which reduce the value of the disconnected part. The counting of such terms is identical to what we did in lemma 11. Recall that these added error terms were related to connected terms that either had an atypical shape or an unlikely partition. The contribution to 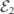 from these terms is proportional to the fraction of atypical logical strings from lemma 10. The contribution from the unlikely partitions is exponentially small in
from these terms is proportional to the fraction of atypical logical strings from lemma 10. The contribution from the unlikely partitions is exponentially small in 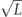 as before.
as before.
There is another class of added errors that contribute to the correction to the disconnected part. Some errors are near the correction Es so that once the errors have been added, they become part of a new connected term. An example is shown in figure F1. This class of terms contains only incoherent-type added errors. Coherent-type added error placed here will still give 0 after we sum over the ways of splitting the errors into the left and right disconnected errors. This is the same as for coherent-type added errors far from the connected logical string. For a likely partition of a short logical string with typical shape, Es will have the same weight as OC. The incoherent-type added errors that join the connected part may either lie near to Es or they may be contained in Es. We will first study the case where the added errors are not contained in Es. These terms are closely related to the situation we just analyzed where the added errors sit next to OU. The condition on the added error is analogous to equation (E.5). Let D denote the added incoherent-type error and  denote the stabilizer group. Then
denote the stabilizer group. Then
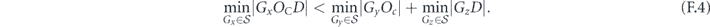
If this condition is satisfied, then the added error becomes part of a new connected term (OUDρOU'D). Together with the new lowest-weight correction OUD forms a new connected logical string. This logical string is similar to the old logical string, but it contains a detour where it veers off to include the error D. This logical string either has an unlikely shape because it includes two closely spaced vertical steps, or the error D has width >γL. In the latter case we also require that the original correction Es included >γL consecutive qubits. This is exponentially unlikely according to the counting we did in lemma 4 and the bound we wrote in equation (191). We conclude that the contribution to the error term  2 from the noise terms we arrive at by adding errors proximate to OC is small.
2 from the noise terms we arrive at by adding errors proximate to OC is small.
This leaves the added errors that lie within Es or one of the operators with the same syndrome and weight. In this case the new connected logical string that results from adding the errors is the same as the old logical string. We will compare the set of terms we arrive at by adding errors in this manner to the set of terms with the same OU but a higher-weight OU'. We will argue that there are more of the terms with higher-weight OU'. We have already neglected such noise terms in lemma 7, so we conclude that the correction to the disconnected part is small.
We start with a connected noise term (OUρOU'), where |OU| = |OU'| = w. We form a higher-weight noise term by adding an incoherent-type error D within one of the operators OC' to produce a new connected noise term (OUDρOU'D). This adds a total of two to the weight of the term. We can place the added error anywhere within one of the operators OC'. The number of possibilities is  . Now consider the possible connected noise terms with the same OU, but instead of choosing OU' with weight w, we set |OU'| = w + 2. Suppose we start with an operator OU' with weight w. We can construct one with w + 2 by adding an extra 'cap' consisting of three qubits around a single plaquette or star. This is illustrated in figure F2, where three possible choices of OU' are drawn with the red dashed line. The number of possible choices is at least
. Now consider the possible connected noise terms with the same OU, but instead of choosing OU' with weight w, we set |OU'| = w + 2. Suppose we start with an operator OU' with weight w. We can construct one with w + 2 by adding an extra 'cap' consisting of three qubits around a single plaquette or star. This is illustrated in figure F2, where three possible choices of OU' are drawn with the red dashed line. The number of possible choices is at least  , because we can place a cap at each location along OU. The full set of possibilities will generally be larger. If we consider a pair of added errors lying within OC', then we compare to the connected noise terms with |OU'| = |OU| + 4. The noise terms where OU and OU' have different weights were discussed in section 6.10. We proved in lemma 7 that the contribution of these terms is negligible. Finally we conclude, just as in lemma 11, that each of the disconnected errors that contribute to the error
, because we can place a cap at each location along OU. The full set of possibilities will generally be larger. If we consider a pair of added errors lying within OC', then we compare to the connected noise terms with |OU'| = |OU| + 4. The noise terms where OU and OU' have different weights were discussed in section 6.10. We proved in lemma 7 that the contribution of these terms is negligible. Finally we conclude, just as in lemma 11, that each of the disconnected errors that contribute to the error 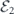 can be matched with a connected noise term that we have already neglected. In other words, the error
can be matched with a connected noise term that we have already neglected. In other words, the error 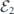 is less than
is less than 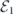 . Therefore, we can say that the disconnected part = 1 and make only a small error for low-weight connected terms. □
. Therefore, we can say that the disconnected part = 1 and make only a small error for low-weight connected terms. □
Figure F1. This figure illustrates a certain type of added error term. We start with a short, typical logical string and partition it into operators OU and OC. Then we would choose some operator OU' (not pictured) with the same weight and syndrome as OU to produce an incoherent term. The errors in the red circle are added to both OU and OU'. The minimal-weight correction is shown as a black dashed line. The added errors are not disconnected but form a new connected term.
Download figure:
Standard image High-resolution imageFigure F2. This figure illustrates the idea of the proof that a certain type of added error term contributes only a small error. Consider a connected logical string that we partition into OU and OC, the solid red and blue lines. The class of added errors we consider are those where the added error lies along OC or one of the operators OC' with the same weight and syndrome. The possible locations for such an added error are marked by the × symbols. We prove that such terms are negligible by comparing to the noise terms where the operator OU' is chosen with weight 2 greater than OU. Three of the possible choices for OU' are drawn with the dashed red lines. In this example there are 12 possible OU' operators and six possible added error terms.
Download figure:
Standard image High-resolution imageAppendix G.: Physical Y errors
In lemma 8 we considered rotations in the X–Z plane where the single-qubit rotation angles were allowed to differ. Here we prove that allowing for rotations partly around the Y axis on the physical qubits will decrease the coherence of the logical noise channel.
Lemma 13. Consider an L × L toric code and a noise channel that consists of single-qubit rotations by an angle θ about an arbitrary axis. Suppose that |sin θ| < 1/L as in lemmas 3 and 5. Then the connected contribution to the logical noise from low-weight terms is most coherent when the single-qubit rotations are about an axis in the X–Z plane. We proved elsewhere that the low-weight connected contribution dominates the logical noise components.
Proof. Let θX, θY, θZ denote the rotation angles about the X, Y, and Z-axis, respectively, so that 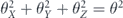 . Of the coherent logical noise components, according to lemmas 14 and 15, the dominant components are the ones
. Of the coherent logical noise components, according to lemmas 14 and 15, the dominant components are the ones 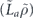 , where
, where 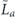 is a logical X or Z operator on one of the encoded qubits. We apply several of our lemmas to restrict the noise terms we consider, just as in theorem 3. Among the noise terms that contribute to the coherent logical noise, we keep the terms with short, typical logical strings and non-exceptional partitions. Among the noise terms that contribute to the incoherent logical noise, we keep the terms where the logical string
is a logical X or Z operator on one of the encoded qubits. We apply several of our lemmas to restrict the noise terms we consider, just as in theorem 3. Among the noise terms that contribute to the coherent logical noise, we keep the terms with short, typical logical strings and non-exceptional partitions. Among the noise terms that contribute to the incoherent logical noise, we keep the terms where the logical string 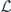 is short and typical,
is short and typical, 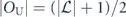 , |OC| = |Es|, and |OU'| = |OU|.
, |OC| = |Es|, and |OU'| = |OU|.
First suppose that θZ = 0. Then the logical 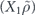 noise component is generated from noise terms (OUρOC) where OU and OC together contain X acting on every qubit along an X1 logical string. Meanwhile, the incoherent logical
noise component is generated from noise terms (OUρOC) where OU and OC together contain X acting on every qubit along an X1 logical string. Meanwhile, the incoherent logical 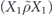 noise component is also generated by X1 logical strings. In theorem 3 we state a bound on the relative magnitude of these logical noise components. Here θX plays the role of θ in equation (233). Under our θX and θY rotation noise model, we also have a non-zero logical
noise component is also generated by X1 logical strings. In theorem 3 we state a bound on the relative magnitude of these logical noise components. Here θX plays the role of θ in equation (233). Under our θX and θY rotation noise model, we also have a non-zero logical 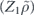 noise component. This is generated by connected noise terms, (OUρOC), where OU and OC together contain both X and Y acting on every qubit along a Z1 logical string. The number of Z1 logical strings with length ℓ is the same as the number of X1 logical strings with length ℓ. However, the weight of the noise terms that contribute to
noise component. This is generated by connected noise terms, (OUρOC), where OU and OC together contain both X and Y acting on every qubit along a Z1 logical string. The number of Z1 logical strings with length ℓ is the same as the number of X1 logical strings with length ℓ. However, the weight of the noise terms that contribute to 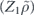 is ℓ2. The contribution of each noise term is
is ℓ2. The contribution of each noise term is 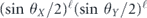 . In contrast, the noise terms that contribute to
. In contrast, the noise terms that contribute to 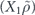 are all proportional to
are all proportional to 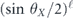 . Therefore,
. Therefore, 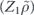 is exponentially smaller in L relative to
is exponentially smaller in L relative to 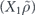 for any choice of rotation axis in the X–Y plane. The
for any choice of rotation axis in the X–Y plane. The 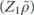 noise component has a negligible effect on the relative magnitudes of the coherent and incoherent logical noise components. We also have an incoherent
noise component has a negligible effect on the relative magnitudes of the coherent and incoherent logical noise components. We also have an incoherent 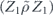 noise component. This is generated by noise terms, (OUρOU'), where OU and OU' contains Y errors along an uncorrectable subset of a Z1 logical string. These noise terms have magnitude
noise component. This is generated by noise terms, (OUρOU'), where OU and OU' contains Y errors along an uncorrectable subset of a Z1 logical string. These noise terms have magnitude 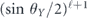 , which is exponentially large relative to the noise terms that contributed to
, which is exponentially large relative to the noise terms that contributed to 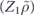 . It follows that the logical coherence is maximized when θY = 0 and θX = θ. We began by supposing θZ = 0. Next, we will consider the case where θX, θY, and θZ are all nonzero.
. It follows that the logical coherence is maximized when θY = 0 and θX = θ. We began by supposing θZ = 0. Next, we will consider the case where θX, θY, and θZ are all nonzero.
Suppose |θZ| ⩾ |θX|. If not, switch the role of X and Z in what follows. Fix a Z1 logical string  . The contribution of the logical string
. The contribution of the logical string  to
to  is a sum over the partitions of
is a sum over the partitions of 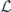 . For each partition (OUρOC), we can replace a Z error in OU with a Y error if we add an X error on the same qubit to OC. Similarly we can replace a Z error in OC by a Y error if we add an X error on the same qubit to OU. The Z syndrome is unchanged, but now we also have a non-trivial X syndrome corresponding to the X error on the chosen site. This does not change how any partitions are decoded, but it does change the weight. The contribution of each partition to
. For each partition (OUρOC), we can replace a Z error in OU with a Y error if we add an X error on the same qubit to OC. Similarly we can replace a Z error in OC by a Y error if we add an X error on the same qubit to OU. The Z syndrome is unchanged, but now we also have a non-trivial X syndrome corresponding to the X error on the chosen site. This does not change how any partitions are decoded, but it does change the weight. The contribution of each partition to 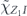 is a sum over all combinations of either a Z error or a Y and an X error on every qubit in
is a sum over all combinations of either a Z error or a Y and an X error on every qubit in 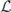 . The terms with Y errors have higher weight. This means they contain extra factors of sin θY/2, which is small since |sin θ| < 1/L. At the same time, the logical string
. The terms with Y errors have higher weight. This means they contain extra factors of sin θY/2, which is small since |sin θ| < 1/L. At the same time, the logical string 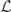 contributes to the
contributes to the 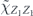 logical noise component. These noise terms include some that feature only Z errors and others with some number of Z errors replaced by Y errors. Unlike the contributions to
logical noise component. These noise terms include some that feature only Z errors and others with some number of Z errors replaced by Y errors. Unlike the contributions to 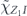 , these terms with Y errors are not higher-weight. There are no extra factors of sin θY/2, and we conclude that the incoherent logical noise components are made larger relative to the coherent logical noise components. Therefore, the logical coherence is maximized when θY = 0.□
, these terms with Y errors are not higher-weight. There are no extra factors of sin θY/2, and we conclude that the incoherent logical noise components are made larger relative to the coherent logical noise components. Therefore, the logical coherence is maximized when θY = 0.□
Appendix H.: Other logical maps
In the section 6.4, we restricted our attention to logical coherent terms of the form 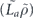 , where La is an X or Z operator on one of the encoded qubits. Now we would like to consider the case where La acts nontrivially on both encoded qubits or as Y on one or both of the encoded qubits.
, where La is an X or Z operator on one of the encoded qubits. Now we would like to consider the case where La acts nontrivially on both encoded qubits or as Y on one or both of the encoded qubits.
Lemma 14. Consider the toric code with minimal-weight decoding and a noise model that consists of uniform single-qubit unitary rotations about a fixed axis. Then the coherent logical noise components, 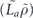 , where
, where 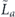 is a Y-type logical operator or
is a Y-type logical operator or 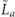 is a non-trivial logical operator on both encoded qubits, are negligible relative to the components where
is a non-trivial logical operator on both encoded qubits, are negligible relative to the components where 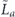 is an X- or Z-type logical operator on one encoded qubit.
is an X- or Z-type logical operator on one encoded qubit.
Proof. Suppose we have 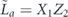 . Logical strings of this type are the product of two operators of the type we have already considered. Each connected noise term that contributes to the logical noise component,
. Logical strings of this type are the product of two operators of the type we have already considered. Each connected noise term that contributes to the logical noise component, 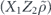 , is a product of a connected noise term that contributes to
, is a product of a connected noise term that contributes to 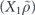 and a connected noise term that contributes to
and a connected noise term that contributes to 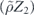 . It follows that up to corrections that come from the disconnected part,
. It follows that up to corrections that come from the disconnected part, 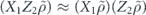 . The logical components,
. The logical components, 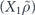 and
and 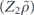 , are both small if error correction is working, so the logical
, are both small if error correction is working, so the logical 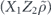 component will be negligible. If
component will be negligible. If 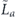 is Y-type operator on the first encoded qubit, the argument is the same, since Y-type logical strings are products of X and Z-type logical strings, Y1 = X1Z1.
is Y-type operator on the first encoded qubit, the argument is the same, since Y-type logical strings are products of X and Z-type logical strings, Y1 = X1Z1.
If we have 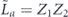 , the logical component
, the logical component 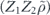 is no longer a product of
is no longer a product of 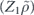 and
and 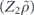 . This is because Z1 and Z2-type logical strings can overlap, and this changes the counting of logical strings of a fixed weight. Figure H1 shows two examples of this kind of logical string. At length 2L, where L is the code distance, there are many connected logical strings because we can have a single connected string that wraps the torus along both directions. If we count the shortest paths between two points in the square lattice separated by distance l1 in the horizontal and l2 in the vertical, we get
. This is because Z1 and Z2-type logical strings can overlap, and this changes the counting of logical strings of a fixed weight. Figure H1 shows two examples of this kind of logical string. At length 2L, where L is the code distance, there are many connected logical strings because we can have a single connected string that wraps the torus along both directions. If we count the shortest paths between two points in the square lattice separated by distance l1 in the horizontal and l2 in the vertical, we get

We can use this to bound the number of weight-2L logical Z1Z2 strings. Fix two sites in the code, qubit i along the vertical edge of the code and qubit j along the horizontal edge. Now count the number of shortest paths that connect these points. We have
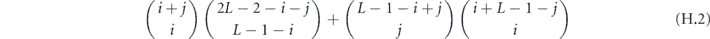
for the two ways of linking the edge points. We simply apply the result from equation (H.1). In the end we find that
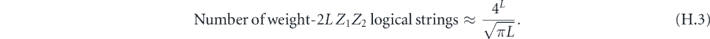
In section 6.5, we counted logical strings that act as X or Z on one of the encoded qubits starting from length L, and we found exponentially many logical strings at higher weights. If we consider weight-2L logical strings, we find order μ2L logical strings, where μ ≈ 2.64 for the 2D square lattice. This is more than 4L, so we have more of the high-weight logical strings that act on only one encoded qubit. Further, in our path counting in lemma 3, we neglected all logical strings of length >L + 2ζ for a constant ζ. The strings of length ⩾2L contribute negligibly for large L. Then we conclude that the logical noise components,  , where La is a Y-type logical operator or acts on both encoded qubits, are negligible relative to the noise components where La acts as X or Z on one of the encoded qubits. □
, where La is a Y-type logical operator or acts on both encoded qubits, are negligible relative to the noise components where La acts as X or Z on one of the encoded qubits. □
Figure H1. Here are two examples of lowest-weight Z1Z2 logical strings,  and
and  , that act as Z on both encoded qubits. Notice that red and green connect the edge points in different (but topologically equivalent) ways.
, that act as Z on both encoded qubits. Notice that red and green connect the edge points in different (but topologically equivalent) ways.
Download figure:
Standard image High-resolution imageAppendix I.: More general coherent terms
We have considered coherent logical noise components  , where
, where 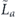 is a logical operator that acts as X or Z on exactly one of the encoded qubits. We must also consider logical noise components
is a logical operator that acts as X or Z on exactly one of the encoded qubits. We must also consider logical noise components 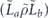 , where
, where 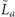 and
and 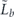 are different non-trivial operators on the encoded qubits.
are different non-trivial operators on the encoded qubits.
Lemma 15. Consider the L × L toric code with noise that consists of single-qubit unitary rotations about a fixed axis by angle θ on every qubit, where |sin θ| is <1/L as in lemma 3. Each coherent logical noise component of the form 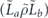 , where
, where 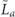 and
and 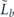 are different nontrivial logical operators, is negligible relative to the coherent logical noise components with
are different nontrivial logical operators, is negligible relative to the coherent logical noise components with  . Each of the more general coherent terms is given by
. Each of the more general coherent terms is given by
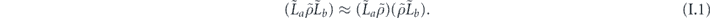
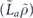 and
and 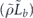 are both small (because we are interested in the regime where error correction succeeds with high probability.) Therefore, we may safely neglect all logical noise components
are both small (because we are interested in the regime where error correction succeeds with high probability.) Therefore, we may safely neglect all logical noise components 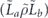 , where
, where  and
and 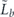 are different nontrivial logical operators.
are different nontrivial logical operators.
Proof. Our approach here is to bound the coherent logical noise components  , where
, where 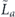 and
and 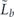 are different nontrivial logical operators, by the coherent logical noise components we have already considered. This follows because the short connected logical strings with different logical action do not overlap much. Overlap here means that the strings contain the same error acting on the same qubits. One possible overlap is between Z1 and Z2 logical strings. Pick a Z1 logical string,
are different nontrivial logical operators, by the coherent logical noise components we have already considered. This follows because the short connected logical strings with different logical action do not overlap much. Overlap here means that the strings contain the same error acting on the same qubits. One possible overlap is between Z1 and Z2 logical strings. Pick a Z1 logical string, 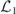 , and a Z2 logical string,
, and a Z2 logical string,  . One string runs left to right, and the other runs top to bottom. If the horizontal string is longer than L, the code distance, then it has vertical steps along it, and these steps may overlap with the vertical logical string. An example is given in figure I1. We assume
. One string runs left to right, and the other runs top to bottom. If the horizontal string is longer than L, the code distance, then it has vertical steps along it, and these steps may overlap with the vertical logical string. An example is given in figure I1. We assume  and
and  both have length ⩽L + 2ζ because of lemma 3. Then we use lemma 9 to restrict to the case where all the steps are one lattice spacing at a time. Any possible overlap is on at most two sites as shown in figure I1. Further, if we consider all possible pairs of a Z1 logical string and a Z2 logical string, only order 1/L strings have any overlap at all, so we can neglect possible overlap.
both have length ⩽L + 2ζ because of lemma 3. Then we use lemma 9 to restrict to the case where all the steps are one lattice spacing at a time. Any possible overlap is on at most two sites as shown in figure I1. Further, if we consider all possible pairs of a Z1 logical string and a Z2 logical string, only order 1/L strings have any overlap at all, so we can neglect possible overlap.
Because the two logical strings  and
and 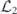 are approximately disjoint, when we sum over partitions, each partition approximately factors into a partition of
are approximately disjoint, when we sum over partitions, each partition approximately factors into a partition of 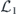 times a partition of
times a partition of 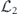 . That is, each connected noise term in the sum for the logical
. That is, each connected noise term in the sum for the logical 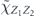 is a partition
is a partition 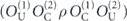 which is approximately equal to
which is approximately equal to 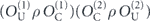 where
where 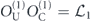 and
and 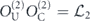 . Therefore,
. Therefore, 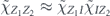 up to small corrections from the overlap between
up to small corrections from the overlap between  and
and  and from the disconnected part. Each of the terms
and from the disconnected part. Each of the terms 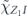 and
and 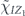 will be ≪1 if we are in a regime where error correction succeeds. Therefore, the
will be ≪1 if we are in a regime where error correction succeeds. Therefore, the 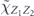 logical noise component will be negligible relative to the
logical noise component will be negligible relative to the 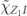 logical noise component. The same holds for the other logical noise components with a nontrivial logical operator on each side of
logical noise component. The same holds for the other logical noise components with a nontrivial logical operator on each side of 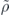 . Then we may safely neglect the more general coherent terms and consider only the
. Then we may safely neglect the more general coherent terms and consider only the 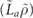 components. □
components. □
Figure I1. Here we have a Z1 and a Z2 logical string. They have an overlap of two qubits, but if we fix one string and consider all possible paths for the other string, we see that only order 1/L have any overlap.
Download figure:
Standard image High-resolution imageAppendix J.: Growth of infidelity
The expression for the average infidelity after m applications of the noise channel from [25] is an upper bound.
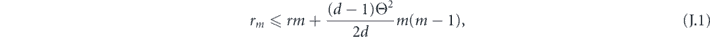
where rm is the average infidelity after m applications of a fixed noise channel, r is the average infidelity after one application of the channel, d is the dimension of the Hilbert space on which the channel acts, and Θ is the coherence angle. For anything save unitary or completely coherent channels, the upper bound has a linear component. We expect that this linear part is not only an upper bound, but that the average infidelity will grow linearly to lowest order.
Working in the Pauli transfer matrix representation, a unital noise channel is written as
When channels are composed, we multiply the Pauli transfer matrices. After applying the same noise channel twice, we have diagonal entries
After m applications of the noise channel, the diagonal entries are
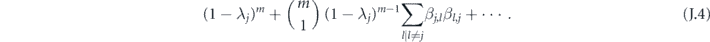
Then the infidelity after composing the channel m times is proportional to
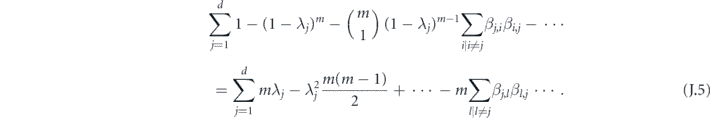
To lowest order the infidelity grows proportional to r, the first term in the upper bound in equation (J.1).
Appendix K.: Diamond distance bound
The diamond distance from identity can be bounded in terms of the average infidelity, r, and the sum of squares of the off-diagonal (coherent) components of the chi matrix.
Lemma 16. In equation (48) we upper bounded the diamond distance from identity for a channel by a function f based on [9]. This function depended on the components of the Pauli transfer matrix for the channel. With a little algebra, we can show
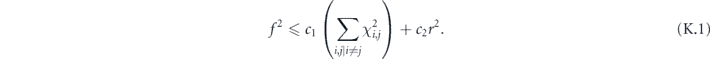
where the constants are given by 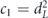 and
and 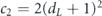 and dL is the dimension of the logical space.
and dL is the dimension of the logical space.
Proof. We start with equation (48), and rewrite the Pauli transfer matrix in terms of chi matrix. We expand 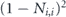 and compare to r2. Equation (50) reads
and compare to r2. Equation (50) reads
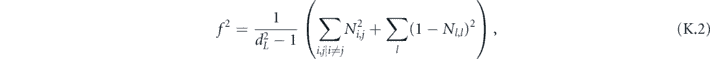
where N is the Pauli transfer matrix representation of the noise channel. The diamond distance from identity is bounded by a constant times f. We can expand f in terms of the chi matrix elements. Recall that we already have lemma 1 concerning the off-diagonal elements. Also, the infidelity r is related to the trace of the Pauli transfer matrix or the (0,0) element of the chi matrix.
We can write the diagonal components of Pauli transfer matrix in terms of the diagonal components of the chi matrix in the following way:
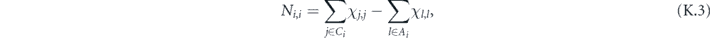
where the set Ci includes all the Pauli operators σj that commute with σi and the set Ai is all Pauli operators σl that anticommute with σi. For example, in the case of a single-qubit channel
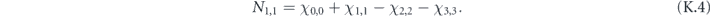
Then we can sum over all the diagonal components of N using the fact that the identity operator commutes with every operator.
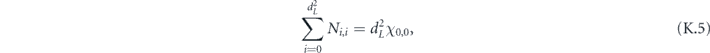
where dL is the dimension of the logical space. Next, we can expand the diagonal term from equation (K.2):
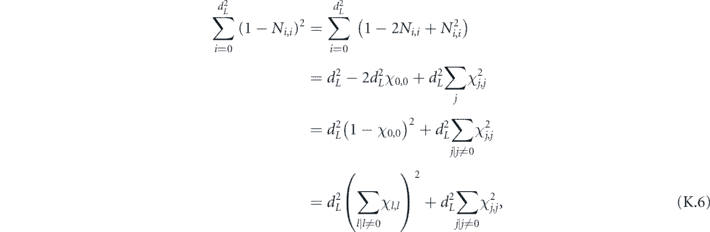
where we have used the trace preservation condition  χi,i = 1. Because the noise channel is unitary, the diagonal components of the chi matrix are real and greater than 0. Then we can bound
χi,i = 1. Because the noise channel is unitary, the diagonal components of the chi matrix are real and greater than 0. Then we can bound
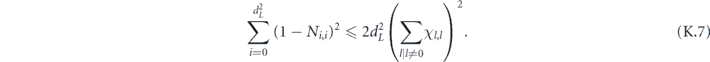
When we substitute into equation (K.2) and use lemma 1 for the off-diagonal terms, we have the following bound on the diamond norm distance from identity:
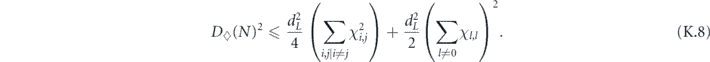
Finally, the average infidelity r is given by
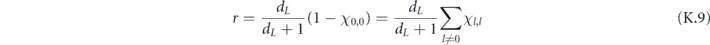
in the chi matrix representation. Equation (K.1) follows.□