Abstract
The study of Weyl semimetals (WSs) has been attracting widely attention due to the fact that the Weyl point (WP) and associated topological invariants enable WSs to exhibit a variety of unusual properties, including robust surface wave and chiral anomaly. However, for the elastic analogue of ideal type-II WS, having the strongly tilted cone dispersion and conical Fermi surface, its realization still remains elusive. Here, we show an elastic type-II WS in three-dimensional (3D) solid phononic crystals (PnCs) with the broken spatial inversion symmetry. The ideal type-II WPs with opposite topological charges (±1), opened Fermi-arc-like surface states and associated robust transport for 3D elastic wave are demonstrated. Furthermore, we reveal the phase transition between the elastic type-II WSs and two valley topological insulators (TIs). At the domain wall of two 3D PnCs with different valley topological phase, the Fermi-circle-like surface states are obtained. Our research provides a platform for the exploration of Weyl physics on a macroscopic mechanical structure.
Export citation and abstract BibTeX RIS
1. Introduction
Driven by the exotic features of being immune against defects and backscattering-suppressed transport, the research interest on topological materials [1–8] has been growing extensively. The simplest three-dimensional topological systems are WSs [9]. In WSs, the WP refers to the crossing point of two bands, which have the linear dispersion in all directions near the Fermi surface in 3D momentum space. They act like monopoles of the Berry flux and being related to a quantized topological charge. A immediate outcome of their nonzero charge is that the perturbations preserving periodicity cannot lift the WP to open a bandgap but only make it move in the bands. In addition, the WPs and the related nonzero topological charges allow WSs exhibiting various remarkable properties, including the robust surface states and the chiral anomaly [10–12]. Especially, the surface band dispersion at the Fermi energy can generate the open arcs connecting projected WPs with the opposite topological charge. Due to the fact that in momentum space, the Berry curvature of WP is strictly zero under the result of parity symmetry and time-reversal symmetry, the existence condition of the isolated WPs must satisfy that at least one of spatial inversion symmetry (SIS) or time-reversal symmetry (TRS) is destroyed [13]. Because this condition can yield to a wide range of physical systems, the Weyl physic has broken through the restrictions of electrons and been developed into artificial periodic crystals for classical waves, such as electromagnetic wave in photonic crystals, acoustic wave in sonic crystals and elastic wave in mechanical crystals. Based on the double-gyroid structures, Lu et al first reported the theoretical prediction and experimental observation of Type-I WPs for electromagnetic wave in 3D photonic system, in which the associated one-way chiral surface states are discovered successfully [14, 15]. By using chiral electromagnetic metamaterial, Xiao et al theoretically investigated the existence of type-II WPs with tilted cone dispersion [16]. Noh et al first experimentally observed the photonic type-II WPs at optical frequencies in which conical diffraction occurring at a single frequency and Fermi arc surface states emerging from the WPs are illustrated [17]. Since then, the exploration of the topological band physics with various unconventional WPs [18–22] and associated intriguing phenomena to have become a hot research focus for many disciplines because it provides an ideal platform for designing modern photonic devices with high-robustness and integrated 3D quantum oscillations [23].
In parallel, as one of the classical waves, the acoustic wave possessing similar characteristic of WPs and topological surface states in 3D PnCs has attracted a lot of attention because of the advantages of robustly manipulating topological surface wave in high-dimensions and multi-planes. Xiao et al first introduced the concepts of WPs into the 3D acoustic system and discovered the acoustic type-I WPs with chiral edge states [24]. Then, Yang et al have theoretically constructed the acoustic type-II WPs by stacking one-dimensional acoustic resonators [25]. Li et al first reported the observation of acoustic WPs in a 3D chiral PnC by experiment, in which the acoustic surface states originated from the WPs and enabled topological one-way transport and the immunity against to defects were demonstrated [26]. Besides, many intriguing phenomena associated with WPs and surface states were explored using artificial phononic structure, such as the interface transport behavior and wavevector selectivity of phonons WPs [27–29]. Ge et al investigated the acoustic WPs and Fermi arcs with the straight-line trajectory and explored the collimation effect of the robust acoustic surface states [30]. He et al first discovered the novel interface behavior of topological negative refraction without reflection for acoustic surface states in 3D Weyl acoustic system through tailoring the surface terminations [31]. Very recently, Zangeneh-Nejad et al have reported another type of acoustic WS, in which the Fermi surface is a flat line and the flat acoustic surface mode of the WS brings the distinctive characteristic of a zero index of refraction along a given direction [32]. Extensive researches of acoustic WS predicted and illustrated the rich topological Weyl physics and prospective applications in novel low-loss acoustic devices [33–36]. Even so, the implementation of Weyl phases for the 3D elastic system is rather challenging. Expect for the proposals of type-I elastic WPs in the chiral truss-structure system by Wang et al [37] and Shi et al [38], the demonstration of ideal type-II WPs and topological phase transition in elastic WS system remains elusive.
Here, an ideal type-II WS for elastic wave is reported in the non-chiral 3D macroscopic solid PnC, in which two pairs of ideal type-II WPs are revealed. Originated from the topological nature of type-II WPs, the anti-chiral Fermi-arc-like surface states of elastic wave and their robust transport are demonstrated. More importantly, by varying the inversion geometric parameters, a phase transition between the elastic type-II WSs and valley TIs is clearly demonstrated. Through the simulation, we show the existence of Fermi-circle-like surface states for the 3D elastic waves at the domain of the two distinct valley PnCs. Finally, the robust transport of elastic Fermi-circle-like surface states is further illustrated. This work largely enriches fundamental physics exploration of the Weyl-physics-based structures for ultrasonic devices in waveguide, splitter and signal communication.
2. Theory and method
Figure 1(a) presents the 3D model of elastic Weyl PnC, which is composed of the cylinders and perforated plates stacked periodically along the z axis. The array of hexagonal blocks of the drilled plate and the connected cylinders are both honeycomb lattice. Figure 1(b) shows the unit cell outlined by the parallelogram, in which the in-plane lattice constant is a = 35 mm and the height lattice constant is h0 = 13.9 mm. The height of the perforated plate is h1 = 7.5 mm. To break the SIS of the elastic system, we introduce a perturbation by simultaneously varying the relative radius of rods and the relative side-lengths of hexagonal blocks. The radii of two adjacent rods are rA = 3.4 mm and rB = 1.6 mm, and the side-lengths of adjacent hexagonal blocks are LA = 9.7 mm and LB = 9.3 mm. Two parameters, Δr = rA − rB and ΔL = LA − LB are used to characterize the breaking level of the spatial inversion symmetry. The material of constructed 3D elastic structure is made by aluminum. The material parameters are Young's modulus EAl=68.9Gpa, density ρAl = 2700 kg m−3 and Poisson's ratio σAl = 0.33, respectively. Moreover, the media for the perforated holes are filled by air, of which material parameters are the density ρa = 1.25 kg m−3 and wave velocity ca = 343 m s−1. When the elastic wave propagates in the 3D periodic structure, we can write the governing equation as
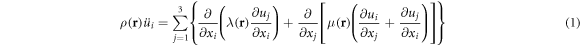
in which ρ(r) is the material density with spatial distributions, and 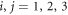 is corresponding to the coordinates x, y, z.
is corresponding to the coordinates x, y, z. 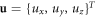 is the displacement vector of three component. r = (x, y, z) is the position vector. λ and μ represent the Lame's coefficients. Three material parameters, the Young's modulus E, Poisson's ratio σ and the Lame's coefficients have the following relationships
is the displacement vector of three component. r = (x, y, z) is the position vector. λ and μ represent the Lame's coefficients. Three material parameters, the Young's modulus E, Poisson's ratio σ and the Lame's coefficients have the following relationships

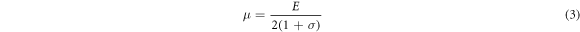
Figure 1. (a) Sketch map of layer-stacked 3D PnC with broken spatial inversion symmetry. (b) The enlarged view of the unit cell model. (c) The corresponding 3D BZ for the elastic Weyl PnC. The green and red spheres mark the opposite topological charges for WPs of elastic wave (d) The equivalent lattice for the tight-binding model.
Download figure:
Standard image High-resolution imageAccording to the Bloch-Floquet wave theory [39], the displacement in periodic medium is expressed as
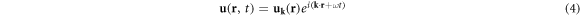
in which k = (kx , ky , kz ) is the Bloch wave vector and uk (r) has the same periodicity as the structure. Because the 3D PnCs are periodic in three spatial directions, the unit cell can be taken. We can substitute equations (4) into (1) and discretize the unit cell with finite elements. A typical eigenvalue equation is obtained in the FEM framework as
in which K and M are stiffness matrix and mass matrix, respectively [40]. Figure 1(c) shows the corresponding 3D Brillouin zone (BZ) in which the red lines outline the first irreducible BZ. The band dispersion for the 3D PnCs is obtained by scanning the points of BZ. Here, combined with the above energy band theory, the band calculations and field distributions are numerically studied by using the finite element method based on COMSOL multiphysics.
To illustrate the idea of this work, a tight-binding model can be equivalently used to describe the stacked 3D PnC along z direction as shown in figure 1(d). We can see that a unit cell includes two different sites (A and B), which correspond to two inequivalent centers of A and B in each layer in figure 1(a). Based on the sublattices A and B, the Hamiltonian of this model could be written in the Pauli matrix form [35]:
where  are the Pauli matrices, and I represents the identity matrix. Moreover, the dx
, dy
, dz
and d0 are expressed as follows:
are the Pauli matrices, and I represents the identity matrix. Moreover, the dx
, dy
, dz
and d0 are expressed as follows:
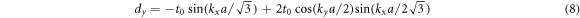
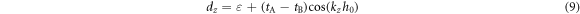

Where the nearest-neighbor hopping t0 denotes the intralayer coupling and keeps constant. The tA and tB are the interlayer coupling, which induced by the circular rods with different radii. The ε denotes the site energy induced by the defined parameter ΔL. From equation (6), the corresponding eigenvalues are  It is known that there exist three cases. First, when tA = tB, the parameter Δr is zero and the term of σz
is independent on the kz
, which indicates that no WP exists in this case [34]. Secondly, when tA ≠ tB and considering dx
= dy
= dz
= 0, the type-II WP is formed due to the band crossing appears and the band dispersion is tilted in kz
direction. The effective Hamiltonian around the WP can be written as:
It is known that there exist three cases. First, when tA = tB, the parameter Δr is zero and the term of σz
is independent on the kz
, which indicates that no WP exists in this case [34]. Secondly, when tA ≠ tB and considering dx
= dy
= dz
= 0, the type-II WP is formed due to the band crossing appears and the band dispersion is tilted in kz
direction. The effective Hamiltonian around the WP can be written as:
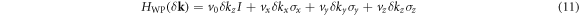
in which νi=x,y,z,0 present group velocities and 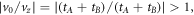 indicating that the type of this WP is type-II [2]. The topological charges for WPs are
indicating that the type of this WP is type-II [2]. The topological charges for WPs are 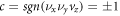 as displayed in figure 1(c). Two pairs of WPs can be expected for the structure in the first BZ, which are represented by the red and green spheres with opposite charges. Thirdly, when tA ≠ tB and considering dx
= dy
= 0 but dz
≠ 0, the Hamiltonian of the model of equation (1) could be seen as a two-dimensional (2D) elastic valley TI slice by regarding the kz
as a parameter variable. At this time, in the light of a fixed kz
along the KH line, the effective Hamiltonian of valley G can be obtained as follows [34]:
as displayed in figure 1(c). Two pairs of WPs can be expected for the structure in the first BZ, which are represented by the red and green spheres with opposite charges. Thirdly, when tA ≠ tB and considering dx
= dy
= 0 but dz
≠ 0, the Hamiltonian of the model of equation (1) could be seen as a two-dimensional (2D) elastic valley TI slice by regarding the kz
as a parameter variable. At this time, in the light of a fixed kz
along the KH line, the effective Hamiltonian of valley G can be obtained as follows [34]:
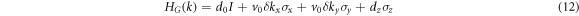
Where 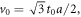 and for a kz
, the valley Chern number can be achieved as
and for a kz
, the valley Chern number can be achieved as 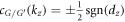 by integrating the Berry curvature near the valley [41]. The above three cases also imply the possibility of transition between the Weyl phase and valley topological phase by inducing the intralayer and interlayer coupling.
by integrating the Berry curvature near the valley [41]. The above three cases also imply the possibility of transition between the Weyl phase and valley topological phase by inducing the intralayer and interlayer coupling.
3. Results and discussion
To present the emergence of the type-II WPs of the elastic wave, it is shown in figure 2(a) that the bulk band dispersions of the 3D elastic PnC with broken SIS. It can be seen that when two symmetry parameters are Δr = 1.8 mm and ΔL = 0.4 mm, two bulk bands are linearly crossed in the high-symmetry KH direction and the crossing point processes the group velocities with the same directions. The enlarged band structure for these two bands and that along the KH high-symmetry line are shown in figures 2(b) and (c), respectively. The WPs are positioned at the fixed kz = 0.52π/h0. Figures 2(d) and (e) further display the perspective view of the 2D band structures near the WP for the elastic wave in kx
-ky
plane and ky
-kz
plane, respectively. It is seen that the directions of group velocities of WP are opposite in the kx
-ky
plane but are same in ky
-kz
plane, which indicates that the crossed point is type-II WP and it is ideal because there are no additional trivial bands coexisting at the frequency of WP. Therefore, the coordinate position of this type-II WP is 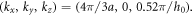 It is mentioned that the essence of forming this type-II WP is because parameters ΔL and Δr have asynchronous effects on the breaking degree of SIS. Moreover, due to the keeping of the mirror symmetry and TRS, the coordinate positions of other three type-II WPs are can be obtained with ,
It is mentioned that the essence of forming this type-II WP is because parameters ΔL and Δr have asynchronous effects on the breaking degree of SIS. Moreover, due to the keeping of the mirror symmetry and TRS, the coordinate positions of other three type-II WPs are can be obtained with , 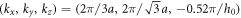 and
and 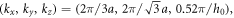 respectively. Therefore, two pair of type-II WPs for elastic wave are found, which provide a chance to explore some interesting physical properties in elastic type-II Weyl system, such as robust surface wave and chiral anomaly.
respectively. Therefore, two pair of type-II WPs for elastic wave are found, which provide a chance to explore some interesting physical properties in elastic type-II Weyl system, such as robust surface wave and chiral anomaly.
Figure 2. (a) The band structure of 3D elastic wave for the Weyl PnCs with ΔL = 0.4 mm and Δr = 1.8 mm. (b), (c) The enlarged view of the two bands and that along the KH high-symmetry line. (d), (e) 3D perspective view of the 2D band structures near the elastic type-II WP in kx -ky plane and ky -kz plane, respectively.
Download figure:
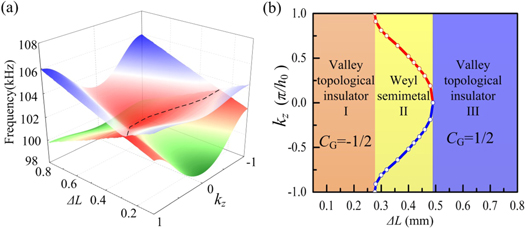
Standard image High-resolution imageTo explore the evolutionary process of the elastic type-II WPs in 3D PnC, the band structure of the points  as the functions of the parameters ΔL and kz
are calculated as shown in figure 3(a). When the parameter ΔL varies in the range of 0.282 mm < ΔL < 0.485 mm, the ideal type-II WPs of elastic wave appear and move on the black dashed line. When ΔL < 0.282 mm, the WPs disappear at the kz
= ±π/h0 and start to open a 3D complete band gap. While ΔL > 0.485 mm, the WPs disappear at the kz
= 0 and also start to form a 3D complete band gap. It is the vanishing of elastic WPs from different positions that makes the gaps for ΔL < 0.282 mm and ΔL > 0.485 mm have the distinct valley topological phases combining with the valley Chern number analysis of above section. Therefore, with the changing of the parameter ΔL, the phases of 3D elastic PnCs are divided into three parts corresponding to the valley topological insulator I, WS II and valley topological insulator III, respectively, which are shown in figure 3(b) presented by the yellow, orange and blue areas, respectively. Most importantly, the calculated results have indicated that the phase transition between the elastic Weyl phase and two elastic valley topological phases happens as the varying of parameter ΔL.
as the functions of the parameters ΔL and kz
are calculated as shown in figure 3(a). When the parameter ΔL varies in the range of 0.282 mm < ΔL < 0.485 mm, the ideal type-II WPs of elastic wave appear and move on the black dashed line. When ΔL < 0.282 mm, the WPs disappear at the kz
= ±π/h0 and start to open a 3D complete band gap. While ΔL > 0.485 mm, the WPs disappear at the kz
= 0 and also start to form a 3D complete band gap. It is the vanishing of elastic WPs from different positions that makes the gaps for ΔL < 0.282 mm and ΔL > 0.485 mm have the distinct valley topological phases combining with the valley Chern number analysis of above section. Therefore, with the changing of the parameter ΔL, the phases of 3D elastic PnCs are divided into three parts corresponding to the valley topological insulator I, WS II and valley topological insulator III, respectively, which are shown in figure 3(b) presented by the yellow, orange and blue areas, respectively. Most importantly, the calculated results have indicated that the phase transition between the elastic Weyl phase and two elastic valley topological phases happens as the varying of parameter ΔL.
Figure 3. (a) 3D dispersion diagrams as evolution of parameters kz and ΔL at the (kx , ky ) = (4π/3a, 0). The black dashed line shows the trajectory of elastic type-II WPs. (b) The phase distribution of the 3D elastic PnCs induced by the kz -dependent parameter for different ΔL. The WS phase II is displayed by the yellow area while the distinct valley topological phase I and III are presented by the orange and blue parts, respectively.
Download figure:
Standard image High-resolution imageDue to the fact that WPs are topological monopoles of the quantized Berry flux carrying the charges +1 and -1, the topological surface states are expected to arise at the finite boundaries. To obtain the surface states of WPs, we consider the case of 3D supercell structure with ΔL = 0.4 mm and Δr = 1.8 mm, which is finite in the y direction but infinite in the x and z directions. We first fix the value of kx and calculate the projected band dispersions along the kz as shown in figure 4. From the figures 4(a) and (b), it can be seen that when kx = π/a, two topological surface states appear in the band gap while no surface state show up at kx = 0 because of the cancellation of the projected WPs with opposite charges [34]. Figure 4(c) shows the displacement field distributions corresponding to the surface state in figure 4(a). The black arrows represent the mechanical energy flow. We can see that two surface states of elastic waves transport along the z direction and they are always of the positive group velocity. It suggests that the surface states in our type-II WP system are of anomalous chirality, which is distinctly different from the chiral surface states originating from the type-I WPs in previous literature [30]. To explore the existing law of the surface states, figure 4(d) presents the Fermi arc trajectory of surface states marked by red line at the 102.8 kHz. It is seen that the Fermi arc trajectory is open. Figure 5 further displays the kx -dependent propagation property of the elastic surface states.
Figure 4. The anomalous chirality and surface states of elastic type-II PnC along the kz -projected direction. The projected band structures with a fixed kx = π/a in (a) and with a fixed kx = 0 in (b), respectively. (c) The displacement field distributions of Q1 and Q2 points in (a) and the black arrows shows the direction of the mechanical energy flow along the z direction. (d) The trajectory of elastic surface states indicated by the grey balls.
Download figure:
Standard image High-resolution imageFigure 5. The transport property of the surface states for 3D elastic wave along the z direction. The point source of excitation is marked by the red star. The kx -dependent propagating property for the surface state of type-II WPs is clearly presented.
Download figure:
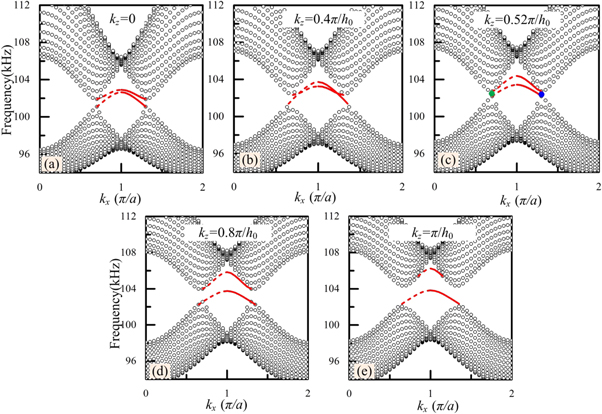
Standard image High-resolution imageNext, we fix the kz value and calculate the projected band dispersions along the kx . Figure 6 shows the band dispersions of supercell at some distinct kz value. It can be seen that for the different kz value, two pairs of the left and right WPs are connected by the surface states, respectively. Moreover, the displacement fields of two surface states marked by the red lines are confined at two different boundaries. With the increasing of kz value, the projection of the WPs varies from the opening to closing and then to opening. Most importantly, the results suggest that for a fixed kz value, two surface states always have the group velocity in same direction, which also shows the anomalous chirality of elastic surface states. To further demonstrate the transport characteristic of these surface states, the case of kz = π/h0 is chosen to carry out the full field numerical simulation. Seeing from the figure 6(e), the gap between two surface states is largest, which is convenient to only stimulate one of the surface states. Figure 7 displays the result of the full displacement field numerical simulation for elastic wave. It is seen from figure 7(a) that a linear boundary is introduced and the excited surface states of elastic wave at 102.8 kHz can well propagate along the zigzag boundary. When introducing the defect on the linear path, we can see that the excited surface states from the left side can bypass the bend angle and propagate to the right side as shown in figure 7(b), indicating a good robustness of topological elastic wave surface states. Moreover, when given a kz = −π/h0, the supercell band dispersion is unchanged but the propagating direction of the elastic surface state is reversed. To reveal the one-way transport of these elastic surface states, figures 7(c) and (d) gives the full field numerical simulation for the cases of kz = π/h0 and kz = −π/h0, respectively. In the middle of the linear path, the four point sources with a phase difference of π/2 are set and the excited frequency is also chosen as 102.8 kHz [26]. For the kz = π/h0, the excited elastic surface state have the positive group velocity and transports along the right direction. But for the kz = −π/h0, the excited elastic surface state have the adverse group velocity and transports along the left direction. Compared to the way to realize the unidirectionality by break the TIS of system in terms of the application of diode effect, our design relying on the topological Weyl theory is much simpler and easier and provide a well ability of directional selectivity for filtering elastic wave. Therefore, the robustness and unidirectional propagation of topological surface states originating from the ideal type-II WPs of 3D elastic wave are clearly demonstrated, which will be great potential in designing the novel ultrasonic devices with the efficient transmission performance.
Figure 6. The anomalous chirality and surface states of elastic type-II PnC along the kx -projected direction. The band structures of supercell at kz = 0 in (a), kz = 0.4π/h0 in (b), kz = 0.52π/h0 in (c), kz = 0.8π/h0 in (d), kz = π/h0 in (e).
Download figure:
Standard image High-resolution imageFigure 7. The robust transport property of the weyl surface states along the x direction. And point source of excitation is marked by the red star. (a) The propagation along the linear boundary. (b) The propagation along the boundary with corner defect. (c) The one-way transport of surface states towards the right with kz = π/h0. (d) The one-way transport of surface states towards the left with kz = −π/h0.
Download figure:
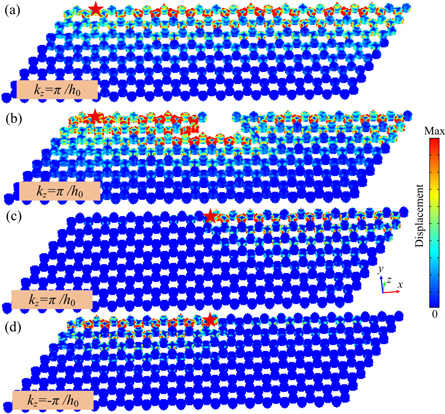
Standard image High-resolution imageThen, we further study the existence of surface states on the interface between PnCs phase I and phase III. For a fixed kz value, the 3D valley TI can be considered as the 2D valley TI slice. Here, we construct the supercell by the 3D PnCs with ΔL = 0.1 mm (phase I) and ΔL = 0.8 mm (phase III). There are two types of interface I-III (phase I locates upper the phase III) and III-I (phase I locates upper the phase III). When the periodic boundary conditions are applied in the x direction, the supercell band dispersions at some kz values for the interfaces III-I and I-III are shown in figures 8(a)–(c) and (d), (e), respectively. It can be seen that for the interface III-I, the trajectory of surface states at the 102.8 kHz is a closed raised circle marked by the red solid line as displayed in figure 8(c). While for the interface I-III, the trajectory is a closed sunken circle marked by the blue dashed line as displayed in figure 8(e). Obviously different from the open Fermi-arc connecting the projections of the WPs with opposite charges, the trajectory of the above surface states is closed Fermi-circle and it appears independently in the complete bulk gap without disturbing by the bulk states.
Figure 8. The supercell band structure for the interfaces constructed by two distinct valley topological phase. (a)–(c) The surface states and corresponding trajectory when the valley topological phase III locates upper the valley topological phase I. (d), (e) The surface states and corresponding trajectory when the valley topological phase III locates lower the valley topological phase I.
Download figure:
Standard image High-resolution imageAfter that, we study the transport property of the Fermi-circle-like elastic wave surface states. The Z-shaped interfaces formed by two distinct 3D PnCs, ΔL = 0.1 mm and ΔL = 0.8 mm with opposite topological phase are constructed to verify the robustness of the Fermi-circle-like surface states. As shown in figures 9(a) and (b), the simulated displacement field distributions at 103 kHz for kz = 0 and kz = π/h0, respectively. The red stars are marked for the position of the point source and it is seen that the stimulated elastic wave can well propagate along the Z-shaped interfaces. In addition, we replace the valley topological phase I with the WS phase II and perform the field numerical simulation at 101.5 kHz seen from figures 9(c) and (d). We can find that when kz = 0, the stimulated elastic wave at 101.5 kHz still transport along the Z-shaped interfaces. But when kz = π/h0, the robust transport is interrupted because the Fermi-circle surface states of elastic wave has merged into the bulk states at this frequency. The results also indicate that the robust transport of the elastic surface states can be controlled by the different topological phase. It has to be mentioned that the robust transport feature of elastic surface states with reflection immunity to the bending of interface could serve as a basis for applications of topological ultrasonic devices, such as waveguide, filter, and signal processing in a network structure.
Figure 9. Simulated wave propagations along the Z-shaped path for kz = 0 (a) and kz = π/h0 (b) at the interface constructed by the PnCs with ΔL = 0.1 mm (phase I) and ΔL = 0.8 mm (phase III). (c)-(d) The corresponding results for the PnCs with ΔL = 0.4 mm (phase II) and ΔL = 0.8 mm (phase III). And point source of excitation is marked by the red star.
Download figure:
Standard image High-resolution imageFinally, we present an experimental prefigure of the 3D elastic topological WS and show the possible practice applications associated with the robust surface states of elastic wave. Most assuredly, although the implementing of experiment for 3D elastic wave is not easy, an effective technical route has been confirmed [41]. It is noted that the 3D experimental sample of Weyl PnCs can be fabricated by laser cutting or 3D printing techniques. Then a ultrasonic experiment could be conduct to test the transmission efficiency including the steps as follows: (i) a pulse generator/receiver (a pair of standard transducers with a central frequency of 100 kHz) creates a short duration large amplitude pulse to excite the elastic waves from the one side; (ii) the signals are received by the corresponding pulse generator/receiver at the other side; (iii) the signal acquired from the two sides is post-amplified and digitized by a Lecroy digital oscilloscope which haves the real-time fast Fourier transform (FFT) capability to obtain the transmission coefficient; (iv) a 3D laser scanning vibromete [42] is applied to capture the vibration displacement field distribution of surface states. The robust topological surface states in 3D elastic structure shows a promising advantage in complex working situation and working planes because various high-frequency and even radio-frequency devices tend to be produced from multidimensional solid structure, such as surface wave spiltters and bulk wave filters in smartphone. The robust transport along the Z-type bending path will be applied in practice. For instance, in terms of a ultrasonic devices with the effect of ultra-long line, the delay time relies on the wave speed and propagation distance. When the wave speed is often certain, the longer propagation distance will produce longer delay line. Therefore, by applying the bending path discussed in our design, we will realize the ultrasonic delay in a long propagation length. Moreover, due to the bending path can be compressed into a small space, reducing the size of device will be another superiority of our structure.
4. Conclusion
In summary, WPs and topological surface states in 3D elastic structure are still in their early periods of formulation and design. Here, by designing the 3D solid PnCs with broken SIS, an ideal type-II Weyl phase of elastic wave have been proposed and the topological phase transition between the two valley TIs and type-II WS is revealed. Moreover, by calculating the supercell band structure, we have shown the elastic Fermi-arc-like surface states, which connects the projections of the type-II WPs with opposite charges at fixed kx or kz , and we also present the Fermi-circle-like surface states of elastic wave in the domain wall of two elastic 3D PnCs with distinct valley topological phases. By performing the full field numerical simulations, we have confirmed the robust transport of the Fermi-arc-like and Fermi-circle-like surface states for the 3D elastic wave. Our study offers fresh insights to 3D topological elastic wave and fills the deficiency of work for the elastic analogue of ideal type-II WSs. Simultaneously, the designed elastic type-II WS will have special advantages for the applications in topological ultrasonic device with the low-loss, high-dimension and multiple working planes.
Acknowledgments
The authors gratefully acknowledge the financial support from National Science Foundation of China under Grant No. 12074114. The authors also gratefully acknowledge the contributions of the Editors and reviewers and their comments have significantly enhanced the quality of this paper.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).