All-PM Yb-doped mode-locked fiber laser with high single pulse energy and high repetition frequency

Ultrafast fiber lasers have attracted the interest of researchers due to their excellent output performance (e.g. broad spectrum, high stability, and ultra-narrow pulse width). They play a significant role in many application fields of laser processing [1–3], medicine [4], spectroscopy [5], and multiphoton imaging [6], etc. However, they are still inferior to conventional solid-state lasers in terms of outputting high energy or high repetition frequency pulses. Therefore, in order to improve the performance of ultrafast fiber laser which can applicated in optical frequency comb and other instruments, we need to increase the fundamental frequency and peak power/energy. Ytterbium-doped fiber lasers (YDFLs) have the advantage of high conversion efficiency and low quantum loss due to the absence of excited state absorption effects during the leap of the ytterbium (Yb) ion [7]. YDFLs have been extensively studied for generating high-energy pulses [8, 9].

Passively mode-locking is usually achieved by using a saturable absorber (SA) without additional intracavity modulation devices. Therefore, passively mode-locked lasers have the advantages of self-starting, compactness, and low cost. SAs are generally divided into SAs based on materials and artificial SAs. However, as time goes on, the performance of the material deteriorates and the high peak power/energy of the ultrashort pulse can damage the material [10]. Common artificial SAs include nonlinear polarization rotation (NPR) [11], nonlinear optical loop mirror (NOLM) [12], and nonlinear amplifying loop mirror (NALM) [13], etc. In 1992, Matsas and Newson reported the first passively mode-locked erbium-doped fiber laser based on NPR [14]. However, the intracavity dispersion of the laser is anomalous dispersion, which induces the laser to output conventional soliton whose energy is not high enough. Thus, researchers began to pay attention to the dissipative soliton obtained as intracavity dispersion is normal dispersion. In 2006, Chong et al demonstrated the first all-normal-dispersion (ANDi) fiber laser mode locked by NPR to generate dissipative soliton directly from the cavity [15]. The dissipative soliton generated in this way has been confirmed to tolerate large nonlinear phase shift accumulation so that wave breaking does not occur, and the soliton can remain single-pulsed at high peak power. However, all single-mode fiber devices make it very sensitive to external environment perturbations (e.g. stress), which will limit the scope of application of the laser. The use of polarization-maintaining (PM) fiber can greatly improve the stability of lasers because the light transmitted in PM fiber can reduce polarization changes due to external stresses. However, the laser will occur group velocity mismatch easily owing to the stress birefringence effect in the PM fiber, making it difficult to achieve all-PM NPR mode locking. Therefore, the use of two-dimensional materials [16], semiconductor saturable absorber mirrors (SESAMs) [17], and other SAs based on materials to achieve all-PM mode-locked fiber lasers have been proposed. But their applications are limited owing to the long response time and low damage threshold.

NOLM and NALM techniques have the advantage of faster response time, higher resistance to environmental perturbations, and higher damage thresholds than SAs based on materials and other artificial SAs [18, 19]. Meanwhile, they can achieve an all-PM structure which greatly enhances their output stability. Adding gain fiber asymmetrically to the interference loop of NOLM allows the NALM technique to obtain more nonlinear phase shifts than the NOLM technique, which makes it easier to achieve mode-locking. It is difficult for all-PM mode-locked fiber lasers using traditional figure-of-8 cavity, whose long cavity length leads to a low output pulse fundamental frequency, to realize self-started mode-locking [20–22]. The figure-of-9 cavity can solve the above problems. The introduction of bias phase shifter can reduce the mode-locked threshold and make it easy to achieve self-started mode-locking [23, 24]. Meanwhile, the pulse repetition frequency is improved by shortening the cavity length. These Yb-doped fiber lasers with figure-of-9 cavity not only output dissipative soliton that can tolerate high nonlinear phase shift, but also achieve high repetition frequency pulses output. They will be the ideal seed source for applications such as high-energy amplifiers and optical frequency combs.

In this paper, we report a figure-of-9 all-PM Yb-doped fiber laser that achieves self-started, stable mode-locking. At one output port of the laser, the pulse duration is 4.53 ps, the spectrum width is 13 nm, and the fundamental frequency is 97.966 MHz. The maximum output power for single-pulse mode-locked operation is 143 mW, corresponding to the single-pulse energy of 1.46 nJ. The output pulses maintain both high repetition frequency and high single-pulse energy. We believe that the laser oscillator displayed in this article can be an ideal seed source for applications such as high-energy amplifiers.

Figure 1 illustrates the configuration of the all-PM Yb-doped fiber laser with a figure-of-9 cavity. We measured the total cavity length to be 1.85 m by adding the 0.27 m spatial part to the 1.58 m fiber part. A 980 nm PM laser diode (LD) is combined with cavity by a 980/1060 nm wavelength division multiplexer (WDM), which is applied to pump the gain fiber. The NALM and linear arm are connected by two collimators (Col 1, Col 2) and a polarization beam splitter (PBS 1). The NALM consists of the above devices and a 0.35 m PM Yb-doped fiber (Yb401, group velocity dispersion (GVD) is 24 ps² km⁻¹) is placed asymmetrically in the NALM. Such a combination of devices can also have the effect of shortening the cavity length and increasing the fundamental frequency of the pulse. Meanwhile, the above-mentioned combination of devices also assumed the role of a 2 × 2 coupler with a 50:50 splitting ratio. The high reflective (HR) mirror, PBS 2, a birefringent filter (d = 7 mm), a phase shifter consisting of a λ/8 waveplate and a Faraday rotator (FR), and Col 1 together form the linear arm. The phase shifter can provide the π/2 phase bias to ensure that the NALM accumulates sufficient nonlinear phase shift for stable self-started mode-locking. The filtering effect provided by birefringent filters can balance the pulse broadening caused by dispersion and self-phase modulation (SPM). The balance between spectrum filtering, SPM, dispersion, and gains is the key to the generation of dissipative soliton. The fibers used to connect the intracavity devices are all PM fiber (PM 980) with GVD of 24 ps² km⁻¹ at 1030 nm. The total cavity dispersion is calculated to be 0.038 ps².

Zoom In Zoom Out Reset image size

Figure 2 shows the variation of reflectivity with nonlinear phase shift in a NALM ring with a 50:50 beam-splitting ratio. The reflectivity of the NALM gradually decreases as the nonlinear phase shift gradually increases as the initial phase shift is 0. This also means that the reflectivity of the continuous wave is higher than that of the pulsed laser, which leads to achieve mode-locking operation difficultly. When the initial phase shift is −π/2, the reflectivity of the NALM increases with the nonlinear phase shift in the cavity at this point, which facilitates the self-started mode-locking [25].

Zoom In Zoom Out Reset image size

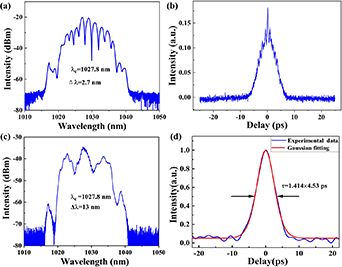
Once we had set the angle of the waveplates to a suitable value and increased the pump power to 713 mW when the coupling efficiency is maximized, self-started mode-locking was successfully achieved. Compared to a typical figure-of-8 cavity without the introduction of a phase shifter, the self-started mode-locking can be realized without additional operation. Figure 3 exhibits the mode-locked characteristics at the pump power of 713 mW. We used an optical spectrum analyzer (OSA) with a wavelength resolution of 0.02 nm (Yokogawa, AQ6370C) to record optical spectrum. The optical spectrum of two output ports, whose spectrum bandwidths are 2.7 nm and 13 nm respectively, is presented in figures 3(a) and (c). Their central wavelengths are both 1027.8 nm. The autocorrection traces of port 1 and port 2 were measured by the intensity autocorrelator (APE, PulseCheck-50), as shown in figures 3(b) and (d). The corresponding pulse duration of output port 2 is 4.53 ps with a Gaussian function fitted.

Zoom In Zoom Out Reset image size

It is worth noting that figures 3(a) and (b) reveal the appearance of modulation signal in the spectrum and the appearance of a shape in the autocorrelation trace similar to pulse splitting, respectively. This is because the light reflected from the linear arm of the laser cavity passes through the NALM ring in two directions and then passes through the polarizing beam splitter where it interferes with the gain-amplified pump light at port 1. Figure 3(c) shows that the spectrum has steep edges, which is a typical characteristic of ANDi lasers [15, 26]. In addition, inhomogeneous modulation in the spectrum can also be observed, which is the result of a combination of SPM, high-order dispersion, and the spectrum filtering effect caused by NALM [22]. The autocorrelation trace displayed in figure 3(d) is not clean and smooth enough, which is because the pulse output from port 2 is still affected by pulse interference. Despite the presence of side flaps on either side of the central peak of the autocorrelation trace, no signal of multi-pulse modulation appears in the spectrum and no pulse splitting is observed on the oscilloscope. Thus, the pulse output at this point is still a single pulse.

We used a digital oscilloscope (Agilent Technologies, DSO9104A) to observe the pulse signal. The radio frequency (RF) spectrum analyzer (Keysight, N9000B) was applied to detect the RF spectrum. Figures 4(a) and (b) show the pulse train in the time domain and RF spectrum of port 2, respectively. As displayed in figure 4(a), we selected the mode-locked pulse train in the 400 ns time range and there is no sign of pulse splitting. Stable mode-locked pulses can be observed. The interval of the pulse is 10.5 ns, corresponding to a pulse fundamental frequency of 97.966 MHz shown in figure 4(b). The signal-to-noise ratio is as high as 57 dB with a resolution bandwidth (RBW) of 36 Hz, which indicates high stability in this mode-locked state.

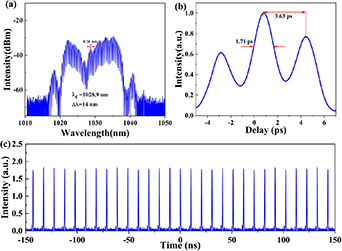
Zoom In Zoom Out Reset image size

Due to the limitation of the core diameter and mode field of the PM980 fiber, the energy of the mode-locked single pulse cannot always increase with the raising of the pump power. Once the maximum mode-locked single pulse energy that the fiber can withstand is exceeded, pulse splitting occurs. We continued to increase the pump power to 777 mW and slightly adjusted the angle of the filter. The output pulse at this point is still a single pulse as observed on the OSA and oscilloscope. The output power is collected by a power meter (Thorlabs, PM100D). At this point, the output power of port 2 is measured at 143 mW. Due to the obtained pulse repetition frequency (97.966 MHz) and output power (143 mW), the single pulse energy can be calculated as 1.46 nJ. As far as we know, it is higher than the previously reported works of figure-of-9 all-PM fiber lasers where the output single pulse energy is less than 1 nJ [27–31]. The recently reported figure-of-9 all-PM fiber laser has high single pulse output energy (>1 nJ), but its pulse repetition frequency is far from the high repetition frequency of nearly 100 MHz [32]. In this work, the output pulses maintain both high repetition frequency and high single-pulse energy. We continued to increase the pump power until 831 mW and found that the intracavity soliton state changed from a dissipative soliton pulse output to a bound state soliton pulse output. The output characteristics are exhibited in figure 5. As shown in figure 5(a), with a central wavelength of 1028.9 nm and an FWHM of 14 nm, the stable modulation with a modulation period of 2.24 nm can be seen in the bound state soliton. Figure 5(b) shows the autocorrelation trace of a bound state soliton with the interval of the pulse of 3.63 ps corresponding to the modulation period of the spectrum. The pulse train of bound state soliton are shown in figure 5(c). The output power measured at port 2 is 211.6 mW and pulse splitting is observed on the oscilloscope, which proves that the output pulse is multi-pulses. Wave breaking leads to multi-pulses operation and the total amount of chirp caused by dispersion and nonlinear effects in ANDi fiber lasers determines whether wave breaking occurs. In normal dispersion fibers, the GVD-induced linear chirp compensates in part for the SPM-induced nonlinear chirp and offsets the wave-breaking effect [33].

Zoom In Zoom Out Reset image size

Nevertheless, with raising pump power, the nonlinear chirp caused by SPM also is enhanced and causes the wave-breaking effect eventually leading to the pulse splitting. Also, an imbalance between the filtering effect of the filter and the SPM can lead to pulse splitting. Increasing pump power makes the spectrum broadening induced by SPM more pronounced. Broader spectrum width leads to progressively higher losses due to spectrum filtering. The losses caused by spectrum filtering can make it impossible for a single pulse to continue to exist and thus pulse splitting occurs. The phenomenon that the FWHM increased with raising pump power due to the SPM effect is observed. As the pump power raised from 713 mW to 831 mW, the FWHM also increased from 13 nm to 14 nm. In addition, the nonlinear phase shift varies with raising pump power causes a redshift in the transmission curve at the output port. The nonlinear phase shift, modulation depth, and linear phase bias will be changed by rotating the waveplate, which ultimately leads to a redshift in the transmission curve [34]. The central wavelength was shifted from 1027.8 nm to 1028.9 nm. We attribute this to the growth in nonlinear phase shift caused by the raising in pump power, which leads to a shift of output central wavelength in the long-wavelength direction.

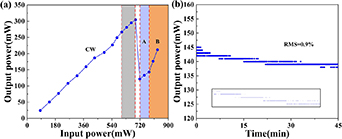
We also found that the Q-switched pulse converts into the mode-locked pulse can be achieved by only increasing the pump power [35]. After realizing stable Q-switched pulse output at the pump power of 598 mW, we slowly increased the pump power to 713 mW, and we found that the Q-switched pulse changed to the mode-locked pulse. The Q-switched range is shown in grey region of figure 6(a). Finally, we used a power meter to measure the output power and output stability of the laser, as displayed in figure 6. The mode-locked range of the laser is 713 mW–831 mW as seen in figure 6(a), and it still reveals a linear increase at the maximum pump power, indicating that the laser has not yet reached the saturation point of the mode-locked state. The single pulse mode-locked operation range of the laser is from 713 mW to 777 mW as shown in A region of figure 6(a). The multi-pulse mode-locked operation range of the laser is from 803 mW to 831 mW as seen in the B region of figure 6(a). When the mode-locked pulse is generated, the energy of the continuous wave is concentrated into the high-power pulse generated periodically for a relatively short period of time. Therefore, although the peak power of a mode-locked laser is high, its average power may be lower than that of continuous wave. Thus when the continuous wave is transformed into the mode-locked pulse, the average power of the laser output may decrease, which can be seen in figure 6(a). Figure 6(b) shows the output power fluctuation of 0.9% root mean square in 45 min when pump power is 777 mW. The inset in figure 6(b) is a detail view which allows the variation of output power to be observed more clearly. As the fiber used in the laser are all PM fiber, we attribute fluctuations in output power to fluctuations in the pump power.

Zoom In Zoom Out Reset image size

The theoretical model of the laser oscillator shown in this paper is as follows. For the pulse evolution process, we use the Ginzburg–Landau equation (GLE) for numerical simulation. The equation is shown below:

$$\begin{equation*}\frac{{\partial \varphi }}{{\partial z}} = - {\text{i}}\frac{{{\beta _2}}}{2}\frac{{{\partial ^2}\varphi }}{{\partial {t^2}}} + {\text{i}}\gamma {\left| \varphi \right|^2}\varphi + \frac{{g - l}}{2}\varphi + \frac{g}{{2\Omega _{\text{g}}^2}}\frac{{{\partial ^2}\varphi }}{{\partial {t^2}}}\end{equation*}$$

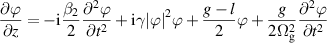
where β₂ is GVD, γ is the nonlinear coefficient, l is the loss coefficient of the fiber, and Ω_g is the gain bandwidth. The gain coefficient in an YDF gain fiber can be described by the following equation:

$$\begin{equation*}g = {g_0}\exp \left( { - \frac{{{{\mathop \smallint \nolimits}}{{\left| \varphi \right|}^2}{\text{d}}t}}{{{P_{{\text{sat}}}}}}} \right)\end{equation*}$$

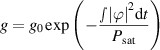
where g₀ is the small signal gain and P_sat is the gain saturation energy.

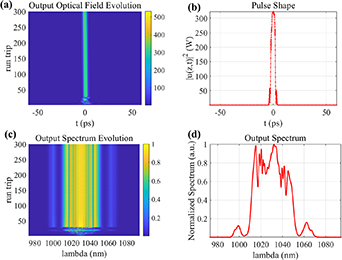
In the numerical simulation, the phase shifter was set as 0 and the mode fields of PM fibers were considered as 6 μm. As shown in figure 7(a), it can be seen that under the balance of the four effects in the cavity, the Gaussian noise gradually evolves into a stable pulse with sidebands during transmission. Figure 7(b) shows the pulse shape of the last run trip in the evolution of figure 7(a). Figure 7(c) shows the spectrum evolution corresponding to figure 7(a). Figure 7(d) shows the spectrum shape of the last run trip in the evolution of figure 7(c). As shown in figure 7(d), it can be observed that there is some modulation in the spectrum, which is very consistent with our outcome of the experiment. We attribute this to that the pulse shape is not perfectly Gaussian, but a pulse shape with sidebands present. This is due to the higher energy inside the cavity. The single pulse energy obtained by numerical simulation is about 1.4 nJ, which differs from our experimental results by only 0.06 nJ. The pulse repetition frequency and pulse width obtained from the simulation are 104 MHz and 5.2 ps respectively, which are very close to the experimental data.

Zoom In Zoom Out Reset image size

In conclusion, we present a mode-locked all-PM figure-of-9 Yb-doped fiber laser based on NALM. With the introduction of a phase shifter in the cavity, the laser oscillator successfully achieves self-started and stable mode-locking. The maximum output power of the mode-locked single pulse is 143 mW at port 2, corresponding to a pulse energy of 1.46 nJ. The fundamental frequency is 97.966 MHz. The ultrashort pulse with high single pulse energy and high fundamental frequency is obtained directly from the laser oscillator. Meanwhile, we numerically simulate the output characteristics of the laser oscillator presented in this paper by using the GLE. The results of numerical simulation are very consistent with the results of the experiment. The sin-gle-pulse energy obtained by numerical simulations differs from our experimental results by only 0.06 nJ. We believe that the laser oscillator demonstrated in this study could be an ideal laser source for high-energy amplifiers and other applications.

This work was supported by the National Major Scientific Research Instrument Development Project of China (51927804).

All data that support the findings of this study are included within the article (and any supplementary files).

The authors declare no conflicts of interest.