The Casimir force between parallel plates separated by anisotropic media with in-plane optical axis

The Casimir effect, which is one of the most significant findings of quantum theory, has long been a topic of great interest in various fields of science and technology [1–6].

In Lifshitz's original theory for the force between dielectric plates the materials were assumed to be isotropic. Therefore, the early research on the Casimir effect was also only focused on isotropic materials. It was only since the works of Parsegian [7] and Barash [8] in 1970s that the study of the impact of anisotropy of materials on Casimir effect has gained momentum. Based on previous works, Munday and his colleagues calculated the Casimir torque between parallel anisotropic plates immersed in liquid, and their recent works showed that this torque could be enhanced by the retardation and an intervening dielectric [9,10]. As a supplementary work, Shao's team analytically calculated the Casimir torque between two birefringent plates with static permittivity [11]. In one of our studies, we calculated the Casimir torque between parallel birefringent plates with frequency-dependent magnetic permeability, and showed that the magnetic properties of the plates could significantly affect the torque [12]. The Casimir torque is not the only effect caused by the anisotropy of the material. The Casimir force can also be affected by it directly. Romanowsky showed that the orientation of the optical axis of highly anisotropic materials could significantly affect the magnitude of the Casimir force [13]. Parashar and his colleagues calculated the Casimir force between two parallel semitransparent δ-function plates and between two parallel anisotropic dielectric slabs [14]. What is more interesting is that the direction of the Casimir force could also be affected by the anisotropy. Based on analytical calculation, Shao claimed that the Casimir force between two uniaxial plates with static permittivity and permeability could be repulsive [15]. In one of our works, the Casimir force between anisotropic metamaterial plates was calculated [16], and the result revealed that the attractive-repulsive transition of the force can happen in some distance ranges. Similar phenomena have also been discovered between liquid-separated dielectric metamaterial and metal [17]. Somers and Munday found that the Casimir force can be repulsive for particular orientations of optical axes even when the two anisotropic slabs are identical [18].

Most of the previous research on the impact of the anisotropy of the material on the Casimir effect has been restricted to the case in which the region between the plates is vacuum or filled with isotropic media. However, the media in this region can also be anisotropic. Some liquid, such as nitrobenzene, can be anisotropic under special circumstances. Moreover, in biology, liquid films between the biomembranes are often anisotropic as well. Therefore, taking the anisotropy of the intervening media into account should prove to be both more interesting and closer to reality. This makes the impact of the anisotropy of the intervening media on the Casimir effect be considered worthy of scholarly attention. Strikingly, very little attention has been paid to this. Parsegian calculated the non-retarded van der Waals interaction energy between two uniaxial slabs acting across a third anisotropic material [7]. Kornilovitch investigated the impact of the angle between the optical axis and the surface normal on the non-retarded van der Waals interaction between parallel slabs immersed in uniaxial media [19]. Both these studies were mainly focused on attractive forces and did not examine the impact of the anisotropy of the intervening media on the Casimir effect. Furthermore, this topic would be more interesting, if the repulsive force or repulsive-attractive transition could happen. In one of our previous studies, the exact impact of the anisotropy of the intervening media on the Casimir force effect was calculated and the result showed that repulsive-attractive transition of the Casimir force could appear in this case and both the magnitude and the direction of the Casimir force were affected by the anisotropy of the intervening media [20]. In a subsequent work [21], we reinvestigated this problem when frequency-dependent permittivities were considered. We also discussed the influence of the external electric field on the Casimir force by affecting the anisotropy of the intervening media though the Kerr effect in that work [21]. The thermal Casimir force between two parallel isotropic plates separated by a uniaxial anisotropic film was investigated by Mostepanenko [22]. This work and our previous works were on the case when the optical axis is perpendicular to the plates (out-of-plane case). In this paper, we are going to focus on the case that the optical axis of the intervening media is parallel to the surfaces of the plates, which is often referred to as in-plane case. This study seeks to find out the general feature of the impact of the anisotropy of the intervening media on the Casimir force and its physical explanation. Therefore, we will calculate the relativistic Casimir force between two isotropic plates separated by a gap filled with a third uniaxial medium in the in-plane case. Then we will examine the relative impact of the anisotropy of the intervening media and explain the reason why it behaves like this. The effect of non-zero temperature on the impact of the anisotropy of the intervening media will also be explored.

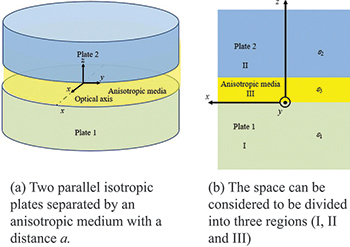
In this section, a detailed calculation of the Casimir force between two parallel isotropic slabs separated by uniaxial material will be given. Consider two parallel plates made of isotropic materials interacting across a uniaxial medium as shown in fig. 1(a). The materials in this paper are assumed to be non-magnetic. The x-y plane is chosen to be parallel to the surfaces of the plates, and the x-axis is chosen to be parallel to the optical axis of the intervening medium. It is convenient to assume the diameters and thicknesses of the plates to be much greater than the separation between them. Therefore, the space could be considered to be divided into three regions (labeled I, II, and III) as shown in fig. 1(b). The dielectric properties of the three regions can be characterized by the corresponding relative permittivities ($\varepsilon_{1}$, $\varepsilon_{2}$ and $\varepsilon_{3}$).

Zoom In Zoom Out Reset image size

The relative dielectric pemittivities of the two isotropic plates can be expressed by diagonal matrices as follows [22]:

$$\begin{eqnarray} \varepsilon_{1} &= \left(\begin{array}{c@{\quad}c@{\quad}c} {\varepsilon_{1} } & 0 & 0\\ 0 & {\varepsilon_{1} }& 0\\ 0 & 0 &{\varepsilon_{1} }\\ \end{array}\right)\!, \end{eqnarray} \tag{ 1 }$$

$$\begin{eqnarray} \varepsilon_{2}&= \left(\begin{array}{c@{\quad}c@{\quad}c} {\varepsilon_{2} } & 0 & 0\\ 0 & {\varepsilon_{2} }& 0\\ 0 & 0 &{\varepsilon_{2} }\\ \end{array} \right)\!. \end{eqnarray} \tag{ 2 }$$

The matrix form for the relative dielectric permittivities of the anisotropic intervening medium is a little complicated. It can be expressed as [9–12,15,16,20–23]

$$\begin{equation} \varepsilon_{3} =\left(\begin{array}{c@{\quad}c@{\quad}c} {\varepsilon_{3\,\vert \vert } } & {\mbox{0}} & 0 \\ {\mbox{0}} & {\varepsilon_{3\bot } } & 0 \\ 0 & 0 & {\varepsilon_{3\,\bot } } \\ \end{array}\right)\!, \end{equation} \tag{ 3 }$$

where $\varepsilon_{\parallel}$ and $\varepsilon_{3\bot}$ are the values of permittivities in the direction parallel and perpendicular to the optical axis, respectively.

To evaluate the Casimir force in our case, we will use the surface mode method. It should be noted that there are many equivalent methods which can be used to calculate the Casimir force in this situation [7–12,14–16,20–22]. We choose this method because it is as practical as other methods and has been used on similar problems many times in our previous works [11,12,15,16,20,21].

Owing to the fact that the three regions in fig. 1(b) are considered to be homogenous, the electric and magnetic field with surface mode q can be written as [20,21,24]

$$\begin{eqnarray} &&\textbf{E}_{q} =iN[a_{q} \textbf{e}_{q} (\textbf{k})-a_{q}^{+} \textbf{e}_{q}^{\ast } (\textbf{k})], \end{eqnarray} \tag{ 4 }$$

$$\begin{eqnarray} &&\textbf{H}_{q} =N[a_{q} \textbf{h}_{q} (\textbf{k})+a_{q}^{+} \textbf{h}_{q}^{\ast} (\textbf{k})], \end{eqnarray} \tag{ 5 }$$

where N is the normalization factor. The parameters a_q and $a^{+}_{q}$ in (4) and (5) are the usual creation and annihilation operators, respectively. $\textbf{k} = (k_{x}, k_{y}, k_{z})$ is the wave vector. We can choose $k_{y} = 0$ without losing generality, thereby we can have $\textbf{k} = (k_{x}, 0, k_{z}) = K_{0}(\alpha, 0, \gamma )$, with $K_{0}=\omega c^{-1}$.

According to the method in [4,12,15,16,20,21], the Casimir interaction energy at zero temperature could be expressed as (since only the intervening medium is considered to be anisotropic, we can let $\phi =0$, which can simplify the equations without losing generality)

$$\begin{equation} E(a)=\frac{\hbar}{4\pi^{2}c^{2}}\int_1^\infty p\mathrm{d}p\int_0^\infty \varepsilon_{3\bot } \xi^{2}[\ln Q_{TE} +\ln Q_{TM}]\mathrm{d}\xi. \end{equation} \tag{ 6 }$$

We can introduce $\delta =\varepsilon_{3\parallel}/\varepsilon_{3\bot} -1$ to describe the anisotropy of the permittivity of the intervening media. The Casimir force between the plates per unit area at zero temperature should be

$$\begin{eqnarray} F(a,\delta )=\,& \frac{\partial E(a)}{\partial a}=\frac{\hbar }{2\pi ^{2}c^{3}}\int_1^\infty {p^{2}\mathrm{d}p\int_0^\infty {\varepsilon_{3\bot }^{3/2} \xi^{3}\mathrm{d}\xi}}\nonumber\\ & {}\times\left[ {\frac{1-Q_{TE} }{Q_{TE} }+\sqrt {1+\delta } \frac{1-Q_{TM} }{Q_{TM} }} \right] \end{eqnarray} \tag{ 7 }$$

with

$$\begin{equation} Q_{TE} =1-\frac{({s_{1} -p})({s_{2} -p})}{({s_{1} +p} )( {s_{2} +p} )}e^{-2pa\xi \sqrt {\varepsilon_{3\bot}}/c} \end{equation} \tag{ 8 }$$

and

$$\begin{eqnarray} Q_{TM}=\,& 1-\left({\frac{( {s_{1} -\frac{\varepsilon_{1} }{\varepsilon _{3\bot } \sqrt {1+\delta } }p})( {s_{2} -\frac{\varepsilon_{2} }{\varepsilon_{3\bot } \sqrt {1+\delta } }p})}{( {s_{1} +\frac{\varepsilon_{1} }{\varepsilon_{3\bot } \sqrt {1+\delta } }p})( {s_{2} +\frac{\varepsilon_{2} }{\varepsilon_{3\bot } \sqrt {1+\delta } }p})}}\right)\nonumber\\ & {}\times e^{-2pa\xi \sqrt {\varepsilon_{3\bot } } \sqrt {1+\delta } /c}. \end{eqnarray} \tag{ 9 }$$

A detailed derivation of (6)–(9) can be found in the supplementary material Supplementarymaterial.pdf (SM).

It is clear that the Casimir force F(a) depends on δ, which reveals the fact that the anisotropy of the intervening medium could affect the Casimir force. It is very interesting that the anisotropy only affects the TM term. If $\delta =0$ eq. (7) becomes

$$\begin{eqnarray} F(a,0)=& \frac{\hbar }{2\pi^{2}c^{3}}\int_1^\infty {p^{2}\mathrm{d}p\int_0^\infty {\varepsilon_{3\bot }^{3/2} \xi^{3}\mathrm{d}\xi}} \nonumber\\ & {}\times \left\{\left[\frac{s_{1} +p}{s_{1} -p}\frac{s_{2} +p}{s_{2} -p}\exp \left(\frac{2pa\xi}{c}\sqrt {\varepsilon_{3\bot}}\right)-1\right]^{-1}\right.\nonumber\\ & \left. +\left[\frac{s_{1} +\frac{\varepsilon_{1}}\varepsilon_{3\bot } ps_{1} -\frac{\varepsilon_{1}}{\varepsilon_{3\bot}}p}{s_{2} +\frac{\varepsilon_{2}}{\varepsilon_{3\bot}}ps_{2} -\frac{\varepsilon_{2}} {\varepsilon_{3\bot}}p}\right.\right.\nonumber\\ & \times\left.\left.\exp \left( {\frac{2pa\xi }{c}\sqrt {\varepsilon _{3\bot }}}\right)-1\right]^{-1}\right\} \end{eqnarray} \tag{ 10 }$$

which is coincident with Lifshitz's result for isotropic materials (eq. 4.14 in [3]).

The result in the previous section shows that the Casimir force can be affected by the anisotropy of the intervening media. In the section, we will analyze the impact of the anisotropy of the intervening media on the Casimir force.

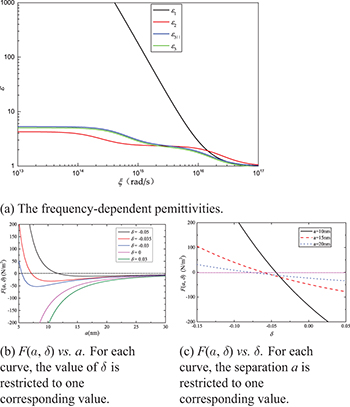
The frequency-dependent permittivity as shown in fig. 2(a) has been used. For plate 1 $(\varepsilon_{1})$, the Drude model is used [4],

$$\begin{equation} \varepsilon (i\xi)=1+\frac{\omega_{p}^{2} }{\xi (\xi +\gamma)}. \end{equation} \tag{ 11 }$$

Zoom In Zoom Out Reset image size

We use the parameters for gold [4]: $\omega_{p}=1.37\times 10^{16}\ \text{rad/s}$ and $\gamma=5.32\times 10^{13}\ \text{rad/s}$.

For plate 2 $(\varepsilon_{2})$ and the intervening material between the plates $(\varepsilon_{3\bot})$, we neglect the dc conductivity of the dielectrics and use the following model [9]:

$$\begin{equation} \varepsilon (i\xi)=1+\frac{C_{IR} }{1+({\xi /\omega_{IR}})^{2}}+\frac{C_{UV} }{1+( {\xi /\omega_{UV}})^{2}}. \end{equation} \tag{ 12 }$$

For $\varepsilon_{2}$, we use the parameters for quartz [9]: $C_{IR}=1.920$, $C_{UV}=1.350$, $\omega_{IR}=2.09\times 10^{14}\ \text{rad/s}$ and $\omega_{UV}=2.04\times 10^{16}\ \text{rad/s}$. For $\varepsilon_{3\bot}$, we use the parameters for bromobenzene [25]: $C_{IR}=2.967$, $C_{UV}=1.335$, $\omega _{IR}=5.47\times 10^{14}\ \text{rad/s}$ and $\omega_{UV}=1.28\times 10^{16}\ \text{rad/s}$. In fig. 2(a), $\delta =0.1$ is used.

The Casimir forces at different separations with different fixed values of δ is shown in fig. 2(b). In fig. 2(b), a positive value of $F(a, \delta )$ indicates that the force is attractive, while a negative value of $F(a, \delta)$ indicates that the force is repulsive. It can be seen that, for a negative value of δ, the force could be attractive at small separation and the magnitude of the force decreases sharply as the separation increases. Finally, the force will switch into repulsive at a larger separation. By contrast, for a positive value of δ, the force is always repulsive for separation above several nanometers. The reason for this behaviour can be explained by the combined effect of dispersion and anisotropy. According to Lifshitz's theory [3,4], in a plate-media-plate system, if the permittivity of the intervening media is intermediate to the other two plates, a repulsive Casimir force can arise and the force should be attractive in other cases. However, in our paper, the intervening medium is anisotropic, which means the permittivity is different in different direction. This makes it difficult to compare the permittivities of the three regions. For the sake of simplicity, we can use the average of $\varepsilon_{3\parallel}$ and $\varepsilon_{3\bot}$ in the arguments discussed below ($\varepsilon_{3}$ is introduced as the average of $\varepsilon_{3\parallel}$ and $\varepsilon_{3\bot}$). Therefore, if $\varepsilon_{1}> \varepsilon_{3}> \varepsilon_{2}$ (or $\varepsilon_{1}< \varepsilon_{3}< \varepsilon_{2}$) is satisfied, the force should be repulsive. Otherwise, the force should be attractive. In fig. 2(a), one can see that in the low imaginary frequency range $\varepsilon_{1}> \varepsilon_{3}> \varepsilon_{2}$, while in the higher frequency range $\varepsilon_{2}> \varepsilon_{1}> \varepsilon_{3}$. Therefore, the force is attractive at small separations where high-frequency modes give rise to the dominant contribution to the total force, and the force is repulsive at larger separations where lower-frequency modes are more relevant. We can also find in fig. 2(b) that, at small separations, a positive δ tends to enhance the repulsive force, while a negative δ tends to supress the repulsive force. This can be understood as the influence of the anisotropy of the intervening media. As can be seen in fig. 2(a), $\varepsilon_{2}$ and $\varepsilon_{3}$ are close in a wide frequency range. Therefore, a small positive δ will slightly increase $\varepsilon_{3}$, which can help the relation $\varepsilon_{1}> \varepsilon_{3}> \varepsilon _{2}$ to remain satisfied. That is why it tends to enhance the repulsive effect. By contrast, a small negative δ will slightly decrease $\varepsilon_{3}$, which might break the relation $\varepsilon_{1}> \varepsilon_{3}> \varepsilon_{2}$ and result in an attractive force. Therefore, the behaviour shown in fig. 2(b) is the result of both anisotropy of the intervening media and the dispersion. This can be seen more clearly in fig. 2(c). For each of the three fixed separations, the force can change its direction as δ changes, which is the influence of the anisotropy of the intervening media. However, for different separation the force switches its sign at a different value of δ, which will not happen if the dispersion is excluded [21].

In order to focus on the impact of the anisotropy of the intervening media, we introduce

$$\begin{equation} \eta =\frac{\Delta F}{|{F(a,0)} |}=\frac{F(a,\delta)-F(a,0)}{|{F(a,0)}|}. \end{equation} \tag{ 13 }$$

$\Delta F$ is the difference in the Casimir force between the case when the anisotropy is taken into account and the case when the intervening medium is isotropic. Therefore, η can be used to evaluate the relative impact of the anisotropy of the intervening media on the Casimir force. A positive ΔF or η indicates that the anisotropy of the intervening media contributes to an attractive force, while a negative $\Delta F$ or η indicates that the anisotropy of the intervening media contributes to a repulsive force.

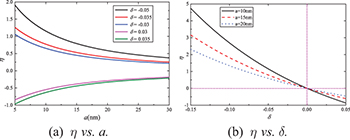
The relative impact of the anisotropy of the intervening media is shown in fig. 3. For positive δ, η is negative, which indicates a "repulsive" contribution to the total force. For negative δ, η is positive which indicates an "attractive" contribution to the force. This is coincident with previous discussions. It can be also noticed in fig. 3(b) that η changes its sign at $\delta =0$, which is the same for all separations. The physical reason for this is the same as we discussed in the previous paragraph. Moreover, this can also be explained by a mathematical way as a supplement. For small δ used in this paper, we can expand eq. (7) by using the Taylor equation at $\delta =0$. Then, the first-order term of δ can show the main contribution of the anisotropy. For any fixed a, the sign of this term will change with the sign of δ. That is the mathematical reason for the behaviours in fig. 3(b).

Zoom In Zoom Out Reset image size

The result calculated by positive δ and negative δ also has some trends in common. As can be found in fig. 3(a), the amplitude of the relative impact of the anisotropy decreases as the separation increases, no matter whether δ is positive or negative. This behaviour can be explained by the dispersion. At small separations, the higher imaginary frequency modes contribute most to the force. As shown in fig. 2(a), the differences between the permittivities are so small in the higher imaginary frequency range that even a tiny δ can cause a significant change to the relations between the pemittivities, which could, furthermore, affect the total force significantly. However, at large distances, the main contribution to the force comes from the modes in the lower imaginary frequency range, where the differences between the permittivities can be very large. Therefore, in this case, anisotropy can hardly cause any notable change to either the relation between pemittivities or the total force. That is why the relative impact of the anisotropy of the intervening media decreases as the separation increases.

It is interesting that we can find similar trends, if we re-examine the results for the out-of-plane case in our previous paper [21] (fig. 5 in [21]). We believe that these two cases may be generalized into one. The anisotropy and dispersion can change the inequality among the permittivities of the 3 regions and furthermore change the magnitude and direction of the total force, and this change decreases with the separation.

As δ may approach 0 at high frequency, we recalculated η numerically with $\delta =0$ for frequencies greater than 10¹⁷ rad/s. The change in the result of η is less than several percent, which means it will not change the main trends of the result.

As mentioned in the second section, the anisotropy only affects the TM term in eq. (7). It would be interesting to examine the thermal effect. In this section, we will discuss how the non-zero temperature affects the impact of the anisotropy of the intervening media on the Casimir force. To calculate the thermal Casimir force, we can just replace the integration over ξ by a summation by means of $\int \mathrm{d}\xi /2\pi \to (k_{B}T/\hbar )\sum_{m}$ with $\xi \to \xi _{m}$ in eq. (7) [12,16],

$$\begin{eqnarray} F^{T}(a,\delta )=\,& \frac{k_{B} T}{\pi c^{3}}\int_1^\infty {p^{2}\mathrm{d}p\sum\limits_{m=0}^\infty {'\,\varepsilon_{3\bot }^{3/2} \xi_{m}^{3} } }\nonumber\\ & {}\times\left[\frac{1-Q_{TE} }{Q_{TE} }+\sqrt {1+\delta } \frac{1-Q_{TM} }{Q_{TM} }\right]\!, \end{eqnarray} \tag{ 14 }$$

where the prime means that the $m = 0$ term is counted with half-weight. Equation (14) can be transformed into the following form:

$$\begin{eqnarray} F^{T}(a,\delta )=\,& F_{m=0}^{T} (a,\delta )+\frac{k_{B} T}{\pi c^{3}}\int_1^\infty {p^{2}\mathrm{d}p\sum\limits_{m=1}^\infty {\varepsilon_{3}^{3/2} \xi_{m}^{3} } } \nonumber\\ & {}\times\left[ {\frac{1-Q_{TE} }{Q_{TE} }+\sqrt {1+\delta } \frac{1-Q_{TM} }{Q_{TM} }} \right] \end{eqnarray} \tag{ 15 }$$

with

$$\begin{eqnarray} F_{m=0}^{T} (a)=\,& \lim\limits_{\xi \to 0} \frac{k_{B} T}{2\pi c^{3}}\int_1^\infty {p^{2}\mathrm{d}p\varepsilon_{3}^{3/2} \xi^{3} }\nonumber\\ & {}\times\left[{\frac{1-Q_{TE} }{Q_{TE} }+\sqrt {1+\delta } \frac{1-Q_{TM} }{Q_{TM} }}\right]\!. \end{eqnarray} \tag{ 16 }$$

The controversy about the thermal Casimir force for real media has raged unabated for decades [5,6]. This controversy focuses on which model should be used for the permittivity of real media to calculate eq. (14). Bimonte demonstrated that the measurement data extrapolated by the plasma model should be used for metal [26]. Following the conclusion in the review article [6], for the dielectrics (plate 2 and the intervening media), we ignore the dc conductivity. In this case, no matter whether the Drude model or the plasma model is used for plate 1, eq. (16) would become

$$\begin{equation} F_{m=0}^{T} (a)=\frac{k_{B} T}{8\pi a^{3}}\sqrt {1+\delta } Li_{3} (X), \end{equation} \tag{ 17 }$$

where Li₃(X) is the polylogarithm function and

$$\begin{equation} X=\left(\frac{\varepsilon_{2} (0)}{\varepsilon_{3} (0)\sqrt {1+\delta } }-1\right)\!\biggl/\!\left(\frac{\varepsilon_{2} (0)}{\varepsilon_{3} (0)\sqrt {1+\delta } }+1\right)\!. \end{equation} \tag{ 18 }$$

The detailed derivation of (17), (18) can be found in the SM. We numerically calculated the Casimir force using both plasma model and Drude model to describe $\varepsilon_{1}$. The results calculated with these two models are so close to each other that, if we plot them in the same figure, they may overlap in most of the range. Therefore, we will only demonstrate the result calculated by the Drude model in figs. 4–6.

Zoom In Zoom Out Reset image size

The numerical result of the thermal Casimir force is shown in fig. 4. When the thermal effect is considered, the attractive-repulsive transition can still happen as the separation of degree of anisotropy changes as shown in fig. 4(a) and (b). The relative impact of anisotropy on the Casimir force is also calculated, and the result is shown in fig. 5. Compare fig. 5(a) and (b) with fig. 3(a) and (b), one may find that the behaviors are similar. It seems that considering the thermal effect will not change the main trends of the result. This is because the separations considered in this paper are small. The cases for large separations were discussed in [22]. The behaviors in figs. 4 and 5 can share the same physical explanation with that in figs. 2 and 3.

Zoom In Zoom Out Reset image size

To examine the effect of non-zero temperature on the impact of anisotropy on the Casimir force, we can compare these results with the result obtained when the thermal effect is ignored. Figures 6(a)–(d) show that the non-zero temperature does affect the impact of anisotropy of intervening media on the Casimir force. As can be seen in fig. 6(a) and (b), considering non-zero temperature (300 K) tends to suppress the magnitude of the relative impact of anisotropy on the Casimir force at smaller distance but to enhance it at larger distance, no matter whether δ is positive or negative. It can be found in fig. 6(c) that at small separation, such as 5 nm, the curve calculated at $T=300\ \text{K}$ has a smaller slope than the curve calculated with the thermal effect ignored, which indicates that the thermal effect in this case tends to suppress the magnitude of the relative impact of anisotropy. By contrast, fig. 6(d) shows that, at 50 nm, the curve calculated at $T=300\ \text{K}$ has a larger slope than the curve calculated with the thermal effect ignored, which indicates that the thermal effect in this case tends to enhance the magnitude of the relative impact of anisotropy. These are consistent with the behaviors in fig. 6(a) and (b). We can also find in fig. 6(c) and (d) that, η still changes its sign at $\delta = 0$, no matter whether the thermal effect is considered of not, which confirms our previous conclusion that the thermal effect will not change the main trends of the result.

Zoom In Zoom Out Reset image size

Previously, we have investigated the impact of the anisotropy of the intervening media on the Casimir force in the configuration of two parallel slabs separated by the anisotropic media.

The relativistic Casimir force was calculated with the surface mode method and frequency-dependent dielectric permittivity was used. The result showed that the attractive-repulsive transition could arise with the change of separation for positive δ. However, for different δ, the force switches direction at different separation. We also noticed that the Casimir force could reverse its direction as the anisotropy changed, but for different separation, the force reverses its direction at different δ. These behaviors are the result of both dispersion and anisotropy of the permittivity of the intervening media.

Based on the result above, the relative impact of the anisotropy of the intervening media on the Casimir force was also calculated. It was found that the anisotropy producing an "attractive" or "repulsive" contribution to the total force is significantly affected by the sign of δ. This can also be explained by the combined effect of both dispersion and anisotropy of the permittivity of the intervening media. It was also concluded that the amplitude of the relative impact of the anisotropy on the Casimir force decreases as the separation increases, which is the result of dispersion.

The thermal Casimir force in this case was also calculated. We found that the thermal effect would not change the main trends of either the force or the relative impact of anisotropy on the Casimir force. However, the thermal effect tends to suppress the impact of anisotropy on the Casimir force at small separation and to enhance it at larger separation, no matter what value δ has.

It might be challenging to observe the above behaviors experimentally, as the anisotropy of a liquid or gas is usually small; still, as a theoretical work, this work remains interesting to many disciplines.

This work was partially supported by the National Natural Science Foundation of China (Grant No. 11605050, Grant No. 91636221, and Grant No. 11604089). GD, QS, and C-YL are grateful to the China Scholarship Council for providing us financial support (Grant No. [2018]5028) to study and carry out research in Canada. They are also grateful to the University of British Columbia for providing us support to finish this paper on UBC Point Grey (Vancouver) campus, Canada. They express special gratitude to Prof. Anna Kindler, Prof. Sunita Chowrira, Dr. Jared Stang, Dr. Fang Wang, Dr. Na Li, and Ms Frankie Zhong for their kindly help in UBC. Land acknowledgments: This paper is finished on the UBC Point Grey (Vancouver) campus, which sits on the traditional, ancestral, unceded territory of the x^wməθk^wəýəm (Musqueam) First Nation.