Transformational supervisor synthesis for evolving systems

Abstract

Supervisory controller synthesis is a means to compute correct-by-construction controllers for discrete event systems. As these systems and their requirements evolve over time, an updated supervisor needs to be computed each time an adaptation takes place. We consider the case that a supervisor has been synthesized for a given model, after which this model is (slightly) adapted. We investigate how we can make use of the previous synthesis result, in order to more efficiently compute the supervisor for the adapted model. We introduce model deltas as a means to describe the difference between pairs of models. Using the model deltas, a notion of atomic adaptations is introduced. For these atomic adaptations, algorithms are provided to compute the supervisor for the adapted model in a transformational manner from the previous synthesis result, rather than performing a completely new synthesis. These atomic adaptations can be iterated over, to transformationally compute a supervisor for model deltas that contain a number of atomic adaptations. To improve efficiency, it is shown how atomic adaptations can be grouped together based on their required computations and be processed at the same time. A running example is used to support the explanations on the functioning of the algorithms. The efficiency of the method is evaluated by means of both an academic and an industrial use case.

1 Introduction

Supervisory control theory, as introduced by Ramadge and Wonham (1987) and Ramadge and Wonham (1989), is a model-based approach to control discrete event (dynamic) systems. Given a plant model (that defines all possible system behavior) and a requirement specification (which defines what plant behavior is allowed), a supervisor can be computed algorithmically (synthesized) that restricts the plant’s behavior so that it is in accordance with the requirements. Depending on the synthesis algorithm, the supervised system has some useful properties, such as safety, nonblockingness, controllability and maximal permissiveness. The benefit of supervisory control theory has been shown in literature for varying fields of industry. Some examples where it is applied to controller design are; A patient support table of a magnetic resonance imaging scanner in Theunissen et al. (2014), chemical process control in Rawlings et al. (2014), lithography machines in van der Sanden et al. (2015), a waterway lock and movable bridge combination in Reijnen et al. (2020), construction robotics in Rosa et al. (2020), and tactical planning for automated vehicles in Krook et al. (2020). Despite the advantages of applying this technique, and the examples thereof shown in case studies, industrial acceptance is still scarce compared to other topics of control theory. Wonham et al. (2018) point to the state space explosion as one of the barriers to industrial acceptance. When the size of the system grows, the time and space (memory) required for synthesis grows exponentially.

We consider the situation sketched in Fig. 1; A supervisor has been synthesized for a particular specification of plant and requirements. Later, a (slight) adaptation is made to the specification, so that we are going to need a new supervisor. In state of practice, a completely new synthesis would be performed on the adapted model. We investigate how to reuse the initial model and synthesis result, in order to more efficiently synthesize a new supervisor, while the supervisor’s desired properties are retained.

Fig. 1

Schematic overview synthesis for evolving system

The reuse of artifacts during (software) development is considered in (software) Product Line Engineering (PLE). Pohl et al. (2005) define: ‘Software product line engineering is a paradigm to develop software applications using platforms and mass customisation.’ By reusing domain artifacts and exploiting product line variability, companies can employ PLE to increase product individualization, reduce development costs, reduce time-to-market, and enhance product quality. Pohl et al. (2005) point to model-based software development as an ideal candidate for employing PLE.

Within the context of PLE, Schaefer et al. (2012) characterize Delta Modeling as a modular approach to model the variability of a system using transformations. A model delta explicitly specifies an adaptation that can be applied to some base model, in order to form a variant model. A particular variant model can be obtained by selecting one or more model deltas and applying them to the base model one-by-one.

Regarding adaptations that are made to software over time, Lehman (1996) has defined the laws of software evolution; these describe what changes typically occur during a software’s lifetime. The laws themselves have evolved over the years, but the law of continuing change has consistently been a part of them. This law states that software controlling a cyber-physical system must continually be adapted, otherwise its functioning becomes progressively less satisfactory.

In this paper, we elaborate on a Transformational Supervisor Synthesis (TSS) method. This type of synthesis uses a base model, its synthesis result and model delta to obtain a supervisor. This supervisor is the same as the would-be supervisor if a completely new synthesis was performed for the variant model, which is defined by the base model and model delta. Note that in this problem statement the model delta is unknown before performing synthesis on the base model. This is a realistic constraint, following from Lehman’s law of continuing change, as well as in the case of iterative and incremental development (Larman and Basili 2003), where system and requirement definitions are adapted during controller development. We introduce a supervisor synthesis algorithm that outputs relevant data that can be used for TSS. We present a notion for model delta, which defines adaptations made between two models, and use this notion to identify atomic adaptations, that are the smallest possible model deltas. For different types of atomic adaptations, we provide TSS algorithms that use the result from a previous synthesis to transformationally compute a supervisor. We show how we can iterate over these atomic adaptations to transformationally obtain a supervisor when multiple atomic adaptations specify the difference between any base and variant model. To improve the efficiency, we will then present an algorithm that groups atomic adaptations together based on their required computations and processes them at the same time. These algorithms are then first applied in an academic experiment in order to analyze their effectiveness. Next, an industrial case study is presented for evolution of a controller that is used in lithography machines. Finally, conclusions are provided based on these results.

1.1 Related work

This paper is strongly based on, and can be seen as an extension to, Thuijsman and Reniers (2020), where the TSS method was first introduced. The extension we present here includes more elaborate examples and explanations, an additional industrial case study, as well as theorems and their accompanying proofs. The algorithms we present here have been updated with respect to Thuijsman and Reniers (2020), some modifications were made on account of obtaining correct results, others for the sake of improving computational efficiency. Tijsse Claase (2020) is also closely related, in which a first attempt of applying TSS to symbolic supervisor synthesis is made, where binary decision diagrams are used to represent the system for efficient supervisor synthesis (Fei et al. 2014).

Within the research area of discrete event systems, PLE is mostly considered in the topic of formal verification or model checking. For example, efficient verification of linear-time temporal logic for variability-intensive systems in Classen et al. (2010) or feature-oriented modular verification of software product lines in ter Beek and de Vink (2014). Khan (2013) investigates evolving Algebraic Petri Nets, how to perform verification on the parts of the system that are affected by the property that is analyzed, and how to identify evolutions that require verification. In ter Beek et al. (2016) and Reniers and Thuijsman (2020), PLE has been applied in supervisory control. In these works a supervisory controller is synthesized for all possible product configurations given by a feature model. The output is one controller with multiple initial locations, were each initial location corresponds to a product configuration. In Reniers and Thuijsman (2020), runtime evolution of the system behavior over the configurations is studied. In contrast to this work, we do not assume a priori knowledge of the possible system configurations and the evolution takes place at design time.

2 Preliminaries

We consider finite state automaton A defined as a 5-tuple: A = (X,Σ,→,X₀,X_m), where X is the finite set of states, of which $X_{0} \subseteq X$ is the set of initial states and $X_{m}\subseteq X$ is the set of marked states. Σ is the finite set of events, also called the alphabet, which is partitioned into sets of controllable and uncontrollable events, respectively Σ_c and Σ_u. Σ^∗ denotes all possible finite strings using events in Σ. → is the finite set of transitions, a transition is a 3-tuple: (x_or,σ,x_tar) ∈ X ×Σ× X, specifying a transition from origin state x_or to target state x_tar over event σ. We denote the existence of a transition (x_or,σ,x_tar) ∈→ by: $x_{\mathit {or}}\xrightarrow { \sigma } x_{\mathit {tar}}$. Likewise, the existence of a sequence of transitions over intermediate states can be addressed by: $x_{\mathit {or}} \xrightarrow { s } x_{\mathit {tar}}$, for s ∈Σ^∗.

The synchronous product of automata A₁ = (X₁,Σ₁,→₁,X_0,1,X_m,1) and A₂ = (X₂,Σ₂,→₂,X_0,2,X_m,2) is defined as: A₁||A₂ = (X₁ × X₂,Σ₁ ∪Σ₂,→₁₂,X_0,1 × X_0,2,X_m,1 × X_m,2), where →₁₂ is constructed by:

$$ \begin{aligned} &((x_{\mathit{or},1},x_{\mathit{or},2}),\sigma,(x_{\mathit{tar},1},x_{\mathit{tar},2})) \in \longrightarrow_{12}, \\ &\text{ if } \sigma \in {\varSigma}_{1} \cap {\varSigma}_{2},\ x_{\mathit{or},1}\rightarrow{ \sigma }_{1} x_{\mathit{tar},1},\ x_{\mathit{or},2}\rightarrow{ \sigma }_{2} x_{\mathit{tar},2}\\ &((x_{\mathit{or},1},x_{2}),\sigma,(x_{\mathit{tar},1},x_{2})) \in \longrightarrow_{12}, \\ &\text{ if } \sigma \in {\varSigma}_{1} \setminus {\varSigma}_{2},\ x_{\mathit{or},1}\rightarrow{ \sigma }_{1} x_{\mathit{tar},1} \\ &((x_{1},x_{\mathit{or},2}),\sigma,(x_{1},x_{\mathit{tar},2})) \in \longrightarrow_{12}, \\ &\text{ if } \sigma \in {\varSigma}_{2} \setminus {\varSigma}_{1},\ x_{\mathit{or},2}\rightarrow{ \sigma }_{2} x_{\mathit{tar},2} \end{aligned} $$

(1)

For a given automaton A, we apply supervisor synthesis to generate a supervisor subautomaton S of A that is reachable, coreachable, controllable, and maximally permissive.

An automaton S = (Y,Σ_S,→_S,Y₀,Y_m) is a subautomaton of A = (X,Σ,→, X₀,X_m) if $Y\subseteq X$, Σ_S = Σ, $\longrightarrow _{S} \subseteq \longrightarrow$, $Y_{0}\subseteq X_{0}$, and $Y_{m}\subseteq X_{m}$. In this work, the subautomata we encounter are restricted to →_S = → ∩ (Y ×Σ× Y ), Y₀ = Y ∩ X₀, and Y_m = Y ∩ X_m.

A state x_r ∈ X is reachable if it can be reached from some initial state; $x_{0}\xrightarrow { s } x_{r}$ for some $x_{0} \in X_{0},\ s \in {{\varSigma }}^{*}$. A state x_cr ∈ X is coreachable if from it a marked state can be reached; $x_{cr} \xrightarrow { s } x_{m}$ for some $x_{m} \in X_{m},\ s \in {{\varSigma }}^{*}$. Supervisor automaton S is called (co-) reachable for plant automaton A, if all its states can be defined as such. An automaton for which all reachable states are coreachable is commonly called nonblocking in literature. We say that for automaton A = (X,Σ,→,X₀,X_m), supervisor automaton S = (Y,Σ_S,→_S, Y₀,Y_m) is controllable if $\longrightarrow \! \cap (Y \times {{\varSigma }}_{u} \times X) {} \subseteq {}\!\! \longrightarrow _{S}$. If S is controllable, the states in Y are also called controllable. Maximally permissive says that S is the maximal subautomaton of A for which coreachability, reachability, and controllability are ensured. Meaning the supervisor does not disable any transitions that do not strictly need to be disallowed.

In addition to the properties of the supervisor mentioned above, problem formulations for supervisor synthesis often include a safety constraint; Along with the plant, some requirement specification on the plant’s behavior is given. The supervisor should restrict the behavior of the plant so that the requirement specification is always satisfied. In such a case, a plantified requirement automaton can be constructed by introducing a non-coreachable sink state. Transitions that are not in accordance with the specification are redirected to this sink state. Given a requirement automaton R = (X,Σ,→,X₀,X_m), the plantified requirement automaton is obtained as follows (Flordal et al. 2007):

$$ R^{\bot} = (X\cup \{\bot\},{{\varSigma}}, \longrightarrow^{\bot},X_{0},X_{m}), $$

(2)

where ⊥∉X is the new sink state and

$$ \longrightarrow^{\bot} = \longrightarrow\! \cup \{ (x,\sigma_{u},\bot) | x\in X, \sigma_{u}\in {{\varSigma}}_{u}, \nexists (x_{\mathit{tar}} \in X) x \xrightarrow{ \sigma_{u} } x_{\mathit{tar}} \}. $$

A safe supervisor can be obtained by synthesizing a coreachable and controllable supervisor on the synchronous product of the plant automata and plantified requirement automata, as proven in Flordal et al. (2007). Other ways of specifying requirements can be plantified as well. For example state exclusion requirements discussed in Markovski et al. (2010) are plantified by removing excluded controllable transitions from the plant, and directing the excluded uncontrollable transitions to the sink state. Therefore, in this work we will consider synthesizing a coreachable supervisor for a single automaton, without loss in generality regarding safety constraints or networks of automata.

We allow automata to be non-deterministic. In the case of non-determinism, we allow the supervisor to be able to disable individual controllable transitions as a result of the removal of unsafe states. So if in the plant a state has two outgoing transitions over the same controllable event, the supervisor subautomaton may contain this state with only one of these outgoing transitions. This is unlike some traditional supervisory control definitions, by for example (Ramadge and Wonham 1989) or (Cassandras and Lafortune 2008), where multiple outgoing events over the same event can not be disabled individually. The distinction between these paradigms is further discussed in Flordal et al. (2007).

2.1 Running example

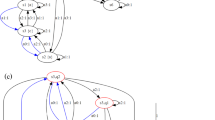
We will consider the plant automaton P of Fig. 2 and requirement automaton R of Fig. 3 as a running example throughout this paper. A solid or dashed arrow respectively indicates a transition by a controllable or an uncontrollable event. The initial states are indicated by the incoming arrows, and the marked states are indicated by a double circle. Requirement automaton R has been plantified, resulting in the plantified requirement automaton R^⊥ in Fig. 4. Constructing the synchronous product P||R^⊥ yields automaton A of Fig. 5. Note that for the remainder of this paper, when we discuss model deltas to this example, they are always to automaton A directly, not to P and R with an implied delta on A.

Fig. 2

Plant automaton P

Fig. 3

Requirement automaton R

Fig. 4

Plantified requirement automaton R^⊥

Fig. 5

Automaton A = P||R^⊥

2.2 Supervisor synthesis algorithm

In Algorithm 1 a supervisor synthesis algorithm is presented. It is based on the algorithm introduced in Ouedraogo et al. (2011). However, we consider Finite State Automata rather than Extended Finite Automata for sake of simplicity. We also omitted the use of forbidden states in the algorithm, as we plantify the requirements. In case the plant behavior is given by multiple plant automata, the input automaton for this algorithm can be obtained by calculating the synchronous product of the plant automata. We present this algorithm using function calls to other algorithms to facilitate reuse of these (sub-)algorithms later in this paper. The algorithm uses a fixpoint computation, provided in Algorithm 2, which iteratively calculates a set of coreachable states G, followed by a set of bad states B, that are non-coreachable or have a sequence of uncontrollable transitions to a non-coreachable state. The calculation to obtain G and B is done by the means of a Backward Reachability Search (BRS), given in Algorithm 3, for which Lemma 1 holds. This is a Breadth First Search algorithm taken from Kleinberg and Tardos (2005) that has a linear runtime complexity. All found states are added to X_ω. The state space is searched in layers. For each state in the current layer, all undiscovered states that have a transition to this state are added to the next layer. After all states in the current layer have been evaluated, the algorithm moves to evaluating the states in the next layer. These steps are repeated until no more new states are found. The algorithm is slightly adapted from Kleinberg and Tardos (2005) to allow a set of starting states, instead of a singular starting state. Also, at the start of the algorithm the transitions are pruned, so that only transitions between states in the input state set X are considered. Transitions from states in the starting set X_α are also removed, as these states are already discovered as the starting set, so analyzing these transitions is not necessary. The functioning of this algorithm is well known so Lemma 1 is not proven here.

Lemma 1

For state set X, alphabet Σ, set of transitions →, and starting state set X_α; BRS(X,Σ,→,X_α) contains all states in X from which a state in X_α ∩ X can be reached, using transitions in →, over states in X, that have an event in Σ.

The bad states B are removed from G. The removal of these states can induce other states to become non-coreachable. Therefore, the algorithm repeats these steps until no further states get removed. At this point, the set of remaining states is defined as good states G, which is the maximal set of controllable and coreachable states, see Lemma 2. Proof for Lemma 2 is provided in Ouedraogo et al. (2011).

Lemma 2

For automaton A = (X , Σ , →, X₀,X_m), and (Y , G) = computeFixpoint(A); G is the maximal controllable and coreachable set of states in X.

Then, in order to generate a reachable supervisor, a Forward Reachability Search (FRS) (Algorithm 4, Lemma 3) is carried out from the set of initial states, resulting in states Y. Essentially BRS is performed with all transitions reversed to search forward instead of backward. Same as for BRS, the accompanying lemma is not proven here. Y is the maximal controllable, coreachable, and reachable subset of X, see Lemma 4.

Lemma 3

For state set X, alphabet Σ, set of transitions →, and starting state set X_α; FRS(X,Σ,→,X_α) contains all states in X that can be reached from a state in X_α ∩ X, using transitions in →, over states in X, that have an event in Σ.

Lemma 4

For automaton A = (X , Σ , →, X₀,X_m), and (Y ,G) = computeFixpoint(A); Y is the maximal controllable, coreachable, and reachable set of states in X.

Proof

Y is the maximal reachable set in G, following from Lemma 3. It is shown by Lemma 2 that G is the maximal controllable and coreachable subset of X. Thus, the maximal reachable subset Y in G is the maximal controllable, coreachable, and reachable subset of X. □

Together, Y, alphabet Σ, the transitions of A between the states in Y, the initial states in Y, and the marked states in Y define the supervisor automaton S. Supervisor S is the maximal subautomaton of A that is reachable, coreachable, controllable; see Theorem 1. The algorithm always computes a supervisor automaton. If there are no reachable, coreachable, and controllable states then the supervisor automaton will contain no states, and hence no transitions.

Theorem 1

For automaton A, and (S,G) = SS(A); S is maximally permissive, controllable, coreachable, and reachable with respect to A.

Proof

By construction, S is the maximal subautomaton of A over states in Y. Y is the maximal controllable, coreachable and reachable set of states in A (Lemma 4). It follows that S is maximally permissive, controllable, coreachable, and reachable with respect to A. □

Next to supervisor S, the synthesis algorithm outputs good state set G, in order to facilitate reuse of this set in other computations. Note that this state set is computed anyways during synthesis, it is not computed specifically for the facilitation of reuse.

2.2.1 Example

When applying the supervisor synthesis algorithm to automaton A of Fig. 5, first the supervisor states and good states are calculated by computeFixpoint (Algorithm 2). The supervisor states are {p₀r₀,p₂r₀}, the good states are {p₀r₀,p₁r₀,p₂r₀,p₃r₀,p₂r₁,p₃r₁}. Next, the supervisor automaton is constructed, which provides the supervisor automaton given in Fig. 6.

Fig. 6

Supervisor S, for (S,G) = SS(A)

For convenience we also provide a visualization of automaton A, where the states are color coded depending on their containment in the state sets resulting from synthesis, in Fig. 7. Supervisor states (Y ) (that are also good states by definition) are displayed white, good states that are not supervisor states (G ∖ Y) are displayed grey, and non-good states (X ∖ G) are displayed black.

Fig. 7

Automaton A, color coded by synthesis result

3 Model delta

For the purpose of TSS we wish to model the difference between the base and variant model. We can represent any adaptation from base to variant automaton as model delta as 10-tuple: Δ= (X⁺, X⁻, Σ⁺, Σ⁻, →⁺, →⁻, ${X_{0}^{+},}$ ${X_{0}^{-},}$ ${X_{m}^{+},}$ ${X_{m}^{-}} )$, which for each of the sets in the 5-tuple definition of automaton A, defines the added (⁺) and removed (⁻) elements of that set. Σ⁺ and Σ⁻ are both partitioned into sets of controllable and uncontrollable events that are added or removed. The following constraints apply to the model delta:

• All removed elements within the model delta, must exist in the base model: $X^{-} \!{}\subseteq {} X,\ {{\varSigma }}^{-} \!{} \subseteq {} {{\varSigma }}, ...$.

• All added elements within the model delta, must not yet exist in the base model: X⁺ ∩ X = ∅, Σ⁺ ∩Σ = ∅,....

• Elements can not simultaneously be added and removed X⁻∩ X⁺ = ∅, Σ⁻∩Σ⁺ = ∅,....

• The initial and marked states of the variant model must exist in the variant state set: $X_{0}^{+}\subseteq (X\cup X^{+})\setminus X^{-},\ X_{m}^{+}\subseteq (X\cup X^{+})\setminus X^{-}$.

• Transitions must go to-and-from states, by defined events: $\longrightarrow ^{\prime } \subseteq X^{\prime }\times {{\varSigma }}^{\prime } \times X^{\prime }$, where $X^{\prime } = (X\cup X^{+})\setminus X^{-},\ {{\varSigma }}^{\prime }=({{\varSigma }}\cup {{\varSigma }}^{+})\setminus {{\varSigma }}^{-}$, and $\longrightarrow ^{\prime }=(\longrightarrow \!\cup \longrightarrow ^{+})\setminus \longrightarrow ^{-}$.

When these constraints are met, we call the model delta valid.

Given base automaton A and model delta Δ, variant automaton $A^{\prime }$ is constructed by: $A^{\prime }=(X^{\prime },{{\varSigma }}^{\prime },\longrightarrow ^{\prime },X_{0}^{\prime },X_{m}^{\prime })$, where: $X^{\prime }=(X\cup X^{+})\setminus X^{-},$${{\varSigma }}^{\prime }=({{\varSigma }}\cup {{\varSigma }}^{+})\setminus {{\varSigma }}^{-},$$\longrightarrow ^{\prime }=(\longrightarrow \!\cup \longrightarrow ^{+})\setminus \longrightarrow ^{-},$$X_{0}^{\prime }=(X_{0}\cup X_{0}^{+})\setminus X_{0}^{-},$$X_{m}^{\prime }=(X_{m}\cup X_{m}^{+})\setminus X_{m}^{-}$. For a valid model delta, and well-defined base automaton, the constructed variant automaton is well-defined.

Furthermore, for any pair of well-defined automata $(A=(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}),A^{\prime }=(X^{\prime }, {{\varSigma }}^{\prime },\longrightarrow ^{\prime },X_{0}^{\prime },X_{m}^{\prime }))$, a valid model delta is constructed as follows: $X^{+}=X^{\prime }\setminus X$, $X^{-}=X\setminus X^{\prime }$, ${{\varSigma }}^{+}={{\varSigma }}^{\prime }\setminus {{\varSigma }}$, ${{\varSigma }}^{-}={{\varSigma }}\setminus {{\varSigma }}^{\prime }$, $\longrightarrow ^{+}=\longrightarrow ^{\prime }\setminus \longrightarrow$, $\longrightarrow ^{-}=\longrightarrow \setminus \longrightarrow ^{\prime }$, $X_{0}^{+}=X_{0}^{\prime }\setminus X_{0}$, $X_{0}^{-}=X_{0}\setminus X_{0}^{\prime }$, $X_{m}^{+}=X_{m}^{\prime }\setminus X_{m}$, $X_{m}^{-}=X_{m}\setminus X_{m}^{\prime }$.

The change of controllability of an event can be modeled by removing all transitions that are labeled by this event, and adding these transitions back with an added event with modified controllability.

We may address a model delta with only its non-empty part. So if we mention a model delta with $X_{0}^{+}=\{x^{\delta }\}$, and no other information, this implies that the other elements in the model delta tuple are empty. In the remainder of this paper, when considering a model delta Δ it is implied that this is a model delta from base automaton A to variant automaton $A^{\prime }$.

4 Atomic adaptations

In this section we consider atomic adaptations, where the difference between the base and variant model can be described by a single, indivisible change in the automaton specification. Formally we can say that a model delta Δ is an atomic adaptation when only one of the tuple-elements is a set of size one, and all other elements are empty; $|{X^{+}}| + |{X^{-}}| + |{{\varSigma }}^{+}| +|{{\varSigma }}^{-}| + | \longrightarrow ^{+}| + |\longrightarrow ^{-}| + | X_{0}^{+} | + |X_{0}^{-} | + |X_{m}^{+}| + |X_{m}^{-}| = 1$.

We consider several types of atomic adaptations, e.g., removing a transition, or adding the marked property to a state, for which we provide an atomic TSS algorithm. The purpose of these algorithms is to calculate the supervisor states and good states of the variant automaton, using the base automaton, its synthesis result, and model delta. Theorem 2 holds for the algorithms. Essentially, the properties of the supervisor ((co-)reachability, controllability, and maximal permissiveness) are retained during atomic TSS. For sake of cohesion, proofs of Theorem 2 for each algorithm are given separately in Appendix Appendix.

Theorem 2

Given base automaton A, fixpoint result (Y,G) = computeFixpoint(A), and atomic adaptation Δ for which the atomic TSS algorithm is given, the atomic TSS algorithm provides a supervisor state set $Y^{\prime }$ and good state set $G^{\prime }$ such that they are equal to the fixpoint result of the variant automaton; $(Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(A^{\prime })$.

Figure 8 shows an overview of the atomic TSS method. It is similar to Fig. 1, only now the names of the artifacts and algorithms that have been introduced are shown. The figure shows that the fixpoint for the variant supervisor can be computed in two ways, either by (1) performing computeFixpoint on the variant automaton directly, or by (2) performing atomic TSS using the base automaton, base supervisor fixpoint, and atomic model adaptation. Either way, the fixpoint result is the same.

Fig. 8

Inputs and outputs for atomic TSS for atomic adaptation Δ

In the following subsections we consider adding or removing the initial property to some state, adding or removing the marked property to some state, and adding or removing a transition respectively. For the cases of removed or added states and events no algorithms are provided. These atomic adaptations are discussed in Section 4.7. After presenting the atomic TSS algorithms in this section, we will show how we can iterate over them in Section 5, where we are also going to group atomic adaptations together to process them at once.

The algorithms are strongly based on Thuijsman and Reniers (2020). In some places minor modifications are made for sake of correctness and efficiency. Some of these modifications are discussed in Tijsse Claase (2020). The authors note that these modifications influence the experimental results presented in Thuijsman and Reniers (2020), however only to a small enough extent that they do not influence the conclusions made on those results. All algorithms are also modified to compute the supervisor state set Y instead of the supervisor S, leading to shorter notations. S can simply be computed from Y, as in line 2 of Algorithm 1.

4.1 Added initial property

We assume the situation that (Y,G) = computeFixpoint(A) has been calculated for base automaton A. Some state of base automaton A has been made an initial state, which is the only adaptation to create variant automaton $A^{\prime }$. In Algorithm 5 the atomic TSS algorithm is provided to compute supervisor states $Y^{\prime }$ and good states $G^{\prime }$ for the variant model, given A, Y, G, and the state with added initial property x^δ. The algorithm uses a switch statement, where the value of a variable, in this case x^δ, is tested for multiple cases. Once a case match is found, the statements associated with the particular case are executed. In case no match is found, the default statements are executed. For all atomic TSS algorithms the switch cases are mutually exclusive, which means that for the given atomic adaptation only one switch case holds, or none and then the default statement is executed.

In Algorithm 5 it can be seen that two cases are considered, the first being that x^δ is in G ∖ Y. A state in G ∖ Y is coreachable and controllable in the base model. It was not reachable in the base model, as in that case it would be part of Y. Due to addition of the initial property, we now know that x^δ is reachable, so it should become part of $Y^{\prime }$. It is possible that more states in G ∖ Y have become reachable due to x^δ being reachable, so an FRS is carried out over states G. We already know that states in Y were reachable, and they will remain reachable in the variant model. As we do not want to reinvest computational effort in finding these states in Y again, the FRS is already initiated with states Y in the starting set along with x^δ, essentially we already start closer to the fixpoint that we wish to find. States in X ∖ G are not considered, as they remain non-coreachable or non-controllable in the variant model. In our running example, we can consider the adaptation to make p₃r₁ initial, which would fit under this particular case. As p₂r₁ is a reachable good state from p₃r₁, both p₃r₁ and p₂r₁ will be added to the supervisor states Y to construct the supervisor states for the variant model $Y^{\prime }$.

Alternatively, x^δ may be in X ∖ G. As we just noted, the adaptation of initial states does not influence the set of coreachable and controllable states. So in this case, we already performed the FRS over the same set G to compute Y. As G did not change, the supervisor and good states remain the same for the variant model. In our example we can consider making p₄r₁ an initial state as such an adaptation. In that variant model, p₄r₁ will remain a non-good state in $X\setminus G^{\prime }$.

Finally, x^δ may be in Y. If this is the case, just like in the previous example the default statement will be executed. x^δ was already found in the FRS of the base model, so also all reachable states from x^δ in G are included in Y. Thus, the supervisor states and good states remain the same for the variant model. In the running example, making p₂r₀ an initial state would be of this case.

4.2 Removed initial property

We consider a similar situation as the previous section, only this time the initial property has been removed from a state instead of added. The atomic TSS algorithm for this case is shown in Algorithm 6.

In the first case of the algorithm, an initial state in Y is removed. This might lead to some states in Y being unreachable in the variant model. However the good states G are not influenced by the initial states, so they remain the same. Also unreachable states will remain unreachable. So an FRS is carried out over the previously reachable states Y, from the new set of initial states for the variant model to compute $Y^{\prime }$. In the running example, the removal of initial property from p₀r₀ would fit in this case. Consequently, there are no initial states left in Y, so for the variant model there are no supervisor states; $Y^{\prime }=\emptyset$. The good states remain the same.

The other case is that the removed initial state is not in Y, considered under the default statement of Algorithm 6. Actually we know that in this case the removed initial state is in X ∖ G, as states in G ∖ Y could not be an initial state, they would already have been in Y as a reachable state in G. As x^δ is not in the maximal controllable and coreachable set in this case, it does not matter if it is reachable, or initial. It will not be part of the good states and supervisor states. In the running example this could be demonstrated by the removal of the initial property from state p₄r₀.

4.3 Added marked property

In Algorithm 7 the atomic TSS algorithm is provided for the case that a state was given the marked property in the model delta from A to $A^{\prime }$.

In the first case the circumstance is considered that a non-good state is now marked. This means that some non-good states may become good and/or supervisor states because they are coreachable in the variant model. All states that were supervisor states and good states will remain so. So a fixpoint computation is instantiated where the supervisor states are already added as marked states and initial states, so this part of the states does not have to be found again in the reachability searches. In the running example we could consider the case that p₁r₁ was made a marked state. During the first iteration of the fixpoint computation it will be found as a good state, as it is marked. It will however be removed from the good states since it has an uncontrollable transition to a bad state. So for this specific example the supervisor and good states will remain the same from base to variant model.

If the state with added marked property is a good state, it was already coreachable, as well as all good states that can reach this state. So giving it a marked property is not going to change the coreachability. Thus the supervisor states and the good states remain the same. In the running example, this would be the case if for instance p₁r₀ was added to the set of marked states.

4.4 Removed marked property

Now the case is considered that a marked state in the base model, is not a marked state in the variant model. The atomic TSS algorithm for this case is given in Algorithm 8.

In the first case the removal of a marked state in G ∖ Y is considered. The supervisor states Y will remain the same, as x^δ is not reachable from such a state, the removal of its marked property does not influence their coreachability. Some good states might not be good states for the variant model, as they may not be coreachable anymore. Therefore a fixpoint computation is performed, with all supervisor states already added as initial states and marked states, so this part of the state space does not have to be searched anymore. In the running example we can consider removing the marked property from p₂r₁. Consequently, the supervisor for the variant model will remain the same, but p₂r₁ and p₃r₁ are not good states for the variant model as they are not coreachable anymore.

The second case considers the situation that the removed marked state is in Y. A new fixpoint computation is performed for the variant model, only the non-good states are not taken into account, as the removal of a marked state will not increase the maximal set of coreachable and controllable states. In the example we can consider removing the marked property of state p₂r₀. As a result, there will be no supervisor states in the variant model, $Y^{\prime }=\emptyset$, and only p₂r₁ and p₃r₁ remain in $G^{\prime }$.

The final case will occur when the marked property is removed from a non-good state. This does not influence the coreachability and controllability of the good states, as they must be coreachable for marked states in G. Also the reachable part of the good states remains the same. So the variant model has the same supervisor states and good states as the base model.

4.5 Added transition

Now we consider the case that only a single transition has been added to the base automaton A to create variant automaton $A^{\prime }$. So all elements in Δ are empty except →⁺ which only contains the transition (x_or,σ,x_tar). Algorithm 9 computes the supervisor and good states for the variant model according to the type of adaptation that is made.

The first case considers an added transition from a state in Y to a state in G ∖ Y. The target and origin state where already coreachable and controllable, so this is not influenced by the addition of the transition. However the target state is now reachable, which it wasn’t before. To find all good states that are now reachable, an FRS is performed to compute the variant supervisor states. The good states remain the same. In the running example we can consider the addition of a transition from p₀r₀ to p₃r₁. In that case, p₃r₁ and p₂r₁ would become supervisor states in the variant model in the addition to the states already in Y. The good states remain unchanged.

Next, the addition of an uncontrollable transition from a good state to a non-good state is considered. The target state was non-coreachable or non-controllable, so transitions to this state need to be disabled. Because an uncontrollable transition is added, it can not be disabled by the supervisor. This means that the origin state is not a good state anymore, and we wish to remove it for the variant model. The state is made non-coreachable by removing all outgoing transitions from it, and removing it from the set of marked states in case it was a marked state. The fixpoint computation is then performed on the state space spanned by the good states, with the origin state of the added transition as non-coreachable. In the running example this could be an added uncontrollable transition from p₂r₁ to p₂⊥. For that adaptation p₂r₁ and p₃r₁ would be removed from the good states to construct the variant good states, and the supervisor states remain the same.

In case the origin state is not a good state, adding the transition that is not a self-loop (x_or≠x_tar) might influence the coreachability of this and other non-good states. States that were supervisor states in the base model will remain so. Thus, a fixpoint computation is performed over the entire state set, where the supervisor states are added to the marked and initial states so that this part of the state space does not need to be searched to reduce computational effort. For the running example we can consider the case that a transition is added from p₄r₁ to p₂r₀, in that case the supervisor states will remain the same, and p₄r₁ is added to the good states to construct the variant good states.

In all other cases, the supervisor states and good states remain the same. For example the addition of a transition from-and-to a supervisor state, all states that are good states will remain coreachable and controllable, and states in G ∖ Y will remain non-reachable. In the example this could be a transition from p₂r₀ to p₀r₀. Another example is adding a self-loop to a non-good state not influencing its non-coreachability or non-controllability. In the running example this may be a transition from p₄r₁ to p₄r₁.

4.6 Removed transition

Here we consider the case that only a single transition has been removed from base automaton A to create variant automaton $A^{\prime }$. Algorithm 10 computes the supervisor states and good states for the variant model according to the state sets the origin and target state of this transition belong to, and the controllability of the transition.

Let us consider a removed transition, that is not a self-loop, for which x_or and x_tar both were in Y. This case is considered first in Algorithm 10. It is possible that due to the removal of this transition, x_or and other states in G might not be coreachable anymore. Also x_tar might not be reachable anymore. However, bad states and non-reachable states will remain as such. Therefore, a fixpoint computation is performed for the variant model, only for the states in G of the base model. As this synthesis is on a reduced state-set, it will require less effort to perform than a completely new synthesis on the variant model. In the running example this could be the removal of transition (p₀r₀,b,p₂r₀), which would lead to no supervisor states for the variant automaton. p₀r₀ would also be removed from the good state set to construct the good states $G^{\prime }$.

Next, we consider a removed transition from a state x_or in G ∖ Y to a state x_tar in G, that is not a self-loop. x_or, and other good states, might become non-coreachable after removal of this transition. However, as these states are not reachable from the supervisor states, these will remain the same for the variant model. To find the set of good states for the variant model, a fixpoint computation is performed over the good states, where the supervisor states are added to the marked and initial states so that this part of the state space is not searched. For the running example, removing transition (p₃r₁,c,p₂r₁) would fall under this case. As a result the supervisor states remain the same from the base to the variant model, but p₃r₁ is removed from the good states to construct the variant good states $G^{\prime }$.

As a third case in Algorithm 10, an uncontrollable transition is removed with origin and target state as not good states. It is possible that the origin state and other states were not good states due to the existence of this transition. We need to perform some additional fixpoint computation in order to find these states. However, we know that all good states that have been found already, will remain good states for the variant model. The same goes for supervisor states. Therefore, computeFixpoint is instantiated with the good states added as marked states, and the supervisor states added as initial states. In the running example the removal of transition (p₀r₁,b,p₂⊥) would fall under this case. In that circumstance, the supervisor states and good states would remain the same for the variant model as the base model.

Finally, for all other cases the supervisor states and good states remain the same between variant and base model. For example, we remove transition (x_or,σ,x_tar) from base model A, for which x_or ∈ X ∖ G and x_tar ∈ Y. We know that in A, the state x_or was coreachable, as the removed transition existed to a state in Y. As (coreachable state) x_or does not exist in the set of good states G, it must be non-controllable. We can reason that the removal of this transition is not going to make it controllable. Thus, Y and G of the base automaton remain the same for the variant automaton. This is also observed in Algorithm 10.

4.7 Other atomic adaptations

Some atomic adaptations were not discussed in the algorithms above. These atomic adaptations are: adding a state, removing a state, adding an event, and removing an event. When these model deltas occur as an atomic adaptation, they do not influence the supervisor states or good states. For example, an added state only influences the synthesis result if there are added transitions towards or from it. Or an event can only be removed, if there are no transitions that are labeled by that event. Otherwise the model delta is not an atomic adaptation, or it is not a valid model delta. Proofs for Lemma 5 are provided in Appendix Appendix.

Lemma 5

For an atomic adaptation that is an: added state, removed state, added event, or removed event, the supervisor states $Y^{\prime }$ of the variant model are equal to the supervisor states Y of the base model, and the good states $G^{\prime }$ of the variant model are equal to the good states G of the base model.

5 Transformational Supervisor Synthesis for any model delta

In this section we will not restrict the model delta to atomic cases anymore; any valid model delta of any size is allowed. A method that iterates over all atomic adaptations is discussed in Section 5.1. A method that groups these atomic adaptations together based on their required computation and processes them at the same time is shown in Section 5.2.

5.1 Iterative Transformational Supervisor Synthesis

In Fig. 9 a modified version of Fig. 8 is shown, which provides a visualization of the idea on which Iterative TSS (ITSS) is based. A non-atomic model delta describes the difference between the base and the variant model. This model delta is split into atomic adaptations, on which the atomic TSS algorithms can be applied, and the variant supervisor fixpoint is computed by iterating over these atomic adaptations.

Fig. 9

ITSS for non-atomic Δ

Algorithm 11 provides an ITSS algorithm, that iterates over the atomic adaptations in the model delta one-by-one. Each time an atomic adaptation is applied using the results of Section 4, and $Y^{\prime }$ and $G^{\prime }$ are computed accordingly. After an adaptation has been applied, the tuples $X_{0}^{\prime },\ X_{m}^{\prime },\ \longrightarrow ^{\prime }$ are updated, so that if we were to construct an intermediate automaton $A^{\prime }=(X^{\prime },{{\varSigma }}^{\prime },\longrightarrow ^{\prime },X_{0}^{\prime },X_{m}^{\prime })$, this automaton is up-to-date for the adaptations applied until that point. This intermediate automaton is then used in the input for the next atomic TSS algorithm. Before iterating over the atomic TSS algorithms, the added states and events are added to the base supervisor and automaton. After the iterations, the set of removed events is removed from the supervisor, as at this point no transitions with this event are left in the supervisor, following from the restrictions specified in Section 3. Because $A^{\prime }$ will not have transitions to-or-from the removed states, and the removed states are not initial or marked, the set of removed states will not be a part of $Y^{\prime }$ (or $G^{\prime }$) at this point of the algorithm. So they do not need to be removed from the supervisor. Algorithm 11 also outputs the variant automaton $A^{\prime }$ of which it produces the synthesis result.

Theorem 3 holds for Algorithm 11. It is similar to Theorem 2 for the atomic model adaptations, only modified to apply for a supervisor automaton S, rather than supervisor states Y. It also considers that the algorithm provides the correct variant automaton as output. The proof for Theorem 3 on Algorithm 11 can be found in Appendix Appendix.

Theorem 3

Given base automaton A, model delta Δ, synthesis result (Y,G) = computeFixpoint(A), and $(\hat {S},\hat {G},\hat {A})=\text {\texttt {ITSS}}(A,Y,G,{{\varDelta }}_{})$; then $\hat {S}=S^{\prime }$, $\hat {G}=G^{\prime }$, and $\hat {A}=A^{\prime }$, for $(S^{\prime },G'{})=\text {\texttt {SS}}(A^{\prime })$.

5.1.1 Order of applying atomic adaptations

There are some restrictions to the order in which the atomic adaptations can be applied during iterative TSS. Essentially, when an atomic adaptation is applied, this atomic adaptation needs to be a valid model delta. Let us consider the following model delta for the running example:

• X⁺ = {p₅r₀},

• Σ⁺ = {e},

• →⁺ = {(p₄r₀,e,p₅r₀)},

• $X^{-} = \emptyset , {{\varSigma }}^{-} = \emptyset , \longrightarrow ^{-} = \emptyset , X_{0}^{+} = \emptyset , X_{0}^{-} = \emptyset , X_{m}^{+} = \emptyset , X_{m}^{-} = \emptyset$.

This model delta represents an added transition with an added event (e) to an added state (p₅r₀) from an existing state (p₄r₀). The model delta can be split into three atomic parts. We observe that the added state and added event need to be added to the automaton first, before the added transition can be added. Otherwise, the transition goes to an undefined state, or uses an undefined event, which means the model delta is not valid.

Therefore, the added states and added events are added first. Now, any state with added or removed initial property and any state with added or removed marked property will exist in this intermediate automaton. Also all added and removed transitions will go between defined states by defined events. Thus these atomic adaptations can be applied in any order. Once these adaptations have been applied, there will be no more transitions towards removed states, or transitions over removed events. Then finally the removed states and removed events can be removed, resulting in the final variant automaton.

The functioning of the atomic TSS algorithms is based on the assumption that the atomic adaptation is a valid model delta by the definitions in Section 3. To support the correct functioning of Algorithm 11, proof that each atomic adaptation that is applied is a valid model delta is given in Appendix Appendix.

The authors note that even though the atomic adaptations of added/removed initial property, added/removed marked property, and added/removed transition can be applied in any order to come up with the same supervisor, the order in which they are applied may impact the computational efficiency. We do not optimize this order here, as the optimal order is likely highly dependent on the particular model and model delta. Therefore the adaptations are applied in the order shown in Algorithm 11, where the atomic TSS algorithms appear in the order in which they are introduced in Section 4.

5.2 Grouped Transformational Supervisor Synthesis

We observe that Algorithm 11 might not be very efficient when many atomic adaptations need to be considered. The main issue is that the SS and FRS algorithms are repeatedly called for input sets that are considerably similar to each other. This may notably occur when the plant description is given by a set of automata {P₁,P₂,...,P_n}. For our synthesis purpose, we take the synchronous product A = P₁||P₂||...||P_n, as mentioned in Section 2. If one of the automata P_i is adapted in an atomic manner, this might result in the model delta Δ to contain many atomic adaptations, due to synchronicity. A lot of these atomic adaptations in the synchronous system will be of the same type, e.g., an added transition in P_i can induce many added transitions in A. Therefore, we want to consider some adaptations at the same time as a group, rather than applying them one-by-one.

We partition the model delta into two disjoint subsets; ${{\varDelta }}^{\times } \uplus {{\varDelta }}^{\circ } = {{\varDelta }}_{}$, where ⊎ denotes the disjoint union of the sets that are in the same field of both tuples. Δ^× contains all atomic adaptations that, when applying the respective atomic TSS algorithm, require the SS or FRS algorithm. Δ^∘ contains all other possible atomic adaptations outside Δ^×, these require no reachability searches. As a result of the construction of the atomic TSS algorithms, all atomic adaptations in Δ^∘ fit under the default cases of these algorithms, and all adaptations in Δ^× match one of the (non-default) case statements in these algorithms. Formally, we can compute Δ^× = (X^+,×, X^−,×, Σ^+,×, Σ^−,×, →^+,×, →^−,×, ${X_{0}^{+,\times },}$ ${X_{0}^{-,\times },}$ ${X_{m}^{+,\times },}$ ${X_{m}^{-,\times }})$ for a model delta Δ= (X⁺, X⁻, Σ⁺, Σ⁻, →⁺, →⁻, ${X_{0}^{+},}$ ${X_{0}^{-},}$ ${X_{m}^{+},}$ ${X_{m}^{-}})$ as follows:

• X^+,× = ∅, X^−,× = ∅, Σ^+,× = ∅, Σ^−,× = ∅

• $\longrightarrow ^{+,\times } = \{(x_{\mathit {or}},\sigma ,x_{\mathit {tar}}) | (x_{\mathit {or}} \in Y \wedge x_{\mathit {tar}} \in G\setminus Y)\vee (x_{\mathit {or}}\in G \wedge x_{\mathit {tar}}\in X\setminus G{} \wedge \sigma \in {{\varSigma }}_{u})\vee (x_{\mathit {or}}\in X\setminus G{} \wedge x_{\mathit {or}} \neq x_{\mathit {tar}})\}$

• $\longrightarrow ^{-,\times } = \{(x_{\mathit {or}},\sigma ,x_{\mathit {tar}}) | (x_{\mathit {or}} \in Y \wedge x_{\mathit {tar}} \in Y \wedge x_{\mathit {or}} \neq x_{\mathit {tar}})\vee (x_{\mathit {or}}\in G\setminus Y \wedge x_{\mathit {tar}}\in G{} \wedge x_{\mathit {or}} \neq x_{\mathit {tar}})\vee (x_{\mathit {or}}\in X\setminus G{} \wedge x_{\mathit {tar}}\in X\setminus G{} \wedge \sigma \in {{\varSigma }}_{u} \wedge x_{\mathit {or}} \neq x_{\mathit {tar}}) \}$

• $X^{+,\times }_{0} = X_{0}^{+} \cap (G\setminus Y)$

• $X^{-,\times }_{0} = X_{0}^{-} \cap Y$

• $X^{+,\times }_{m} = X_{m}^{+} \cap (X\setminus G)$

• $X^{-,\times }_{m} = X_{m}^{-} \cap G$

Δ^∘ is then constructed by all atomic adaptations in Δ outside Δ^×.

When performing Grouped TSS (GTSS), we first want to apply all atomic adaptations in Δ^∘, as we can observe in the atomic TSS algorithms that no reachability searches need to be performed, and the supervisor states and good states remain unchanged. After all atomic adaptations in Δ^∘ have been applied, we find the first atomic adaptation in Δ^× for which, if we were to apply ITSS with model delta Δ^×, one of the case conditions in Algorithms 5-10 holds. Instead of performing the corresponding case statements on only this atomic adaptation, within the case operation we first construct a set ${{\varDelta }}^{\sim }$, that contains all atomic adaptations in Δ^× for which that same case condition in the same atomic TSS algorithm holds. So for example, if we have Δ^× with nonempty set $X_{0}^{+,\times } \cap (G\setminus Y)$, then $X_{0}^{+,\times } \cap (G\setminus Y)$ is a set ${{\varDelta }}^{\sim }$. In addition to just atomic adaptations, the rationale applied in Algorithms 5-10 still holds for sets ${{\varDelta }}^{\sim }$. So, we take set ${{\varDelta }}^{\sim }$, and apply the respective case operation on this set, rather than doing this for each atomic adaptation one-by-one. This might influence the supervisor states and good states. Because the partitioning in Δ^× and Δ^∘ of Δ depends on those state sets, Δ^∘ might be nonempty if we recompute it for the atomic adaptations in Δ that have not been applied yet. Thus, we once more apply adaptations in Δ^∘, and reiterate until all adaptations have been applied.

Figure 10 visualizes the grouped TSS method. First, all atomic adaptations are applied that require no reachability search. Then, a set of atomic adaptations ${{\varDelta }}^{\sim }$ is applied at once. This repetition continues until the entire model delta is applied. At this point, the fixpoint for the variant supervisor has been found.

Fig. 10

GTSS for non-atomic Δ

Algorithm 12 functions as described above. The added events and added states are added in line 1. After these have been applied, they are removed from the model delta. As stated in Section 4.7, these adaptations do not influence the supervisor states and good states, seen in line 3. The model delta is partitioned in Δ^× and Δ^∘ as specified earlier in this section. All adaptations in Δ^∘ are applied in line 6, and subsequently removed from the model delta in line 7. Note that $Y^{\prime }$ and $G^{\prime }$ remain unchanged. In line 8 a set of atomic adaptations ${{\varDelta }}^{\sim }$ is applied; $Y^{\prime }$ and $G^{\prime }$ are calculated accordingly, and $\longrightarrow ^{\prime }$, $X_{0}^{\prime }$, and $X_{m}^{\prime }$ are consequently updated. The calculation of $Y^{\prime }$ and $G^{\prime }$ is done by using slightly modified versions of Algorithms 5-10 that accept sets of atomic adaptations. To avoid redundancy, we only provide the modified version of Algorithm 5 in the example below. The other atomic TSS algorithms are converted in the same manner. The set of atomic adaptations that has been applied, is removed from Δ in line 9. Now Δ^× and Δ^∘ are calculated once again, because the partitioning of the model delta is dependent on $Y^{\prime }$ and $G^{\prime }$ which are now modified. The steps are repeated until all atomic adaptations to $\longrightarrow ^{\prime }$, $X_{0}^{\prime }$, and $X_{m}^{\prime }$ have been applied. Finally, the supervisor automaton for the variant model and the variant automaton are constructed in lines 11 and 12 respectively.

Theorem 4 is proven for Algorithm 12 in Appendix Appendix. In Appendix ?? also the proof is given that Algorithm 12 respects the order of applying adaptations discussed in Section 5.1.

Theorem 4

Given base automaton A, model delta Δ, synthesis result (Y,G) = computeFixpoint(A), and $(\hat {S},\hat {G},\hat {A})=$GTSS(A,Y,G,Δ); then $\hat {S}=S^{\prime }$, $\hat {G}=G^{\prime }$, and $\hat {A}=A^{\prime }$, for $(S^{\prime },G'{})=$SS$(A^{\prime })$.

5.2.1 Example

Let us consider the case that Δ contains three atomic adaptations, all are states with added initial property; $X_{0}^{+} = \{x^{\delta ,1},x^{\delta ,2},x^{\delta ,3}\}$, with x^δ,1 ∈ G ∖ Y, x^δ,2 ∈ G ∖ Y, x^δ,3 ∈ Y. In our running example this could be states p₃r₀, p₃r₁, and p₂r₀ respectively. x^δ,1 and x^δ,2 require FRS, seen in line 3 of Algorithm 5, so they are in Δ^×. x^δ,3 triggers the default case in Algorithm 5, and thus it is in Δ^∘. Therefore, x^δ,3 is applied first, resulting in:

• $X_{0}^{\prime } = X_{0}^{\prime } \cup \{x^{\delta ,3}\}$

• $X_{0}^{+} = X_{0}^{+} \setminus \{x^{\delta ,3}\}$

Note that $Y^{\prime }$ and $G^{\prime }$ are not influenced as x^δ,3 is in Δ^∘.

Now all adaptations in Δ^∘ have been applied. $X_{0}^{+} = \{x^{\delta ,1},x^{\delta ,2}\}$ remains in the model delta. As x^δ,2 and x^δ,3 are both of the same case (line 2 of Algorithm 5), they are in a set ${{\varDelta }}^{\sim }=\lbrace x^{\delta ,1}, x^{\delta ,2}\rbrace$. Consequently, these atomic adaptations will simultaneously be applied. $Y^{\prime }$ and $G^{\prime }$ are calculated in a modified version of Algorithm 5, given in Algorithm 13. $X_{0}^{\prime }$ and $X_{0}^{+}$ are updated as follows:

• $X_{0}^{\prime } = X_{0}^{\prime } \cup {{\varDelta }}^{\sim }$

• $X_{0}^{+} = X_{0}^{+} \setminus {{\varDelta }}^{\sim }$

After applying these adaptations, all atomic model adaptations in the model have been applied and the model delta is empty, and $Y^{\prime }$ and $G^{\prime }$ are the fixpoint result for the variant automaton $A^{\prime }$. For the running example, the good states would remain the same, $G^{\prime }=G$, and $Y^{\prime }$ would be {p₀r₀,p₂r₀,p₃r₀,p₃r₁,p₂r₁}.

6 Experiments

As stated before, we can deal with any valid base automaton and model delta, so the TSS algorithm will always find a supervisor for the variant model. However, there are no guarantees that by applying TSS, we will find the supervisor more efficiently relative to simply performing a completely new synthesis. Therefore, we perform some experiments to investigate the potential reduction in computational effort by applying TSS.

For the experiments, a proof-of-concept implementation of the above synthesis algorithms and models of the case studies we describe below have been made in Matlab.¹

Before discussing case studies, we provide some practical notes in Section 6.1. In Section 6.2 we consider the Transfer Line model as an academic case study, and in Section 6.3 we consider a Lithography Machine Wafer Logistics controller as an industrial case study.

6.1 Practical notes

A proof-of-concept Matlab implementation of the above algorithms has been made. One modification from Thuijsman and Reniers (2020) to this paper, is that now a linear complexity reachability search algorithm is used instead of quadratic. This is to enable a more realistic effort comparison between SS and TSS since linear search algorithms are more widely used than quadratic. In Thuijsman and Reniers (2020), a counter in the reachability search algorithms was introduced to express and compare the time effort of performing synthesis. After implementing the new reachability search algorithms, it was found that the previously used metric was not representative anymore of the time effort of performing synthesis. Experiments were performed with counters at several locations in the code, however none of these counters gave a proper representation of the time effort. Therefore, wall-clock time is used here to represent the time effort of performing synthesis. In order to enable fair comparisons between running times, obvious inefficient parts of the algorithm were improved. Still, the authors note that by using wall clock time instead of a counter makes the results more dependent on the implementation. The experiments were performed on an HP ZBook Studio G4 laptop, using an Intel i7 processor clocked at 2.8 GHz. Regarding memory, Matlab used around 1 GB of memory, regardless of the model size. Filesizes to store the automata and model deltas ranged from a few KB to a few MB.

Each synthesis algorithm requires a monolithic automaton as input, and the transformational synthesis algorithms require a model delta to the variant automaton. In practice, these inputs may not be readily available. E.g., the monolithic automaton A needs to be constructed from a component-wise specification, as discussed in Section 2. This is also the case for the conducted experiments. The inputs are computed in preparation of the experiments. We assume that for the transformational method, the input automaton A is maintained for the next iteration. For each transformational synthesis, $A^{\prime }$ is constructed beforehand in order to compute the model delta. Note that $A^{\prime }$ also needs to be constructed for the baseline case of performing a completely new synthesis. Computing the model delta is done by simple matrix subtractions and requires negligible computational effort. The preparatory computations are not included in the computational effort measurements, because this matches the experiments to the monolithic level discussed in the theoretical part and because computing the synchronous composition is required for all methods.

The construction of A can be done by computing the complete synchronous composition as shown in Eq. 1. Practically however, often only the reachable part of A is constructed. Note that the computed supervisor is the same, as it only contains reachable states. The good state set G is influenced by only using the reachable part of A. Even when all states in X are reachable, it is still beneficial to store set G next to Y. When states are removed from G during synthesis, not all states in G may be reachable anymore through states in G. The model delta may be impacted by considering only the reachable parts of the automata or not. Also the computational effort of performing transformational or non-transformational supervisor synthesis may be impacted. Note that the transformational synthesis method works for both cases, as it allows for any pair of automata A and $A^{\prime }$, independent of how they are constructed. We consider both options in the case studies below.

6.2 Transfer Line

We first consider the Transfer Line model from Wonham and Cai (2019) as an academic case study. In this model, products are being processed by two machines. Machine M1 takes products from the environment, and processes them. After processing, M1 places the product in buffer B1, which can hold up to three products. Machine M2 takes products from B1, processes them, and places them in buffer B2, which can hold only one product. Test unit TU takes products from B2, and tests them. If the product is accepted, it is released from the system. If the product is rejected, it goes back to B1. M1, M2, and TU start by a controllable event, and terminate by an uncontrollable event. Same as in Wonham and Cai (2019), M1, M2, and TU are modeled by plant automata and B1 and B2 by requirement automata. These automata are shown in Fig. 11. The synchronous product over all automata is taken. For plantification, a single sink state is added to this synchronous product, to which all uncontrollable transitions are created whenever one of the requirement automata blocks an uncontrollable event of the plant. The resulting base automaton TL has 65 states and 200 transitions. Supervisor synthesis (Algorithm 1) for this base automaton requires 1.4 milliseconds, which is the mean runtime of 100 executions of SS.

Fig. 11

Transfer Line automata; (a), (b), and (c) are plant automata, (d) and (e) are requirement automata

The following five variant automata, $\mathit {TL}^{\prime }_{1}$ to $\mathit {TL}^{\prime }_{5}$, have been generated by making adaptations to TL.

• $\mathit {TL}^{\prime }_{1}$: Reduced capacity of B1 to two products; state x₃ of automaton B1 removed, and transitions (x₂,2,x₃), (x₂,8,x₃), (x₃,3,x₂) removed.

• $\mathit {TL}^{\prime }_{2}$: Increased capacity of B2 to two products; added a state x₂ and transitions (x₁,4,x₂), (x₂,5,x₁) to B2.

• $\mathit {TL}^{\prime }_{3}$: B1 initially holds one product instead of zero; removed initial property of state x₀, and added initial property to state x₁ in automaton B1.

• $\mathit {TL}^{\prime }_{4}$: TU may send the product to B2 upon completion; added uncontrollable event 9, added transition (x₁,9,x₂) to TU, and added transition (x₀,9,x₁) to B2.

• $\mathit {TL}^{\prime }_{5}$: Capacity of B1 and B2 is two products each; removed state x₃ and transitions (x₂,2,x₃), (x₂,8,x₃), (x₃,3,x₂) from B1, state x₂ and transitions (x₁,4,x₂), (x₂,5,x₁) are added to B2.

As the TSS methods are on a monolithic state space, these adaptations for the individual automata are converted to adaptations on the synchronous state space for the experiments, as discussed in Section 6.1. For the base model and each variant model, all states constructed during the synchronous composition (1) are reachable. Therefore, for these results it does not matter if A is completely constructed as in Eq. 1, or only the reachable part. The experiment cases we presented are the same as presented in Thuijsman and Reniers (2020), however the experiments are executed differently as pointed out in Section 6.1.

For each of the variant automata, the number of states and transitions, as well as the sizes of the nonempty sets in the model delta, are given in Table 1. One might expect that for constructing $\mathit {TL}^{\prime }_{1}$ only states and transitions would be removed. However, it can be observed that some transitions have been added. These are new transitions towards the sink state, as the buffer now may overflow from different states. For each variant model, a supervisor has been synthesized three times. First, doing a completely new synthesis by applying SS given in Algorithm 1, the second and third by using the synthesis result of the base automaton and applying ITSS (Algorithm 11), and GTSS (Algorithm 12) respectively. For each model, the three synthesized supervisors have the exact same automaton specification. For each of the syntheses, the runtime is shown in milliseconds in Table 1. This is the mean over 100 runs for each synthesis. The Coefficient of Variation (CV), calculated by dividing the sample standard deviation over the mean, is shown in between brackets underneath each runtime value as a percentage. Because this example is small, the runtimes are low. Therefore slight absolute variations in runtime result in a high relative variation. The rightmost column shows the percentage change in runtime of using GTSS compared to SS. A positive value indicates an increase in computational effort, and a negative value indicates a reduction. Note that the efficiency of the TSS algorithms will be influenced by the order in which the adaptations are applied, this has not been optimized for the experiments as this would entail a complete new study.

Table 1 Experimental results of performing SS, ITSS, and GTSS on five variant models of the Transfer Line model

We observe that in some cases applying ITSS requires considerably more runtime than applying SS. This was already addressed in Section 5, and led to the introduction of the GTSS algorithm. We observe that for this use case, for most variant models GTSS requires considerably less runtime than ITSS, but still requires more runtime than SS in most cases. The aim of GTSS is to use smaller synthesis calls and reachability searches by using the model delta and previous synthesis result. To do so, GTSS prepares these smaller synthesis calls and reachability searches by operations such as iterating over the model delta and evaluating the switch case statements. Because the model is very small, relatively speaking GTSS requires a lot of time to do the preparation steps, and little time performing the smaller synthesis calls and reachability searches. Therefore GTSS performs poorly compared to SS, that can just perform synthesis directly to the small model. It is expected that for a larger system, GTSS spends relatively less time on the preparation steps, and more on the smaller synthesis calls and reachability searches. Therefore GTSS could be more competitive to SS for these larger systems, since SS will require more runtime as well for the larger systems. We will study a larger system next, in Section 6.3. From a user perspective the runtime differences for the Transfer Line case would be insignificant.

6.3 Lithography Machine Wafer Logistics

Next we present an industrial case study. This case study is performed using models from ASML. ASML is the world-leading manufacturer of lithography machines, which are used in the semiconductor industry to produce integrated circuits. These circuits are printed on silicon wafers. The movement of these wafers through the machine is called the Wafer Logistics, which is studied in van der Sanden et al. (2015) and (van der Schriek 2018). The controller of the Wafer Logistics is constructed using Analytical Software Design (ASD) ((Broadfoot and Hopcroft 2003)). van der Schriek (2018) presents a study on how these ASD models of the components of the Wafer Logistics controller evolve over time. In this study equivalent automata models are constructed in CIF ((van Beek et al. 2014), CIF is part of the Eclipse Supervisory Control Engineering Toolkit®), that are suitable for supervisory controller synthesis. These automata models are constructed for the variation points that the ASD models evolved to over a number of years. We use these automata models here, to investigate the efficiency of TSS in this industrial setting.

Component B of (van der Schriek 2018) is selected to perform the experiments on, based on its large but manageable state space size, the number of variation points, and the variety within the model deltas. The first 11 variation points of this model are taken, to investigate 10 adaptations. Opposed to the Transfer Line experiment, where each variant model was an adaptation of the same base model, we now consider incremental adaptations. So we start with the evolution from B1 to B2, then from B2 to B3, from B3 to B4, and so on. To provide an indication of the model size, B1 contains 5 plant automata, that respectively have:

• 1. 2 states and 2 transitions,

• 2. 2 states and 1 transition,

• 3. 2 states and 3 transitions,

• 4. 15 states and 72 transitions,

• 5. 16 states and 128 transitions.

Model B1 also contains 4 requirement automata, that respectively have:

• 1. 2 states and 2 transitions,

• 2. 2 states and 2 transitions,

• 3. 3 states and 5 transitions,

• 4. 3 states and 5 transitions.

Additionally 3 state transition exclusion invariant requirements (Markovski et al. 2010) are specified. After computing the synchronous composition (1), and adding a sink state for plantification, B1 has 69121 states and 1038228 transitions. Performing SS (Algorithm 1) requires 46.2 seconds, which is the mean over 20 executions of SS.

Unlike the Transfer Line model, for the models of Component B not all states are reachable when automaton A is constructed by Eq. 1. We perform two studies, in Section 6.3.1 we consider the case that the complete automaton is used as an input to the synthesis algorithms and in Section 6.3.2 we consider that only the reachable part of the automaton is used as input.

6.3.1 Complete state space

In this section we perform synthesis on the complete state space that is constructed by performing synchronous composition on the Component B Wafer Logistics model. The experimental results are presented in Table 2. ITSS has not been performed, as its inefficiency compared to GTSS has been discussed in Section 5.2, and shown in the Transfer Line experiments. Note that the runtime is now displayed in seconds instead of milliseconds. Each runtime value is the mean over 20 syntheses. Because of the higher absolute runtimes compared to the Transfer Line use case, the CV is lower in these experiments. Compared to the Transfer Line experiment, we observe that the number of states for Component B increased by three orders of magnitude, for the number of transitions it is four orders of magnitude. Due to this increase in model size, the required runtime has also increased by four orders of magnitude. We observe that for all evolutions in this case study, applying GTSS is more efficient than applying SS to compute the supervisor for the variant model. The efficiency gain ranges from 9 to 29%, and is 20% on average.

Table 2 Experimental results of performing SS and GTSS for evolution of the complete Component B Wafer Logistics model

6.3.2 Reachable state space

In this section we perform synthesis using only the reachable part of synchronous composition of the Component B Wafer Logistics model. The complete state space of model B1 consists of 69121 states and 1038228 transitions. The reachable part of this automaton has 59185 states and 888780 transitions. Note that also the model delta sizes are influenced by only considering the reachable part of the base and variant model automata. The results are shown in Table 3. Each runtime value is the mean over 20 syntheses. Once more, for all evolutions in this experiment applying GTSS is more efficient than applying SS to compute the supervisor for the variant model. Compared to the experiment on the complete state space, discussed in Section 6.3.1, the absolute computational effort to perform synthesis is reduced for both SS and GTSS. Furthermore, the relative efficiency of using GTSS compared to SS was also improved. The efficiency gain ranges from 17 to 36%, and is 27% on average. The authors note that even though in this case study the transformational synthesis method works better when only the reachable states are considered, this may not be so for other models.

Table 3 Experimental results of performing SS and GTSS for evolution of the reachable part of the Component B Wafer Logistics model

7 Conclusions

Supervisory controller synthesis is a means to compute correct-by-construction controllers for discrete event systems. As these systems evolve over time, we want to be able to efficiently generate a supervisor each time the system is adapted. We consider the case that a supervisor has been synthesized for a given base model, after which this base model is adapted to some variant model. Model deltas are used to describe the difference between the base and the variant model. A notion of atomic adaptations is introduced, where the model delta can be described by a single, indivisible change in the automaton specification. For these atomic model adaptations, algorithms are provided to compute the supervisor for the variant model in a transformational manner. The atomic model adaptations can be iterated over to transformationally compute a supervisor for any model delta that contains a number of atomic model adaptations. It is discussed why, and shown in experiments that, only purely iterating over these atomic adaptations is not efficient. Therefore a method is presented where groups of adaptations are considered. By means of both an academic and an industrial case study, we show that in some, but not all, cases the method of GTSS can more efficiently compute the variant model supervisor than SS. The best results for GTSS were found for the larger, industrial, use case.

The methods we presented are based on monolithic synthesis of a fully enumerated state space. To tackle industrial-sized systems, commonly modular methods that split the synthesis problem into smaller sub-problems are applied. It would be interesting to see how the transformational synthesis method we present here translates to those methods. The performance of transformational synthesis could further be improved by, for example, evaluating the adaptations in a smart order, or by imposing restrictions on the model delta. It might also be possible to obtain better results by relaxing the problem constraints, for example not requiring full equality between the results of TSS and SS, but only requiring them to be bisimilar. At the moment we have no way to tell if TSS will be more efficient than simply performing a new synthesis. Optionally, one could run both algorithms in parallel, and stop as soon as on of them is finished. It might also be valuable to have a method that predicts which algorithm will be more efficient. Moreover, perhaps it is possible to have a TSS algorithm that is guaranteed to require less effort than a new synthesis.

Appendices

Appendix: A

In this appendix, we provide the proofs of Theorem 2 for the atomic TSS algorithms provided in this paper. Subsequently the proofs for Lemma 5 are provided for an added state, removed state, added event, and removed event.

1.1 A.1 Added initial property (Algorithm 5)

We denote automaton A = (X,Σ,→,X₀,X_m), $A^{\prime }=(X,{{\varSigma }},\longrightarrow ,X_{0}\cup \{x^{\delta }\},X_{m})$. Additionally, we denote (Y,G) = computeFixpoint(A), $(Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(A^{\prime })$, and $(\hat {Y},\hat {G})=\text {\texttt {TSSAIP}}(A,Y,G,x^{\delta })$.

• For any $(X_{0}, X^{\prime }_{0})\subseteq X\times X$ it holds that $G=G^{\prime }$ when computing $(Y,G)=\text {\texttt {computeFixpoint}}(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}),\ (Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(X,{{\varSigma }},\longrightarrow ,X^{\prime }_{0},X_{m})$, as the initial state does not influence the computation of G. We also observe that for all switchcases in Algorithm 5, $\hat {G}=G$ is computed. It follows that $\hat {G}=G^{\prime }$.

• $Y^{\prime }$ are all reachable states in $G^{\prime }$. Since we have proven that $\hat {G}=G^{\prime }$, it suffices to prove that $\hat {Y}$ are all reachable states in $\hat {G}$ to show that $\hat {Y}=Y^{\prime }$.

  • In case that x^δ is in Y, the state x^δ will already have been found in the FRS (line 8 Algorithm 2), so in this case $\hat {Y}=Y=Y^{\prime }$, which is also found by Algorithm 5.

  • In case that x^δ is in X ∖ G, it will also be in $X\setminus G^{\prime }$. As x^δ is not in $G^{\prime }$, the change of initial property can not influence the reachable part of $G^{\prime }$, so Y = $Y^{\prime }$. This is also found in Algorithm 5. So $\hat {Y}=Y=Y^{\prime }$.

  • In case that x^δ is in G ∖ Y, for the supervisor synthesis of $A^{\prime }$, the reachable part is determined by $Y=\text {\texttt {FRS}}(G^{\prime },{{\varSigma }},\longrightarrow ,X_{0}^{\prime })$, where we know that $G^{\prime }=G$ and $X_{0}^{\prime }=X_{0}\cup \{x^{\delta }\}$. $\hat {Y}$ is calculated by FRS(G,Σ,→,Y ∪{x^δ}). The result of these FRSs is the same, as we know that all states in Y are reachable in G from X₀ from the base synthesis. So $\hat {Y}=Y^{\prime }$.

We can conclude that $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$ for any x^δ ∈ X ∖ X₀, so Theorem 2 holds for Algorithm 5.$\square$

1.2 A.2 Removed initial property (Algorithm 6)

Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow ,X_{0}\setminus \{x^{\delta }\},X_{m})$. Additionally, we denote (Y,G) = computeFixpoint(A), $(Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(A^{\prime })$, and $(\hat {Y},\hat {G})=\text {\texttt {TSSRIP}}(A,Y,G,x^{\delta })$.

• For any $(X_{0},\! X^{\prime }_{0})\!\subseteq \! \!X\!\times \! X\!$ it holds that $G = \!G^{\prime }\!$ when computing (Y,G) = $\text {\texttt {computeFixpoint}}(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}),\ (Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}$ $(X,{{\varSigma }},\longrightarrow ,X^{\prime }_{0},X_{m})$, as the initial state does not influence the computation of G. We also observe that for all switchcases in Algorithm 6, $\hat {G}=G$ is computed. It follows that $\hat {G}=G^{\prime }$.

• $Y^{\prime }$ are all reachable states in $G^{\prime }$. Since we have proven that $\hat {G}=G^{\prime }$, it suffices to prove that $\hat {Y}$ are all reachable states in $\hat {G}$ to show that $\hat {Y}=Y^{\prime }$.

  • In case that x^δ is not in Y, the state x^δ was not in the reachable part of G. Thus, the set of reachable states in G is not influenced by x^δ being initial. So in this case $\hat {Y}=Y=Y^{\prime }$, which is also found by Algorithm 6.

  • In case that x^δ is in Y, for the supervisor synthesis of $A^{\prime }$, the reachable part is determined by $Y=\text {\texttt {FRS}}(G^{\prime },{{\varSigma }},\longrightarrow ,X_{0}^{\prime })$, where we know that $G^{\prime }=G$ and $X_{0}^{\prime }=X_{0}\setminus \{x^{\delta }\}$. $\hat {Y}$ is calculated by FRS(Y,Σ,→,X₀ ∖{x^δ}). The result of these FRSs is the same, as we know that all states in G ∖ Y are not reachable from the base synthesis. So $\hat {Y}=Y^{\prime }$.

We can conclude that $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$ for any x^δ ∈ X₀, so Theorem 2 holds for Algorithm 6.$\square$

1.3 A.3 Added marked property (Algorithm 7)

Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}\cup \{x^{\delta }\})$. Additionally, we denote (Y,G) = computeFixpoint(A), $(Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(A^{\prime })$, and $(\hat {Y},\hat {G})=\text {\texttt {TSSAMP}}(A,Y,G,x^{\delta })$.

• In case that x^δ is in G, it was already in the maximal coreachable and controllable set of states. It will remain so after making it marked, so $G^{\prime }=G$. We observe $\hat {G} = G$ is computed in Algorithm 7, so $\hat {G}=G^{\prime }$. As the initial states did not change, and $G^{\prime }=G$, the reachable part Y will remain the same. So $\hat {Y}=Y=Y^{\prime }$.

• In case that x^δ is in X ∖ G, states in Y remain reachable, coreachable, and controllable. So, computeFixpoint((X,Σ,→,Y ∪X₀,Y ∪X_m∪{x^δ})) = computeFixpoint((X,Σ,→,X₀,X_m∪{x^δ})).

We can conclude that $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$ for any x^δ ∈ X ∖ X_m, so Theorem 2 holds for Algorithm 7.$\square$

1.4 A.4 Removed marked property (Algorithm 8)

Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}\setminus \{x^{\delta }\})$. Additionally, we denote (Y,G) = computeFixpoint(A), $(Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(A^{\prime })$, and $(\hat {Y},\hat {G})=\text {\texttt {TSSRMP}}(A,Y,G,x^{\delta })$.

• We know that x^δ ∈ X_m (model delta is valid). And all states in X_m are coreachable by definition. G was the maximal controllable coreachable set to X_m. After removing x^δ as a marked state; $G^{\prime }\subseteq G$ and $Y^{\prime } \subseteq Y$. So $X\setminus G \subseteq X\setminus G^{\prime }$. Therefore computeFixpoint((G,Σ,→,X₀,X_m∖{x^δ})) = computeFixpoint((X,Σ,→,X₀,X_m∖{x^δ})). Thus, in case x^δ ∈ Y, then $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$.

• In case that x^δ is in G ∖ Y, all states in Y are coreachable and controllable for X_m ∖{x^δ}, as x^δ is not reachable from Y, otherwise it would be contained in Y. Therefore computeFixpoint((G,Σ,→,X₀, (Y ∪X_m)∖{x^δ})) = computeFixpoint((X,Σ,→,X₀,X_m∖{x^δ})). So in case x^δ ∈ G ∖ Y, $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$.

• In case that x^δ∉G, x^δ must have an uncontrollable path to a non-coreachable state, as it is coreachable as a marked state, it would have been in G if it were controllable. States that uncontrollably reach x^δ were removed from G in the base synthesis. G remains the same, and consequently Y will also remain the same, so $\hat {Y}=Y=Y^{\prime }$ and $\hat {G}=G=G^{\prime }$, which is also found by Algorithm 8.

We can conclude that $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$ for any x^δ ∈ X_m, so Theorem 2 holds for Algorithm 8.$\square$

1.5 A.5 Added transition (Algorithm 9)

Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow \!\cup \lbrace (x_{\mathit {or}},\sigma ,x_{\mathit {tar}}) \rbrace ,X_{0},X_{m})$. Additionally, we denote (Y,G) = computeFixpoint(A), $(Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(A^{\prime })$, and $(\hat {Y},\hat {G})=\text {\texttt {TSSAT}}(A,Y,G,(x_{\mathit {or}},\sigma ,x_{\mathit {tar}}))$.

• In case x_or ∈ Y and x_tar ∈ Y, all states in Y remain reachable, coreachable, reachable, and controllable. Also the (co-)reachability and controllability of the states in X ∖ Y remains the same. So $\hat {Y}=Y=Y^{\prime }$ and $\hat {G}=G=G^{\prime }$.

• In case x_or ∈ Y and x_tar ∈ G ∖ Y, the coreachability an controllability of all states remains unchanged. So $\hat {G}=G=G^{\prime }$. All states in Y remain reachable, so FRS(G,Σ,→ ∪{(x_or,σ,x_tar)},Y ) = FRS(G,Σ,→ ∪{(x_or,σ,x_tar)},X₀).

• In case x_or in X ∖ G and x_or≠x_tar, then all states in Y remain (co-)reachable and controllable. Therefore, computeFixpoint((X,Σ,→ ∪{(x_or,σ,x_tar)},Y ∪X₀,Y ∪X_m)) = computeFixpoint((X,Σ,→ ∪{(x_or,σ,x_tar)},X₀,X_m)).

• In case x_or ∈ G and x_tar ∈ X ∖ G. The states in X ∖ G remain non-coreachable or non-controllable. In case that

  • σ ∈Σ_c. The supervisor can disable the added transition. So $\hat {Y}=Y=Y^{\prime }$ and $\hat {G}=G=G^{\prime }$.

  • σ ∈Σ_u. The supervisor can not disable the added transition. Thus x_or is non-controll-able. Because also states in X ∖ G remain non-coreachable or non-controllable, computeFixpoint((G,Σ,→ ∩((G∖{x_or})×Σ×G),X₀∖{x_or},X_m∖{x_or})) = computeFixpoint((X,Σ,→ ∪{(x_or,σ,x_tar)},X₀,X_m)).

• In case x_or ∈ G ∖ Y and x_tar ∈ G the coreachability and controllability of all states does not change; $\hat {G}=G=G^{\prime }$. x_or is non-reachable, so the added transition does not change the reachability of any state. Thus, $\hat {G}=G=G^{\prime }$.

• In case x_or = x_tar, the (co-)reachability and controllability of any state does not change. So $\hat {G}=G=G^{\prime }$ and $\hat {Y}=Y=Y^{\prime }$.

We can conclude that $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$ for any (x_or,σ,x_tar) ∈ (X ×Σ× X) ∖→, so Theorem 2 holds for Algorithm 9.$\square$

1.6 A.6 Removed transition (Algorithm 10)

Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow \setminus \lbrace (x_{\mathit {or}},\sigma ,x_{\mathit {tar}}) \rbrace ,X_{0},X_{m})$. Additionally, we denote (Y,G) = computeFixpoint(A), $(Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(A^{\prime })$, and $(\hat {Y},\hat {G})=\text {\texttt {TSSRT}}(A,Y,G,(x_{\mathit {or}},\sigma ,x_{\mathit {tar}}))$.

• In case x_or ∈ Y, x_tar ∈ Y, and x_or≠x_tar, states in X ∖ G remain non-coreachable or non-controllable. Therefore computeFixpoint((G,Σ,→ ∖{(x_or,σ, x_tar)},X₀,X_m)) = computeFixpoint((X,Σ,→ ∖{(x_or,σ,x_tar)},X₀,X_m)).

• In case x_or ∈ G ∖ Y, x_tar ∈ G, and x_or≠x_tar, states in X ∖ G remain non-coreachable or non-controllable. Also, states in Y remain (co-)reachable and controllable. Therefore, computeFixpoint((G,Σ,→∖{(x_or,σ,x_tar)},Y ∪X₀,Y ∪X_m)) = computeFixpoint((X,Σ,→∖{(x_or,σ,x_tar)},X₀,X_m)).

• In case x_or ∈ X ∖ G, x_tar ∈ X ∖ G, and x_or≠x_tar, states in Y remain (co-)reachable and controllable. States in G remain coreachable and controllable. In case that

  • σ ∈Σ_c, the non-coreachablity or non-controllability of x_or and x_tar do not change. So $\hat {G}=G=G^{\prime }$ and $\hat {Y}=Y=Y^{\prime }$.

  • σ ∈Σ_u, then x_or may have been non-controllable, but may be controllable in the variant model. Because states in Y remain (co-)reachable and controllable, and states in G remain coreachable and controllable; $Y\subseteq Y^{\prime }$ and $G\subseteq G^{\prime }$. Therefore computeFixpoint((X,Σ,→∖{(x_or,σ,x_tar)},Y ∪X₀,G∪X_m)) = computeFixpoint((X,Σ,→∖{(x_or,σ,x_tar)},X₀,X_m)).

• A removed transition from x_or ∈ Y to x_tar ∈ G ∖ Y can not exist, as x_tar was reachable in the base model by this transition, and x_tar would have existed in Y.

• In case x_or ∈ Y and x_tar ∈ X ∖ G, then states in Y remain (co-)reachable and controllable, states in G remain coreachable and controllable, but not reachable, and states in X ∖ G remain non-coreachable or non-controllable. Therefore $\hat {G}=G=G^{\prime }$ and $\hat {Y}=Y=Y^{\prime }$.

• In case x_or ∈ X ∖ G and x_tar ∈ G, then x_or was coreachable in the base model. As it is not in G, x_or must be non-controllable. It will remain as such after removal of the transition (x_or,σ,x_tar). Thus, states in Y remain (co-)reachable and controllable, states in G remain coreachable and controllable, but not reachable, and states in X ∖ G remain non-coreachable or non-controllable. Therefore $\hat {G}=G=G^{\prime }$ and $\hat {Y}=Y=Y^{\prime }$.

• In case x_or = x_tar, the (co-)reachability and controllability of any state does not change. So $\hat {G}=G=G^{\prime }$ and $\hat {Y}=Y=Y^{\prime }$.

We can conclude that $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$ for any (x_or,σ,x_tar) ∈→, so Theorem 2 holds for Algorithm 10.$\square$

1.7 A.7 Added state

In case a state x^δ is added as an atomic model adaptation, there are no transitions to or from this state, because for the base model it holds that $\longrightarrow \subseteq X\times {{\varSigma }} \times X$, and x^δ∉X It is also not an initial state or marked state because for the base model it holds that $X_{0}\subseteq X$ and $X_{m} \subseteq X$. Therefore the added state x^δ is non-coreachable and non-reachable in the variant model. Therefore $Y^{\prime }=Y$, and $G^{\prime }=G$, proving Lemma 5 for an added state.$\square$

1.8 A.8 Removed state

In case a state x^δ is removed as an atomic model adaptation, there are no transitions to or from this state, because for the variant model it holds that $\longrightarrow \subseteq (X\setminus \{x^{\delta }\}) \times {{\varSigma }} \times (X\setminus \{x^{\delta }\})$. It is also not an initial state or marked state because for the variant model it holds that $X_{0}^{\prime }\subseteq X\setminus \{x^{\delta }\}$ and $X_{m}^{\prime } \subseteq X\setminus \{x^{\delta }\}$. Therefore the removed state x^δ is non-coreachable and non-reachable in the base model. Therefore $Y^{\prime }=Y$, and $G^{\prime }=G$, proving Lemma 5 for a removed state.$\square$

1.9 A.9 Added event

In case an event σ is added as an atomic adaptations, there are no transitions over this event, because for the base model it holds that $\longrightarrow \subseteq X\times {{\varSigma }} \times X$, and σ∉Σ. Therefore, adding the event is not going to influence the (co-)reachability or controllability of any state. Thus, $Y^{\prime }=Y$, and $G^{\prime }=G$, proving Lemma 5 for an added event.$\square$

1.10 A.10 Removed event

In case an event σ is removed as an atomic adaptations, there are no transitions over this event in the base model, because for the variant model it holds that $\longrightarrow ^{\prime } \subseteq X\times ({{\varSigma }}\setminus \{\sigma \}) \times X$, and $\longrightarrow ^{\prime }=\longrightarrow$. Therefore, removing the event is not going to influence the (co-)reachability or controllability of any state. Thus, $Y^{\prime }=Y$, and $G^{\prime }=G$, proving Lemma 5 for a removed event.$\square$

Appendix: B

The lemmas in this appendix support Theorem 3 for Algorithm 11. Following from the lemmas, Theorem 3 is proven at the end of this appendix.

Lemma 6

Following each line in Algorithm 11 that directly follows a call to an atomic TSS algorithm (i.e., lines 5,9,13,17,21,25), it holds for the intermediate automaton that is formed by $\hat {A}=(X^{\prime },{{\varSigma }}^{\prime },\longrightarrow ^{\prime },X_{0}^{\prime },X_{m}^{\prime })$ that $\text {\texttt {computeFixpoint}} (\hat {A}) = (Y^{\prime },G^{\prime })$, where $(Y^{\prime },G^{\prime })$ is the result of the atomic TSS algorithm in the line above.

Proof

The correct result (by Theorem 2) of each atomic TSS algorithm is proven in Appendix Appendix. $\hat {A}$ correctly constructs the variant model after applying the atomic model delta, following the definitions in Section 3. □

Lemma 7

Each time an atomic TSS algorithm is initiated by Algorithm 11, the atomic adaptation is a valid model delta for the automaton that is input.

Proof

We subdivide the proof over all calls to the atomic TSS algorithms, Algorithms 5 - 10:

• From Section 3, we know that $X_{0}^{+}\subseteq (X\cup X^{+})\setminus X^{-}$, and $X_{0}^{+} \cap X_{0} = \emptyset$. At the time Algorithm 5 (TSSAIP) is initiated with $x^{\delta } \in X_{0}^{+}$, this is with an automaton with state set $X^{\prime }=X\cup X^{+}$ and initial state set $X_{0}^{\prime }$. It holds that $\{x^{\delta }\}\subseteq X^{\prime }$. It holds that $\{x^{\delta }\} \cap X_{0}^{\prime } = \emptyset$, as x^δ is only added to $X_{0}^{\prime }$ after the call to Algorithm 5 with x^δ as added initial state. We can conclude that $X_{0}^{+} = \{x^{\delta }\}$ is a valid model delta for the automaton that is input when Algorithm 5 is initiated.

• From Section 3, we know that $X_{0}^{-}\subseteq X_{0}$. At the time Algorithm 6 (TSSRIP) is initiated with $x^{\delta } \in X_{0}^{-}$, this is with an automaton with initial state set $X_{0}^{\prime } \subseteq X\cup X^{+}$. x^δ is in $X_{0}^{\prime }$ when Algorithm 6 is called with x^δ, as x^δ is only removed from $X_{0}^{\prime }$ after this call. We can conclude that $X_{0}^{-} = \{x^{\delta }\}$ is a valid model delta for the automaton that is input when Algorithm 6 is initiated.

• From Section 3, we know that $X_{m}^{+}\subseteq (X\cup X^{+})\setminus X^{-}$, and $X_{m}^{+} \cap X_{m} = \emptyset$. At the time Algorithm 7 (TSSAMP) is initiated with $x^{\delta } \in X_{m}^{+}$, this is with an automaton with state set $X^{\prime }=X\cup X^{+}$ and marked state set $X_{m}^{\prime }$. It holds that $\{x^{\delta }\}\subseteq X^{\prime }$. It holds that $\{x^{\delta }\} \cap X_{m}^{\prime } = \emptyset$, as x^δ is only added to $X_{m}^{\prime }$ after the call to Algorithm 7 with x^δ as added marked state. We can conclude that $X_{m}^{+} = \{x^{\delta }\}$ is a valid model delta for the automaton that is input when Algorithm 7 is initiated.

• From Section 3, we know that $X_{m}^{-}\subseteq X_{m}$. At the time Algorithm 8 (TSSRMP) is initiated with $x^{\delta } \in X_{m}^{-}$, this is with an automaton with initial state set $X_{m}^{\prime } \subseteq X\cup X^{+}$. x^δ is in $X_{m}^{\prime }$ when Algorithm 8 is called with x^δ, as x^δ is only removed from $X_{m}^{\prime }$ after this call. We can conclude that $X_{m}^{-} = \{x^{\delta }\}$ is a valid model delta for the automaton that is input when Algorithm 8 is initiated.

• From Section 3, we know that: $\longrightarrow \! \cup [--] \longrightarrow ^{+} \subseteq X^{\prime } \times {{\varSigma }}^{\prime } \times X^{\prime }$, and →⁺ ∩→ = ∅. At the time Algorithm 9 (TSSAT) is initiated with (x_or,σ,x_tar) ∈→⁺, this is with an automaton with state set $X^{\prime }=X\cup X^{+}$ and event set ${{\varSigma }}^{\prime }={{\varSigma }}\cup {{\varSigma }}^{+}$. It holds that $\lbrace (x_{\mathit {or}},\sigma ,x_{\mathit {tar}}) \rbrace \subseteq X^{\prime } \times {{\varSigma }}^{\prime } \times X^{\prime }$. It holds that $\lbrace (x_{\mathit {or}},\sigma ,x_{\mathit {tar}}) \rbrace \cap \longrightarrow ^{\prime } = \emptyset$, as {(x_or,σ,x_tar)} is only added to $\longrightarrow ^{\prime }$ after the call to Algorithm 9 with (x_or,σ,x_tar) as added transition. We can conclude that →⁺ = {(x_or,σ,x_tar)} is a valid model delta for the automaton that is input when Algorithm 9 is initiated.

• From Section 3, we know that $\longrightarrow ^{-}\subseteq \longrightarrow$. At the time Algorithm 10 (TSSRT) is initiated with (x_or,σ,x_tar) ∈→⁻, this is with an automaton with state set $X^{\prime }=X\cup X^{+}$ and event set ${{\varSigma }}^{\prime }={{\varSigma }}\cup {{\varSigma }}^{+}$. (x_or,σ,x_tar) is in $\longrightarrow ^{\prime }$ when Algorithm 10 is called with (x_or,σ,x_tar), as (x_or,σ,x_tar) is only removed from $\longrightarrow ^{\prime }$ after this call. We can conclude that →⁻ = {(x_or,σ,x_tar)} is a valid model delta for the automaton that is input when Algorithm 10 is initiated.

Together, the above cases proof Lemma 7. □

Lemma 8

Each time states are added or removed, or events are added or removed in Algorithm 11, this adaptation is a valid model delta for the automaton it is performed on.

Proof

From Section 3, we know that X⁺ ∩ X = ∅ and Σ⁺ ∩Σ = ∅ The added states and added events are only added once to state set X in Algorithm 11, at the point they are added, this is a valid model delta. The removed states and removed events are removed from automaton $A^{\prime }=(X^{\prime },{{\varSigma }}^{\prime },\longrightarrow ^{\prime },X_{0}^{\prime },X_{m}^{\prime })$ in line 28. At this point, all added transitions are added to $\longrightarrow ^{\prime }$ and removed transitions are removed from →. Also all states with added marked property are added to $X_{m}^{\prime }$, all states with removed marked property are removed from $X_{m}^{\prime }$, all states with added initial property are added to $X_{0}^{\prime }$, and all states with removed initial property are removed from $X_{0}^{\prime }$. So in automaton $A^{\prime }$, $X^{-}\cap X_{m}^{\prime } = \emptyset$, $X^{-}\cap X_{0}^{\prime } = \emptyset$, and $\longrightarrow ^{\prime } \subseteq ((X\cup X^{+})\setminus X^{-}) \times (({{\varSigma }}\cup {{\varSigma }}^{+})\setminus {{\varSigma }}^{-}) \times ((X\cup X^{+})\setminus X^{-})$. In other words, the removed states are not initial or marked, there are no transitions to-or from removed states, and there are no transitions over removed events. Thus, Lemma 8 is proven for Algorithm 11. □

Lemma 9

If final fixpoint result Y in SS is equal to fixpoint result $Y^{\prime }$ in ITSS, then supervisor S is also the same.

Proof

From Lemma 6 it follows that the final fixpoint result $Y^{\prime }$ in ITSS is equal to the final fixpoint result Y in SS. By following the steps of Algorithm 11, it follows that at line 27; ${{\varSigma }}^{\prime }=({{\varSigma }}\cup {{\varSigma }}^{+})$. Line 27 of Algorithm 11 is equal to line 2 of Algorithm 1 when $Y^{\prime }=Y$ and ${{\varSigma }}^{\prime }=({{\varSigma }}\cup {{\varSigma }}^{+}) \setminus {{\varSigma }}^{-}$, thus computing the same automaton S.$\square$

From Lemmas 6-8 it follows that each intermediate result $(Y^{\prime },G^{\prime })$ is correctly constructed in Algorithm 11, so that the final result $(Y^{\prime },G^{\prime })$ is equal to $\text {\texttt {computeFixpoint}}(A^{\prime })$. From Lemma 9 it follows that the supervisor automaton computed by Algorithm 11 is the same as the supervisor automaton computed by Algorithm 1, for the same supervisor states in Y. Together, the lemmas show that Theorem 3 holds. □

Appendix: C

First we proof the application of a set ${{\varDelta }}^{\sim }$ atomic model adaptations in Δ^×, defined in Section 5.2, in the same manner as Appendix Appendix. Following, we provide the proof for Theorem 4 for Algorithm 12.

Lemma 10

For a set ${{\varDelta }}^{\sim }$, the same statements associated with a case statements of Algorithms 5 - 10 can be applied, as long as $\forall \delta \in {{\varDelta }}^{\sim }$ the same case condition holds.

Proof

We structure our proof the same way as Appendix Appendix, for each atomic TSS algorithm the possible ${{\varDelta }}^{\sim }$ in Δ^× is discussed. We denote (Y,G) = computeFixpoint(A), $(Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(A^{\prime })$, and $(\hat {Y},\hat {G})$ is calculated by the TSS algorithm.

• We consider ${{\varDelta }}^{\sim } = X_{0}^{+} \cap (G\setminus Y)$. Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow ,X_{0}\cup {{\varDelta }}^{\sim },X_{m})$.

  • For any $(X_{0}, X^{\prime }_{0})\in X\times X$ it holds that $G=G^{\prime }$ when computing $(Y,G)=\text {\texttt {computeFixpoint}}(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}),\ (Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(X,{{\varSigma }},\longrightarrow ,X^{\prime }_{0},X_{m})$, as the initial state does not influence the computation of G. We also observe that for all switchcases in Algorithm 5, $\hat {G}=G$ is computed. It follows that $\hat {G}=G^{\prime }$.

  • As ${{\varDelta }}^{\sim }\subseteq G\setminus Y$, for the supervisor synthesis of $A^{\prime }$, the reachable part is determined by $Y=\text {\texttt {FRS}}(G^{\prime },{{\varSigma }},\longrightarrow ,X_{0}^{\prime })$, where we know that $G^{\prime }=G$ and $X_{0}^{\prime }=X_{0}\cup {{\varDelta }}^{\sim }$. $\hat {Y}$ is calculated by $\text {\texttt {FRS}}(G,{{\varSigma }},\longrightarrow ,Y\cup {{\varDelta }}^{\sim })$. The result of these FRSs is the same, as we know that all states in Y are reachable in G from X₀ from the base synthesis. So $\hat {Y}=Y^{\prime }$.

• We consider ${{\varDelta }}^{\sim } = X_{0}^{-} \cap Y$. Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow ,X_{0}\setminus {{\varDelta }}^{\sim },X_{m})$.

  • For any $(X_{0}, X^{\prime }_{0})\in X\times X$ it holds that $G=G^{\prime }$ when computing $(Y,G)=\text {\texttt {computeFixpoint}}(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}),\ (Y^{\prime },G^{\prime })=\text {\texttt {computeFixpoint}}(X,{{\varSigma }},\longrightarrow ,X^{\prime }_{0},X_{m})$, as the initial state does not influence the computation of G. We also observe that for all switchcases in Algorithm 5, $\hat {G}=G$ is computed. It follows that $\hat {G}=G^{\prime }$.

  • In case that ${{\varDelta }}^{\sim }\subseteq Y$, for the supervisor synthesis of $A^{\prime }$, the reachable part is determined by $Y=\text {\texttt {FRS}}(G^{\prime },{{\varSigma }},\longrightarrow ,X_{0}^{\prime })$, where we know that $G^{\prime }=G$ and $X_{0}^{\prime }=X_{0}\setminus {{\varDelta }}^{\sim }$. $\hat {Y}$ is calculated by $\text {\texttt {FRS}}(Y,{{\varSigma }},\longrightarrow ,X_{0}\setminus {{\varDelta }}^{\sim })$. The result of these FRSs is the same, as we know that all states in G ∖ Y are not reachable from the base synthesis. So $\hat {Y}=Y^{\prime }$.

• We consider ${{\varDelta }}^{\sim } = X_{m}^{+} \cap X\setminus G$. Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}\cup {{\varDelta }}^{\sim })$.

  • In case that ${{\varDelta }}^{\sim }\subseteq X\setminus G$, states in Y remain reachable, coreachable, and controllable. So, $\text {\texttt {computeFixpoint}}((X,{{\varSigma }},\longrightarrow ,Y\cup X_{0},Y\cup X_{m} \cup {{\varDelta }}^{\sim })) = \text {\texttt {computeFixpoint}}((X,{{\varSigma }},\longrightarrow ,X_{0}, X_{m} \cup {{\varDelta }}^{\sim }))$.

• We consider ${{\varDelta }}^{\sim } = X_{m}^{-} \cap Y$. Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}\setminus {{\varDelta }}^{\sim })$.

  • We know that ${{\varDelta }}^{\sim } \subseteq X_{m}$ (model delta is valid). And all states in X_m are coreachable by definition. G was the maximal controllable coreachable set to X_m. After removing ${{\varDelta }}^{\sim }$ as marked states; $G^{\prime }\subseteq G$ and $Y^{\prime } \subseteq Y$. So all states in $X\setminus G \subseteq X\setminus G^{\prime }$. Therefore $\text {\texttt {computeFixpoint}}((G,{{\varSigma }},\longrightarrow ,X_{0},X_{m}\setminus {{\varDelta }}^{\sim })) = \text {\texttt {computeFixpoint}}((X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}\setminus {{\varDelta }}^{\sim }))$. So in case ${{\varDelta }}^{\sim } \subseteq Y$, $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$.

• We consider ${{\varDelta }}^{\sim } = X_{m}^{-} \cap G \setminus Y$. Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}\setminus {{\varDelta }}^{\sim })$.

  • In case that ${{\varDelta }}^{\sim } \subseteq G\setminus Y$, all states in Y are coreachable and controllable for X_m ∖ x^δ, as states in ${{\varDelta }}^{\sim }$ are not reachable from Y, otherwise they would be contained in Y. Therefore $\text {\texttt {computeFixpoint}}((G,{{\varSigma }},\longrightarrow ,X_{0},(Y\cup X_{m})\setminus {{\varDelta }}^{\sim })) = \text {\texttt {computeFixpoint}}((X,{{\varSigma }},\longrightarrow ,X_{0},X_{m}\setminus {{\varDelta }}^{\sim }))$. So in case ${{\varDelta }}^{\sim } \subseteq G\setminus Y$, $\hat {Y}=Y^{\prime }$ and $\hat {G}=G^{\prime }$.

• We consider ${{\varDelta }}^{\sim } = \longrightarrow ^{+} \cap Y\times {{\varSigma }} \times Y$. Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow \!\cup {{\varDelta }}^{\sim },X_{0},X_{m})$.

  • The coreachability an controllability of all states remains unchanged. So $\hat {G}=G=G^{\prime }$. All states in Y remain reachable, so $\text {\texttt {FRS}} (G{},{{\varSigma }},\longrightarrow \!\cup \lbrace (x_{\mathit {or}},\sigma ,x_{\mathit {tar}}) \rbrace ,Y) = \text {\texttt {FRS}} (G,{{\varSigma }},\longrightarrow \!\cup {{\varDelta }}^{\sim },X_{0})$.

• We consider ${{\varDelta }}^{\sim } = \longrightarrow ^{+} \cap G\times {{\varSigma }}_{u} \times X\setminus G$. Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow \!\cup {{\varDelta }}^{\sim },X_{0},X_{m})$.

  • The states in X ∖ G remain non-coreachable or non-controllable. The supervisor can not disable the added transitions. All states in X_or are non-controllable, where $X_{or} = \{x_{\mathit {or}} | (x_{\mathit {or}},\sigma ,x_{\mathit {tar}})\in {{\varDelta }}^{\sim }, \sigma \in {{\varSigma }}_{u}, x_{\mathit {tar}}\in X\}$. Because also states in X ∖ G remain non-coreachable or non-controllable, computeFixpoint((G,Σ,→ ∩((G∖X_or)×Σ×G),X₀∖X_or,X_m∖X_or)) = computeFixpoint((X,Σ,→ ∪{(x_or,σ,x_tar)},X₀,X_m)).

• We consider ${{\varDelta }}^{\sim } = \{(x_{\mathit {or}},\sigma ,x_{\mathit {tar}})\in \longrightarrow ^{+} |x_{\mathit {or}} \in X\setminus G \wedge x_{\mathit {or}}\neq x_{\mathit {tar}} \}$ Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow \!\cup {{\varDelta }}^{\sim },X_{0},X_{m})$.

  • All states in Y remain (co-)reachable and controllable. Thus we conclude, $\text {\texttt {computeFixpoint}} ((X,{{\varSigma }},\longrightarrow \!\cup \lbrace (x_{\mathit {or}},\sigma ,x_{\mathit {tar}}) \rbrace ,Y\cup X_{0},Y \cup X_{m})) = \text {\texttt {computeFixpoint}} ((X,{{\varSigma }},\longrightarrow \!\cup {{\varDelta }}^{\sim },X_{0},X_{m}))$.

• We consider ${{\varDelta }}^{\sim } = \{(x_{\mathit {or}},\sigma ,x_{\mathit {tar}})\in \longrightarrow ^{-} |x_{\mathit {or}} \in Y \wedge x_{\mathit {tar}}\in Y \wedge x_{\mathit {or}}\neq x_{\mathit {tar}} \}$ Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow \setminus {{\varDelta }}^{\sim },X_{0},X_{m})$.

  • States in X ∖ G remain non-coreachable or non-controllable. Therefore $\text {\texttt {computeFixpoint}} ((G{},{{\varSigma }},\longrightarrow \setminus {{\varDelta }}^{\sim },X_{0},X_{m} )) = \text {\texttt {computeFixpoint}} ((X,{{\varSigma }},\longrightarrow \setminus {{\varDelta }}^{\sim },X_{0},X_{m} ))$.

• We consider ${{\varDelta }}^{\sim } = \{(x_{\mathit {or}},\sigma ,x_{\mathit {tar}})\in \longrightarrow ^{-} |x_{\mathit {or}} \in G\setminus Y \wedge x_{\mathit {tar}}\in G \wedge x_{\mathit {or}}\neq x_{\mathit {tar}} \}$ Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow \setminus {{\varDelta }}^{\sim },X_{0},X_{m})$.

  • States in X ∖ G remain non-coreachable or non-controllable. Also, states in Y remain (co-)reachable and controllable. It follows that $\text {\texttt {computeFixpoint}} ((G{},{{\varSigma }},\longrightarrow \setminus {{\varDelta }}^{\sim }, Y\cup X_{0},Y\cup X_{m})) = \text {\texttt {computeFixpoint}} ((X,{{\varSigma }},\longrightarrow \setminus {{\varDelta }}^{\sim },X_{0},X_{m} ))$.

• We consider ${{\varDelta }}^{\sim } = \{(x_{\mathit {or}},\sigma ,x_{\mathit {tar}})\in \longrightarrow ^{-} |x_{\mathit {or}} \in X\setminus G \wedge x_{\mathit {tar}}\in X\setminus G \wedge \sigma \in {{\varSigma }}_{u} \wedge x_{\mathit {or}}\neq x_{\mathit {tar}} \}$ Automaton A = (X,Σ,→,X₀,X_m), and $A^{\prime }=(X,{{\varSigma }},\longrightarrow \setminus {{\varDelta }}^{\sim },X_{0},X_{m})$.

  • States in Y remain (co-)reachable and controllable. States in G remain coreachable and controllable. The origin states of the removed transition may have been non-controllable, but may be controllable in the variant model. Because states in Y remain (co-)reachable and controllable, and states in G remain coreachable and controllable; $Y\subseteq Y^{\prime }$ and $G\subseteq G^{\prime }$. Therefore $\text {\texttt {computeFixpoint}} ((X,{{\varSigma }},\longrightarrow \setminus {{\varDelta }}^{\sim }, Y\cup X_{0},G \cup X_{m}))=\text {\texttt {computeFixpoint}} ((X,{{\varSigma }},\longrightarrow \setminus {{\varDelta }}^{\sim },X_{0},X_{m} ))$.

For any possible ${{\varDelta }}^{\sim }$ Lemma 10 is proven. □

Lemma 11

Each time $X^{\prime }$, ${{\varSigma }}^{\prime }$, $\longrightarrow ^{\prime }$, $X_{0}^{\prime }$, or $X_{m}^{\prime }$ is constructed in Algorithm 12 (i.e., lines 1,6,8,12), it holds that $\text {\texttt {computeFixpoint}} (X^{\prime },{{\varSigma }}^{\prime },\longrightarrow ^{\prime },X_{0}^{\prime },X_{m}^{\prime }) = (Y^{\prime },G^{\prime })$, for $(Y^{\prime },G^{\prime })$ computed at that point in Algorithm 12.

Proof

We structure our proofs over the different lines where automaton $A^{\prime }$ is constructed.

• Lines 1,12: In case states are added or removed, or events are added or removed in Algorithm 12, the same proofs as for Lemmas 5 and 8 hold here.

• Line 6: This is the same iterative application as in Algorithm 11 (ITSS). The same proofs as for Lemmas 6 and 7 hold here.

• Line 8: The correct result of applying sets ${{\varDelta }}^{\sim }$ is proven for Lemma 10 above. In conjunction with the proof for Lemma 7, this proofs Lemma 11 for line 8.

For each time $X^{\prime }$, ${{\varSigma }}^{\prime }$, $\longrightarrow ^{\prime }$, $X_{0}^{\prime }$, or $X_{m}^{\prime }$ is constructed in Algorithm 12, Lemma 11 is proven. $\square$

From Lemma 11 it follows that each intermediate result $(Y^{\prime },G^{\prime })$ is correctly constructed in Algorithm 12, so that the final result $(Y^{\prime },G^{\prime })$ is equal to $\text {\texttt {computeFixpoint}}(A^{\prime })$. Using the same proof as Lemma 9, it follows that the supervisor automaton computed by Algorithm 12 is the same as the supervisor automaton computed by Algorithm 1, for automaton $A^{\prime }$. Together, this shows that Theorem 4 holds. □