On the dynamic behaviour of a flexible beam carrying a moving mass

Abstract

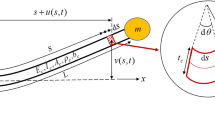
The behaviour of a system containing a mass traveling on a cantilever beam is considered. The mass is induced to move by an applied force as opposed to the case which has been considered in most literature where the position of the moving mass is assumed to be known and independent of the motion of the beam. Furthermore, the system to be discussed has the unique characteristic that the motions of the mass and the beam are coupled. The mathematical model of the system includes two coupled nonlinear integral/partial differential equations which are impossible to solve analytically and are difficult to solve numerically in their original form. As a remedy, the solution is discretized into space and time functions and the equations of motion are reduced to a set of ordinary differential equations. The shape function is chosen so that it satisfies the boundary conditions of the beam as well as the transient conditions imposed by the traveling mass. This choice of the shape function, which considers the mass-beam interaction, provides an improvement over the conventional method of using a simple cantilever beam mode shapes.

The ordinary differential equations of motion using the ‘improved’ shaped functions, are solved numerically to obtain the dynamic behaviour of the system. The results illustrate the validity of the model, and demonstrate the advantages of the ‘improved’ model to the ‘un-improved’ equations.