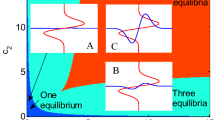
Abstract
The generation and control of animal locomotion is believed to involve central pattern generators — networks of neurons which are capable of producing oscillatory behavior. In the present work, the quadrupedal locomotor central pattern generator is modelled as four distinct but symmetrically coupled nonlinear oscillators. We show that the typical patterns for two such networks of oscillators include 2:1 frequency-locked oscillations. These patterns, which arise through symmetry-breaking Hopf bifurcation, correspond in part to observed patterns of 2:1 frequency-locking of limb movements during electrically elicited locomotion of decerebrate and spinal quadrupeds. We briefly describe how our theoretical predictions could be tested experimentally.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Cohen, A. H., Holmes, P. J., Rand, R. H.: The nature of the coupling between segmental oscillators of the lamprey spinal generator for locomotion: a mathematical model. J. Math. Biol. 13, 345–369 (1982)
Collins, J. J., Stewart, I. N.: Coupled nonlinear oscillators and the symmetries of animal gaits. Mathematics Institute, University of Warwick. (Preprint 1990)
Forrsberg, H., Grillner, S., Halbertsma, J., Rossignol, S.: The locomotion of the low spinal cat. 2: Interlimb coordination. Acta. Physiol. Scand. 108, 283–295 (1980)
Golubitsky, M., Stewart, I. N.: Hopf bifurcation in the presence of symmetry. Arch. Ration. Mech. Anal. 87, 107–165 (1985)
Golubitsky, M., Stewart, I. N.: Hopf bifurcation with dihedral group symmetry: coupled nonlinear oscillators. In: Golubitsky, M., Guckenheimer, J. (eds.) Multiparameter Bifurcation Theory (Contemp. Math., vol. 56, pp. 131–173) Providence, RI: Am. Math. Soc.1986
Golubitsky, M., Stewart, I. N., Schaeffer, D. G.: Singularities and Groups in Bifurcation Theory, vol. II. Berlin Heidelberg New York: Springer 1988
Grillner, S.: Locomotion in vertebrates: central mechanisms and reflex interaction. Physiol. Rev. 55, 247–304 (1976)
Guevara, M. R., Glass, L.: Phase locking, period doubling bifurcations, and chaos in a mathematical model of a periodically driven oscillator: a theory for the entrainment of biological oscillators and the generation of cardiac dysrhythmias. J. Math. Biol. 14, 1–23 (1982)
Jacobson, R. D., Hollyday, M.: Electrically evoked walking and fictive locomotion in the chick. J. Neurophysiol. 48, 257–270 (1982)
Keith, W. L., Rand, R. H.: 1: 1 and 2 : 1 phase entrainment in a system of two coupled limit cycle oscillators. J. Math. Biol. 20, 133–152 (1984)
Kulagin, A. S., Shik, M. L.: Interaction of symmetrical limbs during controlled locomotion. Biophysics 15, 171–178 (1970)
Rand, R., Cohen, A. H., Holmes, P. J.: Systems of coupled oscillators as models of central pattern generators. In: Cohen, A. H., Rossignol, S., Grillner, S. (eds.) Neural Control of Rhythmic Movements in Vertebrates, pp. 333–367. New York: Wiley 1988
Selverston, A. I.: Are central pattern generators understandable? Behav. Brain Sci. 3, 535–571 (1980)
Shik, M. L., Severin, F. V., Orlovskii, G. N.: Control of walking and running by means of electrical stimulation of the mid-brain. Biophysics 11, 756–765 (1966)
Stein, P. S. G.: Swimming movements elicited by electrical stimulation of the turtle spinal cord: the high spinal preparation. J. Comp. Physiol. 124, 203–210 (1978)
Winfree, A. T.: The Geometry of Biological Time. Berlin Heidelberg New York: Springer 1980
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Collins, J.J., Stewart, I.N. Symmetry-breaking bifurcation: A possible mechanism for 2:1 frequency-locking in animal locomotion. J. Math. Biol. 30, 827–838 (1992). https://doi.org/10.1007/BF00176458
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00176458