An adaptation of finite linear viscoelasticity theory for rubber-like viscoelasticity by use of a generalized strain measure

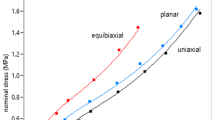
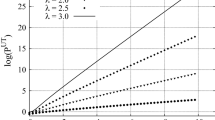
Abstract

In this paper a simplified three-dimensional constitutive equation for viscoelastic rubber-like solids is derived by employing a generalized strain measure and an asymptotic expansion similar to that used by Coleman and Noll (1961) in their derivation of finite linear viscoelasticity (FLV) theory. The first term of the expansion represents exactly the time and strain separability relaxation behavior exhibited by certain soft polymers in the rubbery state and in the transition zone between the glassy and rubbery states. The relaxation spectra of such polymers are said to be deformation independent. Retention of higher order terms of the asymptotic expansion is recommended for treating deformation dependent spectra.

Certain assumptions for the solid theory are relaxed in order to obtain a constitutive equation for uncross-linked liquid materials which exhibit large elastic recovery properties.

Apart from the ‘strain energy’W(I₁,I ₂), which alternatively characterizes the long-time elastic response of solids or the instantaneous elastic response of elastic liquids, only the linear viscoelastic relaxation modulus is required for the first-order theory. Both types of material functions can be obtained, in theory, from simple laboratory testing procedures. The constitutive equations for solids proposed by Chang, Bloch and Tschoegl (1976) and a special form of K-BKZ theory for elastic liquids are shown to be particular cases of the first-order theory.

Previously published experimental data on a cross-linked styrene-butadiene rubber (SBR) and an uncross-linked polyisobutylene (PIB) rubber is used to corroborate the theory.