Abstract
The study aimed to monitor the spatial extent and severity of drought events in the Luni River Basin using Standardized Precipitation Index (SPI), and hence, the long-term monthly precipitation records of 39 rain gauge stations (1973–2016) were used in the study. Both the long-term (24, 12, and 9 months) and short-term (6, 3, and 1 month) SPI were calculated to recognize the drought events and the percentage of the area covered by the severe drought conditions. The nonparametric Mann–Kendall test was performed for trend analysis in drought events to investigate the consistency of drought events. The frequency results of drought events revealed that Jalore station was the highest drought frequency station, while the lowest drought frequency was observed in Vijaynagar station. The annual SPI result showed that the following years witnessed major drought events: 1981, 1984, 1985, 1988, 1989, 1991, 1993, 1999, 2000, 2004, 2005, and 2008. Besides, the results of the Mann–Kendall test showed that a substantial portion of the eastern basin experienced an increase in the intensity of drought, while the western basin experienced a decrease in the severity of the drought. The comprehensive analysis is indicative of climate change, and there is a possibility that such droughts would become more common in the future in the Luni River Basin. The results of this study would help planners to develop sound policy on water resources and also assist in forecasting systems to provide advance warnings.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Drought is a natural hazard found in every climatic region of the world. However, its characteristics and severity vary considerably across the regions [1, 2]. Droughts are more prevalent and severe in arid and semiarid regions and may continue for weeks, months, years, or even decades. Meteorological drought prevails for a short period of time, followed by a catastrophic event due to insufficient precipitation [3]. However, a severe meteorological drought occurs when annual rainfall is less than 25% of the normal rainfall of that region [4]. In addition, drought also occurs due to water shortage, high water utilization, and unplanned utilization of water assets. Most Indian states are severely affected by recurrent and prolonged drought events, resulting in a significant number of negative impacts on water resources, ecosystems, and socioeconomic progress [5, 6]. In relation, agricultural productivity is also reduced due to this natural hazard [7,8,9,10]. Therefore, it is necessary to analyze the spatiotemporal characteristics and severity of droughts in a river basin to ensure proper utilization and sound improvement of water resources, economic progress, and agricultural activity.[11].
Although droughts cannot be avoided, their timely prediction can help to mitigate their adverse effects [12,13,14,15]. Drought events are becoming more recurrent and severe in recent years due to changes in the global climate [16]. Droughts are of various kinds, including agricultural, meteorological, hydrological, and socioeconomic droughts. Over the past few years, the number of scientific studies of drought indices has increased. Additionally, several attempts have been made on comparative analysis of different index methods for assessing drought. Such attempts index methods are the Palmer Drought Severity Index (PDSI) [17], Crop Moisture Index [18], Deciles [19], Rainfall Anomaly Index [20], FAO Water Satisfaction Index [21], Surface Water Supply Index [22], Bhalme and Mooley Drought Index [23], Index of Moisture Adequacy [24], Agro-hydro Potential [25], Standardized Precipitation Index (SPI) [26], and multiple indices of low river flow [27]. The SPI is, however, a compliant drought index recommended by the World Meteorological Organization (WMO). It is commonly used for the observation of drought by Mallya. et al. [28], Ahmad et al. [29], Yan et al. [30], Mondol et al. [31], Sabau et al. [32], Nury and Hasan [33], Rahman and Lateh [34], in the river basins Sebenik et al. [35], David and Davidova [36], Seçkin and Topçu [37], Arunvenkatesh et al. [38] and in Rajasthan by Amrit et al. [39], Reddy and Ganguli [40], Chhajer [41], Mundetia and Sharma [42]. The SPI is considered to be the most effective and reliable index for estimating drought [43]. It can be used for various timescales and regions by using precipitation data of the region [44].
In India, the projection or forecasting of drought conditions was carried out naturally and more extensively by a large number of researchers in Rajasthan [40,41,42, 45,46,47]. Dutta et al. [47] used VCI and SPI to study agricultural drought in Rajasthan and found that the dry season in mid-2002 resulted in crop stress. Mundetia and Sharma [42] keynoted that the Rajasthan is more vagarious drought frequency. They found that mild droughts had a greater tendency than moderate and severe droughts to cause severe drought. Chhajer et al. [41] studied drought in Jaisalmer, Rajasthan, by using SPI and other indices for the spatiotemporal assessment of drought and their characteristics. They also summarized the random appearance of dry and wet meteorological conditions in Jaisalmer, and the conditions have a shorter lifespan. Reddy and Ganguli [40] used gridded (0.5 × 0.5) monthly rainfall data to study the spatiotemporal patterns of drought occurrence in western Rajasthan by using the SPI values of the 6-month timescale (SPI-6). They observed that the number of drought-affected grids of western Rajasthan had been increased during the study period. Amrit et al. [39] monitored drought occurrence in Rajasthan by using the EDI and SPI and executed that the most severe droughts occurred in 1918. Moreover, they noticed that the drought frequency in northern, western, southwestern, and central Rajasthan was one in 3 years, whereas in eastern Rajasthan, it was one in 4 years. Hence, the growing concern about droughts in Rajasthan's Luni River Basin has made it urgent to define in detail the spatiotemporal characteristics and drought trends.
The main focus of the research work is to assess the spatiotemporal drought occurrences and their nature. The SPI_SL_6.exe program recommended by WMO [48] was used to calculate Standardized Precipitation Index. The spline interpolation method was used to obtain the spatial distribution of the drought frequency. The geostatistical analysis tool of ArcGIS 10.3 [49] was used for this purpose. For study, researchers were used 44 years of monthly rainfall data for the calculation of SPI. The present paper tried to conduct a spatial analysis of the meteorological drought attributes and assess temporal drought occurrences. The SPI values at the timescales of 1 month (SPI-1), 24 months (SPI-24), 12 months (SPI-12), 9 months (SPI-9), 6 months (SPI-6), and 3 months (SPI-3) were evaluated. This investigation reveals the extent, spatial patterns, severity of drought, and also identifies the trend in the meteorological drought of the study area. This study will assist water resource managers for improved management activities and policies to reduce the influence of drought in the study area.
2 Description of the study area
Since the last several decades, drought has been a common phenomenon in Rajasthan. Drought is closely related to the lack of rainfall combined with the high temperature in Rajasthan, India. The present study site is the Luni River Basin of Rajasthan, India, where the socioeconomic condition is primarily dependent on agriculture and allied sectors.
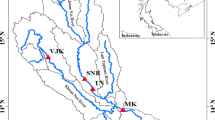
Luni River Basin has a semiarid climatic condition, lies in the parallel to the western part of the Aravalli Ranges, and characterized by high heat flow during summer. The area starches between 24° 30′ 00″ N–27° 10′ 00″ N and 71° 15′ 34″ E–75° 48′ 18″ E and covers an area of 78,380 km2 (Fig. 1). In this area, precipitation occurs mostly from June to September because of the monsoon wind; non-monsoon precipitation is restricted or sporadic in this area. Most of the rivers originate from the oldest fold mountain chains of Aravalli Range. This mountain range serves a primary role in drought occurrences in this river basin. The eastern slope of the Aravalli mountain range obtains the Arabian Sea branch of monsoon first. Moreover, the eastern part of the ranges has higher precipitation, whereas the western part of the range has negligible rainfall. The average annual rainfall distribution has been decreased from the east to the west because of the variations in the relief pattern of the study area.
3 Method and materials
3.1 Data collection and inference of model parameters
The proposed work was processed by using 39 stations rainfall data over the Luni River Basin in Rajasthan from 1973 to 2016. The observed precipitation records were assessed from the archives of the Water Resources Department, Rajasthan. However, some of the stations have missing data, and therefore, we discarded the stations with missing data. After collecting, the data were subjected to check error or missing in the time series and found only less than 1% data were missing which was calculated using multiple imputation method. Several researchers [50,51,52,53] used such data because the quality of the data was maintained by the respective agency. In the study, we adopted ClimDex version 1.3 for further maintaining data quality. In order to control the data quality, unrealistic data and subroutine datasets such as (1) typographic error (i.e., ‘O’ instead of ‘0’) (2) values < 0 (negative rainfall) were identified and corrected. After ensuring that data quality was maintained, station data were more than 90% consistent in carrying out this study.
Homogenization is a key issue in a climate-based analysis. Homogenization is usually a method of removing non-climatic changes in the dataset. A dataset with inhomogeneity creates many problems (biased trend, sudden breaks in the dataset), and therefore, homogeneity testing is performed to address these issues. In the present study, the homogeneity test was performed according to the study by Das et al. [54]. The annual average rainfall (1973–2016) in the study area varies from 198.9 (in Baitu station) to 669.27 mm (in Desuri station) with an average of 1505 mm, The standard deviations of annual rainfall vary from 305.32 (in Bali station) to 101.1 mm (in Phalodi station) (Table 1). By analyzing Table 1, it is observed that the data are positively skewed because the skewness coefficient is larger than zero. Platykurtic and leptokurtic distributions are observed because some values are smaller and some values are larger than zero.
3.2 Standardized Precipitation Index (SPI)
McKee et al. [26] was a key developer of SPI for monitoring the drought events. In this study, SPI was calculated on a 1-, 3-, 6-, 9-, 12-, and 24-month timescale for evaluation of meteorological drought in the Luni River Basin of Rajasthan. Generally, the calculation of SPI is done by setting the probability density function to the total precipitation. It has been done differently for every single month and location. After that, each probability function has been converted into the standard normal distribution [55].
The probability function was used to express the gamma distribution:
here α denotes the appearance of parameters, β represents the range of the parameter, \(x\) denotes the amount of rainfall, and \(\varGamma \left(\alpha \right)\) is the gamma function. The value of \(\alpha\) and \(\beta\) parameters > 0.
The Gamma function \(\varGamma \left(\alpha \right)\) can be expressed as follows:
\(\alpha\) and \(\beta\) parameters must be estimated for adjusting the gamma distribution. Maximum likelihood solutions are used to accurately obtain \(\alpha\) and \(\beta\) as follows [56]:
where
After that, \(\alpha\) and \(\beta\) parameters are adopted to detect the increasing probability distribution function \(G\left(x\right)\) of a given timescale:
By replacing x/\(\widehat{\beta }\) with \(t\), the above equation can be reduced as follows:
Rainfall is not continuous over time. Thus, to account for the zero value obtained when there is no rain. Edwards [57] proposed the true feasibility of non-exceedance \(H\left(x\right)\) can be obtained as follows:
where \(q\) denotes the possibility of a zero event, and \(m\) is the frequency of zeros in the time series dataset of rainfall. Thom [58] stated that \(q\) could be estimated by the following equation:
The present study used the latest SPI program (SPI_SL_6.exe), which is developed by the US National Drought Mitigation Centre of Nebraska University. The SPI severity drought classes are presented in Table 2.
3.3 Mann–Kendall (MK) test
The MK test was performed to assess the presence of monotonic tendency in the SPI time series dataset. The test statistic \((S)\) of a time series \({x}_{1},{x}_{2},{x}_{3}\dots ,\) and \({x}_{n}\) can be calculated using the MK test as [59, 60]:
where n defines the number of rain gauge stations and \({x}_{m}\) and \({x}_{n}\) denote the data point at time n.
Equation 12 was used for the calculation of S variance
where \(n\) is the number of rain gauge stations, \(g\) denotes the total number of tied groups, and \({t}_{p}\) is the number of ties of extent \(p\).
There is a close relationship between statistic \(S\) and Kendall’s \(\tau\) coefficient. The relationship is calculated as follows:
where
If the sample size \(n\) is greater than 10, then \(S\) and \({\mathrm{VAR}}(S)\) is adopted to calculate normalized test statistic \(Z\), applying the following equation:
Generally, the positive and negative values of Z statistics depict the increasing and decreasing trends, respectively. The null hypothesis (Ho) and the alternative hypothesis (HA) depict the no trends and trends, respectively, in the selected time series [61, 62].
4 Results and discussion
4.1 Temporal variation of drought
The SPI-1, 3, 6, 9, 12, and SPI-24 were calculated, and thereafter, the drought events in the Luni Basin of Rajasthan recorded by the 39 rain gauges were distinguished. Table 3 shows the temporal distribution of the annual drought events from 1973 to 2016, and the distribution allows for the recognition of drought periods and their corresponding duration (years). The performance of SPI showed that more than 80% of stations were affected by droughts in the years 1974, 1980, 1981, 1984, 1985, 1986, 1987, 1988, 1991, 1999, 2002, 2004, and 2009. According to the results presented in the table, the most severe drought events occurred in Baitu Station during 1974–91.
The distributions of the SPI for each year are shown in Fig. 2. The results of the SPI showed that few stations exceeded the extreme wet event (SPI > 2) and extreme drought event (SPI < − 2). Based on the short-term SPI (3-and 6-month timescales), several drought periods have occurred during the study period. Specifically, from an agricultural point of view, one of the most severe drought events occurred during the monsoons in June 1984. During this event, more than 23% of the stations of the Luni River Basin were exposed to extreme and severe drought events, as shown in Fig. 2c. Another exceptional drought event occurred in June 1992. During this event, more than 16% of the stations experienced extreme and severe drought during a 3-month timescale. Drought events were observed in September 1974, 1987, and 2002 according to SPI-3 (Fig. 2d), and approximately 67%, 87%, and 46% of the stations were affected by extreme, severe, and moderate droughts, respectively. The incidence of severe and extreme drought (SPI-3) was relatively higher in June and September compared to December and March. Similarly, more than 33% of the stations experienced severe and extreme drought conditions in September 1974, while in September 1987 more than 74% of the stations experienced drought conditions with an SPI value of less than − 1.5. In addition, in September 2002, the analysis of SPI-6 revealed that more than 48% of the stations were affected by extreme and severe drought conditions (Fig. 2f). The annual SPI series also revealed that the drought was experienced in 1974, 1980, 1981, 1982, 1984, 1985, 1986, 1987, 1988, 1989, 1991, 1993, 1999, 2002, 2004, 2005, and 2009. However, the highest frequency of severe and extreme droughts was found in 1974, 1987, 2002, and 2009 (Fig. 2g).
The proportion of stations experiencing meteorological drought events according to the threshold values of SPI-12 specified in Table 3 is presented in Fig. 3. The proportion of stations experiencing meteorological drought events in accordance with the SPI-12 threshold values is presented in Table 3 and Fig. 3. The values showed that approximately 74% of the stations experienced the maximum frequency of mild droughts in 2000. In 1986, almost 49% of the rain gauge stations were affected by moderate drought events. Approximately 31% and 44% of stations affected by extreme and severe drought events in 1987, respectively. The occurrence of drought event was least in 1997 (Fig. 3), followed by 2010 and 2015. However, the maximum number of meteorological drought events was reported in 1974, 1985, 2002, and 2009. The most severe and prolonged drought events in the basin area were identified in 2002. In 2002, SPI-12 showed that approximately 43% of stations had severe and extreme drought conditions.
An overall analysis of the metrological event shows that a mixture of both dry and wet events is identified in the temporal study. Similar findings are found in the study of Mekonen et al. [63], Kalisa et al. [64]. In addition, the temporal study also shows that there are a lot of differences amongst these stations with regard to drought events. This may be due to the differences in climatic and geographic characteristics. Another interesting fact is that most of the stations experienced drought events during the period 1985 to 1990.
4.2 Spatial distribution of drought
The spatial extension of the drought was obtained using a spline interpolation method, as shown in Figs. 4 and 5. The incidence of various categories of drought events varied from regions and timescales. As shown in Figs. 4 and 5, there were a greater number of moderate drought effects compared with severe and extreme drought events between study periods. The highest drought frequency was observed in Dengana Station, where the average drought frequency is 46.58%. The lowest drought frequency was observed at the Vijaynagar station, where the average drought frequency was 35%. For each timescale, the total number of severe (− 1.50 to − 1.99), moderate (− 1.00 to − 1.49), and mild (0 to − 0.99) drought events were considered. The results showed that recurring droughts were mostly observed for the 1-month timescale in the middle portions of the basin (15–23%) (Fig. 4a). For the 3-month timescale, the northeastern and southeastern areas of the basin experienced droughts most frequently (44%–51%) (Fig. 4b). Most of the area of the basin (86.16%) except the northwestern part of the basin, often experienced mild and above category droughts (44–59%) according to the 6-month timescale (Fig. 4c). Conversely, for the 9-month timescale, nearly high recurrences (51%–59%) of mild and above category droughts were seen in the southwestern part of the basin (Fig. 4d). According to SPI-12, the drought events revealed that most of the regions of the basin (except the northwestern part and few pockets of eastern part) experienced the drought most frequently (44–59%), covering about 85.63% of the basin area (Fig. 4e). On the other hand, the longer timescale of SPI-24 showed that recurrent droughts (44–59%) were observed in approximately 66.91% of the basin area and these areas were mostly identified in the northern, eastern, and southwestern parts of the basin (Fig. 4f).
Occurrence of drought events with the severity level, a SPI-3, mild, b SPI-6, mild, c SPI-12, mild, d SPI-24, mild, e SPI-3, moderate, f SPI-6, moderate, g SPI-12, moderate, h SPI-24, moderate, i SPI-3, severe j SPI-6, severe, k SPI-12, severe, l SPI-24, severe, m SPI-3, extreme, n SPI-6, extreme, o SPI-12, extreme, p SPI-24 extreme
The spatial mild drought pattern according to SPI-3 reveals that the drought occurrence mostly reoccurred (34–50%) in approximately 49.57% of the total study area, and these regions were mostly scattered in the southwestern and middle portion of the basin (Fig. 5a). According to SPI-6, a high-recurrence (34–50%) of mild drought zone on an area of 84.33% of the total basin area was observed, and these areas were mainly located in the middle and extreme southern portion of the Luni River Basin (Fig. 5b). According to SPI-12, mild droughts experienced in the focal segment of the southwestern part of the basin with a high recurrence value (34–50%) (Fig. 5c); the area covered approximately 53.79% of the basin. According to SPI-24, a longer timescale, mild droughts were observed in the central portion of the north and northeastern parts of the Luni River Basin with a high-recurrence value (34–50%); the area covered approximately 26.34% of the basin (Fig. 5d).
According to SPI-3, approximately 12% of the basin (Fig. 5e) experienced moderate drought events with a high-recurrence value (6–9%). The area was mainly in the focal segment of the basin. By contrast, a high-recurrence of moderate drought event was also observed in the extreme northwestern and eastern parts of the basin according to SPI-6 (Fig. 5f). According to SPI-12, regions in which moderate drought events occurred most regularly (9–22%) were found in the extreme northeastern and southeastern parts of the basin (Fig. 5g). These areas covered approximately 30% of areas of the basin. According to SPI-24, the moderate drought event zone with high-recurrence values (9–19%) was found mainly in the northwestern, middle-eastern, and also in the southeastern parts, covering approximately 60% area of the basin (Fig. 5h).
According to SPI-3, areas with severe droughts with high recurrence values (1.6–4.9%) were found to be predominantly in the northeast, southeast, southwest, and midwest regions (Fig. 5i) and to cover approximately 55.56% of the basin. Conversely, according to SPI-6, an exceptionally severe drought event (3.28–6.56%) was observed. At this scale, mainly the northern and eastern parts of the basin, with an area of about 45%, experienced severe droughts with high recurrence values (Fig. 5j). As shown in Fig. 5k (SPI-12), the northwestern part of the basin and a small portion of the eastern part experienced severe droughts of high recurrence (6.56–9.84%). The areas covered approximately 13.71% of the basin. According to SPI-24, a severe drought existence zone was found mainly in the western part of the basin, which was approximately 15% of the total area of the Luni River Basin (Fig. 5l).
By contrast, according to SPI-3, approximately 29% of the total basin area experienced extreme drought events with high-recurrence values (1–3%); the area was mainly located in the southwestern parts of the basin (Fig. 5m). According to SPI-6, high occurrence values (2–4%) of severe droughts were observed in the central and southwestern parts of the basin; the area covered 10.69% of the total basin area (Fig. 5n). According to SPI-12, the regions that experienced extreme droughts with high-recurrence values (3–6%) were predominantly situated in extreme northern and eastern parts of the basin; the area was 12% of the total basin area (Fig. 5o). According to SPI-24, an extreme drought occurrence zone with high-recurrence values (3–7%) was mainly situated in the extreme southern and northern portions of the study area. The zone occupied 29.75% of the total basin area (Fig. 5p). Spatial analysis shows that drought events vary from mild to severe drought among the stations. Similar findings were reported by Mundetia and Sharma [42], Dutta et al. [47], and Chhajer et al. [41]. It also recognizes that the western part of the basin is more prone to drought. This may be due to higher temperatures, lower rainfall, and different geographical locations.
4.3 Trend analysis of the SPI values
Figure 6 illustrates the trends in drought intensity according to SPI-6, SPI-9, SPI-12, and SPI-24, obtained by the Mann–Kendall test. The statistically significant trend was identified at three significance levels of 0.01, 0.05, and 0.10. Approximately 46.15%, 38.46%, 30.77%, and 33.33% of the rain gauge stations reported negative trends in SPI-6 (Fig. 6a), SPI-9 (Fig. 6b), SPI-12 (Fig. 6c), and SPI-24 (Fig. 6d), respectively.
Any significant declining trend was not detected in SPI-1. However, only three stations had a significant decreasing trend in SPI-3 values. These stations are Ajmer and Jawaja in the district of Ajmer and Sanchore in Jalore district.
A significant decreasing trend was observed in Ajmer, Jawaja, and Dengana stations at a 99% confidence level (SPI-6). However, a significant decreasing trend was observed at a confidence level of 95% in Srinagar and Sheoganj, and at a confidence level of 90% in Kharchi and Bilara. Significant positive trends were also identified at a confidence level of 99% in Barmer, Pachpadra, Sheo, Jaswantpur, Shergarh, Bhinai, Mangaliwas, Nasirabad, Pisangan, Vijaynagar, Baitu, and Fategarh; at a confidence level of 95% in Pushkar; and at 90% in Sojat and Chohtan (Table 4).
There was a significant decreasing trend in SPI-12 in the stations of Phalodi, Ajmer, Jawaja, Mangaliwas, Srinagar, Vijaynagar, Dengana, and Sheoganj. In SPI-24, similar trends were also found. Northwestern parts of the basin showed statistically significant positive SPI-value trends. In contrast, statistically significant negative trends in the northeastern portion of the basin were identified. However, no trend was detected in the center of the basin. The linear trend of different SPI categories of Dengana station also showed sharp decreasing trends (Fig. 7).
It is interesting to note that SPI-1 and SPI-3 are unable to detect significant trends in drought events. However, SPI-12 and SPI-24 timescales are capable of detecting a significant trend. This means that the ability to detect trends is increased with the increase in SPI timescale. This finding is corroborated with the study of Mahajan and Dodamani [65]. In addition, the detection of significant drought trend is also increased with an increase in the SPI timescale.
5 Conclusion
Drought monitoring and assessment for improved management strategies and policy development are lacking in numbers of underprivilege drought-prone and economically backward regions in India, and such studies are exaggerated the spatial, temporal, and trend behavior of meteorological drought events through the SPI values of the Luni River Basin in Rajasthan. The SPI and the GIS techniques were adopted to identify the significant drought years and also to demarcate the significant drought-prone areas. The maximum drought periods and the corresponding duration were identified, and the results affirm that this basin was affected by some exceptional drought events. The various SPI timescales present distinctive drought periods and their intensities, which play a very crucial role in seasonal drought analysis. By using the data about drought occurrence, severity, spatial pattern, and trend analysis, detailed and efficient management and planning can be developed to mitigate droughts effectively. In summary, the study portrayed that since 1973, severe and extreme droughts occurred during fourteen years in the study area and after 1985, the occurrence of severe and extreme droughts increased. SPI-3 results revealed that the monsoon months are more vulnerable than the other seasons. Moreover, June is more prone to severe droughts, whereas September is more prone to extreme droughts.
The results of Z statistics showed the declining trend in SPI value was observed in the northeastern and southeastern parts of the study area. However, the western portion of the basin depicts an increasing trend of SPI values, while the middle portion of the study area has no identifiable trend.
As low precipitation, high fluctuation in the average rainfall and climate change, especially owing to regional and global warming, has a severe effect on the occurrence of drought. That said, it is crucial to prepare suitable drought management policies and effectively execute these policies with a more prominent association with and support from the government and private associations. The policies are required for the high and very-high drought-affected stations such as Chohtan, Jalore, Bilara, Dengana, Parbatsar, Sheoganj, and Sirohi. The influence of drought is enormous in the basin. In particular, farming and water divisions are the two most influenced aspects of this basin. Thus, the strategies related to the appropriate utilization of surface water and the ideal utilization of groundwater during farming should be consolidated into the moderation strategies and programs to alleviate the influence of droughts in the future, particularly in the severe and extreme drought zones of the various timescales.
Maximum agricultural areas of the watershed are fallen under the severe drought prone due to the adverse effect of Aravalli Mountain, less vegetation cover, and uneven distribution pattern of rainfall. The Aravalli Mountain is influenced not only by the uneven rainfall distribution but also the adverse effect of soil moisture content and led to the developed agricultural drought. Non-suitable land and environmental management strategies affected the climatic condition in this watershed. Finally, this study assessed the trends of drought and its occurrence, and it is expected that this study will be a valuable guide toward understanding the nature of drought and will help in performing efficient management strategies to alleviate the problem of drought in this study area adequately.
References
Wilhite DA (1997) Responding to drought: common threads from the past, visions for the future. Jawra J Am Water Resour Assoc 33:951–959. https://doi.org/10.1111/j.1752-1688.1997.tb04116.x
Buttafuoco G, Caloiero T, Coscarelli R (2015) Analyses of drought events in Calabria (southern Italy) using Standardized Precipitation Index. Water Resour Manag 29:557–573. https://doi.org/10.1007/s11269-0114-0842-5
Pal JS, Small EE, Eltahir EA (2000) Simulation of regional scale water and energy budgets: Representation of subgrid cloud and precipitation processes within RegCM. J Geophys Res Atmos 105:29579–29594. https://doi.org/10.1029/2000JD900415
Venkateswarlu J (1992) Disaster management: a national perspective. Drought network news 4:4–6. International Drought Information Center, University of Nebraska, Lincoln, Nebraska, USA
Glantz MH (1994) Drought follows the plow: cultivating marginal areas. Cambridge University Press, Cambridge
Gumus V, Algin HM (2017) Meteorological and hydrological drought analysis of the Seyhan—Ceyhan River Basins, Turkey. Meteorol Appl 24:62–73. https://doi.org/10.1002/met.1605
Yuan F, Ma M, Ren L, Shen H, Li Y, Jiang S, Kong H (2016) Possible future climate change impacts on the hydrological drought events in the Weihe River Basin, China. Adv Meteorol. https://doi.org/10.1155/2016/2905198
Schubert SD, Suarez MJ, Pegion PJ, Koster RD, Bacmeister JT (1930s) On the cause of the 1930s Dust Bowl. Science 303:1855–1859. https://doi.org/10.1126/science.1095048
Wilhite DA (2000) Drought as a natural hazard: concepts and definitions. In: Wilhite DA (ed) Drought: a global assessment. Routledge, London, pp 3–18
Cook BI, Miller RL, Seager R (2009) Amplification of the North American “Dust Bowl” drought through human-induced land degradation. Proc Natl Acad Sci 106:4997–5001
Thomas T, Nayak PC, Ghosh NC (2015) Spatiotemporal analysis of drought characteristics in the Bundelkhand region of central India using the Standardized Precipitation Index. J Hydrol Eng 20:05015004–5015012. https://doi.org/10.1061/(ASCE)HE.1943-5584.0001189
Agnew C, Warren A (1996) A framework for tackling drought and land degradation. J Arid Environ 33:309–320
Smakhtin VU, Hughes DA (2007) Automated estimation and analyses of meteorological drought characteristics from monthly rainfall data. Environ Modell Softw 22:880–890
Agnew C (1990) Spatial aspects of drought in the Sahel. J Arid Environ 18:279–293
Le Houérou HN (1996) Climate change, drought and desertification. J Arid Environ 34:133–185
Jentsch A, Beierkuhnlein C (2008) Research frontiers in climate change: effects of extreme meteorological events on ecosystems. CR Geosci 340(9–10):621–628
Palmer WC (1965) Meteorological drought. Weather Bureau Research PaDer no. 45, US Dept. of Commerce, Washington, DC, p 58
Palmer WC (1968) Keeping track of index. Weatherwise 21:156–161
Gibbs WJ, Maher JV (1967) Rainfall deciles as drought indicators. Bureau of Meteorology Bulletin No. 48, Commonwealth of Australia, Melbourne
Van Rooy MP (1965) A rainfall anomaly index independent of time and space. Notos 14:43–48
Frere M, Popov GF (1979) Agrometeorological crop monitoring and forecasting. FAO.
Shafer BA, Dezman LE (1982) Development of a Surface Water Supply Index (SWSI) to assess the severity of drought conditions in snowpack runoff areas. In: Proceedings of the (50th) 1982 annual western snow conference. Colorado State University, Fort Collins, pp 164–75
Bhalme HN, Mooley DA (1980) Large-scale droughts/floods and monsoon circulation. Mon Weather Rev 108:1197–1211
Sastri ASRAS (1993) Agricultural drought management strategies to alleviate impacts: examples from the arid and sub humid regions of the Indian Subcontinent. In: Wilhite DA (ed) Drought assessment, management, and planning: theory and case studies. Kluwer Academic Publishers, Dordrecht, pp 65–86
Petrasovits I (1990) General review on drought strategies. In: Proceedings 14th international congress on irrigation and drainage. International Commission on Irrigation and Drainage, Rio de Janeiro, No. 1-C, pp 1–11
McKee TB, Doesken NJ, Kleist J (1993) The relationship of drought frequency and duration to time scales. In: Proceedings of the 8th conference on applied climatology, vol 17. American Meteorological Society, Boston, pp 179–183
Smakhtin VU (2001) Low flow hydrology: a review. J Hydrol 240:147–186
Mallya G, Mishra V, Niyogi D, Tripathi S, Govindaraju RS (2016) Trends and variability of droughts over the Indian monsoon region. Weather Clim Extrem 12:43–68
Ahmad L, Parvaze S, Majid M, Kanth RH (2016) Analysis of historical rainfall data for drought investigation using Standard Precipitation Index (SPI) under temperate conditions of Srinagar Kashmir. Pak J Meteorol 13:29–38
Yan Z, Zhang Y, Zhou Z, Han N (2017) The spatio-temporal variability of droughts using the Standardized Precipitation Index in Yunnan, China. Nat Hazards 88:1023–1042
Mondol M, Haque A, Ara I, Das SC (2017) Meteorological Drought Index Mapping in Bangladesh Using Standardized Precipitation Index during 1981–2010. Adv Meteorol 2017:1–17. https://doi.org/10.1155/2017/4642060
Sabau NC, Man TE, Armaş A, Balaj C, Giru M (2015) Characterization of agricultural droughts using Standardized Precipitation Index (SPI) and Bhalme-Mooley drought index (BDMI). Environ Eng Manag J (EEMJ) 14:1441–1454
Nury AH, Hasan K (2015) Analysis of drought in northwestern Bangladesh using Standardized Precipitation Index and its relation to Southern oscillation index. Environ Eng Res 21:58–68
Rahman MR, Lateh H (2016) Meteorological drought in Bangladesh: assessing, analysing and hazard mapping using SPI, GIS and monthly rainfall data. Environ Earth Sci 75:1026. https://doi.org/10.1007/s12665-016-5829-5
Sebenik U, Brilly M, Šraj M (2017) Drought analysis using the standardized precipitation index (SPI). Actageogr Slov 57:31–49
David V, Davidova T (2015) Analysis of drought events-case study for Blanice River Catchment (Czech Republic). Acta Phys Pol A 128:2B
Seçkin N, Topçu E (2016) Drought analysis of the Seyhan Basin by using Standardized Precipitation Index (SPI) and L-moments. Tarım Bilimleri Dergisi 22:196–215
Arunvenkatesh S, Janapriya S, Rajasekar M, Muthuchamy I (2016) Spatial and temporal analysis of drought characteristics in Parambikulam-Aliyar Sub-basin, Tamil Nadu. Int J Bioresour Stress Manag 7:420–425
Amrit K, Pandey RP, Mishra SK (2014) Study of regional meteorological drought characteristics in Rajasthan. Int J Sci Eng Technol 2014:83–88
Reddy MJ, Ganguli P (2013) Spatio-temporal analysis and derivation of copula-based intensity–area–frequency curves for droughts in western Rajasthan (India). Stoch Env Res Risk Assess 27:1975–1989
Chhajer V, Prabhakar S, Rama CPP (2015) Development of index to assess drought conditions using geospatial data a case study of Jaisalmer district, Rajasthan, India. Geoinform Polon 14:29–40
Mundetia N, Sharma D (2015) Analysis of rainfall and drought in Rajasthan State, India. Glob NEST J 17:12–21
Łabędzki L (2007) Estimation of local drought frequency in central Poland using the Standardized Precipitation Index SPI. Irrigat Drain 56(1):67–77
Capra A, Scicolone B (2012) Spatiotemporal variability of drought on a short-medium time scale in the Calabria Region (Southern Italy). Theoret Appl Climatol 110:471–488
Singh B, Arya CK, Singh J, Mourya KK (2014) Analysis of rainfall data for storage and irrigation planning in humid southeastern plain of Rajasthan in India. J Appl Nat Sci 6:214–219
Tugjamba N (2008) Water scarcity and adaptation strategy under climate change in Luni River Basin, India. Geophys Res Abstr 10:EGU2008-A-03385
Dutta D, Kundu A, Patel NR, Saha SK, Siddiqui AR (2015) Assessment of agricultural drought in Rajasthan (India) using remote sensing derived Vegetation Condition Index (VCI) and Standardized Precipitation Index (SPI). Egypt J Remote Sens Space Sci 18:53–63
Svoboda M, Hayes M, Wood D (2012) Standardized Precipitation Index user guide. World Meteorological Organization, Geneva
ESRI (2015) ArcGIS/ArcMap (version 10.3). New York, Redlands, California, USA.
Das J, Mandal T, Saha P, Bhattacharya SK (2020) Variability and trends of rainfall using non-parametric approaches: a case study of semi-arid area. Mausam 71(1):33–44
Singh B, Rajpurohit D, Vasishth A, Singh J (2012) Probability analysis for estimation of annual one day maximum rainfall of Jhalarapatan area of Rajasthan, India. Plant Arch 12(2):1093–1100
Yadav SK, Nath S, Gautam S (2018) Analysis of rainfall variability in western Rajasthan, India. J Pharm Phytochem 7(4):1592–1595
Poonia S, Rao AS, Singh DV, Choudhary S (2014) Rainfall characteristics and meteorological drought in Hanumangarh district of arid Rajasthan. Ann Plant Soil Res 16(4):279–284
Das J, Mandal T, Saha P (2019) Spatio-temporal trend and change point detection of winter temperature of North Bengal, India. Spat Inf Res 27(4):411–424. https://doi.org/10.1007/s41324-019-00241-9
Guttman NB (1998) Comparing the Palmer drought index and the Standardized Precipitation Index. JAWRA J Am Water Resour Assoc 34:113–121
Thom HCS (1958) A note on the gamma distribution. Mon Weather Rev 86:117–122
Edwards DC (1997) Characteristics of 20th century drought in the United States at multiple time scales (No. AFIT-97–051). Air Force Inst. of Tech Wright-Patterson AFB OH.
Thom HCS (1966) Some methods of climatological analysis. WMO technical note number 81. Secretariat of the World Meteorological Organization, Geneva
Mann HB (1945) Non parametric tests against trend. Econometrica 13:245–259
Kendall MG (1975) Rank correlation methods. Griffin, London
Pearson ES, Hartley HO (1966) Biometrika tables for statisticians, vol 1, 3rd edn. Cambridge University Press, London
Das J, Rahman ATMS, Mandal T, Saha P (2020) Challenges for sustainable groundwater management for large scale irrigation under changing climate in lower Ganga River Basin in India. Groundw Sustain Dev. https://doi.org/10.1016/j.gsd.2020.100449
Mekonen AA, Berlie AB, Ferede MB (2020) Spatial and temporal drought incidence analysis in the northeastern highlands of Ethiopia. Geoenviron Dis 7(1):1–7
Kalisa W, Zhang J, Igbawua T, Ujoh F, Ebohon OJ, Namugize JN, Yao F (2020) spatio-temporal analysis of drought and return periods over the East African region using Standardized Precipitation Index from 1920 to 2016. Agric Water Manag 237:106195
Mahajan DR, Dodamani BM (2015) Trend analysis of drought events over upper Krishna basin in Maharashtra. Aquat Proc 4:1250–1257
Acknowledgements
The authors acknowledge the Water Resources Department, Rajasthan, for providing the rainfall data. Also, the authors would like to thank anonymous reviewers and editor for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Das, J., Gayen, A., Saha, P. et al. Meteorological drought analysis using Standardized Precipitation Index over Luni River Basin in Rajasthan, India. SN Appl. Sci. 2, 1530 (2020). https://doi.org/10.1007/s42452-020-03321-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-020-03321-w