1 Introduction

The recognition of the Trans-European Suture Zone (TESZ) structure, spanning from the East European Platform to the Paleozoic terranes of Western Europe, is key for understanding the geotectonic history of Europe. However, the TESZ is covered by a thick layer of Paleozoic and Mesozoic sediments along almost its entire length, so it is only geophysical data that can provide information on the structure of its deep basement.

Views on this area have changed significantly since W. Teisseyre (based on surface geological studies) and A. Tornquist (contributing the results of magnetic field analysis) introduced the notion of the TT line separating the Precambrian and Paleozoic Platforms. The progress of geophysical methods has produced information on successively deeper layers and the structure of this contact area between the two platforms turned out to be much more complicated than previously supposed. This has affected the terminology describing the area: from the TT line, through the TT zone and, finally, the TESZ. However, in spite of the inflow of a tremendous amount of data, not all geotectonic problems have been solved. One of the vital unresolved questions is whether the Caledonian Deformation Front (CDF) exists and what its position is in relation to the East European Platform margin (Dadlez, 2000). The position of the Variscan Deformation Front (VDF) is also controversial.

Although the seismic survey is the principal research method for studying the Earth’s interior, many vital and complementary data on the distribution of physical parameters in the Earth’s interior are supplied by electromagnetic, gravity and geothermal investigations. These methods are based on the interpretation of potential fields and provide generalized information. Nevertheless, such data may be of great value in the study of deeper parts of the crust, where seismic structures are not so clearly observed because of later tectonic and metamorphic processes.

MV sounding, one of the methods that utilize natural variations of the Earth’s electromagnetic field, enables us to obtain information on electric conductivity and to draw conclusions about physical properties of deep structures. Of particular interest is information on the location of large, widespread and well-conducting structures in the crust at depths that are inaccessible, thus far, for even the deepest drillings. These structures were formed by past tectonic processes and are, in a way, the signature, or record, of these processes. An analysis of the position and origin of these structures allows us to reconstruct the geological buildup of the study area.

Magnetovariational surveys were initiated in Central Europe, first in Germany and then in Poland, Czechoslovakia and Ukraine. The first important results were the documentation and preliminary interpretation of the North German-Polish Conductivity Anomaly (Fleischer, 1954; Schmucker, 1959; Wiese, 1962, 1963; Jankowski, 1967) and the Carpathian Conductivity Anomaly (Jankowski, 1967; Jankowski et al., 1985). In these early, pioneering works very simple methods of interpretation were used, sometimes qualitative rather than quantitative. Later, more sophisticated methods allowed determining more precise models of the conductivity distribution.

The MV results have been routinely presented in the form of the so-called induction arrows or tippers, based on the relation between vertical and horizontal components of the magnetic field at the measuring point. Recently, the transfer function (called HMT) which is a relationship between horizontal components of the magnetic field, at the measuring point and at the reference point, has become increasingly popular. The spatial distribution of some of its invariants enables easy mapping of the position of deep, widespread and well-conducting anomalies. Additionally, the conductivity distribution modeling with the use of HMT is more stable and reliable than the tippers inversion.

2 Geotectonic Background

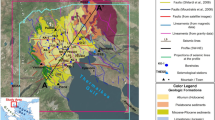
In the tectonics of Europe, the forefield of the East European Platform is a unique area (Fig. 1).

Fig. 1
figure 1

Tectonic sketch map of Central Europe

Full size image

It was formed as a result of consecutive collisions of the smaller Gondwana-derived crustal fragments (microplates) of Avalonia and Armorica (Tait, 1999; Lewandowski, 2003). This area, called the Trans-European Suture Zone (TESZ) (Pharaoh, 1999), intersects the European continent from the Black Sea on the southeast to British Isles on the northwest and is likely to extend further west, reaching the Appalachian orogen on the other side of the Atlantic (Keller and Hatcher, 1999). A particular feature of the TESZ is the deep sedimentary basin that formed during the Permian and the Mesozoic and covered the older rocks. The paleotectonic evolution of the basin was mainly shaped by the collision of the three paleoplates (Laurentia, Baltica and Gondwana) and the formation of the Polish Caledonides which took place from the Late Ordovician to the Silurian (Berthelsen, 1992; Lamarche and Scheck-Wendereroth, 2005).

Most of the tectonic units are a result of the Laramian inversion of the Permian-Mesozoic Polish Basin. The inversion of the central part of the basin in the Tertiary gave rise to the Mid-Polish Anticlinorium, accompanied by two depressions divided into smaller blocks and separated by transverse faults (Kutek, 2001).

Northwest of the south Baltic, the TESZ forks out into several branches of Late Carboniferous and Early Permian troughs, which lie between the trans-European fault (north Germany, south Jutland) and the Sorgenfrei-Tornquist zone (Scania, north Jutland). Subsequently, they were reactivated by extensional motions in the Mesozoic and inversions in the Late Carboniferous and Early Tertiary (Thybo et al., 1990, 2001). The CDF runs farther to the west, close to Rugen (Tanner and Meissner, 1996). Data from Bornholm confirm the different ages and layering on the two sides of the CDF (Meissner and Blundell, 1996). The Caledonian period is the least recognized evolutionary stage of the TESZ because of the considerable thickness of the Permian-Mesozoic and Devonian-Carboniferous sedimentary cover. According to Dadlez et al. (2005), rapid counterclockwise rotation during the Ordovician—Early Silurian caused intense left-lateral shearing stresses in the relatively young crust of the Baltica, particularly in its southern corner. This resulted in splitting and detachment of elongated and narrow slivers of crust and their wandering northwest along the rotating Baltica’s edge. At the same time, the northern drift of Avalonia (and other exotic parts of Gondwana) led to the collision with Baltica. Detached fragments of Baltica docked first at Avalonia and were then re-attached to Baltica in the Silurian. These fragments now form the TESZ basement.

The arguments supporting the presence of the Caledonian orogen to the west of the Baltica stem mainly from the analysis of sub-Devonian profiles in the Rugen region. In the tectonically deformed Ordovician, a layer of turbiditic greywacke, some thousand meters thick, was detected (Katzung, 2001; Giese and Köppen, 2001). East of Rugen, the Lower Palaeozoic formations were not recognized until the Koszalin-Chojnice zone (Dadlez, 1978; Podhalanska, 2007). The presence of formations that were deformed prior to the Devonian, exceeding in thickness the deformed formations of equal age from the western part of the East European Craton, suggests associations of the Koszalin-Chojnice zone with the Rugen zone. The Ordovician convergence and the collision of the Avalonia and Baltica (and hence, indirectly, the Caledonian collision along the northern part of the western rim of the Baltica) have been confirmed by palaeomagnetic studies (Torsvik and Rehnström, 2003). The development of sedimentary basins on the western slope of the Baltica is also an indirect record of the Caledonian tectonic processes within the TESZ (Jaworowski, 2000). Determination of the position and thickness of these very deep-seated basins is extremely difficult and may only be possible with the use of geophysical data.

Our current knowledge of physical parameters of the crust in the TESZ region results from seismic (Guterch and Grad, 2006; Grad et al., 2002) and electromagnetic (Ernst et al., 2008; Schafer et al., 2011) surveys. These surveys confirm the presence of large horizontal contrasts in the distributions of physical parameters and thus make it possible to distinguish the three crustal types that correspond to the East European Platform, the TESZ zone, and the Palaeozoic Platform. The most interesting result of these studies was the finding that in the Polish Basin, rocks of seismic P-wave velocities less than 6.0 km/s and electric conductivities of a few ohmmeters may reach down to depths of 20 km. This corroborates suspicions that the sedimentary cover is very thick and that the rocks occurring in the basin’s basement are probably strongly metamorphic or of volcanic origin. Note that the interpretation of deep seismic and electromagnetic sounding is routinely carried out along 2D profiles across the studied structures. The limited number of such deep profiles makes precise 3D structural interpretation difficult. This paper demonstrates that the interpretation of MV soundings by analyzing the HMT distribution is a good tool for following the 3D course of such deep-seated, well-conducting structures.

3 The Horizontal Magnetic Tensor

The results of MV soundings are routinely presented as tippers T or induction arrows (once called the Wiese vectors). These functions are defined by a linear relationship between the vertical component H z and the horizontal components H x and H y of the magnetic field (Parkinson, 1959; Wiese, 1962):

$$ H_{z} = \bf{T} \, \bf{H}_{h} = \left[ {\it{T}_{x} T_{y} } \right] \, \left[ {\begin{array}{*{20}c} {H_{x} } \\ {H_{y} } \\ \end{array} } \right] $$
(1)

Components T x , T y reflect the horizontal asymmetry of the excess currents of a galvanic and induction nature arising in the Earth due to lateral variations in the electric conductivity (Berdichevsky and Dmitriev, 2008).

The components of matrix T form the induction arrow, both its real and imaginary parts. The real induction arrow is defined in such a way that it is directed from the zones of higher conductivity (current concentration) towards those of lower conductivity (current deconcentration), Wiese convention. Above the anomaly axis, the vertical component H z vanishes, and the tippers become zero; they attain their maximum values on the resistive side above a conductivity contrast. So, maps of real tippers may be most helpful in locating geoelectrical structures, their tracing, and classifying by conductivity. Such a manner of presentation, though helpful to identify individual conducting structures, failed however, in regions with more complicated geology. A detailed discussion on the processing and interpretation of MV data can be found in Egbert (2002) and Berdichevsky et al. (2009) as well as in Zhang et al. (1993) and Ritter and Banks (1998), where the problem of galvanic distortion of the tippers is discussed in detail.

The results of MV sounding can also be presented in the form of the horizontal magnetic tensor (HMT) M. The HMT is a relationship between the horizontal magnetic fields at the observation point r and the reference station r B (Berdichevsky, 1968; Schmucker, 1970; Varentsov, 2005, 2007; Berdichevsky and Dmitriev, 2008):

$$ {\mathbf{H}}_{h} \left( {\mathbf{r}} \right) = {\mathbf{M}}\left( {{\mathbf{r}}\left| {\mathbf{r}} \right._{B} } \right){\mathbf{\rm {\bf{H}}}}_{h} \left( {{\mathbf{r}}_{B} } \right) $$
(2)

Tensor M reflects variations in the geoelectric medium between the reference and the observation sites. We obtain the clearest image of these variations if the reference site is located in an area of normal magnetic field (i.e., above a horizontally homogeneous structure). Otherwise, the effect of inhomogeneities situated around the reference site will be transferred to the entire survey area and superimposed on the effects of inhomogeneities situated around the observation sites (Berdichevsky and Dmitriev, 2008).

Presenting the magnetovariational results in the form of HMT is more informative than in the form of induction arrows (Berdichevsky et al., 2009). An analysis of invariants of this tensor gives us information about the magnetic field induced in the Earth and allows estimating the parameters of the geoelectric structure. A detailed discussion on the properties of magnetic tensor invariants and the information they give us about the structure can be found in Berdichevsky and Dmitriev (2008); here we give just a few examples.

By analogy to Swift (1967) and Bahr (1988) skew parameters for the impedance tensor, it is possible to define a magnetic asymmetry skew parameter which contains information about the dimensionality of the geoelectric structure. If the reference site is located in a horizontally homogeneous zone and the skew parameters are close to zero, it means that the medium under investigation is two-dimensional or quasi two-dimensional and we can estimate the principal (longitudinal and transverse) directions.

A very interesting feature of the HMT is its ability to map the location of well-conducting rocks using spatial distribution of certain rotational invariants. Let us apply the SVD decomposition to the tensor M

$$ {\text{\bf{M}}} = \bf{U}\left[ {\begin{array}{*{20}c} {\lambda_{1} } & {} \\ {} & {\lambda_{2} } \\ \end{array} } \right]{\bf{V}}^{\it{H}} $$
(3)

where the singular values λ1 and λ2 satisfy the condition λ1 > λ2 ≥ 0, and matrices U and V are unitary matrices. We can express the invariants det M and tr M in terms of geometric and arithmetic means, λ G and λ A , of its singular values, λ 1 and λ 2 (Berdichevsky and Dmitriev 2008):

$$ \begin{gathered} \lambda_{G}^{2} = \det {\mathbf{M}} = M_{xx} \, M_{yy} - M_{xy} \, M_{yx} = \lambda_{1} \, \lambda_{2} \hfill \\ 2\lambda_{A} = tr{\mathbf{ M}} = M_{xx} + M_{yy} = \lambda_{1} + \lambda_{2} \hfill \\ \end{gathered} $$
(4)

The geometric and arithmetic means, λ G and λ A , of the singular values of tensor M can be taken as the invariant parameters characterizing the change in the average strength and phase of the horizontal magnetic field on the way from the reference site to the observation site. The most convenient parameter is λ G because it is less subjected to the distorting influence of inhomogeneities around the reference site.

Let the “normal” reference site B N be located in a horizontally homogeneous area and the “anomalous” reference site B A be located in a horizontally inhomogeneous area. According to (4), we get:

$$ \lambda_{G} \left( {{\mathbf{r}}\left| {\mathbf{r}} \right._{{B^{\text{A}} }} } \right) = \frac{1}{{\lambda_{G} \left( {{\mathbf{r}}_{{B^{\text{A}} }} \left| {\mathbf{r}} \right._{{B^{\text{N}} }} } \right)}}\lambda_{G} \left( {{\mathbf{r}}\left| {\mathbf{r}} \right._{{B^{\text{N}} }} } \right). $$

This means that at a given frequency, the values of \( \lambda_{G} \left( {{\mathbf{r}}\left| {\mathbf{r}} \right._{{B^{\text{A}} }} } \right)\,{\text{and}}\,\lambda_{G} \left( {{\text{\bf{r}}}\left| {\text{\bf{r}}} \right._{{B^{\text{N}} }} } \right) \) obtained with the anomalous and normal reference sites, B Aand B N, differ by the same factor \( 1/\lambda_{G} \left( {{\mathbf{r}}_{{B^{\text{A}} }} \left| {\mathbf{r}} \right._{{B^{\text{N}} }} } \right) \), that depends on the positions of the reference sites.

Hence, \( \lambda_{G} \left( {{\mathbf{r}}\left| {\mathbf{r}} \right._{{B^{\text{A}} }} } \right)\,{\text{and}}\,\lambda_{G} \left( {{\mathbf{r}}\left| {\mathbf{r}} \right._{{B^{\text{N}} }} } \right) \)characterize the same relative variations in intensity of the horizontal magnetic field. In this understanding, we associate an increase in \( \left| {\lambda_{G} } \right| \) with the influence of conductive structures (with current concentration) and a decrease in \( \left| {\lambda_{G} } \right| \) with the influence of resistive structures (with current de-concentration).

The situation is clearer when the reference point is located in the normal structure. From the decomposition of matrix M (Eq. 3) it follows that the maximum norm of horizontal magnetic field component at a given point in relation to the norm of normal field is equal to the largest singular value λ1. This is the advantage compared with the parameter \( \left| {\lambda_{G} } \right| = \sqrt{{\lambda_1} {\lambda_2}}\) proposed in Berdichevsky and Dmitriev (2008), which shows us the relationship of average magnetic field (in the two main directions) relative to the normal field. This results in a clearer and more contrasty image of the magnetic field variation. The singular values do not depend on the choice of coordinate system; they depend exclusively on the conductivity distribution within the structure. This means that the spatial distribution of the singular value λ1 over the Earth’s surface is a perfect indicator of the occurrence of well conducting structures.

Although this manner of presentation of MV soundings is advantageous, it is very seldom used because of two requirements that must be fulfilled to calculate the horizontal magnetic tensor directly from registered data. First, the observations must be carried out synchronously in the whole region. Second, the reference point must be selected so that the structure is close to normal, which means it must be situated far enough from the sites where the horizontal conductivity anomalies occur. The fulfillment of these requirements is difficult and considerably increases the cost of the survey.

Yet, it turns out that there is a method for avoiding these inconveniences. This is possible because the magnetic field in a non-conducting atmosphere, and thus at Earth’s surface, is a potential field, and there are spatial relationships (Hilbert transform) between the vertical and horizontal components. This enables a reconstruction of all the magnetic field components from a sufficiently dense set of induction-arrow values (tippers) (Weaver, 1964; Bailey et al. 1974; Banks 1986; Becken and Pedersen, 2003; Jozwiak et al., 2009; Nowozynski, 2011).

Assume that in our Earth model, the three-dimensional structure is size-bounded and embedded in a one-dimensional structure. At infinity, we have a constant, normal field H h alone, and generally, there holds H h  = H n h  + H a h with

$$ {\mathbf{H}}_{h}^{a} \left( {\mathbf{r}} \right) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\frac{{i{\mathbf{k}}}}{{\left| {\mathbf{k}} \right|}}\left( {\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {H_{z}^{a} \left( {\mathbf{r}} \right)e^{ - ik \cdot r} d{\mathbf{r}}} } \right)e^{ik \cdot r} d{\mathbf{k}}} . $$
(6)

where k is the wave number.

Equations 1 and 6 make up a system of linear relationships with which we are able to reconstruct all the anomalous magnetic field components. It is possible to solve this system of equations in an iterative way (Banks 1986; Becken and Pedersen, 2003), but the conjugate gradient method (Jozwiak et al., 2009; Nowozynski, 2011) is more effective.

Performing the calculations for two perpendicular normal magnetic field values, we can now determine the HMT tensor for a reference point r B = ∞ located in infinity:

$$ \left[ {\begin{array}{*{20}c} {H_{x} \left( {\mathbf{r}} \right)} \\ {H_{y} \left( {\mathbf{r}} \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {M_{xx} \left( {{\mathbf{r}}\left| \infty \right.} \right)} & {M_{xy} \left( {{\mathbf{r}}\left| \infty \right.} \right)} \\ {M_{yx} \left( {{\mathbf{r}}\left| \infty \right.} \right)} & {M_{yy} \left( {{\mathbf{r}}\left| \infty \right.} \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {H_{x}^{n} \left( \infty \right)} \\ {H_{y}^{n} \left( \infty \right)} \\ \end{array} } \right] $$

Using normal fields

$$ {\mathbf{H}}^{n1} \left( \infty \right) = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right],{\mathbf{H}}^{n2} \left( \infty \right) = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right], $$

we get:

$$ \left[ {\begin{array}{*{20}c} {M_{xx} \left( {{\mathbf{r}}\left| \infty \right.} \right)} & {M_{xy} \left( {{\mathbf{r}}\left| \infty \right.} \right)} \\ {M_{yx} \left( {{\mathbf{r}}\left| \infty \right.} \right)} & {M_{yy} \left( {{\mathbf{r}}\left| \infty \right.} \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {H_{x}^{n1} \left( {\mathbf{r}} \right)} & {H_{x}^{n2} \left( {\mathbf{r}} \right)} \\ {H_{y}^{n1} \left( {\mathbf{r}} \right)} & {H_{y}^{n2} \left( {\mathbf{r}} \right)} \\ \end{array} } \right] $$

A numerical solution for the system of Eqs. 1 and 3 requires that we know the tipper values on a rectangular grid, while the observational data are usually irregularly spaced. Hence, it is necessary to make an approximation of these data, which can be efficiently done using the regularized spline approximation. Spline approximation f of measured tipper components (ReT x , ImT x , ReT y and ImT y ) has a form:

$$ f\left( {x,y} \right) = \sum\limits_{{k_{x} ,k_{y} }} {f_{{k_{x} ,k_{y} }} } S\left( {\frac{x}{\Updelta x} - k_{x} } \right)S\left( {\frac{y}{\Updelta y} - k_{y} } \right) $$

where S is an infinite cubic spline such that S(0) = 1; S(k) = 0 for k ≠ 0.

Tippers \( f_{k_{x},k_{y}} = f\left( {k_{x} \Updelta x,k_{y} \Updelta y} \right) \) are calculated from measured tippers \( \tilde{f}\left( {x_{k} ,y_{k} } \right) \) using regularized version of the least squares problem:

\( \mathop {\min }\limits_{{f_{{k_{x} ,k_{y} }} }} \, \sum\limits_{k} {\left( {f\left( {x_{k} ,y_{k} } \right) - \left( {\tilde{f}\left( {x_{k} ,y_{k} } \right)} \right)} \right.}^{2} + \sum\limits_{{_{{k_{x} ,k_{y} }} }} {\left[ {\lambda^{2}_{L} \left( {f^{''} \left( {k_{x} \Updelta x,k_{y} \Updelta y} \right)} \right)^{2} + \lambda^{2}_{M} \left( {k_{x} ,k_{y} } \right)\left( {f\left( {k_{x} \Updelta x,k_{y} \Updelta y} \right)} \right)^{2} } \right]} \) where the λ L and λ M parameters control the smoothness and ensure the uniqueness and stability of the solution. These parameters and grid size are chosen so that the tippers approximation error does not exceed their determination error.

The system of Eqs. 1 and 6 is then reduced to a well-conditioned system of linear equations of a large number of unknowns, which can be solved by the conjugate gradient method. This method is always convergent and for a well-conditioned problem, as in our case the convergence is quite rapid. Such a large system with a full matrix is possible to solve only using two-dimensional FFT algorithm. In this work, the calculation for the Central Europe area was performed on the 1,000 × 1,000 grid of nodes placed 1 km apart. The system of equation of 106 complex unknowns was solved two times (for two directions of the normal field) to determine the magnetic tensor M defined by Eq. 3.

As shown by Nowozynski (2011), the procedure briefly described above is very useful and allows us to determine HMT in areas where a sufficient number of data is available. The induction tippers are determined from single field recordings. It is possible both to collect these data systematically over the area of interest and to use ample archival data sets. In addition, the HMT data thus obtained are not affected by possible inhomogeneities near the reference station, as the result obtained is the same as for a reference point at infinity. We can therefore use the distribution of the maximum singular value for mapping the conductive structures.

4 The HMT Reconstructions for the Central European Region

The methodology proposed here was applied to a large data set collected over the last 50 years. The basic part of the collection is the result of MV soundings carried out in Poland during the last 20 years. This collection has been supplemented by archival data from Poland and neighboring countries (Wybraniec et al., 1999). Additional data have been obtained courtesy of H. Brasse, I. Logvinov, and I. Varentsov. The data set is not consistent because the data do not always strictly correspond with the assumed periods of the field variations. The most recent data were calculated by modern numerical methods based on ample experimental material. Older data were obtained by simplified methods. However, for long periods of the field changes (e.g., 1,800 s) the induction tippers varied quite slowly; thus, the final result should not be affected by this inconsistency.

It is also noted that the first attempt to make an integral presentation of archival MV sounding results was made by Wybraniec et al., (1999). However, in the Hilbert transform (3), it was assumed that the horizontal magnetic field H is equal to a normal field, and then the tipper values are equal to the vertical field components H z . This means that, in contrast to the complete iterative process mentioned in the previous section, only the first iteration was done. Furthermore, that data set was much smaller, the authors used only the real parts of tippers, and the calculations were carried out on a coarse grid. Therefore, the results were approximate and many details of the conductivity distribution got lost.

In Fig. 2, we present data in a classical manner, with induction (real) tippers for the period T = 1,800 s. The map displays the Carpathian arc and, less clearly, the so-called North German-Polish anomaly. Of course, a more thorough analysis would make it possible to identify other well-conducting areas, but their locations and shapes are not so obvious. They could be determined in detail only by numerical modeling, which is practically impossible for so widespread 3D structures.

Fig. 2
figure 2

Results of magnetovariational sounding in the form of induction arrows (real part) for T = 1,800 s

Full size image

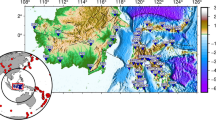
In Fig. 3a, we present the results of transformation of the same data set into the HMT. The figure displays the spatial distribution of the most informative HMT invariant (i.e., the largest singular values), which corresponds to the maximum values of the induced magnetic field. As we can see, the pattern obtained is much more orderly. There are clearly marked, large, elongated, anomalous structures (red in color) in which the amplitudes of the induced magnetic field are twice those in normal regions. This indicates that these are the sites of well-conducting rocks. The long period of field changes (e.g., 1,800 s) for which the calculations were made suggests that we are dealing with deep-seated crustal complexes. To determine the depth of these changes in greater detail, we would have to know the HMT for a larger range of periods. This requires acquisition of data sets for shorter periods than those currently in hand. Nonetheless, by relying on the data obtained to date, we propose hypothetical positions for the VDF and CDF fronts as shown in Fig. 3a.

Fig. 3
figure 3

a Results of magnetovariational sounding as a map of the spatial distribution of the most informative invariants of the horizontal magnetic tensor M (the largest singular value). The high values (red in color) show the locations of conducting structures. Hypothetical locations of the CDF and the VDF are indicated by black lines with triangles. On the right: the results of magnetotelluric soundings on the P2 profile (Ernst et al., 2008) (b) and the PREPAN profile (Ernst et al., 2002) (c), where the spatial distribution of the largest singular value (black for 2D models; red for tipper-reconstruction) is shown below a 2D conductivity model for both cases

Full size image

A more exact determination of the depths of the conducting structures identified by the HMT is possible by comparing the MV results with the 2D MT models at profiles across the structures in question (Fig. 3b, c). This comparison also demonstrates that the calculated values of the HMT for 2D profiles agree with those obtained on the basis of observational data by using the proposed method. We can see that the shape of these two curves is very similar, although the curve of the largest singular value for the HMT reconstructed from tippers is smoother and its amplitudes are somewhat smaller than those calculated using 2D models. This is obviously a result of approximation of real data on a grid covering the study area, but it is necessary to reconstruct the HMT from tippers. However, for both curves we observe a substantial increase above the well-conducting structures, and we can identify their location very clearly.

We can see in Fig. 3b, c that in the Carpathians (PREPAN profile) and Pomeranian zones of the TESZ (P2 profile), the well-conducting structures are modeled at 7–20 km depth (red color in Fig. 3b, c). These are conducting complexes with huge values of integral conductivity, reaching 6,000 S in the Carpathians and even 10,000 S in the TESZ. Unfortunately, we are unable to decide unambiguously what the conductivity mechanism is. It may be ionic-type conductivity, and then we would be dealing with porous rocks saturated with mineralized waters. Yet, this may also be electron-type conductivity, and then we would probably be dealing with black shales or graphite-structures. An analysis made for the Carpathians (Jankowski et al., 2008) indicates that the conducting material is likely to be rocks filled-in with mineral water. In the region of Pomerania, where the conducting complexes lie somewhat deeper, interpretation is more difficult and researchers hold diverse opinions.

Whatever conductivity models are true, these deep-seated, well-conducting formations seem to be genetically linked to geologic structures formed due to Paleozoic diastrophic cycles and they are most likely a result of subsidence of the sedimentary material in the foredeep of these orogens. Such conclusions would be very important because many questions as to the course and range of the Caledonian and Variscan structures still lack an unequivocal answer. Any new information improves the understanding of the geotectonic evolution of a region.

In Fig. 3a, on the map presenting a distribution of conductive structures traced by the MV soundings, we superimposed a map of hypothetical locations of the CDF (as it is usually accepted) adopted after Berthelsen (1992) (dotted line) and with the VDF according to Pozaryski and Karnkowski (1992) (dashed line), Dadlez, 1994 (dotted line) and Narkiewicz and Dadlez (2008) (solid line). Of greatest interest are anomalies that are possibly related to syn-Caledonian structures, currently concealed under a thick cover of younger sedimentary rocks. The Early Paleozoic history of the study area is still enigmatic. It is widely accepted that it was occupied by parts of the north German-Polish Caledonian mobile belt (Ziegler, 1990; Pharaoh, 1999); however, the details of its position and evolution are interpreted in different ways. After Berthelsen (1992), the CDF runs somewhat northeast of the Rugen-Koszalin line, which is confirmed by the borehole data from Rugen (Tanner and Meissner, 1996)], Bornholm (Meissner and Blundell, 1996) and Koszalin-Chojnice zone (Dadlez, 1978; Podhalanska, 2007) (Fig. 3a). If the hypothesis relating the MV anomaly in northwestern Poland to the Caledonian structures is true, our studies allow us to determine the position of CDF more precisely. The position of the identified deep conductive complexes indicates that north of Koszalin the CDF turns west, and runs along the Baltic shore until it reaches Usedom, where it turns north towards Rugen (Fig. 3a; solid line).

Because of a very small amount of geological and geophysical data there is also an ongoing scientific debate about the extent of the Variscan deformation. The Variscan foreland basin of Western Europe continues from Germany eastwards into western Poland, together with the Variscan foreland fold-and-thrust belt on its southern flank, which is an equivalent of the Rhenohercynian zone in Germany. Information on the evolution of the Variscan belt can be derived from the thick Carboniferous sedimentary succession of the adjacent foreland basin completely buried beneath the Permo-Mesozoic cover (Dadlez 1994). The position of VDF is defined first of all on the basis of the borehole data, however the data can be explained alternatively, since there is no precise dating available. Some indications concerning the location of the VDF come also from the geophysical analysis. However, seismic data are very poor too, and image of the gravity field (transition from positive to negative anomalies) is not precise.

The extent of Variscan deformation and the nature of its border with the orogen foreland is the subject of several divergent concepts shown in Fig. 3a. The northernmost and easternmost location of the boundary Variscan orogen was proposed Pozaryski and Karnkowski (1992). On the other hand, Dadlez et al. (1994) adopted the interpretation suggested by Jubitz et al. (1986), and put the VDF position more to the west. In turn, Narkiewicz and Dadlez (2008) believe that the Variscan orogen boundary in the northern section coincides with Pozaryski and Karnkowski’s (1992) concept, while in the east it is intermediate between it and the line drawn by Dadlez et al. (1994).

Analyzing the obtained MV sounding results and comparing the position of identified crustal conductive complexes with the hypothesis of the Variscian orogen extent (Fig. 3a), we find an amazing correlation which suggests that they were formed as a result of subsidence and accumulation of thick sediments on the Variscan foredeep. In the northwestern section, where the VDF position is not controversial, it is localized on the outer side of the conductive complexes (analogous to the CDF location). Basing on this, we propose to continue this line toward the southeast which coincides with the hypothesis suggested by Pozaryski and Karnkowski (1992) and modified by Narkiewicz and Dadlez (2008). We can also conclude more generally that the problem of inclusion or exclusion of these conductive structures from the folds area is crucial for determining the course their extent.

This has been confirmed by the result of seismic project GRUNDY 2003 (Malinowski et al., 2007). On the one hand, the authors argue that they provide some direct seismic evidences for the existence of the Variscan Front and possibly a Variscan thrust plane in the substratum of the Polish Basin coincident with prediction of Dadlez et al. (1994). But the results imaged also a depression, representing the Carboniferous molasse developed in the foreland of the Variscides. However, according to the authors, due to the limited aperture and resolution of the data, we cannot rule out a possibility that this depression, filled by molasses, represents an intermountain basin rather than the Variscan foredeep. In such a case, seismic data have imaged not the VDF itself but the fine structure of the Variscan externides in the form proposed by Pozaryski and Karnkowski (1992): the interwoven flysch belts and internal molasses. This would mean that the seismic results are consistent with our conclusions mentioned above.

Additional information on the course of Caledonian and Variscan folding will be attained from a more detailed analysis of the conductivity mechanism, thickness and precise depth of these complexes of conducting rocks. For such an analysis, it will be necessary to collect rich MV data set for wide period ranges, which is actually under way. It will also be very helpful to create a series of 2D MT models at profiles crossing these structures.

5 Conclusions

The results obtained confirm the usefulness of applying the HMT method to present the results of magnetovariational soundings. A proposed method of transforming tippers into the HMT enables an integral interpretation of many archival sets of experimental data catalogued in the form of induction tippers. An analysis of the spatial distribution of the HMT (notably, of one of the invariants of this tensor (i.e., the largest singular value which corresponds to the maximum value of the induced field amplitude) makes it possible to identify the areas of maximum concentration of telluric currents. These are the areas of well-conducting rocks, and as a result, we present a map displaying the structures characterized by abnormally high electric conductivity values. The procedure is particularly useful for the study of 3D deep structures when 2D inversion algorithms that are in routine use are unable to determine the position of such structures, and the 3D algorithms fail.

Our analysis of the spatial distribution of HMT invariants, resulting from the transformation of a large quantity of archival data from Central Europe, enabled us to determine the location of deep-seated well-conducting basins within the crust. The basins lie at 7–20 km depths and are characterized by very large integral conductivity values, reaching 10,000 S. We cannot resolve the nature of these well-conducting rocks. They may be either porous (fractured or cracked) rocks saturated with mineralized waters or metamorphic sedimentary rocks containing graphite or black shales. The position of these basins points to their close association to the orogeneses occurring in the study area: Caledonian, Variscan, and Alpine. These are probably foredeeps in front of mountain chains formed as a result of the above-mentioned orogeneses. Their identification will contribute to better knowledge of the geotectonic evolution in the TESZ.

Analyzing obtained results, we can conclude that the classification (inclusion or exclusion from the fold area) of the deep conductive complexes is an important argument in the Varicsian orogeny extent analysis. On the basis of our results we are able to determine the CDF position more precisely, especially in the region between Rugen and Koszalin. It seems that north of Koszalin the CDF turns west and runs along the Baltic shore until it reaches Usedom, where it turns north towards Rugen. We proposed also a more eastern location of VDF, on the outer side of identified conductive structures, which complies with the hypothesis suggested by Pozaryski and Karnkowski (1992) and modified by Narkiewicz and Dadlez (2008).