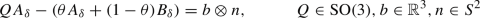The Tapering Length of Needles in Martensite/Martensite Macrotwins

Abstract

We study needle formation at martensite/martensite macro interfaces in shape-memory alloys. We characterize the scaling of the energy in terms of the needle tapering length and the transformation strain, both in geometrically linear and in finite elasticity. We find that linearized elasticity is unable to predict the value of the tapering length, as the energy tends to zero with needle length tending to infinity. Finite elasticity shows that the optimal tapering length is inversely proportional to the order parameter, in agreement with previous numerical simulations. The upper bound in the scaling law is obtained by explicit constructions. The lower bound is obtained using rigidity arguments, and as an important intermediate step we show that the Friesecke–James–Müller geometric rigidity estimate holds with a uniform constant for uniformly Lipschitz domains.

1 Introduction

Shape-memory materials are special alloys that undergo a diffusionless solid-solid phase transformation upon a change of temperature or stress. During nucleation, complex microstructures emerge, and these microscopic patterns seem to be closely linked to macroscopic properties of the materials [3, 9, 32]. The patterns are usually modeled in the framework of the phenomenological theory of martensite [6], based on finite or linearized elasticity. The linearized theory is widely used and has been proven to arise naturally as $\Gamma$-limit of the nonlinear theory for small displacements [26]. While the linearized theory often provides a good approximation to the physical (nonlinear) setting, several mathematical results indicate that in various situations the linear theory can lead to qualitatively different predictions, see e.g. [3, 4, 10, 16, 20, 24].

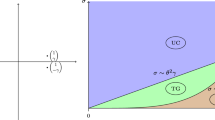
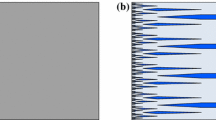
During nucleation of martensite in an austenitic matrix, various interfaces between austenite and martensite or between different martensitic variants are formed. We focus on interfaces between different regions of laminated martensites, so called martensite/martensite macrotwins. At such interfaces, one often observes needle-type microstructures, i.e., laminates where the minority variant drops out at the interface (see Fig. 1 and [12]). We point out that in many experiments, the needles show a more complex topological structure, and in particular branch close to the interface. This leads to different mathematical challenges [13, 35, 36], but we will focus here on simple needle structures as sketched in Fig. 2.

The mathematical treatment of such structures within the framework of the phenomenological theory started with the work in [11, 12, 34, 47, 48]. In [12], the authors used a static variational model based on linearized elasticity and were able to predict the bending angle at which the needle meets the interface, in terms of the measured tapering length of the needle. We point out that the authors here did not intend to make predictions on the tapering length from the theory. Related problems of optimal needle shapes near martensite/martensite or martensite/austenite interfaces have since then been studied extensively, both in the analytical and the numerical literature, see e.g. [11, 15, 21, 22, 29, 39,40,41, 43, 46,47,48,49]. In many numerical simulations, it has been observed that numerical schemes with geometrically linearized elastic energies are unstable or do not reproduce the experimental results while geometrically nonlinear models appear more appropriate.

We follow here the recent approach from the numerical study in [21]. We aim at a better understanding of the length scale of such needle structures, in particular the tapering length. To determine this length in terms of the material parameters, a shape optimization problem for the parametrized needle shape is considered.

Fig. 1

Left: Experimental (high-resolution transmission electron microscopy) image of needles in the $\hbox {Ni}_{65}\hbox {Al}_{35}$ shape-memory alloy, from Boullay, Schryvers and Kohn [12, Fig. 5]. Right: Experimental (optical microscopy with polarized light) image of needles in the $\hbox {Cu}_{14}\hbox {Al}_{3.9}\hbox {Ni}$ shape-memory alloy, courtesy of Chu and James [18, 19]. The two pictures show a similar phenomenon at very different length scales, of the order of a few nanometers on the left, and of a fraction of a millimeter on the right

Let us finally comment on some simplifications that have been proposed in the literature. The most popular simplification is the linearization of the elastic energy (see, e.g., [12]). In this note, we will underline the numerical findings from [21] that the linearized theory is not appropriate to determine the tapering length. More precisely, we show (see Theorem 3.1) that for any energy-minimizing sequence in the geometrically linearized setting, the tapering lengths tend to infinity. This is in accordance with several other numerical findings in which it was observed that the geometrically linear model does not yield the expected results (see [21, 29, 43]).

In [51, 52], a related problem of needle-type microstructures near austenite/martensite interfaces has been investigated. There, the situation is simplified by assuming constant gradient in the very thin needles. Although one does not expect a large contribution to the elastic energy from these small domains, our analysis here indicates that the optimal energy scaling is not preserved under this simplification. Indeed, a significant effect seems to come from rotations at rather large angles (comparable to the shear in the variants).

Fig. 2

Sketch of the geometry. The right picture is based on data from the numerical simulation in [21]

Fig. 3

Sketch of the geometry around a martensite/twinned martensite interface. This geometry is often called a macrotwin

Let us start with a brief qualitative explanation of the relevant effects. We work in two dimensions, and denote the eigenstrains of the two martensitic variants by

(1.1)

We start from the large-scale picture, as summarized in Fig. 2 and 3. On the far right there is a laminate between $A_\delta$ and $B_\delta$, with volume fraction $\theta \in (0,1)$; its average deformation is $F:=\theta A_\delta + (1-\theta ) B_\delta$. On the left of the macro interface we have only variant $A_\delta$, but with a different rotation $Q_*\in \textrm{SO}(2)$. Compatibility of the macro interface implies that $Q_*A_\delta -F$ is rank-one, and the orientation $e_{\theta ,\delta }$ of the macro interface is characterized by the condition $(Q_*A_\delta -F)e_{\theta ,\delta } =0$. This fixes both $Q_*\in \textrm{SO}(2)$ and $e_{\theta ,\delta }$ as functions of $\theta$ and $\delta$, details are given in Lemma 2.1 below (see also Fig. 2). As $Q_*\ne {{\,\textrm{Id}\,}}$, the two regions in the $A_\delta$ variant are not rank-one compatible, $\textrm{rank}(A_\delta -Q_*A_\delta )=2$.

In the geometry of Fig. 2, needles are structures by which the volume fraction of the $A_\delta$ phase varies from 0 close to the macro interface to the asymptotic value $\theta$ at large $x_1$. For this qualitative discussion we use non-orthogonal coordinates and assume that $x_1=0$ corresponds to the macro interface. The entire construction is affine-periodic in the direction of the macro interface, with a periodicity condition given by the macroscopic deformation on the left, $u(x+e_{\theta ,\delta })=Q_*A_\delta e_{\theta ,\delta }=Fe_{\theta ,\delta }$. For definiteness, let us assume that the period is 1, and denote by $\ell >0$ the characteristic length scale in the $x_1$ direction. Given these boundary conditions, one then determines the optimal deformation by minimizing the total elastic energy jointly over the elastic deformation u and the shape of the interfaces, see Fig. 2 for the result in a specific situation. The precise functionals we minimize are introduced below, and given in (3.9) in the geometrically linear case, and in (4.12) for the geometrically nonlinear one. For simplicity, in this introduction we do not include a description of the detailed shape of the interfaces, but only a simplified characterization, based on volume fractions at fixed $x_1$. For any $x_1$, let $a(x_1)$ be the volume fraction (averaged over one period) of the $A_\delta$ phase at given $x_1$; correspondingly $b(x_1)$ for the $B_\delta$ phase. Obviously, $a(x_1)+b(x_1)=1$ for all $x_1$, and by the boundary conditions $a(0)=0$, whereas $a(x_1)\sim {{\theta }}$ and $b(x_1)\sim (1-{{\theta }})$ for $x_1\gg \ell$.

If no rotation is present, and the energy is exactly zero, we necessarily have that $\partial _2u_1=\delta$ in phase $A_\delta$, and $-\delta$ in phase $B_\delta$. The vertical average of $\partial _2 u_1$ over one period is then $(a-b)\delta$, which matches the periodicity requirement only if $a=\theta$ and $b=1-\theta$. We next include infinitesimal rotations in the picture, assuming that the rotation angle depends on $x_1$ but not on $x_2$. In particular, if ${\beta }(x_1)$ is the average lattice rotation angle at given $x_1$, then one has $\partial _2 u_1 = \delta + {\beta }$ in the $A_\delta$ and $\partial _2 u_1 = -\delta + {\beta }$ in the $B_\delta$ phase, with $\partial _1u_2=-{\beta }$ everywhere. Equating the vertical average to the one required by the periodicity leads to

$$\begin{aligned} (a(x_1)-b(x_1))\delta + {\beta }(x_1)=(2{{\theta }}-1)\delta . \end{aligned}$$

(1.2)

This relation between tapering profile and rotation was first studied in [12], it permits in particular to express $\beta$ in terms of a and b. Treating the individual layers as elastic plates, we see that the change in lattice rotation ${\beta }'(x_1)$ generates a bending energy depending on the curvature, and proportional to

$$\begin{aligned} \int _0^\ell \left( \frac{\textrm{d}}{\textrm{d}x_1}{\beta }(x_1)\right) ^2 \textrm{d}x_1. \end{aligned}$$

(1.3)

Inserting the previous expression for ${\beta }$ leads to minimizing

$$\begin{aligned} \delta ^2\int _0^\ell (a'-b')^2 \textrm{d}x_1, \end{aligned}$$

(1.4)

which yields, naturally, $a(x_1)=1-b(x_1)\simeq {{\theta }} x_1/\ell$ for $x_1\in (0,\ell )$. Therefore the total energy is proportional to $\delta ^2\theta ^2/\ell$, and the optimal value for $\ell$ is $\infty$ (see Theorem 3.1 below for a precise statement). The geometrically linear model is unable to predict a finite length scale.

In finite elasticity, one considers an energy density which behaves as

$$\begin{aligned} \min _{R\in \textrm{SO}(2)}|\nabla u-RA_\delta |^2= {\text {dist}}^2(\nabla u ,\textrm{SO}(2)A_\delta ) \sim {\text {dist}}^2(\nabla u A_\delta ^{-1},\textrm{SO}(2)) \end{aligned}$$

(1.5)

in the $A_\delta$ phase, and similarly in the $B_\delta$ phase (see below, and (4.12) in particular, for a precise definition) [5, 8, 44]. A new term enters the picture in the product $RA_\delta$. Indeed, in

$$\begin{aligned} R_{{\beta }} A_\delta = \begin{pmatrix}\cos {\beta } &{}{}\sin {\beta }\\ -\sin {\beta }&{}{}\cos {\beta }\end{pmatrix} \begin{pmatrix}1 &{}{}\delta \\ 0&{}{}1\end{pmatrix} = \begin{pmatrix}\cos {\beta } &{}{\quad }\delta \cos {\beta }+\sin {\beta }\\ -\sin {\beta }&{}{\quad }\cos {\beta }-\delta \sin {\beta }\end{pmatrix} \end{aligned}$$

(1.6)

(and the same with $B_\delta$) there are more nontrivial entries than in the previous description based on linear elasticity. The $\partial _2 u_1$ term, similarly to (1.2) above, prescribes ${\beta }(x_1)$ in terms of $a(x_1)-b(x_1)$; the $\partial _1u_1$ and $\partial _1u_2$ terms are not important for the same reason as above. However, periodicity requires $\partial _2u_2$ to have average 1, so that $|\partial _2u_2-(R_{{\beta }} A_\delta )_{22}|\sim \frac{1}{2}{\beta }^2+\delta {\beta }$. The total energy density is then of order ${\beta }'^2+{\beta }^2\delta ^2$, and balancing terms one obtains that the characteristic length scale is $\ell \sim 1/\delta$. We refer to Proposition 4.3 below for a precise construction. As in (1.2) we have $\beta \sim \delta \theta$, and therefore this results in a total energy scaling as $\theta ^2\delta ^3$, as specified in Theorem 4.2 below.

These results are made precise below. We first formulate a precise mathematical model for the needle geometry following [21, 34, 51], with boundary conditions that fix the long-range structure and the topology but leave the shape of the domain boundaries free. The key assumptions are affine-periodic boundary conditions along the macro interface, a boundary data corresponding to a laminate at large $x_1$, and the fact that the phase boundaries are Lipschitz functions. We then provide, separately in the linear and in the nonlinear case, explicit upper-bound constructions which make the above arguments rigorous. We finally show that these constructions are, up to universal factors, optimal, by providing corresponding lower bounds on the energy. This involves minimizing not only over the elastic deformation, but also over the phase interfaces, and hence over the shape of the domains of the different phases. We present in Sect. 2 the model, in Sect. 3 the linear results, and in Sect. 4 the nonlinear results.

One important difficulty in proving the lower bound is that one has to deal with Sobolev functions on varying domains. Our argument in particular uses a trace theorem, a Poincaré inequality, and a geometric rigidity inequality with constants which are uniform for uniformly Lipschitz domains. Whereas the first two are already present in the literature, the geometric rigidity estimate has, to the best of our knowledge, up to now only been proven with domain-dependent constants, even if uniformity of the constant for certain classes of domains has been formulated in the literature without explicit proof (for example, [2, Prop. 1]), and used in the study of microstructures near austenite/martensite interfaces (see e.g. [51, 52]). We provide in Sect. 5 a full proof of the uniform geometric rigidity inequality for a general class of domains, which we believe to be of independent interest. The key ingredient is a uniform weighted Poincaré inequality, which also permits to easily obtain as byproducts uniform trace and Poincaré estimates.

2 Kinematics and Reduction to a 2D Problem

We describe the crystallographic situation under consideration (see also [12]) building on the crystallographic theory of martensite (see [6]). We consider a macrotwin using two martensitic variants, given by wells $\textrm{SO}(3){U_1}$ and $\textrm{SO}(3){U_2}$. We make the standard assumption that the transformation stretch matrices are positive definite with $\det U_1=\det U_2$ and nontrivial in the sense that $U_1\not \in \textrm{SO}(3)U_2$. If laminates with gradients in the two wells are possible, then the wells are rank-one connected, i.e., there exist ${\tilde{R}}\in \textrm{SO}(3)$, and non-zero vectors a, $n\in {\mathbb {R}}^3$ such that

$$\begin{aligned} \tilde{R}U_2-U_1=\tilde{a}\otimes \tilde{n}. \end{aligned}$$

It is shown in [8] that under these assumptions, we may without loss of generality (up to a linear change of variables) restrict to matrices of the form

$$\begin{aligned} A_\delta :=\text {Id}+\delta e\otimes e^\perp ,\qquad \text { and}\qquad B_\delta :=\text {Id}-\delta e\otimes e^\perp \end{aligned}$$

(2.1)

for some orthogonal unit vectors $e$, $e^\perp \in {\mathbb {R}}^3$ with $\delta >0$. Here, $\delta >0$ measures the shear, and we will focus on the case of small and moderate strains, $|\delta |\leqq 1$, and in particular on the limit $\delta \rightarrow 0$. While we consider the three-dimensional setting, it turns out that in our analysis, we may restrict to a two-dimensional simplification since, as shown in [7], the optimal strains are plane strains, cf. Remark 2.2(iii). Specifically, we shall work in the plane spanned by $e$ and $e^\perp$, and denote by $f\in {\mathbb {R}}^3$ a unit vector perpendicular to that plane. Following [6], the normals to the laminate and macrotwin interfaces can be determined from the crystallographic theory of martensite. For that, we collect the necessary linear algebra results in this section.

2.1 Nonlinear elasticity

In the setting of nonlinear elasticity, the direction of the macro interface is not orthogonal to the one of the laminate, as illustrated in Fig. 2. We denote the orientation of the macro interface (in the plane orthogonal to f) by

$$\begin{aligned} {e_{\delta ,\theta }}:=\frac{1}{\sqrt{1+(\delta \theta )^2}}(e^\perp -\delta \theta e). \end{aligned}$$

(2.2)

This expression arises as the unique (up to a sign) nontrivial solution of the rank-one compatibility condition between $\text {SO}(3)A_\delta$ and the weighted average $\theta A_\delta +(1-\theta )B_\delta$. We summarize the relevant algebraic conditions in the next Lemma. All assertions can be checked by direct computation; see, for example, [5].

Lemma 2.1

Let $(e,e^\perp ,f)$ be an orthonormal basis of ${\mathbb {R}}^3$, $\delta \in {{\mathbb {R}}}{\setminus \{0\}}$, $\theta \in {(0,1)}$, and let $A_\delta$ and $B_\delta$ be the matrices given in (2.1). Then it holds that

• (i) $A_\delta -B_\delta =2\delta e\otimes e^\perp$.

• (ii) The equation

  

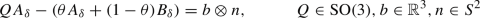  (2.3)

  has four solutions. Two of them are $({{\,\textrm{Id}\,}}, \pm (1-\theta )2\delta e, \pm e^\perp )$, the other two have the form $(Q_*, \pm b_*, \pm e_{\delta ,\theta })$, where $b_*\in {\mathbb {R}}^3$,

  $$\begin{aligned} {e_{\delta ,\theta }^\perp }:=-\frac{e+\delta \theta e^\perp }{\sqrt{1+(\delta \theta )^2}} \end{aligned}$$

  (2.4)

  and

  $$\begin{aligned} \begin{aligned} {Q_*}:=&\frac{1-\delta ^2(1-\theta )^2}{1+\delta ^2(1-\theta )^2}\left( e\otimes e+ e^\perp \otimes e^\perp \right) \\&+\frac{2\delta (1-\theta )}{1+\delta ^2(1-\theta )^2}\left( e^\perp \otimes e-e\otimes e^\perp \right) +f\otimes f. \end{aligned}\end{aligned}$$

  (2.5)

  In particular,

  $$\begin{aligned} {Q_*}A_\delta e_{\delta ,\theta }=(\theta A_\delta +(1-\theta )B_\delta ) {e_{\delta ,\theta }}. \end{aligned}$$

  (2.6)

• (iii) There is a unique $R_0\in \textrm{SO}(3)$ such that

  $$\begin{aligned} {Q_*}A_\delta -R_0B_\delta =a\otimes e\qquad \text { for some }\quad a\in {\mathbb {R}}^3. \end{aligned}$$

  (2.7)

  The rotation $R_0$ is given by

  $$\begin{aligned} R_0= & {} {Q_*}\left( \frac{1-\delta ^2}{1+\delta ^2}\left( e\otimes e+e^\perp \otimes e^\perp \right) +\frac{2\delta }{1+\delta ^2}\left( e\otimes e^\perp -e^\perp \otimes e\right) +f\otimes f\right) \nonumber \\ {}= & {} \frac{1+\delta ^4(1-\theta )^2-\delta ^2(-2+2\theta +\theta ^2)}{(1+\delta ^2)(1+\delta ^2(1-\theta )^2)}(e\otimes e+e^\perp \otimes e^\perp )+\nonumber \\ {}{} & {} \quad +\frac{2\delta (1+\delta ^2(1-\theta ))\theta }{(1+\delta ^2)(1+\delta ^2(1-\theta )^2)}(e\otimes e^\perp -e^\perp \otimes e)+f\otimes f.\end{aligned}$$

  (2.8)

• (iv) All matrices act trivially on f, i.e.,

  $$\begin{aligned} A_\delta f=B_\delta f={Q_*}f=R_0f=f. \end{aligned}$$

  (2.9)

In Sect. 4 we shall consider a macrotwin with normal ${e_{\delta ,\theta }^\perp }$, and twin plane normal $e^\perp$ deep in the laminate on the right hand side of the macrotwin, see Fig. 3.

Remark 2.2

• (i) It follows from (2.2) that ${e_{\delta ,\theta }}\rightarrow e^\perp$ as $\delta \rightarrow 0$, but ${e_{\delta ,\theta }}\ne e^\perp$ for finite $\delta$.

• (ii) If $|\delta |$ and $\theta$ are small, then the rotation ${Q_*}$ as given in (2.5) is a rotation by roughly $2\delta (1-\theta )$, while $R_0$ is a rotation by roughly $-2\delta \theta$. In particular, both rotations are of order $\delta$.

• (iii) Motivated by assertion (iv) of Lemma 2.1, we make the following simplification: We consider only deformations u satisfying $\nabla u f=f$, and, slightly abusing notation, we identify the matrices introduced above with their restrictions to the plane spanned by $e$ and $e^\perp$.

2.2 Linearization

We now turn to the geometrically linearized setting. Precisely, for the small strain case $|\delta |\ll 1$, we linearize around the identity and define the strain matrices

(2.10)

We denote by $\xi _\textrm{sym}:=\frac{1}{2}(\xi +\xi ^T)$ the symmetric part of a matrix, so that

$$\begin{aligned} A^{\textrm{lin}}_\textrm{sym}=\frac{1}{2}(e\otimes e^\perp +e^\perp \otimes e)\quad \text {and }\quad B^{\textrm{lin}}_\textrm{sym}=-\frac{1}{2}(e\otimes e^\perp +e^\perp \otimes e).\qquad \end{aligned}$$

(2.11)

We note the geometrically linearized compatibility properties.

Lemma 2.3

Suppose that $\theta \in (0, 1)$, and let $A^{\textrm{lin}}_\textrm{sym}$ and $B^{\textrm{lin}}_\textrm{sym}$ be given by (2.11). Then it holds that

• (i) $A^{\textrm{lin}}_\textrm{sym}-B^{\textrm{lin}}_\textrm{sym}= e\otimes e^\perp +e^\perp \otimes e$.

• (ii) $\theta A^{\textrm{lin}}_\textrm{sym}+(1-\theta )B^{\textrm{lin}}_\textrm{sym}-A^{\textrm{lin}}_\textrm{sym}={(\theta -1)}(e\otimes e^\perp +e^\perp \otimes e)$.

• (iii) The equation $(A^{\textrm{lin}}_\textrm{sym}-B^{\textrm{lin}}_\textrm{sym}-S)v=0$ has a solution $S\in {\mathbb {R}}^{2\times 2}_\textrm{skw}$ if and only if v is parallel to either $e$ or $e^\perp$.

Proof

The proof follows from a direct calculation. $\square$

In particular, in the geometrically linearized setting, both, the macrotwin and the laminates can have normals $e$ or $e^\perp$. The main difference to the geometrically nonlinear setting is that the compatibility plane between the two variants is aligned with the compatibility plane of the macrotwin.

3 Energy Scaling in the Geometrically Linearized Setting

Following [12], we first consider the geometrically linearized setting. With the strain matrices ${A^{\textrm{lin}}_\textrm{sym}}$ and ${B^{\textrm{lin}}_\textrm{sym}}$ as defined in (2.11), we are led to study the geometrically linearized shape optimization problem involving the displacement. We consider a periodic cell of a macrotwin using linearized kinematics (see, e.g., [3]) and briefly recall the setting. By Lemma 2.3(i), there are two possible directions for ${A^{\textrm{lin}}_\textrm{sym}}/{B^{\textrm{lin}}_\textrm{sym}}$ laminates, given by the normals $e$ and $e^\perp$. Deep in the twinned region on the right-hand side of the macrotwin, we choose the twin planes to be parallel to $e$, and the macrotwin plane parallel to $e^\perp$. Since we work in an orthogonal coordinate system, for the ease of notation, we set $e_1:=e$ and $e_2:=e^\perp$, and for $x\in \text{ span }\{e,e^\perp \}={\mathbb {R}}^2$, we use the notation

$$\begin{aligned} x_1:=x\cdot e_1=x\cdot e,\qquad x_2:=x\cdot e_2=x\cdot e^\perp ,\qquad \text { and }\qquad x=(x_1,x_2). \end{aligned}$$

We describe the needle by the two confining curves $f^\pm :{[0,\infty )}\rightarrow {\mathbb {R}}$ which we assume to be measurable and satisfy

$$\begin{aligned} {f^{-}\leqq f^{+}\leqq f^{-}+1} \quad \text { and }\quad f^+(0)=f^{-}(0){=0}; \end{aligned}$$

(3.1)

see Fig. 4. Note that we do not impose any regularity assumptions on $f^\pm$ but to get closer to the experimental results, we could also impose a length or Lipschitz condition without changing the results, see Remark 3.2(i).

Fig. 4

Sketch of the parametrization of the domain in the geometrically linear setting

We assume that the displacement $v\in W^{1,2}_\textrm{loc}({\mathbb {R}}^2;{\mathbb {R}}^2)$ obeys the periodicity condition

$$\begin{aligned} {v(x+e_2)-v(x)=\left( \theta A^{\textrm{lin}}+(1-\theta )B^{\textrm{lin}}\right) e_2=(-1+2\theta )e_1}, \end{aligned}$$

(3.2)

and we consider the set

$$\begin{aligned} { {\hat{\omega }}_A:=\{x\in {\mathbb {R}}^2:x_1\leqq 0\}\cup \left\{ x\in {\mathbb {R}}^2: x_1>0, x_2\in \bigcup _{k\in {\mathbb {Z}}} \left[ k+f^-(x_1),k+f^+(x_1)\right) \right\} } \end{aligned}$$

(3.3)

and its complement,

$$\begin{aligned} { {\hat{\omega }}_B:=\left\{ x\in {\mathbb {R}}^2: x_1>0, x_2\in \bigcup _{k\in {\mathbb {Z}}} \left[ k+f^+(x_1),k+1+f^-(x_1)\right) \right\} }. \end{aligned}$$

(3.4)

We further assume that there is $\ell >0$ such that for $x_1\geqq \ell$ the deformation coincides with a simple laminate, in the sense that there is $\eta \in {\mathbb {R}}$ such that

$$\begin{aligned} {f^-}(x_1)=\eta \quad \text { and} \quad {f^+}(x_1)=\eta +\theta \quad \text { for } x_1\geqq \ell , \end{aligned}$$

(3.5)

and

$$\begin{aligned} \nabla v(x)={\left\{ \begin{array}{ll} A^{\textrm{lin}}, &{} \text { if } x\in (\ell ,\infty )\times \cup _{k\in {\mathbb {Z}}}(k+\eta ,k+\eta +\theta ),\\ B^{\textrm{lin}}, &{} \text { if } x\in (\ell ,\infty )\times \cup _{k\in {\mathbb {Z}}} (k+\eta +\theta ,k+1+\eta ). \end{array}\right. } \end{aligned}$$

(3.6)

These conditions characterize the class of admissible configurations

(3.7)

As the experimental results indicate that $\ell$ is large (see Fig. 1), we restrict ourselves to the case $\ell \geqq 1$. By periodicity, for the computation of the energy it suffices to integrate over one period, and therefore to consider

$$\begin{aligned} \omega _{A,B}:={\hat{\omega }}_{A,B}\cap \left( {\mathbb {R}}\times (0,1)\right) \end{aligned}$$

(3.8)

(alternatively, one could take for $x_1>0$ only the $k=0$ contribution in (3.3) and (3.4), by periodicity the two choices are equivalent). The elastic shape optimization problem is then to minimize

$$\begin{aligned} {\mathcal {E}}_{\text {lin}}[f^{\pm },v]:= & {} \int _{\omega _A} \frac{1}{2}{\mathbb {C}}(e(v)-{A^{\textrm{lin}}_\textrm{sym}})\cdot (e(v)-{A^{\textrm{lin}}_\textrm{sym}})\textrm{d}x\nonumber \\{} & {} +\int _{\omega _B}\frac{1}{2}{\mathbb {C}}(e(v)-{B^{\textrm{lin}}_\textrm{sym}})\cdot (e(v)-{B^{\textrm{lin}}_\textrm{sym}})\textrm{d}x \end{aligned}$$

(3.9)

over ${\mathcal {A}}_{\text {lin}}^{(\ell )}$. Note that we minimize with respect to both the configuration given by $f^\pm$ and the displacement v. Here we denote the symmetric part of the gradient by $e({v}):=\frac{1}{2}(\nabla {v}+\nabla ^T {v})$, and ${\mathbb {C}}$ represents the elastic modulus which satisfies the standard boundedness and coercivity properties, i.e. $\mathbb C(\xi -\xi ^T)=0$ for all $\xi$ and there exists $\alpha >0$ such that

$$\begin{aligned} \alpha |\xi _\text {sym}|^2\leqq {\mathbb {C}}\xi \cdot \xi \leqq \frac{1}{\alpha }|\xi _\text {sym}|^2\qquad \text { for all }\quad \xi \in {\mathbb {R}}^{2\times 2}. \end{aligned}$$

(3.10)

The energy functional (3.9) does not contain any interfacial energy term penalizing the lengths of the interfaces parametrized by $f^\pm$. Typically such terms are necessary to identify the appropriate length scale on which the twin structures form. In our setting of a periodic cell, however, it is of higher order as long as the curves are sufficiently regular.

We find the following scaling law for the minimal energy.

Theorem 3.1

There is a constant $c>0$ such that for all $\theta \in (0,1/2]$ and all $\ell \geqq 1$, we have

$$\begin{aligned} \frac{1}{c}\frac{\theta ^2}{\ell }\leqq \inf \left\{ {\mathcal {E}}_{\textrm{lin}}[f^{\pm },v]: (f^\pm ,v)\in {\mathcal {A}}_\textrm{lin}^{(\ell )}\right\} \leqq c\frac{\theta ^2}{\ell }. \end{aligned}$$

Remark 3.2

• (i) We derive the scaling law for the minimal energy without regularity assumptions on $f^\pm$ but the upper bound uses only a Lipschitz profile with Lipschitz constant bounded by one.

• (ii) If on the right boundary we impose boundary conditions only on $f^\pm$ (see (3.1)) but not on the deformation (see (3.6)) then there is no minimizing configuration and the infimum of the energy is zero. The reason for that is that in the linearized setting we can have a strain-free ${A^{\textrm{lin}}_\textrm{sym}}/{B^{\textrm{lin}}_\textrm{sym}}$ interface along the macrotwin plane $\{x_1=0\}$ (a fact that will also be used in the proof of the upper bound below). Precisely, consider for $n\in {\mathbb {N}}$ the configuration

  $$\begin{aligned} f^-_{{n}}\equiv 0,\qquad f^+_{{n}}(x_1)={\left\{ \begin{array}{ll} 0,&{}\text { if } x_1\leqq \ell -\frac{1}{n},\\ \theta n x_1+\theta (1-n\ell ),&{}\text { if }\ell -\frac{1}{n}<x_1\leqq \ell ,\\ {\theta }, &{}{\text { if }x_1>\ell ,} \end{array}\right. } \end{aligned}$$

  and displacement $v_n=v$ given for $x\in \omega _{A,B}$ by

  $$\begin{aligned} v(x)= (2\theta -1)x_{{2}} e_1+{\left\{ \begin{array}{ll} 2(1-\theta )x_1e_2,&{}\text { if }x_1\leqq 0,\\ -2\theta x_1e_2,&{}\text { if }x_1> 0, \end{array}\right. } \end{aligned}$$

  and extended to ${\mathbb {R}}^2$ via (3.2). Then $f^\pm _{{n}}$ satisfy (3.1) and (3.5) with $\eta =0$, and v satisfies the periodicity condition (3.2) by construction. Further, $v\in W^{1,\infty }_\textrm{loc}({\mathbb {R}}^2;{\mathbb {R}}^2)$ with

  $$\begin{aligned} e(v)={\left\{ \begin{array}{ll} A^{\textrm{lin}}_\textrm{sym},&{}\text { if } x_1 < 0,\\ B^{\textrm{lin}}_\textrm{sym},&{}\text { if }x_1>0, \end{array}\right. } \end{aligned}$$

  and therefore,

  $$\begin{aligned} 0\leqq {\mathcal {E}}_{\textrm{lin}}[f^\pm _{{n}},v]\leqq \int _{\ell -1/n}^\ell \int _0^{f^+_n(x_1)} \frac{1}{\alpha }\left| A^{\textrm{lin}}_\textrm{sym}-B^{\textrm{lin}}_\textrm{sym}\right| ^2\,\textrm{d}x_2\,\textrm{d}x_1\leqq \frac{\theta }{\alpha n}, \end{aligned}$$

  which implies that $\lim _{n\rightarrow \infty } {\mathcal {E}}_{\text {lin}}[f^\pm _{{n}},v_{{n}}]= 0$.

  We note that the sequence of profiles for these competitors does not have uniformly bounded Lipschitz constants. If one assumes a bound on the Lipschitz constants L of $f^\pm$, then a respective construction has energy $\sim \theta ^2/L$. Hence, for large $\ell$, the construction of the proof of Theorem 3.1 has lower energy.

• (iii) The scaling law in Theorem 3.1 implies that the tapering length of needles is not determined by linearized elasticity. Precisely, setting $\ell =\infty$, the infimum of the energy equals zero, which implies that the optimal tapering length of the needle in this linearized setting is infinite, contradicting the experimental findings.

• (iv) If one interprets the linearized energy as an approximation to the nonlinear energy (cf. (2.10)), the resulting energy scaling is $\delta ^2\theta ^2/\ell$.

Proof

Upper bound. To prove the upper bound, i.e., the second inequality in the assertion, we use a special case of the construction from [12, Figure 4], which makes precise the sketch discussed in the introduction (see (1.2)–(1.4)). We set

$$\begin{aligned} f^{-}(x_1):=0,\quad \eta :=0, \quad \text { and } \quad f^{+}(x_1):={\left\{ \begin{array}{ll} \frac{\theta }{\ell }x_1, &{}\text { if } x_1\in {[0,\ell )},\\ \theta , &{} {\text { if } x_1\geqq \ell .} \end{array}\right. } \end{aligned}$$

(3.11)

Then $f^\pm$ satisfy (3.1) and (3.5). By periodicity, it suffices to describe the associated displacement $v=(v_1,v_2)$ on $\omega _{A,B}$. Consider first $x_1\geqq 0$. We set

$$\begin{aligned} v_1(x):={\left\{ \begin{array}{ll} x_2\left( 1-2\theta \frac{x_1}{\ell }+2\theta \right) -2\theta \frac{x_1}{\ell }+2\theta ,&{}\text { if }\ {0\leqq x_1\leqq \ell \text { and } }0\leqq x_2\leqq \frac{\theta }{\ell }x_1,\\ -\left( 2\theta \left( \frac{x_1}{\ell }-1\right) x_2+x_2\right) +2\theta ,&{}\ \text { if }\ {0\leqq x_1\leqq \ell \text { and } }\frac{\theta x_1}{\ell }< x_2\leqq 1, \end{array}\right. }\qquad \end{aligned}$$

(3.12)

and

$$\begin{aligned} v_2(x):=\frac{\theta }{\ell }x_1^2-2\theta x_1+\theta \ell \qquad \text { for }\ {0\leqq x_1\leqq \ell }. \end{aligned}$$

(3.13)

We then extend the displacement constantly in $x_1$, i.e., we set

$$\begin{aligned} v(x_1,x_2)=v(\ell ,x_2)\quad \text { for }\ x_1> \ell . \end{aligned}$$

As $v(x_1,1)-v(x_1,0)=(2\theta -1)e_1$ we can extend it periodically to ${\mathbb {R}}^2$ using (3.2). Then $v\in W^{1,2}_\textrm{loc}((0,\infty )\times {\mathbb {R}};{\mathbb {R}}^2)$ satisfies (3.2) and (3.6). For the gradients, we have, inside the needle, i.e., for $0\leqq x_1\leqq \ell$ and $0\leqq x_2\leqq \theta x_1 /\ell$ that

$$\begin{aligned} \nabla v(x)=&{}-\frac{2\theta }{\ell }(x_2+1)e_1\otimes e_1+\left( 1-\frac{2\theta x_1}{\ell }+2\theta \right) e_1\otimes e_2\\ {}{}&{} +\left( \frac{2\theta x_1}{\ell }-2\theta \right) e_2\otimes e_1, \end{aligned}$$

and thus,

$$\begin{aligned} e(v)(x)={A^{\textrm{lin}}_\textrm{sym}}-\frac{2\theta }{\ell }(x_2+1)e_1\otimes e_1. \end{aligned}$$

(3.14)

Outside the needle for $0\leqq x_1\leqq \ell$ and $\theta x_1/\ell \leqq x_2\leqq 1$, we have

$$\begin{aligned} \nabla v(x)=-\frac{2\theta x_2}{\ell }e_1\otimes e_1-\left( \frac{2\theta x_1}{\ell }-2\theta +1\right) e_1\otimes e_2+\left( \frac{2\theta x_1}{\ell }-2\theta \right) e_2\otimes e_1, \end{aligned}$$

and thus,

$$\begin{aligned} e(v)(x)={B^{\textrm{lin}}_\textrm{sym}}-\frac{2\theta x_2}{\ell }e_1\otimes e_1. \end{aligned}$$

(3.15)

For $x_1< 0$, we extend v such that the elastic energy in $\{x_1<0\}$ vanishes. We set

$$\begin{aligned}{} & {} v_1(x):=v_1(0,x_2)=2\theta x_2- x_2+2\theta ,\quad \text { and}\\{} & {} v_2(x):=2(1-\theta ) x_1+\theta \ell . \end{aligned}$$

Then $e(v)=A^{\textrm{lin}}_\textrm{sym}$ in $\{x_1<0\}$, v is continuous in ${\mathbb {R}}^2$ and is admissible. By (3.14) and (3.15), we find that there is a constant (not depending on $\ell$ or $\theta$) such that by (3.10)

$$\begin{aligned} {\mathcal {E}}_{\text {lin}}[f^{\pm },v]= & {} \int _{\omega _A\cap \{x_1>0\}}{\frac{1}{2}}{\mathbb {C}}(e(v)-{A^{\textrm{lin}}_\textrm{sym}})\cdot (e(v)-{A^{\textrm{lin}}_\textrm{sym}}){\textrm{d}x}\nonumber \\{} & {} +\int _{\omega _B}{\frac{1}{2}}{\mathbb {C}}(e(v)-{B^{\textrm{lin}}_\textrm{sym}})\cdot (e(v)-{B^{\textrm{lin}}_\textrm{sym}}){\textrm{d}x}\nonumber \\\leqq & {} c\int _{{(0,\ell )\times (0,1)}} \frac{\theta ^2}{\ell ^2}\,\textrm{d}x\leqq c\frac{\theta ^2}{\ell }. \end{aligned}$$

(3.16)

This concludes the proof of the upper bound. For later reference we remark that $f^+$ and $f^-$ are $\theta /\ell$-Lipschitz.

Lower bound. Let $\tilde{c}>0$ be a fixed (small) constant chosen below. Let $(f^\pm ,v)\in {\mathcal {A}}_{\text {lin}}^{{(\ell )}}$ be an arbitrary admissible configuration. If the elastic energy on the left hand side of the interface is large, i.e.,

$$\begin{aligned} \int _{{(-1,0)\times (0,1)}}|e(v)-{A^{\textrm{lin}}_\textrm{sym}}|^2{\textrm{d}x}\geqq \tilde{c}\frac{\theta ^2}{\ell } \end{aligned}$$

then the assertion follows. Hence, from now on, we assume that

$$\begin{aligned} \int _{{(-1,0)\times (0,1)}}|e(v)-{A^{\textrm{lin}}_\textrm{sym}}|^2{\textrm{d}x}< \tilde{c}\frac{\theta ^2}{\ell }. \end{aligned}$$

Thus, by Korn’s inequality, there exists a constant $c_K>0$ and an infinitesimal rotation $W:=w {(e_2\otimes e_1- e_1\otimes e_2)}\in {\mathbb {R}}^{2\times 2}_{\text {skew}}$ with some $w\in {\mathbb {R}}$ such that

$$\begin{aligned} \int _{{(-1,0)\times (0,1)}}\left| \nabla v(x)-{A^{\textrm{lin}}}-W\right| ^2{\textrm{d}x}\leqq \tilde{c} c_K\frac{\theta ^2}{\ell }, \end{aligned}$$

and hence, in particular,

$$\begin{aligned} \int _{{(-1,0)\times (0,1)}}|\partial _2v_1-{1} +w|^2{\textrm{d}x}\leqq \tilde{c}c_K\frac{\theta ^2}{\ell }. \end{aligned}$$

By Fubini’s theorem and Hölder’s inequality, there exists $x_1^*\in (-1,0)$ such that

$$\begin{aligned} \int _0^1|\partial _2v_1(x_1^*,x_2)-{1} +w|{\textrm{d}x_2}\leqq \tilde{c}^{1/2}c_K^{1/2}\frac{\theta }{\ell ^{1/2}}. \end{aligned}$$

(3.17)

By (3.2), this implies that

$$\begin{aligned} \left| (-1+2\theta )-(1-w)\right| =\left| \int _0^1\partial _2v_1(x_1^*,x_2){\textrm{d}x_2}-1+w\right| \leqq \tilde{c}^{1/2}c_K^{1/2}\frac{\theta }{\ell ^{1/2}}.\nonumber \\ \end{aligned}$$

(3.18)

We finally note that using Poincaré’s inequality and (3.17), there exists $b_1\in {\mathbb {R}}$ such that

$$\begin{aligned} \int _0^1\left| v_1(x_1^*,x_2)-(1-w)x_2-b_1\right| {\textrm{d}x_2}\leqq \tilde{c}^{1/2}c_K^{1/2}\frac{\theta }{\ell ^{1/2}}. \end{aligned}$$

With (3.18) we can eliminate w and obtain

$$\begin{aligned} {\int _0^1\left| v_1(x_1^*,x_2)-(2 \theta -1)x_2-b_1\right| {\textrm{d}x_2}\leqq 2\tilde{c}^{1/2}c_K^{1/2}\frac{\theta }{\ell ^{1/2}}.} \end{aligned}$$

(3.19)

We now consider the slice at $x_1=\ell$. By (3.6) and the condition $\theta \leqq 1/2$, there exists an interval $(t,t+1/4)\subset (0,1)$ (depending on $\eta$) of length 1/4 such that $\partial _2v_1(\ell ,\cdot )=(B^{\textrm{lin}})_{12}=-1$ and therefore $v_1(\ell , x_2)=b_2-x_2$ on this interval. However by (3.19) ${v_1}(x_1^*,x_2)$ is close in $L^1$ to a different affine function than ${v_1}(\ell ,x_2)$. We thus estimate the energy from below with this difference using Hölder’s and triangle inequality:

$$\begin{aligned} {\mathcal {E}}_{{\text {lin}}}[f^{\pm },v]\geqq & {} \int _{{(-1,\ell )\times (0,1)}} |\partial _1v_1|^2{\textrm{d}x}\geqq \int _{{(x_1^*,\ell )\times (t,t+\frac{1}{4})}} |\partial _1v_1|^2{\textrm{d}x}\\\geqq & {} \frac{4}{\ell }\left( \int _{{(x_1^*,\ell )\times (t,t+\frac{1}{4})}} |\partial _1v_1|{\textrm{d}x}\right) ^2\\\geqq & {} \frac{4}{\ell }\left( \int _t^{t+1/4}\left| \int _{x_1^*}^\ell \partial _1v_1\,\textrm{d}x_1\right| \,\textrm{d}x_2 \right) ^2\\= & {} \frac{4}{\ell }\left( \int _t^{t+1/4}\left| v_1(\ell ,x_2)-v_1(x_1^*,x_2)\right| \,\textrm{d}x_2\right) ^2. \end{aligned}$$

If $\tilde{c}>0$ is chosen small enough such that $\tilde{c}^{1/2}\leqq \frac{1}{128c_K^{1/2}}$, then, for all $\ell \geqq 1$, by $v_1(\ell ,x_2)=b_2-x_2$ and (3.19),

$$\begin{aligned}{} & {} \int _t^{t+1/4}\left| v_1(\ell ,x_2)-v_1(x_1^*,x_2)\right| \,\textrm{d}x_2\\{} & {} \quad \geqq \int _t^{t+1/4}|b_2-b_1-2\theta x_2|{\textrm{d}x_2}-\int _t^{t+1/4}|v_1(x_1^*,x_2)-{(2\theta -1)}x_2{-b_1}|{\textrm{d}x_2}\\{} & {} \quad \geqq \frac{1}{32}\theta -2(\tilde{c}c_K)^{1/2}\frac{\theta }{\ell ^{1/2}}\geqq \frac{1}{64}\theta , \end{aligned}$$

and hence,

$$\begin{aligned} {\mathcal {E}}_{{\text {lin}}}[f^{\pm },v]\geqq & {} \frac{\theta ^2}{1024\ell }. \end{aligned}$$

This concludes the proof of the lower bound. $\square$

The fact that the minimal energy tends to zero as $\ell \rightarrow \infty$ indicates that we cannot expect existence of minimizers for the problem on the infinite domain. We show that this is indeed the case, at least if we prescribe that the phase boundaries are uniformly Lipschitz.

Proposition 3.3

Let $L\geqq 1$. Then,

• (i) For any $\ell \geqq 1$ there exists a minimizer $(f^\pm ,v)$ of ${\mathcal {E}}_{\textrm{lin}}$ in

  $$\begin{aligned} {\mathcal {B}}_{\textrm{lin}}^{(L,\ell )}:=\left\{ (f^\pm ,v)\in {\mathcal {A}}_{\textrm{lin}}^{(\ell )}:\ f^\pm \ L-\text {Lipschitz}\right\} . \end{aligned}$$

• (ii) For ${\mathcal {B}}_{\textrm{lin}}^{(L)}:=\bigcup _{\ell >0}{\mathcal {B}}_{\textrm{lin}}^{(L,\ell )}$, it holds that

  $$\begin{aligned} \inf _{{\mathcal {B}}^{(L)}_{\textrm{lin}}} {\mathcal {E}}_{\textrm{lin}}=0, \end{aligned}$$

  and there exists no minimizer.

Proof

(i) Let $\ell \geqq 1$. By (3.16) we have $\inf _{{\mathcal {B}}_{\text {lin}}^{(L,\ell )}}{\mathcal {E}}_{\text {lin}}<\infty$. Let $(f^\pm _n, v_n)$ be a minimizing sequence. Then by the Lipschitz condition and (3.1), we have a uniform bound $\sup _n\Vert f_n^\pm \Vert _{C^{0,1}([0,\ell ])}<\infty$. By Arzelà-Ascoli, there exists a subsequence (not relabeled, the same subsequence for $f^+$ and $f^-$) such that $f^\pm _n\rightarrow f^\pm$ uniformly on $[0,\ell ]$, which implies $f^\pm (0)=0$, $(f^+-f^-)(\ell )=\theta$, $f^-\leqq f^+\leqq f^-+1$, and $f^\pm \in C^{0,1}([0,\ell ])$ with $\text {Lip}(f^\pm )\leqq L$. From boundedness of the energy, we get that $\sup _{n}\Vert e(v_n)\Vert _{L^2((-\infty ,\ell )\times (0,1))}<\infty$. Since the periodicity condition (3.2) fixes that the average of $(\nabla v_n)_{12}$ is $-1+2\theta$, this implies a bound on the full gradients, $\sup _n\Vert \nabla v_n\Vert _{L^2((a,\ell )\times (0,1))}<\infty$ for all $a<0$. By adding a constant, we can assume without restriction that all $v_n$ have mean zero over $(0,1)^2$, and thus by Poincaré’s inequality, we obtain a subsequence that converges weakly in $W^{1,2}_\textrm{loc}({\mathbb {R}}^2;{\mathbb {R}}^2)$ to an admissible function $v\in W^{1,2}_\textrm{loc}({\mathbb {R}}^2;{\mathbb {R}}^2)$. The boundary condition and the periodicity condition immediately pass to the limit. It remains to estimate the energy of the limit. Let $\varepsilon >0$. Then, by uniform convergence, there exists $N\in {\mathbb {N}}$ such that for all $n\geqq N$, we have $\text {graph}(f^\pm _n){\subset } B_\varepsilon (f^\pm ):=\{x\in {\mathbb {R}}^2: {\text {dist}}(x,\text {graph}(f^+)\cup \text {graph}(f^-))<\varepsilon \}$. Then, by lower semicontinuity,

$$\begin{aligned}{} & {} \liminf _{n\rightarrow \infty }\int _{\omega _{A}^{(n)}} \frac{1}{2}{\mathbb {C}}(e(v_n)-A^{\textrm{lin}}_\textrm{sym})\cdot (e(v_n)-A^{\textrm{lin}}_\textrm{sym})\textrm{d}x\\{} & {} \quad \geqq \liminf _{n\rightarrow \infty }\int _{\omega _{A}^{(n)}\setminus B_\varepsilon (f^\pm )} \frac{1}{2}{\mathbb {C}}(e(v_n)-A^{\textrm{lin}}_\textrm{sym})\cdot (e(v_n)-A^{\textrm{lin}}_\textrm{sym})\textrm{d}x\\{} & {} \quad \geqq \int _{\omega _{A}\setminus B_\varepsilon (f^\pm )} \frac{1}{2}{\mathbb {C}}(e(v)-A^{\textrm{lin}}_\textrm{sym})\cdot (e(v)-A^{\textrm{lin}}_\textrm{sym})\textrm{d}x, \end{aligned}$$

and analogously in $\omega _B^{(n)}$. Taking $\varepsilon \rightarrow 0$, the assertion follows.

(ii) By the upper bound of Theorem 3.1, we obtain for $\ell \rightarrow \infty$ a sequence $(f^\pm _\ell , v_\ell )\in {\mathcal {B}}_{\text {lin}}^{(L,\ell )}$ such that $\lim _{\ell \rightarrow \infty }{\mathcal {E}}_{\text {lin}}[f^\pm _\ell , v_\ell ]=0$. On the other hand, let $(f^\pm , v)\in {\mathcal {B}}_{\text {lin}}^{(L)}$. Then there exists $\ell >0$ such that $(f^\pm , v)\in {\mathcal {B}}_{\text {lin}}^{(L,\ell )}$, and by the lower bound of Theorem 3.1, ${\mathcal {E}}_{\text {lin}}[f^\pm , v]>0$. $\square$

4 Energy Scaling in the Geometrically Nonlinear Setting

It appears that in the geometrically nonlinear setting, the qualitative behavior of the minimal energy is rather different. On a technical level, the main difference seems to be that the macrotwin habit plane ${e_{\delta ,\theta }}$ is not parallel to a plane of compatibility of the two wells $e^\perp$. Recall that this property was in particular used to extend the test function in the upper bound of Theorem 3.1 with vanishing energy to the left-hand side of the interface.

We first introduce the setting, using the notation from Lemma 2.1. As in Sect. 3, we assume without loss of generality $e:=e_1$ and $e^\perp =e_2$. We recall the definitions

$$\begin{aligned} {e_{\delta ,\theta }}:=\frac{1}{\sqrt{1+(\delta \theta )^2}}(e_2-\delta \theta e_1),\qquad {e_{\delta ,\theta }^\perp }:=-\frac{1}{\sqrt{1+(\delta \theta )^2}}(e_1+\delta \theta e_2). \end{aligned}$$

(4.1)

We shall impose the following periodicity condition on admissible deformations:

$$\begin{aligned} u(x+{e_{\delta ,\theta }})=u(x)+(\theta A_\delta +(1-\theta )B_\delta ){e_{\delta ,\theta }} \qquad \text { for all }x{\in {\mathbb {R}}^2}. \end{aligned}$$

(4.2)

To parametrize the needle shapes, let ${f^\pm }:[0,\infty )\rightarrow {\mathbb {R}}$ be measurable and such that

$$\begin{aligned} {f^-}\leqq f^+\leqq f^-+1\qquad \text { and }\qquad f^+(0)=f^-(0)=0. \end{aligned}$$

(4.3)

(Later on, we will assume that they are L-Lipschitz.)

The periodicity condition (4.2) suggests that we use the non-orthogonal coordinates introduced by the macrotwin, see Fig. 2. We define the linear map $T_{\delta ,\theta }:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$ by

$$\begin{aligned} T_{\delta ,\theta }:= ({e_{\delta ,\theta }}\cdot e_2) e_1\otimes e_1+{e_{\delta ,\theta }}\otimes e_2. \end{aligned}$$

(4.4)

We also define $d,g:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} d(x):= \frac{x\cdot e_2}{{e_{\delta ,\theta }}\cdot e_2} =e_2\cdot T_{\delta ,\theta }^{-1}(x),\qquad {g(x):=-\frac{x\cdot e_{\delta ,\theta }^\perp }{({e_{\delta ,\theta }}\cdot e_2)^2} = e_1\cdot T_{\delta ,\theta }^{-1}(x),} \end{aligned}$$

(4.5)

which is equivalent to

$$\begin{aligned} T_{\delta ,\theta }^{-1}(x)=g(x)e_1+d(x)e_2. \end{aligned}$$

(4.6)

Note that $d(e_1)=0$ and $d({e_{\delta ,\theta }})=1$, so that we can use $\lfloor d(x)\rfloor \in {\mathbb {Z}}$ to label the cell of periodicity that contains x. In turn, $g(x)$ denotes the coordinate along the needle, which corresponds to $x_1$ in the geometrically linear setting. We set

$$\begin{aligned} \begin{aligned} {\hat{\omega }}_{A}:=&\{x\in {\mathbb {R}}^2:x\cdot {e_{\delta ,\theta }^\perp }\geqq 0\}\cup \\&\cup \left\{ x\in {\mathbb {R}}^2: x\cdot {e_{\delta ,\theta }^\perp }<0,\,\, d(x)\in \bigcup _{k\in {\mathbb {Z}}} \left[ k+f^-(g(x)),k+f^+(g(x))\right) \right\} \\ =&T_{\delta ,\theta }\left\{ y\in {\mathbb {R}}^2: y_1\leqq 0 \text { or } y_1>0 \text { and } y_2\in \bigcup _{k\in {\mathbb {Z}}} \left[ k+f^-(y_1), k+f^+(y_1)\right) \right\} \end{aligned}\end{aligned}$$

(4.7)

and

$$\begin{aligned} {\hat{\omega }}_B:={\mathbb {R}}^2\setminus \hat{\omega }_{A}.\end{aligned}$$

(4.8)

By periodicity, for the computation of the energy it suffices to integrate over one period, and therefore to consider the sets

$$\begin{aligned} \omega _{A,B}:={\hat{\omega }}_{A,B}\cap \left\{ x\in {\mathbb {R}}^2: {d(x)}\in (0,1)\right\} =T_{\delta ,\theta }({\mathbb {R}}\times (0,1)). \end{aligned}$$

(4.9)

The class of admissible configurations is given by

$$\begin{aligned} {\mathcal {A}}_{\text {nl}}:=\left\{ (f^\pm ,u): {f^\pm :{\mathbb {R}}\rightarrow {\mathbb {R}}} \text{ satisfy } (4.3),\ {u\in W^{1,2}_{\text{ loc }}({\mathbb {R}}^2;{\mathbb {R}}^2)} \text{ satisfies } (4.2)\right\} . \end{aligned}$$

(4.10)

Note that it depends implicitly on $\delta$ and $\theta$ via (4.2). For $L>0$ we further set

$$\begin{aligned} {\mathcal {A}}_{\textrm{nl}}^L:=\{(f^\pm ,u)\in {\mathcal {A}}_{\textrm{nl}}: f^\pm \text { are }L-\text {Lipschitz}\}. \end{aligned}$$

(4.11)

The resulting variational problem then is to minimize over this set the functional

$$\begin{aligned} {\mathcal {E}}_{\textrm{nl}}[f^\pm ,u]:=\int _{\omega _{A}}W(\nabla u A_\delta ^{-1})\textrm{d}x+\int _{\omega _B}W(\nabla u B_\delta ^{-1})\textrm{d}x. \end{aligned}$$

(4.12)

Here, $W:{\mathbb {R}}^{3\times 3}\rightarrow {[0,\infty )}$ is a typical nonlinear elastic energy density satisfying

$$\begin{aligned} \begin{aligned} \frac{1}{c_W}{\text {dist}}^2(F,\textrm{SO}(2))\leqq W(F) =W(RF)\leqq c_W{\text {dist}}^2(F,\textrm{SO}(2))\\ \quad \text { for all }\ R\in \textrm{SO}(2)\text { and } F\in {\mathbb {R}}^{2\times 2}, \end{aligned}\end{aligned}$$

(4.13)

with some constant $c_W>0$.

Remark 4.1

Note that in contrast to the geometrically linearized setting, we do not assign boundary conditions for the deformation deep in the laminate.

Theorem 4.2

For every $L\geqq 1$ there are constants $c_L>0$ and $\delta _0>0$ such that for all $\theta \in (0,1/2]$ and all $\delta \in (-\delta _0,\delta _0)$, we have

$$\begin{aligned} \frac{1}{c_L}|\delta |^3{\theta ^2}\leqq \inf \{ {\mathcal {E}}_{\textrm{nl}}[f^{\pm },u]: (f^\pm ,u)\in {\mathcal {A}}_\textrm{nl}^L\} \leqq {c_L}|\delta |^3{\theta ^2}. \end{aligned}$$

There is $c_f>0$ such that, if $\delta \ne 0$, the same holds if one imposes that, for $x_1\geqq c_f |\delta |^{-1}$,

$$\begin{aligned} f^-(x_1)=0, \qquad f^+(x_1)=\theta , \qquad {\nabla u}(x)={\left\{ \begin{array}{ll} A_\delta , &{} \text { if } {d(x)}\in (0,\theta ),\\ B_\delta , &{} \text { if } {d(x)}\in (\theta ,1). \end{array}\right. } \end{aligned}$$

(4.14)

Proof

The upper bound follows from Proposition 4.3, the lower bound from Proposition 4.9. $\square$

4.1 Upper Bound

Proposition 4.3

There exists a constant $c>0$ such that for every $\delta \in [-1,1]$ and $\theta \in (0,\frac{1}{2}]$ there are $(f^\pm , u)\in {\mathcal {A}}_{\textrm{nl}}^1$ such that

$$\begin{aligned} {{\mathcal {E}}_{\textrm{nl}}[f^\pm ,u]}\leqq c|\delta |^3{\theta ^2}. \end{aligned}$$

The functions $(f^\pm ,u)$ obey (4.14) for $x_1\geqq c_f|\delta |^{-1}$ for some universal $c_f>0$ (provided $\delta \ne 0$).

Proof

For $\delta =0$, we have $A_\delta =B_\delta ={{\,\textrm{Id}\,}}$, and an affine function $u(x)=x$ has vanishing energy, with $f^+=f^-=0$. Consider now $\delta \ne 0$. Let ${Q_*}$ be as in Lemma 2.1. Left of the interface, in $\{g(x)\leqq 0\}=\{x\cdot {e_{\delta ,\theta }^\perp }\geqq 0\}$, we set

$$\begin{aligned} u(x):={Q_*}A_\delta x. \end{aligned}$$

Note that by (2.6), this definition satisfies the periodicity condition (4.2). Set

$$\begin{aligned} f^{-}(t):=0 \text { for all }t\geqq 0, \end{aligned}$$

(4.15)

and let $f^+:[0,\infty )\rightarrow [0,1)$ be a 1-Lipschitz function with $f(0)=0$, to be determined later. We now describe the deformation. For the ease of notation, we consider a shifted cell of periodicity, i.e.,

$$\begin{aligned} \omega _{A}^*:= & {} \{x\in {\mathbb {R}}^2:g(x)\geqq 0,\ 0\leqq d(x)\leqq f^+(g(x))\},\\ \omega _B^*:= & {} \{x\in {\mathbb {R}}^2: g(x)\geqq 0,\,{f^+}(g(x))-1\leqq d(x)<0\}. \end{aligned}$$

To make an ansatz for the deformation on the right-hand side of the interface, we consider a rotation and a shift as independent parameters. Let $R:[0,\infty )\rightarrow \textrm{SO}(2)$ and $w:[0,\infty )\rightarrow {\mathbb {R}}^2$ be differentiable functions to be determined later, and set

$$\begin{aligned} \phi (t):={(e_2\cdot {e_{\delta ,\theta }})}\int _0^tR(s)e_1\textrm{d}s. \end{aligned}$$

(4.16)

The reason for this choice will become clear in (4.23) below. With these quantities, we define the deformation $u:\omega _A^*\cup \omega _B^*\rightarrow {\mathbb {R}}^2$ as

$$\begin{aligned} u(x):={\left\{ \begin{array}{ll} u_{A}(x),&{}\text { if }x\in {\omega _{A}^*},\\ u_B(x),&{}\text { if }x\in {\omega _B^*}, \end{array}\right. } \end{aligned}$$

(4.17)

where

$$\begin{aligned} \begin{aligned} u_{A}(x)&:=\phi (g(x))+R(g(x))A_\delta {e_{\delta ,\theta }}d(x)+w(g(x))d(x),\\ u_B(x)&:=\phi (g(x))+R(g(x))B_\delta {e_{\delta ,\theta }}d(x)+w(g(x))d(x). \end{aligned}\end{aligned}$$

(4.18)

We note that this yields a continuous function in $\omega _{A}^*\cup \omega _B^*$ since for $d(x)=0$ we have $u_{A}(x)=u_B(x)$. To obtain an admissible configuration, the functions R, $f^+$ and w have to satisfy the following properties: first, $f^+$ should be 1-Lipschitz with

$$\begin{aligned} {f^+(0)=0 \qquad \text { and }}\qquad f^+(t)\in [0,1)\qquad \text { for all }\ t> 0. \end{aligned}$$

(4.19)

Second, this definition, when extended with the periodicity condition (4.2), should generate a continuous function on $\{g(x)\geqq 0\}=\{x\cdot {e_{\delta ,\theta }^\perp }\leqq 0\}$. This requires that

$$\begin{aligned}u_{A}(x+{e_{\delta ,\theta }})-u_B(x)= (\theta A_\delta +(1-\theta )B_\delta ){e_{\delta ,\theta }}\qquad \hbox { if}\ d(x)=f^+(g(x))-1. \end{aligned}$$

Using $d(x+{e_{\delta ,\theta }})=d(x)+1$ and $d(x)+1=f^+(g(x))$ we obtain

$$\begin{aligned} \begin{aligned} u_{A}(x+{e_{\delta ,\theta }})-u_B(x) =&R(g(x))B_\delta {e_{\delta ,\theta }}\\&+f^+(g(x))R(g(x))(A_\delta -B_\delta ){e_{\delta ,\theta }}+w(g(x)), \end{aligned}\end{aligned}$$

(4.20)

so that the periodicity condition is equivalent to

$$\begin{aligned} \begin{aligned} \left( f^+(g(x))R(g(x))-\theta {{\,\textrm{Id}\,}}\right)&\left( A_\delta -B_\delta \right) {e_{\delta ,\theta }}\\ +&\left( R(g(x))-{{\,\textrm{Id}\,}}\right) B_\delta {e_{\delta ,\theta }}+w(g(x))=0. \end{aligned}\end{aligned}$$

(4.21)

Note that on the line $\{g(x)=0\}={\mathbb {R}}e_{\delta ,\theta }$, as $f^+(0)=0$ the function $t\mapsto u(t{e_{\delta ,\theta }})$ is affine. By (2.6), the periodicity condition and $u(0)=0$ it coincides with the expression ${Q_*}A_\delta x$ that we used to define u on $\{g(x)\leqq 0\}$. Equivalently, one can see from (4.21) that $(R(0)-{{\,\textrm{Id}\,}})B_\delta e_{\delta ,\theta }+w(0)=\theta (A_\delta -B_\delta )e_{\delta ,\theta }$, so that (4.17)–(4.18) give $u(te_{\delta ,\theta })=u_B(te_{\delta ,\theta })=R(0)B_\delta te_{\delta ,\theta }+ w(0) t = (\theta A_\delta +(1-\theta )B_\delta ) e_{\delta ,\theta }t$, which by (2.6) equals $Q_*A_\delta e_{\delta ,\theta }t$.

From now on, we restrict to $\{g(x)>0\}$. Before we give the explicit constructions, we provide an estimate for the energy within this ansatz. We observe that $\nabla d = \frac{1}{e_{\delta ,\theta }\cdot e_2}e_2$, $\nabla g = -(e_{\delta ,\theta }\cdot e_2)^{-2}e_{\delta ,\theta }^\perp$, and

$$\begin{aligned} -e_1\otimes e_{\delta ,\theta }^\perp +e_{\delta ,\theta }\otimes e_2=(e_2\cdot e_{\delta ,\theta }) {{\,\textrm{Id}\,}}. \end{aligned}$$

(4.22)

The definition of $\phi$ (see (4.16)) was chosen so that $\phi '=(e_2\cdot e_{\delta ,\theta }) Re_1=(e_2\cdot e_{\delta ,\theta }) RA_\delta e_1$, which – using (4.22) – implies

$$\begin{aligned} \begin{aligned} \phi '(g(x))\otimes \nabla g + R(g(x))A_\delta e_{\delta ,\theta }\otimes \nabla d=&\frac{1}{e_2\cdot e_{\delta ,\theta }} R(g(x))A_\delta ( -e_1\otimes e_{\delta ,\theta }^\perp +e_{\delta ,\theta }\otimes e_2)\\ =&R(g(x))A_\delta . \end{aligned}\end{aligned}$$

(4.23)

Therefore,

$$\begin{aligned}\begin{aligned} \nabla u_{A}(x)=&{\phi '(g(x))\otimes \nabla g} +{R(g(x))A_\delta e_{\delta ,\theta }\otimes \nabla d} +d(x){R'(g(x))A_\delta {e_{\delta ,\theta }}\otimes \nabla g}\\&+d(x) {w'(g(x))\otimes \nabla g} +{w(g(x))\otimes \nabla d}\\ =&R(g(x))A_\delta - {\frac{1}{(e_2\cdot e_{\delta ,\theta })^2}} d(x)\left( R'(g(x))A_\delta {e_{\delta ,\theta }}+w'(g(x))\right) \otimes {e_{\delta ,\theta }^\perp }\\&+\frac{1}{e_{\delta ,\theta }\cdot e_2} w(g(x))\otimes e_2, \end{aligned}\end{aligned}$$

and similarly,

$$\begin{aligned}\begin{aligned} \nabla u_B(x)=&R(g(x))B_\delta - {\frac{1}{(e_2\cdot e_{\delta ,\theta })^2}} d(x)\left( R'(g(x))B_\delta {e_{\delta ,\theta }}+w'(g(x))\right) \otimes {e_{\delta ,\theta }^\perp } \\&+\frac{1}{e_{\delta ,\theta }\cdot e_2} w(g(x))\otimes e_2. \end{aligned}\end{aligned}$$

Hence, the elastic energy of such an admissible test function is estimated by

$$\begin{aligned} {\mathcal {E}}_{\textrm{nl}}{[f^\pm ,u]}\leqq & {} c_W\left( \int _{{\omega _{A}^*}}|\nabla u_{A}(x)-RA_\delta |^2\,\textrm{d}x+\int _{{\omega _B^*}}|\nabla u_B(x)-RB_\delta |^2\,\textrm{d}x\right) \nonumber \\\leqq & {} c \int _0^\infty \left( |R'(t)|^2+|w'(t)|^2+|w(t)|^2\right) \,\textrm{d}t. \end{aligned}$$

(4.24)

Finally, we specify how to choose R, w and $f^+$. We consider the periodicity condition (4.21) and divide it into two equations, testing with $e_1$ and $e_2$. First, we set

$$\begin{aligned} w\cdot e_1=0, \end{aligned}$$

(4.25)

and take the scalar product of (4.21) with $e_1$. Using that $(A_\delta -B_\delta ){e_{\delta ,\theta }}=\frac{2\delta }{\sqrt{1+(\delta \theta )^2}}e_1$ and $B_\delta {e_{\delta ,\theta }}=\frac{e_2-\delta (1+\theta )e_1}{\sqrt{1+(\delta \theta )^2}}$, we obtain, multiplying by $\sqrt{1+(\delta \theta )^2}$ and skipping the arguments g(x) everywhere,

$$\begin{aligned} 2\delta \left( f^+e_1\cdot Re_1-\theta \right) +e_1\cdot Re_2-\delta (1+\theta )e_1\cdot Re_1+\delta (1+\theta )=0. \end{aligned}$$

We let $\alpha := e_1\cdot Re_1$, $\beta :=e_1\cdot Re_2$ and solve this equation for $f^+$, which leads to the definition

$$\begin{aligned} f^+:= & {} \frac{\theta }{\alpha }-\frac{\beta }{2\delta \alpha }+\frac{1+\theta }{2}-\frac{1+\theta }{2\alpha }\nonumber \\= & {} -\frac{1-\theta }{2\alpha }-\frac{\beta }{2\delta \alpha }+\frac{1+\theta }{2}. \end{aligned}$$

(4.26)

Since R is a rotation, we have $|\alpha |=\sqrt{1-\beta ^2}$, and we choose $\alpha =\sqrt{1-\beta ^2}$. Roughly speaking, we expect that for large arguments approximately $\beta =0$ and $\alpha =1$, which correspond to $f^+=\theta$. On the other hand, in view of Remark 2.2(ii) since $R_0$ is a rotation by roughly $-2\delta \theta$, we expect that for small arguments, $\beta \approx 2\delta \theta$ which is positive for $\delta >0$ and negative for $\delta <0$. Hence, we assume that $\frac{\beta }{\delta }$ is monotonically decreasing and $\alpha$ is monotonically increasing, so that by (4.26) also $f^+$ is monotonically increasing. We shall fix the value $\beta (0)$ from the condition $f^+(0)=0$, so that monotonicity of $f^+$ implies $0\leqq f^+\leqq \theta$ everywhere and in particular (4.19).

Rearranging terms, the condition $f^+(0)=0$ is (for $\alpha (0)\ne 0$) the same as

$$\begin{aligned} (1-\theta ) + \frac{\beta (0)}{\delta }=(1+\theta )\alpha (0) . \end{aligned}$$

(4.27)

We choose $\beta (0)$ such that $\beta (0)/\delta >0$, hence squaring and inserting $\alpha ^2=1-\beta ^2$, this is equivalent to

$$\begin{aligned} \left( 1+\delta ^2(1+\theta )^2\right) \left( \frac{\beta (0)}{\delta }\right) ^2+2(1-\theta )\frac{\beta (0)}{\delta }-4\theta =0. \end{aligned}$$

(4.28)

As $\theta \in (0,1/2]$, this quadratic equation has a unique solution with $\beta (0)/\delta >0$. Since the left-hand side is larger than

$$\begin{aligned} \left( \frac{\beta (0)}{\delta }\right) ^2+\frac{\beta (0)}{\delta }-2, \end{aligned}$$

we find that $\beta (0)/\delta \leqq 1$, i.e., $|\beta (0)|\leqq |\delta |$. Analogously, since the left-hand side of (4.28) is larger than

$$\begin{aligned} 2|\beta (0)|^2+|\beta (0)|-2, \end{aligned}$$

we obtain $|\beta (0)|\leqq \frac{4}{5}$. Further, as the first term in (4.28) is positive we have $2(1-\theta )\frac{\beta (0)}{\delta }< 4\theta$, and with $2(1-\theta )\geqq 1$ this leads to $|\beta (0)|\leqq 4\theta \,|\delta |$. Summarizing,

$$\begin{aligned} |\beta (0)|\leqq \min \left\{ |\delta |, 4|\delta |\,{\theta }, \frac{4}{5}\right\} . \end{aligned}$$

(4.29)

We then set, for some $\ell >0$ to be chosen later,

$$\begin{aligned} \beta ( s):={\left\{ \begin{array}{ll} \frac{\ell - s}{\ell }\beta (0)&{}\text { if } s\leqq \ell ,\\ 0&{}\text { otherwise}, \end{array}\right. } \qquad \text { and }\qquad \alpha ( s):=\sqrt{1-\beta ^2( s)}. \end{aligned}$$

(4.30)

Finally, $w\cdot e_2$ is determined from (4.21) by testing with $e_2$. Since $R\in \textrm{SO}(2)$ the definitions of $\alpha$ and $\beta$ imply $e_2\cdot Re_2=\alpha$, $e_2\cdot Re_1=-\beta$. A similar computation as above leads to

$$\begin{aligned} e_2\cdot w=\frac{1}{\sqrt{1+(\delta \theta )^2}}\left( 1-\alpha +\left( 2\delta f^+-\delta (1+\theta )\right) \beta \right) , \end{aligned}$$

(4.31)

which, together with (4.25), defines w. Note that for $s\geqq \ell$, we have $\alpha =1$ and $\beta =0$ which implies that $w(s)=0$. To estimate the energy, we observe that $|\beta (s)|\leqq |\beta (0)|{\leqq \frac{4}{5}}$, which implies $\alpha \geqq \frac{1}{5}$ and $|\alpha '|=\frac{\left| \beta \beta '\right| }{\sqrt{1-\beta ^2}}\leqq 5|\beta '|$. As $|\beta '|( s)=\frac{|\beta (0)|}{\ell }{\leqq \frac{4|\delta |\theta }{\ell }}$ for $s\in (0, \ell )$, from (4.26) we have

$$\begin{aligned} |(f^+)'|\leqq \left| \frac{\alpha '}{\alpha ^2}\right| +\left| \frac{\beta '}{2\delta \alpha }\right| +\left| \frac{\beta \alpha '}{2\delta \alpha ^2}\right| \leqq c \frac{|\beta '|}{|\delta |} {\leqq c_f\frac{\theta }{\ell }} \end{aligned}$$

(4.32)

for some universal constant $c_f>0$, and thus, from (4.31),

$$\begin{aligned} \left| w'\right| \leqq \left| \alpha '\right| +3{|\delta |}\left| \beta '\right| +2|\delta |\,|\beta |\,\left| (f^+)'\right| \leqq c |\beta '| {\leqq c\frac{{|\delta |}\theta }{\ell }}. \end{aligned}$$

Finally, with $1-\alpha =\frac{\beta ^2}{1+\alpha }\leqq \beta ^2\leqq |\delta |\,|\beta |$ and (4.31), we obtain

$$\begin{aligned} |w|\leqq {|1-\alpha |+2{|\delta |}|\beta |} \leqq 3|\delta |\,|\beta |\leqq c\delta ^2\theta . \end{aligned}$$

Hence, using (4.24), we can estimate the energy by

$$\begin{aligned} {\mathcal {E}}_{\textrm{nl}}[f^\pm ,u]\leqq c \int _0^\ell \left( |R'|^2+|w'|^2+|w|^2\right) \,\textrm{d}t \leqq c\left( \frac{\delta ^2\theta ^2}{\ell }+ \ell \delta ^4\theta ^2\right) . \end{aligned}$$

Recalling (4.32), if we choose $\ell :=c_f|\delta |^{-1}$ we obtain that $f^+$ is 1-Lipschitz and ${\mathcal {E}}_{\textrm{nl}}[f^\pm ,u]\leqq c {|\delta |}^3\theta ^2$. $\square$

4.2 Lower Bound

For the lower bound, we need some auxiliary statements.

4.2.1 Technical Preliminaries

For $v\in {\mathbb {R}}^2$ we write $v^\perp :=(-v_2,v_1)$.

Lemma 4.4

There is $c>0$ such that if $\alpha \in {\mathbb {R}}$, $Q\in \textrm{SO}(2)$ and $v\in {\mathbb {R}}^2{\setminus \{0\}}$ are such that

$$\begin{aligned} |Q(v-\alpha v^\perp )-v|\leqq \eta |v| \end{aligned}$$

for some $\eta \geqq 0$, then

$$\begin{aligned} |Q-({{\,\textrm{Id}\,}}+\alpha J)|\leqq \sqrt{2}\, \eta , \end{aligned}$$

where $J:=\begin{pmatrix} 0 &{} -1\\ 1&{}0\end{pmatrix}$.

Proof

This follows immediately by the fact that all matrices considered are conformal. For clarity we present a short explicit computation. By scaling we can assume $|v|=1$. Let $\phi \in (-\pi ,\pi ]$ be such that $Q=\cos \phi {{\,\textrm{Id}\,}}+\sin \phi J$. Then

$$\begin{aligned}\begin{aligned}&\eta ^2\geqq |Q(v-\alpha v^\perp )-v|^2= |v-\alpha v^\perp -Q^Tv|^2=|v-\alpha v^\perp - \cos \phi v+\sin \phi v^\perp |^2\\&= (1-\cos \phi )^2+(\alpha -\sin \phi )^2.\end{aligned} \end{aligned}$$

Then

$$\begin{aligned} |Q-({{\,\text {Id}\,}}+\alpha J)|^2=&{}|(\cos \phi -1){{\,\text {Id}\,}}+ (\sin \phi -\alpha ) J|^2\\ {}{} =&{} 2(1-\cos \phi )^2+2(\sin \phi -\alpha )^2\leqq 2\eta ^2 \end{aligned}$$

concludes the proof. $\square$

The next lemma concerns stability of the rank-one directions.

Lemma 4.5

Suppose that $\delta \in [-1,1]$ and that $Q_{A}, Q_B\in \textrm{SO}(2)$, $t\in S^1$ satisfy $t\cdot e_1>0$ and, for some $\eta >0$,

$$\begin{aligned} |(Q_{A}A_\delta -Q_BB_\delta )t|\leqq \eta . \end{aligned}$$

(4.33)

Then

$$\begin{aligned} |Q_{A}-Q_B|\leqq \frac{{6}}{{t\cdot e_1}}\eta . \end{aligned}$$

(4.34)

Proof

We write $t=t_1e_1+t_2e_2$ and find that $|A_\delta t|+|B_\delta t|\leqq 2(1+|\delta |)\leqq 4$ since $|\delta |\leqq 1$. Assumption (4.33) gives $\left| |A_\delta t|-|B_\delta t|\right| =\left| |Q_AA_\delta t|-|Q_BB_\delta t|\right| \leqq \eta$, and therefore

$$\begin{aligned} \begin{aligned} 4\eta \geqq \left| |A_\delta t|-|B_\delta t|\right| \cdot \left| |A_\delta t|+|B_\delta t|\right| =\left| |A_\delta t|^2-|B_\delta t|^2\right| =4{|\delta |} |t_1t_2|, \end{aligned} \end{aligned}$$

(4.35)

which implies that

$$\begin{aligned} |t_2|\leqq \frac{\eta }{{|\delta |}t_1}. \end{aligned}$$

(4.36)

From $A_\delta ={{\,\textrm{Id}\,}}+\delta e_1\otimes e_2$ and $B_\delta ={{\,\textrm{Id}\,}}-\delta e_1\otimes e_2$ we deduce that

$$\begin{aligned} |A_\delta t-t|=|B_\delta t-t|={|\delta |} |e_2\cdot t|\leqq {\frac{\eta }{t_1}} , \end{aligned}$$

so that, with (4.33),

$$\begin{aligned} \begin{aligned} \frac{|Q_{A}-Q_B|}{\sqrt{2}}=&{}|Q_{A}t-Q_Bt|\\ \leqq&{}|Q_{A}t-Q_{A}A_\delta t|\\ {}&{}+|Q_{A}A_\delta t-Q_BB_\delta t|+|Q_BB_\delta t-Q_Bt|\\=&{} |t-A_\delta t|+|Q_{A}A_\delta t-Q_BB_\delta t|+|B_\delta t-t|\\\leqq&{} {2\frac{\eta }{t_1}}+ \eta \leqq {\frac{3}{t_1}}\eta , \end{aligned} \end{aligned}$$

(4.37)

which concludes the proof.

The next two statements are uniform geometric rigidity and trace statements on domains which are appropriate sections of the sets ${\tilde{\omega }}_A$, ${\tilde{\omega }}_B$ defined in (4.7)–(4.8). For clarity we present here the specific assertion used in the lower bound, postponing to Sect. 5 the proof in a more general context and the specific definition of (L, R)-Lipschitz sets.

Proposition 4.6

For any $L,M>0$ there are constants ${{\hat{L}}, {\hat{R}},} c_{L,M}>0$ with the following property. Let $\ell >0$, $f,g:[0,\ell ]\rightarrow {\mathbb {R}}$ be L-Lipschitz functions. Assume that

$$\begin{aligned} \frac{L\ell }{M} \leqq g({t})-f({t}) \leqq ML \ell \qquad \text { for all } {t}\in [0,\ell ] \end{aligned}$$

(4.38)

and define

$$\begin{aligned} \omega ^{f,g}:=\{x: x_1\in (0,\ell ), f(x_1)<x_2<g(x_1)\}, \end{aligned}$$

(4.39)

fix any $\theta \in (0,\frac{1}{2}]$ and any $\delta \in [-1,1]$. Then the sets $\omega ^{f,g}$ and $T_{\delta ,\theta }(\omega ^{f,g})$ are $({\hat{L}}, {\hat{R}})$-Lipschitz. Further, for any $u\in W^{1,2}(\omega ^{f,g};{\mathbb {R}}^2)$, and any $F\in \{A_\delta ,B_\delta ,{{\,\textrm{Id}\,}}\}$, there is $Q_u^F\in \textrm{SO}(2)$ such that

$$\begin{aligned} \int _{T_{\delta ,\theta }(\omega ^{f,g})} |\nabla u-Q_u^FF|^2 \textrm{d}x \leqq c_{L,M} \int _{T_{\delta ,\theta }(\omega ^{f,g})} {\text {dist}}^2(\nabla u, \textrm{SO}(2)F) \textrm{d}x \end{aligned}$$

(4.40)

and, for some $d_u\in {\mathbb {R}}^2$,

$$\begin{aligned} \int _{T_{\delta ,\theta }(\omega ^{f,g})} |u(x)-d_u-Q_u^FFx|^2 \textrm{d}x \leqq c_{L,M} \int _{T_{\delta ,\theta }(\omega ^{f,g})} {\text {dist}}^2(\nabla u, \textrm{SO}(2)F) \textrm{d}x. \end{aligned}$$

(4.41)

Proof

By Lemma 5.4 the sets $\omega ^{f,g}$ are $(2L+1,R)$-Lipschitz (see Definition 5.1), for some R which depends only on L and M. We observe that the definition (4.4) implies $T_{\delta ,\theta }^{-1}=\sqrt{1+(\delta \theta )^2}({{\,\textrm{Id}\,}}+ \delta \theta e_1\otimes e_2)$, and therefore

$$\begin{aligned} |T_{\delta ,\theta }|\leqq \sqrt{2},\qquad |T_{\delta ,\theta }^{-1}|\leqq \sqrt{2}\left( \sqrt{2}+\frac{1}{2}\right) \leqq 3. \end{aligned}$$

(4.42)

By Lemma 5.3 we obtain that the sets $T_{\delta ,\theta }(\omega ^{f,g})$ are $(6(2L+1),6R)$-Lipschitz. The result for $F={{\,\textrm{Id}\,}}$ follows then immediately from Theorem 5.10.

Consider now $F=A_\delta$. For notational simplicity we prove the statement for $\omega ^{f,g}$, the argument for $T_{\delta ,\theta }(\omega ^{f,g})$ is identical. We define $v\in W^{1,2}(A_\delta \omega ^{f,g};{\mathbb {R}}^2)$ by $v(x):=u(A_\delta ^{-1}x)$, so that $\nabla v(x)=\nabla u(A_\delta ^{-1}x)A_\delta ^{-1}$, which implies

$$\begin{aligned} {\text{ dist }}(\nabla v, \text {SO}(2))(x)={}&{}{\text{ dist }}(\nabla uA_\delta ^{-1}, \text {SO}(2)) (A_\delta ^{-1}x)\nonumber \\\leqq {}&{} |A_\delta ^{-1}| {\text{ dist }}(\nabla u, \text {SO}(2)A_\delta )(A_\delta ^{-1}x). \end{aligned}$$

(4.43)

By Lemma 5.3, using that $|A_\delta |,|A_\delta ^{-1}|\leqq 3$, we obtain that the sets $A_\delta ^{-1}\omega ^{f,g}$ are $(c(2L+1),cR)$-Lipschitz. Therefore Theorem 5.10 implies that there is $Q_u^{A_\delta }\in \textrm{SO}(2)$ such that

$$\begin{aligned} \int _{A_\delta ^{-1}\omega ^{f,g}} |\nabla v-Q_u^{A_\delta }|^2 \textrm{d}x \leqq c_{L,M} \int _{A_\delta ^{-1}\omega ^{f,g}} {\text {dist}}^2(\nabla v, \textrm{SO}(2)) \textrm{d}x. \end{aligned}$$

(4.44)

Using (4.43) and a change of variables, this implies

$$\begin{aligned} \int _{\omega ^{f,g}} |\nabla u-Q_u^{A_\delta }A_\delta |^2 \textrm{d}x \leqq c'_{L,M} \int _{\omega ^{f,g}} {\text {dist}}^2(\nabla u, \textrm{SO}(2)A_\delta ) \textrm{d}x, \end{aligned}$$

(4.45)

and concludes the proof. The case $F=B_\delta$ is identical.

The second bound follows immediately from Theorem 5.8. $\square$

For completeness, we finally note a rescaling property of the trace norm.

Corollary 4.7

(Trace estimate) Let $M_0, L>0$. There exists a constant $C_T$ with the following property: Let $\ell >0$, and let $f,g:[0,\ell ]\rightarrow {\mathbb {R}}$ be L-Lipschitz continuous with $\frac{L\ell }{M_0}< g(t)-f(t)< M_0L\ell$ for all $t\in [0,\ell ]$. Then, setting $\omega _{f,g}:=\{x\in {\mathbb {R}}^2:\ x_1\in (0,\ell ),\ f(x_1)<x_2<g(x_1)\}$, for every $u\in W^{1,2}(\omega _{f,g})$ there exists $d_u\in {\mathbb {R}}$ such that

$$\begin{aligned} \Vert Tu-d_u\Vert ^2_{L^2(\partial \omega _{f,g})}\leqq C_T\ell \Vert \nabla u\Vert ^2_{L^2(\omega _{f,g})}. \end{aligned}$$

Proof

For $\ell =1$, this follows from Lemma 5.4, Theorems 5.8 and 5.9. The general case follows from rescaling $f_\ell :(0,\ell )\rightarrow {\mathbb {R}}$, $f_\ell (t):=\ell f_1(\frac{t}{\ell })$ (similarly for $g_\ell$) and $u_\ell \in W^{1,2}(\omega _{f_\ell ,g_\ell })$ given by $u_\ell (x_1,x_2):=u(x_1/\ell , x_2/\ell )$. $\square$

4.2.2 Proof of the Lower Bound

We start introducing some notation. Recall that the periodicity condition (4.2) is the same as $u(T_{\delta ,\theta }(y+e_2))=u(T_{\delta ,\theta }(y))+ (\theta A_\delta +(1-\theta )B_\delta )T_{\delta ,\theta }(e_2)$. Let ${f^\pm }:[0,\infty )\rightarrow {\mathbb {R}}$ be L-Lipschitz with ${f^-}\leqq {f^+\leqq f^-+1}$. Given $I\subseteq (0,\infty )$ we set

$$\begin{aligned} \begin{aligned} \omega _{A}^I:=&T_{\delta ,\theta }(\{y: y_1\in I, f^-(y_1)<y_2<f^+(y_1)\}),\\ \omega _B^I:=&T_{\delta ,\theta }(\{y: y_1\in I, f^+(y_1)<y_2<f^-(y_1)+1\}) \end{aligned} \end{aligned}$$

(4.46)

and (for $I\subseteq (0,\infty )$ Borel measurable)

$$\begin{aligned} {\mathcal {E}}[I;(f^\pm ,u)]:=\int _{\omega _{A}^I}{\text {dist}}^2(\nabla u,\textrm{SO}(2)A_\delta )\textrm{d}x+ \int _{\omega _B^I}{\text {dist}}^2(\nabla u,\textrm{SO}(2)B_\delta )\textrm{d}x. \end{aligned}$$

(4.47)

Proposition 4.8

Let $L>0$, assume that $f^\pm$ are L-Lipschitz with $f^-\leqq f^+\leqq f^-+1$, and let $I_*\subseteq (0,\infty )$ be an interval of length 1/(4L). For any $u\in W^{1,2}_\textrm{loc}({\mathbb {R}}^2;{\mathbb {R}}^2)$ there is $Q\in \textrm{SO}(2)$ such that

$$\begin{aligned} \int _{\omega _{A}^{I_*}} |\nabla u-QA_\delta |^2 \textrm{d}x + \int _{\omega _B^{I_*}} |\nabla u-QB_\delta |^2 \textrm{d}x\leqq c {\mathcal {E}}[I_*;(f^\pm ,u)]. \end{aligned}$$

(4.48)

The constant may depend on L.

Proof

For brevity in this proof we write ${\mathcal {E}}(I)$ for $\mathcal E[I;(f^\pm ,u)]$. We can assume $L\geqq 1$ in the proof (otherwise we cover $I_*$ with $c_L$ subintervals of length 1/4 and use the result for $L=1$ in each of them).

Fig. 5

Sketch of the sets entering the proof of Proposition 4.8

Step 1: Estimate on $\omega _{A}^{I_*}$. Let $t_*$ be the midpoint of $I_*$ and $\ell _*$ its length. We assume that $(f^+-f^-)(t_*)\geqq \frac{1}{2}$. If not, then $f^ -+1-f^ +\geqq \frac{1}{2}$, and the same argument can be used swapping $A_\delta$ with $B_\delta$ and $(f^+,f^-+1)$ with $(f^-,f^+)$. This implies

$$\begin{aligned} {1\geqq (f^+-f^-)(t) \geqq \frac{1}{2} - 2L \frac{\ell _*}{2}\geqq \frac{1}{4}} \qquad \text { for all } t\in I_*. \end{aligned}$$

(4.49)

We write $\omega _{A}:=\omega _{A}^{I_*}$, and $c_L$ for a generic constant that may change from line to line but depends only on L. Proposition 4.6 can be applied (with $M={4}$) to the set $\omega _{A}$, and there is $Q\in \textrm{SO}(2)$ such that

$$\begin{aligned} \int _{\omega _{A}} |\nabla u-QA_\delta |^2 \textrm{d}x \leqq {c_L}\int _{\omega _{A}} {\text {dist}}^2(\nabla u,\textrm{SO}(2)A_\delta )\textrm{d}x \leqq {c_L}{\mathcal {E}}(I_*). \end{aligned}$$

(4.50)

Note that this concludes the proof in the degenerate case $\omega _B^{I_*}=\emptyset$, i.e., if $I_*\cap \{f^-+1>f^+\}=\emptyset$. In the other case, we note that there is $d_A\in {\mathbb {R}}^2$ such that

$$\begin{aligned} \int _{\omega _{A}} |u(x)-QA_\delta x-d_A|^2 \textrm{d}x\leqq {c_L} {\mathcal {E}}(I_*). \end{aligned}$$

(4.51)

Step 2: Estimate on $\omega _B^{I_*}$. For any Borel set $I\subseteq I_*$ we write, recalling (4.47) and the short-hand notation ${\mathcal {E}}(I)={\mathcal {E}}[I;(f^\pm ,u)]$,

$$\begin{aligned} \hat{{\mathcal {E}}}(I):={\mathcal {E}}(I)+\int _{\omega _{A}^I} |u(x)-QA_\delta x-d_A|^2 \textrm{d}x. \end{aligned}$$

(4.52)

It is clear that ${\mathcal {E}}$ and $\hat{{\mathcal {E}}}$ are measures on $I_*$, and that $\hat{{\mathcal {E}}}(I_*)\leqq {c_L}{\mathcal {E}}(I_*)$. We shall first obtain estimates on suitable subintervals of $I_*$, and then cover $I_*$ by countably many such subintervals. Let $M>0$ be a fixed number, we shall choose $M=16$ below.

Assume that $I\subseteq I_*$ is an interval of length $\ell \in (0, \ell _*]$ such that

$$\begin{aligned} \frac{L\ell }{M} \leqq (f^-+1)-f^+\leqq ML\ell \qquad \text { pointwise on }I, \end{aligned}$$

(4.53)

see Fig. 5. Then by Proposition 4.6 there is $Q_{B}^I\in \textrm{SO}(2)$ such that

$$\begin{aligned} \int _{\omega _{B}^I} |\nabla u-Q_{B}^IB_\delta |^2 \textrm{d}x \leqq {c_L}\int _{\omega _{B}^I} {\text {dist}}^2(\nabla u,\textrm{SO}(2)B_\delta )\textrm{d}x\leqq {c_L} {\mathcal {E}}(I). \end{aligned}$$

(4.54)

By Poincaré and the trace theorem (see Corollary 4.7), there is $d_{B}^I\in {\mathbb {R}}^2$ such that, setting $\gamma _+^I:=T_{\delta ,\theta }(\{(t,f^+(t)): t\in I\})$,

$$\begin{aligned} \int _{\gamma _+^I} |u(x)-Q_{B}^IB_\delta x-d_B^I|^2 d{{\mathcal {H}}}^1\leqq {c_L} \ell \Vert \nabla u-Q_{B}^IB_\delta \Vert _{L^2(\omega _{B}^I)}^2\leqq {c_L}\ell {\mathcal {E}}(I). \end{aligned}$$

(4.55)

Analogously, the trace theorem on ${\hat{\omega }}_{A}^I:= T_{\delta ,\theta }(\{y: y_1\in I, f^+(y_1)-\frac{\ell }{4}<y_2<f^+(y_1)\})$, which by (4.49) and $\ell \leqq \ell _*\leqq 1/4$ is contained in $\omega _{A}^I$, gives

$$\begin{aligned} \int _{\gamma _+^I} |u(x)-QA_\delta x-d_A|^2 \textrm{d}{{\mathcal {H}}}^1\leqq {c_L}\ell \hat{{\mathcal {E}}}(I), \end{aligned}$$

(4.56)

so that with a triangular inequality and ${\mathcal {E}}\leqq \hat{{\mathcal {E}}}$, we obtain

$$\begin{aligned} \int _{\gamma _+^I} |QA_\delta x+d_A-Q_{B}^IB_\delta x-d_B^I|^2 \textrm{d}{{\mathcal {H}}}^1\leqq {c_L} \ell \hat{{\mathcal {E}}}(I). \end{aligned}$$

(4.57)

Therefore there is $v\in {\mathbb {R}}^2$ with $v_1\geqq \frac{1}{3}\ell$ and $|v_2|\leqq L v_1$ such that

$$\begin{aligned} |(QA_\delta -Q_{B}^IB_\delta )v|^2\leqq {c_L}\hat{{\mathcal {E}}}(I). \end{aligned}$$

(4.58)

We apply Lemma 4.5 with $t:=v/|v|$, $Q_{A}:=Q$, $Q_{B}:=Q_{B}^I$, and $\eta :=(c_L\hat{{\mathcal {E}}}(I))^{1/2}/{|v|} \leqq 3(c_L\hat{{\mathcal {E}}}(I))^{1/2}/\ell$. Since

$$\begin{aligned} t_1=\frac{v_1}{|v|}\geqq \frac{1}{\sqrt{1+L^2} }, \end{aligned}$$

we obtain $|Q-Q_{B}^I|\leqq 6\sqrt{1+L^2}\eta$ and therefore

$$\begin{aligned} \ell ^2 |Q-Q_{B}^I|^2\leqq {c_L}\hat{{\mathcal {E}}}(I). \end{aligned}$$

(4.59)

Combining (4.54) and (4.59) we conclude that

$$\begin{aligned} \int _{\omega _{B}^I} |\nabla u-QB_\delta |^2 \textrm{d}x \leqq {c_L} \hat{{\mathcal {E}}}(I). \end{aligned}$$

(4.60)

As ${\mathcal {L}}^2\left( \omega _{B}^{I_*\cap \{f^-+1=f^+\}}\right) =0$, it remains to show that $I_*\cap \{f^-+1>f^+\}$ can be covered (up to null sets) by countably many intervals I with the property (4.53) and finite overlap. For any $t\in I_*\cap \{f^-+1>f^+\}$, the interval

$$\begin{aligned} (t-\frac{f^-(t)+1-f^+(t)}{4L}, t+\frac{f^-(t)+1-f^+(t)}{4L}) \end{aligned}$$

(4.61)

contains t and obeys the property (4.53) with $M=3$. By the Besicovitch covering theorem this family contains a countable set of intervals $(I_k)_k$ which covers $I_*\cap \{f^-+1>f^+\}$ and has finite overlap. The intervals $(I_k\cap I_*)_k$ obey property (4.53) with $M=6$, since ${\frac{f^-(t)+1-f^+(t)}{4\,L} \leqq \frac{1}{4\,L}}=\ell ^*$ implies ${\mathcal {L}}^1(I_k\cap I_*)\geqq \frac{1}{2} {\mathcal {L}}^1(I_k)$. Therefore, by (4.60),

$$\begin{aligned} \begin{aligned} \int _{\omega _{B}^{I_*}} |\nabla u-QB_\delta |^ 2\text {d}x=&\int _{\omega _{B}^{I_*\cap \{f^-+1>f^+\}}}|\nabla u-QB_\delta |^ 2\text {d}x\\ \leqq {}&{c_L} \sum _k \int _{\omega _{B}^{I_*\cap I_k}}|\nabla u-QB_\delta |^ 2\text {d}x\\ \leqq&{}{c_L} \sum _k \hat{{\mathcal {E}}}(I_*\cap {I_k})\leqq {c_L} \hat{{\mathcal {E}}}(I_*) \end{aligned} \end{aligned}$$

(4.62)

and with (4.51) and $\hat{{\mathcal {E}}}(I_*)\leqq {c_L}{\mathcal {E}}(I_*)$ the proof is concluded. $\square$

Proposition 4.9

Let $L>0$. There are $c_L>0$, $\delta _L>0$ such that for all $\theta \in (0,\frac{1}{2}]$, all $\delta \in {[-\delta _L},\delta _L]$, all $(f^\pm ,u)\in {\mathcal {A}}_\textrm{nl}^L$ it holds that

$$\begin{aligned} {\mathcal {E}}_\textrm{nl}[f^\pm ,u]\geqq c_L{|\delta |}^3\theta ^2. \end{aligned}$$

Proof

For brevity, in this proof we write $\mathcal E(I):={\mathcal {E}}[I;(f^\pm ,u)]$ and $E:=\mathcal E_\textrm{nl}[f^\pm ,u]$.

Step 1. Piecewise affine approximation. Consider the intervals

$$\begin{aligned} I_j:=\left( \frac{j}{8L}, \frac{j+2}{8L}\right) . \end{aligned}$$

By Proposition 4.8 there are rotations $Q_j\in \textrm{SO}(2)$ such that, for any $j\in {\mathbb {N}}$, one has

$$\begin{aligned} \int _{\omega _{A}^{I_j}} |\nabla u-Q_jA_\delta |^2 \textrm{d}x+\int _{\omega _{B}^{I_j}} |\nabla u-Q_jB_\delta |^2 \textrm{d}x\leqq {c_L} {\mathcal {E}}(I_j) \end{aligned}$$

(4.63)

with the constant $c_L$ (here and in all following estimates) depending only on L.

We shall use this estimate and the periodicity condition to obtain four different bounds, which are stated in (4.64), (4.65), (4.67) and (4.68).

Step 2. Continuity term. With a triangular inequality, using ${\mathcal {L}}^1(I_j\cap I_{j+1})=1/{(8L)}$ from (4.63), $|Q_j-Q_{j+1}| \leqq |Q_jA_\delta -Q_{j+1}A_\delta |\,|A_\delta ^{-1}|$. and $|A_\delta ^{-1}|\leqq 3$ we obtain

$$\begin{aligned} \sum _{j\in {\mathbb {N}}} |Q_j-Q_{j+1}|^2 \leqq {c_L} {\mathcal {E}}((0,\infty )). \end{aligned}$$

(4.64)

Step 3. Left boundary term. By the trace theorem used in $\omega _{B}^{I_0}$, recalling that $f^-(0)=f^+(0)$, from (4.63) we obtain that for some $d_0\in {\mathbb {R}}^2$

$$\begin{aligned} \int _{(0,1)} |u(t{e_{\delta ,\theta }})-Q_0B_\delta {e_{\delta ,\theta }}t-d_0|^2\textrm{d}{{\mathcal {H}}}^1 \leqq {c_L} {\mathcal {E}}(I_0)\leqq c_L E. \end{aligned}$$

By geometric rigidity and the trace theorem used in $T_{\delta ,\theta }((-1,0)\times (0,2))$ there are $Q_-\in \textrm{SO}(2)$ and $d_-\in {\mathbb {R}}^2$ such that

$$\begin{aligned} {}&{} \int _{(0,2)} |u(t{e_{\delta ,\theta }})-Q_-A_\delta {e_{\delta ,\theta }}t-d_-|^2\text {d}{{\mathcal {H}}}^1\\ {}{}&{} \leqq {c_L} \int _{T_{\delta ,\theta }((-1,0)\times (0,2))} W({\nabla }uA_\delta ^{-1})\text {d}x \leqq c_L E \end{aligned}$$

which, with the periodicity condition, implies

$$\begin{aligned} |Q_-A_\delta {e_{\delta ,\theta }}-v_\theta |\leqq {c_L} E^{1/2}, \end{aligned}$$

where $v_\theta :=(\theta A_\delta + (1-\theta )B_\delta ){e_{\delta ,\theta }}=({{\,\textrm{Id}\,}}+ \delta (2\theta -1)e_1\otimes e_2) {e_{\delta ,\theta }}$. With a triangular inequality,

$$\begin{aligned} |Q_0B_\delta {e_{\delta ,\theta }}-v_\theta |\leqq {c_L} E^{1/2}. \end{aligned}$$

We observe that $B_\delta {e_{\delta ,\theta }}-v_\theta =-\theta (A_\delta -B_\delta ){e_{\delta ,\theta }}=-2\delta \theta e_1/\sqrt{1+\delta ^2\theta ^2}$. As $|v_\theta -e_2|\leqq c{|\delta |}$, $B_\delta {e_{\delta ,\theta }}=v_\theta +2\delta \theta v_\theta ^\perp +O(\delta ^2\theta )$ we have

$$\begin{aligned} |Q_0(v_\theta +2\delta \theta v_\theta ^\perp )-v_\theta |\leqq {c_L\left( E^{1/2} + {\delta ^2\theta }\right) }, \end{aligned}$$

and from Lemma 4.4, we obtain

$$\begin{aligned} |Q_0-{{\,\textrm{Id}\,}}+2\delta \theta J|\leqq {c_L} E^{1/2}+{c_L}{\delta ^2\theta }. \end{aligned}$$

(4.65)

Step 4. Volume term. The periodicity condition (4.2) implies that the average of $\nabla u{e_{\delta ,\theta }}$ over $\omega _{A}^{I_j}\cup \omega _{B}^{I_j}$ coincides with $v_\theta$,

$$\begin{aligned} \frac{1}{{\mathcal {L}}^2(\omega _{A}^{I_j}\cup \omega _{B}^{I_j})} \int _{\omega _{A}^{I_j}\cup \omega _{B}^{I_j}}\nabla u {e_{\delta ,\theta }} \textrm{d}x = (\theta A_\delta + (1-\theta )B_\delta ){e_{\delta ,\theta }} =v_\theta . \end{aligned}$$

From (4.63) we obtain

$$\begin{aligned}{} & {} \left| \int _{\omega _{A}^{I_j}} \nabla u {e_{\delta ,\theta }} \textrm{d}x - {\mathcal {L}}^2(\omega _{A}^{I_j}) Q_jA_\delta {e_{\delta ,\theta }} \right| \\{} & {} +\left| \int _{\omega _{B}^{I_j}} \nabla u {e_{\delta ,\theta }} \textrm{d}x - {\mathcal {L}}^2(\omega _{B}^{I_j}) Q_jB_\delta {e_{\delta ,\theta }} \right| \leqq {c_L}{\mathcal {E}}^{1/2}(I_j). \end{aligned}$$

Therefore, setting $\lambda _j:={\mathcal {L}}^2(\omega _{A}^{I_j})/{\mathcal {L}}^2(\omega _{A}^{I_j}\cup \omega _{B}^{I_j})$ and $w_j:=(\lambda _j A_\delta + (1-\lambda _j)B_\delta ){e_{\delta ,\theta }} =({{\,\textrm{Id}\,}}+ \delta (2\lambda _j-1)e_1\otimes e_2) {e_{\delta ,\theta }}$, we obtain

$$\begin{aligned} \left| Q_j w_j-v_\theta \right| \leqq {c_L} {\mathcal {E}}^{1/2}(I_j). \end{aligned}$$

(4.66)

Since

$$\begin{aligned} w_j-v_\theta =2\delta (\lambda _j-\theta ) (e_1\otimes e_2) {e_{\delta ,\theta }} = \frac{2\delta (\lambda _j-\theta )}{\sqrt{1+\delta ^2\theta ^2}} e_1 \end{aligned}$$

and $|e_1+v_\theta ^\perp |\leqq c{|\delta |}$, we have $|Q_j(v_\theta +2\delta (\theta -\lambda _j)v_\theta ^ \perp )-v_\theta |\leqq c {\mathcal {E}}^{1/2}(I_j)+c\delta ^2 |\lambda _j-\theta |$ and again by Lemma 4.4 we obtain our first volume estimate

$$\begin{aligned} |Q_j-{{\,\textrm{Id}\,}}+2\delta (\theta -\lambda _j)J|\leqq {c_L} \left( {\mathcal {E}}^{1/2}(I_j)+\delta ^2 |\lambda _j-\theta |\right) . \end{aligned}$$

(4.67)

At the same time,

$$\begin{aligned} |v_\theta |^2 =\frac{1+\delta ^2(\theta -1)^2}{1+\delta ^2\theta ^2} \end{aligned}$$

and

$$\begin{aligned} |Q_jw_j|^2=|w_j|^2=\frac{1+\delta ^2(2\lambda _j-\theta -1)^2}{1+\delta ^2\theta ^2}, \end{aligned}$$

so that, from (4.66) and $|w_j|+|v_\theta |\leqq C$, we obtain the second volume estimate

$$\begin{aligned}{} & {} {c_L}{\mathcal {E}}(I_j)^{1/2}\geqq \left| Q_j w_j-v_\theta \right| \cdot \left| Q_j w_j+v_\theta \right| \nonumber \\ {}{} & {} \geqq \left| |w_j|^2-|v_\theta |^2\right| =\frac{4\delta ^2(1-\lambda _j)|\theta -\lambda _j|}{1+\delta ^2\theta ^2}. \end{aligned}$$

(4.68)

Step 5. Conclusion of the proof. Using (4.65) and (4.67) for $j=0$, there is $c_L>0$ (fixed for the rest of the proof) such that

$$\begin{aligned} |\delta |\, |\lambda _0|\leqq {c_L} E^{1/2} + {c_L} {\delta ^2\theta }{+c_L\delta ^2|\lambda _0-\theta |} {\leqq c_L E^{1/2}+2c_L {\delta ^2\theta }+c_L\delta ^2|\lambda _0|.} \end{aligned}$$

Choose $\delta _0>0$ such that $\delta _0\leqq 1/(6c_L)$. Then for $|\delta |\leqq \delta _0$, we have $c_L\delta ^2|\lambda _0|\leqq \frac{1}{6}|\delta |\, |\lambda _0|$, the last term can be absorbed in the left-hand side, and we obtain

$$\begin{aligned} \frac{5}{6}|\delta |\,|\lambda _0| \leqq c_L E^{1/2}+2c_L {\delta ^2\theta }. \end{aligned}$$

If $|\lambda _0|\geqq \frac{1}{2}\theta$ then, using $2c_L {\delta ^2\theta }\leqq \frac{1}{3}{|\delta |}\theta$, we obtain

$$\begin{aligned} {\frac{5}{12}{|\delta |}\theta \leqq c_L E^{1/2}+\frac{1}{3} {|\delta |}\theta }, \end{aligned}$$

so that $E\geqq C{\delta ^2}\theta ^2$, and we are done.

Assume now that $|\lambda _0|\leqq \frac{1}{2}\theta$. By (4.68), for any $j\in {\mathbb {N}}$ such that $|\lambda _j|\leqq \frac{1}{2}\theta$ we have ${\mathcal {E}}(I_j)\geqq {c_L'} \delta ^4\theta ^2$. Therefore there are at most finitely many such j. Let $\ell :=\min \{j\in {\mathbb {N}}: |\lambda _j|>\frac{1}{2}\theta \}$, so that (4.68) gives

$$\begin{aligned} E\geqq c_L'\ell \delta ^4\theta ^2. \end{aligned}$$

(4.69)

Using (4.65) and (4.67) againg for $j=\ell$,

$$\begin{aligned} |Q_\ell -Q_0-2\delta \lambda _\ell J|\leqq c_L'' E^{1/2} +c_L'' \delta ^2\theta +c_L'' \delta ^2|\lambda _\ell |. \end{aligned}$$

As $|2\delta \lambda _\ell J|=2\sqrt{2} |\delta |\,|\lambda _\ell |$, if $\delta _0$ is chosen so that $c_L''\delta _0\leqq \frac{1}{2}$, then

$$\begin{aligned} \begin{aligned} |Q_\ell -Q_0|\geqq&2\sqrt{2}|\delta |\,|\lambda _\ell | - c_L''E^{1/2}-c_L''\delta ^2\theta -c_L'' \delta ^2|\lambda _\ell |\\ \geqq&2|\delta |\,|\lambda _\ell | - c_L''E^{1/2}-c_L''\delta ^2\theta \\ \geqq&{|\delta |\,\theta - c_L''E^{1/2}-c_L''\delta ^2\theta } \geqq \frac{1}{2}{|\delta |}\theta -c_L'' E^{1/2}, \end{aligned}\end{aligned}$$

where in the third step we used $|\lambda _\ell |\geqq \frac{1}{2}\theta$. As above, if $E\geqq (4c_L'')^{-2}\delta ^2\theta ^2$ then we are done. Otherwise $|Q_\ell -Q_0|\geqq \frac{1}{4}{|\delta |}\theta$. With (4.64) and Cauchy-Schwarz we conclude

$$\begin{aligned} c_L''' E\geqq \sum _{j=0}^{\ell -1} |Q_j-Q_{j+1}|^2 \geqq \frac{1}{\ell } |Q_0-Q_\ell |^2 \geqq \frac{1}{16} \frac{\delta ^2\theta ^2}{\ell }, \end{aligned}$$

and therefore, recalling (4.69),

$$\begin{aligned} E\geqq C_L\left( \frac{\delta ^2\theta ^2}{\ell } + \ell \delta ^4\theta ^2 \right) \geqq 2C_L {|\delta |}^3\theta ^2, \end{aligned}$$

which concludes the proof. $\square$

4.3 Existence of Minimizers

In this section, we show existence of minimizers of the shape optimization problem (4.12) on the set defined in (4.11) under the additional assumption that the energy density W is quasiconvex. The notion of quasiconvexity was introduced by Morrey [42] and is a central concept in the calculus of variations since it guarantees existence of minimizers for variational problems of the form $\min _{u} \int W(\nabla u)\,\textrm{d}x$ under rather weak additional assumptions on W, see for example [23, 44] for general presentations.

Proposition 4.10

Let W obey (4.13) and be quasiconvex. Let $L\geqq 1$, $\theta \in (0,\frac{1}{2}]$, $\delta \in [-1,1]$. Then the functional ${\mathcal {E}}_{\textrm{nl}}$ defined in (4.12) has a minimizer in the set ${\mathcal {A}}_{\textrm{nl}}^L$ defined in (4.11).

Proof

We proceed along the lines of the proof of Proposition 3.3(i). Let $(f^\pm _j, u_j)\subset {\mathcal {A}}_{\textrm{nl}}^L$ be a minimizing sequence. By subtracting constants, we can assume without loss of generality that

$$\begin{aligned} \int _{(0,1)\times (0,1)}u_j(x)\,\textrm{d}x=0. \end{aligned}$$

(4.70)

After passing to a subsequence, the functions $f^\pm _j$ converge locally uniformly to L-Lipschitz functions $f^\pm _*$ which by uniform convergence satisfy (4.3). For every $m\in {\mathbb {N}}$, by the lower bound in (4.13), there is a uniform bound on the $L^2$-norms

$$\begin{aligned} \Vert \nabla u_j\Vert _{L^2(T_{\delta ,\theta }((-m,m)^2))}\leqq Cm\left( {\mathcal {E}}((-m,m),(f_j^\pm ,u_j))+m|A_\delta |^2\right) , \end{aligned}$$

and hence, by (4.70), there is a subsequence that converges locally weakly in $W^{1,2}$ to $u_*\in W^{1,2}_{\text {loc}}({\mathbb {R}}^2;{\mathbb {R}}^2)$. By Rellich’s theorem, the limiting function $u^*$ satsifies the periodicity condition (4.2). Let $\omega _{A}^*$ and $\omega _B^*$ denote the respective domains induced by $f_*^\pm$, which are defined as in (4.7)–(4.9). By quasiconvexity of W and the growth condition (4.13), we get lower semi-continuity of the energy restricted to compact sets in $(\omega _A^*\cup \omega _B^*){\setminus } \text {graph}(f^\pm _*){\setminus } ({\mathbb {R}}e_{\delta ,\theta })$, and hence, choosing a diagonal sequence as in the proof of Proposition 3.3, we find, for every $m>0$,

$$\begin{aligned} {\mathcal {E}}((-m,m),(f_*^\pm ,u_*))\leqq \liminf _{j\rightarrow \infty } {\mathcal {E}}((-m,m),(f_j^\pm ,u_j)). \end{aligned}$$

(4.71)

Then

$$\begin{aligned} {\mathcal {E}}((-m,m),(f_*^\pm ,u_*))\leqq \liminf _{j\rightarrow \infty } {\mathcal {E}}({\mathbb {R}},(f_j^\pm ,u_j))= \liminf _{j\rightarrow \infty }{\mathcal {E}}_{\textrm{nl}}[f_j^\pm ,u_j]=\inf _{{\mathcal {A}}_{\textrm{nl}}^L} {\mathcal {E}}_{\textrm{nl}}. \end{aligned}$$

(4.72)

As ${\mathcal {E}}_{\textrm{nl}}[f_*^\pm ,u_*]= {\mathcal {E}}({\mathbb {R}},(f_*^\pm ,u_*))=\sup \{ {\mathcal {E}}((-m,m),(f_*^\pm ,u_*)):m>0\}$, this concludes the proof. $\square$

It would be natural to ask if for a minimizer $(f_*^\pm ,u_*)$ the functions $f_*^\pm (x_1)$ have a finite limit as $x_1\rightarrow \infty$. This does not follow from the above proof. Another open question is whether the condition that $f^\pm$ are Lipschitz is needed, or if it can be replaced by a term of the form

$$\begin{aligned} \sigma \int _0^\infty (\sqrt{1+(f_+'(x_1))^2}+\sqrt{1+(f_-'(x_1))^2}-2)\textrm{d}x_1, \end{aligned}$$

(4.73)

which represents the additional length of the interfaces with respect to the “flat” situation.

5 Korn’s Inequality and Geometric Rigidity for Uniformly Lipschitz Domains

5.1 Uniformly Lipschitz Domains

We show that certain estimates on Sobolev functions hold uniformly for a class of bounded open sets which are uniformly Lipschitz. We focus on bounded sets and use the following definition, which is a variant of the one in [38, Def. 13.11]. For $x\in {\mathbb {R}}^n$, we use the notation $x=(x',x_n)$ with $x'\in {\mathbb {R}}^{n-1}$ and $x_n\in {\mathbb {R}}$.

Definition 5.1

Let $L,R>0$. An open set $\Omega \subseteq {\mathbb {R}}^n$ is (L, R)-Lipschitz if there is $\varepsilon >0$ such that

• (i) $|x-y|< R\varepsilon$ for all $x,y\in \Omega$;

• (ii) For each $x\in \partial \Omega$ there are $f_x\in {{\,\textrm{Lip}\,}}({\mathbb {R}}^{n-1};{\mathbb {R}})$ with ${{\,\textrm{Lip}\,}}(f_x)\leqq L$ and an isometry $A_x:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ such that $B_\varepsilon (x)\cap \Omega =B_\varepsilon (x)\cap V_x$, where

  $$\begin{aligned} V_x:=A_x\{ (y',y_n)\in {\mathbb {R}}^{n-1}\times {\mathbb {R}}: y_n<f_x(y')\}. \end{aligned}$$

  (5.1)

This definition ensures on the one hand uniformity of the Lipschitz constant, on the other hand uniform size of the neighbourhoods in which (5.1) holds with respect to the size of $\Omega$.

Remark 5.2

• (i) The definition is monotonous, in the sense that if $\Omega$ is (L, R)-Lipschitz then it is also $(L',R')$-Lipschitz for any $L'\geqq L$, $R'\geqq R$.

• (ii) From $x\in \partial \Omega$ one immediately obtains that ${\hat{y}}:=A_x^{-1}x$ obeys ${\hat{y}}_n=f({\hat{y}}')$; one can assume without loss of generality that ${\hat{y}}=0$.

• (iii) Condition (ii) implies that the open segment joining $x=A_x{\hat{y}}$ with $A_x({\hat{y}}-\varepsilon e_n)$ belongs to $\Omega$; in particular $R\geqq 1$.

• (iv) Suppose $\Omega \subseteq {\mathbb {R}}^n$ and $\varepsilon >0$ satisfy property (i) of Definition 5.1 and property (ii) with $B_\varepsilon (x)$ replaced by $x+\left( (-\varepsilon ,\varepsilon )^{n-1}\times (-2\varepsilon L,2\varepsilon L)\right)$. Then $\Omega$ is $(L,R_0)$-Lipschitz with $R_0=R\max \{1,1/(2L)\}$. On the other hand, if $\Omega$ is (L, R)-Lipschitz then $\Omega$ satisfies property (ii) of Definition 5.1 with $B_\varepsilon (x)$ replaced by $x+\left( (-\varepsilon _0,\varepsilon _0)^{n-1}\times (-2\varepsilon _0 L,2\varepsilon _0L)\right)$ with $\varepsilon _0:=\frac{\varepsilon }{\sqrt{n}}\min \{1,2L\}$. Similar statements holds for other sets whose size is uniformly controlled by $\varepsilon$.

• (v) One can reduce to the case that only finitely many functions $f_x$ appear, after changing R to 2R. Indeed, if $\Omega \subset {\mathbb {R}}^n$ is (L, R)-Lipschitz then (using the notation of Definition 5.1) the balls $B_{\varepsilon /2}(x)$, $x\in \partial \Omega$, cover $\partial \Omega$. By Vitali’s covering theorem there is a subset $x_1,\dots , x_M$ such that $\partial \Omega \subseteq \cup _{i=1}^M B_{\varepsilon /2}(x_i)$ and $B_{\varepsilon /10}(x_i)\cap B_{\varepsilon /10}(x_j)=\emptyset$ for $i\ne j$. Since $\partial \Omega$ is contained in a ball of radius $R\varepsilon$, we have $M\leqq ({10\cdot R+1})^n$. As for every $x\in \partial \Omega$ there is $i\in \{1,\dots , M\}$ such that $B_{\varepsilon /2}(x)\subseteq B_\varepsilon (x_i)$, only the M functions $f_{x_1},\dots , f_{x_M}$ are relevant.

• (vi) Let $\Omega$ be such that there are open sets $\omega _i$, $i=1,\dots , M$, Lipschitz functions $f_i$ with ${{\,\textrm{Lip}\,}}(f_i)\leqq L$ and isometries $A_i$ such that $\omega _i\cap \Omega =\omega _i\cap V_i$, $V_i:=A_i\{y: y_n<f_i(y')\}$, and assume that there is $\varepsilon >0$ such that for all $x\in \partial \Omega$ there is i with $B_\varepsilon (x)\subseteq \omega _i$. Then property (ii) in Definition 5.1 holds and $\Omega$ is $(L,{{\,\textrm{diam}\,}}(\Omega )/\varepsilon )$-Lipschitz.

Lemma 5.3

Let $\Omega \subseteq {\mathbb {R}}^n$ be (L, R)-Lipschitz, $F\in {\mathbb {R}}^{n\times n}$ an invertible matrix. Then the set $F\Omega \subseteq {\mathbb {R}}^n$ is $(c_F (L+1), c_FR)$ Lipschitz, with $c_F:=|F|\cdot |F^{-1}|$.

Proof

Let $\varepsilon >0$ as in Definition 5.1 for $\Omega$ and set $\varepsilon ':=\varepsilon /|F^{-1}|$. Pick $y\in \partial {(F\Omega )}$ and let $x:=F^{-1}y\in \partial \Omega$. We first show that

$$\begin{aligned} B_{\varepsilon '}(y)\subseteq FB_\varepsilon (x). \end{aligned}$$

To see this, we pick $z\in B_{\varepsilon '}(y)$, consider $z':=F^{-1}z$, and compute $|z'-x|=|F^{-1}(z-y)|\leqq |F^{-1}| |z-y|<\varepsilon$. Therefore $z'\in B_\varepsilon (x)$ and $z\in FB_\varepsilon (x)$. Further, ${{\,\textrm{diam}\,}}(F\Omega )\leqq |F|{{\,\textrm{diam}\,}}\Omega$, hence setting $R':= |F|\,|F^{-1}|R$ we have ${{\,\textrm{diam}\,}}(F\Omega )\leqq R'\varepsilon '$.

Fix again $y\in \partial (F\Omega )$. We need to show that

$$\begin{aligned} (F\Omega )\cap B_{\varepsilon '}(y)=I_y \{w_n<g(w')\}\cap B_{\varepsilon '}(y) \end{aligned}$$

(5.2)

for some isometry $I_y$ and some $g\in {{\,\textrm{Lip}\,}}({\mathbb {R}}^{n-1};{\mathbb {R}})$ with ${{\,\textrm{Lip}\,}}(g)\leqq L'$; the precise value of $L'$ is given below.

We let $x:=F^{-1}y$ as above. By property (ii) in Definition 5.1 there are an isometry $A_x$ and an L-Lipschitz function $f:{\mathbb {R}}^{n-1}\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} \Omega \cap B_\varepsilon (x)=A_x \{z_n<f(z')\}\cap B_\varepsilon (x). \end{aligned}$$

(5.3)

Then $B_{\varepsilon '}(y)\subseteq FB_\varepsilon (x)$ implies

$$\begin{aligned} (F\Omega )\cap B_{\varepsilon '}(y)= (F(\Omega \cap B_{\varepsilon }(x))\cap B_{\varepsilon '}(y)= ( F A_x \{z_n<f(z')\})\cap B_{\varepsilon '}(y). \end{aligned}$$

(5.4)

The isometry $A_x$ can be written as $A_xz=b+Rz$ for some $R\in \text {O}(n)$. We set $\eta :=|FRe_n|\in (0,|F|]$, pick a rotation $Q\in \textrm{SO}(n)$ such that $FRe_n=\eta Qe_n$, and let $T:=Q^TFR\in {\mathbb {R}}^{n\times n}$. Then $FR=QT$ and $QTe_n=\eta Qe_n$, which implies $Te_n=\eta e_n$. We shall show below that

$$\begin{aligned} T\{z_n<f(z')\}=\{w_n<g(w')\}, \end{aligned}$$

(5.5)

with g as stated after (5.2). This implies that

$$\begin{aligned} \begin{aligned} F A_x \{z_n<f(z')\}&=Fb+FR\{z_n<f(z')\} =Fb+QT\{z_n<f(z')\}\\&=Fb+Q\{w_n<g(w')\} =I_y\{w_n<g(w')\},\end{aligned} \end{aligned}$$

(5.6)

where $I_yw:=Fb+Qw$, which together with (5.4) concludes the proof of (5.2) and therefore of the Lemma.

It remains to construct $g\in {{\,\textrm{Lip}\,}}({\mathbb {R}}^{n-1};{\mathbb {R}})$ such that (5.5) holds. We observe that T is invertible, with $|T^{-1}|= |F^{-1}|$ and $T^{-1} e_n=\frac{1}{\eta }e_n$, and write

$$\begin{aligned} T^{-1}(w',w_n)=\left( Sw', \frac{1}{\eta }w_n+s\cdot w'\right) \end{aligned}$$

(5.7)

for some $s\in {\mathbb {R}}^{n-1}$ and $S\in {\mathbb {R}}^{(n-1)\times (n-1)}$, invertible. These obey $\max \{|S|,|s|\}\leqq |T^{-1}|=|F^{-1}|$. Then

$$\begin{aligned} \frac{1}{\eta }w_n+s\cdot w' < f(Sw') \end{aligned}$$

(5.8)

is the same as

$$\begin{aligned} w_n < g(w'):=\eta \cdot ( f(Sw')-s\cdot w'), \end{aligned}$$

(5.9)

so that

$$\begin{aligned} \{z_n<f(z')\}=T^{-1}\{w_n<g(w')\}, \end{aligned}$$

(5.10)

which is the same as (5.5). The function $g:{\mathbb {R}}^{n-1}\rightarrow {\mathbb {R}}$ constructed above is Lipschitz, with ${{\,\textrm{Lip}\,}}(g)\leqq \eta (|S|{{\,\textrm{Lip}\,}}(f)+|s|) \leqq |F|(|F^{-1}|L+|F^{-1}|)$. This concludes the proof. $\square$

Lemma 5.4

Let $f,g:[0,\ell ]\rightarrow {\mathbb {R}}$, $\ell >0$, $L>0$, and set

$$\begin{aligned} \omega _{f,g}:=\{x\in {\mathbb {R}}^2:\ x_1\in (0,\ell ),\ f(x_1)<x_2<g(x_1)\}. \end{aligned}$$

Assume that $\alpha \ell \leqq g-f\leqq \beta \ell$ for some $\alpha ,\beta >0$, and that ${{\,\textrm{Lip}\,}}(f),{{\,\textrm{Lip}\,}}(g)\leqq L$. Then $\omega _{f,g}$ is $(2L+1,R)$-Lipschitz for some R which depends only on $\alpha$, $\beta$ and L.

Proof

Let $\varepsilon :=\frac{\ell }{2(1+L)} \min \{\alpha ,1\}$, $R:=(\beta +1+L)\ell /\varepsilon$. Clearly R depends only on $\alpha$, $\beta$, and L, and its definition ensures that condition (i) in Definition 5.1 holds. The choice of $\varepsilon$ ensures that $|(x_1,f(x_1))-(x_1',g(x_1'))|\geqq \varepsilon$ for all $x_1$, $x_1'\in [0,\ell ]$, so that the top and bottom boundaries can be treated separately.

Fig. 6

Sketch of the rotation in the proof of Lemma 5.4. The shaded area is the one where $y_2<F(y_1)$, the dotted line shows the direction (1, L)

We consider points close to the lower-left corner, in the sense that we show property (ii) of Definition 5.1 for x in (see Fig. 6)

$$\begin{aligned} A_{LL}:=\{0\}\times \left[ f(0),\frac{f(0)+g(0)}{2}\right] \cup \{(x_1,f(x_1)): x_1\in \left[ 0,\frac{1}{2}\ell \right] \} \subseteq \partial \omega _{f,g}; \end{aligned}$$

(5.11)

the other three corners can be treated analogously. We extend f to ${\mathbb {R}}$, setting $f(t)=f(0)$ for $t<0$ and $f(t)=f(\ell )$ for $t>\ell$. By the choice of $\varepsilon$ we see that for all $x\in A_{LL}$ the ball $B_\varepsilon (x)$ does not intersect $\{z: z_2=g(z_1)\}$ and $\{z: z_1=\ell \}$, in the sense that

$$\begin{aligned} B_\varepsilon (x)\cap \omega _{f,g}=B_\varepsilon (x)\cap {\{z\in {\mathbb {R}}^2: z_1>0, z_2>f(z_1)\}}. \end{aligned}$$

(5.12)

After a translation, we can assume $f(0)=0$. In order to make the mentioned boundary the graph of a Lipschitz function we need a nontrivial rotation, as illustrated in Fig. 6. Let $Q\in \textrm{SO}(2)$ be such that $Qe_2$ bisects the angle between $e_2$ and (1, L), which means that Q is a clockwise rotation by $\alpha :=\frac{1}{2} (\frac{\pi }{2}-\arctan L)$. Then there is a unique function $F:{\mathbb {R}}\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} \{z\in {\mathbb {R}}^2: z_2>f(z_1)\}=Q\{y\in {\mathbb {R}}^2: y_2>F(y_1)\}, \end{aligned}$$

(5.13)

obviously $F(0)=0$. One can check that F is $L':=\tan (\frac{\pi }{2}-\alpha )$-Lipschitz, and that $L'=L+\sqrt{1+L^2}\leqq 1+2L$. At the same time, by the definition of Q and $L'$

$$\begin{aligned} \{z\in {\mathbb {R}}^2: z_1>0\}= Q\{y\in {\mathbb {R}}^2: y_2>-L'y_1\}. \end{aligned}$$

(5.14)

Recalling (5.12), we see that it suffices to intersect these two sets. We define ${\tilde{F}}(t):= \max \{-L'y_1, F(y_1)\}$, which is also $L'$-Lipschitz. Then for every $x\in A_{LL}$ we have

$$\begin{aligned} B_\varepsilon (x)\cap \omega _{f,g}=B_\varepsilon (x)\cap Q\{y: y_2>{\tilde{F}}(y_1)\}. \end{aligned}$$

(5.15)

This concludes the proof. $\square$

5.2 Weighted Poincaré Inequality

The next result is a quantitative version of the estimate in [37, Theorem 8.8].

Theorem 5.5

(Weighted Poincaré) Let $\Omega \subseteq {\mathbb {R}}^n$ be a connected, bounded (L, R)-Lipschitz set, $p\in [1,\infty )$. Then for any $u\in W^{1,p}_\textrm{loc}(\Omega ;{\mathbb {R}}^k)$ there is $a\in {\mathbb {R}}^k$ such that

$$\begin{aligned} \Vert u-a\Vert _{L^p(\Omega )} \leqq c_\textrm{WP}\Vert {\text {dist}}(\cdot , \partial \Omega ) \nabla u\Vert _{L^p(\Omega )}. \end{aligned}$$

(5.16)

In particular, $u\in L^p(\Omega ;{\mathbb {R}}^k)$ if the right hand-side in (5.16) is finite. The constant $c_\textrm{WP}$ depends only on n, p, L and R.

We first prove the result in one dimension, by an explicit computation.

Lemma 5.6

Let $I=(a,b)\subseteq {\mathbb {R}}$ be a bounded interval, $\varphi \in C^1(I)$, $E\subseteq I$ with positive measure, $\alpha \in {\mathbb {R}}$, $p\in [1,\infty )$. Then

$$\begin{aligned} \int _I |\varphi -\alpha |^p dt \leqq c_p \frac{{\mathcal {L}}^1(I)}{{\mathcal {L}}^1(E)} \left[ \int _E |\varphi -\alpha |^p \textrm{d}t + \int _I (t-a)^p |\varphi '|^p(t) \textrm{d}t\right] . \end{aligned}$$

(5.17)

The constant $c_p$ depends only on p.

Proof

If the right-hand side is finite, then the function $\varphi$ can be extended continuously to (a, b]. Let $\beta :=\varphi (b)$. For any $x\in I$ by the fundamental theorem of calculus applied to $|\varphi -\beta |^p$ we have

$$\begin{aligned} |\varphi -\beta |^p(x)\leqq p \int _x^b |\varphi (t)-\beta |^{p-1} |\varphi '(t)| \textrm{d}t. \end{aligned}$$

(5.18)

We integrate over all $x\in I$ and use Fubini’s theorem to get that

$$\begin{aligned} \int _a^b |\varphi -\beta |^p(x) \text {d}x&{} \leqq p \int _a^b \int _x^b |\varphi (t)-\beta |^{p-1} |\varphi '(t)| \text {d}t\,\text {d}x\nonumber \\{}&{} =p\int _a^b (t-a) |\varphi (t)-\beta |^{p-1} |\varphi '(t)| \text {d}t. \end{aligned}$$

(5.19)

With Hölder’s inequality,

$$\begin{aligned} \int _a^b |\varphi -\beta |^p(x) \textrm{d}x \leqq p \Vert |\varphi -\beta |^{p-1}\Vert _{L^{p'}(I)} \Vert ({\cdot }-a)\varphi '\Vert _{L^p(I)} \end{aligned}$$

(5.20)

so that, as $\Vert |\varphi -\beta |^{p-1}\Vert _{L^{p'}}=\Vert \varphi -\beta \Vert _{L^p}^{p-1}$,

$$\begin{aligned} \Vert \varphi -\beta \Vert _{L^p(I)} \leqq p\Vert ({\cdot }-a)\varphi '\Vert _{L^p(I)}. \end{aligned}$$

(5.21)

By a triangular inequality,

$$\begin{aligned} |\alpha -\beta | ({\mathcal {L}}^1(E))^{1/p} \leqq \Vert \varphi -\alpha \Vert _{L^p(E)}+\Vert \varphi -\beta \Vert _{L^p(I)}, \end{aligned}$$

(5.22)

so that, with a further triangular inequality,

$$\begin{aligned} \begin{aligned} \Vert \varphi -\alpha \Vert _{L^p(I)}&\leqq |\alpha -\beta | ({\mathcal {L}}^1(I))^{1/p}+\Vert \varphi -\beta \Vert _{L^p(I)} \\&\leqq 2p \frac{({\mathcal {L}}^1(I))^{1/p}}{({\mathcal {L}}^1(E))^{1/p}} \left[ \Vert \varphi -\alpha \Vert _{L^p(E)}+\Vert (t-a)\varphi '\Vert _{L^p(I)}\right] , \end{aligned} \end{aligned}$$

(5.23)

which concludes the proof. $\square$

Lemma 5.7

Let $\Omega \subset {\mathbb {R}}^n$ be (L, R)-Lipschitz, $\varepsilon$ as in Definition 5.1, $x_*\in \partial \Omega$, $r\in (0,\varepsilon /(4+4L)]$, $p\in [1,\infty )$. For any $u\in W^{1,p}_\textrm{loc}(\Omega )$ there is $\alpha \in {\mathbb {R}}$ such that

$$\begin{aligned} \int _{\Omega \cap B_r(x_*)} |u-\alpha |^p\textrm{d}x \leqq c \int _{\Omega } {\text {dist}}^p(x,\partial \Omega )|\nabla u|^p(x) \textrm{d}{x}. \end{aligned}$$

(5.24)

The constant c depends only on n, p, and L.

Proof

By Definition 5.1 we have $B_\varepsilon (x_*)\cap \Omega =B_\varepsilon (x_*)\cap V$, where (as in (5.1)),

$$\begin{aligned} V:=A\{ (y',y_n)\in {\mathbb {R}}^{n-1}\times {\mathbb {R}}: y_n<{f}(y')\} \end{aligned}$$

(5.25)

for some isometry A and L-Lipschitz function $f:{\mathbb {R}}^{n-1}\rightarrow {\mathbb {R}}$. As the assertion is invariant under rotations and translations we can assume that A is the identity and that $x_*=0$; from $x_*\in \partial \Omega$ we then obtain $f(0)=0$.

Let $h:=rL\in (0,\varepsilon /4)$ and consider the cylinder $T:=B'_r\times (-3\,h,-2\,h)$ (see Figure 7). For any $x'\in B'_r$ we have $f(x')\geqq -rL=-h$, and therefore $f(x')-x_n\geqq h$ for all $(x',x_n)\in T$. Further, from $(3\,h)^2+r^2\leqq \frac{9}{16}\varepsilon ^2+\frac{1}{16}\varepsilon ^2=\frac{5}{8}\varepsilon ^2\leqq \varepsilon ^2$ we obtain that $T\subseteq B_\varepsilon \cap V$. As the shape of T (up to uniform rescaling) depends only on L, by the usual Poincaré inequality (for a fixed domain) there is $\alpha \in {\mathbb {R}}$ with

$$\begin{aligned} \int _T |u-\alpha |^p\textrm{d}x \leqq c r^p\int _{T} |\nabla u|^p \textrm{d}x, \end{aligned}$$

(5.26)

with c depending only on n, p, L. For every $x'\in B'_r$ we apply Lemma 5.6 to $u(x', \cdot )$ with $I=(-3h, f(x'))$ and $E=(-3h, -2h)$, and obtain, using $h= {\mathcal {L}}^1(E)\leqq {\mathcal {L}}^1(I)\leqq 4\,h$,

$$\begin{aligned} \int _I |u(x)-\alpha |^p \textrm{d}x_n \leqq c \int _I |f(x')-x_n|^p |\nabla u|^p(x) \textrm{d}x_n + c \int _{E} |u(x)-\alpha |^p\textrm{d}x_n. \end{aligned}$$

(5.27)

Let $U:=(B'_r\times (-3h,\infty ))\cap V$, so that $B_r\cap \Omega =B_r\cap U$ and $U\subseteq B_\varepsilon \cap V=B_\varepsilon \cap \Omega$. We integrate over $x'\in B'_r$, use (5.26) and $rL=h\leqq f(x')-x_n$ for all $(x', x_n)\in T$ to conclude

$$\begin{aligned} \begin{aligned} \int _U |u-\alpha |^p \text {d}x\leqq {}&{}c \int _{B'_r}\int _{(-3h, f(x'))} |f(x')-x_n|^p |\nabla u|^p \text {d}x_n \text {d}x'\\ {}&+ c \int _T |f(x')-x_n|^p |\nabla u|^p \text {d}x\\ \leqq {}&{} c \int _U |f(x')-x_n|^p |\nabla u|^p \text {d}x, \end{aligned} \end{aligned}$$

(5.28)

where the constant c depends only on L, p, and n. We finally show that there is $c_L>0$, depending only on L, such that

$$\begin{aligned} |f(x')-x_n|\leqq c_L {\text {dist}}(x,\partial \Omega ) \qquad \text { for all } x\in U. \end{aligned}$$

(5.29)

Indeed, for any $x\in U$ let $y\in \partial \Omega$ be such that $d:={\text {dist}}(x,\partial \Omega )=|x-y|$. We know that $|f(x')|\leqq h=rL$ and that $x_n\in (-3h, h)$, which imply $|f(x')-x_n|\leqq 4h\leqq \varepsilon$, and with $|x'|<r$ we obtain $|x|\leqq \sqrt{r^2+(3\,h)^2}\leqq \sqrt{\frac{5}{8}}\varepsilon$. We distinguish two cases. If $y\not \in B_\varepsilon$ then $|x-y|\geqq (1-\sqrt{\frac{5}{8}})\varepsilon$ and the proof of (5.29) is concluded (if $c_L$ is sufficiently large). If instead $y\in B_\varepsilon$ then necessarily $y\in \partial V$ and $y_n= f(y')$, which implies $d^2= |y'-x'|^2+|f(y')-x_n|^2$. As f is L-Lipschitz, $f(y')\geqq f(x')-L|x'-y'|$, so that

$$\begin{aligned} d\geqq \max \{|x'-y'|, f(x')-L|x'-y'|-x_n\}. \end{aligned}$$

(5.30)

If $d\geqq \frac{1}{2}(f(x')-x_n)$, then we are done (with any $c_L\geqq 2$). Otherwise, $\frac{1}{2}(f(x')-x_n)> d \geqq (f(x')-x_n)-L|x'-y'|$ implies $Ld\geqq L|x'-y'|\geqq \frac{1}{2}(f(x')-x_n)$ which concludes the proof of (5.29) for any $c_L\geqq 2L$.

Inserting (5.29) and $B_r\cap V\subseteq U$ in (5.28) concludes the proof. $\square$

Fig. 7

Sketch of the geometry in the construction of Lemma 5.7

Proof of Theorem 5.5

It suffices to consider the scalar case; by density it suffices to prove the inequality if u is $C^1(\Omega )$. For brevity, let $A:=\Vert {\text {dist}}(\cdot ,\partial \Omega ) \nabla u\Vert _{L^p(\Omega )}$. Let $\varepsilon$ be as in Definition 5.1 and fix $r_B:=\varepsilon /(12(L+1))$ (the reason will become clear below).

We first show that for every $x\in {\overline{\Omega }}$ there is $\alpha (x)\in {\mathbb {R}}$ such that

$$\begin{aligned} \Vert u-\alpha (x)\Vert _{L^p(B_{r_B}(x)\cap \Omega )} \leqq c A, \end{aligned}$$

(5.31)

with c depending only on n, p, L and R. To see this, we distinguish two cases. If ${\text {dist}}(x,\partial \Omega )\geqq 2r_B$ this follows from the usual Poincaré inequality applied to the ball $B_{r_B}(x)\subset \Omega$, with ${\text {dist}}(\cdot ,\partial \Omega )\geqq r_B$ in $B_{r_B}(x)$. If not, we fix $x_*\in \partial \Omega$ with $|x_*-x|< 2r_B$ and use Lemma 5.7 to $B_{3r_B}(x_*)$ (this is the point where the size of $r_B$ is fixed). As $B_{r_B}(x)\subseteq B_{3r_B}(x_*)$, this concludes the proof of (5.31).

By Vitali’s covering theorem, there is a finite set $x_0,\dots , x_K\in {\overline{\Omega }}$ such that ${\overline{\Omega }}\subset \cup _{k=0}^K B_k$, $B_k:=B_{r_B/2}(x_k)$, with the smaller balls $B_{r_B/10}(x_k)$ pairwise disjoint. In particular, since they are all centered in ${\overline{\Omega }}$ and the diameter of $\Omega$ is bounded by $R\varepsilon$, we obtain $K\leqq (1+10 R\varepsilon /r_B)^n\leqq c R^nL^n$. Let $\alpha _k:=\alpha (x_k)$. We claim that, for every $k=1,\dots , K$, one has

$$\begin{aligned} r_B^{n/p} |\alpha _0-\alpha _k|\leqq c K A. \end{aligned}$$

(5.32)

To see this, fix k, and let $j_0:=0,j_1,\dots , j_H:=k$ be finitely many indices in $\{0,K\}$ such that $B_{j_h}\cap B_{j_{h+1}}\cap \Omega \ne \emptyset$ for all h. They exist since $\Omega$ is connected, which means that there is a continuous curve in $\Omega$ which joins a point of $B_0\cap \Omega$ with a point of $B_k\cap \Omega$; as the curve is compact it is covered by finitely many of the balls. We can further assume the indices $j_h$ to be distinct. Indeed, if $j_h=j_{h'}$ for some $h<h'$, we can remove $h,h+1,\dots , h'-1$ from the set. As there are at most K balls, we obtain $H\leqq K$.

In turn, $B_{j_h}\cap B_{j_{h+1}}\cap \Omega \ne \emptyset$ implies that the larger balls have significant overlap. Indeed, for each $x\in {\overline{\Omega }}$ one has ${\mathcal {L}}^n(\Omega \cap B_{r_B/2}(x))\geqq c_L r_B^n$, and recalling that the radius of the balls $B_k$ is $r_B/2$, we obtain

$$\begin{aligned} c_L r_B^n \leqq {\mathcal {L}}^n(B_{r_B}(x_{j_h})\cap B_{r_B}(x_{j_{h+1}})\cap \Omega ). \end{aligned}$$

(5.33)

Using (5.31) on these two balls and then a triangular inequality,

$$\begin{aligned} r_B^{n/p}|\alpha _{j_h}-\alpha _{j_{h+1}}|\leqq c A, \end{aligned}$$

(5.34)

which, as $H\leqq K$, implies (5.32). Finally, using that the balls $B_0,\dots , B_K$ cover $\Omega$,

$$\begin{aligned} \Vert u-\alpha _0\Vert _{L^p(\Omega )} \leqq \sum _{k=0}^K \left[ \Vert u-\alpha _k\Vert _{L^p(B_k\cap \Omega )} + ({\mathcal {L}}^n(B_k))^{1/p} |\alpha _k-\alpha _0| \right] \leqq c K^2A. \end{aligned}$$

(5.35)

$\square$

Many well-known results from the literature follow easily from the weighted Poincaré inequality and its proof above. We start with a Poincaré inequality (see for example [45, Theorem 1.2]).

Theorem 5.8

(Poincaré inequality) Let $\Omega \subset {\mathbb {R}}^n$ be a connected, bounded (L, R)-Lipschitz set and $p\in [1,\infty )$. Then there exists a constant $c_\textrm{Po}>0$ depending only on n, p, L, and R such that for all $u\in W^{1,p}(\Omega ;{\mathbb {R}}^k)$ there exists $d_u\in {\mathbb {R}}^k$ with

$$\begin{aligned} \Vert u-d_u\Vert _{L^p(\Omega )}\leqq c_\textrm{Po}{{\,\textrm{diam}\,}}(\Omega )\Vert \nabla u\Vert _{L^p(\Omega )}. \end{aligned}$$

Proof

This follows from Theorem 5.5, using that ${\text {dist}}(x,\partial \Omega )\leqq {{\,\textrm{diam}\,}}(\Omega )$ for all $x\in \Omega$. $\square$

With the same strategy as above we can obtain a uniform estimate on the trace operator, as a map from $W^{1,p}$ to $L^p$ of the boundary. Also this result is well-known in the literature; see, e.g., [38, Theorem 18.40].

Theorem 5.9

(Trace) Let $\Omega \subseteq {\mathbb {R}}^n$ be a bounded (L, R)-Lipschitz set, $p\in [1,\infty )$. Then the trace operator $T: W^{1,p}(\Omega ;{\mathbb {R}}^k)\rightarrow L^p((\partial \Omega ,{{\mathcal {H}}}^{n-1});{\mathbb {R}}^k)$ obeys

$$\begin{aligned} \Vert Tu\Vert _{L^p(\partial \Omega )} \leqq c_\textrm{Tr}(d^{1-1/p}\Vert \nabla u\Vert _{L^p(\Omega )} +\frac{1}{d^{1/p}}\Vert u\Vert _{L^p(\Omega )}), \end{aligned}$$

(5.36)

where $d:= {{\,\textrm{diam}\,}}(\Omega )$. The constant $c_\textrm{Tr}$ depends only on n, p, L and R.

Proof

This can be proven along the same lines as Theorem 5.5. One starts showing that, in the setting of Lemma 5.6, one has

$$\begin{aligned} |\varphi (a)-\alpha |^p \leqq c_p \frac{1}{{\mathcal {L}}^1(E)} \int _E |\varphi -\alpha |^p \textrm{d}t + c_p({\mathcal {L}}^1(I))^{p-1}\int _I |\varphi '|^p(t) \textrm{d}t. \end{aligned}$$

(5.37)

To see this, it suffices to observe that for any $t'\in E$ the fundamental theorem of calculus in $(a,t')\subseteq I$ gives

$$\begin{aligned} |\varphi -\alpha |(a) \leqq |\varphi -\alpha |(t') + \int _I |\varphi '|(t) \textrm{d}t. \end{aligned}$$

(5.38)

We take the p-th power, average over all $t'\in E$, and use Hölder’s inequality in the last term to obtain (5.37).

In the next step we observe that, with r as in Lemma 5.7, for any $x\in \partial \Omega$,

$$\begin{aligned} \int _{B_r(x)\cap \partial \Omega } |u-\alpha |^p \textrm{d}{{\mathcal {H}}}^{n-1} \leqq c r^{p-1}\int _\Omega |\nabla u|^p \textrm{d}x+\frac{c}{r} \int _\Omega |u-\alpha |^p \textrm{d}x, \end{aligned}$$

(5.39)

with c depending only on n, p, L. This follows from (5.37) with a change of variables, integrating over the same domain as in Lemma 5.7. The passage to the integral in ${{\mathcal {H}}}^{n-1}$ follows observing that $B_r(x)\cap \partial \Omega$ is the graph of an L-Lipschitz function. The coefficients can be replaced by the corresponding powers of d (by property (iii) in Remark 5.2$\varepsilon \leqq {{\,\textrm{diam}\,}}\Omega$, by property (i) in Definition 5.1${{\,\textrm{diam}\,}}\Omega \leqq R\varepsilon$). Finally, we cover $\partial \Omega$ with no more than $cR^n(\varepsilon /r)^n$ such balls, as in the proof of Theorem 5.5, and conclude the proof. $\square$

5.3 Rigidity

We prove a version of geometric rigidity from [28] and of Korn’s inequality with uniform constant on all (L, R)-Lipschitz sets. Instead of repeating the entire proof, and checking that the variuos constants depend on the domain only through the parameters L and R, we show that the estimate for a general domain can be reduced to the one for a cube. We refer to [14] for the proof for general p and a review of the literature on Korn’s inequality and rigidity. The explicit dependence of the constant on the shape of the domain was analyzed, in the specific case of long and thin domains, in [30, 31]. Korn’s inequality was derived for John domains and related classes using different techniques, see [1, 25, 33] and references therein.

Theorem 5.10

(Uniform rigidity) Let $\Omega \subseteq {\mathbb {R}}^n$ be a connected, bounded (L, R)-Lipschitz set, $p\in (1,\infty )$. Then for any $u\in W^{1,p}(\Omega ;{\mathbb {R}}^n)$ there are $R\in \textrm{SO}(n)$ and $S\in {\mathbb {R}}^{n\times n}_\textrm{skw}$ such that

$$\begin{aligned} \Vert \nabla u-R\Vert _{L^p(\Omega )} \leqq c_\textrm{Rig}\Vert {\text {dist}}(\nabla u,\textrm{SO}(n))\Vert _{L^p(\Omega )} \end{aligned}$$

(5.40)

and

$$\begin{aligned} \Vert \nabla u-S\Vert _{L^p(\Omega )} \leqq c_\textrm{Rig}\Vert \nabla u+\nabla u^T\Vert _{L^p(\Omega )}. \end{aligned}$$

(5.41)

The constant $c_\textrm{Rig}$ depends only on n, p, L and R.

We recall that both estimates do not hold for $p=1$ and $p=\infty$.

Proof

For the case that $\Omega$ is a cube both results are well known. We prove the first inequality, the proof of the second one is almost identical.

The key observation is that the constant depends on the domain only via the weighted Poincaré estimate. The general structure of the argument, using a Whitney decomposition of the domain, is similar to the one used in [28] for the harmonic part. Indeed, there rigidity was first proven in small cubes, and then the second derivative was estimated using harmonic estimates. Here we instead construct a new function (called $\beta$ below) which interpolates between the values of the rotation in each cube, using a partition of unity. This permits to avoid discussing the dependence on the domain of the constants involved in the initial truncation in the proof of [28]. This argument is almost identical to the one used in [17], we repeat it here for completeness.

We intend to construct a partition of unity subordinated to a Whitney covering of $\Omega$, done as in [50, Section VI.1] or [27, Sect. 6.5]. Precisely, we select countably many cubes $Q^j:=x_j+(-r_j,r_j)^n$ such that, letting ${\hat{Q}}^j:=x_j+(-\frac{1}{2} r_j,\frac{1}{2} r_j)^n$ denote cubes with the same center and half the size,

$$\begin{aligned} \chi _\Omega \leqq \sum _j \chi _{{\hat{Q}}^j}\leqq \sum _j \chi _{Q^j}\leqq c \chi _\Omega , \end{aligned}$$

(5.42)

and

$$\begin{aligned} r_j\leqq {\text {dist}}(Q^j,\partial \Omega )\leqq c r_j. \end{aligned}$$

(5.43)

The constant c in (5.42) and (5.43) depends only on the dimension n. These conditions imply that the cubes have finite overlap, and that if $Q^j\cap Q^k\ne \emptyset$ then $1/c\leqq r_j/r_k\leqq c$.

We fix $\varphi ^*\in C^\infty _c((-1,1)^n;[0,1])$ with $\varphi ^*=1$ on $(-\frac{1}{2},\frac{1}{2})^n$, let ${\hat{\varphi }}_j(x):=\varphi ^*((x-x_j)/r_j)$ and $\varphi _j:={\hat{\varphi }}_j/\sum _k {\hat{\varphi }}_k$. Using (5.42) one obtains $\varphi _j\in C^\infty _c(Q^j)$, $\sum _j \varphi _j=1$ in $\Omega$, and $|\nabla \varphi _j|\leqq c/r_j$. By the estimate for the cube, for each j there is $R_j\in \textrm{SO}(n)$ such that

$$\begin{aligned} \Vert \nabla u-R_j\Vert _{L^p(Q^j)} \leqq c_{n,p} \Vert {\text {dist}}(\nabla u,\textrm{SO}(n))\Vert _{L^p(Q^j)}. \end{aligned}$$

(5.44)

We define $\beta :\Omega \rightarrow {\mathbb {R}}^{n\times n}$ as a smooth interpolation between the $R_j$, $\beta :=\sum _j \varphi _j R_j$. Using $\sum _j\varphi _j=1$ in $\Omega$, $\varphi _j\leqq 1$ and the finite overlap,

$$\begin{aligned} \Vert \nabla u-\beta \Vert _{L^p(\Omega )}^p = \Vert \sum _j \varphi _j (\nabla u-R_j)\Vert _{L^p(\Omega )}^p \leqq c\sum _j \Vert \nabla u-R_j\Vert _{L^p(Q_j)}^p. \end{aligned}$$

(5.45)

Using first (5.44) in each cube $Q^j$ and then summing via (5.42) leads to

$$\begin{aligned} \Vert \nabla u-\beta \Vert _{L^p(\Omega )}^p \leqq c \sum _j \int _{Q_j} |\nabla u-R_j|^p \textrm{d}x\leqq c \int _\Omega {\text {dist}}^p(\nabla u,\textrm{SO}(n))\textrm{d}x. \end{aligned}$$

(5.46)

At the same time, the distance between $\nabla u$ and the $R_j$ controls the derivative of $\beta$. Indeed, from $\sum _j\varphi _j=1$ we obtain $\sum _j \nabla \varphi _j=0$ on $\Omega$, so that

$$\begin{aligned} \nabla \beta = \sum _j \nabla \varphi _j R_j=\sum _j \nabla \varphi _j (R_j-\nabla u) . \end{aligned}$$

(5.47)

At this point we recall that $|\nabla \varphi _j|\leqq c/r_j$, and that ${\text {dist}}(Q_j,\partial \Omega )\leqq c r_j$, which implies that

$$\begin{aligned} {\text {dist}}(x,\partial \Omega ) |\nabla \varphi _j|(x)\leqq c \chi _{Q_j}(x) \qquad \text { for all }x\in \Omega . \end{aligned}$$

(5.48)

Therefore

$$\begin{aligned} \begin{aligned} \int _\Omega {\text {dist}}^p(x,\partial \Omega ) |\nabla \beta |^p \textrm{d}x&\leqq c \sum _j \int _{Q_j} {\text {dist}}^p(x,\partial \Omega ) |\nabla \varphi _j|^p |\nabla u-R_j|^p \textrm{d}x\\&\leqq c \sum _j \int _{Q_j} |\nabla u-R_j|^p \textrm{d}x. \end{aligned} \end{aligned}$$

(5.49)

We then apply the weighted Poincaré inequality in Theorem 5.5 and obtain that there is $R_*\in {\mathbb {R}}^{n\times n}$ with

$$\begin{aligned} \Vert \beta -R_*\Vert _{L^p(\Omega )}^p\leqq c \int _\Omega {\text {dist}}^p(x,\partial \Omega ) |\nabla \beta |^p \textrm{d}x\leqq c \int _\Omega {\text {dist}}^p(\nabla u,\textrm{SO}(n))\textrm{d}x. \end{aligned}$$

(5.50)

Finally, we let R be the matrix in $\textrm{SO}(n)$ closest to $R_*$. Then, using that $|R-R_*|={\text {dist}}(R_*,\textrm{SO}(n))\leqq |R_*-\nabla u|(x)+{\text {dist}}(\nabla u(x),\textrm{SO}(n))$ pointwise we obtain

$$\begin{aligned} |R-R_*| ({\mathcal {L}}^n(\Omega ))^{1/p} \leqq c \Vert {\text {dist}}(\nabla u,\textrm{SO}(n))\Vert _{L^p(\Omega )}, \end{aligned}$$

(5.51)

which, together with (5.46) and (5.50), concludes the proof. $\square$