Abstract
The moduli space of nodal Enriques surfaces is irreducible of dimension 9. A nodal Enriques surface is shown to be the quotient of a double cover of the plane by a lift of the Cremona involution. We also show that this gives a straightforward proof of the known description of the automorphism group for the generic such surface.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The goal of this note is to give a simple geometric construction of nodal Enriques surfaces and to show that the known structure of the automorphism group for generic nodal Enriques surfaces can be deduced from it in a straightforward fashion. As a side result we show that these surfaces always have a Nikulin involution. We also determine the transcendental and Picard lattices in the generic nodal case.
1.1 A geometric construction
K3 and Enriques surfaces form a well studied class of compact complex surfaces.Footnote 1 Let us recall that a K3 surface is a simply connected surface with trivial canonical bundle, while an Enriques surface has a K3 surface as a double covering.Footnote 2 The corresponding involution is called an Enriques involution.
It is well known (see e.g., [2] for the complex case) that a general Enriques surface does not contain smooth rational curves of self-intersection \(-2\), also called nodal curves. Since the moduli space of Enriques surfaces has dimension 10, we expect that nodal Enriques surfaces have 9 moduli. From an abstract moduli point of view the notion of a general nodal Enriques surface can be made precise and this leads naturally to an irreducible 9-dimensional moduli space (see Sect. 2.4). The main goal of this paper is to give a simple geometric construction for the corresponding Enriques surfaces.
Although this can be extracted from the results in [6] (see, Remark 3.5), the simple direct construction we propose has not been observed before. Our main result is as follows. It uses the standard plane Cremona transformation c with points of indeterminacy \(p_0,p_1,p_2\) and the blow up P of the plane in these points.
Theorem
-
1.
Let \(X\rightarrow {\mathbf {P}}^2\) be a (minimal desingularization of a) double cover branched in a sextic curve which is invariant under c and which has only ordinary double points at the points \(p_0,p_1,p_2\). Then X is a K3 surface and c lifts on X to a fixed point free involution with quotient a nodal Enriques surface. This construction depends on 9 effective parameters and its general member is a “general nodal Enriques surface”.
-
2.
A K3 surface X which is the double cover of a general nodal Enriques surface admits a second involution such that the resulting quotient of X is a degree 6 del Pezzo surface \(P\subset {\mathbf {P}}^6\). The Enriques involution on X induces an involution on P, the projective plane \({\mathbf {P}}^2\) blown up in three general points \(p_0,p_1,p_2\); this in turn is induced by the standard Cremona transformation c. The branch locus of the resulting cover \(X\rightarrow {\mathbf {P}}^2\) is a sextic curve, invariant under c and having ordinary double points at the three points \(p_0,p_1,p_2\).
We call the double cover \(X\rightarrow P\) a del Pezzo double cover and the corresponding involution a del Pezzo involution. There is a second way to lift the Cremona involution to the K3 double cover X and, surprisingly, this is a Nikulin involution. A Nikulin involution on a K3 surface is a symplectic involution, i.e., one leaving non-zero holomorphic two forms invariant. They were studied by Morrison [11] as a sequel to Nikulin’s study of finite groups of automorphisms of K3 surfaces. Nikulin involutions are also central in the work of van Geemen and Sarti [9]. Every Nikulin involution has eight fixed points leading to a quotient surface with eight nodes; the blow-up of these nodes yields a K3 surface.
To give the proof of the above theorem, we recall in Sect. 2 the moduli description of K3 and Enriques surfaces based on [16]. It is relatively easy to show the first part of the above theorem. We do this next, in Sect. 3, cf. Theorems 3.4 and 3.6. The proof of part (2) – this is Theorem 4.8 – can only be given after considerable work based on a precise lattice theoretic description of the nodal classes on general nodal Enriques surfaces. We have gathered the relevant lattice theory in Appendix A. Although well known among experts, we found it useful to give a concise and self-contained exposition of these results. For technical details we refer to Nikulin’s investigations [12, 14] and the monographs [6, 7].
1.2 Automorphisms
For the generic Enriques surface without nodal curves, the automorphism group is known to be equal to the subgroup of isometries of the Enriques lattice \(M=H^2(Y,{\mathbf {Z}})/\)(torsion) which induce the identity on M / 2M and which, in addition, preserve each of the two connected components of the “light cone” \(\{x\in M\otimes {\mathbf {R}} \mid x\cdot x >0 \}\). Here the “dot” stands for the cup-product pairing. For the complex case see [2], while one should consult [5,6,7] for positive characteristic. Note that this group is infinite.
In the latter works, one can also find a characteristic free description of the automorphism group of the generic nodal Enriques surface. However, in positive characteristic one cannot use the period map for the covering K3-surface, making these results less explicit. For instance, our definition of a “generic nodal” Enriques surface is very explicit in terms of the periods of the universal cover. Secondly, without using transcendental methods it is harder to see when the representation of the automorphism group on the Néron-Severi lattice is faithful. Our precise genericity assumption ensures this faithfulness. In the nodal situation the main result of [5] states that the image of the automorphism group in the isometry group of the Néron-Severi lattice is always contained in the group made explicit in Corollary 5.8 and generically coincides with it. The original proof [5] of this result used computer calculations. Allcock [1] found a simpler group-theoretic proof.
Our geometric construction also gives a relatively easy way to determine the automorphism group of the genericFootnote 3 nodal Enriques surface. See Corollaries 5.6, 5.8 for precise statements. Also in this situation the automorphism group is infinite. See Remark 5.9. Our simplification uses in a crucial way the explicit description of the nodal curves on a generic nodal Enriques surface which we deduce from the geometric model we use.
1.3 Notational conventions
A lattice is a free \({\mathbf {Z}}\)-module of finite rank equipped with a symmetric bilinear integral pairing denoted by a dot. If L is a lattice, and F the field \({\mathbf {Q}},{\mathbf {R}}\) or \({\mathbf {C}}\), the vector space \(L_F=L\otimes F\) inherits this product, likewise denoted by a dot. A sublattice \(M\subset L\) is called primitive if L / M is torsion free. A non-zero element \(x\in L\) is primitive if the lattice it generates is primitive, that is, x is not a non-trivial multiple of some \(y\in L\).
The dual\(L^*\) of the lattice L consists of the group of \(y\in L_{\mathbf {Q}}=L\otimes {\mathbf {Q}}\) for which all products \(y\cdot x \), \(x\in L\) are integral. Obviously \(L\subset L^*\) is a subgroup and the discriminant group of L is the abelian group
For a non-degenerate even lattice L, the pairing on L induces a \({\mathbf {Q}}/2{\mathbf {Z}}\)-valued quadratic form \(\delta _L\) on \(A_L\), the discriminant form. The pair \((A_L,\delta _L)\) is called the discriminant, but we shall be sloppy in that we use this terminology for the group \(A_L\) as well a for the form \(\delta _L\).
We shall use the following standard lattices:
the lattice \(\langle n \rangle \) which is \({\mathbf {Z}}\) equipped with the quadratic form \(x\mapsto nx^2\);
the hyperbolic lattice \(U={\mathbf {Z}}f\oplus {\mathbf {Z}}g\), \(f^2=g^2=0, f\cdot g=1\);
the root lattices \(E_n\) (see, Sect. A.1).
Furthermore, we use the following conventions:
If L is a lattice, \(nL\subset L\) is the sublattice consisting of elements \(nx, x\in L\), while L(n) denotes the lattice with a new product given by n times the product on L.
The orthogonal direct sum of lattices is denoted by \(\perp \).
The group of isometries of a lattice L is denoted by O(L).
If \(S \subset L_{\mathbf {C}}\), its isotropy group within the isometry group is denoted
$$\begin{aligned} O(G)_S= \{g\in O(G) \mid g_{\mathbf {C}}(S)=S \}. \end{aligned}$$A root is an element \(\mathbf {r}\in L\) with \(\mathbf {r}^2=-2\) defining a reflection
$$\begin{aligned} s_\mathbf {r}: L\rightarrow L,\quad s_\mathbf {r}(x)= x+( x\cdot \mathbf {r}) \mathbf {r}\in O(L). \end{aligned}$$\( \Delta (L)=\{\mathbf {r}\in L \mid \mathbf {r}^2=-2 \}\), the collection of roots in L.
\(L_\mathrm{root}= \text {lattice generated by }\Delta (L)\).
\( W(L)= \{\text {the group generated by the reflections}\}\), the Weyl group of L. This is a normal subgroup of O(L).
If M is hyperbolic, that is, has signature (1, n), the “light cone” \(\{x\in M\otimes {\mathbf {R}} \mid x^2>0 \}\) has two connected components. Choose one and call it \(C_M\). Then \(-C_M\) is the other component. We set
$$\begin{aligned} O^\uparrow \!(M)=\{g\in O(M) \mid g C_M=C_M \}, \end{aligned}$$a group of index 2 in O(M). The Weyl group W(M) is a normal subgroup of this subgroup (each reflection preserves the components of the light cone).
\(A(M)= O^\uparrow \!(M)/ W(M)\).
If G is a group of isometries of a lattice L, the automorphism induced by \(g\in G\) on L / nL is denoted by \(g_n\) and we set
$$\begin{aligned} G(n):= \{g\in G \mid g_n ={\mathrm{id}}: L/nL \rightarrow L/nL \} . \end{aligned}$$
2 Preliminaries
2.1 K3 surfaces and Enriques surfaces
As recalled in the introduction, a K3 surface is a simply connected surface X whose canonical bundle \(K_X\) is trivial. A nowhere zero section of \(K_X\) defines a holomorphic 2–form \(\omega _X\), unique up to a multiplicative scalar. The intersection pairing on \(H^2(X,{\mathbf {Z}})\) makes this free abelian group of rank 22 into a lattice whose signature is (3,19). It is unimodular and even, that is, for all \(x\in H^2(X,{\mathbf {Z}})\) the intersection number \(x^2=x\cdot x\) is even. As recalled in Appendix A.4, this characterizes the lattice up to isometry as
which we call the K3–lattice. A choice of an isometry  is called a marking for X.
is called a marking for X.
We employ the following notation:
The transcendental lattice can be characterized as the smallest sublattice T of \(H^2(X,{\mathbf {Z}})\) such that \(T_{\mathbf {C}}\) contains \({\mathbf {C}}\omega _X\). When a marking is given, we frequently confuse \(S_X\) and \(T_X\) with their images in L.
An Enriques surfaceY is a surface with a K3 surface X as an unramified double cover \( u: X \rightarrow Y\). The corresponding involution \(\iota _\mathrm{Enr}\) is called an Enriques involution and one has \(Y= X/\langle \iota _\mathrm{Enr}\rangle \). The morphism u induces an isomorphism

which is not an isometry; one has \(u^*(x)\cdot u^*(y)= 2 x\cdot y\). This can be described abstractly by introducing the Enriques involution on the level of lattices:
One can always choose a marking  such that \(\iota _\mathrm{Enr}^*\) corresponds to \(\sigma \) (see, e.g., [3, Lemma 19.1]). Such a marking is called a marking for the Enriques surfaceY or for the pair \((X,\iota _\mathrm{Enr})\). It follows that such a marking induces an isometry
such that \(\iota _\mathrm{Enr}^*\) corresponds to \(\sigma \) (see, e.g., [3, Lemma 19.1]). Such a marking is called a marking for the Enriques surfaceY or for the pair \((X,\iota _\mathrm{Enr})\). It follows that such a marking induces an isometry
where
is called the Enriques lattice. All classes in this lattice correspond to classes of divisors.
2.2 Involutions on K3 surfaces and on the K3 lattice
Forgetting the lattice structure, an involution \(\tau \) on a free finite rank \({\mathbf {Z}}\)-module K can be characterized by its involution invariant, the triple of non-negative integers \(\vec t(\tau )=(t_+,t_-,t_\mathrm{sw})\) defined by the ranks of the three submodules in any splitting \(K=K_+\oplus K_-\oplus K_\mathrm{sw}\) for which \(s |K_\pm = {\mathrm{id}}_\pm \) and \(K_\mathrm{sw}= U^{\oplus t}\) where U has rank 2 with basis \(\{u,\tau (u)\}\). This triple \(\vec t(\tau )\) is indeed independent of how the splitting is achieved [17]. We determine these invariants for the following three involutions on L:
- 1.
The Enriques involution; it clearly has invariant (0, 2, 10).
- 2.
The Nikulin involution on lattice level, defined as
$$\begin{aligned} \nu (v,u,e,u',e') = (v,u,e',u',e). \end{aligned}$$(4)We have \(\vec t (\nu )=(6,0,8)\).
- 3.
The del Pezzo involution given as follows. Fix a root \(\mathbf {r}\in E_8(-1)\subset L\), the first copy of \(E_8(-1)\), set
$$\begin{aligned} \mu ( v, u, e ,u' , e') = (-v,u', -s_\mathbf {r}e ,u, -s_{\sigma (\mathbf {r})}e'). \end{aligned}$$This involution has invariant (0, 14, 4). Indeed, it preserves each of the two summands \(E_8(-1)\) and on such a summand the reflection \(s_\mathbf {r}\) interchanges two vectors x and \(x-\mathbf {r}\) where x is any vector such that \(x\cdot \mathbf {r}=-1\), while it leaves the orthogonal complement of the plane spanned by these two vectors invariant. Hence \(-s_\mathbf {r}\) as well as \(-s_{\sigma (\mathbf {r})}\) has invariants (0, 6, 1) and \(\mu \) has the stated invariants.
For later use we observe that

where \(s'_\mathbf {r}= -s_\mathbf {r}\) on the first copy of \(E_8(-1)\) and the identity on its orthogonal complement, and likewise for \(s'_{\sigma (\mathbf {r})}\).
The above lattice type involutions come from geometry. The “geometric” Enriques involution, as we have seen, is fixed point free. Nikulin involutions on a marked K3 surface inducing the one on L have 8 isolated fixed points and the quotients, after blowing up the fixed points, are K3 surfaces again. See [11, 13] and [9, Sect. 1.2]. The geometry of the del Pezzo involution will be explained in Sect. 3.2.
Remark 2.1
Involutions on K3 surfaces have been classified [14, Sect. 4], [20]. Apart from the Enriques and the Nikulin type involutions, all other involutions have rational surfaces as quotient. A double cover of the projective plane ramified in a smooth sextic curve is an example of the last type of involution.
2.3 Moduli of K3 and Enriques surfaces
Let X be a K3 surface and \(\omega _X\) a non-vanishing holomorphic 2-form on it. A marking \(\varphi : H^2(X,{\mathbf {Z}}) \rightarrow L\) induces an isometry  . The line \([\varphi (\omega _X) ]\in {\mathbf {P}}(L_{\mathbf {C}})\) defines the period point of \((X,\varphi )\); it belongs to the period domain
. The line \([\varphi (\omega _X) ]\in {\mathbf {P}}(L_{\mathbf {C}})\) defines the period point of \((X,\varphi )\); it belongs to the period domain
The group O(L) acts on \({\widetilde{D}}\).
Moduli of Enriques surfaces \(Y=X/\langle \iota _\mathrm{Enr}\rangle \) can be described by means of the K3-surface X as follows. Choose a marking  for \((H^2(X,{\mathbf {Z}}),\iota _\mathrm{Enr})\) and set
for \((H^2(X,{\mathbf {Z}}),\iota _\mathrm{Enr})\) and set
Since \(\iota _\mathrm{Enr}^*\omega _X=-\omega _X\), the period point of \((X,\varphi )\) then belongs to \({\widetilde{D}} \cap {\mathbf {P}}(L^-_{\mathbf {C}})\). In fact it belongs to an open subset thereof obtained by deleting the points on hyperplanes \(H_\mathbf {r}\subset {\mathbf {P}}(L^-_{\mathbf {C}})\), orthogonal to roots \(\mathbf {r}\in L^-\):

The group
acts on D in a discrete fashion and the quotient
is the moduli space of Enriques surfaces. Note that \(\dim \mathcal M=10\). The class of \([\omega _X]\) in it depends on Y and not on the chosen marking. It is called the moduli point of Y.
2.4 Moduli of nodal Enriques surfaces
Let \(Y=X/\iota _\mathrm{Enr}\) be an Enriques surface. A nodal curve C on Y corresponds to a pair of disjoint nodal curves \(\{B,\iota _\mathrm{Enr}(B)\}\) on X. Let us see how this is reflected on the level of lattices. For clarity, we write the K3-lattice as
where \(M'\simeq M\) is the first sublattice between parentheses in (1). Via the marking, the homomorphism \(u^* : H^2(Y)\rightarrow H^2(X)\) corresponds to the homomorphism
In particular, if \(\mathbf {r}^+\in M\) is the class of a nodal curve on Y, we see that \(u^*(\mathbf {r}^+) = \mathbf {r}+\sigma (\mathbf {r})\in M'\perp \sigma (M')\). This leads to the following terminology for the corresponding roots in L.
Definition 2.2
A pair of roots \(\{\mathbf {r},\sigma (\mathbf {r})\}\) in L for which \(\mathbf {r}\cdot \sigma (\mathbf {r})=0\) is called a \(\sigma \)-adapted pair of roots. If \( \mathbf {r}+\sigma (\mathbf {r})\in M'\perp \sigma (M') \), then \(\{\mathbf {r}, \sigma (\mathbf {r})\}\) is called a strongly \(\sigma \)-adapted pair of roots.
The corresponding two nodal hyperplanes \(H_\mathbf {r}=\mathbf {r}^\perp \) and \(H_{\sigma (\mathbf {r})}=\sigma (\mathbf {r})^\perp \) meet \({\mathbf {P}}(L^-)\) in the same hyperplane which we denote
We set
Remark 2.3
Observe that c can be written in many ways as a difference \(c=\mathbf {s}-\sigma (\mathbf {s})\) of a pair of \(\sigma \)-adapted roots which are not necessarily strongly \(\sigma \)-adapted. For an Enriques surface \(Y=X/\iota _\mathrm{Enr}\) with period point on \(D_c\) such pairs \(\{\mathbf {s},\sigma (\mathbf {s})\}\) consist of algebraic classes on X, but they are not necessarily nodal classes. The classes \(\mathbf {s}+\sigma (\mathbf {s})\) correspond to roots in the Enriques lattice. In fact, below, in Sect. 4.2 we determine these roots.
By Corollary A.9 the group \(O(L,\sigma )\) acts transitively on strongly\(\sigma \)-adapted pairs of roots and so the isomorphism class of \(\mathcal M_c\) does not depend on c. More precisely, if \(c'=\gamma (c)\) for some \(\gamma \in O(L,\sigma )\), we have \(\gamma (D_c)= D_{c'}\) and hence \(\gamma \) induces an isomorphism between \(\mathcal M_c \) and \(\mathcal M_{c'}\). The isomorphism class of this hypersurface is the moduli space of “nodal” Enriques surfaces. We denote it \(\mathcal M_\mathrm{root}\).
On the other hand, suppose we have a strongly \(\sigma \)-adapted pair \(\{\mathbf {s},\sigma (\mathbf {s})\}\) of roots for which \(c'= \mathbf {s}-\sigma (\mathbf {s})\) is different from c. If the period point of Y does not belong to the corresponding hyperplane \(H_{c'}\), the class \(\mathbf {s}\) is not an algebraic class on X and in particular does come from a nodal class on Y. Accordingly, we set:
Points in \(\mathcal M^\mathrm{gen}_\mathrm{root}\) correspond to Enriques surfaces \(Y=X/\iota _\mathrm{Enr}\) whose only nodal classes correspond to strongly \(\sigma \)-adapted pairs \(\{\mathbf {r},\sigma (\mathbf {r})\}\) of roots in the Picard lattice of X with \(\mathbf {r}-\sigma (\mathbf {r})=c\).
3 Del Pezzo double planes
3.1 The standard Cremona transformation and invariant sextics
Consider the projective plane \({\mathbf {P}}^2\) with homogeneous coordinates \((x_0,x_1,x_2)\) and let \(p_0=(1:0:0)\), \(p_1=(0:1:0)\), \(p_2=(0:0:1)\). The standard Cremona transformation centered at \(p_0,p_1,p_2\) is the birational involution given by
Let \(\pi : P \rightarrow {\mathbf {P}}^2 \) the plane blown up in the three points \(p_0,p_1,p_2\) with exceptional curves \(E_i\) mapping to \(p_i\), \(i=0,1,2\) and let \( L_i\) be the proper transform of the coordinate axis \(\{x_i=0\}\).
We now consider sextic curves C having an ordinary double point in each of the points \(p_0,p_1,p_2\) and left invariant by the Cremona transformation. Such a sextic curve is given by a polynomial of the shape
Lemma 3.1
-
(i)
For a general choice of the coefficients \(a_{ijk}\) in (10) the proper transform \({\tilde{C}}\) of the sextic \(C=\{\phi =0\}\) on P is smooth and is disjoint from the fixed point locus of the involution c.
-
(ii)
The family of sextics defined by (10) depends on nine effective parameters.
Proof
-
(i)
A generic member of the family (10) is a sextic which has three ordinary double points at the points \(p_0,p_1,p_2\) and is smooth elsewhere. To see this it suffices to give one member of the family for which this is true. Such a member is the sextic with equation
$$\begin{aligned} x_0^2x_1^2x_2^2 +(x_0^4x_1^2+ x_1^2x_2^4) + (x_0^2x_1^4+x_0^2x_2^4)+(x_1^4x_2^2+x_0^4x_2^2)=0. \end{aligned}$$This can be easily checked; for instance the coordinates of the four fixed points \((1: 1:1),\, (-1:1:1),\, (1: -1:1), \,(1: 1:-1)\) of the Cremona involution don’t satisfy the above equation.
-
(ii)
We first show that if a projective transformation T preserves a generic member C of the family (10), \(T^{12}=1\) and so such T form a finite group G. Indeed, T permutes the singularities of C and hence \(T^6\) fixes each of them. But then \(T^6\) permutes each of the two tangents to C at \(p_j\), \(j=0,1,2\) and so \((T^6)^2\) fixes each of these 6 lines and hence must be the identity. Next, observe that there are 10 coefficients in the equation (10) and hence the family depends on 9 parameters. Since G is finite, this shows that there are nine moduli. \(\square \)
The Cremona transformation induces a biregular involution \(\iota _\mathrm{Cr}:P \rightarrow P\) with \(\iota _\mathrm{Cr}(E_i)= L_i\), \(i=0,1,2\), the proper transform of the coordinate axis \(\{x_i=0\}\). The corresponding divisor classes in the Picard group will be denoted by the corresponding lower case letters. The class of the proper transform L of a line will be denoted by \(\ell \). We have:
Lemma 3.2
-
(i)
\(\iota _\mathrm{Cr}^* e_i= \ell _i = \ell - (e_0+e_1+e_2)+ e_i\), \(i=0,1,2\) and \(\iota _\mathrm{Cr}^*\ell =2\ell -(e_0+e_1+e_2)\).
-
(ii)
\(\iota _\mathrm{Cr}^*\) preserves the class \(-k_P=3\ell -(e_0+e_1+e_2)\) of the anti-canonical bundle; this class is (very) ample.
Proof
-
(i)
The first three equalities are clear. The last equality follows since \(\iota _\mathrm{Cr}\) transforms a line into a conic through the three points \(p_0,p_1,p_2\).
-
(ii)
This follows from (i). For the ampleness of the anti-canonical class, see e.g., [7, Theorem 8.2.3]. \(\square \)
3.2 Del Pezzo double covers admit Enriques involutions
The class of the proper transform in P of a sextic having double points in \(p_0,p_1,p_2\) in the Picard group equals \(6\ell -2(e_0+e_1+e_2)= -2 k_P\) and so is 2-divisible. We thus may form the double cover \(q:X\rightarrow P\) of P branched in the curve \({\tilde{C}}\).
Definition 3.3
A double cover \(q:X\rightarrow P \) of P branched in the proper transform \({\tilde{C}}\) of a sextic (10), is called a del Pezzo double cover and the corresponding involution \(\iota _\mathrm{delP}\), a del Pezzo involution. If \({\tilde{C}}\) is smooth, we speak of a smooth del Pezzo double cover.
Theorem 3.4
Let \(q:X\rightarrow P\) be a smooth del Pezzo cover. The surface X is a K3 surface. The involution \(\iota _\mathrm{Cr}\) lifts to a fixed point free involution \(\iota _\mathrm{Enr}: X\rightarrow X\) commuting with \(\iota _\mathrm{delP}\). The involution  is a Nikulin involution.
is a Nikulin involution.
Proof
Set \(\mathcal F={\mathcal {O}}(-K_P)\), the bundle for which \(\mathcal F^{\otimes 2}= {\mathcal {O}}_{P} ({\tilde{C}})\). Hence \(K_X= q^* (K_P \otimes \mathcal F)={\mathcal {O}}_X\). As a minimal resolution of a plane double cover, X is simply connected and so X is a K3 surface.
The surface X is canonically embedded in the total space F of \(\mathcal F\) as the zero set of the section \(p^*f- s^2\) where \(p: F \rightarrow X\) is the bundle projection, f a section of \(\mathcal F^{\otimes 2}\) vanishing along \({\tilde{C}}\) and s the tautological section of \(p^* \mathcal F\). The involution \(\iota _\mathrm{Cr}\) acts naturally on \(\mathcal F\) and so \(\iota _\mathrm{Cr}\) can be lifted to X in two ways. Since \(\iota _\mathrm{Cr}\) acts fixed point freely on \({\tilde{C}}\), the two involutions on X lifting \(\iota _\mathrm{Cr}\) act without fixed point on \(B=q^{-1}{\tilde{C}}\). Over the 4 fixed points of \(\iota _\mathrm{Cr}\) one has 8 points in X all of which are either fixed or not fixed. In the first case the involution preserves the canonical two-form; in the second case it sends it to its negative. So either we get a Nikulin involution or a fixed point free involution, i.e., an Enriques involution. \(\square \)
On X the inverse images \(q^{-1} E_i\), \(i=0,1,2\) of the 3 exceptional curves \(E_i\) are nodal curves. Their classes in the Picard group will be denoted \({\tilde{e}}_i\). The inverse images \(q^{-1}L_i\), \(i=0,1,2\) of the three rational curves \(L_i\) also are nodal curves with classes, say \({{\tilde{\ell }}}_i\). Then \(\iota _\mathrm{Enr}^*({\tilde{e}}_i)={{\tilde{\ell }}}_i\). Let \({{\tilde{\ell }}}\) be the class of \(q^{-1}(L)\). The intersection behaviour of these classes is as follows:
We say that the six divisors \({\tilde{e}}_i, {{\tilde{\ell }}}_j\) form a doubly bonded hexagon of nodal curves. Its classes are said to form a doubly bonded hexagon of roots. The intersection graph can indeed be depicted as

where the vertices represent classes of selfintersection \(-2\) and where adjacent vertices have inner product 2. We also note that the sum of the divisors in the doubly bonded hexagon is ample, since we have:
To motivate the terminology “del Pezzo involution” for \(\iota _\mathrm{delP}\) we explain the geometry behind this. The anticanonical system \(|-K_P|\) corresponds to the six-dimensional system of cubics passing through \(p_0,p_1\) and \(p_2\) which gives an embedding \(j: P\hookrightarrow {\mathbf {P}}^6\) as a surface of degree 6. This is the standard anticanonical embedding of the del Pezzo surface P. Note that, taking as a basis for \(H^0({\mathcal {O}}_P(-K_P))\) the representing cubics
the branch locus of q has equation
On the other hand, the system \(|- q^* K_P|\) has dimension 7 since the corresponding ample line bundle \(q^* {\mathcal {O}}_P(K_P^{-1})\) on the K3 surface X has degree 12 and Riemann–Roch and Kodaira vanishing then give that the dimension of its space of sections equals \(6+2=8\). See e.g., [3, Ch. VIII.3]. The system \(|- q^* K_P|\) embeds X in \({\mathbf {P}}^7\) as a degree 12 surface; the subsystem of divisors of the form \(q^*D\), D a divisor of \(|-K_P|\) defines a rational map \({\tilde{q}} :{\mathbf {P}}^7\dashrightarrow {\mathbf {P}}^6\) which maps X in a 2-1 fashion onto \(j(P)\subset {\mathbf {P}}^6\). Indeed, there exists \(y\in H^0({\mathcal {O}}_X(- q^* K_P))\) such that \(y^2= \phi \) with \(\phi \) as in (14). If \({\mathbf {P}}^7\) has homogeneous coordinates \((c_0:\dots :c_6:y)\), the del Pezzo involution is induced from \((c_0:\dots :c_6:y)\mapsto (c_0:\dots : c_6:-y)\) and the map \({\tilde{q}}\) which is projection from the point \((0:\dots :1)\) induces q. The Cremona involution is induced from the involution on \({\mathbf {P}}^6\) given by

which lifts to the involutions  on \({\mathbf {P}}^7\); these induce the Nikulin involution, respectively the Enriques involution. This is summarized by the following diagrams.
on \({\mathbf {P}}^7\); these induce the Nikulin involution, respectively the Enriques involution. This is summarized by the following diagrams.

Remark 3.5
From this diagram it follows that the Enriques surface \(Y= X/\iota _\mathrm{Enr}\) has an extra involution, say \(\iota \), induced by \(\iota _\mathrm{delP}\) (or \(\iota _\mathrm{Nik}\)) as depicted below.

The quotient \(Z=P/\iota _\mathrm{Cr}\) has 4 nodes since \(\iota _\mathrm{Cr}\) has 4 isolated fixed points on P. The linear forms \(c_0\), \(c_1+c_2\), \(c_3+c_4\), \(c_5+c_6\) on \({\mathbf {P}}^6\) are \(\iota \)-invariant and the induced projection \({\mathbf {P}}^6 \ni (c_0:c_1:c_2:c_3:c_4:c_5:c_6) \rightarrow (c_0:c_1+c_2:c_3+c_4:c_5+c_6)\in {\mathbf {P}}^3\) realizes the surface Z as the Cayley 4-nodal cubic surface. In [5] this induced involution \(\iota \) is called the “Kantor involution”. Clearly, from the Kantor involution one can obtain the del Pezzo involution, but in the literature we could not find an explicit construction of Enriques surfaces using the del Pezzo double cover.
3.3 Del Pezzo double covers give general nodal Enriques surfaces
Let \(q:X\rightarrow P\) be a del Pezzo double cover. We ask for an explicit isometric embedding of \(q^* S_P\subset S_X\), the sublattice of the Picard lattice of X coming from P, into the K3 lattice \(L=U\perp (U\perp E_8(-1)) \perp (U\perp E_8(-1))\). To that end, let \(\{f,g\}\) be the standard basis of the second copy of U and \(\mathbf {r}\) any root in the first copy of \(E_8(-1)\). We claim:
Theorem 3.6
Let \(q:X\rightarrow P \) be a del Pezzo double cover with corresponding Enriques surface \(Y=X/\iota _\mathrm{Enr}\). Then
- (i)
There is a marking for \((X,\iota _\mathrm{Enr})\), say
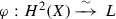 such that $$\begin{aligned} \varphi ({\tilde{e}}_0)= & {} \mathbf {r}, \\ \varphi ( {\tilde{e}}_1 )= & {} g+\sigma (g)-\sigma (\mathbf {r})\\ \varphi ( {\tilde{e}}_2 )= & {} f+ \sigma (f)-\sigma (\mathbf {r})\\ \varphi ({\tilde{\ell }})= & {} f+g+ \sigma (f+g)-\sigma (\mathbf {r}). \end{aligned}$$
such that $$\begin{aligned} \varphi ({\tilde{e}}_0)= & {} \mathbf {r}, \\ \varphi ( {\tilde{e}}_1 )= & {} g+\sigma (g)-\sigma (\mathbf {r})\\ \varphi ( {\tilde{e}}_2 )= & {} f+ \sigma (f)-\sigma (\mathbf {r})\\ \varphi ({\tilde{\ell }})= & {} f+g+ \sigma (f+g)-\sigma (\mathbf {r}). \end{aligned}$$ - (ii)
The classes in the doubly bonded hexagon (11) are embedded in the lattice L in such a way that \(\sigma \) coincides with the action of \(\iota _\mathrm{Enr}^*\). In particular
$$\begin{aligned} \begin{array}{lcl} \iota _\mathrm{Enr}^*{\tilde{e}}_0 = {\tilde{\ell }} -{\tilde{e}}_1-{\tilde{e}}_2 &{}\mapsto _\varphi &{} \sigma (\mathbf {r}) \\ \iota _\mathrm{Enr}^*{\tilde{e}}_1= {\tilde{\ell }} -{\tilde{e}}_0-{\tilde{e}}_2 &{}\mapsto _\varphi &{} f+\sigma (f)-\mathbf {r}\\ \iota _\mathrm{Enr}^* {\tilde{e}}_2 = {\tilde{\ell }} -{\tilde{e}}_0-{\tilde{e}}_1 &{}\mapsto _\varphi &{}g+ \sigma (g)-\mathbf {r}. \end{array} \end{aligned}$$ - (iii)
The class
$$\begin{aligned} -q^* k_P= & {} 3 {\tilde{\ell }} - {\tilde{e}}_0-{\tilde{e}}_1-\tilde{e}_2\mapsto _\varphi \, 2(f+g)+2\sigma (f+g) -\mathbf {r}-\sigma (\mathbf {r}) \\= & {} \varphi ({\tilde{\ell }})+ \sigma ( \varphi ({\tilde{\ell }})) \end{aligned}$$is the class of an ample divisor.
- (iv)
The period point of X belongs to the hyperplane \(H_c\), where \(c=\mathbf {r}-\sigma (\mathbf {r})\) and Y is a nodal Enriques surface. For a general choice of the curve (10) the surface Y is a general nodal Enriques surface, i.e., its moduli point belongs to \(\mathcal M_\mathrm{root}^\mathrm{gen}\).
Proof
We first consider the sublattice of \(L^+\) spanned by \(f^+= f+\sigma (f)\) and \(g^+= g+\sigma (g)\). It is isometric to U(2), the first summand of \(M(2)=U(2)\perp E_8(-2)\). The sublattice of \( H^2(X,{\mathbf {Z}})^{\iota _\mathrm{Enr}^*={\mathrm{id}}}\) spanned by \({\tilde{\ell }}-{\tilde{e}}_1\) and \({\tilde{\ell }}- {\tilde{e}}_2\) is likewise isometric to U(2). The correspondence \({\tilde{\ell }}-{\tilde{e}}_1 \mapsto f^+\), \(\tilde{\ell }- {\tilde{e}}_2 \mapsto g^+\) can be extended to give an isometry

identifying the two summands U(2). Moreover, since any two roots in \(E_8(-1)\) are conjugate under an isometry (see, Appendix A.1), we can choose the isometry in such a way that \({\tilde{e}}_0+\iota _\mathrm{Enr}^*({\tilde{e}}_0)\) maps to \({\mathbf {r}^+}= \mathbf {r}+\sigma (\mathbf {r})\). We now use Cor. A.7 from the Appendix which states that there is a “matching isometry”

such that the pair \((\varphi ^+,\varphi ^-)\) extends to an isometry  compatible with the Enriques involution. By definition, \(\varphi ^-({\tilde{e}}_0 -\iota _\mathrm{Enr}^* (\tilde{e}_0))= \mathbf {r}-\sigma (\mathbf {r})\) and the required properties for \(\varphi \) are a consequence.
compatible with the Enriques involution. By definition, \(\varphi ^-({\tilde{e}}_0 -\iota _\mathrm{Enr}^* (\tilde{e}_0))= \mathbf {r}-\sigma (\mathbf {r})\) and the required properties for \(\varphi \) are a consequence.
(iii) Lemma 3.2 implies that the class \(-q^* k_P\) is ample.
The first assertion in (iv) is a consequence of the existence of this particular marking. Since by Lemma 3.1 the family we constructed has nine effective parameters, and \(\mathcal M_c\) has dimension 9, the general member of the family is a general nodal Enriques surface. \(\square \)
3.4 Comparison of involutions
The three involutions on a del Pezzo double plane, the del Pezzo involution, the Enriques involution and their composition, the Nikulin involution can be compared to their lattice theoretic counterparts.
Corollary 3.7
Let \(q: X\rightarrow P\) be a smooth del Pezzo double plane with corresponding del Pezzo involution \(\iota _\mathrm{delP}\), Enriques involution \(\iota _\mathrm{Enr}\) and Nikulin involution  . The marking \(\varphi \) of Theorem 3.6 intertwines \(\iota _\mathrm{delP}^*\), respectively \(\iota _\mathrm{Enr}^*\) and the lattice variants \(\mu , \sigma \) of the del Pezzo and Enriques involutions, while the marking
. The marking \(\varphi \) of Theorem 3.6 intertwines \(\iota _\mathrm{delP}^*\), respectively \(\iota _\mathrm{Enr}^*\) and the lattice variants \(\mu , \sigma \) of the del Pezzo and Enriques involutions, while the marking  intertwines \(\iota _\mathrm{Nik}^*\) and \(\nu \).
intertwines \(\iota _\mathrm{Nik}^*\) and \(\nu \).
Proof
The marking intertwines \(\iota _\mathrm{Enr}^*\) and \(\sigma \) by construction. Observe that the classes in \(S_X\) invariant under \(\iota _\mathrm{delP}^*\) under the marking all belong to the primitive lattice generated by \(\mathbf {r}\), \(\sigma (\mathbf {r})\), \(f+\sigma (f)\) and \(g+\sigma (g)\). This implies first of all that, as for \(\mu \), the two copies of U are switched (note that \(f-\sigma (f)\) and \(g-\sigma (g)\) are mapped to their opposites). In the first copy of \(E_8(-1)\) the involution \(\iota _\mathrm{delP}^*\) must act as \(-s_\mathbf {r}\) (with only \({\mathbf {Z}}\mathbf {r}\) as invariant sublattice) and, similarly, in the second copy \(\iota _\mathrm{delP}^*\) must act as \(-s_{\sigma (\mathbf {r})}\). This implies that the marking indeed intertwines \(\iota _\mathrm{delP}^*\) and \(\mu \). Since  , by Eq. (5), the marking
, by Eq. (5), the marking  then automatically intertwines \(\nu \) and \(\iota _\mathrm{Nik}^*\). \(\square \)
then automatically intertwines \(\nu \) and \(\iota _\mathrm{Nik}^*\). \(\square \)
4 The K3 cover of a general nodal Enriques surface as a del Pezzo double plane
4.1 Nodal curves and the ample cone
Let \((X,\varphi )\) be any marked K3 surface with period point \([\omega ]\in L_{\mathbf {C}}\). Divisors on a K3 surface X give classes in \(S_X\), the Néron-Severi lattice; effective or ample divisors give effective, respectively ample classes in \(S_X\). By Riemann–Roch, if \(D^2\ge -2\) either D or \(-D\) is effective and so in particular, a root \(\mathbf {s}\in S_X\) is either effective or \(-\mathbf {s}\) is effective, giving rise to the partitioning:
Nodal classes are the effective roots defined by the \((-2)\)-curves, these are precisely the indecomposable roots. The lattice \(S_X\) has signature (1, s) and so we can apply the considerations of Appendix A.5 to \(S_X\). The cone \(\{x\in S_X\otimes {\mathbf {R}} \mid x^2>0 \}\) has two connected components, only one of which contains effective classes. It is called the positive cone\(C_X\). The ample classes form a subcone which can be characterized lattice theoretically as a “fundamental chamber” with respect to the above partitioning of the roots. In this case the fundamental chamber is the ample cone,
The ample cone is completely determined by the nodal classes since these correspond to the indecomposable roots in \( \Delta ^+\). The elements in \(C(\Delta ^+)\cap S_X\) are precisely the ample classes. Conversely, if \(h\in S_X\) is an ample class, we can find back the effective roots
and hence the ample cone.
On an Enriques surface \(Y=X/\langle \iota _\mathrm{Enr}\rangle \) all cohomology classes are classes of divisors:
Any class \(d\in S_Y\) with \(d^2\ge 0\) has the property that either d or \(-d\) is effective. All effective such classes belong to the closure of the positive cone \(C_Y \subset S_Y\otimes {\mathbf {R}}\). As on a K3 surface, on an Enriques surface an indecomposable root is the class of a \((-2)\)-curve. However, if D is a divisor with \(D^2=-2\), it is not true in general that \(\pm D\) is effective. Classes of nodal curves on Y correspond to pairs of disjoint nodal curves \(\{C, \iota _\mathrm{Enr}(C)\}\) on X. So, to study nodal curves, we have to get back to the associated K3 surface. Using this remark, one sees [2, Lemma 2.4] that the natural unramified double cover \( u: X \rightarrow Y \) induces a bijection
4.2 Nodal classes on general nodal Enriques surfaces
Now let \(Y=X/\langle \iota _\mathrm{Enr}\rangle \) be a general nodal Enriques surface with marking  . The nodal classes on \(Y=X/\iota _\mathrm{Enr}\) correspond to strongly \(\sigma \)-adapted pairs of irreducible roots \(\{ \mathbf {s},\sigma (\mathbf {s}) \}\) in the lattice \(\varphi (S_X)\subset L\) (cf. Definition 2.2).
. The nodal classes on \(Y=X/\iota _\mathrm{Enr}\) correspond to strongly \(\sigma \)-adapted pairs of irreducible roots \(\{ \mathbf {s},\sigma (\mathbf {s}) \}\) in the lattice \(\varphi (S_X)\subset L\) (cf. Definition 2.2).
Next, introduce
and similarly for \(\Delta _{+}\subset L^+\). Referring to Remark 2.3, observe that writing \(r_++r_-= 2\mathbf {r}\), we have that \(\{ \mathbf {r},\sigma (\mathbf {r})\} \) is a \(\sigma \)-adapted pair of roots in the lattice L with \(r_\pm = \mathbf {r}\pm \sigma (\mathbf {r})\). For given \(c\in \Delta _-\) we want to determine
as well as the associated set
From Lemma A.9, if \(c = \mathbf {r}-\sigma (\mathbf {r}) \), the nodal class \(\mathbf {r}\) can be chosen at will.
Lemma 4.1
Assume that \(c = \mathbf {r}-\sigma (\mathbf {r}) \) with \(\mathbf {r}\in E_8(-1)\), a root in the first summand \(E_8(-1)\subset L\). Fix a standard basis \(\{f,g\}\) for the second copy of U in L. The set \( \Delta (c)\subset L\) consists of roots \(\{\pm \mathbf {s},\pm \sigma (\mathbf {s})\}\) with
such that \(xy -z(z-1)+ \frac{1}{2}(e')^2=0\). In particular, if \(x=y=\pm 1\) and \(z=0\) then \(e'\) is a root and \(\mathbf {s}\) is orthogonal to \(\mathbf {r}\).
Proof
A root \(\mathbf {s}\) such that \(\mathbf {s}-\sigma (\mathbf {s})= \mathbf {r}-\sigma (\mathbf {r})\) must be of the form \(-\sigma (\mathbf {r})+\ell +\sigma (\ell )\) with \(\ell =u+e \in U\oplus E_8(-1)\). Since \(\mathbf {s}^2=-2\) we must have \(u^2+e^2- \mathbf {r}\cdot e =0\) which implies that \(\mathbf {r}\cdot e\) is even and we apply Lemma A.2 iv) to write \(e = z\mathbf {r}+ e'\), \(e'\in \mathbf {r}^\perp \cap E_8(-1)=E_7(-1)\). Then we find the desired expression. \(\square \)
Corollary 4.2
-
( i)
The lattice N(c) generated by \( \Delta (c)\) is isometric to \(U(2)\perp {\mathbf {Z}}\mathbf {r}\perp {\mathbf {Z}}\sigma (\mathbf {r})\perp E_7(-2)\).
-
(ii)
Roots from the set \(\Delta ^+(c)\) all belong to \({\mathbf {r}^+}+2R\) with \(R= {\mathbf {Z}}\mathbf {r}^+ \perp {\mathbf {r}^+}^\perp \).
-
(iii)
The lattice N generated by \( \Delta ^+(c)\) in M is isometric to
$$\begin{aligned} N= 2{\mathbf {r}^+}^\perp \perp {\mathbf {Z}}{\mathbf {r}^+}. \end{aligned}$$(19)Moreover, the set of roots in N coincides with \( \Delta ^+(c)\).
Proof
-
(i)
The roots \( f+\sigma (f)-\sigma (\mathbf {r}) , g+\sigma (g) -\sigma (\mathbf {r}) ,\mathbf {r}, \sigma (\mathbf {r})\) in \(\Delta (c)\) generate \( {\mathbf {Z}}(f+\sigma (f) )\oplus {\mathbf {Z}}(g+\sigma (g) ) \perp {\mathbf {Z}}\mathbf {r}\perp {\mathbf {Z}}\sigma (\mathbf {r})\), a lattice isometric to \(U(2) \perp {\mathbf {Z}}\mathbf {r}\perp {\mathbf {Z}}\sigma (\mathbf {r})\). Since for any root \(e'\in \mathbf {r}^\perp \cap E_8(-1)\) the root \(f+\sigma (f)+g+\sigma (g)-\sigma (\mathbf {r})+ e'+\sigma (e')\) belongs to \(\Delta (c)\), the lattice N(c) also must contain \(e'+\sigma (e')\) for any \(e'\in E_7(-1)\), since this lattice is generated by its roots. The last set is a lattice isometric to \(E_7(-2)\).
-
(ii)
We have
$$\begin{aligned}&{\mathbf {s}^+} \in \Delta ^+(c)(^1\! / _2) \iff \exists x,y,z\in {\mathbf {Z}}, e'\in E_7(-1) \\&\quad \text { with } \frac{1}{2}(e')^2 - z(z-1) + xy=0 \\&\quad \text { s.t. } {\mathbf {s}^+}= 2x f^+ + 2y g^+ +(2z-1) {\mathbf {r}^+} + 2 {e'}^+ . \end{aligned}$$If follows that \({\mathbf {s}^+} \in {\mathbf {r}^+} + 2 R\).
-
(iii)
Is a direct consequence of (i) and (ii).\(\square \)
Lemma 4.3
Fix a symmetric set of roots \(\mathbf {r}_i \in \mathbf {r}^\perp \cap E_8(-1)=E_7(-1)\), \(i=1,\ldots ,7\), (see Definition A.3) for example those from Example A.4 and put:
Introduce the sets of roots
- (i)
The roots from each of the sets \(\pm \Sigma , \pm \sigma (\Sigma )\) belong to \( \Delta (c)\) and form a maximal orthogonal set of roots in \(\Delta (c)\).
- (ii)
Two distinct roots \(\mathbf {d}, \mathbf {d}'\in \Sigma ^+\) satisfy \(\mathbf {d}\cdot \mathbf {d}'=2\).
Proof
While (ii) is clear, for (i) we first observe that all ten roots \(\delta _j\in \Sigma \) are mutually orthogonal and \(\delta _j- \sigma (\delta _j)=c\) and so \(\Sigma \subset \Delta (c)\) and then also \(-\sigma (\Sigma ) \subset \Delta (c)\). That \(\mathbf {d}\in \Sigma ^+\) is a root is clear, as well as their intersection behaviour. A small calculation shows that these \(\mathbf {d}\) are independent. Since \({\text {rank}}M=10\) this shows that \(\Sigma \) (and also \(-\sigma (\Sigma )\)) forms a maximal orthogonal set of roots in \(\Delta (c)\). \(\square \)
Remark 4.4
Any three roots from the set \(\Sigma \) together with their images under \(\sigma \) form a doubly bonded hexagon of roots.
For the general nodal Enriques surface we observe that the definition is just so that the following holds:
Proposition 4.5
Choose \(c\in L^-\) as above. For a general nodal Enriques surface the nodal curves correspond precisely to the irreducible roots in \(\Delta ^+(c)\). These generate the lattice N given in Eq. (19).
Remark 4.6
In [15] Nikulin defines a certain invariant for Enriques surfaces as follows. Consider the sublattice \(K\subset L^-(\frac{1}{2})\) generated by \(\Delta _-\) (see (16)) and consider the natural homomorphism of groups
which sends the class of \(r_-\) to the class of a corresponding \(r_+\) with \(r_-+r_+\in 2L\). The pair \((K,{\text {Ker}}\xi )\) is Nikulin’s root invariant of the Enriques surface. The root invariant is such that the rank of K is precisely the codimension of the corresponding moduli space in \(\mathcal M\). Note that for a generic Enriques surface the root invariant is (0, 0). For a generic nodal Enriques surface \(K= \langle -2 \rangle \) and since \(\xi \) is injective its root-invariant is \((\langle -2 \rangle ,0)\). In our situation the root invariant is completely determined by the so-called nodality classFootnote 4
We suppose now that Y is an Enriques surface whose moduli point belongs to \(\mathcal M^\mathrm{gen}_\mathrm{root}\). We adapt the marking \(\varphi \) in such a way that the sum h of the roots in the hexagon (12) is an ample class (see, (13) and Theorem 3.6(iii))
Since by (15) both assertions are equivalent, we explain the construction only for the classes on Y.
Lemma 4.7
-
(i)
One has \(h\cdot \mathbf {s}^+\not =0\) for all \({\mathbf {s}^+}\in \Delta ^+(c)(^1\! / _2)\) and there is a marking for Y for which h is ample.
-
(ii)
The roots \({\mathbf {s}^+}\in M\) with \({\mathbf {s}^+}\cdot h=2\) are nodal and so this holds in particular for \({\mathbf {r}^+}\), \(2f^+ -{\mathbf {r}^+}\) and \(2g^+ -{\mathbf {r}^+}\).
Proof
-
(i)
By Lemma 4.2 we have \({\mathbf {s}^+}= \mathbf {r}+ 2 m \) with \(m\in M\) and so \(h\cdot {\mathbf {s}^+} \equiv 2 \bmod 4\) and hence can never be 0. So h is not on a hyperplane orthogonal to one of these roots. Since the only possible nodal classes on Y belong to \(\Delta ^+(c)\), the ample cone \(C^\mathrm{amp}_Y\) corresponds to a connected component \(C_M^+\) of \( M_{\mathbf {R}}-\bigcup _{\mathbf {s}\in \Delta ^+(c)}H_{\mathbf {s}} \). Choose the marking such that \(h\in C^+_M\).
-
(ii)
Since \({\mathbf {s}^+} \cdot h>0\), the root \({\mathbf {s}^+}\) is effective. If it is not nodal, it would be a sum of nodal classes, but since \({\mathbf {s}^+} \cdot h=2\) this is impossible.\(\square \)
In what follows we shall use the above marking to identify \((H^2(X,{\mathbf {Z}}),\iota _\mathrm{Enr}^*)\) and \((L,\sigma )\). We are now ready to prove our second main result:
Theorem 4.8
Let \(Y=X/\iota _\mathrm{Enr}\) be a general nodal Enriques surface. Then X is a del Pezzo double cover with branch locus coming from a sextic curve \(C\subset {\mathbf {P}}^2\). Moreover,
- (i)
the Enriques involution descends to a biregular transformation induced by a standard Cremona transformation of \({\mathbf {P}}^2\). The curve C is invariant under the Cremona transformation and has three ordinary double points in the fundamental points of the Cremona transformation;
- (ii)
the composition of the covering involution and the Enriques involution is a Nikulin involution. In particular, the double cover of any generic nodal Enriques surface admits a Nikulin involution.
With regards to the Néron-Severi and transcendental lattices, one has \(L^++{\mathbf {Z}}c\subset S_X\) and \(T_X\subset c^\perp \cap L^-\) with equality if the Picard number of X equals 11. In that case we have
Proof
-
(i)
We first observe that the del Pezzo involution \(\mu \) preserves the ample class \( {\tilde{h}}= \delta _1+ \delta _2 +\sigma (\delta _0)= f+g+\sigma (f+g)- \sigma (\mathbf {r})\). By the Torelli theorem (e.g., [3, Theorem 11.1]) this implies that there is an involution \(\iota _\mathrm{delP}\) on X inducing \(\mu \). The involution \(\mu \) in addition fixes the nodal classes \(\delta _0, \delta _1, \delta _2\in L\) given by (20). Let \(q: X\rightarrow P'= X/ \iota _\mathrm{delP}\) be the natural quotient map. Since \(P'\) can at most have double point singularities which would give rise to extra nodal curves on X, we see that \(P'\) is smooth. Moreover, from Remark 2.1 we infer that \(P'\) must be a rational surface. To see that it is \({\mathbf {P}}^2\) blown up in three points, we first notice that there an isomorphism \({\mathbf {Q}}\)-vector spaces
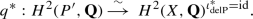
Let \(\ell ,e_0,e_2,e_3 \in H^2(P',{\mathbf {Q}})\) such that \(q^*\ell = {\tilde{h}}\), \(q^*e_0 = \delta _0, q^*e_1= \delta _1,q^*e_2= \delta _2\). Since \(q^*\) multiplies the intersection form with 2 we see that \(\ell ^2=1\) and that the \(e_j\), \(j=0,1,2,\) are classes of exceptional curves on \(P'\). Hence \(H^2(P',{\mathbf {Q}})= {\mathbf {Q}}\ell \perp {\mathbf {Q}}e_0\perp {\mathbf {Q}}e_1\perp {\mathbf {Q}}e_2\) which establishes our claim that \(P'=P\), the projective plane blown up in three points \(p_0,p_1,p_2\). But then \(q: X\rightarrow P\) is a double cover branched in the proper transform \({\tilde{C}}\) of a sextic curve \(C\subset {\mathbf {P}}^2\) having three double points at \(p_j\), \(j=0,1,2\). Since the period point of X belongs to \(\mathcal M^\mathrm{gen}_\mathrm{root}\), the sextic curve has no other singular points. Next, recall that the class of \(-q^* K_P\) corresponds to \( \tilde{h}+\sigma ({\tilde{h}})\) which is fixed under the Enriques involution \(\sigma \). So \(\iota _\mathrm{Enr}\) descends to an involution c on P which on \({\mathbf {P}}^2\) is the Cremona involution. Since \(\sigma \) and \(\mu \) commute, c leaves the branch locus invariant. Hence X is a del Pezzo double cover.
-
(ii)
This is a direct consequence of Theorem 3.4. The statement about \(S_X\) and \(T_X\) for general nodal X are clear. If the Picard number equals 11, one has \(T_X= c^\perp \subset L^-\) which is clearly isometric to \(U\perp U(2)\perp E_7(-2)\). Since \(S_X=T_X^\perp \), by [12, Sect. 1.5] the discriminant form of \(S_X\) is the same as the one for \(T_X(-1)\). By Example A.12 we have that \(S_X\simeq U\perp \langle -4\rangle \perp E_8(-2) \).\(\square \)
Remark 4.9
For any general nodal Enriques surface one can determine the nodal curves D with low degree with respect to the ample class h as follows. As observed, all \((-2)\)-curves D with \(\deg D=2\) are nodal. These are \({\mathbf {r}^+}\), \( d_1=2f^+ -{\mathbf {r}^+}\) and \(d_2=2g^+ -{\mathbf {r}^+}\). Next, consider degree 6. Among those are linear combinations of the preceding nodal curves, found using nodal reflections. We get the following 6 reducible classes of degree 6:
The remaining classes of degree 6 are all of the form \(2f^++2g^+ -{\mathbf {r}^+} + 2e^+\) with \(e^+ \) some root of \(E_7(-1)\) and hence must be nodal. In particular, this holds for the 7 classes \(d_j\), \(j=3,\dots , 9\) defined by (20) and (21).
5 Automorphisms
5.1 Automorphisms of the Enriques lattice
5.1.1 Reduction modulo 2
The product on M defines on the \({\mathbf {F}}_2\)-vector space \(V := M/2M\) an induced \({\mathbf {F}}_2\)-bilinear form b upon setting \( b( {\bar{x}}, {\bar{y}})= x \cdot y \bmod 2 \). The associated quadratic form \(q({\bar{x}}) = \frac{1}{2}x\cdot x \bmod 2\) satisfies \(q({\bar{x}}+{\bar{y}})+q({\bar{x}})+q({\bar{y}})= b({\bar{x}},{\bar{y}})\). By [2, 1.4] there is a surjective homomorphism
The kernel of this homomorphism by definition equals \(O^\uparrow \! (M)(2)\). Roots \(\mathbf {s}\in M\) give classes \({\bar{\mathbf {s}}} \in V\) with \(q({\bar{\mathbf {s}}})=1\). These give the transvections \( t_{{\bar{\mathbf {s}}}} \in O(V, q) \), i.e., \( t_{{\bar{\mathbf {s}}}} (x)=x+ b(x,{\bar{\mathbf {s}}}){\bar{\mathbf {s}}}\).
Lemma 5.1
\( t_{{\bar{\mathbf {s}}}}\) acts trivially on \({\bar{\mathbf {s}}}^\perp \) and conversely, if \(t\in O(V,q)\), \(t\not ={\mathrm{id}}\) acts trivially on \({\bar{\mathbf {s}}}^\perp \) then \( t= t_{{\bar{\mathbf {s}}}} \).
To see this, since \(r_2\) is onto and since all roots in M are conjugate under \(O^\uparrow \! (M)\) we may assume that \({\bar{\mathbf {s}}}= {\bar{f}}+ {\bar{g}} \), where \(\{{\bar{f}}, {\bar{g}}\}\) is the image in V of a basis of the direct summand U of \(M=U\perp E_8(-1)\). Suppose \(t({\bar{f}})= \xi {\bar{f}}+ \eta {\bar{g}} + z\), where z is the class of an element in \(U^\perp \). From \(b( t(x), t(y))= b(x,y)\) one deduces that \(z=0\) and then it easily follows that t switches \({\bar{f}}\) and \({\bar{g}}\) and so \(t= t_{{\bar{\mathbf {s}}}}\).
5.1.2 The group \(\Gamma (c)\)
Note that the reflection \(s_{{\mathbf {r}^+}}\) of M does not belong to \(O^\uparrow \! (M)(2)\). We show that it only depends on \( c=\mathbf {r}- \sigma (\mathbf {r})\in L^-\). Indeed,  sends c to \(-c\) while it induces the identity on \(c^\perp \). Since in M we have
sends c to \(-c\) while it induces the identity on \(c^\perp \). Since in M we have  , its action is indeed determined by c. Consider the extended group
, its action is indeed determined by c. Consider the extended group
We let
be the natural restrictions. We then have:
Lemma 5.2
Introduce the abelian group

Under the restriction \(r^+:O(L,\sigma ) \rightarrow O(L^+)=O(M)\) the group
maps isomorphically to \(\Gamma (c)\subset O(M)\).
Proof
Let \(g\in O(L,\sigma ) \) such that \(r^-(g)\in r^- ( A_c )\). Replacing g by  if necessary, we may assume that \(r^-(g )= {\mathrm{id}}\). We apply the results of Sect. A.3 as follows. We first observe that g induces the identity on \(A_{L^-}\simeq A_{L^+}\) which means precisely that \(r^+(g)\in O(L^+)(2)\). For the converse, one uses Corollary A.7. \(\square \)
if necessary, we may assume that \(r^-(g )= {\mathrm{id}}\). We apply the results of Sect. A.3 as follows. We first observe that g induces the identity on \(A_{L^-}\simeq A_{L^+}\) which means precisely that \(r^+(g)\in O(L^+)(2)\). For the converse, one uses Corollary A.7. \(\square \)
We next translate this in terms of M. Recall that the class
by definition is the nodality class determined by the root \({\bar{\mathbf {r}}}^+\). It depends only on \(c=\mathbf {r}-\sigma (\mathbf {r})\). Observe that the mod 2 reduction of \(s_{\mathbf {r}^+}\) is the transvection \(t_{{\bar{r}}}\in O(V,q)\) and so, by Lemma 5.1 we have
5.1.3 The Reye lattice
Note that since \({\mathbf {r}^+}\) is a root, \(q({\bar{\mathbf {r}}})=1\), while \(b({\bar{\mathbf {r}}}, {\bar{\mathbf {r}}})=0\). So \({\bar{\mathbf {r}}}^\perp \subset V\) is a 9-dimensional subspace containing \({\bar{\mathbf {r}}}\). This leads to the following notion, introduced by Cossec and Dolgachev [5].
Definition 5.3
Let \(\pi : M \rightarrow (V,q)\) be the projection. The lattice
is called the Reye lattice.
From now on we suppose, as before, that \(\mathbf {r}\) is a root in the first copy of \(E_8(-1)\) giving \(\mathbf {r}^+\) in the corresponding copy of \(E_8(-1)\subset M\).
We need the following result.
Lemma 5.4
The group \(\Gamma (c) \subset O^\uparrow \!(M)\) stabilizes the set of roots \( \Delta ^+(c)\) in the sublattice \(N\subset M\) it generates. Moreover, it preserves the Reye lattice \(R_{10}\).
Proof
For simplicity we write R instead of \(R_{10}\). Suppose that \(g\equiv {\mathrm{id}}\bmod 2M\). Any c-nodal root \({\mathbf {s}^+}\) belongs to \({\mathbf {r}^+} + 2R\) and so \(g({\mathbf {s}^+})\in {\mathbf {r}^+} + 2R \). Clearly \(s_{{\mathbf {r}^+}}\) preserves the set of c-nodal roots. It follows that any \(g\in \Gamma (c)\) fixes \({\bar{\mathbf {r}}}\in V\) and hence preserves \({\bar{\mathbf {r}}}^\perp \). But this means precisely that g preserves the Reye lattice. \(\square \)
5.2 Automorphisms of the generic nodal Enriques surface
Fix a marking for \((X, \iota _\mathrm{Enr})\) and identify \( ( C^\mathrm{amp}_X)^{\iota _\mathrm{Enr}^*={\mathrm{id}}}=C^\mathrm{amp}_Y \) (see (15)) with its image in \(M\otimes {\mathbf {R}}\) under the marking. The marking induces a representation of \({\text {Aut}}(Y)\) on the lattice M and we set
The marking sends the holomorphic 2 form on X to the corresponding line \([\omega _X]\). Any automorphisms g of X induces an automorphism of the transcendental lattice \(T_X\) and preserves the plane \(P_X \subset T_X\otimes {\mathbf {R}}\) spanned by the real and imaginary parts of \(\omega _X\). The intersection form is positive definite on this plane and it follows that g has finite order on \(T_X\) since \(T_X\) is the smallest sublattice of \(H^2(X,{\mathbf {Z}})\) with \(P_X\subset T_X\otimes {\mathbf {R}}\). Hence g acts on the complex line \({\mathbf {C}}\omega _X \) as multiplication by an \(\ell \)-th root of unity \(\epsilon _\ell \) ,which is at the same time an eigenvalue for \(g^*|T_X\). Since the characteristic polynomial of this action has degree equal to \({\text {rank}}T_X\le 12\) we must have \(\varphi (\ell )\le 12\), where \(\varphi \) denotes the Euler function. This leads to the number field
Proposition 5.5
Let \(Y=X/\iota _\mathrm{Enr}\) a general nodal Enriques surface, say with period point in \(D_c^0\), \(c=\mathbf {r}-\sigma (\mathbf {r})\), \(\mathbf {r}\) a \(\sigma \)-separated root in L. Suppose that X has Picard number 11 and that, in addition, the period point is not contained in any proper linear subspace of \({\mathbf {P}}(c^\perp \cap L^-)\subset {\mathbf {P}}(L^-)\) defined over the field k. Then \({\text {Aut}}(Y)\) maps injectively to its image \(\Gamma _Y\subset O^\uparrow \! (M) \). Moreover, \(\Gamma _Y=\Gamma (c) \cap O^\uparrow (Y)\).
Proof
The global Torelli theorem for K3 surfaces [3, Theorem 11.1] implies that
The argument of [2, Lemma 2.9] shows that the assumption on the period point implies that \(g\in {\text {Aut}}(Y)\) acts on \(T_X\) as \(\pm {\mathrm{id}}\). Since the Picard number of X is 11, Theorem 4.8 tells us that \(T_X=c^\perp \cap L^-\). Since g must also preserve c up to sign, we deduce that in that case \(g|L^- \in r^-(A_c)\). So, by Lemma 5.2\(g\in \Gamma (c)\). Conversely, every \(g\in \Gamma (c)\) induces \(\pm {\mathrm{id}}\) on \(T_X\) and in particularly it preserves \([\omega _X]\). If \(g_{\mathbf {R}}\) also preserves the ample cone of Y, it sends an ample invariant class in \(C^\mathrm{ample}_X\) to an ample class. But \(g_{\mathbf {R}}\) permutes the chambers of the Weyl group and so if \(g_{\mathbf {R}}C^\mathrm{ample}_X\cap C^\mathrm{ample}_X\not =\varnothing \), the entire ample cone \(C^\mathrm{ample}_X\) must be preserved. So by (25) we have \(g\in {\text {Aut}}(Y)\). It follows that the image of \({\text {Aut}}(Y)\) in \(O^\uparrow \!(Y)\) under the inclusion (25) equals \(\Gamma (c)\cap O^\uparrow \!(Y)\). \(\square \)
We now make explicit the condition that \(C^\mathrm{amp}_Y\) be preserved. Set
This is the group generated by the reflections \(s_\mathbf {s}\), \(\mathbf {s}\in \Delta ^+(c)\). Since \(C^\mathrm{amp}_Y\) is a fundamental domain for the action of \(W_\mathrm{nodal}\) on the “light cone” \(C_M\), we have
Corollary 5.6
Remark
If we replace c by \(c'=\gamma (c)\) for some \(\gamma \in O(L,\sigma )\), then \(\Gamma (c')=\gamma \Gamma (c)\gamma ^{-1}\) and \(W(N(^+(c'))=\gamma W(N^+(c))\gamma ^{-1}\), and so the above isomorphism for \({\text {Aut}}(Y)\) is canonical up to \(O(L,\sigma )\)-conjugacy.
Following [5, 7] the group \(\Gamma _Y\) can be described more explicit. We give a simplified argument. For simplicity we write R for the Reye lattice instead of \(R_{10}\). Recall that by Lemma A.5(ii) we have \(O^\uparrow \!(R)= O^\uparrow \!(M) _{R} \). We need an auxiliary result.
Lemma 5.7
\(W_\mathrm{nodal}\) is contained in \(O^\uparrow \!(R)= O^\uparrow \!(M) _{R} \) and it is the smallest normal subgroup therein generated by \(s_{\mathbf {r}^+}\).
Proof
Lemma 5.4 tells us that \(\Gamma (c)\) and hence \(W_\mathrm{nodal}\) preserves the Reye lattice so that \(W_\mathrm{nodal}\subset O^\uparrow \!(R)\).
Next we consider the conjugacy class of \(s_{\mathbf {r}^+}\). Within M all roots are conjugate. We want to show that a c-nodal root \(\mathbf {s}= \mathbf {r}^+ +2y\), \(y\in R\) is conjugate to \(\mathbf {r}^+\) by an element in O(M) that preserves the Reye lattice. So pick \(u\in O(M)\) with \(u(\mathbf {s})= \mathbf {r}^+\). The Reye lattice can be characterized as
Consequently, if \(x\in R\) we find \(u (x) \cdot \mathbf {r}^+ = u(x)\cdot u(\mathbf {s})= x \cdot \mathbf {s}\equiv x\cdot \mathbf {r}^+ \equiv 0 \bmod 2\) and so \(u(x)\in R\). So, indeed, all c-nodal roots of M are conjugate within \(O^\uparrow \!(M)_R\). Since \(u s_{\mathbf {s}} u^{-1}= s_{u(\mathbf {s})}\), applied to c-nodal roots \(\mathbf {s}\), this shows that \(W_\mathrm{nodal}\) is the smallest normal subgroup of \( O^\uparrow \!(R)\) containing the reflection \(s_{\mathbf {r}^+}\). \(\square \)
From this result, Corollary 5.6, the characterisation (24) of \(\Gamma (c)\), and Lemma A.5(iii) we deduce:
Corollary 5.8
[5, 7] Let \(\Gamma _{2,4,6}\) be the T-shaped graph of Fig. 2 and let \(\text { Cox}( T_{2,4,6})\) be its Coxeter group, i.e., the group generated by the reflections defined by its nodes.
There is an isomorphism
Remark 5.9
-
1.
The Coxeter group \(\text { Cox}( T_{2,4,6})\), as any hyperbolic Coxeter group containing an isotropic vector, is infinite, as we see as follows. Referring to Fig. 2, the obvious subdiagram \(\widetilde{E_7}\) contains a primitive isotropic vector which was called f in the course of the proof of Lemma A.2. For \(y\in f^\perp \) the Eichler–Siegel transformation
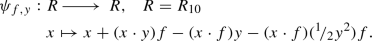
belongs to \(\text { Cox}( T_{2,4,6})_f\), hence preserves \(f^\perp \). Moreover, since \(\psi _{f,y} =\psi _{f,y+f} \) we may write \(\psi _{f,{\bar{y}}}\), \({\bar{y}} \in f^\perp /{\mathbf {Z}}f\). One easily verifies
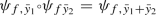
and so \(\text { Cox}( T_{2,4,6})\) contains a free abelian group of rank equal to the rank of \(f^\perp /{\mathbf {Z}}f\), i.e., of rank 8.
-
2.
The group \(\Gamma _Y\subset \text { Cox}( T_{2,4,6})\) obviously contains the congruence subgroup \(\text { Cox}( T_{2,4,6})(2)\). The index of the latter in \(\Gamma _Y\) is \(2^8\). This was first observed in [5]. See also [8].
Notes
In this note we stay entirely within the realm of complex surfaces.
Enriques surfaces, contrary to K3 surfaces, are always projective.
“Generic” has the precise meaning given in Proposition 5.5. In the moduli space of the general nodal Enriques surfaces these belong to the complement of countably many subvarieties.
Allcock [1] calls this “nodal class”. For obvious reasons for us this is not an appropriate notion.
For \(E_{10}(-1)\), the Enriques lattice, this is also true, see the proof of A.8.
References
Allcock, D.: Congruence subgroups and Enriques surface automorphisms. arXiv:1601.00103 [math.AG] (2016)
Barth, W., Peters, C.: Automorphisms of Enriques surfaces. Invent. Math. 73, 383–411 (1983)
Barth, W., Hulek, K., Peters, C., Van de Ven, A.: Compact complex surfaces, Second edition. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. Springer, Berlin (2004)
Bourbaki, N.: Éléments de mathématique. Fasc. XXXIV. Groupes et algbres de Lie. Chapitre IV: Groupes de Coxeter et systèmes de Tits. Chapitre V: Groupes engendrs par des réflexions. Chapitre VI: systèmes de racines. Actualits Scientifiques et Industrielles, 1337 Hermann, Paris (1968)
Cossec, F., Dolgachev, I.: On automorphisms of nodal Enriques surfaces. Bull. Amer. Math. Soc. 12, 247–249 (1985)
Cossec, F., Dolgachev, I.: Enriques surfaces I. Progress in Math. Birkhäuser Verlag, Boston (1989)
Dolgachev, I.: Classical algebraic geometry. Cambridge University Press, Cambridge (2012)
Dolgachev, I.: A brief introduction to Enriques surfaces, in Development in Moduli theory, Kyoto-2013, Advanced Studies in Pure Math., 69 (2016) arXiv:1412.7744
van Geemen, B., Sarti, A.: Nikulin involutions on K3 surfaces. Math. Z. 255, 731–753 (2007)
Kondō, S.: Enriques surfaces with finite automorphism groups. Japan. J. Math. (N.S.) 12, 191–282 (1986)
Morrison, D.: On K3 surfaces with large Picard number. Invent. Math. 75, 105–121 (1986)
Nikulin, V.: Integral symmetric bilinear forms and some of their geometric applications. Math. USSR Izv. 14, 103–167 (1980)
Nikulin, V.: Finite automorphism groups of Kählerian surfaces of type K3. Trans. Moscow Math. Soc. 38(2), 71–135 (1980)
Nikulin, V.: On quotient groups of the automorphism groups of hyperbolic forms by the subgroups generated by 2-reflections. Algebraic-geometric applications. J. Soviet Math 22, 1401–1475 (1983)
Nikulin, V.: On a description of the automorphism groups of Enriques surfaces. Soviet Math. Dokl. 30, 282–285 (1984)
Pjateckiǐ-Šapiro, I.I., Šafarevič, I.R.: Torelli’s theorem for algebraic surfaces of type K3. Izv. Akad. Nauk SSSR Ser. Mat. 35, 530–572 (1971)
Reiner, I.: Integral representations of cyclic groups of prime order. Proc. AMS. 8, 142–146 (1957)
Serre, J.-P.: A Course in Arithmetic, Graduate Texts in Math. Springer, Berlin (1973)
Vinberg, E.: Some examples of crystallographic groups in Lobachevsky spaces. Mat. Sb. 78, 633–639 (1969)
Zhang, D.-Q.: Quotients of K3 surfaces modulo involutions. Japan. J. Math. (N.S.) 24(2), 335–366 (1998)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Ngaiming Mok.
To the memory of Wolf Barth.
Some lattice theory
Some lattice theory
1.1 The \(E_n\)-lattices
We use the description of the root lattices \(E_n(-1)\) as given in [7] which differs from the classical description but turns out to be better adapted to calculations. Consider \({\mathbf {R}}^{n+1}\) equipped with the standard Lorentz inner product given in coordinates (ranging from 0 to n) by \((x_0,x_1,\dots ,x_n)\cdot (y_0,y_1,\dots ,y_n)= x_0y_0-(\sum \nolimits _{j=1}^n x_jy_j)\) and let \(E^{1,n} \) be the lattice \({\mathbf {Z}}^{n+1}\subset {\mathbf {R}}^{n+1}\) with the induced Lorentz product, and put
For \(n=6,7,8\) this gives the “negative” of the root lattices \(E_n\). For \(n=9\) the form has a one-dimensional radical spanned by k and for \(n=10\) the lattice has signature (1, 9). Below we show that the latter is isometric to the Enriques lattice M. The above description of \(E_n\) makes it easy to deal with roots. See e.g., [7, Section 8.2.3]. For instance, we have:
Lemma
With \(\{e_0,\dots ,e_n\}\) the standard basis for \({\mathbf {R}}^{n+1}\), a root basis for \(E_n(-1)\) is given by the roots \( \alpha _0=(1,-1,-1,-1,0,\dots , 0)\) and \(\alpha _j =e_{j+1}- e_{j}\), \(j=1,\dots , n-1\).
We shall use a basis of roots in \(E_7(-1)\) and \(E_8(-1)\). The Dynkin diagrams together with their extensions are as follows.

With the numbers \(m_j\) below the nodes \(\alpha _j\), the vector \( \sum \nolimits _{j=0}^{n} m_j \alpha _j\), \(n=7,8\) spans the isotropic subspace of the extended lattices \(\widetilde{E_n(-1)}\) and so, if we delete \(\alpha _n\) from this sum, the resulting vector
is a root orthogonal to all roots from the Dynkin diagram except the one connecting to \(\alpha _n\). Using this, we see that the Enriques lattice is isometric to \(E_{10}(-1)\) (Fig. 1).
Indeed, the leftmost part of the diagram is \(\widetilde{E_8}(-1)\) and \(\{\gamma _8 +\alpha _8,\gamma _8 +\alpha _8+ \alpha _9\}\) span a hyperbolic plane orthogonal to the \(E_8(-1)\) formed by \(\{\alpha _0,\dots ,\alpha _7\}\).
Using the preceding expression for the roots, a small calculation shows that for \(n\not =9\)
generates the discriminant group. Since \( y^2= \frac{n-10}{9-n} \equiv \frac{8-n}{9-n} \mod 2{\mathbf {Z}}\), it follows that we have:
Lemma A.1
For \(n\not =9\) the discriminant of \(E_n(-1)\) equals \(({\mathbf {Z}}/(9-n){\mathbf {Z}}, \frac{8-n}{9-n} \mod 2{\mathbf {Z}})\), and hence \(E_8(-1)\) and \(E_{10}(-1)\) are unimodular, \(A_{E_7(-1)}=({\mathbf {Z}}/2{\mathbf {Z}},\frac{1}{2})\) and \(A_{E_6(-1)}= ({\mathbf {Z}}/3{\mathbf {Z}}, \frac{2}{3})\).
We assemble some further useful facts:
Lemma A.2
-
(i)
For \(n=7,8\) we have \(O(E_n(-1))=W(E_n(-1))\); for \(n=10\) we have that \( O^\uparrow \!(E_{10}(-1))= W(E_{10}(-1))\).
-
(ii)
The orthogonal complement of a root in \(E_8(-1)\) is isometric to \(E_7(-1)\).
-
(iii)
Given a root \(\mathbf {r}\in E_8(-1)\), the sublattice
$$\begin{aligned} {\mathbf {Z}}\mathbf {r}\perp \mathbf {r}^\perp = {\mathbf {Z}}\mathbf {r}\perp E_7(-1) \end{aligned}$$consists of those \(e\in E_8(-1)\) for which \(e\cdot \mathbf {r}\) is even.
-
(iv)
For \(n=6,7,8 \) the Weyl group \( W(E_n(-1))\) acts transitively on the set of roots.Footnote 5
Proof
For (i) and (iv) see [7, Section 8.2.3]. Assertion (ii) and (iii) are clear for the special root \( \gamma _ 8 \) (cf. (26)) and since all roots are conjugate under the isometry group, this implies the assertion for all roots. \(\square \)
We furthermore need special sets of roots in \(E_n(-1)\) called symmetric:
Definition A.3
A set of k roots \(b_1,\dots ,b_k\in E_n(-1)\) for which \(b_i \cdot b_j=-1\), \(i\not =j\) is called a symmetric set of k roots.
Example A.4
The following roots
form a symmetric set of roots in \(E_7(-1)\).
1.2 The Reye lattice
Consider the T-shaped graph \(T_{2,4,6}\) formed by the leftmost 10 nodes of the graph of Fig. 2. Here \(\beta _i^2=-2\), \(i=0,\dots ,9\) and \(\mathbf {r}^+\) is a root with \(\mathbf {r}^+ \cdot \beta _9=-2\), as indicated by the dotted double line. We show the following.
Lemma A.5
-
(i)
The Reye lattice \(R_{10}:= E_7(-1) \perp { \langle -2 \rangle }\perp U \) is isometric to \(T_{2,4,6}\). In this isometry the summand \(\langle -2 \rangle \) corresponds to \(\mathbf {r}^+\).
-
(ii)
Every \(u \in O^\uparrow \!(R_{10})\) extends uniquely as an isometry of M. Hence \(O^\uparrow \!(M)_{R_{10}}=O^\uparrow \!(R_{10})\).
-
(iii)
Let \(\text { Cox}_{2,4,6}\) be the Coxeter group defined by the diagram \(T_{2,4,6}\), i.e. the group generated by the reflections in the roots of \(T_{2,4,6}\). We have
$$\begin{aligned} W(R_{10})= O^\uparrow \!(R_{10})= \text { Cox}_{2,4,6} \ltimes N( s_\mathbf {r}) , \end{aligned}$$where \(N( s_\mathbf {r}) \) is the minimal normal subgroup containing \(s_{\mathbf {r}^+}\).
Proof
-
(i)
\(T_{2,4,6}\) has an obvious Dynkin subdiagram of type \({\widetilde{E}}_7(-1)\) with \(\beta _7\) in the role of \(\alpha _7\). Hence \(f=\gamma _7+\beta _7\) is isotropic in \({\widetilde{E}}_7(-1)\) but \(f\cdot \beta _8=1\), \(f\cdot \beta _9=0\). Hence \(f, f+\beta _8+\beta _9\) span a hyperbolic plane orthogonal to \(E_7(-1)\) and to the root \(\mathbf {r}^+=f + \beta _9\). Hence \(T_{2,4,6}\) is indeed isometric to \(E_7(-1)\perp U \perp \langle -2 \rangle \).
-
(ii)
Since the generating reflections from \(\text { Cox}_{2,4,6}\) come from roots in M this is obvious.
-
(iii)
Let P be the lattice spanned by \(\mathbf {r}^+\) and \(\beta _9\). It is left invariant by the two reflections \(s_{\mathbf {r}^+}\) and \(s_{\beta _9}\). Observe
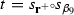 preserves the plane P and in the basis \(\{\mathbf {r}^+,\beta \}\) the automorphism t|P has matrix $$\begin{aligned} \begin{pmatrix} 3 &{} 2\\ -2 &{} -1 \end{pmatrix}, \end{aligned}$$
preserves the plane P and in the basis \(\{\mathbf {r}^+,\beta \}\) the automorphism t|P has matrix $$\begin{aligned} \begin{pmatrix} 3 &{} 2\\ -2 &{} -1 \end{pmatrix}, \end{aligned}$$which has infinite order. Hence the natural division of the nodes in the extended Dynkin diagram into the 10 nodes of \(T_{2,3,6}\) and \(\mathbf {r}^+\) is such that
 either has order 2 or \(\infty \). We then apply [19, Lemma 1].\(\square \)
either has order 2 or \(\infty \). We then apply [19, Lemma 1].\(\square \)
1.3 On isometries of L and M
We investigate the K3 lattice L and the behaviour of its isometries with respect to the Enriques involution \(\sigma \). The sublattices of L on which \(\sigma =\pm {\mathrm{id}}\) are denoted \(L^\pm \). Recall that \(L^+ \simeq M(2)\) and \(L^- \simeq U \perp M(2)\) where \(M= U\perp E_8(-1)\). We consider the question as to whether a pair of isometries of \(L^\pm \) extend to give an isometry on L. To answer this question, introduce the isometry

inducing the group isomorphism  between the discriminant groups. The following result is well known ( [12, Cor. 1.5.2.]):
between the discriminant groups. The following result is well known ( [12, Cor. 1.5.2.]):
Proposition A.6
A given pair of isometries \(\gamma ^\pm \in O(L^\pm )\) extend to an isometry \(\gamma :L\rightarrow L\) if and only if for the induced isometries \({\bar{\gamma }}^\pm \) of the discriminants one has  .
.
Corollary A.7
Let \(\gamma ^+ \in O(L^+)\) be given and define \( \gamma ^-\in O(L^-)\) by
With \( r^\pm : O(L,\sigma )\rightarrow O(L^\pm ) \) the obvious restriction maps, there is a unique isometry \(\gamma \) of L for which \(r^\pm \gamma =\gamma ^\pm \) on \(L^\pm \). Moreover \(\gamma \) commutes with \(\sigma \).
Proof
This follows immediately from the preceding discussion, except that we need to see that \(\gamma \) commutes with \(\sigma \). This follows since it does so on the sublattice \(2L\subset L\) (write \(2x= (x+\sigma (x))+(x-\sigma (x))\) ). \(\square \)
We finish with a property of isometries of the Enriques lattice M.
Lemma A.8
The group O(M) acts transitively on roots.
Proof
We apply the analog of Witt’s theorem [12, Theorem 1.14.4]. This theorem states that one can primitively embed a lattice T of signature \((t^+,t^-)\) in a unimodular lattice S of signature \((s^+,s^-)\) in a unique way up to isometries of S, provided that the conditions \(s^+-t^+>0,\, s^--t^->0\), \({\text {rank}}S -{\text {rank}}T\ge {\text {rank}}A_T+2\) hold. In our case \(S=M\), \(T={\mathbf {Z}}r_+\), \(t^+=0,t^-=1\), \(s^+=1,s^-=9\), \(A_T={\mathbf {Z}}/2{\mathbf {Z}}\) and the condition is fulfilled. \(\square \)
Recalling Definition 2.2 and using Corollary A.7 we then deduce:
Corollary A.9
Strongly \(\sigma \)-adapted pairs of roots in L are conjugate under the action of \(O(L,\sigma )\).
1.4 On even indefinite lattices
As is well known (see e.g., [18, Chapter 5]), even indefinite unimodular lattices are uniquely determined by their signature. The building blocks are \(U, E_8\) and \(E_8(-1)\). The K3 lattice, having signature (3, 19) thus equals \(U^3\perp E_8(-1)^2\). For non-unimodular lattices L, there is an extra invariant, the discriminant form \(\delta _L\). Nikulin has given criteria ensuring uniqueness for even indefinite lattices L with given signature and discriminant form. It uses the “signature \(\mod 8\)” or Arf-invariant\(\tau (q)\) of a quadratic form on a finite groups. This is an integer modulo 8 with the property that \(\tau (q_L)\equiv \text {index of } L\pmod 8\). We quote the result [12, Corollary 1.13.3]:
Theorem A.10
There is a unique indefinite even non-degenerate lattice L with signature \((t_+,t_-)\) and discriminant form \((A_L,\delta _L)\) whenever
the signature \(t_+-t_-\) of L and of \(\delta _L\) are the same modulo 8;
\({\text {rank}}L \ge 2+|A_L| \).
Before we can apply this, we need to introduce some \({\mathbf {Q}}/2{\mathbf {Z}}\)-valued quadratic forms on finite abelian groups.
Notation A.11
-
1.
For a prime p and a an integer prime to p, we let \(q_{a, p^k}\) be the group \({\mathbf {Z}}/p^k {\mathbf {Z}}\) with form \(x\mapsto \frac{a}{p^k} x^2\).
-
2.
The group \({\mathbf {Z}}/2^k{\mathbf {Z}}\oplus {\mathbf {Z}}/2^k{\mathbf {Z}}\) equipped with the quadratic form \(({\bar{x}},{\bar{y}})\mapsto \frac{1}{2^{k-1}} xy \) with \(x,y\in {\mathbf {Z}}\) representatives for \({\bar{x}}, {\bar{y}}\), gives the discriminant form for the lattice \(U(2^k)\) and will be denoted \(u_{2^k}\). It has Arf invariant 0.
-
3.
The group \({\mathbf {Z}}/2^k{\mathbf {Z}}\oplus {\mathbf {Z}}/2^k{\mathbf {Z}}\) equipped with the quadratic form \((x,y)\mapsto \frac{1}{2^{k-1}} (x^2+xy+y^2)\) is denoted \(v_{2^k}\). It has Arf-invariant 1.
Observe that it follows immediately that a \({\mathbf {Q}}/2{\mathbf {Z}}\)-valued form on the group \(({\mathbf {Z}}/2^k{\mathbf {Z}})^8\) of rank 8 has Arf-invariant 0 precisely for \(u_{2^k}^4\) or \(q_{\pm 1,2^k}^8\).
Next we observe that, given a lattice L of rank r with discriminant form \(q_{a, p^k}\), the modified lattice \(L(p^s)\) has discriminant group \({\mathbf {Z}}/{\mathbf {Z}}p^{k+s}\oplus ({\mathbf {Z}}/{\mathbf {Z}}p^{s})^{r-1}\). This follows easily from the theory of elementary divisors applied to the Gram matrix for the lattice \(L(p^s)\). It is more complicated to find the induced quadratic form on the discriminant. For \(p=2\) the Arf-invariant facilitates the calculation; can can use e.g. that the Arf-invariant is zero if and only if the form represents 0. We have seen (Lemma A.1) that the discriminant form of \(E_7(-1)\) is \(q_{1,2}\), a form with Arf-invariant \(1 \pmod 8\), confirming that \(1\equiv -7 \bmod 8\). There is a unique form on \({\mathbf {Z}}/2{\mathbf {Z}}\oplus {\mathbf {Z}}/2{\mathbf {Z}}\) with Arf-invariant 0, namely \(u_{2}\). Using this, it follows that \(E_7(-2)\) has discriminant \(q_{1,2^2}\oplus u_{2}^3\). Finally, note that the discriminant form of \(E_8(-2)\) represents zero: the quadratic form vanishes on the vector \( (1,-1,0,0,0,0,0,0,0)\in (k^\perp )^*= E^{1,8}/{\mathbf {Z}}k\) and hence on its class in \(q_{E_8(2)}\). It follows that \(q_{E_8(2)}= u_2^4\).
Example A.12
Consider \(L_1= U \perp U(2)\perp E_7(-2)\). This lattice has signature (2, 9) and discriminant \(u_2\oplus q_{1,2^2} \oplus u_{2}^3\) and satisfies the conditions of the theorem. Consider now the form \( q_{-1,2^2}\oplus u_{2}^4= -q_{L_1}\). It also satisfies the conditions of the theorem, this time for signature (1, 10). So there is a unique even lattice \(L_2\) of this signature and with \(q_{L_2}=- q_{L_1}\). To determine it, note that we just saw that \(E_8(-2)\) has Arf-invariant 0 so that its discriminant is \(u_2^4\). It follows that \(L_2= U\perp \langle -4\rangle \perp E_8(-2)\).
1.5 Hyperbolic lattices
We recall here some well known properties of groups generated by reflections in the vector space \(N_{\mathbf {R}}\) associated to an even hyperbolic lattice N, i.e., a lattice whose signature is (1, n). See e.g., [4, 14, Sect. 1.1].
Recall that the half cone \(C_N\) is a connected component of the “light cone” of elements \(x\in N_{\mathbf {R}}\) with \(x\cdot x >0\). The reflections \(s_\mathbf {r}\), \(\mathbf {r}\) a root in N preserve the cone \(C_N\) and generate a normal subgroup of \(O^\uparrow \!(N)\), the Weyl group \( W(N)\subset O^\uparrow \!(N)\) with quotient group
A fundamental domain for the action on \(C_N\) can be obtained as follows. Choose a partition \(\Delta (N)= \Delta ^+\cup -\Delta ^+\) for the set \(\Delta (N)\) of roots in N into “positive” and “negative” roots. Such a partition can be assumed to be stable under taking sums: a root which is a sum of roots from \(\Delta ^+\) belongs to \(\Delta ^+\). Roots which cannot be written as such a sum are called indecomposable. W(N) is generated by reflections in the indecomposable roots. For two different indecomposable roots \(\mathbf {r},\,\mathbf {s}\) we have \(\mathbf {r}\cdot \mathbf {s}\ge 0\).
The roots \(\mathbf {r}\in \Delta (N)\) define hyperplanes \(H_\mathbf {r}=\mathbf {r}^\perp \in N\otimes {\mathbf {R}}\) which divide \(C_N\) in “chambers”, by definition the components of the complements of their union in \(N_{\mathbf {R}}\). The fundamental domain is then the closure of the fundamental chamber
A fundamental domain is thus determined by a partition into positive and negative roots. Conversely, given any chamber C gives such a partition: take an element y in its interior, then the roots in N having positive intersection with y are the positive roots in a partition and C is the intersection of the positive half spaces defined by these roots. Consequently we have
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.




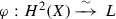 such that
such that 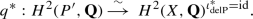
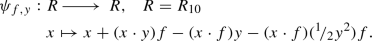
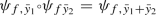


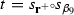 preserves the plane P and in the basis
preserves the plane P and in the basis 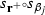 either has order 2 or
either has order 2 or