1 Introduction and motivation

Application of the positron annihilation spectroscopy to studies of matter is based on the unique properties of a positron as a probe at the atomic level. The positron annihilates with an electron and mainly two energetic quanta are emitted almost in opposite directions, which take over the total energy and momentum of the pair. Because thermalized positron occupies the lowest energy level in its band, the measurement of the total quanta momentum, i.e., the angular correlation of these quanta, is determined by the electron momentum in the annihilation place. Due to the positive charge, the positron is also sensitive to the local distortion of electron density, which is when the open volume defects, vacancies and their clusters are present in the structure. The angular correlation of annihilation quanta (ACAR) and the complementary Doppler broadening (DB) of the annihilation line are the main measured positron annihilation characteristics which are related to the local electron states in a matter. Another characteristic, the positron lifetime (PALS), depends mainly on the local electron density. Nevertheless, before annihilation the positron, as a mobile particle, scans a certain volume of the implanted sample, first as an energetic particle, in the implantation and thermalization process, and then during a random walk as a thermalized one. Thus, the annihilation characteristics reflect the local properties of the sample but they are averaged over the volume. This is not taken into account in the simple positron trapping model proposed by Brandt [1], Bergersen and Stott [2], and Connors and West [3], which is commonly used in the analysis of the PALS or DB spectra. In this model it is assumed that the defects which trap positrons with a certain rate are distributed homogeneously. Additionally, they localize only thermalized positrons. The extension of this model to the diffusion trapping model allows taking into account the fact that defects are distributed in a certain way in the volume. This problem was attacked theoretically and experimentally by many authors; some of them are listed in Refs. [4–8]. The size of the scanned volume depends on the positron diffusion length which is equal about 0.1 μm. However, positrons used for PALS or DB measurements are mainly emitted from the radioactive sources into matter and distributed over the implantation profile. Its total depth is about hundreds of micrometers and depends on the positron energy and density of the matter [9, 10]. If the studied sample exhibits a non-homogeneous defect distribution across the implantation profile and/or the path of random walk, then the measured annihilation characteristics must be sensitive to it.

The aim of the paper is to illustrate both effects in experimental studies. They concern a so-called subsurface zone (SZ) in the pure magnesium which is formed by dry sliding against another body. The SZ occurs below the surface exposed to the different technological processes and can extend up to hundreds of micrometers. Properties of the SZ are interesting because it is created directly by the processes at the worn surface which are difficult to characterize and because it is then an entering surface for positrons during measurements. We intended to find out the thermal stability of the SZ and to show how it is affected by the annealing process. In the first part of the paper we discuss the theoretical considerations of influence of the defect distribution on the positron annihilation characteristics. In the second part the experimental results concerning our studies of the SZ in pure magnesium are presented.

2 How the annihilation characteristics reflect the inhomogeneity of the probed samples

2.1 Inhomogeneity across the implantation profile

Let us consider a flat semi-infinite sample and positrons which enter through the plane xy and penetrate the depth in the z direction, as depicted in Fig. 1a. Commonly in the experiments, positrons are emitted from the β + decay nuclides located directly on the plane xy. They are emitted in the full solid angle. Additionally, we assume that only the layer of the sample between z and z+dz is uniform. The positron annihilation characteristics do not depend on the x and y coordinates. They change only in the z-direction. It is helpful to define the positron implantation profile p(z) as the probability of finding a thermal positrons at the end of the implantation and thermalization process, initially implanted with the energy E at the depth between z and z+dz from the entrance surface of the sample. Thus the total number of positrons emitted in the unit time in the sample is expressed as

$$ n = \sum_{i = 1}^{\infty} n_i = \int_{0}^{\infty} p(z)n(z)\, dz, $$
(1)

where n i is the number of positrons thermalized in the ith layer at the depth z i , while n(z) is the number of positrons in the layer at the depth between z and z+dz. Due to the annihilation the quantities n and n(z) are functions of time as well. From this we can conclude that the normalized positron annihilation lifetime spectrum is expressed as

$$ \biggl( - \frac{1}{n_{0}}\frac{dn}{dt} \biggr) = \int_{0}^{\infty} p(z) \biggl( - \frac{1}{n_{0,z}}\frac{dn(z)}{dt} \biggr) \,dz, $$
(2)

where n 0 is the total number of positrons implanted in the probed sample and n 0,z corresponds to their number at the depth between z and z+dz. Multiplying both sides of this relation by time and integrating over the time from zero to infinity we obtain the robust parameter which characterizes the PALS spectrum, i.e., the mean positron lifetime:

$$ \bar{\tau} _{m} = \int_{0}^{\infty} p(z)\,\bar{\tau} (z) \,dz, $$
(3)

where \(\bar{\tau} (z)\) represents the local mean positron lifetime, which reflects the local properties of the sample in the layer at the depth from z to z+dz. The DB spectrum is commonly characterized be the line shape parameter, i.e., the S-parameter, which is defined as the ratio of the area under the fixed center part of the annihilation line to the area under the whole annihilation line. Similar considerations allow us to obtain the S-parameter as the weighted function over the implantation profile:

$$ S_{m} = \int_{0}^{\infty} p(z)S(z)\,dz, $$
(4)

where S(z) is the value of the S-parameter in the layer. In the single measurement we are able to detect only the S m -parameter or τ m , not the depth profiles of the positron annihilation characteristics, i.e., \(\bar{\tau} (z)\) and S(z).

Fig. 1
figure 1

The scheme of the processes with the positrons at different scales

Full size image

In order to detect these profiles, the following strategies can be applied. The direct measurement of the S(z) profile is possible using the technique we call Depth Scanning of the positron Implantation Profile (DSIP). This technique allows to select a layer using a narrow slit made in the lead or tungsten shields. The HpGe detector behind the slit records the annihilation radiation coming only from positrons thermalized in the selected slab [11]. However, the scanning depth is limited to the total positrons implantation depth, which depends mainly on their energy and the density of the studied sample. No detection of the positron lifetime profile using the slit technique was done yet. Another strategy requires varying the energy of implanted positrons, from the dependency of the measured S m -parameter to the positron energy one could deduce about the S(z) profile. However, this strategy needs application of the high energetic positron beam, which is not commonly used. The commonly used low-energy positron beam of tens of keV allows to scan only the depth of few micrometers. The last strategy is much simpler. One can remove from the top of the sample a layer of a certain thickness by etching. Sequenced etching and measurement let us to obtain the dependency of S m on the total thickness of the etched layers, denoted as d, which is expressed as

$$ S_{m}(d) = \int_{d}^{\infty} p(z - d)S(z)\,dz, $$
(5)

and

$$ \bar{\tau} _{m}(d) = \int_{d}^{\infty} p(z - d)\bar{\tau} (z)\, dz. $$
(6)

These give us a possibility to deduce information about the depth profiles \(\bar{\tau} (z)\) and S(z). However, this strategy is not often used by authors [12, 13].

It was shown experimentally [9] and confirmed by Monte Carlo simulations [10] that for positrons emitted from a nuclide with a single β + decay the p(z) function can be written with a certain accuracy in the form

$$ p(z) = \mu\exp( - \mu z ), $$
(7)

where μ is the linear absorption coefficient which depends on the endpoint energy of the β + spectrum, the density of the implanted sample and its atomic number [10]. In this case, Eqs. (5) and (6) can be solved analytically:

$$ S(z) = S_{m}(z) - \frac{1}{\mu} \frac{dS_{m}(z)}{dz}, $$
(8)

and

$$ \bar{\tau} (z) = \bar{\tau} _{m}(z) - \frac{1}{\mu} \frac{d\bar{\tau} _{m}(z)}{dz}. $$
(9)

For large value of coefficient μ the second term can be neglected and the obtained in the sequenced etching measurement S m -parameter or \(\bar{\tau}_{m}\) dependency coincidence with the profile S(z) or \(\bar{\tau} (z)\). In some cases, where the surface of the sample was damaged, for instance in the dry sliding, we found the exponential type of dependency, i.e., \(S_{m}(z) = a\exp( - \frac{z}{d_{0}} ) + S_{\mathrm{b}}\) [13]. From Eq. (8) it is simple to show that it corresponds also to the exponential dependency of the S-parameter on the depth z: \(S(z)= a( 1 + \frac{1}{\mu d_{0}} )\exp( - \frac{z}{d_{0}} ) + S_{\mathrm{b}}\). For the linear type of dependency, S m (z)=a(z max−z)+S b for 0≤z≤z max and S m (z)=S b for z>z max, it corresponds to the linear dependency: \(S(z) = a(z_{\max} - z) + S_{\mathrm{b}} + \frac{a}{\mu}\). Generally, for large value of coefficient μ, i.e., low value of positron implantation range, the sequenced etching measurements allow to obtain the correct depth profiles of the S-parameter or the mean positron lifetime. However, for small values of μ the experimentally obtained results only slightly differ from the original one if the latter is linear or exponential type of dependency. For other types of dependencies it cannot be true. Equation (7) is also not correct when the positron implantation profile (7) is expressed in more accurate form [10]. Nevertheless, in typical sequenced etching experiments it is difficult to distinguish the accuracy which could reveal the deviation from Eqs. (8) and (9).

It is well established that the S-parameter is sensitive to the open volume type of defects then both relations (8) and (9) can be useful for the study of the defect distribution generated in the process like cold working, thermal shock quenching, flex-fatigue or irradiation with heavy ions or X-rays, sliding and friction, machining or sandblasting processes. In those cases the processes generates a certain defect distribution in the sample interior, which can be studied using the positron techniques. As mentioned above, one can use the energetic positrons to send them to the desired depth from the entering surface instead of the sequenced etching measurement or DSIP technique. Equations (5) and (6) are valid also for that case; however, the appropriate implantation profile should be taken into considerations instead of the relation (7).

2.2 Inhomogeneity across the diffusion length

After implantation and thermalization, positrons begin a random walk. The sample may exhibit inhomogeneity, like point defects, grains and grain boundaries or small precipitations across the diffusion length which is about 0.1 μm [5, 14]. Let us consider first small, homogeneous spherical particles of radius R being immersed in the uniform and homogeneous region, Fig. 1b. Positrons can finish their implantation path in the interior of the particle or in its surroundings. Assuming that the size of the particle is larger than the positron diffusion length, the measured S-parameter is

$$ S_{m} = (1 - \delta)S_{\mathrm{s}} + \delta S_{\mathrm{p}}, $$
(10a)

and the measured mean positron lifetime

$$ \bar{\tau} _{m} = (1 - \delta)\tau_{\mathrm{s}} + \delta\tau_{\mathrm{p}}, $$
(10b)

where the S-parameter and the positron lifetime inside the particle are equal to S p and τ p and in the surrounding region S s and τ s, respectively; δ=V p/(V s+V p) is the volume fraction of particles with V p and V s the total volumes of the particles and surrounding, respectively. However the relation (10a–10b) is not appropriate to the description of data in general, because positrons are mobile and they penetrate some volume before annihilation. That simple relation must be modified when the radius of the particles is comparable with the positron diffusion length. Taking into account also that positron inside the particle of radius R can diffuse to its surface and escape with a certain transition rate to the surrounding region, we obtain the following relation for the measured S-parameter within this model [15]:

$$ S_{m} = S_{\mathrm{s}} + \delta(S_{\mathrm{p}} - S_{\mathrm{s}}) \biggl[ 1 - \frac{3L_{ +}}{R}\frac {L(R/L_{ +} )}{1 + \frac{L_{+}}{\alpha\tau_{\mathrm{p}}}L(R/L_{ +} )} \biggr], $$
(11a)

and the corresponding relation for the measured mean positron lifetime (see Refs. [8] and [16]):

$$ \bar{\tau} _{m} = \tau_{\mathrm{s}} + \delta(\tau_{\mathrm{p}} - \tau_{\mathrm{s}}) \biggl[ 1 - \frac{3L_{ +}}{ R}\frac{L(R/L_{ +} )}{1 + \frac{L_{ +}}{\alpha\tau_{\mathrm{p}}}L(R/L_{ +} )} \biggr], $$
(11b)

where L(z)=coth(z)−1/z is the Langevin function, L + is the positron diffusion length expressed as \(L_{ +} = \sqrt{D_{ +} \tau_{\mathrm{p}}}\) with D + the positron bulk diffusion coefficient and τ p the positron lifetime in the particle, τ s is the positron lifetime in the surrounding region. It is worth noticing that the measured S m -parameter and \(\bar{\tau} _{m}\) are the functions of the particle of radius R and the properties of the boundary between the particle and its surrounding represented by the α-parameter which is the transition rate of positrons from the particle to the surrounding. For α→∞ all the positrons that reach the boundary go into the surroundings. When α→0 the boundary reflects the positrons, and the relation (11a) tends to (10a–10b).

A simple model can be useful also for another case, when e.g., cold worked metals and alloys start recovering their properties towards the initial one in the annealing process. After deformation the microstructure is highly destroyed and can be approximated as statistically uniform region full of dislocations and other defects which can localize the positrons. However, the restoration process involved by subsequent annealing induces occurrence of new dislocation-free grains formed within the deformed or recovered regions. This is the partial recrystallization process. The new grains can be treated each as the particle in the model above. When the sample is fully recrystallized, i.e., the dislocations introduced during deformation were removed, it still contains grain boundaries, which are thermodynamically unstable. The annealing process results in a grain growth, in which the smaller grains are consumed by larger ones. For such a case we propose another model.

Let us assume that the positron can annihilate inside a spherical grain, but during the diffusion process it can reach the grain boundary where it can be trapped, see Fig. 1c. We assume that the volume fraction of the grain boundaries is negligible. For that case the measured S-parameter is the following function of the S-parameter inside the grain, S g, and at the grain boundary, S b [8]:

$$ S_{m} = S_{\mathrm{g}} + 3(S_{\mathrm{b}} - S_{\mathrm{g}}) \frac{L_{ +}}{R}\frac{L(R/L_{ +} )}{1 + ( \frac{L_{ +}}{\alpha\tau_{\mathrm{b}}} )L(R/L_{ +} )}, $$
(12a)

and the corresponding value of the measured mean positron lifetime is:

$$ \bar{\tau} _{m} = \tau_{\mathrm{g}} + 3(\tau_{\mathrm{b}} - \tau_{\mathrm{g}})\frac{L_{ +}}{ R}\frac{L(R/L_{ +} )}{1 + ( \frac{L_{ +}}{\alpha\tau_{\mathrm{b}}} )L(R/L_{ +} )}, $$
(12b)

where τ b, τ g are the positron lifetime in grain and in the grain boundary, and \(L_{+} = \sqrt{D_{ +} \tau_{\mathrm{b}}}\). Note that Eq. (12a) is a case of Eq. (11a) with δ=1. In reality, the grains are not spheres, but polyhedrons, as in Fig. 1c; however, assumption of the spherical grains let us to solve analytically the positron diffusion equations; in another case only the Monte Carlo simulation can be used [14]. It is also possible to consider the grain which contains the homogeneous distributed vacancies, which can trap the positrons with the rate κ v . Vacancies certainly reduce the diffusion length which now is expressed as \(L_{ +}' = \sqrt{D_{ +} \tau_{\mathrm{f}}/(1 + \kappa_{v}\tau_{\mathrm{f}})}\), where τ f is the positron lifetime in vacancies-free grain region or lifetime in bulk (-free) state. Following the calculations presented in Refs. [8] and [16], the measured value of the S-parameter and the mean positron lifetime are given:

(13a)

and

(13b)

where S v , τ v , S b, τ b, S f and τ f denote the S-parameter and the positron lifetime for positrons annihilated only being trapped at a vacancy, at the grain boundary and in bulk, respectively. Note that the S m parameter in Eqs. (12a) and (13a) is an identical decreasing function of the grain radius. We believe that these equations can be applied to the study of processes where the grain size of a polycrystalline sample alters under certain conditions.

Following Burke and Turnbull [18] and other authors, the grain growth kinetics in the recrystallization process can be expressed by the formula

$$ \bar{R}^{n} = \bar{R}_{0}^{n} + ct, $$
(14)

where \(\bar{R}\) is the mean radius of an individual grain after annealing time t, n is the grain growth exponent close to 2, c is the temperature-dependent quantity proportional to the mobility of grain boundaries described by the Arrhenius formula \(M = M_{0}\exp ( - \frac{Q}{k_{\mathrm{B}}T} )\) where Q is the activation energy of boundary migration, T is the temperature and k B is the Boltzmann constant [17–19]. Substituting the mean radius obtained from Eq. (14) into Eq. (12a–12b), we are able to describe the change of the S m -parameter or mean positron lifetime in the isothermal and isochronal measurements. Additionally, this gives an opportunity to determine the activation energy of Q.

Čižek et al. [20] proposed another approach to the description of the recrystallization process in the ultrafine grained copper samples in the isochronal annealing. The authors took into account the positron diffusion in the spherical, non-distorted grains the volume fraction of which was described by the Göhler–Sachse’s equation [21] instead of the commonly used Avrami–Johnson–Mehl’s equation [17, 22]. By sophisticated analysis of the positron the authors obtained the activation energy of recrystallization in the ultrafine grained copper samples of about 1.0±0.1 eV. Application of Eqs. (12b) and (14) with n=2 also gives the reasonable description (regression coefficient r 2=0.987) of their data presented in Fig. 5 in Ref. [20] (only the mean positron lifetime) with the energy of grain boundary migration of 1.5±0.3 eV. The value is higher but still within the accuracy. The activation energy of grain boundary migration reported by other authors in coarse-grained copper is about 1.1 eV [17, 22]. In our former studies for the copper, single crystal after a deep plastic deformation (84 % deformation) using these equations gave the value of 1.18±0.02 eV [15]. Keeping in mind that the mechanism of the boundary migration depends on many factors, for instance the grain misorientation [17], one can conclude that the obtained activation energies are acceptable.

2.3 Standard trapping model

The commonly used model assumes that the one-dimensional defects are uniformly distributed in the host, see Fig. 1d. A difference of the electrons concentration in the perfect lattice and defects induces the differences in the measured annihilation characteristics. The standard trapping model takes into account only annihilation and trapping rates at different defects [1–3]. For one type of defect, e.g. vacancy, the S-parameter can be given (see Ref. [23]) as

$$ S_{m} = \frac{S_{\mathrm{b}} + S_{v}\kappa_{v}\tau_{\mathrm{b}}}{1 + \kappa_{v}\tau _{\mathrm{b}}}, $$
(15)

and for the mean positron lifetime:

$$ \bar{\tau} _{m} = \frac{1 + \kappa_{v}\tau_{v}}{1 + \kappa_{v}\tau _{\mathrm{b}}}\tau_{\mathrm{b}}, $$
(16)

where S b, τ b, S v , τ v , are the S-parameters and the positron lifetime in bulk and in a vacancy, respectively; and κ v is the trapping rate at the vacancy. No spatial distribution of vacancies, only their concentration C v is reflected in the trapping rate:

$$ \kappa_{v} = v C_{v}, $$
(17)

where v is the specific trapping rate which expresses the transition rate of the positron from the free to the localized at vacancy state. (Note, for very large grain radius Eqs. (13a) and (13b) coincide with Eqs. (15) and (16), respectively.) The concentration of vacancies can change due to different processes and this is reflected in the changes of the directly measured S m  parameter or \(\bar{\tau}_{m}\) according Eqs. (15) and (16), respectively. With the increase of temperature T vacancies can be thermally generated. Their concentration in the equilibrium is

$$ C_{v} = \exp \biggl[ - \frac{G_{\mathrm{F}}}{k_{\mathrm{B}}T} \biggr], $$
(18)

where G F denotes the Gibbs energy of the vacancy formation. The relation (18) together with (16) and (17) is used for determination of the formation enthalpy H F, because G F=H F−TS F, where S F is the formation entropy (not including the configuration entropy).

When vacancies are generated in the non-equilibrium processes, it is observed that in the recovery process induced by temperature and annealing time their initial concentration is decreasing. One can consider a simple model that vacancies are migrating to the sinks which are located at the grain boundary. For spherical grains of radius R, from the diffusion equation one can obtain that the vacancy concentration decreases as follows [24]:

$$ C_{v} = \frac{6\,C_{0}}{\pi^{2}}\sum_{k = 1}^{\infty} \frac {1}{k^{2}}\exp \biggl[ - k^{2}\pi ^{2}t \frac{D(T)}{R^{2}} \biggr], $$
(19)

where C 0 is the initial concentration, t is annealing time, and D is the diffusion coefficient of migrating vacancy, which is the function of temperature:

$$ D(T) = D_{0}\exp \biggl( - \frac{H_{m}}{k_{\mathrm{B}}T} \biggr), $$
(20)

where H m denotes the vacancy migration enthalpy and D 0 is the pre-exponential diffusion constant. This allows incorporating the spatial distribution of vacancies into the simple trapping model. This model allows describing the experimental results obtained in the isothermal and isochronal measurements of the highly deformed Ag [24] and stainless steel [25].

The review of the models points out a wide application of the annihilation methods to variety of problems at different scales. Due to the positron implantation profile one can study the defect distribution induced during surface treatment, for instance blasting or dry sliding, in the depth of hundreds of micrometers in the sequenced etching experiment. Positron diffusion at the range of 0.1 μm gives the possibility to study small particles and the typical grain structure of the material in the range of few micrometers. The recrystallization process induced by annealing of plastically deformed material is an example for such study. The uniform distribution, for instance of the thermally generated vacancies of atomic size being in the equilibrium in the host, is also studied successfully by the positron techniques. For years this was the important application of the positron annihilation spectroscopy.

3 Experimental details

3.1 Sample preparation

For demonstration of the effect of inhomogeneity on the measured characteristics we have chosen the samples of pure magnesium whose surfaces were damaged in the dry sliding and compression. Samples of magnesium of 99.8 % purity (purchased from Goodfellow) were disc-shaped 10 mm in diameter and 3 mm thick. Before treatments, they were annealed in the flow of N2 gas at a temperature of 400 °C for 3 hours, and then slowly cooled to room temperature. After annealing, the samples were etched in a 5 % solution of acetic acid in distilled water to reduce their thickness by 100 μm and clean their surface. This procedure allowed to remove defects that occurred during manufacturing. In fact, in the positron lifetime spectrum measured for virgin samples, only one lifetime component, equal to 225±1 ps, was resolved. This corresponds well with the data reported in the literature as the bulk value for magnesium (see, e.g. Ref. [26]). After that, the sample was located in a tribotester, and a rotated disc made of martensitic steel (steel 1.355 hardness about 670 HV0.1) of diameter 50 mm was pressed to its surface with the 25 N load during 1 min. The treatment was performed in air, no oxidation was observed. The velocity of the disc relative to the surface of the sample was 5 cm/s. During this test we obtained the value of the friction coefficient equal to 0.24 and the specific wear rate, defined as worn volume per unit sliding distance per unit load, equal to (8.0±0.8)×10−13 m3 N1 m−1. Another virgin sample of pure magnesium was compressed in a flat shape to reduce its thickness to about 40 %. For compression, the hydraulic press of 10 MPa was used. After 15 seconds, the pressure was released. Such samples were measured using the positron lifetime technique.

3.2 Positron lifetime measurements

Magnesium is a low electron density metal; also, the plastic deformation of its hpc lattice is induced by motion of dislocations and minor twinning deformation. This causes them to have a weakly reflected S-parameter (see Ref. [27]). Then, instead of the measurement of this parameter or using the DISP technique, we applied the positron lifetime measurements as more accurate.

For the measurements we used as a positron source the 22Na isotope enveloped into a 7-μm thick Kapton foil. Its activity was 32 μCi. One should note that the positrons emitted from the source have sufficient energy (E max=544 keV) to penetrate a certain depth of the sample. For magnesium, the linear absorption coefficient for positrons is equal to ca. 1/144 μm−1 [10]. A distance of 144 μm can be taken as the thickness of the layer penetrated by positrons during measurements, because 64 % of emitted from this source positrons are stopped in this layer. For that reason this technique is not sensitive to surface defects and we will ignore the near-surface inhomogeneities, mechanically mixed layer and oxide effects in future considerations.

For recording the positron lifetime spectra we used the conventional fast-fast spectrometer. The spectrometer was constructed of BaF2-based detectors and standard ORTEC electronic units; the time resolution of the system was 260 ps (FWHM). The positron source was located between two identical magnesium samples, and this sandwich was positioned in front of the scintillator detectors of the positron lifetime spectrometer. The positron lifetime spectrum was measured during 24 hours to obtain more than 2×106 counts in the spectrum. All obtained spectra were deconvoluted using the LT code [28], subtracting the background and the source components.

4 The results of annealing measurements

4.1 The sample exposed to compression

In the first experiment, the isochronal annealing of the compressed sample (40 % of a thickness reduction) using a uniaxial hydraulic press was performed. The sample was annealed at constant temperature during 1 hour, cooled to the room temperature and then the positron lifetime spectrum was measured. All spectra were deconvoluted using a single lifetime component; its value vs. the annealing temperature is depicted in Fig. 2 (black squares). All obtained values are below 254 ps. This value is attributed to the positron lifetime trapped at single vacancy, and it is above the bulk value [26]. We argue that in the case of magnesium the obtained positron lifetime is the averaged value over different states where positron can be trapped mainly at dislocation jogs, i.e., breaks or step, which occur at their lines or vacancies located close to the dislocation lines. (The interesting review of the positron and dislocations interaction the reader can find in the Byrne’s paper [29].) Then the measured positron lifetime can be treated as the mean value over different states where the annihilation process occurs and based on the relations (16) and (17) we can conclude that this value is well linked with the defect concentration. Using a spectrometer with slightly better time resolution, del Rio et al. [30] were able to resolve two lifetime components: ca. 253 and 188 ps in their lifetime spectra for the magnesium sample deformed plastically up to a thickness reduction of 40 %. However, their values of the mean positron lifetime are almost equal to those obtained by us.

Fig. 2
figure 2

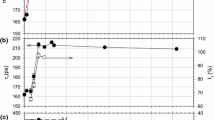
The positron lifetime as a function of the temperature in the isochronal annealing measurement for pure magnesium sample exposed to the compression (black squares) (40 % of a thickness reduction) and sample exposed to the sliding (gray circles). The solid curve represents the best fit of Eqs. (12b) and (14) to the experimental points obtained for the compression sample. The arrows indict temperatures for which the depth profiles of the samples exposed to the dry sliding were measured in sequenced etching procedure and the results are presented in Figs. 3a, b. In inset, the calculated mean grain radius according Eq. (14) with the parameters obtained from the fit of Eq. (12b) to the experimental points obtained for compression sample

Full size image

The measured positron lifetime, depicted in Fig. 2 (black squares), decreases with the increasing annealing temperature and at the temperature of about 300 °C reaches the bulk lifetime value. Many authors observed such a behavior for different metals: Cu [31, 32], Ni [33], Ta, Nb, Ni, Fe, Zr [34], Al, Mo [35], Ag [24] and stainless steel [36, 37] and Mg [30, 38] exposed to the plastic deformation. They attributed it to the vacancy migration of the recovery and recrystallization processes in the sample. This was supported by other methods: for instance, the measurements of the electrical resistivity correlate well with the characteristic decreases of the annihilation characteristics, as it is for deformed magnesium [39, 40]. Another example is the recrystallization temperature for aluminum of commercial purity is about 200 °C, and the positron measurements of the S-parameter of deformed aluminum, reported in [35], indicate the decreases slightly below 200 °C. However, the recrystallization temperature depends on the purity and degree of deformation and deviations can be expected. In Fig. 2 we can notice the positron lifetime reaches the bulk value for the temperature above 300 °C, and this temperature we can assume to be the recrystallization temperature, i.e., the sample after deformation rebuilt its properties to new, defect-free grains. No open volume defects, which trap positrons are observed above this temperature? One should emphasize that almost identical recovery dependencies of the mean positron lifetime, Fig. 2, were obtained by del Rio et al. [30]; however, they observed slightly lower temperature of the complete recover stage, i.e., 250 °C. Nevertheless, this discrepancy is within the accuracy of the annealing temperature in both measurements.

For description of the data presented in Fig. 2 (black squares) we propose to use Eqs. (12b) and (14). Additionally, it was assumed: n=2 and L +=0.70 μm [27], τ b=225 ps, and τ g=237 ps. The best fit to the experimental points with the parameters given above is depicted in Fig. 2 by the solid line. The description of the experimental data using both these relations seems to be adequate. The interesting parameter is the activation energy Q which controls boundary migration in the model. From the fit we obtain the value of Q=0.56±0.18 eV. This value is quite reasonable. We can compare it with the activation energy for migration of high-energy grain boundaries in pure Zn, which is also hpc lattice metal and has a similar melting point. In this case it is equal to 0.65 eV and it is close to the value obtained from our data [17, 41]. The parameters allow us to obtain the mean radius as a function of annealing temperature directly from Eq. (14). In the inset of Fig. 2 the dependency is drawn. This is only a draft approximation of the real grain size, which is not spherical and exhibits a certain size distribution [17]. Using a simple relation (Eg. (2) in Ref. [30]), del Rio et al. [30] obtained the value of 1.36±0.04 eV which links the central temperature of the recovery (for magnesium it is equal to 150 °C) and the activation energy. They did not discuss this value in detail; however, it seems that it can be treated as the activation energy for the recovery and/or recrystallization process. Nevertheless, this value corresponds to the values obtained for copper samples mentioned above. In this case the central temperature of the recovery is about 300 °C [20]. It is difficult to accept that the recrystallization kinetics of both the metals are similar.

4.2 The sample exposed to the sliding

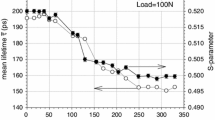
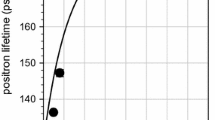
The compression induces more or less uniform plastic deformation and generates the uniform defect distribution in the whole volume of the sample (see Fig. 4 in Ref. [42]). The dry sliding, in opposite, induces the defects only in the SZ whereas the interior of the sample remains unchanged. The sample was exposed to the sliding conditions presented in Sect. 3.1 and then the positron lifetime spectra were measured in the sequenced etching procedure. Similarly as above, the samples were etched in a 5 % solution of acetic acid in distilled water to achieve the reduction of their thickness by about 40 μm. No effect of the etching process on the measured spectra was observed. The single lifetime component was resolved in all spectra; this value we treat as the mean positron lifetime. Figure 3a presents the depth profile. As it was claimed above, the mean positron lifetime reflects the defects concentration of localized positrons. The characteristic exponential decay is well recognized in Fig. 3a. We associate it with the decrease of the defect concentration with the depth increase. The detected defects are mainly vacancies localized close or on dislocation lines. For description of the experimental data, depicted in Fig. 3a, we apply the relation (9), assuming the following form for the net depth distribution of the measured mean positron lifetime: \(\bar{\tau} (z) = a + b\exp( - z/d_{0})\). The solid line in this figure represents the best fit and the values of the adjustable parameters are as follows: a=(225±0.2) ps, b=(32.5±4) ps and d 0=(42.4±5.2) μm. It was assumed that the linear absorption coefficient for the 22Na positrons in magnesium is equal to ca. μ=1/144 μm−1. The description is satisfactory, and the parameters correspond well with those obtained in our former studies [42].

Fig. 3
figure 3

The positron lifetime of the depth profile measured using the sequenced etching experiment. In (a) the profile obtained for the sample exposed to the dry sliding, no annealing was performed. The solid line represents the best fit of the exponential function with the parameters given in text. In (b) the depth profile, obtained in a similar way like in (a) but before the samples were annealed at temperatures 150, 225 and 300 °C. The dashed lines represent the best fit of the sum of the exponential decay and the Gaussian function to the experimental points for the selected temperature. The obtained in such way dependences were inserted into the right part of Eq. (9). The obtained from this equation local mean positron lifetimes as the function of the depth for samples exposed to the dry sliding and then annealed, are presented in (c)

Full size image

Having the sample with the SZ produced by dry sliding described above, it was performed the isochronal annealing measurement like for the sample exposed to the compression. In Fig. 2, the gray circles represent the obtained values of the positron lifetime as the function of the annealing temperature. The obtained dependency differs from that of the previous samples. In the temperature range between 20 and 200 °C the decrease of the positron lifetime is similar to that for the compressed samples; however, above 250 °C its value saturates at about 229 ps and remains almost constant up to the temperature of 500 °C. Above this temperature the dependency drops to the bulk value indicating recovery of the sample microstructure. It indicates that the significant difference between the two dependencies depicted in Fig. 2 originates from the fact that recovery and recrystallization processes in the SZ follow in another way.

The results presented in Fig. 2 are related to the changes of the mean positron lifetime directly in the zone of the thickness of about 144 μm adjoining the worn surface. Its thickness is the value of the average positron implantation depth. For detection of the changes in the deeper zones we measured the depth profiles of the positron lifetime in the samples exposed to dry sliding and annealed at three selected temperatures, 150, 225 and 300 °C during 1 hour (marked in Fig. 2 by arrows). The results are presented in Fig. 3b. One can notice the characteristic evolution of the depth profile. After annealing, the positron lifetime at the worn surface gradually decreases with the increase of the annealing temperature but at the depth of about 80 μm the positron lifetime increases creating a bump on the dependencies curve. That is true for the temperatures of 150 and 225 °C, however for the temperature of 300 °C the bump disappears. Nevertheless the positron lifetime in the zone adjoining the worn surface does not drop to the bulk value. Such a dependency was observed previously for copper. The measurements of the depth profile of the S-parameter using the non-destructive technique DSIP (see above) for the copper samples exposed to dry sliding revealed similar bump induced by annealing at 400 °C. It was observed at the depth of ca. 80 μm from the worn surface, see Fig. 4 in [43]. However, the results from Fig. 3b need to be recalculated using the relation (9) where the positron implantation profile is taken into account because of a small value of the linear absorption coefficient, μ, for magnesium.

In order to perform the recalculation of the measured positron lifetime and find its net value at each depth, the following strategy is proposed. First we fit a function which is the sum of the exponential decay and the Gaussian function in the bump region with some adjustable parameters to the experimental points, see Fig. 3b. At this stage the proposed function has no physical meaning, however it allows to describe the obtained dependency as a smooth analytical relation suitable for future handling. The dashed lines represent the best fit of this sum to the experimental points for each temperature. Then we introduce this sum into the right side of Eq. (9), which allows us obtaining the net dependency of the mean positron lifetime which is depicted in Fig. 3c. The obtained dependencies show (see inset in Fig. 3c) that at the depth between 60 and 100 μm the positron lifetime gradually increases with the increasing annealing temperature and at 225 °C the bulge occurs. However the minimum at the depth of 40 μm well visible in Fig. 3b is not seen. At the worn surface, the mean positron lifetime increases with the increasing annealing temperature but at the temperatures of 225 and 300 °C decreases to the value of about 250 ps.

Del Rio et al. [30] deduced from their studies that in pure magnesium exposed to the plastic deformation, two types of defects which trap positrons are present. At low degree of deformation up to 8 % only the dislocations with the positron lifetime of about 244 ps are observed; for 40 % the jogs, the size of which is close to the vacancy size with the positron lifetime of 253 ps, are the major traps. This value is observed at the worn surface in our samples annealed at 225 and 300 °C, Fig. 3c; however, annealing at 150 °C induces the increase of the positron lifetime at the surface to the value of 268 ps. Hautojärvi et al. [38] detected the positron lifetime of 350 ps in their pure magnesium samples exposed to the plastic deformation at low temperature, which was attributed to the multiple vacancies. Thus it is not excluded that at the worn surface, where the degree of deformation is highest, the increase of the temperature induces coalescence of jogs to vacancy clusters.

The annealing at 300 °C sustains the depth profile which still exhibits the exponential dependency but its total depth is shortened to 80 μm, whereas the original depth profile was extended up to depth of 125 μm, Fig. 3a. This profile vanishes only when the temperature reaches a value higher than 500 °C and the existence of this defect profile is responsible for the results presented in Fig. 2 for the sample after dry sliding.

4.3 The discussion

The rough explanation of the observed dependencies can be as follows. We argue that dry sliding generates the stream of dislocations at the worn surface which is expanded in the interior of the sample. Moving they cross each other and vacancies or interstitial atoms are created [44]. The dislocations and vacancies are distributed in the depth of the sample. Their concentration gradually decreases with the depth increase. The exponential dependency detected in the sequenced measurements, Fig. 3a, points out that they are stopped at a certain depth: it is a well-known effect that the increase of number of dislocations accompanies the increase of the hardness. Additionally, the hardness distribution, which roughly follows the defect depth profile, is well detected in the SZ as well [42]. When the sample is annealed, then the recovery is connected with motion, and rearrangement and annihilation of dislocations occur. Usually dislocations contain jogs and during their motion new vacancies or interstitial atoms are generated. This can explain the increase of the mean positron lifetime after annealing of the sample at 150 °C, Fig. 3c. The concentration of dislocations in deeper zones is lower, so they can move freely, and more point defects can be created when closer to the worn surface. This can explain the generation of the characteristic bump at the depths of 60 and 100 μm observed in our measurements.

It is worth noticing that similar bump on the dependency of the mean positron lifetime on the annealing temperature was also observed by other authors for deformed metals by rolling at room temperature: Ta, Nb, Ni, Fe [34] and Cu [43]. The slight increase of the mean positron lifetime before the characteristic drop to the bulk value was interpreted as the evidence for the migration of single vacancies.

The annealing at 300 °C initiates nucleation and growth of the new, free of dislocation and defect, grains. The bump disappears, however at the depth below 80 μm from the worn surface the restoration is not complete and defects still exist. We argue that the gradient of their concentration makes the nucleation of the new grains hard up to the temperature of 500 °C. This indicates the unique properties of the SZ created during the dry wear sliding. We think that application of the EBSD (Electron Backscatter Diffraction) which allows to obtain a 2D map of grains and their texture over large areas comparable to positron techniques should shed more light on the presented phenomena. This technique was already applied to the study of recrystallization process in hot worked magnesium [45].

5 Conclusions

Variety of the structural elements including, defects, grains, particles and interfaces at different scale levels are present in the metallic samples exposed to the compression or sliding. They can be evaluated during annealing and this can be monitored using positron techniques. This is possible because positrons before annihilation randomly walk and scan quite large volume of the sample. Additionally, emitted from the radioactive source they are spread over even larger area or depth, i.e., the positron implantation depth. This can be useful for detecting defects, mainly point defects, grain and their spatial distribution created for instance during different technological processes.

The positron lifetime measured for the pure magnesium exposed previously to compression decreases with the increase of the annealing temperature in isochronal measurements and at the temperature of about 300 °C reaches the bulk value. This dependency corresponds to the similar dependencies detected for other metals. The proposed theoretical model which takes into account the growth of the new defect free grain radius allows to describe the obtained data and extract the activation energy of the boundary migration equal to Q=0.56±0.18 eV.

In pure magnesium, similarly like in other metals, the defect depth profile induced during the dry sliding exhibits exponential decay with the depth increase. However, the annealing at temperatures of 150 and 225 °C shows the change of the profile shape indicating that at depths of 60 and 80 μm defects are generated instead of annealing. At 300 °C this effect disappears. Nevertheless, the defects are still present in the zone adjoined to the worn surface. One should emphasize that the defects survive the annealing up to the temperatures slightly above 500 °C. This behavior is in contradiction to the annealing of defects induced during compression; it this case the complete structure restoration takes place at 300 °C.

One should emphasize that the complete recovery of the SZ takes place at the temperature above 500 °C. This is in contradiction to the recovery of the samples exposed to compression which is completed at the lower temperature, i.e., 300 °C.