Quantifying the influence of natural climate variability on in situ measurements of seasonal total and extreme daily precipitation

Abstract

While various studies explore the relationship between individual sources of climate variability and extreme precipitation, there is a need for improved understanding of how these physical phenomena simultaneously influence precipitation in the observational record across the contiguous United States. In this work, we introduce a single framework for characterizing the historical signal (anthropogenic forcing) and noise (natural variability) in seasonal mean and extreme precipitation. An important aspect of our analysis is that we simultaneously isolate the individual effects of seven modes of variability while explicitly controlling for joint inter-mode relationships. Our method utilizes a spatial statistical component that uses in situ measurements to resolve relationships to their native scales; furthermore, we use a data-driven procedure to robustly determine statistical significance. In Part I of this work we focus on natural climate variability: detection is mostly limited to DJF and SON for the modes of variability considered, with the El Niño/Southern Oscillation, the Pacific–North American pattern, and the North Atlantic Oscillation exhibiting the largest influence. Across all climate indices considered, the signals are larger and can be detected more clearly for seasonal total versus extreme precipitation. We are able to detect at least some significant relationships in all seasons in spite of extremely large (> 95%) background variability in both mean and extreme precipitation. Furthermore, we specifically quantify how the spatial aspect of our analysis reduces uncertainty and increases detection of statistical significance while also discovering results that quantify the complex interconnected relationships between climate drivers and seasonal precipitation.

1 Introduction

Globally, extreme precipitation in the observational record has been shown to contain nonstationarities over the past fifty to one hundred years (Hartmann et al. 2013; Donat et al. 2016; Papalexiou and Montanari 2019), and this result has been verified in numerous studies over the contiguous United States (CONUS; Kunkel 2003; Easterling et al. 2017; Risser et al. 2019a). As such, there is a keen interest in attributing these trends to specific climate drivers, often anthropogenically-based (Min et al. 2011; Zhang et al. 2013; Fischer and Knutti 2015). However, an important component of detecting trends and subsequently attributing them to anthropogenic climate change is an appropriate characterization of the natural variability inherent to extreme precipitation from the observational record. Furthermore, a robust quantification of the natural variability in extreme precipitation from the observational record is relevant for improving seasonal and subseasonal predictability as well as evaluating climate models’ ability to capture these relationships.

The literature contains a large number of studies that explore the relationship between climate variability and extreme precipitation, for example the El Niño–Southern Oscillation (ENSO; Gershunov 1998; Cayan et al. 1999; Gershunov and Cayan 2003; Cannon 2015), the Pacific Decadal Oscillation (PDO; McCabe and Dettinger 1999), the Atlantic Multidecadal Oscillation (AMO; Enfield et al. 2001), the North Atlantic Oscillation (NAO; Durkee et al. 2008), the Pacific North American pattern (PNA; Archambault et al. 2008), and the Artic Oscillation (AO; Goswami et al. 2006). Almost all of these studies explore individual relationships between a single climate index and extreme precipitation; furthermore, such analyses often compare years from high/positive phases of the index versus low/negative phases of the index (similar to the so-called “composite analysis” in Zhang et al. 2010), which discretizes the fundamentally continuous relationships between the indices and extreme precipitation. Alternatively, Zhang et al. (2010) and Armal et al. (2018) develop statistical methods that simultaneously explore the joint relationships between a set of climate indices and extreme precipitation. Zhang et al. (2010) use a nonstationary extreme value analysis over CONUS wherein certain aspects of the generalized extreme value (GEV) distribution vary according to ENSO, NAO, and PDO. Armal et al. (2018) jointly explore the influence of ENSO, NAO, PDO, AMO, and global mean temperature on the frequency of extreme precipitation over CONUS, but do not explicitly evaluate the relationships between the drivers and extreme precipitation. Instead, these drivers are used as a proxy for natural variability in an assessment to determine where there is a meaningful anthropogenic influence on the frequency of extreme precipitation.

All of these studies maintain an underlying reliance on weather station data over CONUS, and while Zhang et al. (2010) and Armal et al. (2018) importantly consider joint relationships between climate variability and extreme precipitation their methods do not explicitly include a spatial component. As such, their results are limited to the weather station locations themselves and can neither resolve how these relationships translate to a high spatial resolution nor take advantage of the innate spatial coherence of these relationships. Resolving these relationships to a high spatial resolution is critical for understanding the behavior of extreme precipitation at their native scales which is often what is most relevant for impacts, and failing to borrow strength spatially can result in an unnecessarily large signal-to-noise ratio (SNR) in the resulting estimates (see, e.g., Risser et al. 2019b who achieve a reduction in the SNR by a factor of about two by using a spatial analysis). Furthermore, spatially-complete and spatially-resolved estimates of these relationships are needed for evaluating modern high-resolution climate models (e.g., the HighResMIP experiment, Haarsma et al. 2016). In lieu of incorporating a spatial statistical approach to in situ measurements, one must rely on gridded daily products of precipitation for model evaluation (see, e.g., Wehner 2013). While gridded products are the most appropriate data source to use for evaluating climate models (Chen and Knutson 2008; Gervais et al. 2014), a number of recent analyses specifically quantify potential errors when using daily gridded products to characterize local extremes (King et al. 2013; Timmermans et al. 2019; Risser et al. 2019b).

To address all of these issues, in this paper we use long-term records of high quality in situ measurements of daily precipitation to jointly consider seasonal relationships with a set of climate drivers. A critical component of our method is that we provide a single framework for characterizing the historical signal (anthropogenic forcing) and noise (natural variability) in seasonal mean and extreme precipitation. Our analysis utilizes the spatial extreme value analysis developed in Risser et al. (2019b) which allows us to explore the various relationships at their native scales. Furthermore, after accounting for a set of climate drivers, we develop a method for isolating the influence of individual drivers on the magnitude and frequency of extreme events using a posterior predictive approach which statistically constructs climate scenarios for comparison. We then use a data-driven approach to quantify uncertainty and test the significance of individual relationships between climate drivers and extreme precipitation (following Risser et al. 2019a), resulting in a high-resolution “probabilistic” data product for each climate driver considered that quantifies its relationship with extreme precipitation and indicates where the relationship is statistically significant. The initial motivation (and primary contribution) of this work involves seasonal extreme precipitation, but we also present results from a parallel analysis of seasonal mean precipitation and compare the mean versus extreme relationships.

Here, in Part I of this work, we focus on summarizing the natural variability of precipitation, with attribution of anthropogenic influences reserved for a separate analysis in Part II (Risser et al., “Quantifying the influence of anthropogenic forcing on in situ measurements of seasonal and extreme daily precipitation”, in prep.). The detectability for natural modes of variability is mostly limited to DJF and SON, particularly for extreme precipitation, with the El Niño/Southern Oscillation, the Pacific–North American teleconnection pattern, and the North Atlantic Oscillation exhibiting the largest influence. It is important to note that we have at least some detection of statistical significance in all seasons in spite of extremely large (> 95%) background variability in both mean and extreme precipitation. In this paper, we define background variability to be any residual variability not characterized by anthropogenic forcings (e.g., greenhouse gases), other external forcings (e.g., solar or volcanic), and known large-scale modes of climate variability (e.g., ENSO or the PNA), e.g., due to chaos in the atmosphere; see Sect. 4.1 for further details. Finally, we identify several areas where our methodology provides new insights, including a discussion around the ways in which our approach improves upon single-station and composite analyses and arrives at new results that reveal the complex, interconnected nature of the relationships between climate drivers and precipitation.

The paper proceeds as follows: in Sect. 2, we describe and justify the modes of climate variability that we will consider in the paper, as well as the data sources (both in situ measurements of precipitation and climate variability indices). Section 3 describes our statistical methods, and results are presented and discussed in Sect. 4. Section 5 concludes the paper.

2 Data sources and modes of climate variability

2.1 In situ measurements of precipitation

The weather station data used for this study consist of measurements of daily precipitation from the GHCN-D database (Menne et al. 2012). Specifically, we use measurements from the $n=2504$ weather station records (of 21,269 total) that have at least 66.7% non-missing daily values over December 1, 1899 to November 30, 2017. Denote these stations as ${\mathcal {S}}$; the geographic distribution of the stations in ${\mathcal {S}}$ is shown in Fig. C.1. For each year $t \in \{ 1900, \dots , 2017\}$, each station $\mathbf{s}\in {\mathcal {S}}$, and each season (subscript suppressed for simplicity) we extract two quantities:

• 1. the seasonal average daily precipitation rate $Z_t(\mathbf{s})$ (mm $\hbox {day}^{-1}$), and

• 2. the seasonal maximum daily precipitation total $Y_t(\mathbf{s})$ (mm), also referred to as seasonal Rx1Day,

as long as there are at least 66.7% non-missing daily values for the station in the season/year of interest; otherwise, the extreme/mean measurement is set to NA. Note that the index t refers to a “season year” where, for example, the DJF season for 1950 is comprised of December 1949 to February 1950. Also, while allowing any proportion of missing values (here, 1/3) will necessarily bias extremes downward, as long as the measurements are missing at random this will not significantly influence estimates of return values (see Appendix C of Risser et al. 2019a). As an aside, we also considered analyzing extreme seasonal five-daily totals (often referred to as Rx5Day) and found that the results were consistent whether using either Rx1Day versus Rx5Day (see Appendix 2 for further details).

2.2 Candidate climate variability indices

Based on the large body of literature summarized in Sect. 1, the set of climate variability indices that could be considered for our analysis are numerous. However, given that we seek to construct a single framework for evaluating a set of joint relationships between the indices and extreme precipitation, a process-based a priori understanding is critical. This problem is exacerbated by the fact that there are a variety of ways to incorporate climate variability in a nonstationary extreme value analysis model (e.g., shifts and/or rescaling in the overall distribution) and, furthermore, given the large number of potential climate variability indices, it is important to choose a set of candidate sources of variability to preserve degrees of freedom for fitting statistical models.

The set of candidate indices or drivers considered in our analysis are the natural logarithm of atmospheric carbon dioxide concentration, the ENSO Longitude Index, the Pacific/North American pattern, the Arctic Oscillation (sometimes referred to as the North Annular Mode), the Atlantic Multidecadal Oscillation, the North Atlantic Oscillation, and the stratospheric aerosol optical depth due to volcanoes (denoted vSAOD). This set of indices have been carefully chosen based on the existing literature (see below) as representative of different relatively independent/uncorrelated sources of climate variability (e.g., Atlantic, Pacific, etc.). With the exception of the Atlantic Multidecadal Oscillation, we have opted to include high-frequency modes of variability in order to optimize the year-to-year variance explained (as opposed to low-frequency modes of variability, which would optimize predictability). The high-frequency counterpart of the AMO is the Atlantic Meridional Mode (AMM): unfortunately, the AMM is only available back to 1948 based on the fact that its calculation requires 10 m winds over ocean regions between 75 E and 15 W, 21 S to 32 N. The AMO is correlated with the AMM on the seasonal timescale during 1948-present (roughly 0.65 in DJF, MAM, and JJA and 0.8 in SON), and furthermore AMO is a reasonably suitable replacement for the AMM in explaining variability in tropical cyclones (Huang et al. 2018). As a final note, our analysis quantifies joint relationships between this set of drivers and precipitation in each season; however, the DJF analysis excludes the Arctic Oscillation due to its strong coupling with (and high correlation with) the North Atlantic Oscillation (see also Rogers and McHugh 2002, who find that the NAO and the AO are largely inseparable during the winter months but form distinct regional patterns in the spring, summer, and autumn seasons).

In spite of the breadth of our analysis, there are a number of indices that are known to influence extreme precipitation over CONUS that we have excluded from consideration. For example, Wang et al. (2017) introduce the so-called dipole index (DPI), which describes the amplitude of a quasi-stationary centered over CONUS. O’Brien et al. (2019) showed that in California, this mode of variability accounted for by far the largest fraction of extreme precipitation at the seasonal timescale. However, the statistics of DPI appear to be fairly nonstationary over time (specifically, there was recently a sharp increase in its variance), which complicates its use as a non-anthropogenic source of natural variability. In addition, there are many indices with known relationships to seasonal total and daily extreme precipitation, such as the Madden–Julian Oscillation (Jones 2000; Zhou et al. 2012; DelSole et al. 2017), the quasi-biennial oscillation (Mundhenk et al. 2018; Gray et al. 2018), and ocean eddies (Sugimoto et al. 2017; Jan et al. 2017), but measurements of these indices are not available (or trustworthy) before the satellite era. Given that we set out to conduct a century-long analysis, these indices are excluded for now, although we plan to explore these sources of variability in a follow up analysis focused on a shorter time record.

It should be noted that because climate indices are obtained from various observational and reanalysis datasets, there could be non-negligible uncertainties in the indices used in this study. While one could develop a statistical analysis to account for such uncertainties, this is not straightforward and is beyond the scope of this paper. Instead, we note that we have only chosen indices that have low uncertainty between data sources (e.g., PNA and AO agree nicely from the different observational sources, while the QBO showed essentially complete disagreement). Furthermore, since any uncertainty in the indices would likely increase as one goes further back in time, we conducted a sensitivity analysis which showed that the signals identified are consistent whether the analysis considers 1950-present or 1900-present (see Appendix 1). This result gives us confidence that the longer-term results included in the paper are robust to uncertainties in the index values.

For each of the following indices, we obtain monthly mean values over 1900–2017 (as described below), and then construct the seasonal average time series for each of December–January–February (DJF), March–April–May (MAM), June–July–August (JJA), and September–October–November (SON). The seasonal average time series and seasonal correlations among the indices are provided in the Supplement (Figs. C.2 and C.3, respectively). The exception is atmospheric carbon dioxide, for which we use the same annually-averaged time series for each seasonal analysis.

2.2.1 Pacific sources of variability

El Niño–Southern Oscillation The most well-known and widely studied mode of natural variability stemming from the Pacific oceanic basin is known as the El Niño–Southern Oscillation (ENSO). ENSO is a coupled ocean–atmosphere interaction that cycles between its positive (El Niño) and negative (La Niña) phases every 2–7 years (Philander 1985). During El Niño events, an initial equatorial East/Central Pacific positive sea surface temperature (SST) anomaly weakens the tropical zonal SST gradient in turn reducing the strength of the Walker circulation and associated trade winds (Lindzen and Nigam 1987). The weakening of the Walker circulation further allows the positive SST anomaly to grow and migrate eastward resulting in a positive ocean–atmosphere feedback known as the Bjerknes feedback (Bjerknes 1969). The anomalously warm SSTs proximal to the climatologically cool waters of the East Pacific cold tongue/upwelling region result in steep zonal SST gradients, which in turn, initiate and fuel strong and sustained deep convection (Hoerling et al. 1997; Sabin et al. 2013). The anomalous convective activity excites a quasi-stationary Rossby wave train that alters the configuration of the global atmosphere driving remote temperature and precipitation responses both near and far alike (Horel and Wallace 1981; Dai and Wigley 2000; Alexander et al. 2002). In particular, for CONUS, the quasi-stationary northeast Pacific Aleutian low is strengthened resulting in enhanced stormtrack activity and vapor transport, which in turn, drive extreme precipitation and alter climatological precipitation patterns CONUS wide (Chiodi and Harrison 2013; Patricola et al. 2020). During El Niño years, wintertime intense precipitation occurs more frequently across the western US, the southwest, the Gulf Coast including Florida, and the Central US, while the intermountain west, the northern Great Plains and the Ohio river valley tend to experience the opposite (Patricola et al. 2020; Carleton et al. 1990; Schubert et al. 2008; Larkin and Harrison 2005; Cannon 2015). To a large extent, ENSO impacts are most prominent during the boreal winter in the midlatitudes and extra-tropics, however, a summer signal in precipitation frequency has been detected across the northern US (Higgins et al. 2007).

Across the large number of indices used to quantify ENSO, we choose to use the ENSO Longitude Index (ELI, Williams and Patricola 2018), which is a sea surface temperature-based index that summarizes the average longitude of deep convection in the Walker Circulation. Unlike, e.g., the Niño3.4 index, ELI compactly characterizes the different spatial patterns or “flavors” of observed and projected ENSO events. In addition to its connection to physical mechanisms, Patricola et al. (2020) show that the ELI maximizes the predictability of both mean and extreme precipitation over CONUS. This is because ELI characterizes the zonal shifts in deep convection that initiate the Rossby wave train response that influences mid-latitude precipitation. Monthly ELI values are calculated from 1854 to present based on the ERSSTv5 data set following Williams and Patricola (2018). Large values of ELI correspond to El Niño conditions, while small values of ELI correspond to La Niña conditions.

Pacific/North American Pattern The leading mode of Pacific atmospheric variability is known as the Pacific/North American (PNA) pattern and is defined as the second Rotated Empirical Orthogonal Function (EOF) of 500mb heights between 20$^\circ$ N and 90$^\circ$ N (Wallace and Gutzler 1981; Barnston and Livezey 1987). The PNA is most active during the boreal winter, where in its positive phase is associated with low pressure anomalies over the north Pacific and southeastern US and high pressure anomalies over the western US The PNA pattern is most active during the boreal winter, but can also alter precipitation patterns in the Spring and Autumn shoulder seasons. Leathers et al. (1991) undertake a comprehensive study of PNA-precipitation correlations across CONUS and find February/March anticorrelation across the Ohio river valley and the Northeast, and similar anticorrelation across much of the western US/Great Plains regions from OND season. Harding and Snyder (2015) found that the negative phase of the PNA strengthens the Great Plains low level jet which tends to enhance precipitation over the North Central US, and further, that negative PNA events less than one standard deviation are associated with the majority of heavy 5-day precipitation events. Furthermore, the negative PNA has been linked with the Midwest flood events of June–July 1993 and May–June 2008 (Patricola et al. 2015).

The Pacific Decadal Oscillation (PDO) is another mode of Pacific variability that has been studied in depth with respect to its influence on precipitation over the US (e.g., Zhang et al. 2010). However, we chose to include the PNA in our analysis instead of PDO for several reasons. First, as a technical matter, the PDO shows strong seasonal correlation in the winter and spring with PNA, and hence a statistical analysis should only include one of these indices (also, PDO is highly correlated with ENSO in all seasons). More importantly, Newman et al. (2016) show the PDO is not an independent mode but rather an integrator of independent signals at different spatio-temporal scales. The PNA, on the other hand, is an independent mode of variability (1st EOF of 500mb heights) and has direct physical linkage to extreme precipitation. The physical mechanisms by which PDO drives extreme precipitation are nebulous at best due to the characteristic timescales involved.

Measurements of the Pacific/North American pattern (PNA) are available from NOAA’s Climate Prediction Center (https://www.cpc.ncep.noaa.gov/products/precip/CWlink/pna/month_pna_index2.shtml), but measurements are only provided from January, 1950 to present. We obtain measurements for the first part of the 20th century based on the 20th Century Reanalysis version 2 (20CRV2c; https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Plot/) which covers 1851–2011. Note that to make these two data sources comparable, we use NOAA’s monthly mean PNA index constructed using the modified pointwise method (see the above link for further detail). The monthly time series from these two data sources show strong agreement during their overlapping time periods (with a correlation of 0.965). The final monthly time series used in this analysis consists of the 20CRV2c time series for 1900–1949, the arithmetic mean of the 20CRV2c and NOAA time series for 1950–2011, and the NOAA time series for 2012–2017.

2.2.2 Atlantic sources of variability

Atlantic Multidecadal Oscillation The Atlantic Multidecadal Oscillation (AMO) describes fluctuations in sea surface temperatures between the north and equatorial Atlantic which occur on the order of 60–70 years, and feature a warm/cool northern/equatorial Atlantic in the positive AMO phase and the opposite pattern in the negative phase (Schlesinger and Ramankutty 1994; Kerr 2000). The AMO is most often defined as an area averaged, detrended, 10-year low-pass filtered time-series of north Atlantic SSTs, which allow the low-frequency character to be separated from seasonal to interannual SST fluctuations which can be introduced by atmospheric forcing (Schlesinger and Ramankutty 1994; Enfield et al. 2001). However, we note that there are different methods to detrend SSTs and thus quantify the AMO in the observational records (Frankignoul et al. 2017). While calculation methods can slightly affect the magnitudes of observed AMO, the timing of observation-based AMO phase shifts is relatively insensitive to calculation methods (Enfield and Cid-Serrano 2010). Here we use the traditional AMO index as defined by Enfield et al. (2001) because it is relatively convenient to use (Zhang et al. 2019) and well documented by NOAA’s Earth System Research Laboratory. Many studies have focused on quantifying the various climatic impacts stemming from the AMO. For example, McCabe et al. (2004) found that the positive phase of the AMO increased the probability for 20-year drought frequency across most of CONUS, but in particular the southwest and Great Lakes regions. Enfield et al. (2001) found that the Mississippi River outflow and the Lake Okeechobee (Florida) inflow vary by 10% and 40% respectively between the positive and negative phases of the AMO with the seasonal correlation with precipitation highest in the summer. Further, they found that the precipitation patterns associated with ENSO are also affected by the AMO phase, motivating the need for a joint analysis among these two modes of variability.

A time series of the AMO is available from NOAA’s Earth System Research Laboratory (https://www.esrl.noaa.gov/psd/data/timeseries/AMO/) based on the monthly Kaplan sea surface temperature (SST) data set. Specifically, the AMO is calculated as the area-weighted average SST anomaly over the North Atlantic ocean (approximately 0$^\circ$ N to 70$^\circ$ N) with the climate change signal removed by detrending the averaged SST data.

North Atlantic Oscillation The North Atlantic Oscillation (NAO) is an internal mode of atmospheric variability describing a meridionally oriented dipole pressure pattern centered over the north Atlantic ocean (Hurrell et al. 2003). The NAO is often quantified using a station-based difference in sea level pressures over the north Atlantic or a regionally defined EOF analysis. Results of the EOF-based description typically yield the NAO as the first leading mode of variability of sea-level pressures (or other levels) in the northern hemisphere (Hurrell and Deser 2010; Nigam and Baxter 2015). Regardless of how the NAO is defined, results indicate that there is no preferred timescale on which the NAO varies and thus the NAO can show a large amount of seasonal variability as well as interannual and decadal variability (Hurrell and Deser 2010). Due to its center of action over the north Atlantic, the NAO’s strongest climatological impacts affect Europe, in the same way the PNA center of action being over the Pacific primarily affects North America. However, studies have shown that the NAO can have notable impacts across North America, particularly from the central US to the eastern seaboard. For example, the negative NAO phase is associated with anomalous northerly flow over the eastern US and lower atmospheric pressures conducive to increased storminess (Wallace and Gutzler 1981; Hurrell 1995). Similarly, Hartley and Keables (1998) found that the negative phase of the NAO can drive exceptionally high snowfall totals during New England winters.

NAO index values (from Jones et al. 1997) were obtained from the web site of the Climate Research Unit (CRU) of the University of East Anglia (https://crudata.uea.ac.uk/cru/data/nao/), which provides monthly values from 1821 to present.

2.2.3 Long-term secular trends

The natural logarithm of atmospheric carbon dioxide concentration is chosen as a physically-based covariate for describing long-term secular trends in the distribution of mean and extreme precipitation due to the radiative forcing of the climate system by anthropogenic greenhouse gases. As has been well-established since the seminal work by Arrhenius (1897), the radiative forcing by and global mean temperature response to increasing CO${}_2$, the primary anthropogenic greenhouse gas (IPCC 2013), is proportional to the logarithm of the concentration of CO${}_2$ (Etminan et al. 2016). Globally-averaged or local surface temperature is another covariate commonly used to quantify changes in seasonal precipitation. However, temperature-based covariates include both natural and anthropogenic forcings, while atmospheric $\hbox {CO}_2$ reflects a purely human influence. Since we explicitly include a set of natural modes of variability in the analysis, it makes more sense to characterize trends via a covariate that isolates the anthropogenic effect on the global climate system.

The measurements of atmospheric carbon dioxide ($\hbox {CO}_2$) concentrations are a combined time series of data used as input for climate models (from the International Institute for Applied Systems Analysis or IIASA; see https://tntcat.iiasa.ac.at/RcpDb) and the record from the Mauna Loa Observatory (MLO). The MLO measurements are the most widely used data set of $\hbox {CO}_2$ concentrations, but unfortunately these measurements begin in 1958. The IIASA values, on the other hand, cover a much longer record (starting in 1765) and are also based on observations, although the IIASA only provides annually averaged measurements. The annually-averaged MLO time series and the IIASA values are almost identical for their overlapping period (with a Pearson correlation of $>0.99$), and so we use the IIASA values for 1900–1957 and the arithmetic mean of the two time series for 1958–2017. Note that unlike the other indices, which consider seasonal average time series, for $\hbox {CO}_2$ we use the same annual time series for each seasonal analyses.

2.2.4 Other sources of variability

Arctic oscillation (AO). The AO is defined as the non-seasonal leading EOF mode of sea level pressures poleward of 20$^\circ$ N (Thompson and Wallace 2000). The AO positive phase features negative surface pressure anomalies and enhanced westerly winds creating a strong polar vortex. The negative AO phase results in the opposite pattern thereby leading to a weak polar vortex, which is associated with cold air outbreaks where cold polar air masses can more easily advect south to the midlatitudes. In addition to the AO causing surface temperature impacts, it is also associated with precipitation impacts as well. Guan and Waliser (2015) found that during the AO negative phase, wintertime atmospheric river (AR) frequency is enhanced in the subtropical Pacific offshore of the western US, in turn driving increased AR related precipitation in California. Further, during the negative AO phase, increased summertime precipitation occurs throughout the central US due to an equatorward shift of the eddy driven jet (Hu and Feng 2010).

Measurements of the Arctic oscillation are available from NOAA’s National Centers for Environmental Information (https://www.ncdc.noaa.gov/teleconnections/ao/), but unfortunately the measurements are only provided from January, 1950 to present. To obtain measurements for the first part of the 20th century, we use the AO index calculated from the 20th Century Reanalysis version 1 (20CR; from https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Plot/) which covers 1871–2012. The monthly time series from these two data sources show strong agreement during their overlapping time periods (with a correlation of 0.987). The final monthly time series used in this analysis consists of the 20CR time series for 1900–1949, the arithmetic mean of the 20CR and NOAA time series for 1950–2012, and the NOAA time series for 2013–2017.

Stratospheric aerosol optical depth due to volcanoes (vSAOD) Volcanic eruptions are a highly intermittent but important type of variability that affect global precipitation patterns. By introducing reflective aerosols into the stratosphere that persist for several years, volcanic eruptions reduce the amount of sunlight absorbed by the climate system, cool the Earth’s surface, and thereby reduce the energy available for evaporation (Robock 2000). The resulting reduction in global land precipitation and increased incidence of droughts have been detected for volcanic eruptions during the 20th century (Gillett et al. 2004; Lambert et al. 2005) including the most recent major eruption by Mt. Pinatubo in 1991 (Trenberth and Dai 2007). The appropriate index to characterize the radiative forcing and resulting reduction in global mean surface temperature is the aerosol optical depth (AOD), a unitless measure of the amount of light reflected by stratospheric aerosols. For the AODs$< 1$ typical of volcanic eruptions, to a good approximation the reduction in sunlight is proportional to AOD.

For the first part of the historical record, we utilize the AOD data set from Sato et al. (1993) which provides measurements of global monthly mean AOD at 550nm from January, 1850 to October, 2012 (data accessed from https://data.giss.nasa.gov/modelforce/strataer/). A more up-to-date time series of volcanic SAOD is provided by Schmidt et al. (2018) and Mills et al. (2016) (data provided via personal communication with Dr. Anja Schmidt), which covers January, 1975 to December, 2015. Finally, for the last 2 years (2016–2017), we use a constant measurement of 0.004, because in recent years the global average is approximately 0.004 (Schmidt et al. 2018; Friberg et al. 2018) and the volcanic activity in 2016 and 2017 has been at similar levels as the previous years. As with the other indices, we take the arithmetic mean of the monthly time series for the overlapping time window (January, 1979 to October, 2012).

3 Statistical methods

3.1 Spatial extreme value analysis

We now outline a framework for characterizing changes over time in the climatology of extreme precipitation, as well as quantifying uncertainty and determining statistical significance. The core of the methodology used here is the spatial extreme value analysis outlined in Risser et al. (2019b), which enables a characterization of the spatially-complete climatology of extreme precipitation based on measurements from irregularly observed weather stations. Two features are novel about this approach: first, one can estimate the distribution of extreme precipitation even for locations where no in situ measurements are available; second, the analysis can be applied even for a large network of weather stations over a heterogeneous spatial domain like CONUS, which is critical for the results in this paper. Furthermore, the underlying Gaussian process models provide a natural method for resolving the information provided by a set of in situ measurements to their native scales (i.e., a high-resolution grid) in such a way that the spatial length scale of the interpolation varies across the geographic domain (i.e., we use a second-order nonstationary covariance function; see Risser 2016).

For a full description of the methodology used, we refer the reader to Risser et al. (2019b). (Note that all of the following is applied separately to each 3-month season.) In summary, the method consists of two steps: first, one obtains estimates of the climatological features of extreme precipitation in each season based on measurements from an individual weather station using the generalized extreme value (GEV) family of distributions. When considering the approximately 90 daily measurements in a given season, the cumulative distribution function (CDF) of $Y_t(\mathbf{s})$ (which is the seasonal maximum daily precipitation measurement in year t at station $\mathbf{s}$) can be well-approximated by a member of the GEV family

$$\begin{aligned} G_{\mathbf{s}, t}(y) \equiv {P}(Y_t(\mathbf{s}) \le y) = \exp \left\{ -\left[ 1 + \xi _t(\mathbf{s})\left( \frac{y - \mu _t(\mathbf{s})}{\sigma _t(\mathbf{s})}\right) \right] ^{-1/\xi _t(\mathbf{s})} \right\} \end{aligned}$$

(1)

(Coles et al. 2001, Theorem 3.1.1, page 48), defined for $\{ y: 1 + \xi _t(\mathbf{s})(y - \mu _t(\mathbf{s}))/\sigma _t(\mathbf{s}) > 0 \}$. The GEV family of distributions (1) is characterized by three space-time statistical parameters: the location parameter $\mu _t(\mathbf{s}) \in {\mathcal {R}}$, which describes the center of the distribution; the scale parameter $\sigma _t(\mathbf{s})>0$, which describes the spread of the distribution; and the shape parameter $\xi _t(\mathbf{s}) \in {\mathcal {R}}$. The shape parameter $\xi _t(\mathbf{s})$ is the most important for determining the qualitative behavior of the distribution of daily rainfall at a given location. If $\xi _t(\mathbf{s})<0$, the distribution has a finite upper bound; if $\xi _t(\mathbf{s}) >0$, the distribution has no upper limit; and if $\xi _t(\mathbf{s}) = 0$, the distribution is again unbounded and the CDF (1) is interpreted as the limit $\xi _t(\mathbf{s}) \rightarrow 0$ (Coles et al. 2001).

Technically, the GEV distribution is only the asymptotic (limiting) distribution for the sample maximum as the block size approaches infinity. In practice, of course, one has finite sample sizes, and in a block maxima framework there is a fundamental tradeoff between small block sizes (resulting in increased bias but smaller variance) and large block sizes (leading to a better approximation but larger variance). In this work, we choose seasonal blocks of approximately 90 measurements; however, a 90-day season may have many fewer “independent” measurements of precipitation, due to either zero rainfall days, missing data, or the temporal autocorrelation innate to a time series of daily weather. When limiting oneself to return periods well within the range of the data (we later consider 10-year return values, which satisfies this criteria), Risser et al. (2019a) (Appendix C) verify that the GEV approximation is appropriate for seasonal maxima, in the sense that the bias is small and the bootstrap uncertainties are well-calibrated, even when the number of independent measurements of daily precipitation in a season is quite small.

While many studies subset the observational record to focus on years with a specific phase of a climate variability index (e.g., the composite analysis in Zhang et al. 2010), we instead utilize the entire observational record to both include all phases of each index and also disentangle the joint relationships between the various indices and extreme precipitation. Our approach to relating year-to-year changes in the seasonal CDF of extreme precipitation to the candidate set of climate variability indices identified in Sect. 2 (and similar to the analyses in Zhang et al. 2010; Risser and Wehner 2017) is to explicitly model changes in the GEV parameters as varying according to $\log$ $\hbox {CO}_2$, ELI, AO, PNA, vSAOD, AMO, and NAO. In what follows, we assume that the center of the extreme value distribution changes linearly with these modes of variability while the scale and shape parameters are fixed over time; all quantities vary spatially over the domain. In other words, we assume

$$\begin{aligned} \mu _t(\mathbf{s})= & {} \mu _0(\mathbf{s}) + \mu _1(\mathbf{s}) [\log \text {CO}_2]_t + \mu _2(\mathbf{s}) [\text {ELI}]_t + \mu _3(\mathbf{s}) [\text {AO}]_t \nonumber \\&+ \mu _4(\mathbf{s}) [\text {NAO}]_t + \mu _5(\mathbf{s}) [\text {PNA}]_t + \mu _6(\mathbf{s}) [\text {AMO}]_t + \mu _7(\mathbf{s}) [\text {vSAOD}]_t, \nonumber \\ \sigma _t(\mathbf{s})= & {} \sigma (\mathbf{s}), \nonumber \\ \xi _t(\mathbf{s})= & {} \xi (\mathbf{s}), \end{aligned}$$

(2)

where $[\text {X}]_t$ indicates the measurement of index X in year t. We henceforth refer to $\mu _0(\mathbf{s})$, $\{\mu _j(\mathbf{s}): j = 1, \dots , 7\}$, $\sigma (\mathbf{s})$, and $\xi (\mathbf{s})$ as the climatological coefficients for location $\mathbf{s}$, as these values describe the climatological distribution of extreme precipitation in each year. Note that modeling changes in the center of the GEV distribution in this way is related to multiple (mean) regression. While statistically modeling the shape parameter as a constant over time is common (e.g., Cooley et al. 2007; Risser and Wehner 2017), we choose to also model the scale parameter as constant over time (unlike Zhang et al. 2010). The various climate variability indices clearly may influence the width of the GEV distribution for some parts of CONUS; however, overall there is a “degrees of freedom” consideration wherein adding statistical parameters to an analysis with a fixed amount of data results in a loss of efficiency in estimation. Furthermore, related attribution studies opt for a more parsimonious representation that does not attempt to characterize changes in the GEV scale parameter (Min et al. 2011; Westra et al. 2013; Zhang et al. 2013). To specifically assess the choice of how to model the scale parameter, we conducted a sensitivity analysis wherein the scale was allowed to change log-linearly with all the climate drivers. We then assessed the quality of this statistical model versus the constant scale model as defined in Eq. (2) via the Akaike Information Criteria (AIC), which is a metric for determining which statistical model best describes variability in observed data, as well as the proportion of variance explained (see Sect. 3.3). The results are shown in Table D.1; overall, the constant scale statistical model is better in terms of AIC, and also explains essentially the same amount of variability. Therefore, we choose to focus on changes in the center of the GEV distribution in this analysis.

Once we have estimated the climatological coefficients independently at each station, the second step of our analysis is to apply a spatial statistical approach using second-order nonstationary Gaussian processes to infer the underlying climatology over a fine grid via kriging. This approach is applied to each climatological coefficient separately and yields gridded fields of best estimates of the climatological coefficients, denoted

$$\begin{aligned} \Big \{ {\widehat{\mu }}_0(\mathbf{g}), \{{\widehat{\mu }}_j(\mathbf{g}): j = 1, \dots , 7\}, {\widehat{\sigma }}(\mathbf{g}), {\widehat{\xi }}(\mathbf{g}) : \mathbf{g}\in {\mathcal {G}} \Big \}, \end{aligned}$$

(3)

where ${\mathcal {G}}$ is the $0.25^\circ$ grid of $M=13073$ grid cells over CONUS. These gridded estimates summarize the information contained in the seasonal maxima regarding their relationship with the various climate indices and present this information at the native scales of precipitation extremes (i.e., at a high resolution). While the coefficients $\{{\widehat{\mu }}_j(\mathbf{g}): j = 1, \dots , 7\}$ could be used to infer the strength of the relationship between each index and extreme precipitation, we instead quantify how each index individually influences the distribution of extremes in two ways: first, by exploring differences in 10-year return values (following, e.g., Risser et al. 2019a), and second, by exploring changes in the return probability of a fixed magnitude event (i.e., the risk ratio; see for example Risser and Wehner 2017). These two metrics evaluate changes in the magnitude and frequency, respectively, of extreme events, and provide useful insights in to how the climate indices influence extremes. We now provide further details on each analysis.

For the first comparison, we compare estimated return values for a large versus small value of an individual climate index while holding all other indices constant. In other words, we use the fitted statistical model and best estimates in Eq. (3) to construct artificial climate “scenarios” by plugging in the desired climate index values. Let $\mathbf{X}_{k-}$ and $\mathbf{X}_{k+}$ represent vectors of climate index values where index $k \in \{\text {ELI}, \text {AO}, \text {NAO}, \text {PNA}, \text {AMO}, \text {vSAOD}\}$ is set to its seasonal 5th and 95th climatological value (over the entire 1900–2017 period), respectively, and all other indices are fixed at their seasonal climatological mean; this isolates the effect of an individual driver while simultaneously accounting for variability in precipitation due to all other drivers in the analysis. The change in return value of interest for index k at grid cell $\mathbf{g}$ is denoted

$$\begin{aligned} \varDelta _k(\mathbf{g}) = {w_\mathbf{g}(\mathbf{X}_{k+})} - {w_\mathbf{g}(\mathbf{X}_{k-})}, \end{aligned}$$

(4)

where $w_\mathbf{g}(\mathbf{X}_{(\cdot )})$ is the 10-year return value at grid cell $\mathbf{g}$ when the climate indices are fixed at the conditions specified by $\mathbf{X}_{(\cdot )}$. The return value specifies that the seasonal Rx1Day will exceed $w_\mathbf{g}(\mathbf{X}_{(\cdot )})$ once every 10 years, on average; so, $\varDelta _k(\mathbf{g})$ describes how the magnitude of a fixed probability extreme daily event changes based on individual drivers. Given the form of the CDF in (1), we can write down a formula for our best estimate of the return period ${\widehat{w}}_\mathbf{g}(\mathbf{X}_{(\cdot )})$ in terms of the best estimates of the climatological coefficients from (3):

$$\begin{aligned} {\widehat{w}}_\mathbf{g}(\mathbf{X}_{(\cdot )}) = \left\{ \begin{array}{ll} {\widehat{\mu }}_{\mathbf{X}_{(\cdot )}}(\mathbf{g}) - \frac{{\widehat{\sigma }}(\mathbf{g})}{{\widehat{\xi }}(\mathbf{g})}\big [1 - \{-\log (1-1/10)\}^{-{\widehat{\xi }}(\mathbf{g})}\big ], &{} {\widehat{\xi }}(\mathbf{g}) \ne 0 \\ {\widehat{\mu }}_{\mathbf{X}_{(\cdot )}}(\mathbf{g}) - {\widehat{\sigma }}(\mathbf{g}) \log \{-\log (1-1/10)\}, &{} {\widehat{\xi }}(\mathbf{g}) = 0, \end{array} \right. \end{aligned}$$

(5)

(Coles et al. 2001), where ${\widehat{\mu }}_{\mathbf{X}_{(\cdot )}}(\mathbf{g})$ is the estimated location parameter from (2) using the best estimates from (3) evaluated at the conditions specified by $\mathbf{X}_{(\cdot )}$.

For the second comparison, we use the so-called risk ratio to summarize how each index individually influences the probability of a fixed magnitude extreme event. The risk ratio is actually a ratio of probabilities, each of which describes the likelihood of a fixed event occurring in a particular climate scenario; the risk ratio is often used in event attribution studies to compare a world with anthropogenic influences (e.g., greenhouse gas emissions) versus a world without these forcings (National Academies of Sciences et al. 2016). Instead, we use the risk ratio as a way to compare the probabilities of experiencing an extreme precipitation event for a large versus small value of an individual climate index while holding all other indices constant; again, this isolates the effect of an individual driver while simultaneously accounting for variability in precipitation due to all other drivers in the analysis. As before, we use vectors of climate index values $\mathbf{X}_{k-}$ and $\mathbf{X}_{k+}$ to summarize high versus low values of index k; the risk ratio for index k at grid cell $\mathbf{g}$ is then

$$\begin{aligned} RR_k(\mathbf{g}) = \frac{p_\mathbf{g}(\mathbf{X}_{k+}, {\overline{w}}_\mathbf{g})}{p_\mathbf{g}(\mathbf{X}_{k-}, {\overline{w}}_\mathbf{g})}, \end{aligned}$$

(6)

where $p_\mathbf{g}(\mathbf{X}_{(\cdot )}, {\overline{w}}_\mathbf{g})$ is the probability of the seasonal maxima exceeding a threshold ${\overline{w}}_\mathbf{g}$ at grid cell $\mathbf{g}$ when the climate indices are fixed at the conditions specified by $\mathbf{X}_{(\cdot )}$. If $RR_k(\mathbf{g})>1$, this means that an extreme event is more likely for large values of index k; if $RR_k(\mathbf{g})<1$, this means that an extreme event is more likely for small values of index k. If $RR_k(\mathbf{g}) =1$, then an extreme event is equally likely for small and large values of index k, implying that the influence of index k on extreme precipitation is negligible. Given that $p_\mathbf{g}(\mathbf{X}_{(\cdot )}, {\overline{w}}_\mathbf{g})$ is the inverse of the return period, we can write down a formula for our best estimate of the return probability ${\widehat{p}}_\mathbf{g}(\mathbf{X}_{(\cdot )}, {\overline{w}}_\mathbf{g})$ in terms of the best estimates of the climatological coefficients from (3):

$$\begin{aligned} {\widehat{p}}_\mathbf{g}(\mathbf{X}_{(\cdot )}, {\overline{w}}_\mathbf{g}) = \left\{ \begin{array}{ll} 1 - \exp \left\{ - \big [1- {\widehat{\xi }}(\mathbf{g})({\widehat{\mu }}_{\mathbf{X}_{(\cdot )}}(\mathbf{g}) - {\overline{w}}_\mathbf{g})/{\widehat{\sigma }}(\mathbf{g}) \big ]^{-1/{\widehat{\xi }}(\mathbf{g})} \right\} , &{} {\widehat{\xi }}(\mathbf{g}) \ne 0, \\ 1 - \exp \left\{ - \exp \big \{ ({\widehat{\mu }}_{\mathbf{X}_{(\cdot )}}(\mathbf{g}) - {\overline{w}}_\mathbf{g})/{\widehat{\sigma }}(\mathbf{g}) \big \} \right\} , &{} {\widehat{\xi }}(\mathbf{g}) = 0 \end{array} \right. \end{aligned}$$

(7)

(Coles et al. 2001), where again ${\widehat{\mu }}_{\mathbf{X}_{(\cdot )}}(\mathbf{g})$ is the estimated location parameter from (2) using the best estimates from (3) evaluated at $\mathbf{X}_{(\cdot )}$. The threshold ${\overline{w}}_\mathbf{g}$ in (7) depends on location; for this value we use the climatological 10-year return value:

$$\begin{aligned} {\overline{w}}_\mathbf{g}= \left\{ \begin{array}{ll} {\widehat{\mu }}_{\overline{\mathbf{X}}} - \frac{{\widehat{\sigma }}(\mathbf{g})}{{\widehat{\xi }}(\mathbf{g})}\big [1 - \{-\log (1-1/10)\}^{-{\widehat{\xi }}(\mathbf{g})}\big ], &{} {\widehat{\xi }}(\mathbf{g}) \ne 0 \\ {\widehat{\mu }}_{\overline{\mathbf{X}}} - {\widehat{\sigma }}(\mathbf{g}) \log \{-\log (1-1/10)\}, &{} {\widehat{\xi }}(\mathbf{g}) = 0, \end{array} \right. \end{aligned}$$

where $\overline{\mathbf{X}}$ is a vector of the 1900-2017 average climate index values. In other words, ${\overline{w}}_\mathbf{g}$ represents a “typical” 10-year event over 1900-2017 at each spatial location $\mathbf{g}$.

While we have included the natural logarithm of $\hbox {CO}_2$ in (2) to account for long-term secular trends in the distribution of extreme precipitation, in this paper we focus on characterizing the natural variability due to the other climate indices considered and specifically do not explore changes in return values for the effect of anthropogenic climate change (as is done in, e.g., Risser and Wehner 2017). Given that there are non-negligible trends in extreme precipitation over the past several decades (Hartmann et al. 2013; Donat et al. 2016; Papalexiou and Montanari 2019; Kunkel 2003; Easterling et al. 2017) it is important to account for long-term trends in our statistical model. A thorough analysis of the anthropogenic influence on extreme precipitation in this framework is presented in Part II of this methodology (Risser et al., “Quantifying the influence of anthropogenic forcing on in situ measurements of seasonal and extreme daily precipitation”, in prep.).

The best estimates of the climatological coefficients in (3) fully specify our best estimates of the change in return values, ${\widehat{\varDelta }}_k(\mathbf{g})$, as well as the risk ratios, ${\widehat{RR}}_k(\mathbf{g})$, for $k \in \{\text {ELI}, \dots , \text {vSAOD}\}$ (and separately for each season). However, we still need to quantify uncertainty in these estimates and conduct a hypothesis test at each grid cell, which furthermore involves accounting for the multiplicity in testing. For each of these components we utilize methodology from Risser et al. (2019a): the block bootstrap is used to quantify uncertainty in the estimated change in return values; a reshuffling or permutation approach is used to conduct hypothesis testing; and a variant of the Benjamini and Hochberg (1995) procedure (described in Risser et al. 2019a) is used to account for multiplicity in testing. One slight variation on the hypothesis testing procedure should be noted: in this analysis, we actually set out to determine the significance of each individual climate variability index (unlike Risser et al. 2019a, who seek to determine significant overall trends). In other words, for $k \in \{\text {ELI}, \dots , \text {vSAOD}\}$, the hypotheses of interest are

$$\begin{aligned} H_0(\mathbf{g}): \varDelta _k(\mathbf{g}) = 0 \quad \text {vs.} \quad H_1(\mathbf{g}): \varDelta _k(\mathbf{g}) \ne 0 \end{aligned}$$

(8)

for the change in return values and

$$\begin{aligned} H_0(\mathbf{g}): RR_k(\mathbf{g}) = 1 \quad \text {vs.} \quad H_1(\mathbf{g}): RR_k(\mathbf{g}) \ne 1 \end{aligned}$$

(9)

for the risk ratios. For index k, the null distribution for both (8) and (9) is obtained by reshuffling the index values over 1900 to 2017 (which breaks any relationship between the index and extreme precipitation) but maintaining the original values of all other indices (maintaining any residual relationship between the other indices and extreme precipitation). In this way, we can isolate the influence of index k and generate the correct null distribution. As in Risser et al. (2019a), we determine the statistical pointwise significance of the risk ratios for both “low” (i.e., controlling the rate of false discoveries at $q = 0.33$) and “high” (i.e., controlling the rate of false discoveries at $q = 0.1$) confidence statements. These thresholds for significance are chosen as reasonable limits for bounding the proportion of type I errors, with $q = 0.33$ yielding a less conservative statement and $q = 0.1$ yielding a more conservative statement.

3.2 Spatial analysis of seasonal total precipitation

A parallel analysis is conducted to similarly identify the time-varying climatology of seasonal mean precipitation. Define $Z_t(\mathbf{s})$ to be the average daily precipitation rate (mm $\hbox {day}^{-1}$) in year t at station $\mathbf{s}\in {\mathcal {S}}$; then, using a multiple regression framework, we can statistically model

$$\begin{aligned} Z_t(\mathbf{s})= & {} \beta _0(\mathbf{s}) + \beta _1(\mathbf{s}) [\log CO_2]_t + \beta _2(\mathbf{s}) [\text {ELI}]_t + \beta _3(\mathbf{s}) [\text {AO}]_t \nonumber \\&+ \beta _4(\mathbf{s}) [\text {NAO}]_t + \beta _5(\mathbf{s}) [\text {PNA}]_t + \beta _6(\mathbf{s}) [\text {AMO}]_t + \beta _7(\mathbf{s}) [\text {vSAOD}]_t + \varepsilon _t(\mathbf{s}), \end{aligned}$$

(10)

where $\beta _0(\mathbf{s})$ is an intercept term that describes the average precipitation rate when all of the indices are fixed at zero, the $\{ \beta _j(\mathbf{s}): j = 1, \dots , 7\}$ are regression coefficients that describe changes in the mean precipitation rate, and $\varepsilon _t(\mathbf{s})$ is an error term assumed to be temporally independent and identically distributed as Gaussian with mean zero and variance $\tau ^2(\mathbf{s})$, i.e., $\varepsilon _t(\mathbf{s}) {\mathop {\sim }\limits ^{\text {iid}}}N(0, \tau ^2(\mathbf{s}))$. Applying a similar analysis as Risser et al. (2019b) to the seasonal mean precipitation rate, we can again first estimate the regression coefficients at each station and then apply the same spatial statistical model to resolve best estimates of the coefficients over a high-resolution $0.25^\circ$ grid over CONUS. As with the extremes analysis, we conducted a sensitivity analysis wherein the residual error standard deviation $\tau (\mathbf{s})$ was allowed to change log-linearly with all the climate drivers and then assessed the quality of this statistical model versus the constant error variance model as defined in Eq. (10) via the Akaike Information Criteria (AIC) and the proportion of variance explained (see Sect. 3.3). The results are also shown in Table D.1; overall, the constant residual error standard deviation statistical model is better in terms of AIC, and also explains essentially the same amount of variability. Therefore, we maintain the constant error model for the remainder of this analysis.

As with the extremes analysis, while we could use the estimated coefficients $\{{\widehat{\beta }}_j(\mathbf{g}): j = 1, \dots , 7; \mathbf{g}\in {\mathcal {G}}\}$ to summarize the various relationships, we instead quantify the change in seasonal totals for a large versus small value of each index while holding all other indices constant. In other words, we again use the results to construct “statistical” climate scenarios by plugging in the desired climate index values. Again let $\mathbf{X}_{k-}$ and $\mathbf{X}_{k+}$ represent vectors of climate index values where index $k \in \{\text {ELI}, \dots , \text {vSAOD}\}$ is set to its seasonal 5th and 95th climatological value (i.e., over the entire record), respectively, and all other indices (including the $\hbox {CO}_2$) are fixed at their seasonal climatological mean. Our best estimate of the seasonal total for the statistical climate scenario defined by $\mathbf{X}_{(\cdot )}$ at grid cell $\mathbf{g}$ is ${{\widehat{m}}_\mathbf{g}(\mathbf{X}_{(\cdot )})} = \mathbf{X}_{(\cdot )} {\widehat{{\varvec{\beta }}}}(\mathbf{g})$, where ${\widehat{{\varvec{\beta }}}}(\mathbf{g}) = \big ({\widehat{\beta }}_0(\mathbf{g}), \dots , {\widehat{\beta }}_7(\mathbf{g})\big )$, and we quantify the change in seasonal totals using a simple difference:

$$\begin{aligned} {\widehat{\theta }}_k(\mathbf{g}) = {\widehat{m}}_\mathbf{g}(\mathbf{X}_{k+}) - {\widehat{m}}_\mathbf{g}(\mathbf{X}_{k-}). \end{aligned}$$

(11)

Our hypotheses of interest are now

$$\begin{aligned} H_0(\mathbf{g}): \theta _k(\mathbf{g}) = 0 \quad \text {vs.} \quad H_1(\mathbf{g}): \theta _k(\mathbf{g}) \ne 0, \end{aligned}$$

which we can test using a similar reshuffling or permutation framework as described in Sect. 3.1 to quantify uncertainty, ascribe statistical significance, and account for multiplicity in testing.

3.3 Proportion of variance explained

In spite of the fact that we have carefully chosen a candidate set of seven climate variability indices to explore in this paper, the point remains that the global climate system has many more degrees of freedom for year-to-year variability seasonal mean and extreme precipitation than explained by the indices considered here. As such, it is important to quantify the proportion of variability explained by the statistical models specified by (2) and (10). For the seasonal mean analysis using multiple regression, it is straightforward to summarize this quantity using the usual $R^2$, defined for each station $\mathbf{s}\in {\mathcal {S}}$ as $R^2(\mathbf{s}) = 1 - {SSE(\mathbf{s})}/{SST(\mathbf{s})}$, where

$$\begin{aligned} SST(\mathbf{s}) = \sum _{t=1}^T \left( Z_t(\mathbf{s}) - \frac{1}{T}\sum _{t=1}^T Z_t(\mathbf{s}) \right) ^2 \end{aligned}$$

is the total sum of squares (total variability) in the seasonal mean precipitation and

$$\begin{aligned} SSE(\mathbf{s}) = \sum _{t=1}^T \left( Z_t(\mathbf{s}) - {\widehat{Z}}_t(\mathbf{s})\right) ^2 \end{aligned}$$

is the sum of squared error between the data ($Z_t(\mathbf{s})$) and the predicted seasonal mean (${\widehat{Z}}_t(\mathbf{s})$) from the statistical model given by (10). For the GEV analysis, we can instead use a likelihood-ratio based metric of $R^2$ (Magee 1990), defined for each station $\mathbf{s}\in {\mathcal {S}}$ as

$$\begin{aligned} R^2_\text {LR}(\mathbf{s}) = 1 - \exp \left\{ -\frac{2}{T} \log [{\widehat{L}}_N(\mathbf{s})/{\widehat{L}}_S(\mathbf{s})] \right\} , \end{aligned}$$

where ${\widehat{L}}_N(\mathbf{s})$ is the GEV likelihood for the nonstationary model defined in (2) and ${\widehat{L}}_S(\mathbf{s})$ is the GEV likelihood for a stationary model fit to the same seasonal maxima. We use the smoothed coefficients to calculate both $R^2$ values given that we have a moderate number of covariates for a relatively small data set (at most $T=118$ years) and using the independently estimated coefficients would likely result in inflated $R^2$ from overfitting the data. For the seasonal mean and extreme analyses, we actually calculate $R^2$ values for the “full” models (2) and (10) as well as individual driver models. This allows us to get a sense of the variability explained by each individual driver as well as the full statistical model.

4 Results

Fig. 1

Best estimates of the change in the magnitude of 10-year return values for daily precipitation (mm) for high versus low values of each climate index across each season. Green values indicate locations where extremes are larger for large/positive values of the index; brown values indicate locations where extremes are larger for small/negative values of the index. The hatching indicates statistical significance of the change. Note: the AO is excluded from the DJF analysis due to its strong coupling (and high correlation) with the NAO

Rather than discuss the seasonal mean and extreme relationships one by one, we instead focus on how our methodology provides new insights into quantifying relationships between climate drivers and precipitation. First, in Sect. 4.1, we summarize and discuss variability explained in the underlying precipitation data by the statistical analysis of responses to climate variability modes. Then, recall that in Sect. 1 we identified two limitations of related papers that explore relationships between observed precipitation and climate variability indices: (a) conducting single-station analyses, and (b) using composite analyses. In Sects. 4.2 and 4.3, respectively, we specifically identify how our methodology improves upon these two limitations and yields unique value-added information, including results that quantify the ways in which the relationships between climate drivers and precipitation are more complicated than might have been expected.

Maps of the relationships between each climate driver and seasonal precipitation for all seasons, indices, and metrics (mean and extreme), including significance, are shown in Figs. 1, 2, and 3 . The seasonal 5th and 95th percentile index values used to create the maps are given in Table D.2. Figure 1 shows the isolated change in the magnitude of 10-year return values for daily precipitation (given in mm) for each index as quantified by (4); Fig. 2 shows the isolated multiplicative change in the probability of the climatological 10-year return value (i.e., the risk ratio), specific to each index, as quantified by (6); and Fig. 3 shows the isolated change in seasonal total precipitation (mm) for each index as quantified by (11). In Figs. 1 and 3 , green values indicate locations where extremes/means are larger for large/positive values of each index; brown values indicate locations where extremes/means are larger for small/negative values of each index. In Fig. 2, purple values indicate locations where extremes are more likely for large/positive values of each index; red values indicate locations where extremes are more likely for small/negative values of each index.

Fig. 2

Best estimates of the multiplicative change in the probability of the climatological 10-year return value (i.e., the risk ratio; no units) for high versus low values of each climate index across each season. Purple/pink values indicate locations where extremes are more likely for large/positive values of the index; red/yellow values indicate locations where extremes are more likely for small/negative values of the index. The hatching indicates statistical significance of the change. Note: the AO is excluded from the DJF analysis due to its strong coupling (and high correlation) with the NAO

Fig. 3

Best estimates of the change in seasonal total precipitation (mm) for high versus low values of each climate index across each season. Green values indicate locations where seasonal totals are larger for large/positive values of the index; brown values indicate locations where seasonal totals are larger for small/negative values of the index. The hatching indicates statistical significance of the change. Note: the AO is excluded from the DJF analysis due to its strong coupling (and high correlation) with the NAO

4.1 Variability explained by statistical models

The goal of the $R^2$ analysis outlined in Sect. 3.3 is to determine how much of the year-to-year variability in seasonal mean and extreme precipitation from the GHCN record is explained by the modes of variability identified in Sect. 2.2, both collectively (i.e., for the trend models in Eqs. (2) and (10)) and individually (i.e., for trend analyses that only use a single driver; these individual relationships are explicitly not the focus of this paper, but are included for reference). The various $R^2$ values are shown in Table 1 for each season, where the reported numbers are averaged over all $n=2504$ CONUS weather stations. Overall, the proportion of variance explained is higher for the seasonal total analysis relative to the extremes analysis, with the most predictability in DJF and SON. While ELI and PNA generally have the largest variance explained individually, it is noteworthy that the proportion of variance explained is very low for both the individual drivers and the full statistical analysis of responses to climate variability modes. For the seasonal total analysis, between 7 and 11% of the year-to-year variability is explained by our trend model; for the seasonal extremes analysis, just 3–5% of the year-to-year variability is explained. Of course, the variance explained by the modes of variability (individually and collectively) varies over CONUS: for example, the statistical model with all drivers explains over 20% of the variance in DJF seasonal total precipitation in the Ohio and Mississippi River Valleys but less than 3% in the Mountain West (see Fig. C.4 in the Appendix). Nonetheless, the CONUS averages suggest that, overall, a relatively small proportion of year-to-year variability is explained by the chosen set of climate indices.

Table 1 Proportion of variance ($R^2$) explained by each individual climate driver as well as all climate drivers simultaneously for each season, averaged over CONUS, for both the seasonal total (ordinary least squares) analysis and Rx1Day (GEV) analysis

To frame the following discussion, it will be helpful to define two terms that partition the year-to-year variability in seasonal mean and extreme precipitation. First, define driven variability to characterize year-to-year variability due to anthropogenic forcings (e.g., greenhouse gases), other external forcings (e.g., solar or volcanic), and known large-scale modes of climate variability (e.g., ENSO or the PNA). Second, define background variability to be any remaining residual variability not characterized by the aforementioned modes (e.g., due to chaos in the atmosphere). The idea here is that the total year-to-year variability in seasonal mean and extreme precipitation would be the sum of the driven and background variability.

The statistical analyses defined by (2) and (10) assume that the set of drivers considered as inputs to the statistical models (i.e., $\hbox {CO}_2$, ELI, AO, NAO, PNA, AMO, and vSAOD) appropriately characterize the driven variability in precipitation from the GHCN record. In other words, the $R^2$ values for the “All drivers” row of Table 1 are our best estimate of the proportion of driven variability in the observations. The immediate question that arises is: why are these $R^2$ values (7–11% for means and 3–5% for extremes) so small? There are two possible explanations: either we have failed to include one or more drivers/modes of climate variability that, if included in the analysis, would significantly increase the proportion of variance explained (i.e., the proportion of driven variability), or the background variability for seasonal precipitation over CONUS is large enough that it may not be possible to explain more than 5–10% of the total year-to-year variability using indices like the ones considered in this paper.

An analysis of global climate model runs can be used to assess how much of the variability is driven for seasonal mean and extreme precipitation. Specifically, we use an ensemble of AMIP-style (Atmospheric Model Intercomparison Project) climate model simulations from version 5.1 of the Community Atmospheric Model global atmosphere/land climate model, run in its conventional $\approx$1$^{\circ }$ longitude/latitude configuration (Neale et al. 2012; Stone et al. 2018) originally carried out as part of the World Climate Research Programme’s (WCRP) Climate Variability Programme’s (CLIVAR) Climate of the 20th century Plus Project (C20C+). We utilize the historical simulations, which are driven by observed boundary conditions of atmospheric chemistry (greenhouse gases, tropospheric and stratospheric aerosols, ozone), solar luminosity, land use/cover, and the ocean surface (temperature and ice coverage). This set of runs has the same boundary conditions but stochastically perturbed initial conditions. The data and further details on the simulations are available at http://portal.nersc.gov/c20c; we use 41 ensemble members that cover the 55-year period from 01/1959 to 12/2013. The idea is to use these simulations to get a sense of the “true” driven variability in seasonal mean and extreme precipitation.

For the observational analysis described in this paper, we fit real data with a single realization of the temperature-driven indices and a single time-evolving lower boundary condition (the ocean skin temperature). Given this construction, the background variability is dominated by weather and subseasonal synoptic variability in climatic conditions. This observational construction maps naturally onto the CAM5.1 AMIP-style runs, where likewise the within-year variability has a single realization of the SST boundary condition, a single realization of temperature-driven indices, and by design the in-year variability across the ensemble is entirely associated with variability introduced by ${\mathcal {O}}(\varepsilon )$ perturbations to the initial conditions amplified by inherent atmospheric chaos. As such, these simulations provide a test bed for determining the magnitude of driven variability in precipitation by comparing the variability across all years to the variability across realizations for a single year. To quantify the driven/background variability, for each CAM5.1 grid cell over CONUS we calculate two quantities for seasonal total and Rx1Day:

$$\begin{aligned} V_\text {B} = \frac{1}{55} \sum _{t=1}^{55} V_{\text {B},t}, \quad V_\text {T} = \frac{1}{41} \sum _{e=1}^{41} V_{\text {T},e}, \end{aligned}$$

where $V_{\text {B},t}$ is the within-year variance of all ensemble members in year t and $V_{\text {T},e}$ is the across-year variance in ensemble member e. As the subscripts suggest, $V_{\text {B},t}$ quantifies the background variability, i.e., that which is not forced by SST, aerosol, sea ice, CO${}_{2}$ variability (because the these boundary conditions are the same in each year) and any other external forcing, while $V_{\text {T},e}$ quantifies both driven and background variability. Averaging over all years (for $V_\text {B}$) and ensemble members (for $V_\text {T}$) allows us to approximate the proportion of driven variability in seasonal precipitation as simulated by this model, as

$$\begin{aligned} R_M^2 = 1 - \frac{V_\text {B}}{V_\text {T}}, \end{aligned}$$

(here the notation suggest a model-based estimate of the proportion of driven variability), where we set $R_M^2 = 0$ if ${V_\text {B}}/{V_\text {T}}>1$. As with the $R^2$ values in Table 1, we then average over all CONUS grid cells; see Table 2. For the variance-based $R_M^2$ calculations, the proportion of driven variability is roughly 5–9% for seasonal total precipitation and 2–3% for seasonal Rx1Day, which is consistent with the observational results in Table 1. The $R^2_M$ values are roughly the same if we instead calculate the background and total variability using the interquartile range (IQR; the IQR is a more robust measure of variability when the underlying data are highly skewed, as is the case with seasonal precipitation). Note that these results are consistent with those in Dittus et al. (2018), who also use the C20C+ ensemble to explore the proportion of variance explained by ocean forcing in temperature and precipitation extremes (see Figure 2 of Dittus et al. 2018). As might be expected, Dittus et al. (2018) find that the variance explained for temperature extremes is substantially higher than for precipitation extremes.

Table 2 CONUS grid cell average of the proportion of driven variability in seasonal total precipitation and Rx1Day as simulated by the large ensemble of CAM5.1–1$^\circ$ runs

Given the large proportion of simulated background variability (> 90% for seasonal total precipitation and > 95% for seasonal Rx1Day), we can be confident that our statistical model with only seven climate variability indices is doing a very good job of quantifying driven variability in observed seasonal mean and extreme precipitation. In other words, this analysis verifies that the driven variability truly is only about 5–10% of the total variability in observed seasonal precipitation, and the inclusion of additional climate indices would not drastically increase the $R^2$ values in Table 1.

4.2 Benefits of using a spatial analysis

As discussed in Sect. 1, many observational analyses that explore relationships between climate variability indices and precipitation maintain an underlying reliance on weather station data. In most cases these take the form of single-station analyses, which ignore important spatial autocorrelations in the relationships between precipitation and the climate indices. As a result, the single-station analyses cannot resolve the relationships to a fine grid and, more seriously, have larger uncertainties (see, e.g., Risser et al. 2019b). Given that the signals we are trying to identify are relatively small (as evidenced by the analysis in Sect. 4.1), it is essential to take advantage of the spatial nature of these relationships to maximize detection.

In this subsection, we demonstrate the reduction in uncertainty and increased detection that is enabled via the spatial component of our analysis. For both of these results, we compare the GEV and mean regression coefficients as well as bootstrap/permutation estimates obtained at the $n=2504$ GHCN station locations from a single-station analysis (i.e., when the analyses are conducted using the precipitation measurements from a single station only) versus the corresponding quantities from the spatial analysis described in this paper which explicitly models the spatial dependence underlying the precipitation data.

4.2.1 Reduction in bootstrap uncertainty

Table 3 Ratio of bootstrap standard errors for the multiple mean regression (“Mean reg.”, i.e., $\{ \beta _j(\mathbf{s}): j = 1, \dots , 7\}$) and GEV (i.e., $\{ \mu _j(\mathbf{s}): j = 1, \dots , 7\}$) coefficients for each climate index/driver, averaged over the $n=2504$ GHCN stations over CONUS, comparing a single-station station analysis versus the spatial analysis proposed in this paper (spatial standard errors divided by single-station standard errors)

One of the important results from Risser et al. (2019b), which describes the statistical methods used in this paper, is that using a spatial analysis can significantly reduce the uncertainty in estimates of return values relative to a single-station analysis. We would expect a similar reduction in uncertainty for both the GEV and multiple mean regression analyses conducted in this paper, specifically with respect to the climate driver coefficients $\{ \mu _j(\mathbf{s}): j = 1, \dots , 7\}$ and $\{ \beta _j(\mathbf{s}): j = 1, \dots , 7\}$. Table 3 shows the ratio of bootstrap standard errors (obtained via the block bootstrap as described in Risser et al. 2019b) for the mean and GEV coefficients, comparing the spatial analysis standard errors with the corresponding quantity from a single-station analysis and averaging over the $n=2504$ GHCN stations in CONUS. Across all seasons and drivers, there is a major reduction in uncertainty for both the mean and extreme analysis: for example, on average the standard errors for the ELI GEV coefficient in DJF from the spatial analysis are 60% of the single-station analysis standard errors, for a reduction of 40%. Unsurprisingly, the reduction is larger for the GEV analysis relative to the multiple mean regression analysis. Furthermore, there are interesting differences across seasons: the reduction in uncertainty is generally larger in JJA than DJF, particularly for the mean regression coefficients. In general, applying a spatial analysis results in a reduction of uncertainty by about 30–45% for the extremes analysis and about 15–30% for the mean analysis. While we do not explicitly compare the coefficient estimates themselves, the implication is that a spatial analysis can significantly reduce uncertainty and hence increase the resulting signal-to-noise ratio of the analysis.

4.2.2 Increased detection of statistical significance

Fig. 4

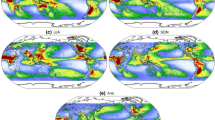
Proportion of the $n=2504$ GHCN stations over CONUS with significant relationship identified between each climate driver and precipitation for a single-station analysis vs. the spatial analysis proposed in this paper. The proportions are shown for detecting significance for the change in extreme magnitude (top; i.e., the change in 10-year return value $\varDelta _k(\mathbf{s})$), the change in extreme frequency (middle; i.e., the risk ratio $RR_k(\mathbf{s})$), and the change in seasonal total (bottom; i.e., $\theta _k(\mathbf{s})$)

While the bootstrap standard errors quantify uncertainty in the relationships between precipitation and the various drivers, the hypothesis testing used to assess statistical significance also involves the permuted estimates and their uncertainties (see Risser et al. 2019a). To assess the influence of the spatial analysis on detection of statistical significance, we can compare the proportion of the $n=2504$ GHCN stations over CONUS for which we can determine a significant relationship (for at least the “low” confidence statement) with each climate index. These proportions are shown in Fig. 4 for all seasons, showing detection for the change in extreme magnitude (top; i.e., the change in 10-year return value $\varDelta _k(\mathbf{s})$), the change in extreme frequency (middle; i.e., the risk ratio $RR_k(\mathbf{s})$), and the change in seasonal total (bottom; i.e., $\theta _k(\mathbf{s})$). Generally speaking, the spatial analysis results in greater detection of statistical significance across all seasons, drivers, and mean/extreme analysis. This is particularly true for the extremes analysis, where the proportion of stations with a significant relationship is uniformly larger with respect to the non-anthropogenic drivers for both the change in frequency and change in magnitude of extremes. In some cases this increase is substantial: for example, only about 15% of the weather station locations have a significant relationship between PNA and the change in extreme magnitude for SON with the single-station analysis, while the PNA relationship is significant for about 70% of stations when using the spatial analysis. The difference in detectability is smaller for the change in seasonal total precipitation, although the spatial analysis always detects a larger signal for the non-anthropogenic drivers than the single-station analysis.

4.3 Comparison with a composite analysis

As discussed in Sect. 3.1, we use the fitted statistical model to construct artificial climate “scenarios” by plugging in a desired set of climate index values. In this sense, our approach could be considered an “emulator” of the climatology of seasonal precipitation. The primary way we use this is to isolate individual drivers, i.e., comparing return values, return probabilities, or seasonal totals using vectors of the climate index values $\mathbf{X}_{k-}$ and $\mathbf{X}_{k+}$ where index $k \in \{\text {ELI}, \dots , \text {vSAOD} \}$ is set to its seasonal 5th and 95th value over the entire 1900-2017 period, respectively, and all other indices are fixed at their seasonal climatological mean. The fact that we are able to isolate the effect of a single driver while simultaneously accounting for all other drivers is a distinguishing feature of our analysis, and thus this type of comparison is at the center of our results and represents our best estimate of the true isolated relationship between each index and seasonal precipitation. For clarity, we refer to the various change metrics $\varDelta _k(\mathbf{g})$ (Eq. 4), $RR_k(\mathbf{g})$ (Eq. 6), and $\theta _k(\mathbf{g})$ (Eq. 11) from Sect. 3 as the isolated change metrics for index k.

However, many related studies from the literature instead conduct a so-called “composite analysis,” where one considers the effect of a single driver (e.g., ENSO) on some aspect of precipitation by taking a year or set of years with particularly extreme El Niño conditions and comparing with another set of years with particularly extreme La Niña conditions. For example, Zhang et al. (2010) conduct a composite analysis by selecting years with the five highest and lowest index values and calculating a difference in the average extreme precipitation from each set of years. Zhang et al. (2010) acknowledge an important limitation of this approach, namely, that the signals associated with a particular index in a composite analysis could be confounded with another co-occurring mode of oceanic or atmospheric variability in the selected years. Additionally, the analysis of daily extremes in Patricola et al. (2020) involves a spatial analysis much like the one used in this paper, but only includes the ELI index. Such an approach is a generalization of the composite analysis used in Zhang et al. (2010) (and others), but still cannot separate the effect of ELI from other modes that may co-occur with ELI.

On important benefit of the emulator framework described in this paper is that we can reproduce the composite analysis directly and explicitly quantify if and when a particular relationship identified in a composite analysis is in fact confounded with another mode or modes of variability. Instead of isolating a single driver, we can identify the specific years with extreme values of a specific index and maintain the value of the other indices that actually occurred in those years. Using the same framework we can define composite change metrics, e.g., for the change in extreme magnitude,

$$\begin{aligned} \varDelta ^C_k(\mathbf{g}) = {w_\mathbf{g}(\mathbf{X}^C_{k+})} - {w_\mathbf{g}(\mathbf{X}^C_{k-})}, \end{aligned}$$

(12)

where now the composite vector $\mathbf{X}^C_{(\cdot )}$ is defined as follows: for index $k \in \{\text {ELI}, \dots , \text {vSAOD} \}$,

• 1. Identify the years $t^+$ and $t^-$ where index k experiences its extreme states. For an index like ELI, this would correspond to large (El Niño) and small (La Niña) values; for an index like AMO, this would correspond to large positive phase and large negative phase values.

• 2. Define $\mathbf{X}^C_{k+} = \big ([\log \text {CO}_2]_{t^+}, [\text {ELI}]_{t^+}, \dots , [\text {vSAOD}]_{t^+}\big )$ and $\mathbf{X}^C_{k-} = \big ([\log \text {CO}_2]_{t^-}, [\text {ELI}]_{t^-}, \dots , [\text {vSAOD}]_{t^-}\big )$.

To average over the specific conditions that occur in a single year (and following Zhang et al. 2010), we can take an average of the return values from a set of 5 years for high/low values of index k: the estimated return value that goes in the above calculation is

$$\begin{aligned} {\widehat{w}}_\mathbf{g}(\mathbf{X}^C_{k+}) = \frac{1}{5}\sum _{i = 1}^5 {\widehat{w}}_\mathbf{g}\big ([\log \text {CO}_2]_{t^+_i}, [\text {ELI}]_{t^+_i}, \dots , [\text {vSAOD}]_{t^+_i}\big ), \end{aligned}$$

where $\{ t^+_i: i = 1, \dots , 5 \}$ are the 5 years such that the average value of index k experiences its 95th percentile; similarly for ${\widehat{w}}_\mathbf{g}(\mathbf{X}^C_{k-})$ using the years $\{ t^-_i: i = 1, \dots , 5 \}$ where the average value of index k experiences its 5th percentile. Furthermore, since in this framework the return value can be written as in (5), the composite change from (12) can be decomposed into components for each forcing:

$$\begin{aligned} {{\widehat{\varDelta }}}^C_k(\mathbf{g}) = {{\widehat{\mu }}}_1(\mathbf{g}) \cdot \frac{1}{5}\sum _{i = 1}^5 \left( [\log \text {CO}_2]_{t^+_i} - [\log \text {CO}_2]_{t^-_i} \right) + \cdots + {{\widehat{\mu }}}_7(\mathbf{g}) \cdot \frac{1}{5}\sum _{i = 1}^5 \left( [\text {vSAOD}]_{t^+_i} - [\text {vSAOD}]_{t^-_i} \right) . \end{aligned}$$

(13)

As such, the composite change metric allows us to quantify the composite relationship of index k with extreme precipitation while specifically isolating any drivers that may be aliasing onto the composite metric.

Fig. 5

Best estimates of the isolated change ${{\widehat{\varDelta }}}_k(\mathbf{g})$ and composite change ${{\widehat{\varDelta }}}^C_k(\mathbf{g})$ in the magnitude of 10-year return values for daily precipitation due to ELI in DJF (mm; a) as well as their difference (mm; b). c Contains the additive contribution of each driver to the composite change: in other words, the composite change in a is the sum of the components in c. In a, green values indicate locations where extremes for El Niño conditions; brown values indicate locations where extremes are larger for La Niña conditions

To illustrate the different conclusions that might be drawn from the isolated vs. composite change, we consider the estimated relationship between ELI and the magnitude of extreme events in DJF. In Fig. 1, we note a curious result for the isolated change: there is essentially no signal for ELI in DJF over California (a similar lack of signal shows up in Fig. 2 for the change in extreme frequency), with only a very small portion of southern California experiencing a significant increase in the magnitude of extremes under El Niño conditions. This would seem to contradict much of the literature on ENSO and extreme precipitation in California, for example, the analyses in Zhang et al. (2010) (see their Figure 1, 2, and 3); the daily extremes analysis in Patricola et al. (2020) (see their Figure 6); and the GEV analysis in Cannon (2015) (see their Figure 3).

For reference, the estimated isolated and composite relationships between ELI and the magnitude of extreme events in DJF is also shown in Fig. 5, albeit without significance hatching. The isolated change in Fig. 5a is a copy of the plot from Fig. 1, and shows the lack of signal over California. The composite change, also in Fig. 5a, is calculated by averaging over two 5 year periods, the first representing El Niño conditions and the second representing La Niña conditions (the specific years and index values are in Table D.3). The difference plot (isolated change minus composite change) in Fig. 5b illuminates major differences in the estimated relationship between ELI and extreme precipitation depending on how the change is quantified. In other words, if we use the composite change, the El Niño effect is overestimated in much of California and Texas and severely underestimated in much of the central US. More seriously, the sign of the effect is wrong in much of California and over Indiana, Illinois, and Kentucky. Interestingly, the negative anomaly and error in sign for Indiana, Illinois, and Kentucky that shows up in the composite change is also present in Zhang et al. (2010), Cannon (2015), and Patricola et al. (2020).

To assess which drivers are contributing to these differences, we can decompose the composite change into its various components as described in (13); see Fig. 5c. Recall that the composite change in Fig. 5a is the sum of the components in Fig. 5c. While the color limits are different, note that the ELI component in Fig. 5c is identical to the isolated change for ELI in Fig. 5a. It is clear that, given the specific AMO, PNA, and vSAOD conditions in the specific years that ELI attains its small and large values (see Table D.3), the AMO, PNA, and vSAOD significantly alter the perceived influence of ELI on precipitation extremes, particularly in California, Texas, and much of the central US. The primary index aliasing onto the ELI signal for California is actually AMO, while the PNA is the primary aliasing factor for the central US.

Focusing in on the California result, to consider this from another angle we also calculate the proportion of variance explained by the statistical models averaged over California only (see Table D.4 in the Appendix). From this table, it is clear that AMO and PNA can influence the precipitation response in California in DJF (albeit with small $R^2$). Furthermore, the $R^2$ in DJF for ELI alone is significantly smaller than the $R^2$ for the all drivers model, indicating that the full set of indices increases the predictability of seasonal precipitation over California (and indeed the same holds for CONUS; see Table 1).

In summary, we reiterate that the relationships between climate drivers and seasonal precipitation are often more complicated than they may initially appear. The fact that we can recreate many of the results from the literature on ENSO versus extreme precipitation with our composite analysis verifies that the relationships between the modes of variability and precipitation do not occur in isolation. Of course, an El Niño event does not occur in a vacuum: as such, we do not suggest that the composite analyses in the literature are “wrong.” Instead, a more nuanced analysis reveals that it is important to account for co-varying modes when attempting to disentangle the isolated relationships between a specific driver and precipitation.

5 Discussion

In this paper, we have developed a spatial analysis for in situ measurements of seasonal mean and extreme precipitation that quantifies joint relationships with a set of natural and anthropogenic climate indices. Critically, we use a single framework for characterizing the historical signal (anthropogenic forcing) and noise (natural variability) in seasonal mean and extreme precipitation. We furthermore frame our approach as an emulator, develop a method for characterizing the influence of individual drivers, and use a data-driven approach to quantify uncertainty and assess statistical significance for changes in the distribution of mean and extreme precipitation. In spite of significant noise in seasonal mean and extreme precipitation, we are able to detect statistically significant relationships for means and extremes in all seasons even though the proportion of variance explained by large-scale modes of variability is less than might have been anticipated from previous studies. We also demonstrate several ways in which our approach improves upon single-station and/or composite analyses and furthermore yields new results that explicitly reveal the complex, interconnected relationships between climate drivers and precipitation.

As mentioned in Sect. 4, we have opted to forgo a detailed discussion of the specific relationships revealed in Figs. 1, 2, and 3 as this was beyond the scope of the current paper. Nonetheless, the relationships identified in the maps contain important insights into the ways the various climate drivers impact seasonal precipitation and could form the basis for future exploration or climate model evaluation. As such, similar to the climatological data product of Risser et al. (2019b), we plan to publish the relevant fields used to create the maps in Figs. 1, 2, and 3 as a high-resolution “probabilistic” data product for each climate driver that quantifies its isolated relationship with mean and extreme precipitation and indicates where the relationship is statistically significant.

In Sect. 4.1, we briefly discussed how the total proportion of variability explained in seasonal mean and extreme precipitation changes across CONUS. This is true both overall (again see Fig. C.4) and for the influence of individual drivers. For example, volcanic aerosols explain only around 1% of variability when averaging over CONUS (across mean/extreme precipitation and all seasons; see Table 1) but up to 10% for seasonal mean precipitation in the Mountain West and Pacific Coast (in JJA) and the Southwest (in DJF). Maps of the proportion of variance explained for each state specific to the influence of volcanic aerosols are shown in Fig. C.5; this figure reiterates the fact that volcanic aerosols do not result in a uniform outcome in expectation, particularly at the regional scale. Note that the signals we see in the Northwest US appear to be consistent with increased rainfall and stream flow identified in Iles and Hegerl (2014) and Iles and Hegerl (2015).

The results of our analysis suggest that evaluation of teleconnections in climate models may benefit from using isolated—rather than composite—change metrics. The comparison between the isolated and composite change metrics in Sect. 4.3 shows that compositing techniques, which are prevalent in the literature (Gershunov and Barnett 1998; Zhang et al. 2010; Patricola et al. 2020), likely alias signals from other important modes of variability. AMIP-style simulations control for SST variability, but they do not necessarily control for atmospheric background variability like the PNA. Fig. 5c shows that negative PNA exterts a strong drying on the midwestern US, which aliases onto the ENSO composite shown in Fig. 5a. This implies that an AMIP simulation with a PNA pattern that differs from observations would show a different spatial pattern of extreme precipitation during ENSO years than observations. Such a difference might not necessarily be associated with a model error, if the difference in the PNA pattern is simply due to internal atmospheric variability. The situation is even more complicated for CMIP-style simulations, in which the various modes of variability co-vary in a different way than observations. Deser et al. (2017) propose the use of large ensembles of simulations to isolate the ENSO signal. We propose that the methodology described in this manuscript could be used to simultaneously isolate the effects of ENSO—and other modes of variability—in climate simulations; this would allow a more fair comparison with observations.

The emulator framework developed in this paper is used to identify the isolated and composite change metrics for each climate index. Both of these change metrics involved constructing “statistical” climate scenarios by characterizing the climatology of mean and extreme precipitation for an arbitrary combination of the climate indices that did not actually occur in the historical period. In a similar way, we could also use our results as a predictive model in (at least) two ways. First, for a particular grid cell or region in CONUS we could identify the combination of climate drivers that maximizes or minimizes seasonal precipitation. For example, looking at Fig. 1, it appears that the magnitude of extreme daily precipitation in California in MAM is maximized under El Niño conditions, the positive phase of the AO, the negative phase of the NAO, the positive phase of the AMO, and the negative phase of the PNA. Second, conditional on knowledge of the various climate indices in an upcoming season, our data product could be used to identify areas with high risk of departing significantly from the mean or extreme climatology. Such a prediction would assume that the relationships identified over 1900–2017 would continue to hold in the future, which should be a relatively safe assumption in the near future.

The linear regression-based approach used in our analysis of course cannot capture nonlinear responses to climate variability due to its assumption of symmetry. Of the climate modes considered, ENSO is one that is well known for asymmetric teleconnections (see, e.g., Hoerling et al. 1997; Gershunov 1998), and this unaccounted for asymmetry could contribute to the large background variability. One possible way to explore this would be to split the ENSO Longitude Index into two separate covariates: one for positive ELI anomalies and another for negative ELI anomalies; this would break the requirement that the ELI response is symmetric. This of course then raises the issue of how you would deal with near-zero ELI anomalies, where the (small) response might arguably be symmetric. We plan to explore further development of the methodology to account for asymmetries and nonlinearities as future work.

Finally, as discussed in Sect. 1, while our methodology includes characterization of the anthropogenic influence on seasonal mean and extreme precipitation we have so far only discussed the influence of the non-anthropogenic drivers. A forthcoming manuscript will specifically address the anthropogenic attribution question. However, the results already described in this paper have important implications for detection and attribution of a human influence on grid-scale seasonal precipitation over CONUS. First, we have quantified the difficult signal-to-noise problem for detecting an anthropogenic influence at the weather station level: from Table 1, the variance explained by $\hbox {CO}_2$ is $\approx 1\%$ of the total variance. One of the reasons why the literature on $\hbox {CO}_2$ influence on precipitation is so internally inconsistent may be due to compositing techniques, in this case compositing time periods with high $\hbox {CO}_2$ minus low $\hbox {CO}_2$. As Table 1 shows, the multiple drivers that “come along for the ride” in such a compositing approach are, at a minimum, comparable to $\hbox {CO}_2$ (and in DJF, up to nearly 10 $\times$ larger). These will alias onto the signal of interest, that from $\hbox {CO}_2$ alone. Given that the noise is very large (> 90%) for both seasonal mean and extreme precipitation, this suggests that we might have a difficult time detecting and attributing trends in mean and extreme precipitation at the grid scale level over CONUS. Nonetheless, as with the natural variability indices explored in the current paper, we are able to detect at least some human influence on extreme precipitation in spite of the significant noise in the underlying data.

Appendices

Appendix 1: Sensitivity to start time

In order to assess the sensitivity of our results to the start time, we conducted two analyses: first, exploring GEV coefficient estimates when starting the analysis in $\{1900, 1910, \dots , 1950\}$ (but without the full hypothesis testing procedure); and second, comparing the results when starting in 1900 versus 1950 with the full uncertainty quantification and permutation/testing analysis. An important point to note is that we use the same selection criteria for the GHCN stations regardless of the start time (i.e., a GHCN station is included if and only if it has at least 66.7% non-missing daily values over the length of the record) and, given the nature of the GHCN record, the number of eligible stations increases monotonically with time (see Table 4 for the number of stations that meet this criteria per decade). In other words, the choice of start year presents a tradeoff between more spatial information (more stations) and more temporal information (more years of data).

Table 4 Number of GHCN stations over the contiguous United States that have at least 66.7% non-missing daily values over the period from the start year to 2017

1.1 Comparison 1: compare decades without hypothesis testing

As a fast initial comparison, we first assess standardized GEV coefficient estimates (i.e., estimates divided by their standard error) for the statistical model given in (2), where the analysis starts in one of $\{1900, 1910, \dots , 1950\}$ and runs through 2017. In order to make this analysis less computationally demanding, instead of applying the full spatial analysis described in the main text we use the local likelihood functionality in climextRemes, which incorporates spatial smoothing but does not interpolate the station results. For each start period, using the set of stations that meet our selection criteria (see Table 4), we obtain smoothed maximum likelihood estimates of the GEV coefficients for each driver as well as their standard errors. Then, for each station, we calculate z-scores for each driver (estimate divided by standard error) and aggregate spatially across all CONUS stations in the analysis.

The resulting box plots of z-scores are shown in Fig. C.6; for simplicity we only show box plots for the natural logarithm of $\hbox {CO}_2$, ELI, NAO, and PNA. In general, the signal-to-noise ratio (SNR; summarized by the z-scores) exhibits a slight attenuation as the start time moves from 1900 to 1950; in other words, the box plots shrink and move towards zero with increasing start time. This generally holds for all of the drivers in the plot, but is particularly pronounced for, e.g., log $\hbox {CO}_2$ in MAM and PNA in DJF. Interestingly, this is not always the case: for example, the signal is quite robust to start time for ELI in DJF. Furthermore, for seasons/drivers where there is essentially no signal (e.g., ELI in JJA), the box plots are centered on zero regardless of the start time.

This SNR attenuation suggests that it would be better to start the analysis in an earlier time period, most likely 1900. However, this analysis by itself does not fully characterize the uncertainty since we do not pursue the permutation/null distribution analysis; on the other hand, note that in general the attenuation is monotone. As such, we next explore the full spatial analysis with hypothesis testing for the two extreme start times considered so far, namely 1900 and 1950.

1.2 Comparison 2: compare 1900 vs. 1950 start with spatial analysis

For this comparison, we now apply the full analysis described in the main text to the seasonal maxima starting in both 1900 and 1950. Recall that these two analyses present a stark trade-off between more spatial information (5202 stations for 1950 versus 2504 stations for 1900) and more temporal information (68 years for 1950 versus 118 years for 1900); however, for the 1900 start time we might hope that the spatial aspect of the analysis is helpful in accounting for the loss of spatial information. In fact, we also conducted a third analysis that again starts in 1950 but uses a detrended version of the natural driver variables (i.e., with low frequency variation removed). The idea here is that when considering a shorter time period, there may be low frequency variability in the natural driver variables that could mask the long-term secular trend described by log $\hbox {CO}_2$ (which is nearly linear over 1950–2017); for example, note that the AMO time series in Fig. C.2 are nearly linear over 1950–2017. As with the previous subsection, to simplify our discussion we focus on the natural logarithm of $\hbox {CO}_2$, ELI, NAO, and PNA.

Figure C.7 shows scatterplots of the risk ratio estimates (comparing the probability of exceeding the 10-year climatological return value for high vs. low index values) after applying the full spatial analysis for 1900 versus 1950 (panel a; the 1950 analysis uses the “raw” indices) and starting in 1950 but using “raw” versus detrended indices (panel b), as well as the 1–1 line. These scatterplots aggregate pairwise risk ratio estimates for the 13073 grid cells. First, in panel a, note that in general the coefficient estimates are clustered around the 1–1 line, particularly for ELI, NAO, and PNA, indicating that the estimated risk ratios are robust to the start time. Of course there is some variability about the 1–1 line, but there do not appear to be any systematic biases for the natural indices. The story is slightly different for log $\hbox {CO}_2$: here, the scatterplots appear to be stretched more along the y-axis relative to the x-axis, particularly for DJF and SON, indicating that there is a larger anthropogenic effect for the 1950 start time. This is not entirely surprising, since log $\hbox {CO}_2$ is nearly linear over 1950–2017; in any case, the effect is not too severe. Next, panel b of Fig. C.7 shows the same risk ratio estimates for 1950 using the “raw” index values versus estimates based on using detrended index values; again, the scatterplot shows pairs of estimates for each grid cell. Again the estimates are tightly clustered around the 1-1 line, particularly for the natural indices, with much less variability around the 1–1 line relative to panel a. The variability around the 1–1 line is slightly larger for log $\hbox {CO}_2$, but again there do not appear to be any significant biases.

Figure C.7 provides confidence that the actual risk ratio estimates are robust to the start time. However, these scatterplots only assess the signal; it is also important to assess the magnitude of the noise and our ability to detect statistically significant relationships between the drivers and extreme precipitation. To this end, Fig. C.8 shows the proportion of CONUS where we can detect a significant relationship between the same set drivers (the natural logarithm of $\hbox {CO}_2$, ELI, NAO, and PNA) and extreme precipitation for each start time (i.e., the number of grid cells that are significant divided by the total number of grid cells). (Note: this plot also shows detectability for Rx5Day; see Sect. B.) In almost all cases where a relationship is detectable at all, there is a larger signal for the analysis that starts in 1900; this is uniformly the case for the natural variability indices. For example, note that ELI in SON and PNA in DJF, MAM, and SON can detect a much larger proportion of CONUS as having significant relationships for 1900 relative to either of the 1950 analyses.

In summary, from the sensitivity analyses in this section we can be confident that the estimated signal is robust to the start time (Fig. C.7 shows that risk ratio estimates are approximately the same for starting in 1900 vs. 1950, with or without detrending the natural indices), and furthermore the noise is such that we can better detect signals when starting the analysis in 1900. In other words, the spatial analysis preserves the signal in the presence of less spatial data (i.e., having only 2504 stations for the 1900 start time versus 5202 stations for the 1950 start time) while the increased temporal information helps us to reduce the noise such that our detection power is stronger. Hence, we use the 1900 start time for our main analysis in the paper.

Appendix 2: Metrics for quantifying extremes

A final open question for this analysis is how to best summarize extreme precipitation from a single season. While in principle there are a large number of metrics for summarizing extreme precipitation (e.g., the ETCCDI effort; Alexander 2016) in a GEV framework we maintain a focus on block (here, seasonal) maxima. Nonetheless, we still need to choose a time window to take maxima over, e.g., daily maxima (Rx1Day), versus longer cumulative maxima like 5-day running maxima (termed Rx5Day). The seasonal Rx1Day is potentially a more familiar metric, but seasonal Rx5Day involves aggregating over multiple days and therefore may help reduce noise in the data.

In order to explore this question more thoroughly, we also conducted the full analysis using Rx5Day extracted from the same set of stations, again for each of the time periods considered in Sect. A. First, in Fig. C.9, we show spatial pattern correlations in the grid cell risk ratio estimates based on Rx1Day and Rx5Day for the 1900 start time, as before focusing on the natural logarithm of $\hbox {CO}_2$, ELI, NAO, and PNA in each season. All of the pattern correlations exceed 0.6, with most in excess of 0.8 and several in excess of 0.9; in other words, the spatial patterns of the estimated impact for each index on extreme precipitation is very similar regardless of whether we consider daily maxima or five-daily running maxima. Next, we can again look at Fig. C.8, which shows the proportion of CONUS that exhibits a significant relationship between each driver and extreme precipitation for both Rx1Day and Rx5Day. The signal is largely the same for Rx1Day and Rx5Day, in the sense that for seasons/drivers where we can detect a significant signal for Rx1Day we see a similar signal for Rx5Day. (In this figure we again see a preference for starting in 1900 relative to 1950 for Rx5Day.) There are some differences in the magnitude of the proportion that we can determine significant relationships for the 1900 start time, e.g., more of the map is significant for Rx5Day when looking at ELI and PNA in DJF. However, using Rx5Day does not lead to uniformly larger signals: for example, ELI and $\hbox {CO}_2$ in SON show a larger signal for Rx1Day.

Ultimately, there appears to be a lack of strong evidence for choosing either metric (daily maxima vs. five-daily maxima) for this analysis: spatial patterns of the signal are approximately the same for both Rx1Day and Rx5Day (based on Fig. C.9) and detectability is comparable for both metrics (based on the analysis summarized in Fig. C.7). Therefore, we opted to focus on Rx1Day for the analysis in the main text for two reasons: (1) Rx1Day is a more familiar metric to a general reader, and (2) five-daily running maxima are more sensitive to missing values in the observational record (i.e., we select the seasonal Rx5Day from all 5-day periods with no missing values; hence, the seasonal Rx5Day values could be biased due to the proportion of missing data allowed by our selection criteria).