Introduction

Amino acids are chemical entities containing an amine group and a carboxylic acid group and a side chain that varies between different amino acids. They form proteins, which are critical to life, and have many important functions in living cells. Twenty naturally occurring amino acids with different physicochemical and biochemical properties are the structural building blocks of proteins. A wide diversity of properties of amino acids have been investigated through a large number of experiments and theoretical studies. Each of these amino acid properties can be represented by a vector of 20 numerical values, and we refer to it as an amino acid index. Nakai et al. (1988) came up with 222 amino acid indices from published literature and investigated the relationships among them using hierarchical clustering analysis. Subsequently, Tomii and Kanehisa (1996) enriched the AAindex database with 42 amino acid mutation matrices and released as the AAindex2. Recently, 47 amino acid contact potential matrices have been reported as AAindex3.Footnote 1 The database is continuously updated by Kawashima et al. (1999, 2008) and Kawashima and Kanehisa (2000). Currently, 544 amino acid indices are released in AAindex1 database (see footnote 1). Selection of the minimal/optimal set of amino acid indices for different bioinformatics applications is a difficult task and often involves adhoc/sub-optimal choices. It is, therefore, necessary to group similar indices in clusters and label representative cluster-indices. Moreover, apart from AAindex database, Chou’s pseudo amino acid composition (PseAA) (Chou 2001) and its several variants, described in Nanni et al. (2010), have been used as an alternative tool to deal with sequence-related systems and protein-related problems (Chou 2009; Nanni et al. 2010; Georgiou et al. 2009, 2010; Pape et al. 2010; Wang et al. 2010). Clustering (Hartigan 1975; Jain and Dubes 1988; Oliveira and Pedrycz 2007) is a widely used technique in data mining application for discovering patterns in underlying data, which partitions the input space into K regions depending on some similarity/dissimilarity metric, where the value of K may or may not be known a priori. Clustering can be performed in two different modes: (1) crisp and (2) fuzzy. In crisp clustering, the clusters are disjoint and nonoverlapping in nature. Any pattern may belong to one and only one class in this case. In fuzzy clustering, a pattern may belong to all the classes with a certain fuzzy membership grade. Due to the overlapping nature of the AAindex1 database, we decided to work on the field of evolutionary partitional fuzzy clustering methods. Moreover, it has been observed by our recent experimental study that no single method outperforms all others over a wide array of different applications (Plewczynski et al. 2010b). Thus, the consensus of all methods is typically applied to provide the best solution. Therefore, we propose a consensus fuzzy clustering (CFC) technique, which analyzes the AAindex1 database for known and unknown number of clusters by exploiting the capability of recently developed fuzzy clustering techniques. It has also been observed that the index encoding scheme of cluster medoids, used in the fuzzy c-medoids (FCMdd) (Krishnapuram et al. 1999) algorithm, provides better results over real valued encoding scheme of cluster centres as used in fuzzy c-means (FCM) (Bezdek 1981). Thus, the different advanced hybridization forms of FCMdd, like differential evolution-based fuzzy c-medoids (DEFCMdd) (Maulik et al. 2010; Maulik and Saha 2009) clustering, and genetic algorithm-based fuzzy c-medoids (GAFCMdd) (Maulik et al. 2010; Maulik and Saha 2009; Maulik and Bandyopadhyay 2000) clustering algorithms are tested. In the case of finding the optimal number of clusters, automatic differential evolution-based fuzzy clustering (ADEFC) (Maulik and Saha 2010) and variable length genetic algorithm (Bandyopadhyay and Pal 2001)-based fuzzy clustering (VGAFC) (Maulik and Bandyopadhyay 2003) are used, which measure the Xie–Beni (XB) (Xie and Beni 1991) index in fitness computation. Thereafter, the consensus result of all methods is taken by a majority voting procedure. Effectiveness of the proposed method is demonstrated quantitatively and visually. Also Wilcoxon rank sum test (Hollander and Wolfe 1999) is conducted to judge the statistical significance and statbility of clusters found by the proposed method. In bioinformatics research on protein sequences, the AAindex1 database has been used in wide range applications, e.g., prediction of post-translational modification (PTM) sites of proteins (Plewczynski et al. 2008; Basu and Plewczynski 2010), protein subcellular localization (Huanga et al. 2007; Tantoso and Li 2008; Liao et al. 2010; Laurila and Vihinen 2010), immunogenicity of MHC class I binding peptides (Tung and Ho 2007; Tian et al. 2009), protein SUMO modification site (Liu et al. 2007; Lu et al. 2010), coordinated substitutions in multiple alignments of protein sequences (Afonnikov and Kolchanov 2004), HIV protease cleavage site prediction (Ogul 2009; Nanni and Lumini 2009), and many more (Jiang et al. 2009; Liang et al. 2009; Soga et al. 2010; Chen et al. 2010; Pugalenthi et al. 2010). In all these cases, selection of proper amino acid indices is crucial, where this paper also attempts to make a humble contribution. The notable work, available in the literature so far, on clustering of amino acid indices is by Tomii and Kanehisa (1996) and Kawashima et al. (2008). They categorized 402 indices into six groups using hierarchical clustering technique. Those clusters/groups represent alpha and turn propensities, beta propensity, composition, hydrophobicity, physicochemical properties and other properties. However, there is no work available on clustering of the latest AAindex database, consisting of 544 amino acid indices. To address this issue, three standardized sets of high-quality indices (HQIs) are generated in our current work by analyzing the AAindex1 database using a CFC technique.

Description of fuzzy clustering algorithms and validity measures

Algorithms for known number of clusters

Fuzzy c-means clustering

The FCM algorithm (Bezdek 1981) is a widely used technique that uses the principles of fuzzy sets to evolve a partition matrix U(X) while minimizing the measure

$$ J_{m} = \sum^{n}_{j=1} \sum^{K}_{k=1} u^{m}_{k,j} D^{2}(z_{k},x_{j}),\quad 1\leq m\leq \infty $$
(1)

where n is the number of data objects, K represents number of clusters, u k,j is cluster membership of jth point in the kth cluster and m denotes the fuzzy exponent. D(z k , x j ) denotes the distance of point x j from the kth cluster centre z k . FCM algorithm starts with random initial K cluster centres, and then at every iteration, it finds the fuzzy membership of each data points using the following equation:

$$ u_{k,i} = \frac{\left(\frac{1}{D(z_{k},x_{i})}\right)^{\frac{1}{m-1}}} {\sum^{K}_{j=1} \left(\frac{1}{D(z_{j},x_{i})}\right)^{\frac{1}{m-1}}}, \quad {\rm for}\quad 1\leq k \leq K,\quad 1\leq i\leq n $$
(2)

The cluster centres are recomputed using the following equation:

$$ z_{k} = \frac{\sum_{i=1}^{n} u_{k,i}^{m} x_{i}}{\sum_{i=1}^{n} u_{k,i}^{m}}\quad 1\leq k \leq K $$
(3)

The algorithm terminates when there is no further change in the cluster centres. Finally, each data point is assigned to the cluster to which it has maximum membership.

Fuzzy c-medoids clustering

The FCMdd (Krishnapuram et al. 1999) algorithm is the extension of FCM (Bezdek 1981) algorithm replacing cluster means with cluster medoids. A medoid is defined as follows: Let \(V = \left\{v_{1}, v_{2}, \ldots, v_{i} \right\}\) be a set of z objects. The medoid of V is an object \(O \in V\) such that the sum of distances from O to other objects in V is minimum. The aim of FCMdd algorithm is to cluster the dataset \(X = \left\{ x_{1}, x_{2}, \ldots, x_{n} \right\}\) into K partitions so that the J m (Eq. 1) is minimized. The FCMdd algorithm also iteratively estimates the partition matrix U(X) followed by computation of new cluster medoids. It starts with random initial C medoids, and then at every iteration it finds the fuzzy membership of each object to every cluster using the Eq. 2. Based on the membership values, the cluster medoids are recomputed as follows:

$$ p_{k} = {\rm argmin}_{1 \leq j \leq n} \sum^{n}_{i=1} u^{m}_{k,i} D(x_{j},x_{i}),\quad 1 \leq k \leq K $$
(4)

and

$$ z_{k} = x_{pk}, 1 \leq k \leq K $$
(5)

The algorithm terminates when there is no significant improvement in J m value. Finally, assignment of each data point is performed in a manner identical to that of FCM.

Differential evolution-based fuzzy c-medoids clustering

In DEFCMdd (Maulik et al. 2010; Maulik and Saha 2009) clustering, the medoids of the clusters are encoded in the vector. For initializing a vector, C medoids are randomly selected from n data points. The fitness of a vector indicates the degree of goodness of the solution, which is defined by J m . The objective is, therefore, to minimize the J m index for achieving proper clustering. Subsequently, the medoids encoded in a vector are updated using Eqs. 3 and 5. The process of mutation and crossover follows Eqs. 6 and 9.

$$ \vartheta_{k}(t+1) = \vartheta_{m}(t) + F(\vartheta_{r}(t) -\vartheta_{j}(t)) $$
(6)

Here ϑ m (t), ϑ r (t) and ϑ j (t) are randomly taken vectors from the current population (indicated by t time stamp) with the d dimensions for the mutant vector ϑ k (t + 1). F is the scaling factor usually \(\in\) [0,1]. If the index value of ϑ k (t + 1) lies beyond the permissible range of \(\left\{1,\ldots, n \right \}\) then it is scaled using one of the following two operations:

$$ \vartheta_{k}(t+1) - n $$
(7)

and

$$ \vartheta_{k}(t+1) + n $$
(8)

To increase the diversity of the perturbed parameter vectors, crossover is introduced.

$$ U_{jk}(t+1) = \left\{ \begin{array}{l} \vartheta_{jk}(t+1) \\ \quad{\rm if}\,{\rm rand}_{j}(0,1) \leq {\rm CR}\quad{\rm or}\quad j={\rm rand}(k)\\ \vartheta_{jk}(t)\\ \quad{\rm if}\,{\rm rand}_{j}(0,1) > {\rm CR}\quad{\rm and}\quad j \not= {\rm rand}(k)\\ \end{array}\right. $$
(9)

In Eq. (9), rand j (0,1) is the jth evaluation of a uniform random number generator with outcome \(\in\) [0, 1]. CR is the crossover rate \(\in\) [0, 1], which has to be determined by the user. rand(k) is a randomly chosen index \(\in\left\{1, 2,\ldots, d\right\},\) which ensures that U k (t + 1) gets at least one parameter from ϑ k (t + 1). To make the population for the next generation, the trial vector U k (t + 1) is compared with the target vector ϑ k (t) using the greedy criterion. If vector U k (t + 1) yields a better fitness value than ϑ k (t), then U k (t + 1) is set to ϑ k (t); otherwise, the old value ϑ k (t) is retained. The algorithm is terminated after a fixed number of generations. The algorithm is outlined in Fig. 1.

Fig. 1
figure 1

DEFCMdd algorithm

Full size image

Genetic algorithm-based fuzzy c-medoids clustering

GA-based fuzzy c-medoids (GAFCMdd) (Maulik et al. 2010; Maulik and Saha 2009; Maulik and Bandyopadhyay 2000) clustering algorithm also uses the same encoding policy as DEFCMdd to represent the vectors. The fitness of each chromosome is computed using Eq. 1. Subsequently, the medoids encoded in a chromosome are also updated using Eqs. 3 and 5. Conventional proportional selection has been implemented on the population. The standard single point crossover is applied stochastically with probability μc. Each chromosome also undergoes mutation with a fixed probability μm. Termination condition is the same as the other algorithm. The elitism model of GAs has been used, where the best chromosome seen till the current generation is stored in a location within the population. The best chromosome of the last generation provides the solution to the clustering problem. Figure 2 demonstrates the GAFCMdd algorithm.

Fig. 2
figure 2

GAFCMdd algorithm

Full size image

Algorithms for unknown number of clusters

Automatic differential evolution-based fuzzy clustering

Automatic differential evolution-based fuzzy clustering (Maulik and Saha 2010) has been developed on the framework of differential evolution (DE). The technique uses a masker along with the initial population of DE, which contains 0’s and 1’s. The value 1 in the masker cell indicates that the encoded medoids in the same position of the vector is valid, otherwise not. Fitness of the each vector is computed by XB index (Xie and Beni 1991). Let \(\left\{z_{1}, z_{2}, \ldots, z_{K} \right\}\) be the set of K cluster medoids encoded in a vector. The XB index is defined as a function of the ratio of the total variation σ to the minimum separation sep of the clusters. Here σ and sep can be written as

$$ \sigma(U,Z;X) = \sum_{k=1}^{K}\sum_{i=1}^{n} u_{k,i}^{2}\,D^{2}(z_{k},x_{i}), $$
(10)

and

$$ {\rm sep} (Z) = min_{i \neq j} {\parallel z_{i} -z_{j} \parallel^{2}}, $$
(11)

where ∥.∥ is the Euclidean norm, and D(z k , x i ), as mentioned earlier, is the distance between the pattern x i and the cluster medoid z k . The XB index is then define as

$$ XB (U,Z;X) = \frac{\sigma(U,Z;X)}{n \times {\rm sep} (Z)} $$
(12)

Note that when the partitioning is compact and good, value of σ should be low while sep should be high, thereby yielding lower values of the XB index. The objective is, therefore, to minimize the XB index for achieving proper clustering. Moreover, the process of mutation, crossover and selection are the same as in DE, and it terminates after a fixed number of generations.

Variable length genetic algorithm-based fuzzy clustering

A variable string length GA (VGA)-based clustering technique has been developed by Maulik and Bandyopadhyay (2003) on the framework of genetic algorithm (GA), where real valued encoding of cluster centres is used. However, index-encoding of cluster medoids is implemented due to context of this article. The algorithm automatically evolves the number of clusters as well as the partitioning and minimizes the XB cluster validity index. Since the number of clusters is considered to be variable, the string lengths of different chromosomes in the same population are allowed to vary. The selection, crossover and mutation operations are also performed in each generation. Elitism is also incorporated to keep track of the best chromosome obtained so far.

Cluster validity indices

Minkowski Score (Jardine and Sibson 1971), Kappa Index (Cohen 1960) (these indices are applied when true cluster is known), and Silhouette Index (S(C)) (Rousseeuw 1987) are used for evaluating the performance of the clustering algorithms.

Minkowski Score

The performances of the clustering algorithms are evaluated in terms of the Minkowski Score (MS) (Jardine and Sibson 1971). This is a measure of the quality of a solution given the true clustering. Let T be the “true” solution and S the solution we wish to measure. Denote by n 11 the number of pairs of elements that are in the same cluster in both S and T. Denote by n 01 the number of pairs that are in the same cluster only in S, and by n 10 the number of pairs that are in the same cluster in T. Minkowski Score (MS) is then defined as:

$$ {\rm MS} = \sqrt{\frac{n_{01} + n_{10}}{n_{11} + n_{10}}} $$
(13)

For MS, the optimum score is 0, with lower scores being “better”.

Kappa index

The kappa index was developed by Cohen (1960) and used by the medical community as a useful measure of classification accuracy. The score of the method is derived from the contingency table called confusion matrix, where each element C ij is the number of records pertaining to cluster i that have been automatically classified in cluster j. So the diagonal elements correspond to the records that have been correctly classified. Overall accuracy (% correct) and kappa index are computed by Eqs. 14 and 15, respectively.

$$ \% \ {\rm correct} = \frac{\sum_{k}C_{kk}}n\times 100 $$
(14)
$$ {\rm kappa} = \frac{n \sum_{k}C_{kk} - \sum_{k} C_{k+} C_{+k}}{n^{2} - \sum_{k} C_{k+} C_{+k}} $$
(15)

where C k+ = ∑ j C kj , C +k  = ∑ i C ik and n is the number of data points. Kappa values range from 0 to 1. Higher value of kappa (close to 1) indicates better accuracy.

Silhouette index

Silhouette index (Rousseeuw 1987) reflects the compactness and separation of the clusters. Given a set of n samples \(S = \left\{s_{1}, s_{2},\ldots, s_{n} \right\}\) and a clustering of the samples \(C = \left\{C_{1}, C_{2}, \ldots,C_{K}\right\},\) the silhouette width S(s i ) for each sample s i belonging to cluster C j denotes a confidence measure of belongingness, and it is defined as follows:

$$ S(s_{i})=\frac{b(s_{i}) - a(s_{i})}{{\rm max}\left\{a(s_{i}), b(s_{i})\right\}} $$
(16)

Here a(s i ) denotes the average distance of the sample s i from the other samples of the cluster to which sample s i is assigned, and b(s i ) represents the minimum of the average distances of sample s i from the samples of the clusters \(C_{l}, l = 1, 2,\ldots, K,\) and l ≠ j. The value of S(s i ) lies between −1 and 1. Large value of S(s i ) (approaching 1) indicates that the sample s i is well clustered. Overall silhouette index S(C) of a clustering C is defined as

$$ S(C)=\frac{1}{n}\sum_{i=1}^{n} S(s_{i}) $$
(17)

Greater value of S(C) (approaching 1) indicates that most of the samples are correctly clustered and this, in turn, reflects better clustering solution.

Proposed consensus fuzzy clustering algorithm

We have analyzed the AAindex1 database in two different phases. Phase I explores the capability of fuzzy clustering methods for known number of clusters. Thereafter, a consensus result is obtained through majority vote over all fuzzy clustering methods implemented. These phases are described in greater detail below.

Phase I

In this phase, the results of hierarchical clustering for 402 AA indices have been verified by fuzzy clustering algorithms. For this purpose, different fuzzy clustering techniques, like DEFCMdd clustering, GAFCMdd clustering, FCMdd and FCM have been used. Each of these algorithms is executed separately for producing the fuzzy partitions and then different cluster validity measures have been used for the evaluation of the algorithms. Different steps of this phase are described below as well as highlighted in Fig. 3 by red color.

  1. Step 1:

    Input the AAindex1 database of 402 indices with the known number of clusters.

  2. Step 2:

    Execute N number of fuzzy clustering algorithms.

  3. Step 3:

    Evaluate the performance of N number of fuzzy clustering algorithms using different validity measure to ensure that the number of clusters used in Step1 are stable.

Fig. 3
figure 3

Block diagram of the proposed method

Full size image

Phase II

This phase is more advanced than the earlier phase. The enhanced AAindex1 database of 544 indices has been used. The database is tested by ADEFC and variable length genetic algorithm-based fuzzy clustering (VGAFC) techniques for finding optimal number of clusters automatically. After that, the earlier fuzzy clustering techniques are used to fix the optimal number of clusters as stable clusters. Finally, the results of all six fuzzy clustering methods are used to create a consensus using majority voting procedure. The phase II of the proposed method is described below and its block diagram is shown in Fig. 3.

  1. Step 1:

    Use enhanced database of AAindex1 for predicting the number of clusters.

  2. Step 2:

    Execute M number of automatic fuzzy clustering methods to determine the number of clusters.

  3. Step 3:

    Evaluate the performance of M number of fuzzy clustering algorithms using different validity measures.

  4. Step 4:

    Execute N number of fuzzy clustering methods with the predicted number of clusters found in Step 2 to ensure that the number of clusters are stable.

  5. Step 5:

    Repeat the Step 3 of Phase I to evaluate the performance of N number of fuzzy clustering algorithms.

  6. Step 6:

    It is divided into two sub-steps. One is for creating equivalence among all different solutions, and the other for a consensus result among those solutions.

    1. (a)

      Before creating the consensus clustering result among M + N number of methods, reorganization of data points is required to make them consistent with each other. Thus, the cluster j in the first solution should be equivalent to cluster j in all the other solutions. For example, the solution string \(\left\{aabbccc\right\}\) is equivalent to \(\left\{bbccaaa \right\}.\) The reorganization is done in such a way that each δ i , where \(i =2,3, \ldots,M+N\) and δ i is a solution string, becomes consistent with δ1.

    2. (b)

      Apply consensus method on the label vectors δ i , \(i =1,2,\ldots,M+N\) to obtain the final clustering label vector δ. The majority voting is used to create the consensus clustering result, and it is performed as follows: assign each point \(k = 1,\ldots, n\) to the cluster j where the label j appears the maximum number of times among all the labels for the point k in all the δ i .

Experimental results

Description of AAindex1 database

The AAIndex1 currently contains 544 amino acid indices. Each entry consists of an accession number, a short description of the index, the reference information and the numerical values for the properties of 20 amino acids.

Distance measures

The Pearson correlation-based distance measure has been used as this is the commonly used distance metric for clustering AAindex1 database (Tomii and Kanehisa 1996; Kawashima et al. 2008). Given two sample vectors, s i and s j , Pearson correlation coefficient Cor(s i , s j ) between them is computed as:

$$ {\rm Cor}(s_{i},s_{j})=\frac{\sum_{l=1}^{p} (s_{il}-\mu_{s_{i}})(s_{jl}-\mu_{s_{j}})}{\sqrt{\sum_{l=1}^{p} (s_{il}-\mu_{si})^{2}}\sqrt{\sum_{l=1}^{p} (s_{jl}-\mu_{sj})^{2}}}. $$
(18)

Here μ s_i and μ s_j represent the arithmetic means of the components of the sample vectors s i and s j , respectively. Pearson correlation coefficient defined in Eq. 18 is a measure of similarity between two samples in the feature space. The distance between two samples s i and s j is computed as 1 − mod(Cor(s i , s j )), which represents the dissimilarity between those two samples.

Visualization

In this article, for visualization of the datasets, well-known visual assessment of clustering tendency (VAT) representation (Bezdek and Hathaway 2002) is used. To visualize a clustering solution, first the points are reordered according to the class labels given by the solution. Thereafter, the distance matrix is computed on this reordered data matrix. In the graphical plot of the distance matrix, the boxes lying on the main diagonal represent the clustering structure.

Input parameters

The population size and number of generation used for DEFCMdd, GAFCMdd, ADEFC and VGAFC algorithms are 20 and 100, respectively. The crossover probability (CR) and mutation factors (F) for DEFCMdd and ADEFC are set to 0.8 and 1, respectively. For GAFCMdd and VGAFC, the crossover and mutation probabilities are taken to be 0.8 and 0.3, respectively. The FCMdd and FCM algorithms are executed till it converges to the final solution. Also for the probabilistic/stochastic nature, each algorithm has run for 50 times to show consistency in producing the better results. Note that the input parameters used here are fixed either following the literature or experimentally (Maulik and Bandyopadhyay 2000, 2003; Maulik and Saha 2009; Maulik et al. 2010). The performance of the clustering methods is evaluated by measuring Minkowski Score (MS) (Jardine and Sibson 1971), Kappa index (Cohen 1960), and Silhouette Index (Rousseeuw 1987).

Results and discussion

To analyze the AAindex1 database, different fuzzy clustering algorithms are used in two phases and the average results of 50 consecutive runs of those algorithms are reported in Tables 1, 2, and 3. Here, phase 1 is conducted for the known number of clusters of 402 AA indices. The results are reported in Table 1, which shows the quality of different fuzzy clustering algorithms in terms of cluster validity measures. It is also observed from Table 1 that the DEFCMdd provides better results. However, in phase II, CFC outperforms the others. Hence, Tables 2 and 3 have been designed to show the effectiveness of different fuzzy clustering algorithms. At the beginning of phase II, the enhanced AAindex1 database of 544 indices is examined by ADEFC and VGAFC techniques. The number of clusters found by these two methods is mentioned in Table 2. Table 2 also shows that ADEFC provides better results over VGAFC in terms of validity measures. However, the number of clusters found by both of these algorithms is similar. Thereafter, different fuzzy clustering algorithms (for known number of clusters) are then evaluated by comparing the clustering results of ADEFC and reported in Table 3. Effectiveness of the results is demonstrated by confusion matrix and boxplot in Figs. 4 and 5, respectively. Moreover, for the enhanced database of AAindex1, it has also been observed that the optimal number of clusters is ‘8’ whereas, earlier it was ‘6’ for reduced database of AAindex1. The true clusters plot are shown in Fig. 6 for ADEFC and hierarchical clustered result. It also very clear from Fig. 6 that the ADEFC performs better for producing the optimal number of clusters.

Table 1 Average values of cluster validity indices for AAindex1 database of 402 indices in Phase I
Full size table
Table 2 Number of clusters predicted and average values of cluster validity indices for AAindex1 database of 544 indices in Phase II
Full size table
Table 3 Average values of cluster validity indices for AAindex1 database of 544 indices in Phase II
Full size table
Fig. 4
figure 4

The best Confusion matrix produced by a DEFCMdd for 402 indices, b consensus fuzzy clustering for 544 indices, out of 50 runs

Full size image
Fig. 5
figure 5

Boxplot of different clustering algorithms. a ‘6’ clusters for 402 indices, b ‘8’ clusters for 544 indices, out of 50 runs

Full size image
Fig. 6
figure 6

True clusters plot of AAindex1 database using VAT representation. a ‘6’ clusters for 402 indices, b ‘8’ clusters for 544 indices found by ADEFC

Full size image

Tables 4, 5 and 6 represent the in-depth analysis of each cluster produced by ADEFC and CFC algorithms, respectively. Table 4 shows that the earlier clustering results have been fragmented into different clusters for ADEFC algorithm, and this observation is also supported by other algorithms in Table 5. For example, in Table 5, the number of AAindex1 indices belonging to cluster 4 are 96, 91, 93, 96, 92, 98 based on seven different algorithms. Moreover, the mapping of the clusters found by CFC is given in Table 6. The name of the clusters is provided based on the mapping of known clusters and predicted clusters, which gives us three new clusters, named as electric properties, residue propensity and intrinsic propensities. These names are given by in-depth study of each AA index. For electric properties and residue propensity, most of the indices came from original clusters called alpha and turn propensities and hydrophobicity, respectively. The electric properties describe isoelectric point and polarity of amino acid indices, whereas molecular weight, average accessible surface area and mutability are described by residue propensity. However, intrinsic propensities are formed mostly by the unclustered AA indices, and it describes hydration potential, refractivity, optical activity and flexibility. It is also observed that original clusters are fragmented into other clusters to some extent. The cluster called other properties has now been resolved by assigning them in alpha and turn propensities and physicochemical properties. Moreover, names of the current eight clusters are electric properties, hydrophobicity, alpha and turn propensities, physicochemical properties, residue propensity, composition, beta propensity, and intrinsic propensities.

Table 4 Name of the clusters of AAindex1 database
Full size table
Table 5 Number of AAindex1 indices in each cluster for different algorithms
Full size table
Table 6 Mapping of consensus clusters
Full size table

High-quality indices

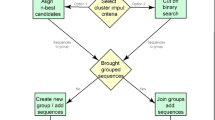
To provide different subsets of HQIs from the consensus clusters, three different approaches are used. For computing the HQIs 8 (HQI8), medoids (centres) of each cluster are considered and these become AA indices called BLAM930101, BIOV880101, MAXF760101, TSAJ990101, NAKH920108, CEDJ970104, LIFS790101, MIYS990104. Similarly for HQI24 and HQI40, three and five AA indices are considered from each cluster, respectively. For computing HQI24, including the cluster medoids, two other indices farthest from the medoids are taken from each cluster. These two farthest indices are less significant for that cluster, which gives more diversable properties of amino acid to that subset. Similarly for HQI40, including the indices computed in HQI24 for each cluster, other two nearest indices of the medoids are considered, that gives strength to the property of medoids indices. All of these HQIs, HQI8, HQI24 and HQI40 are separately given in the supplementary with their amino acid values. Computational process of HQIs is illustrated by Fig. 7.

Fig. 7
figure 7

Illustrated the computational process of HQIs for two clusters, ‘star’ points are considered for HQI2, ‘star +square’ points are considered for HQI6, and ‘star + square + circle’ points are considered for HQI10. In our case, number of clusters is 8, hence, we got HQI8, HQI24 and HQI40

Full size image

Statistical significance test

A non-parametric statistical significance test called Wilcoxon’s rank sum test (Hollander and Wolfe 1999) for independent samples has been conducted at the 5% significance level to show that the statistical significance and clusters found by CFC did not arise by chance. For this purpose, results are obtained by comparing pairs of algorithms, in particular, CFC is compared to each four methods (for phase II). For phase I, there are actually only three pairs of comparisons (one less than in phase II), since DEFCMdd is compared to three other methods. Each group consists of the Minkowski Score (MS) produced by 50 consecutive runs of the corresponding algorithm.

To establish that this goodness is statistically significant, Table 7 reports the p values produced by Wilcoxons rank sum test for comparison of two groups (one group corresponding to DEFCMdd and another group corresponding to some other algorithm in phase I and in phase II, one group corresponding to CFC and another group corresponding to some other algorithm) at a time. As a null hypothesis, it is assumed that there is no significant difference between the median values of two groups. Whereas, according to the alternative hypothesis there is a significant difference in the median values of the two groups. The test reflects the stability and reliability of the algorithm. All the p values reported in the table are less than 0.05 (5% significance level). For example, the rank sum test between the algorithms CFC and DEFCMdd in phase II produced a p value of 0.0012, which is very small. This is strong evidence against the null hypothesis, indicating that the better median values of the performance metrics produced by CFC are statistically significant and have not occurred by chance. Similar result is obtained for other case and for all other algorithms compared to CFC, establishing the significant superiority of the proposed method, which also gives that the clusters formed were not the result of random chance.

Table 7 p values produced by Wilcoxon’s rank sum test comparing DEFCMdd and CFC with other algorithms in Phase I and Phase II
Full size table

Conclusion

Summarizing, this article poses two different issues. First, we propose a novel classification method based on fuzzy clustering and second, to provide three subsets of HQIs to the research community from large AAindex1 database. For the first purpose, several recently developed fuzzy clustering techniques are used to analyze the currently released AAindex1 database. We found novel clusters that divide the AAindex1 database on more clear and biologically meaningful way. The novel clusters describe some of the properties of amino acids like isoelectric point, polarity, molecular weight, average accessible surface area, mutability, hydration potential, refractivity, optical activity and flexibility. We also resolved the problem of unknown amino acid indices by assigning them to clusters that have defined biological meaning. Thereafter, majority voting among the all fuzzy clustering methods are taken to create a consensus clusters. After applying the above procedure, we prepared three datasets of HQIs. The first dataset of HQI8 contains eight HQIs, which belongs at the medoids (centres) of each cluster. Similarly, HQI24 and HQI40 contain 24 and 40 indices, respectively. For HQI24, two most less significant indices are taken from each cluster to provide the versatility of subset. However, HQI40 gives the more strength to the medoids indices. These three datasets of HQIs are very effective for machine learning applications of protein sequences, where the short fragments of chains of amino acids can be encoded very easily and effectively. As a scope of further research, developed code of CFC can be used for other bioinformatics applications that utilize amino acids physico-chemical features for machine learning or data mining classification tasks. Representation of amino acids using vector of real numbers can be further explored in physical chemistry, e.g., in computational studies of polymers (Plewczynski et al. 2007; Rodriguez-Soca et al. 2010; Lu et al. 2007), of selecting inhibitors for a given protein target (Plewczynski et al. 2006, 2010a, b), for PTMs prediction (Plewczynski et al. 2008; Basu and Plewczynski 2010) as well as for finding co-expressed genes (Liu et al. 2008; Kim et al. 2006) in large-scale microarray experiments. The authors are currently working in these directions.