Relationship between vortex structures and shear localization in 3D granular specimens based on combined DEM and Helmholtz–Hodge decomposition

Abstract

The paper presents three-dimensional simulation results of granular vortex structures in cohesionless initially dense sand during quasi-static plane strain compression. The sand behaviour was simulated using the discrete element method (DEM). Sand grains were modelled by spheres with contact moments to approximately capture the irregular grain shape. The Helmholtz–Hodge decomposition of the displacement vector field obtained with DEM was used. The variational discrete multiscale vector field decomposition allowed for separating a vector field into the sum of three uniquely defined components: curl free, divergence free and harmonic. A direct correlation between vortex structures and shear localization was studied. The simulation results showed that vortex structures were closely connected to spontaneous shear localization. They localized early in locations wherein a shear zone ultimately developed. They were affected by the specimen depth.

1 Introduction

Localization of deformation in the form of narrow zones of intense shearing is a basic phenomenon in granular materials [1,2,3,4,5]. Localization under shear may occur in the interior domain in the form of a spontaneous shear zone as a single shear zone, a multiple or a regular pattern of zones. It may be also created at interfaces in the form of an induced single wall shear zone. Localized shear inside of materials is closely related to an unstable behaviour of the entire earth structure. In continuous and discontinuous numerical calculations and laboratory experiments, shear localization is usually identified in granular bodies by grain rotations or micro-polar rotations or by an increase of void ratio in initially dense ones [4]. An understanding of the mechanism of the formation of shear zones is important since they act as a precursor of the ultimate soil failure. Thus it is of major importance to predict them very early for the safety of earth structures and soil behaviour optimization.

Recently Tordesillas et al. [6] and Kozicki and Tejchman [7, 8] have shown that shear localization may be predicted through so-called granular vortex structures defined as the roughly swirling (rotating) motion of several grains around a common central point. The collective particles rotated almost as rigid bodies, however the single particles inside did not rotate. The vortices were calculated at early stages in the pre-peak deformation regime. A dominant mechanism responsible for the vortex formation was the breakage of force chains [6, 9]. The collapse of main force chains lead to a formation of larger voids and appearance of vortices and their build-up to a formation of smaller voids and disappearance of vortices. The vortex motion continuously appeared and disappeared during granular flow. This kinematic mode appeared to be prevalent in grains during granular flow. The calculations in [6,7,8,9] were carried out under 2D conditions only. The 2D vortices were frequently observed in experiments on granular materials (Couette shear [10], plane strain compression [11] and simple shear [12, 13]) and in calculations using the discrete element method (DEM) [14,15,16,17,18,19,20,21,22,23]. They became apparent in experiments and calculations (mainly in shear zones in the residual state) when the motion associated with uniform (affine) strain was subtracted from the actual granular deformation. They are reminiscent of turbulence in fluid dynamics [16], however the grain rotation is several ranges of magnitude smaller than the fluid vortex rotation. In addition, their life time is also shorter than of eddies during turbulent fluid flow. Moreover, granular flow is too slow to induce inertial forces characteristic for turbulences in fluid.

Motivation behind our present work is to calculate centres of 3D granular vortex structures and to find their relationship with shear localization in a deforming granular specimen (in contrast to the previous simplified 2D computations in [7,8,9]). The 3D vortex structures have not been calculated in granulates yet. When identifying granular vortex structures in a three-dimensional kinematic field in dry sand during quasi-static plane strain compression, a novel approach was used based on the combined Helmholtz–Hodge decomposition (HHD) of a displacement vector field [24, 25] and the discrete element method (DEM) [26]. The plane strain compression test is one of the most important geotechnical laboratory tests to experimentally investigate both strength and shear localization in granular materials [4]. The analyses were carried out with spheres with contact moments [7] which were introduced to account for the effect of particle shape angularity, e.g. resistance to relative rotations due to particle interlocking. In order to accelerate the computation time, some simplifications were assumed in analyses: large spheres with contact moments, linear sphere distribution, linear normal contact model and no particle breakage [7]. The calculations were solely carried out with initially dense sand. A three-dimensional discrete element model YADE developed at University of Grenoble by Donze and his co-workers was applied [27,28,29].

In our previous paper [8] we calculated exactly the cores of 2D granular vortex structures in initially dense sand during a quasi-static 2D passive wall translation using the same approach. HHD proved to be an objective, universal and effective technique for identifying the centres of 2D vortex structures during granular flow that was directly based on single grain displacement increments from DEM (but not on displacement fluctuations). The method did not use any additional non-objective parameters. It found the centres of all vortex structures. However it did not determine the size of vortex structures. A strong connection between the location of vortex structures and progressive shear localization was found in simulations. The vortex structures were the precursor of shear localization since they clearly concentrated in the area where shear zones ultimately later formed. Thus the ultimate shear zone pattern has already been detected in early loading stages. The vortex structures allowed to identify shear localization significantly earlier than, e.g. based on single grain rotations which were always the most reliable indicator of shear localization. They developed from the beginning of the deformation process. The vortex centres solely emerged in shear zones. They had a tendency to move along shear zones and their number varied (it was larger on average at the residual state). The right-handed vortices were dominant in the curved shear zone and left-handed ones were dominant in the radial shear zone. In the residual state, local regions of dilatacy and contractancy alternately happened along shear zones with a dominance of local dilatancy. In addition, our preliminary analyses of plane strain compression in [8] detected 2D vortex structures very early at the location where a spontaneous shear zone ultimately occurred. Note that core regions of vortex structures may be detected using different methods (e.g. [6, 9, 31,32,33]).

The innovative points of the present paper are: (a) the calculation results of cores (rotational centres) of 3D granular vortex structures using an objective method from fluid dynamics (that has not yet been applied to granular materials), (b) the comparison between 3D and 2D vortex structures and (c) the investigations of the algorithm’s accuracy for finding the centres of 3D vortices. The vortex structures were directly related to the occurrence of spontaneous shear localization in the granular specimen. The numerical results of vortex structures and local volume changes along a granular shear zone were qualitatively compared with the experimental outcomes of plane strain compression on sand by Abedi et al. [11] and Chupin et al. [30].

The current paper is structured as follows. We first provide a brief summary of our explicit DEM model (Sect. 2). We next report on some DEM results of plane strain compression in sand (Sect. 3). The mathematical algorithm of HHD is described in Sect. 4. Then we demonstrate first 2D (Sect. 5) and later 3D results of HHD (Sect. 6) that demonstrate the efficacy of our approach to identify centres of vortex structures. Sect. 7 qualitatively compares the numerical results with the experimental ones. Finally, we draw conclusions as to the significance of our numerical results in the context of shear localization and failure in granular bodies (Sect. 8).

2 Three-dimensional DEM model

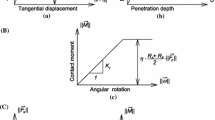
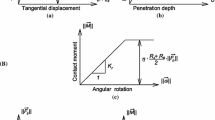
In order to simulate the behaviour of real sand, the 3D spherical discrete element model YADE, developed at University of Grenoble [27,28,29] was used. DEM includes the simple mathematical treatment of engineering problems (complex global constitutive relationships are replaced by simple local contact laws) and has the natural predisposition to account for the material non-uniformity. The outstanding advantage of DEM is the ability to explicitly handle the discrete/heterogeneous nature of granular materials by modelling particle-scale properties, including size and shape, which play an important role in shear localization. The disadvantages are an enormous computational cost and an extensive calibration based on experimentally measured macro-scale properties. The algorithm used in the present DEM, which is based on a description of particle interactions in terms of force laws [26], involves in general two main steps. First, based on constitutive laws, interaction forces between discrete elements are computed. Second, the Newton’s second law is applied to determine for each element the resulting acceleration, which is then time integrated to find the new position. This process is repeated until the simulation is finished. YADE takes advantage of the so-called soft-particle approach, i.e. the model allows for particle deformation, which is modelled as an overlap of particles. A linear elastic normal contact model was used only. In compression, the normal force was not restricted and could increase indefinitely. A choice of a very simple linear elastic normal contact was intended to capture on average various contacts possible in real sands. Figure 1 shows the mechanical response of the linear contact model [27,28,29]. The DEM model [27,28,29] (Fig. 1) may be summarized as follows:

$$\begin{aligned}&\vec {F}_{n}=K_{n}U\vec {N}, \end{aligned}$$

(1)

$$\begin{aligned}&\vec {F}_s=\vec {F}_s + \varDelta \vec {F}_{s} \quad \hbox {with} \quad \varDelta \vec {F}_{s} =K_s \varDelta \vec {X}_s, \end{aligned}$$

(2)

$$\begin{aligned}&K_n =E_c \frac{2R_A R_B }{R_A +R_B }\quad \hbox {and} \quad K_s =v_c E_c \frac{2R_A R_B }{R_A +R_B }, \end{aligned}$$

(3)

$$\begin{aligned}&\Vert {\vec {F}}_{\mathrm{s}} \Vert - \Vert \vec {F}_{\mathrm{n}} \Vert \times \tan \mu \le 0, \end{aligned}$$

(4)

$$\begin{aligned}&\varDelta \vec {M} =K_r \varDelta \vec {\omega }, \end{aligned}$$

(5)

$$\begin{aligned}&K_r =\beta \times K_s \times R^{2}=\beta \times K_s \times R_A R_B , \end{aligned}$$

(6)

$$\begin{aligned}&\Vert {\vec {M}} \Vert -\eta \frac{R_A +R_B }{2} \Vert \vec {F}_n \Vert \le 0, \end{aligned}$$

(7)

$$\begin{aligned}&\vec {F}_{damped}^k = \vec {F}^k - \propto _{d} \cdot sgn(\vec {v}^k) | \vec {F}^k | \quad \hbox {and} \nonumber \\&\vec {M}_{\mathrm{damped}}^k = \vec {M}^k - \alpha \cdot \hbox {sgn}({\omega }^k)| \vec {M}^k |, \end{aligned}$$

(8)

Fig. 1

Mechanical response of linear contact model without (A) and with contact moments (A + B) ([27,28,29]): a tangential contact model, b normal contact model and c rolling contact model and C loading and unloading path (tangential and rolling contact), ${\vec {F}}_{{s}}$—tangential force vector between elements, ${\vec {F}}_{{n}}$—normal force vector between element, ${\vec {M}}$—contact moment vector, $K_{s}$ - tangential stiffness, $K_{n}$—normal stiffness, $K_{r}$—rolling stiffness, U—penetration depth, $\vec {\omega }$- tangential displacement vector, - angular rotation vector, $\mu$—inter-particle friction angle, $\eta$—limit rolling coefficient

where $\vec {F}_n$- the normal force vector, $\vec {F}_s$- the tangential force vector, $K_{n}$—the normal stiffness, $K_{s}$—the tangential stiffness, U—the penetration depth between discrete elements, $\vec {N}$—the unit normal vector at the contact point, $\Delta \vec {X}_s$—the incremental tangential displacement vector, $E_{c}$—the modulus of elasticity of the grain contact, $\upsilon _{c}$—Poisson’s ratio of the grain contact, $R_{A}$ and $R_{B}$—the contacting grain radii, $\mu$—the inter-particle friction angle, $K_{r}$—the rolling stiffness, $\varDelta M$—the contact moment increment, $\Delta \vec {\omega }$—the angular rotational increment vector, $\beta$—the dimensionless rolling stiffness coefficient, R—the equivalent grain radius, $\eta$ - the dimensionless rolling coefficient that specifies the limit friction moment of the rolling motion, $\alpha$—damping parameter, $\vec {F^{k}}$ and $\vec {M^{k}}$- the $k^{\mathrm{th}}$ components of the residual force and moment vector, $\vec {v}^k$ and $\vec {\omega }^k$ - the $k^{th}$ components of the translational and rotational velocity.

No forces were transmitted when grains were separated. The elastic contact constants were specified from the experimental data of a triaxial compression sand test and could be related to the modulus of elasticity of grain material E and its Poisson ratio v [34, 35]. In Eq. 5, the angular rotational increment vectors do not depend on the spherical grain radii in contrast to equations that take the different radii into account [36, 37]. The rolling stiffness $K_{r}$ in Eq. 5 is related to the tangential stiffness $K_{s}$ in Eq. 3 by the formula in [38]. Because the proposed DEM is a fully dynamic formulation, a local non-viscous damping scheme was applied [39] in order to dissipate excessive kinetic energy in a discrete system and facilitate convergence towards quasi-static equilibrium (Eq. 8). The effect of damping was insignificant in quasi-static calculations [34, 35]. Although a non-linear contact law is more realistic, a linear contact law provides similar results with the significantly reduced computation time [35] and therefore was used in the present simulations.

The following five main local material parameters are necessary in our DEM simulations: $E_{c}$ (modulus of elasticity of the grain contact), $v_{c}$ (Poisson’s ratio of the grain contact), $\mu$ (inter-particle friction angle), $\beta$ (rolling stiffness coefficient) and $\eta$ (limit rolling coefficient). In addition, a particle radius R, particle mass density $\rho$ and numerical damping parameter $\alpha$ are required. The DEM material parameters: $E_{c}$, $v_{c}, \mu ,\beta ,\eta$ and $\alpha$ were calibrated using the corresponding homogeneous axisymmetric triaxial laboratory test results on Karlsruhe sand with the different initial void ratio and lateral pressure by Wu [40]. The procedure for determining the material parameters in DEM was described in detail by Kozicki et al. [34, 35]. The index properties of Karlsruhe sand are: mean grain diameter $d_{{ 50}}=0.50$ mm, grain size between 0.08 mm and 1.8 mm, uniformity coefficient $U_{c}=2$, maximum specific weight $\gamma _{d}^{max}=17.4\hbox { kN/m}^{3}$, minimum void ratio $e_{min}=0.53$, minimum specific weight $\gamma _{d}^{min}=14.6~\hbox {kN/m}^{3}$ and maximum void ratio $e_{max}=0.84$. The sand grains are classified as sub-rounded/sub-angular. The following material constants were found in DEM by fitting numerical outcomes with experimental ones during homogeneous triaxial compression: $E_{c}=0.3$ GPa, $v_{c} =0.3$, $\mu =18^{{\circ }}$, $\beta =0.7$, $\eta =0.4~\rho =2.55\hbox { g/cm}^{3}$ and $a=0.08$. Note that the constants $E_{c}$ and $v_{c}$ do not correspond to the elastic constants of grains [34, 35]

3 DEM results of plane strain compression

Our numerical outcomes with respect to 3D vortex structures were related to quasi-static plane strain compression with initially dense sand. The results of 3D DEM calculations were described in detail in [7]. The granular specimen used in DEM had the same size as in the experiments [1], namely: the width $b=4$ cm, height $h=14$ cm and depth $l=8$ cm (out-of-plane direction) (Fig. 2). The linear grain distribution curve was assumed; the grain diameter range was between 1.25 mm and 3.75 mm with the mean grain diameter of $d_{\mathrm{50}}=2.5$ mm. The total assembly contained 56,000 polydisperse particles with the same material constants. The initial void ratio was the same as in the experiments ($e_{o}=0.53$). The flexible vertical walls [7] were assumed to model the membrane surrounding the specimen in experiments (Fig. 2). Both the front and rear specimen sides $4\times 14 \hbox { cm}^{2}$ were blocked in a perpendicular direction to the specimen to enforce plane strain conditions. The bottom surface $4\times 8\hbox { cm}^{2}$ was fixed in a vertical direction and the top surface $4\times 8\hbox { cm}^{2}$ was subjected to the constant vertical displacement $u_{1}$. Along the top, bottom and membrane granular surfaces, the inter-particle friction angle was $\mu =0$. During the loading process, the constant confining pressure of $\sigma _{c}=200$ kPa was applied through the flexible membrane.

Fig. 2

Sand specimen $4\times 14\times 8\hbox { cm}^{3}$ between two vertical flexible membranes during plane strain compression: a initial state, b deformed state and c vertical mid-sectional slice with area of $4\times 14~\hbox {cm}^{2 }$ and thickness of $5 \times d_{\mathrm{50}}$ (1.25 cm) [7] (note that membrane is transparent to make granular specimen visible)

Figure 3 demonstrates one typical evolution of the mobilized internal friction angle (calculated with principal stresses from Mohr’s equation) versus the vertical normal strain $\varepsilon _{1}=u_{1}/h$ and volumetric strain $\varepsilon _{v}$ versus $\varepsilon _{{ 1}}$ for the granular specimen [7]. Figures 4 and 5 show the distribution of sphere rotations $\omega$ and void ratio e at four different values of axial strain in the vertical mid-section slice with the area of $4\times 14\hbox { cm}^{2 }$ and thickness of $5\times d_{{ 50}}$ (1.25 cm with $d_{{ 50}}=2.5$ mm) cut out from the granular specimen [7] (Fig. 2c). Both the quantities were calculated from the volumetric cell $V_{c}=5d_{{ 50}}\times 5d_{{ 50}}\times 5d_{{ 50}}$ moved by $d_{{ 50}}$ in two directions within the slice in order to create a 2D grid of the averaged values in the cell. The cell size, which was smaller than the shear zone thickness $t_{s}$, was chosen with preliminary calculations. The averaging cell larger than $V_{c}$ caused the results too diffusive and with the smaller cell volume $V_{c}$, the results started to too strongly fluctuate.

The DEM results (Fig. 3) exhibit a stress-strain response that is typical of densely packed granular systems. Similarly as in real experiments [1], the initially dense specimen showed an asymptotic behaviour; first it exhibited small elasticity, hardening (connected first to contractancy and then dilatancy), reached a peak of $\phi _{max}=46^{{\circ }}$ at about of $\varepsilon _{1}=5\%$, gradually softened and dilated reaching a residual state of $\phi _{max}=30^{{\circ }}$ at the large vertical strain of 25–30% (Fig. 3a). At the residual state, the volume changes were insignificant (Fig. 3b). The coordination number was initially about 5 and decreased down next to 3.8 during shearing due to dilatancy. During deformation a single internal inclined shear zone spontaneously occurred inside the sand specimen that governed system dynamics after the peak stress. It was marked by shear strain, larger grain rotation and volume increase (Figs. 4, 5). The thickness of the inclined interior shear zone $t_{s}$ was determined on average as about $t_{s}=25$ mm ($10\times d_{{ 50}})$ in the residual state for $\varepsilon _{1}=30\%$, based on the shear strain distribution data (shear strain was pronounced in the shear zone and negligible beyond the shear zone). The calculated shear zone inclination to the bottom was $60^{\mathrm{o}}$ at $\varepsilon _{1}=10\%$ and $67^{{\circ }}$ at $\varepsilon _{1}=30\%$. In the calculated shear zone, the mean void ratio and grain rotation were: $e>0.65$ and $\omega >25^{{\circ }}$. The void ratio distribution was strongly non-uniform in the shear zone (Fig. 5). The specimen globally dilated in the shear zone up to the residual state. In the residual state for $\varepsilon _{1}=30\%$, the resultant void ratio changed between 0.70–0.80 in the shear zone and between 0.53–0.60 outside (Fig. 5d). The maximum resultant rotation in the shear zone at the peak ($\varepsilon _{1}=5\%$) was about $\omega =5^{{\circ }}$ and at the residual state for $\varepsilon _{1}=30\%$ between $\omega =50^{{\circ }}$–55$^{{\circ }}$. Based on both the cumulative rotation (Fig. 4) and void ratio (Fig. 5), the internal inclined shear zone may be noticed close to the stress-strain peak ($\varepsilon _{1}=5\%$).

Fig. 3

DEM results for plane strain compression with sand ($e_{o}=0.53$, $\sigma _{c}=200$ kPa, $d_{\mathrm{50}}=2.5$ mm, $E_{c}=0.3$ GPa, $\vartheta _{c}=0.3$, $\mu =18^{{\circ }}$, $\beta =0.7$, $\eta =0.4$) for one numerical simulation: a mobilized internal friction angle $\phi$ versus normalized vertical displacement of specimen top $\varepsilon _{1}=u_{1}/h$ and b volumetric strain $\varepsilon _{v}$ versus $\varepsilon _{1}$ (h—initial specimen height) [7]

Fig. 4

DEM results for plane strain compression test with sand ($e_{o}=0.53$, $\sigma _{c}=200$ kPa, $d_{\mathrm{50}}=2.5$ mm)—average cumulative grain rotation distribution in degrees in granular specimen for vertical normal strain $\varepsilon _{1}$: a 5%, b 10%, c 20% and d 30% (white squares denote spots without grains) [7]

Fig. 5

DEM results for plane strain compression test with sand ($e_{o}=0.53$, $\sigma _{c}=200$ kPa, $d_{\mathrm{50}}=2.5$ mm) - average cumulative void ratio distribution in granular specimen for vertical normal strain $\varepsilon _{1}$: a 5%, b 10%, d 20%, and d 30% [7]

The experimental curves were satisfactorily reproduced in our DEM simulations of initially dense sand [7] in spite of the fact that the real grain shape, mean grain size and grain size distribution of Karlsruhe sand were not taken into account and the assembling process generated a higher coordination number than in experiments [41]. The calculated shear zone (location, width and inclination) and maps of void ratio (Fig. 5) were also realistic with respect to the experiments. The DEM results of resultant grain rotations (Fig. 4) were qualitatively in agreement with other tests on granular bodies including shear localization wherein single grain rotations were measured in artificial granular materials [4].

4 Helmholtz–Hodge decomposition (HHD)

4.1 Method of calculations

The Helmholtz–Hodge decomposition (HHD) of vector fields, one of the fundamental theorems in fluid dynamics [24, 25, 42], describes a displacement vector field in terms of its curl-free and divergence-free components based on potential functions. The unique Helmholz-Hodge decomposition of each smooth 3D vector field $\vec {\xi }$ yields the following formula

$$\begin{aligned} \vec {\xi }=\vec {\nabla }u +\vec {\nabla } \times \vec {v}+\vec {h}, \end{aligned}$$

(9)

where $\nabla =\left( {\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}} \right) ^{T}$ is the gradient, $\nabla \cdot =\Big (\frac{\partial }{\partial x}+\frac{\partial }{\partial y}+\frac{\partial }{\partial z} \Big )$ denotes the divergence operator, $\nabla \times$ is the curl operator, u denotes the scalar potential field, $\vec {v}$ is the vector potential field and $\vec {h}$ denotes the harmonic vector field. The gradient of the scalar potential function $\vec {\nabla }u$ is called the curl-free component and is related to expansion/contraction (because is irrotational) while the curl of the vector potential function $\vec {\nabla }\times \vec {\mathrm{v}}$ is called the divergence-free component and is related to vorticity, a vector that describes the local rotational motion at a point and pure shear (because is incompressible). The harmonic component which contains the non-integrable component of the field is related to pure translation.

The decomposition of the discrete vector field $\vec {\xi }$ (obtained with DEM simulations) was separately solved for each component of u and $\vec {v}$ by finding the minimum of 2 following quadratic functionals [42] by means of the variational calculus principle [43]

$$\begin{aligned} F\left( u \right) =\frac{1}{2}\mathop \smallint \nolimits _{\varGamma } (\vec {\nabla }u- \vec {\xi })^2 dV \end{aligned}$$

(10)

and

$$\begin{aligned} G(\vec {{v}}) =\frac{1}{2} \mathop \smallint \nolimits _{\varGamma } (\vec {\nabla }\times \vec {v}- \vec {\xi })^2 dV, \end{aligned}$$

(11)

where

• $\varGamma$ is the domain where the vector field $\vec {\xi }$ is defined – the total volume of all tetrahedrons (or triangle areas) where the Delaunay triangulation was performed,

• u is the discrete scalar potential at the node $'i'\, u\left( {\vec {r}}\right) = \sum _{i} \phi _i (\vec {r})u_i$,

• $\vec {v}$ is the discrete vector field at the node $'i'\, \vec {v}(\vec {r})=\sum _i \phi _i (\vec {r}){\vec {v_l}}$,

• $\phi _i \left( {\vec {r}} \right)$ is the piecewise-linear basis function (shape function) valued 1 at ${\vec {r_l}}$ (the i-th node) and valued 0 at all other nodes,

• $\vec {r}$ is the spatial coordinate in $\varGamma$ using the Cartesian coordinate system $\vec {r}=(x,y,z)$.

The minimum of the quadratic functionals $\hbox {F}(u)$ and $\hbox {G}(\vec {v})$ was found by requiring that their functional derivatives are zero

$$\begin{aligned} \frac{\partial F\left( u \right) }{\partial u_i}=\frac{1}{2}\frac{\partial }{\partial u_i }\mathop \int \nolimits _{\varGamma } (\vec {\nabla }u- \vec {\xi })^2 dV=0 \end{aligned}$$

(12)

and

$$\begin{aligned} \frac{\partial G\left( {\vec {v}} \right) }{\partial v_i}= \frac{1}{2} \frac{\partial }{\partial v_i} \mathop \int \nolimits _{\Gamma } (\vec {\nabla } \vec {\times v}- \vec {\xi })^2 dV=0. \end{aligned}$$

(13)

Solving for $u(\vec {r})$ using the variational calculus :

$$\begin{aligned} 0= & {} \frac{\partial F\left( u \right) }{\partial u_i }=\frac{1}{2}\mathop \int \nolimits _{\varGamma } \frac{\partial }{\partial u_i }(\vec {\nabla }u - \vec {\xi })^2 dV=,\nonumber \\= & {} \frac{1}{2}\mathop \int \limits _{\varGamma } 2(\vec {\nabla } u-\vec {\xi })\cdot \frac{\partial }{\partial u_i }(\vec {\nabla } u-\vec {\xi })dV \nonumber \\= & {} \mathop \int \limits _{\varGamma } (\vec {\nabla } u-\vec {\xi })\cdot \frac{\partial }{\partial u_i }\left( \vec {\nabla } \left( \mathop \sum \limits _j \phi _i \left( \vec {r} \right) u_j \right) -0\right) dV= \nonumber \\= & {} \mathop \int \nolimits _{\varGamma } (\vec {\nabla }u- \vec {\xi } ) \cdot (\vec {\nabla } \phi _i (\vec {r}))dV. \end{aligned}$$

(14)

Thus Eq. 14 becomes

$$\begin{aligned} \mathop \int \nolimits _{\varGamma } \vec {\nabla } \phi _i (\vec {r}) \cdot \vec {\nabla } u (\vec {r}) dV= \mathop \int \nolimits _{\varGamma } \vec {\nabla } \phi _i (\vec {r}) \cdot \vec {\xi }(\vec {r}) dV, \end{aligned}$$

(15)

and similarly for $\vec {v}$

$$\begin{aligned} \mathop \int \nolimits _{\varGamma } \vec {\nabla } \phi _i (\vec {r}) \times (\vec {\nabla } \times \vec {v}(\vec {r}))dV =\mathop \int \nolimits _{\varGamma } \vec {\nabla } \phi _i (\vec {r}) \times \vec {\xi } (\vec {r})dV. \end{aligned}$$

(16)

The integrals in Eqs. 15 and 16 were re-written in a discrete form as a sum over tetrahedron volumes for each i-th node, creating a set of linear equations (one equation per node) that was solved for the unknows $u_{i }\hbox { and }\vec {v}_{i}$ using standard methods (e.g. inverting matrix or conjugate gradient)

$$\begin{aligned}&\mathop \sum \nolimits _{T_k \in N\left( i \right) } (\vec {\nabla } \phi _i)_k \cdot (\vec {\nabla }u)_k | T_k | \nonumber \\&\quad = \mathop \sum \nolimits _{T_k \in N (i)} (\vec {\nabla }\phi _i)_k \vec {\cdot \xi _k} | T_k |, \end{aligned}$$

(17)

$$\begin{aligned}&\mathop \sum \nolimits _{T_k \in N\left( i \right) } (\vec {\nabla } \phi _i)_k \times (\vec {\nabla }\times \vec {v})_k | T_k | \nonumber \\&\quad = \mathop \sum \nolimits _{T_k \in N (i)} (\vec {\nabla }\phi _i)_k \times \vec {\xi _k} | T_k |, \end{aligned}$$

(18)

where $\left| {T_k } \right|$—the tetrahedron volume (triangle area), $\vec {(\nabla }\phi _i )_k$- the vector orthogonal to the tetrahedron face f (triangle edge f for 2D cases) opposite to the i-th node in the k-th tetrahedron (triangle), pointing towards the i-th node with the magnitude of $\frac{area\left( f \right) }{3\left| {T_k } \right| } \quad \left( {\hbox {or}~\frac{\hbox {length}\left( f \right) }{2\left| {T_k } \right| }\hbox { for }2\hbox {D cases}} \right)$, N(i)—the set of all tetrahedrons (triangles) containing the i-th node. A variational calculus approach was used [43] that allowed for finding the unknown vector fields $\vec {\nabla }u$ and $\vec {\nabla }\times \vec {v}$ by examining the difference between them and the known vector field $\vec {\xi }$ that was obtained in DEM simulations (Eqs. 10, 11). By demanding that this difference is minimum (the minimum was found by assuming that the derivatives of the functionals were equal to zero, Eqs. 12 and 13), the vector fields ${\vec {\nabla }}u$ and ${\vec {\nabla }} \times \vec {v}$ were explicitly determined. The explicit calculation for ${\vec {\nabla }}u$ was given in Eqs. 14 and 15 and for ${\vec {\nabla }} \times \vec {v}$ in Eq. 16. The accurate discrete multiscale Helmholz-Hodge decomposition of vector fields on arbitrary tetrahedral grids was proposed by Tong et al. [42]. In order to create a grid, the centre of each sphere was a node in the Delaunay triangulation and the i-th node had the coordinate $\vec {r_l }$. Then the discrete piecewise-constant vector field $\vec {\xi }(\vec {r_l })=\mathop \sum \nolimits _k \psi _k \left( {{\vec {r}}} \right) \vec {\xi _k}$ was created by assigning the constant vector value $\vec {\xi _k }$ to each k-th tetrahedron ($\psi _{k}$ is the piecewise-constant basis function equal to 1 inside the k-th tetrahedron and 0 otherwise). This value was calculated as the average of sphere displacement increments $\vec {d_n }$ which constituted each tetrahedron $\vec {\xi _k }=1/4\mathop \sum \nolimits _{n=1}^{n=4} \vec {d_n }$ in the 3D case or each triangle $\vec {\xi _k }=1/3\mathop \sum \nolimits _{n=1}^{n=3} \vec {d_n }$ in the 2D case. Since u and $\vec {v}$ are the piecewise linear functions described using a piecewise-linear basis shape function $\phi _i \left( {{\vec {r}}} \right)$, their derivatives $\nabla$ will be piecewise-constant, hence the solution for the piecewise-constant $\vec {\xi }({\vec {r}})$ discrete vector field is exact [42]. Equations 17 and 18 describe the i-th row of 2 sparse matrices and were numerically solved for the unknowns $u_{i }\hbox { and } \vec {v}_{i}$ using the Eigen library with a bi-conjugate gradient stabilized solver [44]. The third component of Eq. 9 (the harmonic vector field) was determined as $\vec {h}=\vec {\xi }-\vec {\nabla }u-\vec {\nabla } \times \vec {v}$. All displacement vectors in the Helmholtz–Hodge decomposition (the vector field $\vec {\xi }$ in Fig. 6) were calculated from the differences of sphere positions for two different strains $\varepsilon _{1}$: ($x_{2}, y_{2}, z_{2})$ for $\varepsilon _{1}^{2}$ and ($x_{1}, y_{1}, z_{1})$ for $\varepsilon _{1}^{1}$, where $\varepsilon _{1}^{2} -\varepsilon _{1}^{1}=0.02\%$. This strain increment corresponded to $IT=1000$ iterations. The value of IT was based on earlier simulations [9]. For ${IT}>1000$ the results of vortices were similar. The calculated vector fields were plotted using the line integral convolution method [45]. No additional smoothing techniques [42] were used in the detection’s method to find sinks, sources and vortices.

4.2 Boundary conditions

In order to obtain a unique solution, appropriate boundary conditions have to be assumed [25]. The system of linear equations in HHD was solved using the following general boundary conditions: ${\vec {\nabla }}\times \vec {v}$ (divergence-free component - incompressible component) was tangential to the domain boundary $\vec {v}|_{\partial \mathrm{T}}=0$ and ${\vec {\nabla }}u$ (curl-free component - irrotational component) was orthogonal to the boundary domain $u|_{\partial \mathrm{T}} =0$. The proof of uniqueness and orthogonality for these boundary conditions, called N-P (normal-parallel) boundary conditions, which should be always maintained for flow problems, may be found in [46]. Note that a change of these boundary conditions suggested in [47] may create an invalid or ill-posed problem [48]. The so-called Hodge–Morrey–Friedrichs boundary conditions may be also used [25]. The boundary conditions obviously influence vector fields close to specimen boundaries. In particular when the number of particles is low; vortex structures may be solely detected in the specimen centre since the vector field ${\vec {\nabla }} \times \vec {v}$ is forced by boundary conditions to be parallel to boundaries. In our previous calculations of the passive wall translation [7], the number of spheres along the height and length of the granular specimen was high enough (200–400) and the effect of boundaries proved to be insignificant on the distribution of vortices. In the present paper due to a relatively small number of particles along the specimen width b during plane strain compression ($\approx 16=b/d_{\mathrm{50}}=40/2.5$), the effect of boundary conditions during calculations of vortex structures was weakened by introducing extra particles outside boundaries [47] (Fig. 6). The extra nodes were added in a tetrahedral (3D) grid with a node distance of 4.5 mm using the criterion that each extra node had to be at the distance of 4 mm or greater from centres of spheres in the specimen. These nodes were added with the maximum distance of up to 50 mm around the granular specimen (Fig. 6). The incremental displacement vector $\vec {\xi }$ in these artificial nodes was calculated by the Gaussian averaging with true specimen nodes only (using the averaging radius of $80\hbox { mm }(=2\times b))$. Some large vectors in Fig. 6 appeared if single grains suddenly underwent excessive displacements.

Fig. 6

2D displacement vectors of single spheres (input vector field in Eq. 10) in arbitrary vertical cross-section of granular specimen including artificial extra nodes around for weakening boundary conditions ($\varepsilon _{1}=10\%$) (displacement vectors are enlarged by factor 200) [8]

5 Numerical 2D results using HHD/DEM approach

In the first step, the 2D calculations were carried out during plane strain compression in order to compare them with our earlier 2D results regarding the passive wall translation [8]. The 2D vortices were computed in the vertical cross-sectional slice with the area of $4\times 14\hbox { cm}^{2 }$ and thickness of $5 \times d_{\mathrm{50}}$ of Fig. 2c that was located at the specimen mid-depth l. The coordinates of each sphere (x, y, z) were projected onto the plane using the coordinates (x, y). Thus, all spheres were included in the slice with the thickness of $5\times d_{\mathrm{50}}$ (no averaging was performed over the volume). The results of the displacement vector field $\vec {\xi }$, scalar field gradient ${\vec {\nabla }}u$ (curl-free component related to compressibility), vector field curl ${\vec {\nabla }}\times \vec {v}$ (divergence-free component related to vorticity) and harmonic vector field $\vec {h}$ (related to pure translation) based on DEM results of Sect. 3 are presented in Figs. 7, 8, 9 and 10.

Fig. 7

DEM results: A mobilized internal friction angle $\phi$ versus normalized vertical displacement of specimen top $\varepsilon _{1}=u_{1}/h$ with marked strain points and B evolution of 2D displacement vector field $\vec {\xi }$ in granular specimen area $x\times y$ during vertical normal strain $\varepsilon _{1}$: a 1%, b 1.5%, c 2%, d 3%, e 4%, f 5%, g 10%, h 20% and i 30% (varying scale denotes incremental displacement vector length in [mm/iteration])

Fig. 8

Evolution of 2D vector field curl ${\vec {\nabla }} \times \vec {v}$ (divergence-free component related to vorticity) in granular specimen area $x\times y$ for vertical normal strain $\varepsilon _{1}$: a 1%, b 1.5%, c 2%, d 3%, e 4%, f 5%, g 10%, h 20% and i 30% (varying scale denotes component of vector potential $\vec {v}$ perpendicular to specimen in [$\hbox {mm}^{2}/\hbox {iteration}$]), green circles describe centres of right-handed vortices and red circles denote centres of left-handed vortices) (color figure online)

Fig. 9

Evolution of 2D scalar field gradient ${\vec {\nabla }}u$ (curl-free component related to contractancy/dilatancy) in granular specimen area $x\times y$ during vertical normal strain $\varepsilon _{1}$: a 1%, b 1.5%, c 2%, d 3%, e 4%, f 5%, g 10%, h 20% and i 30% (green circles denote sources (centres of local dilatancy regions) and red circles denote sinks (centres of local contractancy regions)) (color figure online)

Fig. 10

Evolution of 2D harmonic vector field $\vec {h}$ in granular specimen area $x \times y$ during vertical normal strain $\varepsilon _{1}$: a 1%, b 1.5%, c 2%, d 3%, e 4%, f 5%, g 10%, h 20% and i 30% (varying scale denotes incremental vector length h)

Figure 7 shows the evolution of the displacement vector field $\vec {\xi }$ during deformation $\varepsilon _{1}$ (the sphere displacement increment directions are marked by the white arrows). The scale attached denotes the sphere displacement vector length during $IT=1000$ iterations in [mm/iteration], ranging from 0 up to 0.1 mm/iteration. Based on the incremental displacement vector length and vector direction changes, the displacement field inside the specimen (mid-region) started to be non-uniform from the beginning of deformation. An inclined internal shear zone was already well visible along the specimen width for $\varepsilon _{1}=2\%$ (Fig. 7b). Beyond the internal shear zone the material was practically rigid. Based on the displacement vectors, one can recognize some right-handed vortex structures whose size is limited to the width of the shear zone.

The evolution of the vector field curl ${\vec {\nabla }} \times \vec {v}$ (divergence-free component related to vorticity) during deformation $\varepsilon _{1}$ is presented in Fig. 8. The scale denotes the component of the vector potential $\vec {v}$ perpendicular to the specimen in [$\hbox {mm}^{2}$/iteration]), changing from $-\,0.50 \hbox { mm}^{2}$/iter up to $0.05~\hbox {mm}^{2}$/iter. The green circles describe the local minima of the scalar field $\Vert v\Vert$ (equivalent to centres of right-handed vortices) and red circles the local maxima of the scalar field $\Vert v\Vert$ (equivalent to centres of left-handed vortices). These local extrema of the scalar field $\Vert v\Vert$ were defined in such a way that the values of $\Vert v\Vert$ in all neighbouring nodes in the mesh created by the Delaunay triangulation were smaller/larger than $\Vert v\Vert$ at the node in question. The diameter of each circle indicates the relative magnitude of extremum points.

The vortex structures emerged from the beginning of the specimen deformation. Initially their centres were seemingly randomly located. However, by $\varepsilon _{1}\ge 1\%$, they were quickly aligned along the line of the ultimate location of the spontaneous shear zone (Fig. 8a–c). In the range of $\varepsilon _{1}=$ 3–4% they were more concentrated around the shear zone mid-point (Fig. 8d, e) before a final shear direction was chosen. Thus the final shear zone turned out to be encoded in the grain kinematics far before the stress peak ($\varepsilon _{1}=5\%$). This outcome is in accordance with our earlier calculation results for plane strain compression based on displacement fluctuations [7] and calculation results based on bottlenecks in force transmission through the contact network [49]. The right-handed vortices (green circles) dominated during progressive shear deformation. The left-handed vortices (red circles) were evidently in minority. The distance of vortex-centres and their intensity along the shear zone was varying in time. Some single vortices also occurred (very intermittently) beyond the shear zone. Note that the size of vortex structures could not be directly deduced from HHD since the vortex structures corresponded to points only that were associated with their rotational centres. The size of vortices may be detected with the aid of other methods, based on the vector displacement field of single particles [6, 50,51,52]].

The evolution of the scalar field gradient ${\vec {\nabla }}u$ (curl-free component related to compressibility) during deformation $\varepsilon _{1}$ is described in Fig. 9. The green circles describe the sources (local minima of the scalar potential u - centres of local dilatancy regions) and the red circles denote the sinks (local maxima of the scalar potential u—centres of local contractancy regions). The magnitude of sources and sinks was again expressed by the different diameter of green and red circles. The scale attached denotes the scalar potential u in [$\hbox {mm}^{2}$/iteration] (sign (-) - sources in the scalar potential field u, sign (+) – sinks in the scalar potential field u), varying between $-0.1\hbox { mm}^{2}/\hbox {iter}$ and $0.25\hbox { mm}^{2}/\hbox {iter}$.

The local dilatancy (sources) and local contractancy extremum points (sinks) started to develop in the shear zone region for $\varepsilon _{1}>1\%$ (thus clearly before the stress peak $\varepsilon _{1}=1\%$, Fig. 3b). During progressive shear deformation, the sources and sinks alternately happened inside of the shear zone area. The magnitude of sources and sinks was the smallest in the residual state (Fig. 9i). This outcome is in accordance with the alternating distribution of local void ratio in shear zones during DEM calculations [9]. Note that local dilatant regions are usually connected to the collapse of main force chains and creation of vortices, and local contractant regions are linked with the build-up of main force chains and disappearance of vortices [9].

Finally Fig. 10 shows the evolution of the harmonic increment vector field $\vec {h}$ during deformation $\varepsilon _{1}$. The scale denotes the vector length in [mm/iteration] changing from 0 mm up to 0.06 mm. The evolution $\vec {h}$ was practically the same independently of $\varepsilon _{1}$ since the top boundary continuously moved at the same displacement increment. Some irregularities in the harmonic field appeared due to large vectors (see Fig. 6) since the vector field of sphere displacements was not smoothed. The irregularities were the most pronounced in the shear zone (Fig. 10f–i). The 2D results depicted in Figs. 7, 8, 9 and 10 were very similar as those during passive wall translation [8].

6 Numerical 3D results using combined HHD/DEM approach

This section includes the numerical results of vortex structures in 3 dimensions in the granular specimen (including 56,000 spheres with contact moments) subjected to plane strain compression (with $IT=1000$). Figure 11 shows the three-dimensional vector field curl ${\vec {\nabla }} \times \vec {v}$ during evolving deformation. The tubes shown link all local extrema (vortex structures). A simple algorithm was used to connect these local extrema. In the half-space determined by the direction of the vector $\vec {v}$ at the current node, all nodes connected with the current node through a Delauney’s triangulation edge were checked. Since the starting node was a local maximum, all other node values were smaller. One node with the largest magnitude vector ${\vert }\vec {v}{\vert }$ was selected and if it was smaller by $\delta =5\%$ or less than the value $\left| {\vec {v}} \right|$ at the current node, a tubular connection was formed. If it was smaller more than $\delta =5\%$, the formation of tubular connections between nodes was stopped. In the next step, the node to which a tubular connection was formed, was considered a current node and previous instructions were repeated in a loop. A different algorithm for finding ridges in 3D vector fields might be also used (e.g. by Krissian et al. [53]). The steps were repeated until all paths from all local extrema were traced. Later the algorithm was repeated for the opposite direction of $\vec {v}$. Note that the three-dimensional vector field curl ${\vec {\nabla }}\times \vec {v}$ of Fig. 11 was shown in two 3D views for $\varepsilon _{1}=4\%$ and $\varepsilon _{1}=5\%$ (Fig. 11g, i) where some single steep tubes occurred. The tubes were mainly inclined or horizontal (Fig. 11). The single steep tubes in Fig. 11g, i were due to the occurrence of single intermittent vortices beyond the shear zone (see also Figs. 12, 14, 15) and the tube detection algorithm which enforced them to link all local extremum points.

Fig. 11

Three-dimensional vector field curl ${\vec {\nabla }}\times {\vec {v}}$ (divergence-free component related to vorticity) in granular specimen during plane strain compression for vertical normal strain $\varepsilon _{1}$: a $\varepsilon _{1}=0\%$, b $\varepsilon _{1}=0.5\%$, c $\varepsilon _{1}=1.0\%$, d $\varepsilon _{1}=1.5\%$, e $\varepsilon _{1}=2\%$, f $\varepsilon _{1}=3\%$, g $\varepsilon _{1}=4\%$, h $\varepsilon _{1}=4.5\%$, i $\varepsilon _{1}=5\%$, j $\varepsilon _{1}=10\%$, k $\varepsilon _{1}=20\%$ and l $\varepsilon _{1}=30\%$ (dark green circles describe centres of right-handed vortices and red circles denote centres of left-handed vortices, green tubes are lines which link centres of vortices for parameter $\delta =5\%$, tube diameter is proportional to ${\vert }\vec {v}{\vert }$, note that two different 3D views are shown for $\varepsilon _{1}=4\%$ and $\varepsilon _{1}=5\%$) (color figure online)

Figures 12, 13, 14 and 15 present the centres of vortex structures at 4 different specimen vertical cross-sections (mid-depth, front side, rear side and 2/3 depth of the granular specimen) with increasing vertical normal strain $\varepsilon _{1}$. The circles with the different diameters in Figs. 12, 13, 14 and 15 denote the spots where the vertical cross-sectional slices intersected the 3D tubes of Fig. 11. The circle diameters do not again represent the spatial size of vortices (that are not defined in the present paper) but the magnitude of the vector ${\vert }\vec {v}{\vert }$, related to the rotational velocity around the vortex axis. The threshold value of $\delta =$ 2–5% was tested. The larger values of $\delta$ resulted in too many tubes (contributing to an obscure image).

The 3D results are certainly more exact that the 2D results, since a significantly larger number of spheres was captured in 3D computations (56,000 spheres against 8000 spheres in the 2D slice), that caused a smoother vector field and smaller calculation errors. Slightly less vortex structures occurred in the shear zone and beyond the shear zone in 3D conditions than in 2D ones (compare Fig. 8 with 12, 13, 14 and 15). However, the 2D vortex calculations were performed for the slice of the thickness of $5\times d_{\mathrm{50}}$ by ignoring the z-coordinate of each sphere. Since all sphere coordinates were projected onto the plane, it might happen therefore that two spheres, which were at the distance of $5 \times d_{\mathrm{50}}$ on the opposite sides of the slice, could lie very next to each other. Since their real 3D distance was large, they might move in significantly different plane-projected directions. When two nodes, close to each other in the 2D $\xi$-vector field, moved in significantly different directions, a disturbance in the vector field occurred that contributed to the larger number of vortices.

In 3D analyses the right-handed vortices (green circles) were again in the clear majority during the progressive deformation (Figs. 11, 13, 14, 15) as in 2D calculations (Fig. 8) due to the shear direction in the shear zone. The left-handed vortices appeared again episodically. The 3D vortex structures occurred in the shear zone and were spatially non-uniform along the specimen depth (their number was different in 4 vertical cross-sections, Figs. 12, 13, 14, 15). Their centres happened mainly at the position of the final shear zone and they appeared from the beginning of deformation. Initially their number was extremely high and their distribution was random in the entire specimen (Fig. 11a, b). Later they started to coalesce around the eventual, single, persistent shear zone (Fig. 11c, d). In the range of $2\%\le \varepsilon _{1}\le 4.5\%$ (Fig. 11e–h), they mostly gravitated toward the shear zone centre (except of $\varepsilon _{1}=4\%$), and then from $\varepsilon _{1}=5\%$ (Fig. 11i) onward they coalesced again (Figs. 11j–l). The number of all left-handed and right-handed vortex cores in the entire 3D specimen as the function of the vertical normal strain $\varepsilon _{1}$ may be seen in Fig. 16.

Fig. 12

Three-dimensional vector field curl ${\vec {\nabla }}\times {\vec {v}}$ (divergence-free component related to vorticity) in granular specimen during plane strain compression at its front side for different vertical normal strain $\varepsilon _{1}$: a $\varepsilon _{1}=1\%$, b $\varepsilon _{1}=1.5\%$, c $\varepsilon _{1}=2\%$, d $\varepsilon _{1}=3\%$, e $\varepsilon _{1}=4\%$, f $\varepsilon _{1}=5\%$, g $\varepsilon _{1}=10\%$, h $\varepsilon _{1}=20\%$ and i $\varepsilon _{1}=30\%$ (scale denotes component of vector potential $\vec {v}$ perpendicular to specimen in [$\hbox {mm}^{2}$/iteration]), green circles describe centres of right-handed vortices

Fig. 13

Three-dimensional vector field curl ${\vec {\nabla }}\times {\vec {v}}$ (divergence-free component related to vorticity) in granular specimen during plane strain compression at its mid-depth for different vertical normal strain $\varepsilon _{1}$: a $\varepsilon _{1}=1\%$, b $\varepsilon _{1}=1.5\%$, c $\varepsilon _{1}=2\%$, d $\varepsilon _{1}=3\%$, e $\varepsilon _{1}=4\%$, f $\varepsilon _{1}=5\%$, g $\varepsilon _{1}=10\%$, h $\varepsilon _{1}=20\%$ and i $\varepsilon _{1}=30\%$ (scale denotes component of vector potential $\vec {v}$ perpendicular to specimen in [$\hbox {mm}^{2}$/iteration]), green circles describe centres of right-handed vortices

Fig. 14

Three-dimensional vector field curl ${\vec {\nabla }}\times {\vec {v}}$ (divergence-free component related to vorticity) in granular specimen during plane strain compression at its rear side for different vertical normal strain $\varepsilon _{1}$: a $\varepsilon _{1}$=1%, b $\varepsilon _{1}$=1.5%, c $\varepsilon _{1}=2\%$, d $\varepsilon _{1}=3\%$, e $\varepsilon _{1}=4\%$, f $\varepsilon _{1}=5\%$, g $\varepsilon _{1}=10\%$, h $\varepsilon _{1}=20\%$ and i $\varepsilon _{1}=30\%$ (scale denotes component of vector potential $\vec {v}$ perpendicular to specimen in [$\hbox {mm}^{2}$/iteration]), green circles describe centres of right-handed vortices (color figure online)

Fig. 15

Three-dimensional vector field curl ${\vec {\nabla }}\times {\vec {v}}$ (divergence-free component related to vorticity) in granular specimen during plane strain compression at 2/3 depth for different vertical normal strain $\varepsilon _{1}$: a $\varepsilon _{1}=1\%$, b $\varepsilon _{1}=1.5\%$, c $\varepsilon _{1}=2\%$, d $\varepsilon _{1}=3\%$, e $\varepsilon _{1}=4\%$, f $\varepsilon _{1}=5\%$, g $\varepsilon _{1}=10\%$, h $\varepsilon _{1}=20\%$ and i $\varepsilon _{1}=30\%$ (scale denotes component of vector potential $\vec {v}$ perpendicular to specimen in [$\hbox {mm}^{2}$/iteration]), green circles describe centres of right-handed vortices) (color figure online)

Fig. 16

Three-dimensional DEM results for plane strain compression showing number of: a single right-handed vortices and b single left-handed vortices N b in entire 3D granular specimen against vertical normal strain $\varepsilon _{1}$ ( $\delta =5\%$)

The maximum number of right-handed vortices was 2–15 before the peak stress ($\varepsilon _{1}\le 5\%$) and about 40–50 after the peak stress ($\varepsilon _{1}\ge 5\%$) (Fig. 16a). Their number decreased from the beginning of deformation up to the stress peak ($\varepsilon _{1}=5\%$), increased up to $\varepsilon _{1}=10\%$ and then remained the same up to $\varepsilon _{1}=30\%$. The maximum number of episodic left-handed vortices was about 20 (Fig. 16b).

Figure 17 presents the period $T=1/f$ of right-handed vortices in the entire specimen against the global vertical strain in the range of $\Delta \varepsilon _{1}=$ 0–30% (Fig. 17a) and $\Delta \varepsilon _{1}=$ 20–30% (in the residual state) (Fig. 17b) using the Fourier transformation. The values of T were not related to time but to the strain $\varepsilon _{1}$ due to a quasi-static problem considered (regardless of the dynamic nature of DEM). In both the strain ranges of $\Delta \varepsilon _{1}=$ 0–30% (full range, Fig. 17a) and $\Delta \varepsilon _{1}=$ 20–30% (residual region, Fig. 17b), the predominant period of right-handed vortices was about 6% of $\varepsilon _{1}$ in the entire specimen. The smaller regular periods of right-handed vortices were also observed in the range of $\Delta \varepsilon _{1}=$ 20–30% (Fig. 17b). Similar predominant periods of vortices (4% of $\varepsilon _{1})$ were also calculated during a quasi-static passive wall translation [7].

Fig. 17

Three-dimensional DEM results for plane strain compression with sand showing number of single right-handed vortices N in entire 3D granular specimen as function of period of vertical normal strain $\varepsilon _{1}$ in range of: a $\Delta \varepsilon _{1}=$ 0–30% (full range) and b $\Delta \varepsilon _{1}=$20–30% (residual range) based on Fourier transformation ($\delta =5\%$)

With a lower threshold value of the parameter $\delta =2\%$, the distribution of vortex centres was similar, however slightly less connecting tubes between local extrema were computed. The predominant period of vortices was the same for the vertical normal strain range $\varepsilon _{1}$ of 0–30% and slightly smaller for the vertical normal strain range $\varepsilon _{1}$ of 20–30% (Fig. 18).

Fig. 18

Three-dimensional DEM results for plane strain compression with sand showing number of single right-handed vortices N in entire 3D granular specimen as function of period of vertical normal strain $\varepsilon _{1}$ in range of: a $\Delta \varepsilon _{1}=$ 0–30% (full range) and b $\Delta \varepsilon _{1}=$ 20–30% (residual range) based on Fourier transformation ($\delta =2\%$)

The calculation results of Sects. 5 and 6 clearly indicate that the vortex-motion kinematics should be explicitly considered in granular materials within continuum mechanics modelling, since it is a preferable motion type during granular flow (granular material tends to organize its flow into a collection of vortices, similarly to fluids).

7 Comparison with experiments

In plane strain compression laboratory tests on a sand specimen by Abedi et al. [11] and Chupin et al [30] ($b=4$ cm, $h=14$ cm, $l=8$ cm and $d_{\mathrm{50}}=0.84$ mm), the digital image correlation (DIC) technique was used to detect vortex structures and volumetric strain non-uniformity in the spontaneous inclined shear zone in the residual state. DIC is a non-contact experimental technique to measure surface displacements on a deforming solid [54]. In order to determine the vortices in the form of a rotational motion of several grains around its central point, the displacement fluctuation vectors of small clusters of grains were calculated from the mean displacement vector field. A systematic vortex formation and vortex disappearance was observed in the inclined shear zone after the stress-strain peak that propagated from the left side up to the right side. The vortices were short-lived. The maximum 5 right-handed vortices and left-handed vortices temporarily occurred in the shear zone. They had a periodic character. In addition, a pattern of nearly periodic spatial variation of local volume changes (including dilatant and contractant regions) along the length of the shear zone was also observed in the critical state. Our calculations showed that vortex structures and local volume changes were observed to occur in the shear zone throughout the entire deformation regime (note that [11] and [30] did not report experimental observations before the peak). The computed number of vortex structures was also significantly higher than this in experiments. This difference between the calculation outcomes and experimental results is due to: a) a different method used to detect vortices, b) a smaller mean grain diameter $d_{\mathrm{50}}$ in the experiment $d_{\mathrm{50}}=0.84$ mm (in DEM: $d_{\mathrm{50}}=2.5$ mm) and c) a lack of the real sand grain shape in DEM. Our numerical detection method (based on single grain displacements) is an objective method that detects the centres of all vortex structures independently of their size. The experimental detection’s method was however based on displacement fluctuations of small clusters of grains (not single grains) and was strongly limited by the accuracy of DIC. Moreover DIC is sensitive to the assumed subset size and image length resolution [54].

8 Conclusions

The following conclusions may be offered from DEM simulations of 3D granular vortex structures in initially dense sand during quasi-static plane strain compression:

• The occurrence of vortex structures was closely related to shear localization. The vortices proved to be an early precursor of shear localization since their centres concentrated in the region where the shear zone ultimately formed. They developed throughout deformation. They mainly emerged in the main inclined internal shear zone and were strongly non-uniform in a spatial arrangement. Vortices rotating in a clock-wise direction mainly occurred due to the shearing direction. Left-handed vortices were rarely observed. Thus, the vortex structures allowed identification of shear localization earlier than, for example, based on single grain rotations or an increase of void ratio.

• The number of 3D vortices spatially and temporarily changed along the specimen depth.

• The centres of local regions of dilatancy and contractancy alternately happened in the shear zone with a dominance of local dilatant regions.

• An early prediction possibility of shear localization through the formation of vortex structures creates an interesting perspective for a detection of impending failure in granular bodies within continuum mechanics (inherently connected with shear localization).