Introduction

Rainfall is a highly significant piece of hydrologic data. Such data are recorded as observational data through comprehensively designed rainfall station networks. However, rainfall records are often incomplete because of missing rainfall data in the measured period, or insufficient rainfall stations in the study region. To resolve the problems of such partial rainfall data, probable rainfall data can be estimated through spatial interpolation techniques.

Various spatial interpolation techniques have already been employed in related fields. Such techniques can be divided into geographical statistics and non-geographical statistics. Examples include nearest neighbor (NN), Thiessen polygons, splines and local trend surfaces, global polynomial (GP), local polynomial (LP), trend surface analysis (TSA), radial basic function (RBF), inverse distance weighting (IDW), and geographically weighted regression proposed by Fotheringham et al. (2002), which are all classified as non-geographical statistics. On the other hand, various forms of Kriging method are classified as geographical statistics (Lam 1983; Jeffrey et al. 2001; Price et al. 2000; Li and Heap 2008; Yeh et al. 2011).

As this article aims to discuss the spatial interpolation of rainfall, the research literature carried out by Naoum and Tsanis (2004) on the interpolation of rainfall in the island of Crete, Greece was reviewed. The research had developed a new Geographical Information System (GIS)-based spatial interpolation module that adopts a multiple linear regression (MLR) technique. This technique can be compared with other methods, such as splin_regularized, spline_tension, IDW, kriging, and second-order polynomial. When estimating precipitation at ungauged locations, the MLR models provided better estimations than the other spatial interpolation techniques. Li et al. (2006) used the annual precipitation over a span of 30 years between 1961 and 1990 from 2114 meteorological stations in China. The data were compared with its respective nearby regions and analyzed through spline, ordinary kriging (OK), and IDW. The result in cross-validation tests shows that the precision of interpolated results are very high. The relative mean errors of three methods were 8.31, 8.76 and 8.76%, respectively ranking as OK > IDW = spline. Similar results of OK > Spline > IDW (the mean absolute error, MAE are 42.94, 44.79, and 49.86) The study carried out by Chu et al. (2008) reported a similar trend.

Segond et al. (2007) indicated that high spatial and temporal rainfall resolutions are required for urban drainage and urban flood modeling applications. Through IDW, the spatial rainfall field can be obtained when data over a whole catchment are interpolated. When using such method, the results were proven satisfactory as the stimulated data at individual sites preserved properties which mimicked the observed statistics at an acceptable level for practical purposes. Garcia et al. (2008) reported that Multiquadric–biharmonic (MQB) methods surpass IDW methods in terms of interpolation accuracy for both convective and mixed/stratiform events in the study regarding the North American monsoon season over a dense gauge network in the southwestern United States. However, it is found that the order in the IDW method is more important as under certain conditions, results obtained are just as accurate as the MQB method. Dong et al. (2009) used OK, co-kriging (CK), and IDW to interpolate daily precipitation in Qingjiang river basin of China. Daily precipitation data from 36 rainfall stations in June 2006 were analyzed, and the result demonstrated that CK was superior to OK and IDW. The author explained that IDW was unable to take the spatial dependencies of adjacent rain gauges in the basin into account. A similar conclusion was also reached in another case study in Xinjiang, China. The study suggested that the CK method is the most superior compared with RBF, IDW, Kriging methods based on the results of annual precipitation in 75 weather stations from 1995 to 2008 (Zhong 2010). A model composed of OK and entropy with probability distribution function is proposed to relocate the rainfall network and to obtain the optimal design with the minimum number of rain gauges by Yeh et al. (2011).

Nevertheless, several researchers have contrasting views in this area of study. Dirks et al. (1998) compared four spatial interpolation methods using rainfall data from a network of 13 rain gauges on Norfolk Island. The more computationally demanding method of Kriging provided no significant advantage over any of the much simpler IDW, Thiessen, or areal-mean methods. This further indicates that in order to assimilate some characteristics of spatially varying rainfall, the inverse distance method is the most advantageous for interpolations using spatially dense networks. In another case study, the daily precipitation data from 72 meteorological stations between 1961 and 2000 in Northeast China were analyzed using OK and IDW methods with the weighting of longitude and latitude, and gradient of height plus IDW (GIDW). For daily precipitation, the results showed that the precision of the evaluated value with IDW is greater than OK and GIDW (Zhuang and Wang 2003). Hsieh et al. (2006) used daily summer rainfall records from 20 rain gauges stations between 1990 and 2000 to predict the spatial rainfall distribution in the Shih-Men Watershed in Taiwan using two schemes as OK and IDW. The results indicated that IDW (mean error = 0.04) produced more accurate representations of spatial distribution of rainfall than OK (mean error = 0.54). Kurtzman et al. (2009) aimed at improving the spatial interpolation of daily precipitation for hydrologic models. Different parameterizations of IDW and a local weighted regression (LWR) method were tested in a mountainous terrain in the eastern Mediterranean using 16 years of daily data. The LWR took into account of the weighting factors of elevation which are the explanatory variable and distance, elevation factors, and aspect difference. The IDW interpolation was preferred over the LWR scheme in 27 out of 31 validation gauges. Wu et al. (2010) analyzed and compared five typical interpolation models: IDW, OK, GP, LP, and RBF. The results show that OK and IDW are suitable methods for maximum and minimum precipitations respectively; the results were consistent with the 30 years worth of data in 599 climate stations situated in Texas, US as analyzed by Kong and Tong (2008). A similar research was carried out by Li et al. (2010) utilizing the mean yearly precipitation of 72 meteorological stations from 1971 to 2008 in Zhejiang, China. Different interpolation methods such as the combining stepwise regression and IDW, kriging, spline, and trend were tested. The result demonstrated that the combination of stepwise regression and IDW showed the highest accuracy in prediction, and was better than other methods.

From the above review and comparison of the related researches on spatial interpolation techniques of rainfall, a conclusion can be drawn. According to the comparisons, each method has its advantages and disadvantages based on its objectives, and hence the optimal interpolation method to be adopted varies for different proposals. In general, OK is only suitable for normal distributions; the advantage the IDW method is its usefulness when the distribution of the estimated parameters is not a normal distribution.

In this article, the IDW method is used to interpolate the spatial rainfall distribution in the middle of Taiwan. The choice of the IDW exponent was found to be more significant than the choice of whether or not to use elevation as explanatory data (Kurtzman et al. 2009). In most cases, the critical influence parameter of IDW is the distance. For this reason, elevation of rainfall stations is not considered in this study. The study aims at improving interpolation accuracy of rainfall using IDW, which is concerned with parameters adjustment including the power (α value) and search radius.

Materials and methods

Study area and data

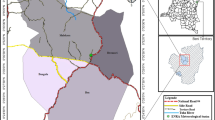
In this study, the region of the middle of Taiwan was chosen as the main research area. There are 46 rainfall stations distributed in this region. Figure 1 shows the schematic diagram of the rainfall stations spatial distribution in the middle of Taiwan. The rainfall stations are managed by two organizations. The 33 rainfall stations, which are shown as blue points in Fig. 1, are managed by Water Resources Agency (WRA), Ministry of Economic Affairs, while the remaining 13 rainfall stations, which are shown as red points in Fig. 1, are managed by TIA.

Fig. 1
figure 1

Location of 46 rainfall stations in the middle of Taiwan. Blue and red dots denote the rainfall stations managed by the WRA and Taichung Irrigation Association, respectively. (Color figure online)

Full size image

For the purpose of using IDW to interpolate spatial rainfall, long-term observed rainfall data were necessary for analysis in the process. Therefore, the daily rainfall data of 30 years from 1981 to 2010 were adopted in this study.

IDW

IDW is based on the concept of Tobler’s first law (the first law of geography) from 1970. It was defined as everything is related to everything else, but near things are more related than distant things. The IDW was developed by the U.S. National Weather Service in 1972 and is classified as a deterministic method. This is due to the lack of requirement in the calculation to meet specific statistical assumptions, thus IDW is different from stochastic methods (e.g., Kriging and TRA).

The IDW method is also for multivariate interpolation. Its general idea is based on the assumption that the attribute value of an unsampled point is the weighted average of known values within the neighborhood (Lu and Wong 2008). This involves the process of assigning values to unknown points by using values from a scattered set of known points. The value at the unknown point is a weighted sum of the values of N known points. In this study, the IDW method is used to interpolate spatial data, which is based on a concept of distance weighting. It can be used to estimate the unknown spatial rainfall data from the known data of sites that are adjacent to the unknown site (Bedient and Huber 1992; Burrough and McDonnell 1998; Goovaerts 2000; Li and Heap 2008). The IDW formulas are given as Eqs. 1 and 2.

$$ \hat{R}_{\text{p}} = \sum\limits_{i = 1}^{N} {w_{i} R_{i} } $$
(1)
$$ w_{i} = \frac{{d_{i}^{ - \alpha } }}{{\sum\limits_{i = 1}^{N} {d_{i}^{ - \alpha } } }} $$
(2)

where \( \hat{R}_{\text{p}} \) means the unknown rainfall data (mm); R i means the rainfall data of known rainfall stations (mm); N means the amount of rainfall stations; w i means the weighting of each rainfall stations; d i means the distance from each rainfall stations to the unknown site; α means the power, and is also a control parameter, generally assumed as two as used by Zhu and Jia (2004) and Lin and Yu (2008), or as six as set by Gemmer et al. (2004). Several researches (e.g., Simanton and Osborn 1980; Tung 1983) have experimented with variations in a power, examining its effects on the spatial distribution of information from precipitation observations. For this reason, α value is conducted in the range of zero to five with an incremental interval value of 0.1 in this article.

Cross-validation

As IDW is the chosen method to interpolate spatial rainfall data for this article, cross-validation is essential to validate critical parameters that could affect the interpolation accuracy of rainfall data. In this case, α value and search radius were evaluated for optimal parameters. This insures the overall utility of the IDW models and enables optimal data prediction that is comparable to the observed data.

Cross-validation, also called rotation estimation, is a technique for assessing how generalized the results of a statistical analysis are with respect to an independent dataset. Common types of cross-validation methods include k-fold cross-validation, twofold cross-validation, repeated random sub-sampling validation, leave-one-out cross-validation (LOOCV), etc. It is mainly used in settings where the objective is to gain a prediction, and estimating how accurately a predictive model will perform in practice (Devijver and Kittler 1982; Seaman 1983; Geisser 1993; Kohavi 1995). Cross-validation has been widely applied in studying the accuracy of prediction methods in precipitation fields. Related research studies include Gyalistras (2003), Feng et al. (2004), Lloyd (2005), Li et al. (2006), Hsieh et al. (2006), Chu et al. (2008), Wang et al. (2008), and Kong and Tong (2008).

Cross-validation can be defined as a method for estimating the accuracy of an inducer by dividing the data into k mutually exclusive subsets (the “folds”) of approximately equal size. The inducer is trained and tested k times. Each time it is trained on the data-set minus a fold and tested on that fold. The accuracy estimate is the average accuracy for the k folds (Cressie 1993; Kohavi and Provost 1998). In general, LOOCV involves using a single observation from the original sample as the validation data, and the remaining observations as the training data. This is repeated such that each observation in the sample is used once as the validation data. This is the same as a K-fold cross-validation with K being equal to the number of observations in the original sample. Because of considering tenfold cross-validation is commonly used (McLachlan et al. 2004). Thus, for the cross-validation purpose of this study, from the total of 46 rainfall stations, the 12 rainfall stations that belonged to the Taichung Irrigation Association (TIA), within Taichung irrigation area (Fig. 2) were adopted for this study.

Fig. 2
figure 2

Distribution of 12 rainfall stations for cross validation

Full size image

Performance assessment

In this study, the root mean squared error (RMSE) was adopted to assess the IDW models performances. The RMSE is also called root-mean-square deviation (RMSD), a measure frequently used on the differences between values predicted by a model or an estimator and the values actually observed from the thing being modeled or estimated. RMSE is a robust measure of accuracy. These individual differences are also called residuals, and the RMSE is served to aggregate them into a single measure of predictive power. The RMSE is applied widely in various fields as follows: in hydrogeology, RMSE is used to evaluate the calibration of a groundwater model; in meteorology, to see how effectively a mathematical model predicts the behavior of the atmosphere; in GIS, the RMSE is one of the measures used to assess the accuracy of spatial analysis and remote sensing. In this study, the RMSE was used to evaluate the optimal model of IDW. At the same time, coefficient of correlation (r) was also used for evaluate whether the estimated data fits observed data. The formulas of RMSE and r are considered by Phogat et al. (2010) and Traore et al. (2010) and given as Eqs. 3– 4:

$$ {\text{RMSE}}_{i} = \sqrt {\frac{1}{n}\sum\limits_{t = 1}^{n} {\left[ {R_{i} (t) - \hat{R}_{i} (t)} \right]} } ;\quad {\text{RMSE}}_{i} \ge 0. $$
(3)
$$ r = \frac{{\sum\nolimits_{t = 1}^{n} {\left( {R_{i} (t) - \overline{{R_{i} }} } \right)\left( {\hat{R}_{i} (t) - \overline{{\hat{R}_{i} }} } \right)} }}{{\sqrt {\sum\nolimits_{t = 1}^{n} {\left( {R_{i} (t) - \overline{{R_{i} }} } \right)^{2} } \sum\nolimits_{t = 1}^{n} {\left( {\hat{R}_{i} (t) - \overline{{\hat{R}_{i} }} } \right)^{2} } } }};\quad 1 \ge r \ge - 1 $$
(4)

where: \( \hat{R}_{i} (t) \) means spatial rainfall values interpolated using IDW in the unknown rainfall station (i); \( R_{i} (t) \) means observed rainfall data in the unknown rainfall station (i); n means numbers of year (t) adopted, n was equal to 30 in this study.

Analysis procedure

There are 46 rainfall stations used for interpolate rainfall data by IDW models, adopting cross-validation as an appropriate method to assess the accuracy of spatial interpolated rainfall data. 25% of the 46 rainfall stations were selected for a cross-validation process. The selection of rainfall stations was based on the conditions of isotropic and maximum search radius to increase the evaluated groups in a cross-validation process. For this reason, the 12 rainfall stations that are managed by the TIA were selected to conduct the model testing of validity using cross-validation. These 12 rainfall stations were selected in following of Taichung, Zhunlan, Taian, Yuemei, Ciyao, Yuanli, Rinan, Dajia, Danan, Dongshi, Fengyuan and Dadu. Rainfall data required were continuous daily data in the period of 1981–2010 (30 years). Table 1 shows the distance between respective rainfall stations, and is used to calculate the weighting of individual rainfall station to the objective rainfall station. To determine the optimal search radii (O.S.R.) of IDW of the 12 rainfall stations, 11 search radii (10–110 km) were executed (Table 2). The italicized numbers in Table 2 represent the optimal number of rainfall stations nearby the objective that were selected for daily rainfall interpolation. Figure 3 shows the schematic diagram of different groups in Taichung rainfall station as an example. It illustrates that different rainfall stations within different selected search radii can used for interpolate rainfall data. For example, 19 and 45 rainfall stations falls within the selected search radius of 30 and 70 km for rainfall data interpolation. We compared and analyzed the data with seven groups, assessing the relationship between prediction accuracy with search radius (the number of selected rainfall stations). This was used for further calculations in cross validation. Finally, RMSE was used for determining optimal parameters: α value and search radius of IDW. This is done through data verification testing which must be conducted subsequent to all procedures of cross-validation. The data verification testing then compared the data interpolated with observed data. To express the applicability of IDW models, the results of rainfall data interpolation using IDW were all determined by r.

Table 1 Distance (km) between 46 rainfall stations to the 12 objective rainfall stations for calculation of the individual weighting
Full size table
Table 2 Optimal numbers of rainfall stations evaluated by different search radii (10–110 km) of 12 objective rainfall stations
Full size table
Fig. 3
figure 3

Schematic diagram of rainfall station groups of different search radius—use Taichung rainfall station for example

Full size image

Results and discussions

To interpolate the unknown rainfall data, 12 rainfall stations (Table 2) were assumed as unknowns and rainfall data estimated using IDW in a common parameter of α = 0–5.0. As the adopted data expressed as daily rainfall, all interpolated data results were also expressed as daily rainfall data. Every different group of each rainfall station was estimated individually using only the observed data respective to individual rainfall station’s search radius. After interpolation of daily rainfall levels, data were then compiled accordingly to create data expressed as ten-day rainfall, monthly rainfall and annual rainfall.

To identify the optimal parameters of IDW, α value and research radius, and the minimum RMSE were calculated. Table 3 shows the minimum RMSE in the forms of both monthly rainfall and annually rainfall. At the same time, the O.S.R. and α value were recorded in the condition of the minimum RMSE. Comparing the annual O.S.R. and monthly α values, the results showed two phenomena. Firstly, in a viewpoint of annual O.S.R., 75% O.S.R. were within 10–20 km, there was only one anomaly (80 km) which occurred in Fengyuan rainfall station; it deemed the use of numerous rainfall stations unnecessary for data interpolation under most conditions. Nevertheless, the greater result accuracy occurred when only four to five rainfall stations were considered such as Zhunlan, Ciyao, Rinan, and Dongshi rainfall stations as opposed to incorporating data from all 45 rainfall stations. A similar trend also occurred with monthly rainfall levels. The results revealed that the interpolation accuracy of rainfall was greater with increasing rainfall stations and to an optimal up-limit. However, the interpolation accuracy can become inferior when the number of rainfall stations considered exceeds the optimal value. In all cases of this article, when considering all 45 stations, less than 20 stations, and less than 10 stations, the optimal number of rainfall stations 8, 83 and 58%, respectively. Excessive number of rainfall stations considered for interpolate rainfall could cause the data to become meaningless. Such results are similar to previous researches such as those conducted by Li et al. (2006), Lin and Yu (2008), and Chu et al. (2008) which the optimal number of rainfall stations were 10, 13 and 15 respectively.

Table 3 Optimal parameters of IDW for interpolation of spatial rainfall data
Full size table

The second phenomenon was that the optimal α value varied greatly from zero to five. There was only a 1.92% probability met and that the optimal α was equal to 2.0. It revealed that the prediction accuracy of rainfall could not the optimal when using α value at 2.0. Even at a 2.0 α value, it is only a general consent but cannot be considered scientific. The result in this article have identical views with several researches including one by Chu et al. (2008) reported the optimal α value was equal to 3.31 when 15 rainfall stations were considered to measure a case of Gansu, China. Wang et al. (2008) also reported a case in China where the prediction accuracy of annual rainfall had the highest significance when the α value was considered in the range of three to five. However, Dirks et al. (1998) showed that the exact choice of the numerical value of the power has minimal effect on the resulting errors providing data using the α values within the range of 1.5–4. It was an inconsistent argument with this article, because several optimal α values of this article occurred in the range 0–1.5 and even at 4–5. Table 2 also showed that the annual RMSE existed in the range of 29.5–44.9. Figure 4 displays a series of 12 sub-diagrams on the RMSE variation at different search radii (10–110 km) and α value (from zero to five with an increment interval of 0.1). The finding was a large RMSE variation of different groups (search radius) occurred when α approach zero, the RMSE variation also reduced with the increase in α. This showed that the minimum variation occurred at the largest α value, regardless of the number of rainfall stations used for interpolation. However, the minimum variation of RMSE remains uncertain on based of the optimal α and search radius. Therefore the optimal α and search radius must be further measured.

Fig. 4
figure 4

RMSE variation of different search radii (10–110 km) and α value (0–5) of 12 rainfall stations

Full size image

Figure 5 diagrams the RMSE variation of different groups using annual optimal α value in each month. These results show that all 12 rainfall stations follows the same trend: the RMSE value was relatively lower in dry seasons (from October to April) than in flood seasons (from May to September), it denoted that the data obtained during dry seasons are more accurate than in flood seasons. This point of view in this study is consistent with the study done by Kong and Tong (2008). It would therefore consider that spatial rainfall interpolated in flood season is inferior to the data interpolated during dry seasons due to extreme rainfall events. However, another research had indicated that IDW was better than kriging and suggested for spatial rainfall prediction in summer (Hsieh et al. 2006). The relationship between the interpolated rainfall values and the true observed data was also evaluated. Figure 6 showed a significant accuracy of the predicted data during low rainfall value, and the deviation increased gradually with increased rainfall. The trend could explain the cause of high RMSE values occurring during flood seasons (Fig. 5). The phenomenon implied large deviations were caused from extreme rainfall events in the flood season.

Fig. 5
figure 5

RMSE variation of different search radii (10–110 km) using annual optimal α value in each month of 12 rainfall stations

Full size image
Fig. 6
figure 6

Scatter plots of monthly interpolation of spatial rainfall data

Full size image

Finally, for the purpose of evaluating the suitability of using IDW for interpolated data, daily rainfall data interpolated were accumulated into 36 ten-day rainfall values from 1 year, and was compared with the observed data. The coefficient of correlation (r) was utilized as an indicator to evaluate the fittingness of IDW. Cross-validation methods were applied to 12 optimal monthly α values and a single annual one on an individual basis. The r can be expressed as r m and r a. 30-years worth of average data (1981–2010) presented in the form of 10-day interpolated rainfall were compared with observed data in Fig. 7. The result showed that r m and r a were all higher than 0.95 in 12 rainfall stations. It was evident that, rainfall interpolations using IDW showed significant similarities with the observed data, either using optimal monthly α values or as independent annual values. Therefore an argument can be drawn from this study: that IDW is a suitable method for rainfall interpolation under the conditions that optimal α and search radius must be measured.

Fig. 7
figure 7

Comparison of observation and interpolation of spatial rainfall data using optimal monthly and annual α values

Full size image

Conclusion

In this article, the authors have three findings about using IDW for interpolate spatial rainfall: (i) The predicted accuracy of rainfall interpolated can be improved through the α value adjustment, and that the α value usually is not equivalent to two. Therefore, for the purpose of increasing prediction accuracy, searching an optimal α value as a preparation step is necessary. (ii) The number of known rainfall station is also another influential parameter; most cases show that the prediction accuracy increases with the increasing numbers of known rainfall station. However, the accuracy of rainfall data interpolation could be reduced by the interference from the use of excessive rainfall stations. Nevertheless, radius of influence is important to effective interpolation of rainfall data. The optimal result is based on only using rainfall stations within the radius of influence. (iii) Application of IDW for spatial rainfall data interpolation, results show the prediction accuracy are better during dry seasons (October to April) than in flood seasons (May–September). It reveals that IDW has significant prediction ability in small rainfall events than in extreme rainfall events. In summary, through analyzing the optimization steps of α value and radius of influence, IDW is deemed as a suitable spatial interpolation method of rainfall.