Modeling the landslide-generated debris flow from formation to propagation and run-out by considering the effect of vegetation

Abstract

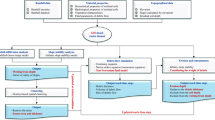
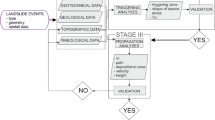
This study aimed to investigate the formation and propagation processes of a landslide-generated debris flow within a small catchment while considering the effects of vegetation. This process is divided into three stages: rainfall infiltration, slope failure, and debris flow routing, according to their different mechanisms. Existing models that involve the effect of vegetation for each stage, including Richards’s model, infinite slope stability model, and the enhanced two-phase debris flow model (Pudasaini 2012), were coupled. The tridiagonal matrix algorithm and finite volume method were applied to solve these equations, respectively. Finally, the approach was tested by application to the 2018 debris flow event in the Yindongzi catchment, China. The results showed that the proposed comprehensive model could effectively describe the behaviors of each stage during the formation and propagation processes of landslide-generated debris flows in vegetated area. The roles of vegetation on each stage, such as root water uptake and root soil reinforcement, were also analyzed by performing several scenarios.

Appendix A HLLC Riemann Approximate Solver for Two-phase Equations

In matrix form, the conservation law of the two-phase model equations can be expressed as follows:

$$ \frac{\partial \mathbf{w}}{\partial t}+\frac{\partial \mathbf{f}}{\partial x}+\frac{\partial \mathbf{m}}{\partial y}=\mathbf{s}+\mathbf{q} $$

(A1)

where w, f, m, s, and q are vectors representing the conserved variables, the fluxes in the x and y directions, and the source terms in the x and y directions, respectively. A one-dimension problem in x direction can be obtained by dividing equation (A1) based on the operator-splitting technique and its explicit time-marching conservative finite-volume form is expressed as the following:

$$ {\mathbf{w}}^{n+1}={\mathbf{w}}^n-\frac{\varDelta t}{\varDelta x}\left({\mathbf{f}}_e-{\mathbf{f}}_w\right)+\varDelta t{\boldsymbol{s}}^n $$

(A2)

where the superscript n is the time level, ∆t is the time step, f_e and f_w are the fluxes through the eastern and western cell interface in x direction, and ∆x is the side lengths of a grid cell in x direction. By using the HLLC scheme, the internal flux, e.g., f_e, is computed as follows:

$$ {\mathbf{f}}_e=\left\{\begin{array}{c}{\mathbf{f}}_l\kern3.999998em if\kern0.2em 0\le {S}_l\\ {}{\mathbf{f}}_{\ast l}\kern1.6em if\kern0.2em {S}_l\le 0\le {S}_m\\ {}{\mathbf{f}}_{\ast r}\kern1.6em if\kern0.2em {S}_m\le 0\le {S}_r\\ {}{\mathbf{f}}_r\kern3.899998em if\kern0.2em {S}_r\le 0\end{array}\right. $$

(A3)

where f_l and f_r are the interface fluxes on both sides of the east cell interface, which are calculated from the left and right Riemann states w_l and w_r; S_l, S_m, and S_r represent the speeds of the left, middle, and right waves, respectively, for a local Riemann problem; and f_*l and f_*r represent the left and right sides of the contact wave and can be expressed as follows:

$$ {\mathbf{f}}_{\ast l}=\left(\begin{array}{c}{f}_{\ast 1}\\ {}{f}_{\ast 2}\\ {}{v}_l{f}_{\ast 1}\end{array}\right),{\mathbf{f}}_{\ast r}=\left(\begin{array}{c}{f}_{\ast 1}\\ {}{f}_{\ast 2}\\ {}{v}_r{f}_{\ast 1}\end{array}\right) $$

(A4)

where v_l and v_r are the left and right tangential velocity components of the Riemann states. Then, the fluxes f_* in the middle region are needed to calculate f_*l and f_*r by using the constructed variables and can be obtained from the Harten-Lax-van Leer (HLL) formula:

$$ {\mathbf{f}}_{\ast }=\frac{S_r{\mathbf{f}}_l-{S}_l{\mathbf{f}}_r+{S}_r{S}_l\left({\mathbf{w}}_r-{\mathbf{w}}_l\right)}{S_r-{S}_l} $$

(A5)

Considering the dry bed condition from the two-rarefaction approximate Riemann solver, the wave speeds are calculated as follows:

$$ {\displaystyle \begin{array}{c}{S}_l=\left\{\begin{array}{c}{u}_r-2{c}_r\kern10em if\kern0.2em {h}_l=0\\ {}\min \left({u}_l-{c}_l,{u}_{\ast }-{c}_{\ast}\right)\kern4.599998em if\kern0.2em {h}_l>0\end{array}\right.\\ {}{S}_r=\left\{\begin{array}{c}{u}_l+2{c}_l\kern10em if\kern0.2em {h}_r=0\\ {}\max \left({u}_r+{c}_r,{u}_{\ast }+{c}_{\ast}\right)\kern3.999998em if\kern0.2em {h}_r>0\end{array}\right.\\ {}{S}_m=\frac{S_l{h}_r\left({u}_r-{S}_r\right)-{S}_r{h}_l\left({u}_l-{S}_l\right)}{h_r\left({u}_r-{S}_r\right)-{h}_l\left({u}_l-{S}_l\right)}\end{array}} $$

(A6)

where c is the speed of gravity waves; u_l, u_r, h_l, and h_r are the components of the left and right Riemann states for a local Riemann problem; and u_* and h_* are the components of the middle Riemann states, which are calculated as follows:

${u}_{\ast }=\frac{1}{2}\left({u}_l+{u}_r\right)+{c}_l-{c}_r\kern0.5em ;\kern0.5em {h}_{\ast }=\frac{1}{g_z}{\left(\frac{1}{2}\left({c}_l+{c}_r\right)+\frac{1}{4}\left({u}_l-{u}_r\right)\right)}^2$ (A7)

As derived by Pudasaini (2012), the speeds of gravity waves for solid and fluid phases, c_s and c_f, can be given by:

$$ \left\{\begin{array}{c}{c}_s^2={\beta}_s\left({h}_s+\frac{1}{2}{h}_f\right)\\ {}{c}_f^2={\beta}_f\left({h}_f+\frac{1}{2}{h}_s\right)\end{array}\right. $$

(A8)

Compared with standard expression of gravity wave speed in shallow water, the form of c_s and c_f indicates that the gravity wave speed in mixture mass flows of one phase is influenced by another phase. The time step should satisfy the demand of two phases dynamic computing simultaneously

$$ \varDelta t=\min \left(\varDelta {t}_s,\kern0.5em \varDelta {t}_f\right); which\kern0.70em \varDelta {t}_{s,f}\le \min \left(\frac{cfl\cdot \eta }{\max \left(\left|{\mathbf{u}}_{\left(s,f\right)}\right|+\sqrt{g_z{h}_{\left(s,f\right)}}\right)}\right) $$

(A9)

where cfl is the Courant number, whose value should be less < 1 and a small value of 0.5 is adopted and η is the ratio of the area of the grid to its perimeter.