Classical and non-classical time history and spectrum analysis of soil-structure interaction systems

Abstract

The problem of non-classical dynamic analysis of structures resting on flexible bases is studied in this paper. Because of presence of the underlying soil in the dynamic model of structure that acts like an energy sink, the damping matrix is not proportional to structural mass and stiffness and theoretically a non-classical approach should be followed in modal analysis. Considering one to twenty-story buildings, two types of soils, and several suits of ground motions each containing ten earthquake records specifically selected for each building, the seismic responses are calculated using a time history modal analysis in this paper. Three cases are considered: fixed-base buildings with classical analysis, flexible-base buildings with classical and non-classical analysis. It is shown that the code-based soil-structure interaction (SSI) analysis for the fundamental mode is not always safe. Also, on each soil type, instances of importance of accounting for the non-classical nature of the SSI system are clarified. Cases for which the base flexibility should be considered for the higher modes too are distinguished. Finally, simple correction factors are derived for converting the fixed-base responses of moment frames, resting on surface foundations on medium and soft soils, to the responses including soil-structure interaction effects.

Appendices

Appendix 1: Equations of motion

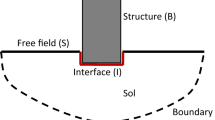
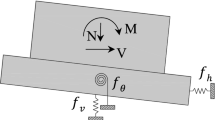
The equations of motion of the system of Fig. 1 can be written as follows:

$$\left[ M \right] \left\{ {\begin{array}{*{20}c} {\{ {\ddot{u}}\} } \\ {{\ddot{u}}_{b} } \\ {\ddot{\psi }} \\ \end{array} } \right\} + \left[ C \right] \left\{ {\begin{array}{*{20}c} {\{ \dot{u}\} } \\ {\dot{u}_{b} } \\ {\dot{\psi }} \\ \end{array} } \right\} + \left[ K \right] \left\{ {\begin{array}{*{20}c} {\{ u\} } \\ {u_{b} } \\ \psi \\ \end{array} } \right\} = - \left\{ {\begin{array}{*{20}c} {\left\{ m \right\}} \\ {m_{b} + \mathop \sum \limits_{1}^{n} m_{i} } \\ {\mathop \sum \limits_{1}^{n} m_{i} h_{i} } \\ \end{array} } \right\}{\ddot{u}}_{g} \left( t \right) = \{ p(t)\}$$

(24)

in which:

$$\left[ M \right] = \left[ {\begin{array}{*{20}c} {[m]} & {\{ m\} } & {\{ mh\} } \\ {\{ m\}^{T} } & {m_{b} + \mathop \sum \limits_{1}^{n} m_{i} } & {\mathop \sum \limits_{1}^{n} m_{i} h_{i} } \\ {\{ mh\}^{T} } & {\mathop \sum \limits_{1}^{n} m_{i} h_{i} } & {I + \mathop \sum \limits_{1}^{n} m_{i} h_{i}^{2} } \\ \end{array} } \right]$$

(25)

$$\left[ C \right] = \left[ {\begin{array}{*{20}c} {[c]} & {\{ 0\} } & {\{ 0\} } \\ {\{ 0\}^{T} } & {c_{uu} } & 0 \\ {\{ 0\}^{T} } & 0 & {c_{\psi \psi } } \\ \end{array} } \right]$$

$$\left[ K \right] = \left[ {\begin{array}{*{20}c} {[k]} & {\{ 0\} } & {\{ 0\} } \\ {\{ 0\}^{T} } & {k_{uu} } & 0 \\ {\{ 0\}^{T} } & 0 & {k_{\psi \psi } } \\ \end{array} } \right]$$

and:

$$\left[ m \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {m_{1} } \\ \\ \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} & & \\ \end{array} } \\ {\begin{array}{*{20}c} {m_{2} } & & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} { } & \ddots & \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} \\ \\ \\ \end{array} } \\ {\begin{array}{*{20}c} \\ \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ \\ \end{array} } & {\begin{array}{*{20}c} \\ \\ \end{array} } & {\begin{array}{*{20}c} {m_{n - 1} } \\ \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} \\ {m_{n} } \\ \end{array} } \\ \end{array} } \right]$$

$$[c] = \left[ {\begin{array}{*{20}c} {c_{1} } \hfill & { - c_{2} } \hfill & \cdots \hfill & 0 \hfill & 0 \hfill \\ { - c_{2} } \hfill & {c_{1} + c_{2} } \hfill & { - c_{3} } \hfill & 0 \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & {c_{{n - 1}} + c_{{n - 2}} } \hfill & { - c_{n} } \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & { - c_{n} } \hfill & {c_{n} + c_{{n - 1}} } \hfill \\ \end{array} } \right]$$

(26)

$$[K] = \left[ {\begin{array}{*{20}c} {k_{1} + k_{2} } \hfill & { - k_{2} } \hfill & \cdots \hfill & 0 \hfill & 0 \hfill \\ { - k_{2} } \hfill & {k_{2} + k_{3} } \hfill & { - k_{3} } \hfill & 0 \hfill & 0 \hfill \\ \vdots \hfill & { - k_{3} } \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ 0 \hfill & \vdots \hfill & \cdots \hfill & {k_{n} + k_{{n + 1}} } \hfill & { - k_{{n - 1}} } \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & { - k_{{n - 1}} } \hfill & {k_{n} } \hfill \\ \end{array} } \right]$$

and:

$$\left\{ m \right\} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {m_{1} } & {m_{2} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {m_{n} } \\ \end{array} } \\ \end{array} } \right]^{T}$$

(27)

$$\left\{ {mh} \right\} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {m_{1} h_{1} } & {m_{2} h_{2} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {m_{n} h_{n} } \\ \end{array} } \\ \end{array} } \right]^{T}$$

$$\left\{ u \right\} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{1} } & {u_{2} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {u_{n} } \\ \end{array} } \\ \end{array} } \right]^{T}$$

$$I = I_{b} + \mathop \sum \limits_{i = 1}^{n} I_{i}$$

In the above equations, $m_{i} \;{\text{and}}\; m_{b}\; \left( {i = 1, 2, \ldots ,n; n = {\text{number of stories}}} \right)$ are mass of the ith floor and the foundation, respectively, $h_{i}$ is the height of the ith floor from the base, $I_{i}$ and $I_{b}$ are respectively the mass moments of inertia of the ith story and the foundation, $c_{i}$ and $k_{i}$ are the damping coefficient and the lateral relative stiffness of the ith story, respectively, $c_{jj}$ and $k_{jj}$ with $j = u$ or $\psi$ are respectively the damping and stiffness impedances of the supporting medium in translational and rotational directions, $u_{i}$, $u_{b}$ and $u_{g}$ are the horizontal displacements of the ith story, the foundation, and ground with respect to a fixed reference, respectively, $\psi$ is the rotational component of motion of foundation, and a dot represents derivation with respect to time.

Appendix 2: The free vibration response characteristics

The homogeneous solution of Eq. (24) can be written as:

$$\{ U\} = \{ \psi \} e^{rt}$$

(28)

in which r and $\left\{ \psi \right\}$ are the characteristic value and vector, respectively, and $\{ U\}$ is defined in Eq. (2). Substitution of (28) in (24) with p(t) = 0 gives:

$$\left( {r^{2} \left[ M \right] + r\left[ C \right] + \left[ K \right]} \right)\left\{ \psi \right\} = \{ 0\}$$

(29)

Foss (1958) showed that the characteristic Eq. (29) can be reduced to:

$$\left( {r\left[ A \right] + \left[ B \right]} \right)\left\{ Z \right\} = \{ 0\}$$

(30)

in which:

$$\left\{ Z \right\} = \left\{ {\begin{array}{*{20}c} {{\text{r}}\{ \psi \} } \\ {\{ \psi \} } \\ \end{array} } \right\}$$

(31)

$$\left[ A \right] = \left[ {\begin{array}{*{20}c} {[0]} & {[{\text{M}}]} \\ {[{\text{M}}]} & {[{\text{C}}]} \\ \end{array} } \right]_{{2{\text{N}} \times 2{\text{N}}}}$$

$$\left[ {\text{B}} \right] = \left[ {\begin{array}{*{20}c} { - [M]} & {[0]} \\ {[0]} & {[{\text{K}}]} \\ \end{array} } \right]_{{2{\text{N}} \times 2{\text{N}}}}$$

The dimension of Eq. (30) is 2 N where N = n + 2 with the additional two DOF’s of the foundation included. Its solution results in N complex conjugates for r and $\uppsi$. If $r_{j}$ and $\bar{r}_{j}$ are a pair of characteristic values and $\{\uppsi\}$ and $\{ {\bar{\psi }}\}$ a pair of characteristic vectors where the over bar denotes complex conjugate, then the following relations are introduced:

$$\left. {\begin{array}{*{20}c} {r_{j} } \\ {\bar{r}_{j} } \\ \end{array} } \right\} = - q_{j} \pm \tilde{p}_{j}$$

(32)

$$\left. {\begin{array}{*{20}c} {\{ \psi_{j} \} } \\ {\{ \bar{\psi }_{j} \} } \\ \end{array} } \right\} = \{ \phi_{\text{j}} \} \pm i\{ \chi_{j} \}$$

in which $i = \sqrt { - 1}$, $q_{j}$ and $\tilde{p}_{j}$ are real constants, and, $\{ \phi_{\text{j}} \}$ and $\{ \chi_{j} \}$ are N-component real vectors. Then the new parameters $p_{j}$ and $\xi_{j}$ are defined as follows:

$$p_{j} = \sqrt {q_{j}^{2} + \tilde{p}_{j}^{2} }$$

(33)

$$\upxi_{\text{j}} = \frac{{q_{j} }}{{p_{\text{j}} }}$$

Then:

$$\left. {\begin{array}{*{20}c} {r_{j} } \\ {\bar{r}_{j} } \\ \end{array} } \right\} = - \xi_{j} p_{j} \pm i\tilde{p}_{j}$$

(34)

$${\tilde{\text{p}}}_{j} = p_{\text{j}} \sqrt {1 -\upxi_{\text{j}}^{2} }$$

Substituting Eq. (32) in (28) results in:

$$\left\{ {{\text{U}}_{\text{j}} } \right\} = e^{{ -\upxi_{\text{j}} p_{\text{j}} t}} \left( {\{ \phi_{\text{j}} \} \pm i\{ \chi_{\text{j}} \} } \right)e^{{ \pm {\tilde{\text{p}}}_{j} t}}$$

(35)

The displacement response in Eq. (35) consists of two parts: the damped amplitude and the oscillation function, which are as follows:

$${\text{Displacement}}\;{\text{amplitude}} = e^{{ -\upxi_{\text{j}} p_{\text{j}} t}} (\{ \phi_{\text{j}} \} \pm i\{ \chi_{j} \} )$$

(36)

$${\text{Oscillation}}\;{\text{function}} = e^{{ \pm {\tilde{\text{p}}}_{j} t}} = \cos ({\tilde{\text{p}}}_{j} t) \pm i\sin ({\tilde{\text{p}}}_{j} t)$$

(37)

Equation (36) shows that $\xi_{j}$ is the damping ratio of the jth mode while $p_{\text{j}}$ and ${\tilde{\text{p}}}_{j}$ show the undamped and damped frequencies of the jth mode, respectively, all being positive values.

The total response in the jth mode (j = 1, 2, …, N) can be calculated combining contributions from both complex conjugates as:

$$\{ U_{j} \} = C_{j} \{ \psi_{j} \} e^{{r_{j} t}} + \bar{C}_{j} \{ \bar{\psi }_{j} \} e^{{\bar{r}_{j} t}}$$

(38)

in which $C_{j}$ is a complex constant. Equation (38) can be simplified as:

$$\left\{ {U_{j} } \right\} = 2Re[C_{j} \{ \psi_{j} \} e^{{r_{j} t}} ]$$

(39)

in which Re denotes real value. Summing the combinations of all modes, the total response at each degree of freedom can be written as:

$$\left\{ U \right\} = 2\mathop \sum \limits_{j = 1}^{N} Re\left[ {C_{j} \{ \psi_{j} \} e^{{r_{j} t}} } \right]$$

(40)

Using modal orthogonality conditions, it can be shown that (Veletsos and Ventura 1986):

$$C_{j} = \frac{{r_{j} \{ \psi_{j} \}^{T} \left[ M \right]\left\{ {U(0)} \right\} + \{ \psi_{j} \}^{T} \left[ C \right]\left\{ {U(0)} \right\} + \{ \psi_{j} \}^{T} \left[ M \right]\left\{ {\dot{U}\left( 0 \right)} \right\}}}{{2r_{j} \{ \psi_{j} \}^{T} \left[ M \right]\{ \psi_{j} \} + \{ \psi_{j} \}^{T} \left[ C \right]\{ \psi_{j} \} }}$$

(41)

in which $\left\{ {U(0)} \right\}$ and $\left\{ {\dot{U}\left( 0 \right)} \right\}$ are the vectors of initial displacement and initial velocity of the system.

Appendix 3: The displacement response to base acceleration

Response of the system of Fig. (1) to a base acceleration that is equivalent to a constant initial velocity at all horizontal degrees of freedom, can be calculated from Eqs. (40) and (41) with the following initial values:

$$\left\{ {U\left( 0 \right)} \right\} = \{ 0\} ,\left\{ {\dot{U}\left( 0 \right)} \right\} = \left\{ {\begin{array}{*{20}c} 1 \\ \vdots \\ 1 \\ \begin{aligned} 1 \hfill \\ 0 \hfill \\ \end{aligned} \\ \end{array} } \right\}v_{0}$$

(42)

in which $\nu_{0}$ is the value of the initial velocity. Substituting Eq. (42) in (41) results in:

$$B_{j} = \frac{{\{ \psi_{j} \}^{T} \left[ M \right]\left\langle {\begin{array}{*{20}c} 1 & \ldots \\ \end{array} \begin{array}{*{20}c} 1 & 1 & 0 \\ \end{array} } \right\rangle_{n + 2}^{T} }}{{2r_{j} \{ \psi_{j} \}^{T} \left[ M \right]\{ \psi_{j} \} + \{ \psi_{j} \}^{T} \left[ C \right]\{ \psi_{j} \} }}$$

(43)

in which $B_{j} = C_{j} /\nu_{0}$. Now, Eq. (43) is substituted in (40) to result in:

$$\left\{ U \right\} = 2\mathop \sum \limits_{j = 1}^{N} Re[B_{j} \{ \psi_{j} \} v_{0} e^{{r_{j} t}} ] .$$

(44)

To write the response in the real form, the amplitude in (44) is decomposed as follows:

$$2B_{j} \{ \psi_{j} \} = \left\{ {\beta_{j}^{v} } \right\} + i\{ \gamma_{j}^{v} \}$$

(45)

in which $\left\{ {\beta_{j}^{\nu } } \right\}$ and $\left\{ {\gamma_{j}^{\nu } } \right\}$ are real and imaginary parts of the term on the left. Substituting (45) in (44) gives:

$$\{ U\} = \mathop \sum \limits_{j = 1}^{N} e^{{ - \xi_{j} p_{j} t}} \left[ {\left\{ {\beta_{j}^{v} } \right\} \cos \left( {\tilde{p}_{j} t} \right) - \{ \gamma_{j}^{v} \} \sin \left( {\tilde{p}_{j} t} \right)} \right]v_{0}$$

(46)

The unit impulse response function for the system is introduced as:

$$h_{j} ({\text{t}}) = \frac{1}{{{\tilde{\text{p}}}_{j} }}e^{{ -\upxi_{\text{j}} p_{\text{j}} t}} \sin \left( {{\tilde{\text{p}}}_{j} t} \right)$$

(47)

The derivative of Eq. (47) is:

$$\dot{h}_{j} ({\text{t}}) = e^{{ -\upxi_{\text{j}} p_{\text{j}} t}} \left[ {\cos \left( {{\tilde{\text{p}}}_{j} t} \right) - \frac{{\upxi_{\text{j}} }}{{\sqrt {1 -\upxi_{\text{j}}^{2} } }}\sin \left( {{\tilde{\text{p}}}_{j} t} \right)} \right]$$

(48)

Replacing (47) and (48) in (46) results in:

$$\{ U\} = \mathop \sum \limits_{j = 1}^{N} \left[ {\left\{ {\alpha_{j}^{v} } \right\} p_{j} h_{j} (t) - \{ \beta_{j}^{v} \} \dot{h}_{j} \left( t \right)} \right]v_{0}$$

(49)

in which:

$$\left\{ {\alpha_{j}^{v} } \right\} =\upxi_{\text{j}} \left\{ {\beta_{j}^{v} } \right\} - \sqrt {(1 -\upxi_{\text{j}}^{2} )} \{ \gamma_{j}^{v} \}$$

(50)

For calculating the response at $t_{0} = \tau$ to a base acceleration ${\ddot{u}}_{g} (t)$, the velocity $\nu (\tau )$ is computed as:

$$v\left( t \right) = - {\ddot{u}}_{g} \left( \tau \right)d\tau$$

(51)

If Eq. (51) is substituted in (49) and integrated to the arbitrary time $t$, the dynamic response will be resulted as Eq. (4).

Appendix 4: The base shear

To calculate the base shear due to ground motion, first the vector of lateral story forces is computed using (24) as:

$$\left\{ f \right\} = \left[ M \right]\{ {\ddot{U}}\}^{total} = - (\left[ K \right]\left\{ U \right\} + [C]\{ \dot{U}\} )$$

(52)

$\left\{ {\dot{U}} \right\}$ and $\left\{ U \right\}$ are determined from (44) and replaced in (52) to give:

$$\left\{ {f(t)} \right\} = 2\mathop \sum \limits_{j = 1}^{N} Re\left\{ {\left[ {\left[ K \right]\left\{ {\psi_{j} } \right\} + r_{j} [C]\left\{ {\psi_{j} } \right\}} \right]B_{j} v_{0} e^{{r_{j} t}} } \right\}$$

(53)

Using the homogenous form of (24) with (28) in (53), $f\left( {\,t\,} \right)$ is written as:

$$\left\{ {f(t)} \right\} = - 2\mathop \sum \limits_{j = 1}^{N} Re\left\{ {r_{j}^{2} \left[ M \right]\{ \psi_{j} \} B_{j} v_{0} e^{{r_{j} t}} } \right\}$$

(54)

Using Eqs. (45), (47), and (48) in (54) and integrating, give the vector of lateral forces as follows:

$$\left\{ {f(t)} \right\} = \mathop \sum \limits_{j = 1}^{N} e^{{ - \xi_{j} p_{j} t}} \left[ M \right]\left\{ {\left[ {\left( {p_{j}^{2} - 2\xi_{j}^{2} p_{j}^{2} } \right)\left( {\left\{ {\beta_{j}^{v} } \right\} \cos \left( {\tilde{p}_{j} t} \right) - \{ \gamma_{j}^{v} \} \sin \left( {\tilde{p}_{j} t} \right)} \right)} \right] + \left[ {\left( { - 2i\xi_{j} p_{j}^{2} \sqrt {1 - \xi_{j}^{2} } } \right)\left( {\left\{ {\beta_{j}^{v} } \right\} \sin \left( {\tilde{p}_{j} t} \right) + \{ \gamma_{j}^{v} \} \cos \left( {\tilde{p}_{j} t} \right)} \right)} \right]} \right\}v_{0}$$

(55)

in which:

$$\left\{ {\omega_{j}^{v} } \right\} =\upxi_{j} \left\{ {\gamma_{j}^{v} } \right\} + \sqrt {1 -\upxi_{j}^{2} } \left\{ {\beta_{j}^{v} } \right\}$$

(56)

Equation (55) can also be written as:

$$\left\{ {f(t)} \right\} = \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{N}} \left\{ {\alpha_{j}^{Mv} } \right\} p_{\text{j}} V_{j} ({\text{t}}) + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{N}} \left\{ {\beta_{j}^{Mv} } \right\}\dot{D}_{j} \left( {\text{t}} \right) + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{N}} \left\{ {\omega_{j}^{Mv} } \right\} p_{\text{j}} V_{j} ({\text{t}}) + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{N}} \left\{ {\gamma_{j}^{Mv} } \right\}\dot{D}_{j} \left( {\text{t}} \right)$$

(57)

where:

$$\left\{ {\alpha_{j}^{Mv} } \right\} = \left( {p_{j} + 2\xi_{j}^{2} p_{j} } \right)\left[ M \right]\left\{ {\alpha_{j}^{v} } \right\}$$

$$\left\{ {\beta_{j}^{Mv} } \right\} = \left( {p_{j} + 2\xi_{j}^{2} p_{j} } \right)\left[ M \right]\left\{ {\beta_{j}^{v} } \right\}$$

$$\left\{ {\omega_{j}^{Mv} } \right\} = \left( { - 2\xi_{j} p_{j}^{2} \sqrt {1 - \xi_{j}^{2} } } \right)\left\{ {\omega_{j}^{v} } \right\}$$

(58)

$$\left\{ {\gamma_{j}^{Mv} } \right\} = \left( { - 2\xi_{j} p_{j}^{2} \sqrt {1 - \xi_{j}^{2} } } \right)\left\{ {\gamma_{j}^{v} } \right\}$$

Then the base shear is computed as the summation of lateral story forces resulting in Eq. (6).

Appendix 5: Characteristics of the selected records

The earthquake records selected with the criteria of this study are described in the following table.

Order	NGA no.	EQ. name	Date	Station	Soil type	Distance (km)	Max Acc. (g)
1	169	Imperial Valley-06	10/15/79	DELTA	D	22.0	0.28
2	178	Imperial Valley-06	10/15/79	El Centro Array #3	E	12.85	0.26
3	726	Superstition Hills-02	11/24/87	Salton Sea Wildlife Refuge	E	25.88	0.13
4	732	Loma Prieta	10/18/89	APEEL 2—Redwood City	E	43.23	0.08
5	777	Loma Prieta	10/15/79	HOLLISTER CITY HALL	D	27.6	0.23
6	778	Loma Prieta	10/18/89	Hollister Differential Array	D	24.8	0.26
7	786	Loma Prieta	10/18/89	Palo Alto—1900 Embarc	D	30.81	0.21
8	806	Loma Prieta	10/18/89	Sunnyvale Colton Ave	D	24.23	0.21
9	953	Northridge-01	01/17/94	Beverly Hills—14145 Mulhol	D	17.15	0.55
10	987	Northridge-01	1/17/94	LA—Centinela St	D	28.3	0.25
11	995	Northridge-01	01/17/94	LA—Hollywood Stor FF	D	24.03	0.37
12	996	Northridge-01	01/17/94	LA—FARING RD	D	20.81	0.34
13	1001	Northridge-01	01/17/94	LA—S Grand Ave	D	33.99	0.27
14	1003	Northridge-01	01/17/94	LA—Saturn St	D	27.01	0.45
15	1038	Northridge-01	1/17/94	Montebello Bluff	E	45.03	0.15
16	1044	Northridge-01	01/17/94	Newhall—Fire Sta	D	5.92	0.70
17	1063	Northridge-01	1/17/94	Rinaldi Receiving Sta	D	6.5	0.63
18	1085	Northridge-01	01/17/94	SYLMAR-CONVERTER STA-EAST	D	5.19	0.65
19	1087	Northridge-01	01/17/94	Tarzana—Cedar Hill A	D	15.6	0.99
20	1107	Kobe, Japan	01/16/95	Kakogawa	D	22.5	0.35
21	1111	Kobe, Japan	01/16/95	Nishi—Akashi	E	7.08	0.49
22	1113	Kobe, Japan	01/16/95	Osaj	E	21.35	0.08
23	1116	Kobe, Japan	01/16/95	Shin—Osaka	E	19.15	0.23
24	1119	Kobe, Japan	01/16/95	Takarazu	E	0.27	0.71
25	1120	Kobe, Japan	01/16/95	Takatori	E	1.47	0.65
26	1180	Chi–Chi, Taiwan	09/20/99	CHY002	E	24.96	0.13
27	1183	Chi–Chi, Taiwan	09/20/99	CHY008	E	40.43	0.12
28	1186	Chi–Chi, Taiwan	09/20/99	CHY014	D	34.18	0.24
29	1187	Chi–Chi, Taiwan	09/20/99	CHY015	D	38.13	0.16
30	1194	Chi–Chi, Taiwan	09/20/99	CHY025	E	19.07	0.15
31	1196	Chi–Chi, Taiwan	09/20/99	CHY027	E	41.99	0.06
32	1197	Chi–Chi, Taiwan	09/20/99	CHY028	D	3.12	0.79
33	1199	Chi–Chi, Taiwan	09/20/99	CHY032	E	35.43	0.09
34	1201	Chi–Chi, Taiwan	09/20/99	CHY034	D	14.82	0.30
35	1203	Chi–Chi, Taiwan	09/20/99	CHY036	D	16.04	0.26
36	1204	Chi–Chi, Taiwan	09/20/99	CHY039	E	31.87	0.11
37	1205	Chi–Chi, Taiwan	09/20/99	CHY041	E	19.83	0.46
38	1228	Chi–Chi, Taiwan	09/20/99	CHY076	E	42.15	0.08
39	1233	Chi–Chi, Taiwan	09/20/99	CHY082	E	36.09	0.07
40	1236	Chi–Chi, Taiwan	09/20/99	CHY088	D	37.48	0.18
41	1238	Chi–Chi, Taiwan	09/20/99	CHY092	E	22.69	0.10
42	1240	Chi–Chi, Taiwan	09/20/99	CHY094	E	37.1	0.06
43	1246	Chi–Chi, Taiwan	09/20/99	CHY104	E	18.02	0.18
44	1478	Chi–Chi, Taiwan	09/20/99	TCU033	D	40.88	0.18
45	1483	Chi–Chi, Taiwan	09/20/99	TCU040	E	22.06	0.13
46	1484	Chi–Chi, Taiwan	09/20/99	TCU042	D	26.31	0.21
47	1492	Chi–Chi, Taiwan	09/20/99	TCU052	D	0.66	0.35
48	1496	Chi–Chi, Taiwan	09/20/99	TCU056	E	10.48	0.14
49	1503	Chi–Chi, Taiwan	09/20/99	TCU065	D	0.57	0.66
50	1504	Chi–Chi, Taiwan	09/20/99	TCU067	D	0.62	0.41
51	1507	Chi–Chi, Taiwan	09/20/99	TCU071	D	5.8	0.62
52	1508	Chi–Chi, Taiwan	09/20/99	TCU072	D	7.08	0.40
53	1509	Chi–Chi, Taiwan	09/20/99	TCU074	D	13.46	0.45
54	1529	Chi–Chi, Taiwan	09/20/99	TCU102	D	1.49	0.24
55	1536	Chi–Chi, Taiwan	09/20/99	TCU110	E	11.58	0.18
56	1537	Chi–Chi, Taiwan	09/20/99	TCU111	E	22.12	0.11
57	1538	Chi–Chi, Taiwan	09/20/99	TCU112	E	27.48	0.08
58	1541	Chi–Chi, Taiwan	09/20/99	TCU116	E	12.38	0.17
59	1542	Chi–Chi, Taiwan	09/20/99	TCU117	E	25.42	0.13
60	1553	Chi–Chi, Taiwan	09/20/99	TCU141	E	24.19	0.09
61	1602	DUZCE, Turkey	11/12/99	BOLU	D	12.04	0.77
62	1605	DUZCE, Turkey	11/12/99	DUZCE	D	6.58	0.43