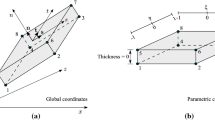
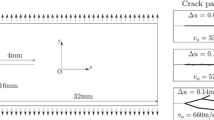
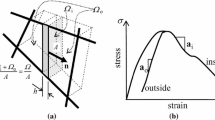
Abstract
Experimental data indicates that the limiting crack speed in brittle materials is less than the Rayleigh wave speed. One reason for this is that dynamic instabilities produce surface roughness and microcracks that branch from the main crack. These processes increase dissipation near the crack tip over a range of crack speeds. When the scale of observation (or mesh resolution) becomes much larger than the typical sizes of these features, effective-medium theories are required to predict the coarse-grained fracture dynamics. Two approaches to modeling these phenomena are described and used in numerical simulations. The first approach is based on cohesive elements that utilize a rate-dependent weakening law for the nodal cohesive forces. The second approach uses a continuum damage model which has a weakening effect that lowers the effective Rayleigh wave speed in the material surrounding the crack tip. Simulations in this paper show that while both models are capable of increasing the energy dissipated during fracture when the mesh size is larger than the process zone size, only the continuum damage model is able to limit the crack speed over a range of applied loads. Numerical simulations of straight-running cracks demonstrate good agreement between the theoretical predictions of the combined models and experimental data on dynamic crack propagation in brittle materials. Simulations that model crack branching are also presented.
Similar content being viewed by others
References
Abraham FF (2005). Unstable crack motion is predictable. J Mech Phys Solids 53: 1071–1078
Adda-Bedia M (2004). Brittle fracture dynamics with arbitrary paths. II. Dynamic crack branching under general antiplane loading. J Mech Phys Solids 52: 1407–1420
Adda-Bedia M (2005). Brittle fracture dynamics with arbitrary paths. III. The branching instability under general loading. J Mech Phys Solids 53: 227–248
Barenblatt GI (1962). The mathematical theory of equilibrium of cracks in brittle fracture. Adv Appl Mech 8: 55–129
Buehler M, Abraham FF and Gao H (2003). Hyperelasticity governs dynamic fracture at a critical length scale. Nature 426: 141–146
Buehler M and Gao H (2006). Dynamical fracture instabilities due to local hyperelasticity at crack tips. Nature 439: 307–310
Camacho GT and Ortiz M (1996). Computational modeling of impact damage in brittle targets. Int J Solids Struct 33: 2899–2938
Camacho GT and Ortiz M (1997). Adaptive Lagrangian modeling of ballistic penetration of metallic targets. Comput Methods Appl Mech Eng 142: 269–301
Dugdale DS (1960). Yielding of steel sheets containing slits. J Mech Phys Solids 8: 100–104
Erdogan F and Sih GC (1963). On the crack extension in plates under plane loading and transverse shear. J Basic Eng, Trans ASME 85: 519–527
Fineberg J, Gross SP, Marder M and Swinney HL (1991). Instability in dynamic fracture. Phys Rev Lett 67: 457–460
Fineberg J, Gross SP, Marder M and Swinney HL (1992). Instability in the propagation of fast cracks. Phys Rev B 45: 5146–5154
Flory P (1961). Thermodynamic relations for high elastic materials. Trans of the Faraday Soc 57: 829–838
Goldstein RV and Salganik RL (1974). Brittle fracture of solids with arbitrary cracks. Int J Frac 18: 507–523
Liu X and Marder M (1991). The energy of a steady-state crack in a strip. J Mech Phys Solids 39: 947–961
Morris JP, Rubin MB, Blair SC, Glenn LA and Heuze FE (2004). Simulations of underground structures subjected to dynamic loading using the distinct element method. Eng Comput 21: 384–408
Morris JP, Rubin MB, Block GI, Bonner MP (2006) Simulations of fracture and fragmentation of geologic materials using combined FEM/DEM Analysis. J Impact Eng 33: 463–473
Nuismer RJ (1975). An energy release rate criterion for mixed-mode fracture. Int J Frac 11: 245–250
Pandolfi A, Krysl P and Ortiz M (1999). Finite element simulations of ring expansion and fragmentation: The capturing of length and time scales through cohesive models of fracture. Int J Frac 95: 279–297
Rubin MB (1995) Numerical solution of two- and three-dimensional thermomechanical problems using the theory of a Cosserat point. J Math and Phys (ZAMP) 46, Special Issue, S308–S334. In: Casey J and Crochet MJ. Theoretical, experimental, and numerical contributions to the mechanics of fluids and solids, Brikhauser Verlag, Basel
Rubin MB (2000) Cosserat theories: shells, rods and points, solid mechanics and its applications, vol 79, Kluwer, The Netherlands
Sharon E and Fineberg J (1996). Microbranching instability and the dynamic fracture of brittle materials. Phys Rev B 54: 7128–7139
Sharon E and Fineberg J (1999). Confirming the continuum theory of dynamic brittle fracture for fast cracks. Nature 397: 333–335
Sih GC (1974). Strain-energy-density factor applied to mixed-mode crack problems. Int J Frac 10: 305–321
Xu X-P and Needleman A (1994). Numerical simulations of fast crack growth in brittle solids. J Mech Phys Solids 42: 1397–1434
Xu X-P and Needleman A (1995). Numerical simulations of dynamic interfacial crack growth allowing for crack growth away from the bond line. Int J Frac 74: 253–275
Xu X-P and Needleman A (1996). Numerical simulations of dynamic crack growth along an interface. Int J Frac 74: 289–324
Yoffe EH (1951). The moving Griffith crack. Philos Mag 42: 739–750
Zhou F, Molinari JF and Shioya T (2005). Rate-dependent cohesive model for simulating dynamic crack propagation in brittle materials. Engineering Fracture Mechanics 72: 1383–1410
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Block, G., Rubin, M.B., Morris, J. et al. Simulations of dynamic crack propagation in brittle materials using nodal cohesive forces and continuum damage mechanics in the distinct element code LDEC. Int J Fract 144, 131–147 (2007). https://doi.org/10.1007/s10704-007-9085-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-007-9085-2