1 Introduction

Carrier transport properties (for example, DC conductivity, Hall resistance, etc.) are one of the most fundamental parameters for understanding the performance of an electronic device. The electron transport can be characterized, for example, by using electromagnetic waves in the terahertz (THz) region [1, 2]. This technique enables mapping of the carrier transport in a wafer with a high spatiotemporal resolution without the need of ohmic connections. In addition, advances in the generation of ultrashort optical pulses have enabled us to evaluate the complex conductivity of a material directly by time-domain measurements without the need of using the Kramers-Kronig relation. By using this method, optical parameters of various electronic device materials including semiconductors have been derived from the complex transmittance [3,4,5] and time-domain spectroscopy in the Faraday configuration [6,7,8,9,10].

For industrial applications where device quality control is necessary, the electronic properties in each layer of a device are more significant than the electronic properties of bulk samples or thin films of a single material. In particular, for large-area devices based on SiC and GaN, uniform properties throughout the film are strongly required [11]. Since electronic devices are usually prepared on highly doped substrates, which are opaque in the THz frequency region, polarization-resolved reflection measurements, such as those in ellipsometry [12,13,14] and magneto-optical Kerr effect (MOKE) spectroscopy [15,16,17,18], are powerful methods for device inspection. Ellipsometry characterizes the complex reflectance of p-polarized and s-polarized light with a large angle of incidence [19, 20] and is widely used for the characterization of dielectric constants in the range from ultraviolet to infrared regions. Furthermore, ellipsometry in the THz region is also useful, and many bulk samples and thin films have been characterized by this method [21]. For example, Boosalis et al. performed ellipsometry in the THz region on Si p-n junction structures [22]. They characterized multilayer samples based on the reflectance characteristic of the surface mode [23], which is an electromagnetic wave that is guided at the interface between the conductive layer and the depletion layer. However, the p- and n-layers cannot be distinguished in ellipsometry measurements, and this causes a large deviation between the evaluated and actual electronic properties of each layer. In addition, in many semiconductors, the holes have a large effective mass and a short scattering time [24], and therefore the surface mode along the p-layer can be leaky. As a result, the signal of the p-layer may be buried in that of the n-layer in the device structure of a polar semiconductor, and thus the device structures that can be characterized by this method are limited.

On the other hand, MOKE spectroscopy can be used for a highly sensitive evaluation of the electronic transport properties of particular layers such as the n- and p-layers in a p-n junction, because the signs of the MOKE signals of p- and n-layers are opposite [25]. In MOKE spectroscopy, the change in the polarization of the THz pulse reflected from the sample is measured by a time-domain spectroscopy. Here, the rotation of the polarization direction can be enhanced at the resonance frequency of magnetic plasmons by applying a magnetic field [26]. Since the polarization modulation by the magnetic field for a p-layer is expected to be weak due to the low mobility, MOKE spectroscopy measurements of devices have been performed by using large angles of incidence like in ellipsometry [17, 18]. Uprety et al. measured the Hall effect of a Si-based photovoltaic device in the THz region under oblique incidence [27]. They evaluated the minority carrier mobility of the sample under 1-sun illumination and evaluated the carrier transport properties of the n-type emitter and p-type wafer.

Here, we consider that MOKE measurements at normal incidence have two important advantages for device characterization, where the wavevector of the incident THz pulse is parallel to the applied magnetic field. One reason for this is that a high spatial resolution can be achieved since the spot size of the incident THz pulse is the smallest at normal incidence. A further reason is the simpler analysis of the data obtained at normal incidence. When a magnetic field is applied perpendicularly to a thin film, the complex conductivity tensor can be diagonalized resulting in two eigenvalues for the two circular polarization states. In this case, the signal obtained in the MOKE measurement corresponds to a differentiation of the complex reflectance with respect to the frequency [25]. In this report, we demonstrate that MOKE spectroscopy in the THz frequency range is a powerful method for evaluating the carrier densities of a particular layer of a p-n junction. We also calculate the expected MOKE signals (i.e., the spectra of the ellipticity and polarization rotation angles) and find that the contribution of the p-layer to the MOKE signal is enhanced in a p-i-n structure. This can be explained by the intensity distribution of the incident THz electric field in the device. For the experimental verification, we perform measurements on GaAs epitaxial layers and photovoltaic devices with a p-i-n structure by using a circularly polarized THz wave.

2 Theoretical MOKE Signals of Different Samples

In our numerical calculations, we assume devices composed of several semiconductor layers with different electronic conduction properties. In general, the complex refractive index \( \overset{\sim }{n} \) of an isotropic semiconductor in the THz frequency regime is expressed by the following equation:

$$ {\overset{\sim }{n}}^2={\upepsilon}_{\mathrm{b}}+\frac{A}{\omega_{TO}^2-{\omega}^2- i\omega {\gamma}_{TO}}+\frac{i\overset{\sim }{\sigma}\left(\omega \right)}{\upepsilon_0\omega } $$
(1)

Here, ϵb is the background dielectric constant, and the second term on the right-hand side is the contribution from the transverse optical (TO) phonon determined by the resonance frequency of the TO phonon mode ωTO, its damping constant γTO, and a proportionality coefficient A. The third term is the contribution from the conductivity of free charge carriers. If we use the approximation for long wavelengths, the complex conductivity \( \overset{\sim }{\sigma}\left(\omega \right) \) can be described according to the Drude model as

$$ \overset{\sim }{\sigma}\left(\omega \right)=\frac{e^2 n\tau /{m}^{\ast }}{1- i\omega \tau} $$
(2)

Here, e is the elementary charge, and n, m∗, and τ are the free carrier density, the effective mass, and the average scattering time, respectively. Previously we evaluated the THz conductivity properties of GaAs-based photovoltaic devices without an applied magnetic field [28, 29], and we analyzed them with the parameters summarized in Table 1. In our present work, we perform the calculations using the same parameters. We consider a complex index of refraction corresponding to the carrier type and carrier density in each layer of the device. When a magnetic field B is applied to a semiconductor, the cyclotron motion of the free carriers perpendicular to the magnetic field causes anisotropy in the optical constants. This case is convenient because the conductivity tensor can be diagonalized using the basis of the two circular polarization states in the direction perpendicular to the magnetic field [25]. In Eq. 3, we define the cyclotron-active and cyclotron-inactive complex conductivities, \( {\overset{\sim }{\sigma}}_A\left(\omega \right) \) and \( {\overset{\sim }{\sigma}}_I\left(\omega \right) \), by using Eq. 2 and the cyclotron frequency ωc = eB/m∗:

$$ {\overset{\sim }{\sigma}}_A\left(\omega \right)=\overset{\sim }{\sigma}\left(\omega -{\omega}_c\right) $$
(3-a)
$$ {\overset{\sim }{\sigma}}_I\left(\omega \right)=\overset{\sim }{\sigma}\left(\omega +{\omega}_c\right) $$
(3-b)
Table 1 Material properties of GaAs used in our calculations
Full size table

For the derivation of the MOKE signal in the case of circular polarization, we assume that linearly polarized light impinges on the sample. The ellipticity angle and polarization rotation angle of the reflected light are denoted by η and θ, respectively. The linearly polarized light can be expressed by a sum of clockwise (R) and counterclockwise (L) circularly polarized fields, \( {E}_0\left({\overrightarrow{e}}_L+{\overrightarrow{e}}_R\right) \), where E0 is constant and we define the bases of the circularly polarized field as \( {\overrightarrow{e}}_L \) and \( {\overrightarrow{e}}_R \). Here, we assume that the wavevector of the incident light is parallel to the applied magnetic field. The light reflected from the sample can be expressed as \( E{\prime}_0\left({e}^{-\eta + i\theta}{\overrightarrow{e}}_L+{e}^{\eta - i\theta}{\overrightarrow{e}}_R\right) \), where E′0 describes the electric field strength of the reflected beam. Note that in the case of electrons, the cyclotron-active conductivity needs to be chosen clockwise circular polarization and cyclotron-inactive conductivity needs to be chosen for counterclockwise circular polarization. For the holes, the opposite rule needs to be applied. Thus, the complex reflectance of the semiconductor multilayer device can be calculated by using the complex refractive index \( {\overset{\sim }{n}}_{A/I} \) obtained by substituting Eq. 3 for \( \overset{\sim }{\sigma}\left(\omega \right) \) in Eq. 1 for each layer. From the time-domain MOKE measurements, the frequency-domain spectra of the ellipticity angle η and polarization rotation angle θ can be determined. These angles are related to the Fresnel reflection coefficients for circularly polarized light according to [30]

$$ \frac{r_R-{r}_L}{r_R+{r}_L}=\tanh \left(\eta - i\theta \right)\approx \eta - i\theta $$
(4)

Figure 1(a) shows the calculated spectra of η (red curve) and θ (blue curve) for an n-GaAs epitaxial layer with an applied magnetic field of B=0.4 T. The calculation results for a p-GaAs epitaxial layer are shown in Fig. 1(b). In these calculations, we assumed a 4-μm-thick epi-layer on a semi-insulating GaAs substrate. We used carrier densities of 3.0 × 1017 cm−3 (n-GaAs) and 1.6 × 1018 cm−3 (p-GaAs) and the same plasma frequency \( {\omega}_p=\sqrt{n{e}^2/{m}^{\ast }{\epsilon}_0} \) of 19 THz. While the cyclotron frequencies of the electrons and holes are ωc=0.17 THz and 0.032 THz, respectively, the values of η at cyclotron frequencies exhibit no distinct peak in the reflection geometry. On the other hand, η exhibits a peak near the effective plasma frequency \( {\omega}_p^{\ast}\approx {\omega}_p/\sqrt{\epsilon_b} \) of 5.2 THz in the n-GaAs epitaxial layer as shown Fig. 1(a). Since the effective plasma frequency is shifted by ±ωc by applying a magnetic field, the spectra of η and θ correspond to the first and second derivatives of the change in the complex reflectance spectrum induced by the magnetic field, respectively. In Fig. 1(b) for the p-GaAs epitaxial layer, the signs of η and θ are opposite to those for the n-GaAs epitaxial layer. Furthermore, their magnitudes are about 1 mrad, which is much smaller than the magnitudes calculated for the n-type layer. The small magnitudes are a result of a damped magneto-plasmon at the plasma frequency due to both a short average scattering time of holes and a small cyclotron frequency (derived from the large effective mass), as shown in Table 1. Therefore, a strong magnetic field is usually required for an accurate MOKE measurement of a p-GaAs epitaxial layer. On the other hand, as shown below, MOKE measurements on p-i-n structures are more sensitive to the p-layer.

Fig. 1
figure 1

Frequency-domain spectra of η (red curve) and θ (blue curve) for (a) an n- and (b) a p-GaAs epitaxial layer with an applied magnetic field of B=0.4 T

Full size image

The inset of Fig. 2(a) shows the sample structure used for the calculation of the MOKE signal of a p-i-n junction: the bottom layer is an n+-GaAs substrate with a carrier density of 3 × 1018 cm−3, the next layer is an n-GaAs layer with a thickness of 3 μm and a carrier density of 2 × 1017 cm−3, then an intrinsic GaAs layer with a thickness of 0.5 μm was introduced, and the top layer is a 0.66-μm-thick p-GaAs layer. We changed the carrier density of the p-GaAs layer (0.5 × 1018, 1.0 × 1018, and 1.5 × 1018 cm−3) to evaluate the sensitivity of the MOKE signals with respect to the p-layer. Figure 2(a) shows the spectra of η and θ for B=0.4 T. By comparing with the spectra shown in Fig. 1(a) and 1(b), we find that the signal intensity of the p-i-n structure is stronger by about an order of magnitude while the spectral width is narrower. It can be seen that the signal intensity of η gradually increases with the carrier density of the p-layer, and the spectral shape of θ also changes slightly. These changes occur due to the direct contribution of the p-layer. Note that the slight changes induced by the p-layer are, however, much stronger than the amplitudes observed in Fig. 1(b). On the other hand, if the sign of the cyclotron frequency of the p-layer in this structure was inverted, the signal would hardly change (Fig. 2(b)). The comparison between Fig. 2(a) and 2(b) suggests that the MOKE signal in Fig. 2(a) is mainly due to the interface of the i/n layer, and we have to discuss the additional contribution of the p-layer to the MOKE signal.

Fig. 2
figure 2

(a) η (red curve) and θ (blue curve) for a p-i-n structure in a magnetic field of B=0.4 T. (b) η and θ of the same structure in the case of an inverted cyclotron frequency of the p-layer

Full size image

The THz spectroscopy results for a p-i-n photovoltaic device without an applied magnetic field in our previous work show that a THz wave can be detected with high sensitivity if photocarriers are generated near the depletion layer [28]. Since the THz pulse is mainly reflected at the boundary of the n+-substrate, constructive interference of the internal reflections at the p-i-n layers occurs near the plasma frequency. The THz field is enhanced near the surface at the resonance frequency, causing a larger MOKE signal for the p-i-n structure than that for the epi-film. Figure 3 shows the intensity distributions of the electric field at 6.4, 7.1, and 5.2 THz for the n- and p-type epitaxial layers and the p-i-n structure, respectively. These distributions were calculated by using the transfer-matrix method [31]. In the epi-films, the amplitude of the THz field at the surface is small because it is reflected at the surface. On the other hand, in the p-i-n structure, the electric field amplitude reaches its maximum near the p-layer and the depletion layer owing to interference. This can enhance the MOKE signal significantly. Therefore, a remarkable response due to the p-layer is apparent in Fig. 2(a).

Fig. 3
figure 3

Amplitude of the electric field at (a) a frequency of 6.4 THz for the n-GaAs epitaxial layer, (b) at 7.1 THz for the p-GaAs epitaxial layer, and (c) at 5.2 THz for the p-i-n structure

Full size image

3 Experimental Setup

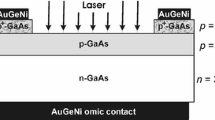
Figure 4 shows the schematic overview of our experimental setup. We evaluated the Kerr ellipticity angle η and the Kerr rotation angle θ by extracting the values of the circularly polarized complex reflectance at normal incidence for different values of the applied magnetic field. As light source, we used an amplified Ti/sapphire laser (Spectra Physics, Spitfire) with a pulse width of 35 fs, a repetition rate of 1 kHz, and a pulse energy of 3.5 mJ. The optical beam was divided into two beams by a beam splitter; the pulses of the transmitted beam were used for the THz wave generation and the pulses of the other beam were used for the electro-optic (EO) sampling [32]. The THz wave (generated by a two-color air plasma) was focused on the sample at normal incidence after it had passed through a wire-grid polarizer and had been converted into a circularly polarized THz wave by single 45°-right-angled Si prism [25]. The THz wave reflected from the sample was converted into linearly polarized light by passing through the Si prism again. Since the obtained polarization direction is perpendicular to the axis of the wire-grid polarizer, the THz wave was reflected by the wire-grid polarizer and was focused onto a crystal for EO sampling. As the EO crystal, we used a 0.3-mm-thick (110)-oriented GaP plate. The THz-induced change in the birefringence of the EO crystal was digitized for each shot using a λ/4 plate, a Wollaston prism, and a balance detector. The THz wave detected in this setup is linearly polarized but contains information on the complex reflectance of the sample with respect to circularly polarized light. The detectable frequencies were in the range from 0.5 to 7.0 THz. The region of the optical path of the THz wave was filled with dry air. A rotatable disk with magnets was placed above the sample to apply a magnetic field.

Fig. 4
figure 4

The schematic overview of our experimental setup

Full size image

Since the wavevector of the incident light in this setup is parallel to the direction of the magnetic field, we obtain the relations rR/L(+B) = rL/R(−B) as well as σR/L(+B) = σL/R(−B) [33]. Therefore, we can rewrite Eq. 4 as

$$ \frac{r_R\left(+B\right)-{r}_R\left(-B\right)}{r_R\left(+B\right)+{r}_R\left(-B\right)}\approx \frac{\Delta {r}_R}{2{r}_R(0)}\approx \eta - i\theta $$
(5)

In order to modulate the magnetic field, the disk with four neodymium magnets was rotated by a DC brushless motor (Oriental Motor, US2-26JA-A-2). This disk was also used in Ref. [30] and the magnets had a diameter of 10 mm. The rotation speed and phase of the disk were monitored by a magnetic proximity sensor (ASA electronics industry, AH002-S). The sample was placed 1 mm away from the front face of the magnets, and we modulate the magnetic field at a frequency of 20 Hz. To obtain physically meaningful time profile of the THz wave, we excluded the disk angles where the sample lies at an edge of the magnet to avoid data including inhomogeneous magnetic field distributions within the THz wave spot [30]. The induced magnetic field of |B| = 0.40 T on the surface of the samples was estimated from the MOKE signals in this experiment. Since we used an integration time of 10 min, it was possible to measure the polarization rotation with an accuracy of 0.5 mrad at 0.5 THz. The dynamic ranges estimated from the power spectra were 2 mrad at 1 THz, approximately 10 mrad at 4 THz, and 50 mrad at the measurement limit of 7 THz.

We experimentally confirmed the enhancement in the MOKE signal explained in Section 2 by investigating different devices. We performed measurements on two GaAs photovoltaic devices with a p-i-n structure (with different i-layer thicknesses) and GaAs epitaxial layers grown on a semi-insulating GaAs substrate by molecular beam epitaxy. We already reported the complex reflectance spectra of one of the p-i-n structures in the THz regime in Ref. 28, and the THz radiation and I–V characteristics in Ref. 29.

4 Experimental Results and Discussion

Figure 5(a) shows the time-domain THz waveform reflected from an n-GaAs epitaxial layer without an applied magnetic field, \( {E}_R^0 \) (black curve), and its change induced by the magnetic field modulation, \( \Delta E={E}_{\mathrm{R}}^{+\mathrm{B}}-{E}_R^{-B} \) (red curve, × 10). Figure 5(b) shows the data of a p-GaAs epitaxial layer. The samples investigated here are an n-GaAs epitaxial layer with a thickness of 4 μm and a carrier density of 3.4 × 1017 cm−3 and a p-GaAs epitaxial layer with a thickness of 2 μm and a carrier density of 3.7 × 1018 cm−3, both grown on semi-insulating GaAs substrates with almost the same plasma frequency [28]. We find that the values of ∆E of the n-GaAs epitaxial layer are larger than those of the p-GaAs epitaxial layer and exhibit a phase shift of −π/2 with respect to \( {E}_R^0 \). We calculated the Fourier transforms of these signals to obtain the spectra for \( \Delta E/2{E}_R^0=\eta - i\theta \). Figure 5(c) and 5(d) show the spectra of both η and θ for the n- and p-GaAs epitaxial layers, respectively. It can be seen that the general features of the Kerr ellipticity η (red circles) of the p-type film have an opposite sign with respect to the corresponding features of the η of the n-type film. The Kerr rotation angle θ (blue squares) also exhibits such a behavior. Note that the MOKE signal of the p-GaAs epitaxial layer is overall smaller than that of the n-GaAs epitaxial layer, in spite of the same plasma frequency. This is due to the short scattering time and the large effective mass of the holes as described in Section 2. We also calculated the η and θ spectra that are expected from the responses of the conduction carriers in the epi-films. The solid line in Fig. 5(c) is the fitting result for a scattering time of 0.33 ps and a carrier density of 2.7 × 1017 cm−3. The deviation between the estimated carrier density and the design value of 3.4 × 1017 cm−3 is probably due to a fluctuation in the growth condition such as the substrate temperature. The solid line in Fig. 5(d) is the calculated spectrum for a scattering time of 0.032 ps and a carrier density of 3.1 × 1018 cm−3. Unfortunately, the signal in the high-frequency region is smaller than the noise level in our system.

Fig. 5
figure 5

The THz waveform reflected from (a) an n- and (b) a p-GaAs epitaxial layer without an applied magnetic field is shown by the black curve (\( {E}_R^0 \)). The change in the THz wave due to the modulation of the magnetic field by the rotating disk is shown by the red curve (∆E, multiplied by × 10 for better visibility). The corresponding η and θ spectra are shown in (c) and (d). Here, the solid curves show the calculated spectra

Full size image

Figure 6(a) and (b) show the η and θ spectra for p-i-n structures with intrinsic layer thicknesses of 100 nm and 500 nm, respectively. The samples are GaAs-based photovoltaic devices that contain, from top to bottom, a 0.66-μm-thick p-layer with a carrier density of 1.0 × 1018 cm−3, an intrinsic layer, a 3-μm-thick n-layer with a carrier density of 2.0 × 1017 cm−3, and an n+-substrate (3.0 × 1018 cm−3). The MOKE signals obtained from these devices have amplitudes that are an order of magnitude larger than those of the epi-films in Fig. 5(c) and (d). Furthermore, they also exhibit narrower spectra. This enhancement in the signal intensity is due to the interference between the THz wave reflected at the highly doped n+-substrate and the p-layer surface, as explained in Fig. 3. Therefore, we conclude that the MOKE spectroscopy in the THz frequency range is a powerful technique for the characterization of the electronic transport properties of particular layers in a p-i-n structure. Although this work only evaluated the carrier densities, the transport properties such as the conductivity can be derived from Eq. 2. We evaluated the contributions from the n- and p-layers to the signal by calculating η − iθ with the characteristic values of the phonons and carriers in Table 1. Based on Fig. 2(b), we consider that the peak frequency of the MOKE signal is mainly determined by the interface of the i/n-layer. Therefore, the carrier density of the n-layer and the electron scattering time were set to 1.3 × 1017 cm−3 and 0.092 ps, respectively. These values are the same as those used in Ref. 28. The deviation of this estimated carrier density of the n-layer from the design value of 2.0 × 1017 cm−3 is almost the same as that for the abovementioned epi-film. To evaluate the response of the p-layer in the device, we used the carrier density of the p-layer as the fitting parameter and the solid curves in Fig. 6(a) are the calculated spectra for the p-i-n structure with a 100-nm-thick i-layer and a p-layer with a carrier density of 0.6 × 1018 cm−3. The red curve roughly reproduces the experimental η values, but the predicted spectral width of θ (blue curve) is slightly smaller than the experimentally confirmed spectral width. The solid curves in Fig. 6(b) are the calculated spectra for the p-i-n structure with a 500-nm-thick i-layer and a p-layer with a carrier density of 1.2 × 1018 cm−3, and both η and θ are sufficiently well reproduced. The obtained carrier densities were different from the carrier density of the design structure (1.0 × 1018 cm−3), but this degree of deviation can be attributed to a fluctuation in the growth conditions such as the substrate temperature.

Fig. 6
figure 6

η and θ spectra for two p-i-n structures with different intrinsic layer thicknesses of (a) 100 nm and (b) 500 nm. The solid curves show the fitting results

Full size image

From both our calculations and experiments, we concluded that the MOKE signal of the p-layer in a p-i-n structure is large due to the constructive interference between the reflections at the substrate and the top p-layer in this layered structure. The obtained spectra of η and θ approximately represent the first and second derivatives of the complex reflectance, respectively. The complex reflectance changes in accordance with the carrier density of the p-layer and the MOKE signal is sensitive to these changes. This also implies the possibility of an accurate and quantitative evaluation of the p-layer in our device. Finally, we discuss the accuracy of the carrier density determined by fitting the data in Fig. 6. We evaluated the error by the least squares method and obtained (0.6 ± 0.2) × 1018 cm−3 and (1.2 ± 0.1) × 1018 cm−3 for the carrier densities of the p-layers in the samples with depletion layer widths of 100 nm and 500 nm, respectively. These values are close to the design values and much better than the usual error in THz ellipsometry using oblique incidence (which is almost twice as large, e.g., see Ref. 21). Thus, we conclude that this method allows us to evaluate the carrier density with high accuracy and that the MOKE spectroscopy in the THz frequency range is useful for evaluating the carrier transport characteristics of particular layer of a p-n junction.

5 Conclusion

We have demonstrated that the MOKE at normal incidence in the THz frequency range is useful for evaluating the carrier densities of the n- and p-layers of a p-n junction. We calculated the MOKE signals for GaAs epitaxial layers and a p-i-n structures and found that the MOKE signal for the p-GaAs epitaxial layer cannot be evaluated with high sensitivity due to the p-layer’s small hole mobility. On the other hand, we found that, in the p-i-n structure, the contribution of the p-layer is better reflected in the MOKE signal due to the interference between the THz waves reflected at the highly doped substrate and the surface. To verify this effect experimentally, we performed MOKE spectroscopy on GaAs epitaxial layers and p-i-n structures and evaluated the carrier densities of the n- and p-layers. Our technique allows the characterization of the important electronic transport properties with a small spot size (corresponding to the diffraction limit) without measuring a reference mirror. It is also applicable to systems based on high-repetition lasers of low-cost laser systems. Therefore, a high-speed mapping of electronic transport properties with a high spatial resolution is possible, which is promising for large-area devices.