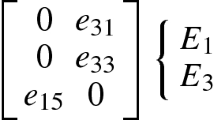Abstract
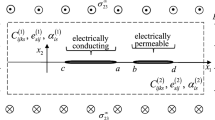
The paper addresses a plane problem for an infinite plane consisting of two different piezoceramic half-planes with an interfacial crack with smooth contact zones and subjected to the uniformly distributed electromechanical loading applied at infinity. Methods of complex-variable theory are used to reduce the problem to a Dirichlet-Riemann mixed homogeneous boundary-value problem. Its solution is found in closed form. A system with one crack that has one or two contact zones is calculated. Expressions for stresses, electric-flux density, and displacement discontinuities at the interface are written. Equations for the determination of the length of the contact zones and expressions for the stress intensity factors at the crack tips are derived
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. T. Grinchenko, A. F. Ulitko, and N. A. Shul’ga, Electroelasticity, Vol. 5 of the five-volume series Mechanics of Coupled Fields in Structural Members [in Russian], Naukova Dumka, Kyiv (1989).
J. Dundurs and M. Comninou, “Review of and outlook for interphase-crack studies,” Mekh. Komp. Mater., No. 3, 387–396 (1979).
A. A. Kaminskii, L. A. Kipnis, and V. A. Kolmakova, “On the Dugdale model for a crack at the interface of different media,” Int. Appl. Mech., 35, No. 1, 58–63 (1999).
V. V. Loboda and A. E. Sheveleva, “Determining prefracture zones at a crack tip between two elastic orthotropic bodies,” Int. Appl. Mech., 39, No. 5, 566–572 (2003).
N. I. Muskhelishvili, Some Basic Problems in the Mathematical Theory of Elasticity [in Russian], Nauka, Moscow (1966).
E. L. Nakhmein and B. M. Nuller, “Pressure of system of punches upon an elastic half-plane under the general conditions of contact coupling and sliding,” Prikl. Mat. Mekh., 52, No. 2, 284–293 (1988).
V. I. Ostrik and A. F. Ulitko, “Circular interfacial crack with frictional contact of surfaces,” Mat. Metody Fiz.-Mekh. Polya, 47, No. 1, 84–94 (2004).
I. V. Simonov, “Crack at an interface in a uniform stress field,” Mech. Komp. Mater., 21, No. 6, 950–957 (1986).
A. F. Ulitko and V. I. Ostrik, “Interfacial crack with frictional contact of faces,” Visn. Kyiv. Univ., Ser. Fiz.-Mat. Nauky, No. 2, 133–141 (2002).
G. P. Cherepanov, “Stress state in an inhomogeneous plate with cuts,” Izv. AN SSSR, Otd. Tekhn. Nauk Mekh. Mashinostr., No. 1, 131–137 (1962).
M. Comninou, “The interface crack,” J. Appl. Mech., 44, 631–636 (1977).
K. P. Herrmann and V. V. Loboda, “On interface crack models with contact zones situated in an anisotropic bimaterial,” Arch. Appl. Mech., 69, 311–335 (1999).
K. P. Herrmann and V. V. Loboda, “Fracture-mechanical assessment of electrically permeable interface cracks in piezoelectric bimaterials by consideration of various contact zone models,” Arch. Appl. Mech., 70, 127–143 (2000).
S. A. Kaloerov, “Determining the intensity factors for stresses, electric-flux density, and electric-field strength in multiply connected electroelastic anisotropic media,” Int. Appl. Mech., 43, No. 6, 631–637 (2007).
V. L. Karlash, “Planar electroelastic vibrations of piezoceramic rectangular plate and half-disk,” Int. Appl. Mech., 43, No. 5, 547–553 (2007).
I. V. Kharun and V. V. Loboda, “A set of interface cracks with contact zones in a combined tension-shear field,” Acta Mech., 166, 43–56 (2003).
V. S. Kirilyuk, “Stress state of a piezoelectric body with a plane crack under antisymmetric loads,” Int. Appl. Mech., 42, No. 2, 152–161 (2006).
V. S. Kirilyuk and O. I. Levchuk, “Electrostressed state of a piezoceramic body with a paraboloidal cavity,” Int. Appl. Mech., 42, No. 9, 1011–1020 (2006).
V. V. Loboda, “The quasi-invariant in the theory of interface crack,” Eng. Fract. Mech., 44, 573–580 (1993).
Y. E. Pak, “Linear electroelastic fracture mechanics of piezoelectric materials,” Int. J. Fract., 54, 79–100 (1992).
M. L. Williams, “The stresses around a fault or cracks in dissimilar media,” Bull. Seismol. Soc. Amer., 49, 199–204 (1959).
Author information
Authors and Affiliations
Additional information
__________
Translated from Prikladnaya Mekhanika, Vol. 44, No. 3, pp. 66–74, March 2008.
Rights and permissions
About this article
Cite this article
Govorukha, V.B., Herrmann, K.P. & Loboda, V.V. Electrically permeable crack with contact zones between two piezoelectric materials. Int Appl Mech 44, 296–303 (2008). https://doi.org/10.1007/s10778-008-0041-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-008-0041-2