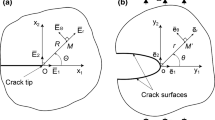
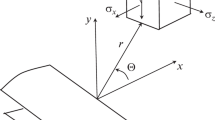
A body with a fracture process zone at the crack front is considered. The constitutive equations relating the components of the stress vectors at points on the opposite boundaries of the fracture process zone and the components of the vector of relative displacements of these points are derived. A local fracture criterion is formulated. A boundary-value problem for a plate made of a nonlinear elastic orthotropic material with a mode I crack is stated in terms of the components of the displacement vector. By solving the problem numerically, it is revealed how the fracture process zone develops under loading. Features of the deformation field at the end of the fracture process zone are established. The critical load on the plate that causes the crack to grow is determined.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
O. S. Bogdanova, A. A. Kaminsky, and E. E. Kurchakov, “Fracture process zone at the front of a crack in a solid,” Dop. NAN Ukrainy, No. 5, 25–33 (2017).
E. E. Kurchakov, “Stress–strain relations for nonlinear anisotropic medium,” Int. Appl. Mech., 15, No. 9, 803–807(1979).
E. E. Kurchakov, “Thermodynamic validation of the constitutive equations for a nonlinear anisotropic body,” Dop. NAN Ukrainy, No. 5, 46–53 (2015).
H. Hencky, “Development and modern state of plasticity theory,” Prikl. Mat. Mekh., 4, No. 3, 31–36 (1940).
L. Banks-Sills, N. Travitzky, D. Ashkenazi, and R. Eliasi, “A methodology for measuring interface fracture properties of composite materials,” Int. J. Fract., 99, No. 3, 143–160 (1999).
A. A. Kaminsky and O. S. Bogdanova, “Long-term crack-resistance of orthotropic viscoelastic plate under biaxial loading,” Int. Appl. Mech., 31, No. 9, 747–753 (1995).
A. A. Kaminsky and E. E. Kurchakov, “Influence of tension along a mode I crack in an elastic body on the formation of a nonlinear zone,” Int. Appl. Mech., 51, No. 2, 130–148 (2015).
A. A. Kaminsky and M. F. Selivanov, “On modeling of subcritical crack growth in viscoelastic body under point forces,” Int. Appl. Mech., 53, No. 5, 538–544 (2017).
E. E. Kurchakov, “Experimental study of the plastic zone at the front of a mode I crack,” Int. Appl. Mech., 54, No. 2, 213–219 (2018).
A. Love, Treatise on the Mathematical Theory of Elasticity, The University Press, Cambridge (1927).
A. Needleman, “A continuum model for void nucleation by inclusion debonding,” J. Appl. Mech., 54, No. 3, 525–531 (1987).
K. Park and G. H. Paulino, “Cohesive zone models: A critical review of traction-separation relationship across fracture surfaces,” Appl. Mech. Rev., 64, No. 11, 1–20 (2011).
G. N. Savin, and A. A. Kaminsky, “The growth of cracks during the failure of hard polymers,” Sov. Appl. Mech., 3, No. 9, 22–25 (1967).
V. Tvergaard and J. W. Hutchinson, “The influence of plasticity on mixed mode interface toughness,” J. Mech. Phys. Solids, 41, No. 6, 1119–1135 (1993).
A. A. Wells, “Critical tip opening displacement as fracture criterion,” in: Proc. Crack. Propagation Symp., 1, Granfield (1961), pp. 210–221.
F. H. Wittmann, K. Rokugo, E. Bruehwiler, H. Mihashi, and P. Simonin, “Fracture energy and strain softening of concrete as determined by means of compact tension specimens,” Mater. Struct., 21, No. 1, 21–32 (1988).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prikladnaya Mekhanika, Vol. 55, No. 1, pp. 26–43, January–February,2019.
Rights and permissions
About this article
Cite this article
Kaminsky, A.A., Kurchakov, E.E. Fracture Process Zone at the Tip of a Mode I Crack in a Nonlinear Elastic Orthotropic Material. Int Appl Mech 55, 23–40 (2019). https://doi.org/10.1007/s10778-019-00931-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-019-00931-9