1 Introduction

Housing market is a very unique asset market as demand for housing comes from both demand for investment return and demand for a shelter/accommodation. When viewed as an investment vehicle, housing market is simply part of the market economy. When viewed as a social tool to provide shelter, it becomes a major concern for most governments as pressure from the society for more affordable housing is always high. Such social pressure is especially mounting in societies where the private sector housing market is prone to overheating and excessive demand. Hong Kong, being an open economy with no control on hot money, is one of these speculation-prone markets. More importantly, housing market activities in this city, as represented by transaction volume, also fluctuate vigorously with housing price levels. Real estate investors as well as home buyers are getting more and more interested in knowing the correlation among the major elements in the housing market, in particular between transaction volume and price so as to make a more informed investment or home purchase decision. In addition, because of this volatile market housing movement in Hong Kong, the government tends to be more concerned with fine-tuning the market, especially in the recent few years. Demand suppression measures have been devised and delivered to the housing market in Hong Kong by the government since the latter part of 2012. These measures include tightening mortgage credit availability, additional tax on non-local purchasers as well as tax on short-term speculative gains. The government has emphasized that they would not like to administratively “control” housing price directly as this goes against the reputation of the free economy adopted in Hong Kong. It is hoped that by suppressing demand, and hence transaction volume, it will ultimately lead to downward adjustment of market price level. At the same time, when market expectation of housing price appreciation diminishes, it also reduces or defers home purchase decisions. In this way, sometimes it may even contradict the policy objective of encouraging more homeownership with a sustained low and affordable price level when the desire to purchase shrinks with the drop of housing price. It is therefore imperative for policymakers to understand the correlation between housing price movements and housing transaction activities in order for a more effective housing policy to be formulated.

Correlation between asset price and transaction volume has always been an interesting research topic in the study of most capital markets. Transaction volume represents the intensity of market interest in that commodity, and hence the demand. Usually, when there is an increased interest in such commodity, as represented by an increase in transaction volume, the sustained surge of demand will push up the market price of such commodity, assuming supply is not extremely responsive to this upsurge in demand. On the other hand, one may also argue that the increase in demand, hence transaction activity, is induced by an increase in price especially in the investment market where ordinary investors may be triggered to invest by the price signal. In particular, analyses in the stock market have been focusing on the market dynamics evolving around price movements, liquidly, and trading intensity or transaction volume (Diamond and Verrecchia 1987; Huffman 1992; Easley and O’Hara 1992; Liesenfeld et al. 2006; Gerhold et al. 2014). One reason for this interest in the stock market is the availability of data as transaction activities in most of the stock markets are relatively intense on a daily basis and both transaction volume and price movements are centrally recorded in the local stock exchange. Stock markets in various regions of the global economy therefore have become an important laboratory for the examination of such correlation, with different degrees of impacts and correlation found (Sharma 2006; Liu and Zhu 2009; McGowan and Muhammad 2012; Yang and Wu 2014). Interestingly, not all of these studies come to a consensus on how these elements in the financial market interact with each other, such as the correlation between price movement and transaction times (Diamond and Verrecchia 1987; Easley and O’Hara 1992). In addition, similar relationship has also been tested in other financial markets such as futures (Wang et al. 1997) and currency (Sarwar 2003), as well as the real estate market (Arbel et al. 2009; Shi et al. 2010). In any case, market participants with different levels of information advantage and sensitivity seem to react quite differently (Gerhold et al. 2014).

Transaction volume in the capital markets may also be exogenously stimulated by changes in government regulations. Deregulations on the stock market which result in lower transaction costs have been shown to have a positive impact on the transaction volume, which in turn affect price volatility (Liu and Zhu 2009). Regulatory and policy changes in the capital markets therefore are instrumental to the volatility observed in these markets due to their impacts on market transaction volume and the subsequent impact on price movements. Such regulatory and policy changes alter the information structure in the market such that players with different degrees of information exposure need time to adjust their strategy, respectively. Changes in the market structure such as change in stock index composition and landscape may also have an impact on “abnormal market-adjusted returns” (Wilkens and Wimschulte 2005), which in turn may affect the price volatility–trading volume correlation.

Examination of such correlation provides important information for people in the market to understand the causation effect among major variables as well as the delicate dynamics of the housing market (Arbel et al. 2009; Widlak and Tomczyk 2010; Wong et al. 2013). In theory, investors tend to be more cautious in their investment decision when price is going down, and more inclined to make a purchase when price begins to go up due to potential capital gains in the future. Shi et al. (2010) have examined this correlation in most large cities in New Zealand and concluded as an investment strategy that when transaction volume comes down substantially, housing price will soon follow in the same direction, and vice versa. Hence, when the housing market is receiving an intensified attention leading to more and more transaction activities, it is also foreseeable that price level will follow suit. Consequently, high housing price may stimulate more interest from investment funds seeking for higher return in this market, leading to a sustained level of intensive market transaction activities. However, in the housing market, there is a further factor to consider, namely affordability. When prices are too high, most prospective homeowners may find it difficult to afford a housing unit for their occupation purpose. Hence, it is expected that when prices are coming down from the peak, housing price level should become more appealing and affordable to these prospective homeowners. This also forms the basis for the pro-interventionist argument that government has a duty to fine-tune housing price so as to allow more people to become homeowners at an affordable level.

We intend to examine such correlation between housing price movements and transaction volume/activity in Hong Kong using the Granger causality test framework with a core objective of getting a better understanding of the housing market behavior in this city so that more effective government housing policy could be devised. We need to examine whether and how housing price movements impact on transaction volume/market activities, and vice versa. This is important as the results will help estimate the effectiveness of government homeownership policy in Hong Kong. For instance, if housing price Granger causes transaction volume to change in opposite direction, government intervention that aims at suppressing housing price might see a higher desire for the citizens to become homeowners once price level begins to drop. Nevertheless, if transaction volume does not Granger cause housing price to change, any measures such as limiting credit availability or curbing housing demand may not be capable of moderating runaway housing price situation. We will discuss these issues later after the examination of the empirical results.

Although there is a general consensus that housing price and transaction volume do have a certain positive correlation, the magnitude and causation direction between these two elements vary from market to market, or from district sector within a market to another sector (Clayton et al. 2010; Ling, et al. 2009; Tu et al. 2009). What seems to be interesting is that such positive correlation is only found in the buyer’s and sellers’ behavior in the housing/residential sector, but not in other sub-sectors of the real estate market such as the commercial sector (Leung and Feng 2005). More specifically, housing market with inelastic supply nature will tend to observe Granger causality between housing price and transaction volume in both directions (Clayton et al. 2010). This means in any housing market where supply is relatively elastic, price will Granger cause transaction volume to change, but probably not vice versa. Given the nature of housing development is usually associated with a lag time due to the need to convert potential site into habitable floor space, as well as procedural delay in housing development in most economies, short-term inelastic supply is a common phenomenon. In this way, short-term and long-term relationship between housing price and transaction volume may differ in correlation outcome and magnitude (Shi et al. 2010). On the other hand, some study has shown that changes in transaction volume do not seem to be correlated with the rate of entry into the housing market (de Wit et al. 2013).

Such correlation between price changes and changes in transaction activity/intensity may be due to a number of reasons. For instance, falling housing price will reduce existing homeowners’ home equity value. When these homeowners want to sell their houses, they have to ensure that the proceeds from selling the house would be adequate for repaying their outstanding loans, or there will be problem of negative asset value. Hence, higher asking prices due to loss aversion behavior in a slow market will in return increase the time on market of the house and eventually reduce the transaction volume. In addition, market information also plays an important role in it (Gerhold et al. 2014). Wong et al. (2013) also find that when information in market transaction activities is more abundant, participants would rely relatively more on information from the immediate neighborhood. Their findings show that property prices do not only depend on various property attributes but also on the neighboring properties transacted previously. When people see an active market in the neighborhood, they tend to be more confident to enter into the market, and hence this will add fuel to the upward rising housing price movement. Yiu et al. (2009) on the other hand find that transaction cost level has a bearing on the relationship between price and transaction volume, especially in the first-hand market and hence a market with very intensive transaction volume might not necessarily provide good price information when such market is dominated by “noise traders.”

Moreover, it has been argued that rising price level allows homeowners to be more confident financially to commit down payment for a new house with an intention to trade up or move in the near future (Leung et al. 2002). This is because when housing price is on the upward trend, homeowners who wish to trade up or move may want to lock the purchase price of the new flat as soon as possible by committing to pay down payment before they have sold their existing house. In this way, they may be able to achieve an even higher selling price for their existing house without the worry of seeing the value of their new house inflated during that period.

In this paper, we are going to examine the price–transaction volume correlation observed in the Hong Kong housing market by means of a vector autoregressive (VAR) model. We will apply quarterly housing transaction data in Hong Kong from the beginning of 1993 to the end of 2014. The objectives are to establish whether there is such positive price–transaction volume correlation in a rather active market in Hong Kong, and to study the lead–lag relationship of these two elements. In this study, transaction activity or transaction volume is defined as number of transaction. We fit the two endogenous variables namely the price and transaction volume variables into a bivariate VAR model and conduct the Granger causality test, and supplemented by an autoregressive distributed lag model (ARDL) model. We are able to show that, as elaborated below, housing price Granger causes transaction volume in the housing market of Hong Kong, but not vice versa. Based on all these results, we question the current government housing policy which aims mainly at suppressing demand and hence transaction intensity, if the objective was to bring housing price level to a more affordable level. Housing policy should aim at effectuating the supply channel so that there is a clear signal of constant and effective supply of housing units, which will eventually help stabilize housing price.

2 Housing price and transaction activity in the Hong Kong

Before examining the correlation between the housing price movement and transaction activities in Hong Kong, we will provide a brief overview of these two elements in this market. Hong Kong is a small city with a total land area of about 1,100 square kilometers. However, due to the mountainous topology, developable land area for housing a huge 8 million population is only less than half of this area. This makes Hong Kong one of the most densely developed cities in the world. This also keeps housing demand from end users on a constantly high level while at the same time also makes residential properties a good investment asset. The housing market has basically been very active since the mid-80’s due to high-speed growth in the economy, with the exception of a short period after 1989, and a much longer period of stagnation that started after the Asian Financial Crisis in 1998 and extended into the SARS pandemic in 2003. Housing price in the recent years after 2010 has been rising rapidly with the influx of investors from mainland China until the end of 2012 when the government of Hong Kong started a few drastic anti-speculation measures to cool down the demand. However, housing price still sustains at a high level today. In November 2010 and October 2012, the Hong Kong government levied two rounds of special tax on residential property transaction known as the Special Stamp Duty (SSD), which was considered by the market as a drastic measure in Hong Kong to curb speculations. These taxes were designed to fight short-term speculation so that people who resell their properties within 2 years will face a sliding scale tax ranging from 10 % on resale value if the resale is within 6 months from the date of purchase, to 5 % if the property is held for 1 year but resold within 24 months from the date of purchase. In addition, there is also the Buyers’ Stamp Duty (BSD) introduced in October 2012 which is a flat rate of 15 % on the value of the property if the buyer is not a permanent Hong Kong resident. The cooling down measures did not stop there. To rein in the runaway property prices in spite of several rounds of SSD and BSD measures, the government further doubled the tax rates for all second-home buyers since February 2013 for properties resold within 6 months of purchase. Such cooling measure was known as Double Stamp Duty (DSD) and received a lot of criticisms in the market as well. Despite all these cooling measures, the residential property prices continue to grow though the speed is less dramatic. The impact of these demand-suppressed policies therefore remains doubtful.

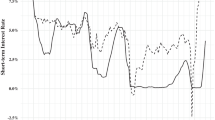
From Fig. 1 below, we can see that housing transaction volume basically follows the ups and downs of the price movements in the past three decades in Hong Kong, except a divergence of price–volume relationship observed amidst the recent rounds of demand suppression measures. This close correlation between housing transaction volume and housing price allows us to examine further the causal relationship between them. Having established such causal relationship, we can then further examine the implications of government housing policy that will have impacts on either or both of these elements.

Fig. 1
figure 1

Divergence of housing prices and transaction volume in recent rounds of demand management measures. The number of transaction is denoted as SP, and housing price index is denoted as HP in this paper. For more details about the cooling measures implemented by the Hong Kong SAR Government, one may vide the economic report Box 4.1, 4.2 at the link http://www.hkeconomy.gov.hk/en/pdf/er_12q4.pdf; and also Box 3.1 at the link http://www.hkeconomy.gov.hk/en/pdf/er_13q1.pdf

Full size image

3 Research design and data

3.1 Granger causality test with the mix of I(0) and I(1) processes

The standard Granger causality test (Granger 1969) was developed for analyzing the dynamic relationship between two stationary time series variables. A key assumption of the test is the stationarity of the variables, which however is not always satisfied in reality, with no exception to the housing market data in our study. If some of the data are non-stationary, then the Wald test statistic generated from the Granger causality test would not follow its usual asymptotic Chi-square distribution. The resulting nonstandard distribution would bias the test results even with a large sample size. With the mix of stationary and non-stationary processes, the conventional first differencing approach will “over-difference” the stationary series which is not appropriate for directly carrying out the causality test with the first difference VAR model.

For this reason, it is necessary to adopt a modified Granger causality procedure proposed by Toda and Yamamoto (1995), Dolado and Lütkepohl (1996), and Saikkonen and Lütkepohl (1996) or their equivalents. In fact, these modified Granger causality procedures are sometimes referred as the “modified Wald test” in the statistical literature. For expository purpose, we will illustrate what the modified Granger causality testing procedure proposed by Toda and Yamamoto (1995) is and how the procedure is applied to study the relationship between transaction (denoted as SP, which means sale and purchase agreements) and the housing prices (HP).

First, a pth-order vector autoregressive (VAR) model is established:

$$HP_{t} = a_{0} + a_{1} HP_{t - 1} + \cdots + a_{p} HP_{t - p} + b_{1} SP_{t - 1} + \cdots + b_{p} SP_{t - p} + u_{t}$$
(1a)
$$SP_{t} = c_{0} + c_{1} SP_{t - 1} + \cdots + c_{p} SP_{t - p} + d_{1} HP_{t - 1} + \cdots + d_{p} HP_{t - p} + v_{t}$$
(1b)

where HP is housing prices index; SP is transactions volume in terms of number of signed sale and purchase agreements filed at the Land Registry; u and v are unobserved residuals that capture demand shocks; and a, b, c, and d are the coefficients to be estimated. Second, different lag lengths (p) are tried, and the optimal length is determined by the usual information criteria, such as the Akaike information criterion (AIC) and Schwarz information criterion (SIC). One can further check whether the residuals follow a white noise process using the Breusch–Godfrey serial correlation or Lagrange multiplier tests. This is to ensure that the VAR model is dynamically stable so that a time series receiving a “shock” will eventually die down to what it was before.Footnote 1 Third, the Augmented Dickey and Fuller (1979) and Kwiatkowski et al. (1992) tests are used to check whether each of the time series variables is stationary. Let the maximum order of integration for the group of variables be d max, if one variable is integrated of order 0 (i.e., I(0)) and the other is I(1), then d max = 1. If the variables have the same order of integration, then Johansen’s methodology is required to test whether the time series are cointegrated. Fourth, based on the optimal lag length and maximum order of integration found above, a (p + d max)th-order VAR is estimated. Finally, for (1a), a null hypothesis of b 1 = b 2 =\(\cdots\)= b p  = 0 is set, meaning SP does not Granger cause HP. Similarly, for (1b), a null hypothesis of d 1 = d 2 =\(\cdots\)= d p  = 0 means HP does not Granger cause SP. In each case, a rejection of the null implies there is Granger causality. The null hypotheses will be tested using the Wald statistic, which is asymptotically Chi-square distributed with p degree of freedom under the null hypothesis. It is noteworthy that the coefficients of the extra d max lags have to be excluded from the Wald tests since these additional lags are merely used to correct for estimation bias.

3.2 Data

Our dataset consists of the quarterly residential property transactions and the private housing prices index in Hong Kong. The time series data we used in this study start from 1993 first quarter (Q1) to the last quarter of 2014(Q4). This period is chosen because it covers the most fluctuating segments of the housing market history in Hong Kong, including the overheated period from 1993 to 1997 followed immediately by stagnation until 2005, when the market recovered gradually before it hit the financial tsunami in 2008, but only for a short period. The market went up again with the influx of investment hot money, especially from mainland Chinese investors at an unprecedented rate since 2009. In addition, this period also covers the two definitive different regimes of governance structure in Hong Kong. Hong Kong was a British colony before 1997 and was very often accused of adopting the “high-land price” policy that favoured developers. After 1997, the city became a special administrative region (SAR) of China, with a city government composed of local Hong Kong residents appointed by Beijing. The Hong Kong SAR government always tries to draw a line from the colonial era that they are more concerned with the welfare of the citizens.

We obtained the residential price index from the Rating & Valuation Department (RVD) in Hong Kong for our Granger causality analysis. The index essentially covers all private sector housing transactions, both new and second-hand sales, in Hong Kong. It will be our measure for price movements. Another variable under our study is the housing transaction data. The data series is gathered from the Land Registry (LandReg) which is an official government body recording transactions for all types of property sale. Only the sale and purchase agreements for residential properties are included in this study.

Hence, in this analysis, there are only two variables, namely housing price and housing transaction volume. Initially, we did a pilot test with some other macroeconomic variables such as mortgage rate, unemployment rate, GDP, and stock market index. Since only a handful of these variables, noticeably mortgage rate and stock market index, are statistically significant and in order not to digress from the main discussion focus of this paper, i.e., the correlation between housing price movements and housing transaction activity, we decided to adopt a two-variable model instead.

The descriptive statistics of our data series are shown in Table 1. Some stylized facts are worthwhile to pinpoint here. Over the entire sample period, the average price index level of the residential housing was at 129. Before the current property market cycle, the housing price index (HP) was averaged at 103, while the mean of price index rose by 38 to 142 %. As regards the transaction, the number of residential property transaction (SP) slightly increased from 22,641 per quarter before year 2003 to 23,098 per quarter afterward. The demand suppression measures since 2010 effectively weighed on the trading volume in the housing market. From 2011 to 2014, the sale and purchase agreement of residential properties filed by Land Registry averaged at 17,500 per quarter, far lower than the long-term average trading volume experienced since 2003. Meanwhile, in terms of the first- and second-hand market composition, the first-hand market accounted for about one-fifth of the total market transactions in the city.

Table 1 Descriptive statistics
Full size table

3.3 Stationarity between the transactions and housing price

To examine whether the two variables, namely price and transaction, are stationary, we test each time series to determine its order of integration. Ideally, this should involve using a test for which the null hypothesis is non-stationarity (such as the ADF test) as well as a test for which the null is stationarity (such as the KPSS test) for cross-checking purpose. Therefore, we conduct an augmented Dickey and Fuller (1979) test together with the Kwiatkowski et al. (1992) test. Table 2 shows that the ADF test result fails to reject the null of unit root for the residential price index (HP), implying that the price index is non-stationary or not mean-reverting process. KPSS test results also confirm the residential price index is a non-stationary first order of integration I(1) process. Meanwhile, the result for transaction (SP) series is able to marginally reject null hypothesis of having a unit root at 10 % significance level in the ADF test which implies the transaction series could possibly be a stationary or mean-reverting process. The KPSS test tries to further confirm the SP is a stationarity I(0) process with the test statistics is unable to reject the null of stationarity.

Table 2 Testing for stationarity of housing prices index and transaction variables
Full size table

3.4 Causality between the transactions and housing price

The modified Toda and Yamamoto (1995) Granger causality test outlined above is used to test empirically whether the relationship between housing prices and transaction exists over time. Our Granger causality test results in Table 3 show that transaction activities/transaction volume in the housing market of Hong Kong did not Granger cause housing price movements in the market during the test period.

Table 3 Insignificant causality results from transaction to housing prices
Full size table

In addition, since our test period spans over 20 years in which there were substantial fluctuations observed, one may need to further decipher the correlation between housing price and transaction during the various sub-periods in this dataset. To address this issue, we further divide our dataset into two different periods covering two property cycles, namely the period of 1993Q1–2002Q4 and 2003Q1–2014Q4. Evidently, the results remain intact.

Moreover, in order to ensure our causality test results are valid in both the primary (first hand/IPO) and secondary housing markets, we further carry out our causality tests by subdividing our transaction (SP) time series into primary (FIRST) and secondary (SECOND) transactions. The results listed in Table 4 dovetail with our overall dataset results in which the transaction volume did not Granger cause housing prices in the Hong Kong housing market during the test period.

Table 4 Causality results remained intact in the primary and secondary market
Full size table

Further, it is noteworthy that in our analysis, housing price (HP) did Granger cause transaction volume (SP) in the housing market of Hong Kong in our entire sample during the test period. This is consistent with the empirical tests conducted by Clayton et al. (2010). Interestingly, such causation appears to be more pronounced in the primary sales market which implies purchase decision on new properties is more sensitive to the residential price movement in general. We think there a number of reasons for this phenomenon. First of all, there is, in general, a relatively stronger investment demand in new properties. Investors are relatively fond of new properties as home purchasers usually will prefer new projects that come with completely new configuration and appliances; hence, resale potential for these new properties is higher from an investment point of view. In addition, some developers may even provide preferential packages for buyers of their new projects, such as rebates to cover government extra stamp duties, which they cannot find in the second-hand housing market. Very often than not, property agents will even forfeit commission fees from the buyers of new properties as developers will also cover this cost, which again is not possible in the second-hand market. Since transaction cost has an important bearing on market interest (Yiu et al. 2009), when transaction cost for investing in the new property sub-market is lower, investors will be much more inclined and keen to purchase new flats when they see price level is on the upward trend, as this implies a potentially higher expected return. This can be confirmed from our analysis in the secondary market that price movements did not have a significant influence on second-hand property transactions. This also echoes with our observation that there are more end users in the second-hand market. Their buying decision does not solely hinge on the price movements as most of them are more concerned with their immediate need for accommodation.

4 Robustness check on the short-run and long-run relationship between housing prices and transactions

4.1 Cointegration of a mix of I(0) and I(1) processes: ARDL model and bounds test

The empirical outcomes based on the modified Granger causality test need to be further verified in order for us to confirm the short-run and long-run dynamics between the housing prices and transaction volume in this market. In addition, to address the issue of the correlation between housing prices and transaction volume in the concurrent period, we further employ the “autoregressive distributed lag” (ARDL) model and its corresponding bounds test (Pesaran and Shin 1998; Pesaran et al. 2001) to examine the short-run and long-run relationships (i.e., the cointegration relationship) between the housing prices and transaction volume.

ARDL models have been applied in various studies for decades while more recently such model setup has been demonstrated to provide a very useful vehicle for testing the presence of long-run relationships between time series, in particular with the presence of a mixture of stationary I(0) and non-stationary I(1) processes. In its basic form, an ARDL (p,q) regression model is specified as follows in the context of this study:

$$HP_{t} = \, \beta_{0} + \beta_{1} HP_{t - 1} + \cdots + \beta_{p} HP_{t - p} + \, \alpha_{0} SP_{t} + \, \alpha_{1} SP_{t - 1} + \alpha_{q} SP_{t - q} + \varepsilon_{t}$$
(2)

where ε t is a random disturbance term which is serially independent.

The model is named as “autoregressive” as HP t is explained partly by lagged value of itself together with the current value of SP t as well as a “distributed lag” component of SP t−1+ \(\cdots\)+SP t−q . Sometimes, the current value of SP t itself may be excluded from the distributed lag part which is dependent on the model selection criterion discussed below. However, what we are mostly concerned with should not be just a stand-alone coefficient of SP t but its cointegrated equation for accessing the short-run dynamics as well as the “bounds test” results for its long-run relationships. That will be fully discussed below.

One may wonder why we need the ARDL(p,q) model? In the presence of lagged values of the dependent variable as regressors, ordinary least square (OLS) estimation of an ARDL model could be biased. If the disturbance term, ε t , is autocorrelated, the OLS will also be an inconsistent estimator. In this scenario, the instrumental variables estimation and its equivalent treatments are usually employed for addressing the issues. ARDL (p,q) is one of such equivalent in time series studies. In the 1960s and 1970s, time series researchers made use of distributed lag (DL(q), or ARDL(0,q)) models to avoid the adverse effects of the multicollinearity due to the inclusion of many lags of regressors. The technique was common in reducing the number of parameters by imposing restrictions on the pattern (or “distribution”) of values that α-coefficients in Eq. (2) could take.

A well-known set of restrictions was made by the Koyck (1954) for the estimation of DL (∞) model. These restrictions imposed a polynomial rate of decay on α-coefficient. This enabled the model to be manipulated into a new one that was autoregressive, but with an error term that followed a moving average (MA) process. That is the ARMA model we usually see in the time series literatures. Almon (1965) puts up another set of restrictions for the coefficients in a DL(q) model. Her approach was based on Weierstrass’s approximation theorem, which tells us that any continuous function can be approximated by a polynomial of some order. Dhrymes (1981) provides a very thorough discussion of distributive lag models.

In our study, if we know that all of our time series HP and SP are stationary process and hence I(0), we can simply model the data in their levels by OLS estimation. Another scenario is that we know all of our time series are integrated into the same order (e.g., I(1)), but they are not cointegrated (i.e., a linear combination of these series is integrated of order zero). We can also differentiate each series and estimate a standard regression model with OLS. Alternatively, if we know that all of the series are integrated of the same order, they are cointegrated. In this case, we can estimate two types of models: (i) an OLS model using the levels of the data which provides the long-run equilibrating relationship between the variables; or (ii) an error-correction model (ECM) that represents the short-run dynamics of variables.

In our study, since HP level is non-stationary while the SP level is a stationary process, the situation is not as straightforward as the three situations stated above. Therefore, ARDL(p,q) and bounds test come into play. The ARDL (p,q) and bounds testing method proposed by Pesaran and Smith (1998) and Pesaran et al. (2001) have several merits over many conventional cointegration testing, such as Engle–Granger two-step method (1987) and Johansen test (1991). The ARDL model and bounds testing technique can be used with a mixture of I(0) and I(1) data. The method is easy to implement and intuitive to interpret as the model only involves a single-equation setup. Different variables can be assigned with different lag lengths as they enter the model, in particular the concurrent period variables.

In order to make the ARDL model and bounds testing easy for readers to follow, we try to outline the fundamental steps in specifying the model and the test. First, we have to ensure that none of the variables in the model are I(2) process which will invalidate the method proposed. Next, we need to formulate a conventional error-correction model except that the error-correction termFootnote 2 is being replaced by the variables HP t−1 and SP t−1 without restricting their coefficients:

$$\Delta HP_{t} = \beta_{0} + \varSigma \, \beta_{i} \Delta HP_{t - i} + \varSigma \gamma_{j} \Delta SP_{t - j} + \theta_{0} HP_{t - 1} + \theta_{1} SP_{t - 1} + e_{t}$$
(3)

And then, we are required to determine the appropriate lag structure for the model by using one or more of the “information criteria” including Akaike information criterion (AIC), Schwarz (Bayes) criterion (SC), Hannan–Quinn information criterion (HQ), etc. These criteria are based on a log-likelihood value with a penalty term for penalizing the inclusion of more lags. The form of penalty varies with each criterion. It usually starts with −2log(L) and then penalizes by a term dependent on lags used, so the smaller the value of an information criterion, the better the result. We will adhere to using Schwarz (Bayes) criterion which is a consistent model selector and take into account of not to “over-select” the maximum lags as AIC does. One of the key assumptions in the ARDL model and bounds test of Pesaran et al. (2001) is that the errors of Eq. (3) must be serially independent which can be checked by the Lagrange multiplier test to examine the null hypothesis that the errors are serially independent, against the alternative hypothesis that the errors are either AR(m) or MA(m).

Simply put, the bounds test is to conduct a F-test of the hypothesis, H 0 : θ 0 = θ 1 = 0; against H0 is not true. As in conventional cointegration testing, we test for the absence of a long-run equilibrium relationship between the variables. This absence coincides with zero coefficients for HP t−1 and SP t−1 in Eq. (3). A rejection of null hypothesis H0 implies that we have a long-run relationship. The distribution of the test statistics is again nonstandard under a mixture of I(1) and I(0) processes, (i.e., it depends on the cointegrating rank of the system) even though we have an infinitely large sample size in the asymptotic case. That problem is similar to the standard Wald test problem we have discussed previously for the conventional Granger causality test. As discussed above, we attempt to adopt the Toda and Yamamoto (1995) procedure to ensure that the Wald test statistics is modified to be asymptotically Chi-square. Likewise, an exact critical value for the F-test is not available for an arbitrary mixture of I(0) and I(1) processes. Fortunately, Pesaran et al. (2001) supply bounds on the critical values for the asymptotic distribution of such F-statistics. For various situations, Persaran et al. give the lower and upper bounds on the critical values. In each case, the lower bound (i.e., I0 bound noted in Table 5) is based on the assumption that all of the variables are I(0), and the upper bound (i.e., I1 bound noted in Table 5) is based on the assumption that all of the variables are I(1). Indeed, the true case may be lying somewhere in between these two extreme bounds. If the F-statistic exceeds the upper bound, we can conclude that we have cointegration of our two variables and hence a long-run relationship. Otherwise, if the computed F-statistic is below the lower bound of Persaran’s critical values, we would conclude that no cointegration is observed and it would be another piece of hard evidence confirming our hypothesis that transaction intensity does not have a long-run relationship with housing prices. Assuming that we have found a cointegration relationship, then we have to further fit an ECM which is the model that represents the short-run dynamics.

Table 5 Results on ARDL models and error-correction models
Full size table

4.2 Empirical results on the short-run/long-run dynamics for housing prices and transactions

The ARDL (2,4) model in our paper is selected to explain housing prices in terms of its lagged values, as well as the current and lagged values of housing transaction volume, as specified in Eq. (3). It is noteworthy that we have tried to specify 72 different ARDL models by allowing a maximum of eight lags for housing prices and transaction volume as well as the current value of transaction volume (i.e., 8 × 9 = 72). The model which minimizes the Schwarz criterion is selected, and the corresponding results are appended in the column (1) of Table 5. In addition, we have also checked the errors of the model as serially independent and dynamically stable to ensure that the parameter estimates will be consistent. The model is then applied to perform the bounds test with the null hypothesis that there is no long-run relationship existing between the variables (i.e., the coefficient for log HP t−1 and SP t−1 = 0, or H 0 : θ 0 = θ 1 = 0). The F-statistics is only 0.923 which is far below the lower bound (I0 bound) of Pesaran et al. (2001)’s critical bound values at 10 % level of significance. That means, we are quite confident to say that there is no long-run relationship existing for housing prices, even we include the lagged value of housing prices and transactions volume along with the current value of transactions volume. To further show the short-run dynamics of transaction volume on housing prices, we specify the error-correction term in column (2) of Table 5, thus the lagged cointegration equation. The coefficient of the lagged cointegration is insignificant and positive. That means, we cannot conclude the existence of any short-run dynamics, having taken into account a strong and significant current value of HP and SP in the ARDL model.

To complete our entire ARDL analysis, we follow exactly the same procedure for specifying the ARDL model with the transaction volume (SP) as the dependent variables. The results are appended in columns (3) and (4) in Table 5. The significant results of the bounds test at 10 % level of significance (i.e., F-statistics 5.566) indicate a long-run relationship from housing prices to transaction volume, and it is coherent with the findings discussed in our modified Granger causality analysis. The significant coefficient for lagged cointegration equation (i.e., CointEq(-1)) in column (4) indeed confirms that there could possibly be a short-run relationship for transaction volume on housing prices, but not vice versa.

5 Housing policy implications for Hong Kong

Adopting a free and open economic system, the government of Hong Kong has never been involved in the development side of the real estate market, except for the building of public housing flats which are regarded more as a social policy given public housing now provide shelters for almost half of the population. Housing policy, from the government perspective, in this city has always been centered on the provision of public/welfare housing which the government has the control and resources to execute. On the other hand, the government of Hong Kong has always maintained strong power in controlling land supply directly, given the leasehold land tenure system, and hence housing supply indirectly in the private sector. After a new regime of government in 1997 emerged with the return of the sovereignty to China, the Hong Kong government started to put more emphasize on monitoring the land market and to some extent controlling of the performance of the housing market such as the so-called 85,000 housing units supply policyFootnote 3 which ended disastrously.

Ever since the private sector housing market in Hong Kong started to resurrect its pre-1997 hyperactive state toward the end of 2009, the government has made a pledge to stop speculative activities from making housing price level out of touch with the general public. The government has subsequently taken various measures, especially in the late 2012 when investment demand had pushed housing price level to a near burst-bubble state. These measures are described by the government as “demand-control” oriented so that access to finance for home purchase will be limited and holding cost for speculating on housing properties will be increased. What is interesting is the fact that the government has emphasized that they do not want to intervene into market price movements directly and have no intention of administratively capping housing price at any level. A core objective of these measures, therefore, is to cool down and curb investors’ demand on housing properties, so that reduction in the overall demand, hence transaction activities, will drive property price down naturally. Eventually, it is hoped that the price level will become more affordable through the adjustment of the market mechanism.

However, our analysis shows that this may not be the expected outcome of the government housing policy, not at least in the short run. Our empirical analysis indicates that housing price Granger causes housing transaction volume, but not vice versa, especially in the first-hand housing sub-market. Government housing policy that initially aims at controlling housing demand, and hence transaction intensity, as a means to pull down housing price to an affordable level may not work, especially when such policy aims solely at tightening credit accessibility and taxing on capital gains. This was what happened in Hong Kong in the recent few years.

Tightening mortgage lending facilities affects first-time home purchasers more than investors who are in general financially more resourceful. On the other hand, increasing stamp duty as a form of capital gains tax on short-term transactions only decreases supply in the second-hand market, causing housing price to be sustained at the existing high level. Thus, reducing transaction activities due to the curbed demand in the market from the initiation of anti-speculation measures in late 2012 did not immediately bring down housing price to an affordable level to achieve higher homeownership for the general public. Meanwhile, the government is trapped in the mounting demand from the general public for more drastic measures to lower housing price and request from the real estate agency industry to lift these administrative measures due to the shrinking business.

If the causal relationship between housing price and transaction is unidirectional flowing from housing price movements, then the government would need to realign its housing policy to focus more on housing price changes. Since administrative capping on housing price movement is an extreme and counterproductive action, a better option is to allow housing price to achieve “soft landing” in the market. This can be achieved by supplying more land to the housing market, streamlining the planning mechanism to expedite urban regeneration process (Li et al. 2015) and allowing higher development intensity in the housing market. Though housing supply takes time, a positive message showing unwavering government policy in guaranteeing sufficient supply to the market will have an impact on market speculation as market perception of a constant rising supply scenario will not help speculative activities.

6 Concluding remarks

Housing market is often analyzed in a sociopolitical context in which the state plays an important role. In this paper, we analyzed the ways Hong Kong government intervened in the housing market by examining the causal relation between housing price movements and housing transaction activities. Based on a time series of 20 years or so, we found that housing price movements in Hong Kong do Granger cause housing transaction volume, but not vice versa. Housing consumers are keen to buy and sell housing units when housing price is on the upward trend. On the other hand, any exogenous factors causing transaction activities to shrink do not really impact on housing price movements in this market.

Considering the special characteristics of the market structure such as the lack of central trading market, homogeneity of product, and high transaction cost in search for the best product, the housing market has been infamous for its inefficiency. With such a degree of inefficiency, players’ mentality in the market becomes instrumental to the fluctuations of market prices (Evans 1995). Under such circumstances, government intervention may be desired via urban economic policies to solve the adverse consequences (Warren 2000). Effective housing policies initiated by the government, especially in a market where the government also owns the freehold titles of almost all land and hence the supply of land, should take into the account of the market dynamics in terms of the causal relationship between housing price movements and demand intention (in the form of transaction volume). Our analysis shows that this market dynamic is one way in Hong Kong so that suppressing demand by administrative measures described in this paper did not quite bring the expected outcome of falling property price. Housing price sustained at a high level in the course of the year 2013 in spite of the shrinking market transaction under the unveiled “demand-control” measures. It was not until when latent supply of housing flats that had been building up in the market as a response to sustained high demand since 2009 started to emerge at the beginning of 2014, coupled with sign of potential rise in interest rate in the USA as well as unprecedented downward adjustment in the stock markets in Mainland China in Mid-2015 that all worked together to slow down the housing market in Hong Kong.

Similar to other research, this paper was completed within a set of limitations. First of all, concurrent relationship between housing prices and transactions was not put into our analysis as the focus of this paper is the examination of the effects of “demand suppression” measures on housing prices, not the instant response of housing prices to the transaction movement. Also, the analytical framework is a two-variable model, without consideration of other macroeconomic factors, for the same rationale that this paper is more focused on the causal relationship between price movements and transaction volume. Future research should incorporate these other factors individually or collectively, to examine how housing prices and transaction activities react to changes in these factors, such as stock market performanceFootnote 4 and mortgage rate, which were shown to be significant in our pilot analysis.