Skip to main content
SpringerLink
Log in

A study of one dimensional nonlinear diffusion equations by Bernstein polynomial based differential quadrature method

  • Original Paper
  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

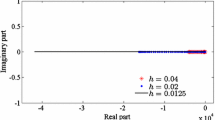
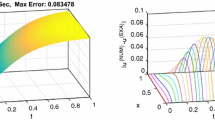
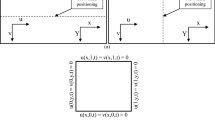
Abstract

The purpose of this work is to study numerical solutions of nonlinear diffusion equations such as Fisher’s equation, Burgers’ equation and modified Burgers’ equation by applying Bernstein differential quadrature method (BDQM). These nonlinear diffusion equations occur in many applications of theoretical, engineering and environmental sciences. Therefore, finding numerical solutions of these equations is very important. In BDQM, Bernstein polynomials are used as base functions to find weighting coefficients of differential quadrature method. We have applied BDQM on eleven different test problems taken from the literature and the computed results confirm that BDQM is an efficient method for finding solution of nonlinear partial differential equations. It is found that BDQM produces very good results even at small number of grid points.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Sir R.A. Fisher, The wave of advance of advantageous genes. Ann. Eugen. 7, 355–369 (1937)

  2. J.M. Burgers, A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. I, 171–199 (1948)

    Article  Google Scholar 

  3. H. Bateman, Some recent researches on the motion of fluids. Mon. Weather Rev. 43, 163–170 (1915)

    Article  Google Scholar 

  4. J.M. Burgers, A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1, 171–199 (1948)

    Article  Google Scholar 

  5. J.D. Cole, On a quaslinear parabolic equations occurring in aerodynamics. Q. Appl. Math. 9, 225–236 (1951)

    Article  Google Scholar 

  6. E. Hopf, The partial differential equation \(u_{t} + uu_{x}=\mu u_{xx}^{\prime }\). Commun. Pure Appl. Math. 3, 201–230 (1950)

    Article  Google Scholar 

  7. D.D. Ganji, H. Tari, H. Babazadeh, The application of He’s variational iteration method to nonlinear equations arising in heat transfer. Phys. Lett. A 363, 213–217 (2007)

    Article  Google Scholar 

  8. H. Brezis, F. Browder, Partial differential equations in the 20th century. Adv. Math. 135, 76–144 (1998)

    Article  Google Scholar 

  9. A.G. Bratsos, A fourth-order numerical scheme for solving the modified Burgers equation. Comput. Math. Appl. 60, 1393–1400 (2010)

    Article  Google Scholar 

  10. O.V. Vasilyev, S. Paolucci, A dynamically adaptive multilevel wavelet collocation method for solving partial differential equations in a finite domain. J. Comput. Phys. 125, 498–512 (1996)

    Article  Google Scholar 

  11. X.Y. Wang, Exact and explicit solitary wave solutions for the generalized Fisher’s equation. Phys. Lett. A 131, 277–279 (1988)

    Article  Google Scholar 

  12. I. Dag, A. Sahin, A. Korkmaz, Numerical investigation of the solution of Fisher’s equation via the B-spline Galerkin method. Numer. Methods Partial Differ. Equ. 26, 1483–1503 (2010)

    Google Scholar 

  13. Y. Qiu, D.M. Sloan, Numerical solution of Fisher’s equation using a moving mesh method. J. Comput. Phys. 146, 726–746 (1998)

    Article  Google Scholar 

  14. S. Ting-Yu, C. Rong-Jun, G. Hong-Xia, An element-free Galerkin (EFG) method for generalized Fisher equations (GFE). Chin. Phys. B 22(6), 060210 (2013)

    Article  Google Scholar 

  15. R.C. Mittal, R.K. Jain, Numerical solutions of nonlinear Fishers reaction-diffusion equation with modified cubic B-spline collocation method. Math. Sci. 7, 1–10 (2013)

    Article  Google Scholar 

  16. V. Chandraker, A. Awasthi, S. Jayaraj, A numerical treatment of Fisher equation. Procedia Eng. 127, 1256–1262 (2015)

    Article  Google Scholar 

  17. S. Succi, A note on the Lattice Boltzmann versus finite difference methods for the numerical solution of the Fisher’s equation. Int. J. Mod. Phys. C 25, 1340015 (2014)

    Article  Google Scholar 

  18. Jalil Rashidinia, Ali Barati, Numerical solutions of one-dimensional non linear parabolic equations using Sinc collocation method. Ain Shams Eng. J. 6, 381–389 (2014)

    Article  Google Scholar 

  19. A. Korkmaz, I. Dag, Shock wave simulations using sinc diffrerential quadrature method. Eng. Comput. 28, 654–674 (2011)

    Article  Google Scholar 

  20. A. Bashan, S.B.G. Karako, T. Geyikli, Approximation of the KdVB equation by the quintic B-spline differential quadrature method. Kuwait J. Sci. 42 67–92 (2015)

  21. A. Korkmaz, A.M. Aksoy, I. Dag, Quartic B-spline differential quadrature method. Int. J. Nonlinear Sci. 11, 403–411 (2011)

    Google Scholar 

  22. R.C. Mittal, R. Jiwari, Numerical study of Fisher’s equation by using differential quadrature method. Int. J. Inf. Syst. Sci. 5, 143–160 (2009)

    Google Scholar 

  23. Z. Zong, K.Y. Lam, A localized differential quadrature (LDQ) method and its application to the 2D wave equation. Comput. Mech. 29, 382–391 (2002)

    Article  Google Scholar 

  24. S. Tomasiello, Numerical stability of DQ solutions of wave problems. Numer. Algorithms 57, 289–312 (2011)

    Article  Google Scholar 

  25. A. Korkmaz, I. Dag, Polynomial based differential quadrature method for numerical solution of nonlinear Burgers equation. J. Frankl. Inst. 348, 2863–2875 (2011)

    Article  Google Scholar 

  26. A. Korkmaz, I. Dag, Cubic B-spline differential quadrature methods and stability for Burgers’ equation. Eng. Comput. 30, 320–344 (2013)

    Article  Google Scholar 

  27. B. Saka, I. Dag, A numerical study of the Burgers’ equation. J. Frankl. Inst. 345, 328–348 (2008)

    Article  Google Scholar 

  28. K. Rahman, N. Helil, R. Yimin, Some new semi-implicit finite difference schemes for numerical solution of Burgers equation. in International Conference on Computer Application and System Modeling, vol 14 (2010), pp. 451–455

  29. Z. Rong-Pei, Y. Xi-Jun, Z. Guo-Zhong, Modified Burgers’ equation by the local discontinuous Galerkin method. Chin. Phys. B 22, 030210(1–5) (2013)

  30. Mohamed A. Ramadan, Talaat S. El-Danaf, Numerical treatment for the modified Burgers’ equation. Math. Comput. Simul. 70, 90–98 (2005)

    Article  Google Scholar 

  31. A. Bashan, S.B.G. Karako, T. Geyikli, B-spline differential quadrature method for the modified Burgers’ equation. J. Sci. Eng. 12, 1–13 (2015)

    Google Scholar 

  32. A.S.J. Al-Saif, F.A. Al-Saadawi, Bernstein differential quadrature method for solving the unsteady state convection diffusion equation. Indian J. Appl. Res. 3, 2248–555X (2013)

  33. A.S.J. Al-Saif, F.A. Al-Saadawi, A new differential quadrature methodology based on Bernstein polynomials for solving the equations governing the unsteady flow of polytropic gas. J. Phys. Sci. Appl. 5, 38–47 (2015)

  34. A.S.J. Al-Saif, F.A. Al-Saadawi, An improved ADI-DQM based on Bernstein polynomial for solving two dimensional convection diffusion equations. Math. Theory Model. 3, 2225–0522 (2013)

  35. R. Bellman, B.G. Kashef, J. Casti, Differential quadrature: a technique for the rapid solution of nonlinear partial differential equations. J. Comput. Phys. 10, 40–52 (1972)

    Article  Google Scholar 

  36. A.K. Singh, V.K. Singh, O.P. Singh, The Bernstein operational matrix of integration. Appl. Math. Sci. 3(49), 2427–2436 (2009)

    Google Scholar 

  37. R.T. Farouki, V.T. Rajan, Algorithms for polynomials in Bernstein Form. Comput. Aided Geom. Des. 5, 1–26 (1988)

    Article  Google Scholar 

  38. G.G. Lorentz, Bernstein Polynomials (Chelsea Publishing, New York, 1986)

    Google Scholar 

  39. A.A. Dascioglu, N. Isler, Bernstein collocation method for solving nonlinear differential equations. Math. Comput. Appl. 18, 293–300 (2013)

    Google Scholar 

  40. J.R. Quan, C.T. Chang, New insights in solving distributed system equations by the quadrature methods-I. Comput. Chem. Eng. 13, 779–788 (1989a)

    Article  CAS  Google Scholar 

  41. J.R. Quan, C.T. Chang, New insights in solving distributed system equations by the quadrature methods-II. Comput. Chem. Eng. 13, 1017–1024 (1989b)

    Article  CAS  Google Scholar 

  42. Shu Chang, Differential Quadrature and its Application in Engineering (Athenaeum Press Ltd, Great Britain, 2000)

    Google Scholar 

  43. M.K. Jain, S.R.K. Iyengar, R.K. Jain, Numerical Methods. New age international publishers, ISBN (13):978-81-224-2707-3 (1984)

  44. J.G. Verwer, W.H. Hundsdorfer, B.P. Sommeijer, Convergence properties of the Runge–Kutta–Chebyshev method. Numer. Math. 57, 157–178 (1990)

    Article  Google Scholar 

  45. A.-M. Wazwaz, A. Gorguis, An analytic study of Fisher’s equation by using Adomain decomposition method. Appl. Math. Comput. 154, 609–620 (2004)

    Google Scholar 

  46. T. Kawahara, M. Tanaka, Interactions of traveling fronts, an exact solution of a nonlinear diffusion equation. Phys. Lett. A 97, 311–314 (1983)

  47. J. Sherratt, On the transition from initial data traveling waves in the Fisher-KPP equation. Dyn. Stab. Syst. 13(2), 167–174 (1998)

    Article  Google Scholar 

  48. P. Brazhnik, J. Tyson, On traveling wave solutions of Fisher’s equation in two spatial dimensions. SIAM J. Appl. Math. 60(2), 371–391 (1999)

    Google Scholar 

  49. S.S. Nourazar, M. Soori, A. Nazari-Golshan, On the exact solution of Newell–Whitehead–Segel equation using the homotopy perturbation method. Aus. J. Basic Appl. Sci. 5, 1400–1411 (2011)

    Google Scholar 

  50. W.K. Zahra, W.A. Ouf, M.S. El-Azab, Cubic B-spline collocation algorithm for the numerical solution of Newell–Whitehead–Segel type equations. Electron. J. Math. Anal. Appl. 2, 81–100 (2014)

    Google Scholar 

  51. J.D. Cole, On a quasi-linear parabolic equation in aerodynamics. Q. Appl. Math. 9, 225–236 (1951)

    Article  Google Scholar 

  52. H. Nguyen, J. Reynen, A space-time finite element approach to Burgers’ equation, in Numerical Methods for Non-Linear Problems, vol. 2, ed. by C. Taylor, E. Hinton, D.R.J. Owen, E. Onate (Pineridge Publisher, Swansea, 1982), pp. 718–728

    Google Scholar 

  53. A. Asaithambi, Numerical solution of the Burgers’ equation by automatic differentiation. Appl. Math. Comput. 216, 2700–2708 (2010)

    Google Scholar 

  54. A.A. Soliman, The modified extended tanh-function method for solving Burgers’type equations. Phys. A 361, 394–404 (2006)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, IIT Roorkee, Roorkee, Uttarakhand, 247667, India

    R. C. Mittal & Rajni Rohila

Authors
  1. R. C. Mittal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rajni Rohila
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rajni Rohila.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mittal, R.C., Rohila, R. A study of one dimensional nonlinear diffusion equations by Bernstein polynomial based differential quadrature method. J Math Chem 55, 673–695 (2017). https://doi.org/10.1007/s10910-016-0703-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10910-016-0703-y

Keywords

Search

Navigation