Approximation of Supremum of Max-Stable Stationary Processes & Pickands Constants

Abstract

Let $X(t),t\in \mathbb {R}$ be a stochastically continuous stationary max-stable process with Fréchet marginals $\Phi _\alpha , \alpha >0$ and set $M_X(T)=\sup _{t \in [0,T]} X(t),T>0$. In the light of the seminal articles (Samorodnitsky in Ann Probab 32(2):1438–1468, 2004; Adv Appl Probab 36(3):805–823, 2004), it follows that $A_T=M_X(T)/T^{1/\alpha }$ converges in distribution as $T\rightarrow \infty$ to $\mathcal {H}^{1/\alpha } X(1)$, where $\mathcal {H}$ is the Pickands constant corresponding to the spectral process Z of X. In this contribution, we derive explicit formulas for $\mathcal {H}$ in terms of Z and show necessary and sufficient conditions for its positivity. From our analysis, it follows that $A_T^\beta ,T>0$ is uniformly integrable for any $\beta \in (0,\alpha )$. For Brown–Resnick X, we show the validity of the celebrated Slepian inequality and discuss the finiteness of Piterbarg constants.

Appendix: Tilt-Shift and inf-argmax Formula

Next we present the tilt-shift formula which is initially shown for the special case of Brown–Resnick max-stable processes with log-normal Z in [5]. The inf-argmax formula mentioned above is shown in [14], we present below a shorter proof.

Lemma 5.1

Let $X(t),t\in \mathbb {R}$ be a max-stable process with Fréchet marginals $\Phi _\alpha$, de Haan representation (1.1) and càdlàg sample paths.

• i) If X is stationary, then for any nonnegative 0-homogeneous $\mathcal {D}/\mathcal {B}(\mathbb {R})$-measurable functional H we have

  

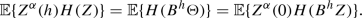  (5.1)

• ii) If (5.1) holds for any $h\in \mathbb {R}$, then X with representation (1.1) is stationary.

Proof of Lemma 5.1

i) As in [6] we have that the stationarity of X implies the shift invariance of the exponent measure, i.e., for any $h\in \mathbb {R},A \subset \mathcal {D}$

If A is 0-homogeneous (meaning $cA=A, c>0$) set in $\mathcal {D}$, then since further implies that for any $h\in \mathbb {R}$ using $z^\alpha = \int _0^\infty \mathbb {I}( r z >1) \alpha r^{-\alpha -1} \,dr$ valid for any $z\in (0,\infty )$ we obtain

hence the claim for any 0-homogeneous $\mathcal {D}/\mathcal {B}(\mathbb {R})$-measurable functional H follows easily.

ii) If (5.1) holds, then for any $n\ge 1, t_i \in \mathbb {R}, x_i>0, i\le n$ since $\inf \arg \max$ functional is 0-homogeneous and $\mathcal {D}/\mathcal {B}(\mathbb {R})$-measurable, by (1.2) we have

where we used (5.1) in the second last line above. Consequently, X is stationary and thus the proof if complete. $\square$