On PAC-Bayesian bounds for random forests

Abstract

Existing guarantees in terms of rigorous upper bounds on the generalization error for the original random forest algorithm, one of the most frequently used machine learning methods, are unsatisfying. We discuss and evaluate various PAC-Bayesian approaches to derive such bounds. The bounds do not require additional hold-out data, because the out-of-bag samples from the bagging in the training process can be exploited. A random forest predicts by taking a majority vote of an ensemble of decision trees. The first approach is to bound the error of the vote by twice the error of the corresponding Gibbs classifier (classifying with a single member of the ensemble selected at random). However, this approach does not take into account the effect of averaging out of errors of individual classifiers when taking the majority vote. This effect provides a significant boost in performance when the errors are independent or negatively correlated, but when the correlations are strong the advantage from taking the majority vote is small. The second approach based on PAC-Bayesian $C$-bounds takes dependencies between ensemble members into account, but it requires estimating correlations between the errors of the individual classifiers. When the correlations are high or the estimation is poor, the bounds degrade. In our experiments, we compute generalization bounds for random forests on various benchmark data sets. Because the individual decision trees already perform well, their predictions are highly correlated and the $C$-bounds do not lead to satisfactory results. For the same reason, the bounds based on the analysis of Gibbs classifiers are typically superior and often reasonably tight. Bounds based on a validation set coming at the cost of a smaller training set gave better performance guarantees, but worse performance in most experiments.

1 Introduction

A random forest is one of the most successful machine learning algorithms (Breiman 2001). It is easy to use and to parallelize and often achieves high accuracies in practice (Fernández-Delgado et al. 2014). In a survey on the machine learning competition website kaggle.com,¹ 46% of 16.000 surveyed users claimed to use the algorithm in their daily work. A random forest for classification predicts based on the (possibly weighted) majority vote of a set (an ensemble) of weaker classifiers, concretely decision trees. The model was first presented by Breiman (2001), who provides an initial analysis and some theoretical bounds, showing that the strength of the random forest depends on the strength of individual trees and their correlation. Despite its popularity in practice, the algorithm is still not well understood theoretically (Arlot and Genuer 2014; Biau 2012; Denil et al. 2014), the main reason being that the model is difficult to analyse because of the dependencies between the induced partitions of the input space and the predictions within the partitions (Arlot and Genuer 2014). The conceptually simpler purely random forests (Breiman 2002) avoids these dependencies by creating a random partitioning independent of the training data. This is done by selecting features and splits at random. Biau et al. (2008) show the purely random forests to be consistent under some assumptions on the distribution of the input variables. Several modification of the random forest have been introduced in the literature, most of them being in between the standard random forest and the purely random forest in the sense that extra randomness is added to get independent partitions (Geurts et al. 2006; Genuer 2010). For instance, Wang et al. (2016) introduce the Bernoulli random forests, which relies on Bernoulli random variables for randomly choosing the strategy for partitioning the input space, and prove this model to be consistent. Likewise, Denil et al. (2014) give a variant based on sampling of predictions in a partition for determining best splits, and prove this variant to be consistent. Theoretical bounds on the expected loss have been considered by Genuer (2010) in the case of regression tasks when the input space is one-dimensional. Arlot and Genuer (2014) consider the generalization error for the purely random forest in relation to the number of trees. All these have nice analytical properties, but these come at the expense of degradation in empirical performance compared to the standard random forest. Accordingly, the original random forest still remains the best choice in practice (Wang et al. 2016), despite the lack of strong theoretical guarantees.

This study considers the application of theoretical bounds based on PAC-Bayesian analysis to the standard random forest as given by Breiman (2001). Here PAC stands for the Probably Approximately Correct frequentist learning model (Valiant 1984). PAC-Bayesian approaches are usually used for analysing the expected loss of Gibbs classifiers. Gibbs classifiers are randomized classifiers that make predictions by applying a hypothesis drawn from a hypothesis class $\mathcal {H}$ according to some distribution $\rho$ on $\mathcal {H}$ (McAllester 1998; Seeger 2002; Thiemann et al. 2017). While generalization bounds for Gibbs classifier may at first not seem directly applicable to majority vote classifiers, they are in fact closely related. It can be shown that the loss of a $\rho$-weighted majority vote classifier is at most twice that of the associated Gibbs classifier, meaning that any bound for a Gibbs classifier leads to a bound for the majority vote (Germain et al. 2015). However, such adaptation of the bounds for Gibbs classifiers typically provides relatively weak bounds for majority vote classifiers, because the bounds for Gibbs classifiers do not take into account dependencies between individual classifiers. One of the main reasons for the good performance of majority vote classifiers is that when the errors of individual classifiers are independent they tend to average out (Breiman 2001). Therefore, the majority vote may perform very well even when the individual classifiers are weak (i.e., only slightly better than random guessing). In this case, application of PAC-Bayesian bounds for the Gibbs classifier to the majority vote yields suboptimal results.

This has motivated the development of PAC-Bayesian bounds designed specifically for averaging and majority vote classifiers (Germain et al. 2015; McAllester 1999; Oneto et al. 2018). One such bound is the $C$-bound, given by Germain et al. (2015), which is based on the margin of the classifier. In contrast to the bounds for Gibbs classifiers, the $C$-bound takes the correlations between the individual classifiers into account and could potentially yield tighter bounds in the case described above. However, in the case with strong individual classifiers and high correlation (as is the case for random forests), the $C$-bound deteriorates (Germain et al. 2015) – in contrast to the Gibbs classifier bounds.

In this study, several of the above mentioned bounds are applied to the standard random forest setting, where trees are trained using bagging, that is, using different random subsets of the training data (Breiman 2001, 1996a). Since validation sets for individual trees are constructed as part of the training procedure when using bagging, the theoretical bounds come “for free” in the sense that no separate data needs to be reserved for evaluation. We compare the quality of bounds obtained in this setting with bounds obtained by leaving out a validation set for evaluation. We also consider optimization of the weighting of the voters by minimization of the theoretical bounds (Thiemann et al. 2017; Germain et al. 2015).

2 Background

We consider supervised learning. Let $S= \{(X_1,Y_1), \ldots , (X_n, Y_n)\}$ be an independent identically distributed sample from $\mathcal {X}\times \mathcal {Y}$, drawn according to an unknown distribution $D$. A hypothesis is a function $h: \mathcal {X}\rightarrow \mathcal {Y}$, and $\mathcal {H}$ denotes a space of hypotheses. We evaluate a hypothesis h by a bounded loss function $\ell : \mathcal {Y}^2 \rightarrow [0,1]$. The expected loss of $h$ is denoted by $L(h) = {\mathbb {E}}_{(X,Y)\sim D}\left[ \ell (h(X),Y)\right]$ and the empirical loss of $h$ on a sample $S$ is denoted by ${{\hat{L}}}(h, S) = \frac{1}{n}\sum ^{n}_{i=1} \ell (h(X_i),Y_i)$. In this study, we focus on classification. Given a set of hypotheses $\mathcal {H}$ and a distribution $\rho$ on $\mathcal {H}$, the Gibbs classifier${h_G}$ is a stochastic classifier, which for each input X randomly draws a hypothesis $h\in \mathcal {H}$ according to $\rho$ and predicts $h(X)$ (Seeger 2002). The expected loss of the Gibbs classifier is given by $L^{\text { {Gibbs}}}({h_G})= {\mathbb {E}}_{h\sim \rho }\left[ L(h)\right]$, and the empirical loss of ${h_G}$ on a sample $S$ is given by ${{\hat{L}}}^{\text { {Gibbs}}}({h_G},S) = {\mathbb {E}}_{h\sim \rho }\left[ \hat{L}(h, S)\right]$.

Closely related to the random Gibbs classifier are aggregate classifiers, whose predictions are based on weighted aggregates over $\mathcal {H}$. The $\rho$-weighted majority vote${h_M}$ predicts ${h_M}(X) = {\text {argmax}}_{Y\in \mathcal {Y}} \sum _{h\in \mathcal {H}\wedge h(X)=Y}\rho (h)$. When discussing majority vote classifiers, it is convenient to define the margin realised on a pattern (X, Y) (Breiman 2001):

$$\begin{aligned} \mathcal {M}_\rho (X,Y) = {\mathbb {P}}_{h\sim \rho }\left[ h(X)=Y\right] -\max _{j\ne Y}{\mathbb {P}}_{h\sim \rho }\left[ h(X)=j\right] , \end{aligned}$$

(1)

and the expected value of the margin $\mathcal {M}_\rho = {\mathbb {E}}_{(X,Y)\sim D}\left[ \mathcal {M}_\rho \left( X,Y\right) \right]$. Note, that a large margin indicates a strong classifier. The expected loss of ${h_M}$ is then given by $L^{\text { { {MV}}}}({h_M})= {\mathbb {P}}_{(X,Y)\sim D}\left[ \mathcal {M}_\rho (X,Y) \le 0\right]$, and the empirical loss ${{\hat{L}}}^{\text { {MV}}}({h_M},S) = {\mathbb {P}}_{(X,Y)\sim S}\left[ \mathcal {M}_\rho (X,Y) \le 0\right]$, where we use $(X,Y)\sim S$ to denote a uniform distribution over the sample.

The Kullback–Leibler divergence between two distributions $\pi$ and $\rho$ is denoted by ${{\,\mathrm{KL}\,}}(\rho \Vert \pi )$ and between Bernoulli distributions with biases p and q by ${{\,\mathrm{kl}\,}}(p\Vert q)$. Furthermore, let ${\mathbb {E}}_D[\cdot ]$ denote ${\mathbb {E}}_{(X,Y)\sim D}[\cdot ]$ and ${\mathbb {E}}_{\rho }[\cdot ]$ denote ${\mathbb {E}}_{h\sim \rho }[\cdot ]$. Finally, $u$ denotes the uniform distribution.

2.1 Random forests

Originally described by Breiman (2001), the random forest is a majority vote classifier, where individual voters are decision trees. In the standard random forest setting, every voter has equal weight (i.e., $\rho = u$). Let $T\subset \mathcal {X}\times \mathcal {Y}$ denote training patterns drawn according to $D$. A random forest is constructed by independently constructing decision trees$h_1, h_2, \ldots , h_m$ (Hastie et al. 2009), where each $h_i$ is trained on $T_i\subseteq T$. A tree is constructed recursively, starting at the root. At each internal node, a threshold $\theta$ and a feature j are chosen, and the data set $T'$ corresponding to the current node is then split into $\{X\, |\, X_j \le \theta \}$ and $\{ X\, |\, X_j > \theta \}$. $\theta$ and j are chosen according to some splitting criterion, usually with the goal of maximizing the information gain for each split, making the new subsets more homogeneous (Hastie et al. 2009). Splitting is stopped when a node is completely pure (only one class is present) or by some other stopping criterion (e.g., maximum tree depth). The tree construction is randomized (Breiman 1996a, 2001). First, the selection of data sets $T_i$ for training individual trees is randomized. They are generated by the bagging procedure described below. Second, only a random subset of all features is considered when splitting at each node (Breiman 2001; Hastie et al. 2009).

Bagging is a general technique used for aggregated predictors (Breiman 1996a), which generates the training sets $T_i$ for the individual predictors by sampling $|T|$ points from $T$ with replacement. The individual training sets $T_1,T_2,\ldots$ are known as bootstrap samples. Because of sampling with replacement, not all patterns of $T$ are expected to be in each $T_i$. Let ${\bar{T}}_i = T\setminus T_i$ denote the patterns not sampled for $T_i$. ${\bar{T}}_i$ can now be used to give an unbiased estimate of the individual classifier $h_i$. The expected number of unique patterns in $T_i$ is approximately $\left( 1-\frac{1}{e}\right) |T| \simeq 0.632|T|$, leaving us with slightly more than one third of the training patterns for the validation sets (Breiman 1996a).

Bagging also allows us to compute out-of-bag (OOB) estimates. For each training pattern $(X,Y) \in T$, a majority vote prediction is computed over all voters $h_i$ with $(X,Y)\not \in T_i$. The empirical loss computed over these predictions is known as the OOB estimate, which we denote by ${{\hat{L}}}_{\text {OOB}}^{\text { {MV}}}({h_M},T)$. Empirical studies have shown that the OOB estimate on the training data is a good estimator of the generalization error (Breiman 1996b).

Furthermore, the sets ${\bar{T}}_1, {\bar{T}}_2, \ldots , {\bar{T}}_m$ can be used to compute the empirical error of the associated $\rho$-weighted Gibbs classifier ${h_G}$ by

$$\begin{aligned} {{\hat{L}}}_{\text {OOB}}^{\text { {Gibbs}}}({h_G},T) = {\mathbb {E}}_\rho \left[ \frac{1}{|{\bar{T}}_i|}\sum _{(X,Y)\in {\bar{T}}_i} \ell \left( h_i(X),Y\right) \right] , \end{aligned}$$

and by considering ${\bar{T}}_i \cap {\bar{T}}_j$, we can also estimate the correlation between trees $h_i$ and $h_j$, an important ingredient in bounds for majority vote classifiers.

3 PAC-Bayesian bounds for majority vote classifiers

We now give an overview of the PAC-Bayesian bounds we apply to bound the expected loss of random forests. PAC-Bayesian bounds have a form of a trade-off between $\rho$-weighted empirical loss of hypotheses in $\mathcal{H}$ and the complexity of $\rho$, which is measured by its Kullback–Leibler divergence from a prior distribution $\pi$. The prior must be selected before the data is observed and can be used to incorporate domain knowledge, while the posterior $\rho$ can be chosen based on the data.

3.1 PAC-Bayesian bounds for gibbs classifiers

The $\rho$-weighted majority vote classifier ${h_M}$ is closely related to the $\rho$-parameterized Gibbs classifier ${h_G}$. Whenever the majority vote makes a mistake, it means that more than a $\rho$-weighted half of the voters make a mistake. Thus, the expected loss of the majority vote classifier $L^{\text { { {MV}}}}({h_M})$ is at most twice the expected loss of the Gibbs classifier $L^{\text { {Gibbs}}}({h_G})$,

$$\begin{aligned} L^{\text { { {MV}}}}({h_M})\le 2 L^{\text { {Gibbs}}}({h_G}) \end{aligned}$$

(2)

(Mcallester 2003; Langford and Shawe-Taylor 2002; Germain et al. 2015). Therefore, any bound on $L^{\text { {Gibbs}}}({h_G})$ provides a bound on the corresponding $L^{\text { { {MV}}}}({h_M})$. We consider the following inequality originally due to Seeger (2002), which we refer to as the PBkl-bound (PAC-Bayesian kl):

Theorem 1

(PBkl-bound, Seeger 2002) For any probability distribution $\pi$ over $\mathcal{H}$ that is independent of S and any $\delta \in (0,1)$, with probability at least $1-\delta$ over a random draw of a sample S, for all distributions $\rho$ over $\mathcal{H}$ simultaneously:

A slightly tighter bound can be obtained by using

$$\begin{aligned} \xi (n) = \sum ^n_{k=0} \left( {\begin{array}{c}n\\ k\end{array}}\right) \left( \frac{k}{n}\right) ^k \left( 1-\frac{k}{n}\right) ^{n-k} \end{aligned}$$

(3)

instead of $2\sqrt{n}$ in the bound above, because we have $\sqrt{n} \le \xi (n) \le 2\sqrt{n}$ (Maurer 2004).

In order to use Theorem 1 in the bagging setting, we need to make a small adjustment. The empirical Gibbs loss ${{\hat{L}}}^{\text { {Gibbs}}}({h_G},T)$ is computed using ${\bar{T}}_1, {\bar{T}}_2, \ldots$, and since these sets have different sizes, in order to apply the PBkl-bound, we use $n= \min _i\left( |{\bar{T}}_i|\right)$. That this is a valid strategy can easily be seen by going through the proof of Theorem 1, see Thiemann et al. (2017).

Theorem 1 may also be applied to the final majority vote classifier ${h_G}$ if a separate validation set is left out. In this case, $|\mathcal {H}| = 1$, ${{\,\mathrm{KL}\,}}(\rho \Vert \pi ) = 0$, and $\hat{L}^{\text { {Gibbs}}}({h_M},S) = {{\hat{L}}}^{\text { {MV}}}({h_M},S)$. A separate validation set implies that the data available at training time has to be split, and, therefore, the actual training set gets smaller. While ${{\hat{L}}}^{\text { {Gibbs}}}({h_M},S)$ may be larger due to the smaller training data set size, the bound does no longer suffer from the factor 2 in (2). We will consider this way of bounding $L^{\text { { {MV}}}}({h_M})$ as an additional baseline denoted as SH-bound (Single Hypothesis). Note that this bound requires the separate validation set and, thus, cannot be applied in the bagging setting.

3.2 PAC-Bayesian bounds for majority vote classifiers

The PBkl-bound provides a tight bound for the Gibbs classifier, but the associated bound for the majority vote classifier may be loose. This is because the bound for the Gibbs classifier does not take correlation between individual classifiers into account. The individual classifiers may be weak (i.e., $L(h_i)$ close to $\frac{1}{2}$) leading to a weak Gibbs classifier, but if the correlations between the classifiers are low, the errors tend to cancel out when voting, giving a stronger majority vote classifier (Germain et al. 2015). The generalization bounds for Gibbs classifiers do not capture this, as they depend only on the strength of the individual classifiers. In order to get stronger generalization guarantees for majority vote classifiers, we need bounds that incorporate information about the correlations between errors of classifiers as well, as already pointed out by Breiman (2001).

Germain et al. (2015) propose to use the $C$-bound for this purpose, which is based on the margin of the majority vote classifier. They consider only the case where the output space is binary, $\mathcal {Y}= \{-1,1\}$, and (1) becomes $\mathcal {M}_\rho (X,Y) = Y\left( \sum _{h\in \mathcal {H}} \rho (h) h(X)\right)$. With the first moment $\mathcal {M}_\rho = {\mathbb {E}}_D\left[ \mathcal {M}_\rho (X,Y)\right]$, the second moment is given by $\mathcal {M}_{\rho ^2} = {\mathbb {E}}_D\left[ \left( \mathcal {M}_\rho (X,Y)\right) ^2\right] = {\mathbb {E}}_{h_1,h_2\sim \rho ^2}\left[ {\mathbb {E}}_D\left[ h_1(X)h_2(X)\right] \right]$. Then the $C$-bound for the expected loss of the $\rho$-weighted majority vote classifier reads:

Theorem 2

($C$-bound, Germain et al. 2015) For any distribution $\rho$ over $\mathcal {H}$ and any distribution $D$ on $\mathcal {X}\times \{-1,1\}$, if $\mathcal {M}_\rho > 0$, we have

$$\begin{aligned} L({h_M}) \le 1 - \frac{\mathcal {M}_{\rho }^2}{\mathcal {M}_{\rho ^2}}. \end{aligned}$$

The theorem follows from the one-sided Chebyshev inequality applied to the loss of ${h_M}$. As the first and second moments are usually not known, Germain et al. offer several ways to bound them empirically. They start by showing that

$$\begin{aligned} \mathcal {M}_\rho = 1-2 L^{\text { {Gibbs}}}({h_G}) \end{aligned}$$

(4)

meaning that the first moment of the margin can be bounded by the use of the PBkl-bound (Theorem 1). For the second moment, we have that

$$\begin{aligned} \mathcal {M}_{\rho ^2} = 1-2 d_{\rho }, \end{aligned}$$

(5)

where $d_{\rho }= \frac{1}{2}\left[ 1-{\mathbb {E}}_D\left[ \left( {\mathbb {E}}_\rho \left[ h(X)\right] \right) ^2\right] \right]$ is the disagreement between individual classifiers. Together with the $C$-bound, the relations above confirm the observations made by Breiman (2001): the strength of ${h_M}$ depends on having strong individual classifiers (low $L^{\text { {Gibbs}}}({h_G})$, i.e., large $\mathcal {M}_\rho$) and low correlation between classifiers (high disagreement $d_{\rho }$, i.e., low $\mathcal {M}_{\rho ^2}$).

By (4), the first moment of the margin can be bounded by the use of the PBkl-bound (Theorem 1), while by (5) the second moment can be bounded using a lower bound on $d_{\rho }$. With ${\hat{d}}_{\rho }^S$ denoting the empirical disagreement computed on $S$, $d_{\rho }$ can be lower bounded by the smallest d satisfying (Germain et al. 2015)

Like in the case of Theorem 1, solutions to the above inequality can be computed by a root-finding method. This leads to the following empirical $C$-bound, which we denote the $C1$-bound:

Theorem 3

($C1$-bound, Germain et al. 2015) For any probability distribution $\pi$ over $\mathcal {H}$ that is independent of $S$ and any $\delta \in \left( 0,1\right)$, with probability at least $1-\delta$ over a random draw of a sample $S$, for all distributions $\rho$ over $\mathcal {H}$ simultaneously

$$\begin{aligned} L^{\text { { {MV}}}}({h_M})\le 1 - \frac{\left( 1-2b\right) ^2}{(1-2d)}. \end{aligned}$$

Here $b$ is an upper bound on $L^{\text { {Gibbs}}}({h_G})$, which can be found by Theorem 1, and d is a lower bound on $d_{\rho }$.

The $C1$-bound allows direct bounding of $L^{\text { { {MV}}}}({h_M})$. However, Germain et al. (2015) also provide another bound based on Theorem 2, which does not require bounding $L^{\text { {Gibbs}}}({h_G})$ and $d_{\rho }$ separately. First, we let $e_\rho = {\mathbb {E}}_{h_1,h_2\sim \rho ^2}\left[ {\mathbb {E}}_D\left[ I\left( h_1(X)\ne Y\right) I\left( h_2(X)\ne Y\right) \right] \right]$ denote the expected joint error and ${\hat{e}}_{\rho }^{S}$ denote the empirical joint error computed on $S$. Then the loss of the associated Gibbs classifier can be written as $L^{\text { {Gibbs}}}({h_G})= \frac{1}{2}\left( 2e_\rho +d_{\rho }\right)$. The next bound is then based on bounding $d_{\rho }$ and $e_\rho$ simultaneously, by bounding the ${{\,\mathrm{KL}\,}}$-divergence between two trivalent random variables. A variable X is trivalent if ${\mathbb {P}}\left( X=x_1\right) = p_1$, ${\mathbb {P}}\left( X=x_2\right) = p_2$ and ${\mathbb {P}}\left( X=x_3\right) =1-p_1-p_2$, and similar to , denotes the ${{\,\mathrm{KL}\,}}$-divergence between two trivalent random variables with parameters $(p_1,p_2,1-p_1-p_2)$ and $(q_1,q_2,1-q_1-q_2)$.

Using the above and a generalization of the PAC-Bayes inequality to trivalent random variables, Germain et al. derive the following bound, which we refer to as the $C2$-bound:

Theorem 4

($C2$-bound, Germain et al. 2015) For any probability distribution $\pi$ over $\mathcal {H}$ independent of $S$ and any $\delta \in \left( 0,1\right)$, with probability at least $1-\delta$ over a random draw of a sample $S$, for all distributions $\rho$ over $\mathcal {H}$ simultaneously

$$\begin{aligned} L^{\text { { {MV}}}}({h_M})\le \sup _{d,e}\left( 1 - \frac{\left( 1-\left( 2e+d\right) \right) ^2}{1-2d}\right) , \end{aligned}$$

where the supremum is over all d and e satisfying

(6)

Again, we need to make adjustments in order to apply the $C1$-bound and $C2$-bound in the bagging setting. When lower bounding the disagreement and the joint error in Theorem 4, we consider the empirical disagreement ${\hat{d}}_{\rho }^{T}$ (and joint error ${\hat{e}}_{\rho }^{T}$) between $h_i$ and $h_j$ estimated on ${\bar{T}}_i \cap {\bar{T}}_j$ and choose $n= \min _{i,j}\left( |{\bar{T}}_i\cap {\bar{T}}_j|\right)$ accordingly.

3.3 Optimizing the posterior distribution

Aside from providing guarantees on expected performance, PAC-Bayesian bounds can be used to tune classifiers. The prior distribution $\pi$ must be chosen before observing the data, but we are free to choose the posterior distribution $\rho$ afterwards, for instance one could choose $\rho$ such that the empirical loss ${{\hat{L}}}^{\text { {MV}}}({h_M},S)$ is minimized.

Breiman has applied boosting (Schapire and Singer 1999) to random forests in order to optimize the weighting of the vote, finding that it improved the accuracy in some cases (Breiman 2001). We instead consider optimization of the posterior by minimizing the theoretical bounds (Thiemann et al. 2017; Germain et al. 2015). However, none of the bounds provided above can easily be used to directly optimize $\rho$, because they are non-convex in $\rho$ (Thiemann et al. 2017). Thiemann et al. (2017) and Germain et al. (2015) came up with two different ways to resolve the convexity issue.

Thiemann et al. apply a relaxation of Theorem 1 based on Pinsker’s inequality, which leads to the following result that we refer to as the $\lambda$-bound:

Theorem 5

($\lambda$-bound, Thiemann et al. 2017) For any probability distribution $\pi$ over $\mathcal{H}$ that is independent of $S$ and any $\delta \in (0,1)$, with probability at least $1-\delta$ over a random draw of a sample $S$, for all distributions $\rho$ over $\mathcal{H}$ and $\lambda \in (0,2)$ simultaneously

$$\begin{aligned} L^{\text { {Gibbs}}}({h_G})\le \frac{{{\hat{L}}}^{\text { {Gibbs}}}({h_G},S)}{1 - \frac{\lambda }{2}} + \frac{{{\,\mathrm{KL}\,}}(\rho \Vert \pi ) + \ln \frac{2 \sqrt{n}}{\delta }}{\lambda \left( 1-\frac{\lambda }{2}\right) n}. \end{aligned}$$

(7)

They show that the $\lambda$-bound is convex in $\rho$ and in $\lambda$ (but not jointly convex). They give an iterative update procedure, which alternates between updating $\lambda$ and $\rho$, and prove that, under certain conditions, the procedure is guaranteed to converge to the global minimum.

Germain et al. (2015) state a version of the $C$-bound that is suited for optimization of $\rho$. However, the bound is restricted to self-complemented hypothesis classes and posteriors aligned on the prior. A hypothesis class is said to be self-complemented, if $h\in \mathcal {H}\Leftrightarrow -h\in \mathcal {H}$, where $-h$ is a hypothesis that always predicts the opposite of h (in binary prediction). A posterior $\rho$ is said to be aligned on $\pi$ if $\rho (h) + \rho (-h) = \pi (h) + \pi (-h)$. Thus, the final statement of the bound, which we denote by $C3$-bound, becomes:

Theorem 6

($C3$-bound, Germain et al. 2015) For any self-complemented hypothesis set $\mathcal {H}$, any probability distribution $\pi$ over $\mathcal {H}$ independent of $S$ and any $\delta \in \left( 0,1\right)$, with probability at least $1-\delta$ over a random draw of a sample $S$, for all distributions $\rho$ aligned with $\pi$ simultaneously

$$\begin{aligned} L^{\text { { {MV}}}}({h_M})\le 1-\frac{\left( 1-2r\right) ^2}{(1-2d)}, \end{aligned}$$

where

$$\begin{aligned}&r = \min \left( \frac{1}{2},{{\hat{L}}}^{\text { {Gibbs}}}({h_G},S)+\sqrt{\frac{\ln \frac{2\xi (n)}{\delta }}{2n}}\right) , \\&d = \max \left( 0,{\hat{d}}_{\rho }^S-\sqrt{\frac{\ln \frac{2\xi (n)}{\delta }}{2n}}\right) . \end{aligned}$$

The authors show how to minimize the bound in Theorem 6 over the posterior $\rho$, by solving a quadratic program. The quadratic program requires a hyperparameter $\mu$, used to enforce a minimum value of the first moment of the margin. $\mu$ can be chosen by cross validation (Germain et al. 2015). Furthermore, they note how the restriction to aligned posteriors acts as regularization.

For both the $\lambda$-bound and the $C3$-bound, we need to make the same adjustments as for the PBkl-bound and the $C$-bound, that is, we choose $n= \min _{i,j}\left( |{\bar{T}}_i\cap {\bar{T}}_j|\right)$. When applying the optimization procedure of the $C3$-bound, we also need to make sure that the $\mathcal {H}$ is self-complemented; given a set of hypotheses, this can be done by copying all hypotheses and inverting their predictions.

Table 1 Overview of the bounds that we apply in Sect. 4 with references to the corresponding theorems in Sect. 3

4 Experiments

We have applied the bounds of Sect. 3, summarized in Table 1, in different random forest settings. First, we considered the standard setting with bagging and used the sets ${\bar{T}}_1, {\bar{T}}_2, \ldots$ for evaluation and computation of the bounds as described in Sect. 3. The posterior distribution $\rho$ was taken uniform and not optimized. Then we considered a setting with a separate validation set $T_{\text { {val}}}$. The majority vote bounds suffer from the low number of training patterns available for evaluating the correlation between classifiers. Therefore, we also evaluated the quality of the bounds when a separate validation set $T_{\text { {val}}}$ was set aside before training. $T_{\text { {val}}}$ was then used in addition to ${\bar{T}}_1,{\bar{T}}_2,\ldots$, when evaluating and computing the bounds. Again, the posterior distribution $\rho = u$ was not optimized. Finally, we looked at random forests with optimized posteriors. We used bagging and the bounds in Theorems 5 and 6 to optimize the posterior distribution $\rho$.

For all settings, the accuracy of the final majority vote classifier ${h_M}$ is also of interest. Hence, a separate test set $T_{\text { {ext}}}$ is left out in each setting. This set is used only for evaluating the final classifier by ${{\hat{L}}}^{\text { {MV}}}({h_M},T_{\text { {ext}}})$. We are mainly concerned with the tightness of the bounds when individual voters are strong. Therefore, all features are considered in each split during the training of the random forest (using Gini impurity as splitting criterion), and trees are trained until all leaves are pure [see, e.g., Gieseke and Igel (2018), for arguments why this can be beneficial].

To study how the bounds depend on the strengths of the individual classifiers, we varied the maximum tree depth and the number of features considered in each split in the first two settings. This allows us to investigate the evolution of the bounds as the strength of individual classifiers increases by going from decision stumps to full-grown trees. We either set the number of random features considered for splitting to the maximum number or, to further weaken the classifiers, to a single random feature. We restricted these experiments to two data sets.

Experiments were run on several binary UCI data sets (see left part of Table 2). For each data set, all patterns with one or more missing features were removed. Since the $C$-bound is only analysed for binary classification, we restrict ourselves to binary tasks. The number of trees $m$ for any data set of size $N$ was chosen as the largest value from $\{100,200,500,1000\}$ that was smaller than $N/4$.

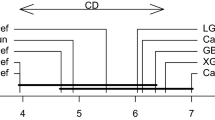
For each setting, $N/2$ patterns were randomly sampled for $T_{\text { {ext}}}$. In the first and third settings, all remaining patterns were used for training. In the second setting, a further $N/4$ patterns were sampled for $T_{\text { {val}}}$, with the remaining patterns used for training, see Fig. 1 for an illustration.

When evaluating the bounds, we chose $\pi = u$ and $\delta = 0.05$.

Table 2 The PBkl-bound, $C1$-bound, $C2$-bound and SH-bound computed for the binary UCI data sets in the bagging and validation set settings

Fig. 1

Overview of data split for each of the three settings. Note, that the bounds computed on $T$, as well as the optimization in the third setting, are only based on the hold-out sets, ${\bar{T}}_i$

4.1 Random forest with bagging

We started with the original random forest setting, where an individual tree $h_i$ is trained on a bootstrap sample $T_i$ of size $|T|$, drawn with replacement from the training set $T$ consisting of half the data with the other half $T_{\text { {ext}}}$ used for evaluating the final classifier. As mentioned, the posterior distribution $\rho$ was chosen uniform. In this experiment, $T$ comprised all available data. The empirical Gibbs loss was evaluated using ${\bar{T}}_i = T\setminus T_i$ and the empirical disagreement and joint error between two trees $h_i$ and $h_j$ using ${\bar{T}}_i \cap {\bar{T}}_j$.

We considered the PBkl-bound and the two empirical $C$-bounds, $C1$-bound and $C2$-bound, with sample sizes n calculated as described in Sect. 3. Furthermore, the trained classifier ${h_M}$ was evaluated on $T_{\text { {ext}}}$.

Table 2 (middle) lists the results. The test score ${{\hat{L}}}^{\text { {MV}}}({h_M},T_{\text { {ext}}})$ provides an estimate of the accuracy of the classifier. The PBkl-bound always gave the tightest bounds. For 6 out of the 14 data sets the bound was below 0.5. The better performance of the PBkl-bound is explained by the high accuracy of the individual trees. As mentioned by Germain et al. (2015) and discussed in Sect. 3, the $C$-bound degrades when the individual classifiers are strong. Thus, the PBkl-bound including the factor of 2 coming from (2) is tighter. Furthermore, for the $C$-bounds the bagging setting is particularly difficult, because there is only a small amount of data available for estimating correlations. This is especially true for the $C2$-bound, since it relies only on the intersection between the two samples ${\bar{T}}_i$ and ${\bar{T}}_j$, which may be small.

In the bagging setting we get the bounds “for free” in the sense that all evaluations are based on the ${\bar{T}}_i$ sets, which are by-products of the training, and we do not have to set aside a separate validation set. Thus, more data is available for selecting the hypothesis.

Figure 2 shows the evolution of the bounds as the strength of the individual voters varies for the data sets Letter:AB and Mushroom. Voter strength was controlled by increasing the maximum allowed tree depth until only pure trees were obtained, and by feature selection during splits, that is, using either the best feature (stronger voters) or a random feature (weaker voters).

Fig. 2

Evolution of bounds depending on voter strength (measured by Gibbs risk) on data sets Letter:AB (top) and Mushroom (bottom) in the bagging setting, using the best feature for splits (left) or a random feature (right). In addition, the empirical disagreement ${\hat{d}}_{\rho }$ between the trees is plotted

From the figure, we see that the PBkl-bound is tighter than both the $C1$-bound and the $C2$-bound, even though the $C$-bounds are expected to perform better, when individual classifiers are weak. However, this theoretical advantage is outweighed by the low amount of data available for bounding the disagreement/joint error, that is, $n= \min _{i,j}\left( |{\bar{T}}_i\cap {\bar{T}}_j|\right)$ is very small, leading to loose bounds.

4.2 Random forest with a separate validation set

As a reference, we considered the scenario where a separate validation set $T_{\text { {val}}}$ was set aside before the random forest was trained, which allows for a better estimate of the correlations in the $C$-bounds. Recall that a separate test set $T_{\text { {ext}}}$ was set aside for evaluating the classifier beforehand. Now the remaining half of the data set was split into two equal sized parts, $T$ and $T_{\text { {val}}}$. The random forest was then trained on $T$ as before using bagging, but the empirical Gibbs loss and disagreement were now measured on the sets ${\bar{T}}_1,{\bar{T}}_2,\ldots$ combined with $T_{\text { {val}}}$. We also considered the setting in which only $T_{\text { {val}}}$ was used for computing the bounds. This, as expected, led to slightly worse bounds. The results can be found in Table 4 in the “Appendix A”. As in the previous setting, we had to take care when applying the bounds. Again, the sample sizes n for the theorems were calculated as described in Sect. 3, but now with extra $N/4$ points available. As before, we applied the PBkl-bound, the $C1$-bound and the $C2$-bound, but now with the addition of the SH-bound. Having the separate validation set allowed us to apply this single hypothesis bound, which is based only on $T_{\text { {val}}}$.

Table 2 (right) lists the results. Again, the loss of ${h_M}$ on $T_{\text { {ext}}}$ is given as an estimate of the accuracy of the classifier. As before, we see that the PBkl-bound was tighter than the $C$-bounds in almost all cases, and again the explanation lies in the strength of the individual classifiers. We also see that the $C2$-bound was tighter than $C1$-bound. This is in accordance with the observation by Germain et al. (2015) that the $C2$-bound is often tighter when there is an equal amount of data available for estimating the empirical Gibbs loss and the empirical correlation between any two classifiers. However, we see in all cases that the single hypothesis bound gives the best guarantees. This indicates that the PBkl-bound does indeed suffer from not taking correlations into account, even if it outperforms the $C$-bounds.

Comparing the results to the bounds obtained in the previous experiment, we see that, with the exception of the SH-bound, the bounds overall were very similar, some bounds better, some worse. This can be explained by the trade-off between using data for training the classifier and using data for evaluating the classifier as part of computing the bounds. In the previous experiment, more data was used to train the random forest, which typically gives a better classifier (as also indicated by the performance on the test set $T_{\text { {ext}}}$), resulting in a lower empirical Gibbs loss. Still, in this experiment the bound can be tighter because more data is used to evaluate the classifiers. This is demonstrated in Fig. 6 in “Appendix B” which shows a comparison of the two settings on two exemplary data sets, Letter:DO and Adult. The figure illustrates the difference in tightness of the bounds.

The SH-bound provides the best guarantees for all data sets across both experiments, indicating that the other bounds are still too loose. The SH-bound does not come for free though, as data must be set aside, whereas the bounds computed in the bagging setting often provide useful guarantees and a better classifier.

The dependence of the bounds on the strengths of the individual voters is shown in Fig. 3 for the data sets Letter:AB and Mushroom. As in the previous setting, maximum tree depth and feature selection at splits (using the best or a random feature) were used to control voter strength.

Fig. 3

Evolution of bounds depending on voter strength (measured by Gibbs risk) on data sets Letter:AB (top) and Mushroom (bottom) in the setting with a separate validation set, using the best feature for splits (left) or a random feature (right). In addition, the empirical disagreement ${\hat{d}}_{\rho }$ between the trees is plotted

Even when individual voters got weaker, the SH-bound remained tighter. As expected, the $C2$-bound now outperformed the PBkl-bound when individual voters are weak and disagreement is high. However, to observe this effect it was necessary to consider a single random feature for splitting. Considering the best feature with shallow trees also results in weak voters, but because of lower disagreement (due to trees being very similar), the $C$-bounds are still loose.

Comparing to the bagging setting, we see the impact of having extra data from the left out validation set, $T_{\text { {val}}}$, when evaluating the bounds. Still, the PBkl-bound remained tighter for strong voters, that is, when the Gibbs risk is close to zero.

4.3 Random forest with optimized posterior

Finally, we optimized the posteriors based on the $\lambda$-bound (Theorem 5) and the $C3$-bound (Theorem 6). The former was updated by iterative application of the update rules given by Thiemann et al. (2017). For the latter, we made sure that the hypothesis set is self-complemented (Germain et al. 2015) by adding a copy of all trained trees with their predictions reversed. The quadratic program was then solved using the solver CVXOPT (Andersen and Vandenberghe 2019).

Table 3 Loss on $T_{\text { {ext}}}$ obtained when $\rho$ is chosen by minimizations of the $\lambda$-bound ($\rho =\rho _\lambda$) and the $C3$-bound ($\rho =\rho _{C}$), compared to loss obtained with $\rho =u$

For each experiment, we split the data set into a training set $T$ and an external test set $T_{\text { {ext}}}$not used in the model building process, see Fig. 1. We only considered larger benchmark data sets, because $T$ and $T_{\text { {ext}}}$ needed to be of sufficient size. The random forest was then trained using bagging, and the posteriors were then optimized using the individual sets ${\bar{T}}_1,{\bar{T}}_2,\ldots$. We selected the hyperparameter $\mu$ for the quadratic program of Theorem 6 that minimized the OOB estimate. Once the optimal $\rho$ was found, the random forest with optimized weights was evaluated on $T_{\text { {ext}}}$. A random forest with uniform posterior was trained and evaluated in the same setting as a baseline.

Table 3 lists the loss on $T_{\text { {ext}}}$ for the seven largest data sets when optimizing $\rho$ by minimization of the $\lambda$-bound and $C3$-bound. $\rho _\lambda$ and $\rho _{C}$ denotes the optimal posteriors found using the optimization with the $\lambda$-bound and the $C3$-bound respectively. Note that for $\rho _{C}$, the hypothesis set is modified such that it is self-complemented.

For the optimization using the $\lambda$-bound, we see that, except on the Tic-Tac-Toe data set, the test loss for the optimized posterior was equal or slightly higher. The reason is that, because the $\lambda$-bound does not consider interactions between ensemble members, it tends to put most weight on only a few trees. Thus, the effect of cancellation of errors vanishes.

Figure 4 demonstrates that indeed most of the probability mass was centered on the few trees.

Fig. 4

Optimized distribution $\rho _\lambda$ and for each tree i the error on the subset ${\bar{T}}_i$ of the training data not used for building the tree. Shown are the results for the Credit-A data set using 50 trees

However, recomputing the PBkl-bound, $C1$-bound and $C2$-bound using posterior $\rho _\lambda$, we observed that the PBkl-bound (and actually also the $C$-bounds) became tighter, indicating that the bounds are still quite loose.

Optimizing using the $C$-bound in Theorem 6 does not suffer from the probability mass being concentrated on very few tress, because of the restriction to posteriors aligned on the prior (which is uniform in our case) and the fact that the individual trees were rather strong. The probability mass can only be moved between a tree and its complement. If $h_i$ has a small loss, $\rho _C(h_i)$ is close to $1/m$, since $-~h_i$ is very weak. Figure 5 shows an example. The algorithm selected almost exclusively the strong classifiers, and due to the required alignment, the $\rho _C$ was basically the uniform distribution on the original (non-self-complemented) hypothesis set, explaining the similarities in accuracy and bounds.

Fig. 5

Optimized distribution $\rho _C$ and for each tree i the error on the subset ${\bar{T}}_i$ of the training data not used for building the tree. Shown are the results for the Credit-A data set using 100 self-complemented trees

5 Conclusions

PAC-Bayesian generalization bounds can be used to obtain rigorous performance guarantees for the standard random forest classifier used in practice. No modification of the algorithm is necessary and no additional data is required because the out-of-bag samples can be exploited. In our experiments using the standard random forest, bounds inherited from the corresponding Gibbs classifiers clearly outperformed majority vote bounds that take correlations between ensemble members into account. The reason is that the individual decision trees are already rather accurate classifiers, which makes it difficult to estimate the correlations of errors. As expected, we could observe the opposite result when using weaker individual classifiers. However, this required enough disagreement between the classifiers (which we enforced by increasing randomization) and using a separate validation set, because the out-of-bag samples alone provided not enough data for reliably estimating the correlation between two voters. We also replaced the majority vote by a weighted majority vote and optimized the weights by minimizing the PAC-Bayesian bounds. This led to better performance guarantees, but weaker empirical performance.

When we split the data available at training time into a training and a validation set, we can use the hold-out validation set to compute a generalization bound. In our experiments, this led to considerably tighter bounds compared to the PAC-Bayesian approaches. However, because less data was available for training, the resulting classifiers performed worse on an external test set in most cases. Thus, using a validation set gave us better performance guarantees, but worse performance.

Our conclusion is that existing results that are derived for ensemble methods and take correlations of predictions into account are not sufficiently strong for guiding model selection and/or weighting of ensemble members in majority voting of powerful classifiers, such as decision trees. While the $C$-bounds are empirically outperformed by the generalization bounds based on the Gibbs classifier, the latter ignore the effect of cancellation of errors in majority voting and, thus, are of limited use for optimizing a weighting of the ensemble members and guiding model selection. Therefore, more work is required for tightening the analysis of the effect of correlations in majority voting. Nevertheless, to our knowledge, the PAC-Bayesian approach in this study provides the tightest upper bounds for the performance of the canonical random forest algorithm without requiring hold-out data.

Appendices

A Extra results for second setting

Table 4 lists the bounds and losses obtained in the validation set setting using only $T_{\text { {val}}}$ for computing the bounds.

Table 4 The PBkl-bound, $C1$-bound, $C2$-bound and SH-bound computed for the binary UCI data sets in the validation set setting, where only $T_{\text { {val}}}$ is used for computing the bounds

B Comparison plots for the bagging and validation set settings

Figure 6 shows the comparison of the bounds obtained for the Letter:DO and Adult data set. The figure includes all three settings: using only the hold-out sets from bagging (${\bar{T}}$), using only the validation set ($T_{\text { {val}}}$), and using a combination of both (${\bar{T}}$+$T_{\text { {val}}}$)

Fig. 6

Comparison of the bounds obtained for a random forest with 500 trees trained on the Letter:DO data set. Comparison of the bounds obtained for a random forest with 500 trees trained on the Letter:DO data set (left) and for a random forest with 1000 trees trained on the Adult data set (right)