Adaptive infinite dropout for noisy and sparse data streams

Abstract

The ability to analyze data streams, which arrive sequentially and possibly infinitely, is increasingly vital in various online applications. However, data streams pose various challenges, including sparse and noisy data as well as concept drifts, which easily mislead a learning method. This paper proposes a simple yet robust framework, called Adaptive Infinite Dropout (aiDropout), to effectively tackle these problems. Our framework uses a dropout technique in a recursive Bayesian approach in order to create a flexible mechanism for balancing between old and new information. In detail, the recursive Bayesian approach imposes a constraint on the model parameters to make a regularization term between the current and previous mini-batches. Then, dropout whose drop rate is autonomously learned can adjust the constraint to new data. Thanks to the ability to reduce overfitting and the ensemble property of Dropout, our framework obtains better generalization, thus it effectively handles undesirable effects of noise and sparsity. In particular, theoretical analyses show that aiDropout imposes a data-dependent regularization, therefore, it can adapt quickly to sudden changes from data streams. Extensive experiments show that aiDropout significantly outperforms the state-of-the-art baselines on a variety of tasks such as supervised and unsupervised learning.

1 Introduction

Bayesian modelling has become a powerful tool in machine learning and has been utilized in a wide range of applications such as text mining (Blei et al., 2003; Van Linh et al., 2017), recommendation systems (Le et al., 2018; Van Linh et al., 2020), social network (Gopalan et al., 2013; Mehrotra et al., 2013), computer vision (Fei-Fei & Perona, 2005), bioinformatics (Rogers et al., 2005), etc. Based on assumptions about data, we can straightforwardly build a model with hidden variables and observations. The inferred posteriors of the hidden variables expose data characteristics that can used in applications.

There are numerous inference methods (MacKay & Mac Kay, 2003; Zhang et al., 2018) to work well in a static environment in which there is no change in data in the entire training process. However, in modern applications such as social networks, and E-commerce, data is generated continually and is collected in infinitely many mini-batches (known as the streaming environment). The prevailing characteristics of data are big, noisy and sparse. Moreover, the various kinds of concept drifts (such as sudden, incremental, and recurring concept drifts Gama et al., 2014; Krawczyk & Cano, 2018), in which the statistical characteristics of new data change, can happen. Therefore, developing an effective learning method poses challenging problems in the streaming environment. Firstly, traditional inference methods which implement an iterative procedure on all data are impossible to work on data streams. It is necessary for a method to adapt to new data quickly without revisiting the past data. As a result, it must deal with the stability-plasticity dilemma (Mermillod et al., 2013). The dilemma requires a learning method to be stable to effectively exploit acquired knowledge when working on new data whose characteristics are similar to those of the past data. Simultaneously, it should be plastic when concept drift happens. Secondly, noisy and sparse data (Nguyen et al., 2021; Ha et al., 2019; Mai et al., 2016; Tuan et al., 2020) makes a lot of difficulties for learning methods. While sparse data does not provide an unclear context, noisy data can mislead the methods. Consequently, the generalization ability of a learned model can be limited. In this paper, we focus on these challenges.

Some recent studies (Broderick et al., 2013; Duc et al., 2017; Masegosa et al., 2017; McInerney et al., 2015; Tran et al., 2021; Van et al., 2022) have provided solutions to learning from data streams. Those methods enable Bayesian models, which are designed for static conditions, to work with data streams. The recursive Bayesian approach (Ahn et al., 2019; Broderick et al., 2013; Duc et al., 2017; Masegosa et al., 2017; McInerney et al., 2015; Nguyen et al., 2018) has emerged as an effective solution and has been paid a great deal of attention by researchers. The main idea is that the learned posterior from a mini-batch is used as the prior in the next one. Therefore, this approach provides a flexible mechanism to exploit acquired knowledge in the current mini-batch without revisiting past data. However, the existing studies are still limited when facing the above challenges. We found that streaming variational Bayes (SVB) (Broderick et al., 2013) could suffer from the phenomenon of overconfident posterior after receiving a large enough amount of data. Concretely, the posterior variance would become arbitrarily small leading to point-mass posterior concentration. This arguably cause several critical issues in the online Bayesian updates including poor uncertainty representation of the underlying data-generating distribution, and lack of the flexibility to adapt to the sudden changes in data streams. Hierarchical power prior (HPP) (Masegosa et al., 2017, 2020) is more plastic to learn a new concept, however, it does not have any efficient way to work on noisy and sparse data. Other recursive Bayesian-based studies (Nguyen et al., 2021; Duc et al., 2017; Tran et al., 2021; Van et al., 2022) require external knowledge to deal with the challenges.

In this paper, we propose a novel framework called Adaptive Infinite Dropout (aiDropout) which enables a wide range of models to work in streaming environments. Our framework is based on the recursive Bayesian approach and dropout technique (Srivastava et al., 2014) to create an effective solution to learning from data streams. It has several benefits. Firstly, aiDropout has an easy mechanism to balance the information between old and new data throughout the data stream, which helps tackle the stability-plasticity dilemma. Secondly, we theoretically prove that Dropout in aiDropout induces a data-dependent regularization, which allows each parameter component to have its own search space to capture geometric properties, especially highly discriminative characteristics, of the data features. This is extremely important when data comes continuously with high uncertainty, which has the possibility of concept drifts or undesirable properties such as noise and sparsity. Thirdly, Dropout in our method works as an ensemble of an exponential number of learners, which is very useful in making good predictions for future data. These advantages help our method obtain better generalization. Finally, because the data inevitably changes over time, the drop rate should be adapted according to the data. Our method provides a mechanism to automatically tune the drop rate and therefore obtains better generalization and more practicality.

We empirically evaluate the performance of aiDropout compared to the existing state-of-the-art streaming methods by using two base models: (1) latent Dirichlet allocation (LDA) (Blei et al., 2003) for topic modelling and (2) Naïve Bayes (NB) (Russell and Norvig 2016) for classification. The extensively experimental results on both learning tasks show the superior effectiveness of aiDropout.

Roadmap: Section 2 briefly provides closely related work. We formally describe the aiDropout framework in Sect. 3 and its applications in Sect. 4. Non-trivial findings of aiDropout are described in Sect. 5. Section 6 presents extensive experiments and a conclusion is made in Sect. 7.

2 Related work

Several studies have addressed the inference problem on data streams. They are divided into two notable approaches: Stochastic optimization and recursive Bayesian update. The first one (Hoffman et al., 2013; Hughes & Sudderth, 2013; Kim et al., 2019; McInerney et al., 2015; Theis & Hoffman, 2015) considers the inference problem as a stochastic optimization problem in which the objective function is the expectation of the likelihood. In particular, stochastic variational inference (SVI) (Hoffman et al., 2013) aims to optimize the empirical expectation by sampling data instances from the uniform distribution on a fixed dataset, which is impractical in the streaming environment. To address this limit, population variational Bayes (PVB) (McInerney et al., 2015) assumes that data streams are generated by consecutively sampling $\nu$ (population size) data instances from the population distribution $F_{\nu }$ instead of the uniform distribution. However, $\nu$ must be manually adjusted to achieve better performances. Meanwhile, the second approach assumes that the learned knowledge from a mini-batch is considered as prior knowledge in the next one (Ahn et al., 2019; Broderick et al., 2013; Chérief-Abdellatif et al., 2019; Kirkpatrick et al., 2017; Kurle et al., 2020; Nguyen et al., 2018; Masegosa et al., 2017; Zenke et al., 2017). Streaming variational Bayes (SVB) (Broderick et al., 2013) uses the variational distribution learned in the previous mini-batch as the prior distribution for the current one. However, we find that SVB can become too stable in many cases and therefore can be unable to learn new information once trained from large enough data. To address the drawback of SVB, hierarchical power prior (HPP) (Masegosa et al., 2017, 2020) uses a forgetting factor relating to the degree of forgetting the old knowledge at the current mini-batch. Unfortunately, because this forgetting factor is considered as a hidden variable, the model in HPP is non-conjugate, leading to difficulties in inferring complicated Bayesian models. In addition, a lot of studies (Ahn et al., 2019; Kirkpatrick et al., 2017; Nguyen et al., 2018; Zenke et al., 2017) apply the recursive Bayesian approach to deal with multiple tasks. In this paper, we only concentrate on addressing the problem in data streams without changing tasks.

In terms of dealing with sparse and noisy data, none of these mentioned methods pays careful attention to this problem. Following the recursive Bayesian approach, some recent studies (Nguyen et al., 2021; Duc et al., 2017; Tran et al., 2021; Van et al., 2022) have proposed methods based on exploiting external/prior knowledge which is derived from a pre-trained model or human knowledge. Albeit those methods show promising results in coping with extremely short texts, their performances depend heavily on the quality of prior knowledge. Moreover, it is difficult to find external knowledge which is suitable for data streams. In contrast, by adopting the dropout technique in the streaming environment, our proposed method can tackle the problem of noise and sparsity efficiently without using external knowledge.

Dropout (Hinton et al., 2012) is well-known as a powerful regularization technique (Mou et al., 2018) for preventing overfitting by discouraging the co-adaptation of features. Moreover, dropout provides an efficient way to approximately combine an exponential number of learners, working as a form of ensemble learning. The idea of dropout is to randomly drop a subset of features at each iteration during training. At first, the drop rate is manually tuned, which demands to use grid-search, a prohibitive operation with large network models. To address this problem, some methods (Gal et al., 2017; Kingma et al., 2015; Liu et al., 2019) have been proposed to automatically determine the drop rate. Dropout has achieved great success in various machine learning models, e.g., neural networks (Srivastava et al., 2014), SVM (Chen et al., 2014), matrix factorization (Zhai & Zhang, 2015), topic models (Ha et al., 2019). However, the applications of Dropout are still limited to a static data environment. In parallel to our work, Guzy and Woźniak (2020) showed that dropout helps deal with recurring concept drift because dropout leads to using submodels generated for each concept. However, this work only focused on deterministic neural networks and lacked an adaptive mechanism. Moreover, the random selection of features in adaptive Random Forest (Gomes et al., 2017) achieves good performance in streaming environments. Therefore, exploiting adaptive dropout for learning Bayesian models on data streams is hopeful. In this paper, we explore Dropout for training Bayesian models to address the challenges in the streaming data. Our analysis about the role of Dropout as regularization applies well to a large class of Bayesian models, extending existing works (Baldi & Sadowski, 2014; Helmbold & Long, 2015; Mianjy et al., 2018; Rifai et al., 2011; Wager et al., 2013; Wang et al., 2013) to significantly wider contexts.

3 Adaptive infinite dropout for Bayesian models

In this section, we first introduce how to apply dropout to a general Bayesian model to work on data streams. Then, we present a strategy to learn drop rate.

Fig. 1

Graphical representation for iDropout and aiDropout

3.1 Infinite dropout

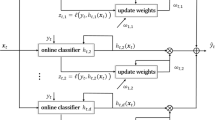
We consider a general model $B(\beta ,z,x)$ (Hoffman et al., 2013; McInerney et al., 2015) which consists of global variable $\beta$, the set of observations $x= x_{1:M}$ and the set of hidden variables $z=z_{1:M}$. More explicitly, each data instance (observation) $x_i$ has a hidden variable $z_i$ to encode the hidden feature of $x_i$. Meanwhile, the global variable $\beta$ is shared among all of the data instance $x_{1:M}$. Bayesian methods aim to infer the posterior distribution of hidden variables $p(\beta , z | x)$ when given a fixed dataset. Undoubtedly, this can not work with data streams where the data comes in an infinite sequence of mini-batches $C = \{D^1, D^2, \cdots , D^t, \cdots \}$ and each mini-batch t consists of M observed data points: $D^t = \{x_1^t, x_2^t, \cdots , x_M^t \}$.

We need to extend the model to also describe the dynamics of data streams. Here we assume that only the global variable $\beta$ evolves over time, which we indicate with superscript t, i.e., $\beta ^t$. We introduce a transition model $p(\beta ^t | \beta ^{t-1})$ to describe the transformation between two consecutive mini-batches:

$$\begin{aligned} p(\beta ^t_k | \beta ^{t-1}_k) = \mathcal {N}(.|\beta ^{t-1}_k, \sigma ^2I) \end{aligned}$$

(1)

where k is the row index of $\beta ^{t-1}$ and I is the identity matrix of size V. The variance $\sigma ^2$ is a hyperparameter, which describes our assumption about the fluctuation of $\beta _k$ between two consecutive mini-batches.

We assume that $\beta$ is represented by a $K \times V$ matrix. Dropout is utilized in our framework as follows. In each mini-batch t, we drop randomly some elements of matrix $\beta ^t$. This is implemented by using a hyperparameter called drop matrix $\pi ^t$ to make the element-wise product with $\beta ^t$, then going through a transformation: $\tilde{\beta }^t = f(\beta ^t \odot \pi ^t)$. Transformation f should be chosen to assure that $\tilde{\beta }^t$ can replace $\beta$ in model $B(\beta ,z,x)$ at each mini-batch t (in the later subsections, we use softmax to be the transformation). Given the new global variable $\tilde{\beta }^t$ at each mini-batch t, the generative process of all data points is similar to the original model B (Fig. 1a). In order to keep the randomness of Dropout, we use a different drop matrix at each mini-batch. Each element $\pi ^t_{ij}$ of $\pi ^t$ is generated using one of two options:

• 1. Bernouli dropout: $p(\pi ^t_{ij} = 1) = 1 - p$, $p(\pi ^t_{ij} = 0) = p$

• 2. Inverted dropout:

  $$\begin{aligned} p(\pi ^t_{ij} = {1}/{(1-p)}) = 1 - p, p(\pi ^t_{ij} = 0) = p \end{aligned}$$

  (2)

in which p is drop rate. Note that when $\beta ^t$ is used at test time, it has to be rescaled by $\mathbb {E}[\pi ^t_{ij}]$. By doing this scaling, $2^{K \times V}$ models with shared parameters can be combined into a single model to be used at test time, which works as a form of ensemble learning.

Learning: At each mini-batch t, we make a point estimate for $\beta ^t$ by maximizing $\log p(\beta ^t|\beta ^{t-1}, \pi ^t, D^t)$, where $\beta ^{t-1}$ is learned from the previous mini-batch:

$$\begin{aligned} \begin{aligned} \hat{\beta }^t&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}, \pi ^t, D^t) \right\} \\&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t, D^t|\beta ^{t-1}, \pi ^t) \right\} \\&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + \log p(D^t|\pi ^t, \beta ^t) \right\} \end{aligned} \end{aligned}$$

(3)

While the direct optimization of $p(D^t|\pi ^t, \beta ^t)$ is intractable, it is significantly easier to optimize than the complete data likelihood $\int _{z^t} p(D^t, z^t|\pi ^t, \beta ^t)$. By introducing a variational distribution $q(z^t|\phi ^t)$ defined over the local variables $z^t$, we then have:

$$\begin{aligned} \begin{aligned} \log p(D^t|\pi ^t, \beta ^t)&= \log \int _{z^t} p(D^t, z^t|\pi ^t, \beta ^t)dz^t = \log \int _{z^t} q(z^t|\phi ^t) \frac{p(D^t, z^t|\pi ^t, \beta ^t)}{q(z^t|\phi ^t)}dz^t\\&\ge \int _{z^t} q(z^t|\phi ^t) \log \frac{p(D^t, z^t|\pi ^t, \beta ^t)}{q(z^t|\phi ^t)}dz^t = E_{q(z^t|\phi ^t)}\left[ \log \frac{p(D^t, z^t|\pi ^t, \beta ^t)}{q(z^t|\phi ^t)} \right] \end{aligned} \end{aligned}$$

(4)

By substituting (4) into (3), our objective function can be rewritten as:

$$\begin{aligned} \begin{aligned} \{ \hat{\beta }^t, \hat{\phi }^t\} = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t, \phi ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + E_{q(z^t|\phi ^t)}\left[ \log \frac{p(D^t, z^t|\pi ^t, \beta ^t)}{q(z^t|\phi ^t)} \right] \right\} \end{aligned} \end{aligned}$$

(5)

The learning process is composed of two phases. We first infer the local variables by inheriting from the original model B, and then update the global variable. Algorithm 1 briefly describes the learning process.

3.2 Learning drop rate

Difference from the previous subsection in which $\pi ^t$ is sampled from a fixed Bernoulli distribution, we will infer the posterior of $\pi ^t$. The prior distribution for $\pi ^t$ is a Bernoulli distribution parameterized by $p^t$ (Fig. 1b). Our goal here is to maximize log $p(\beta ^t|\beta ^{t-1}, p^t, D^t)$ at each mini-batch t:

$$\begin{aligned} \begin{aligned} \hat{\beta }^t&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}, p^t, D^t) \right\} \\&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t, D^t|\beta ^{t-1}, p^t) \right\} \\&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + \log p(D^t|p^t, \beta ^t) \right\} \end{aligned} \end{aligned}$$

(6)

To automatically determine the posterior of $\pi ^t$ and hyperparameter $p^t$, we use the empirical Bayesian method and introduce the variational distribution $q(\pi ^t|\lambda ^t) = Bernoulli(\lambda ^t)$ where $\lambda ^t$ is the variational hyper-parameter of Bernoulli distribution. Therefore, we have a lower bound on $\log p(D^t|p^t, \beta ^t)$:

$$\begin{aligned} \begin{aligned}&\log p(D^t|p^t, \beta ^t) = \log \sum _{\pi ^t} p(D^t, \pi ^t|p^t, \beta ^t) = \log \sum _{\pi ^t} q(\pi ^t|\lambda ^t) \frac{p(D^t, \pi ^t|p^t, \beta ^t)}{q(\pi ^t|\lambda ^t)}\\&\qquad\qquad\qquad \ge \sum _{\pi ^t} q(\pi ^t|\lambda ^t) \log \frac{p(D^t, \pi ^t|p^t, \beta ^t)}{q(\pi ^t|\lambda ^t)} = \sum _{\pi ^t} q(\pi ^t|\lambda ^t) \log \frac{p(D^t|\pi ^t, \beta ^t)p(\pi ^t|p^t)}{q(\pi ^t|\lambda ^t)}\\&\qquad\qquad\qquad = E_{q(\pi ^t|\lambda ^t)}\left[ \log p(D^t|\pi ^t, \beta ^t) \right] - KL\left[ q(\pi ^t|\lambda ^t)||p(\pi ^t|p^t) \right] \\ \end{aligned} \end{aligned}$$

(7)

By introducing (7) into (6), the objective function can be written as:

$$\begin{aligned} \begin{aligned} \{ \hat{\beta }^t, \hat{\lambda }^t, \hat{p}^t \}&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t, \lambda ^t, p^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + E_{q(\pi ^t|\lambda ^t)}\left[ \log p(D^t|\pi ^t, \beta ^t) \right] \right. \\&\quad \left. - KL\left[ q(\pi ^t|\lambda ^t)||p(\pi ^t|p^t) \right] \right\} \end{aligned} \end{aligned}$$

(8)

While the KL term has a closed-form expression, it is not straightforward to estimate the expected log-likelihood $\mathbb {E}_{q(\pi ^t)}\log p(D^t|\beta ^t, \pi ^t)$, and more importantly the derivative of this second term with respect to the variational distribution parameter $\lambda ^t$ due to the difficulty in applying reparameterization trick (Kingma & Welling, 2014) to discrete random variables. There are some studies (Grathwohl et al., 2018; Jang et al., 2017; Maddison et al., 2017; Yin et al., 2019) to handle the learning problem from discrete latent variables. We select a simple solution that exploits the Gumbel-Softmax distribution (Jang et al., 2017), a continuous distribution, which helps us to do reparameterization for discrete variables. The original Gumbel-Softmax trick is intended to approximate samples from a categorical distribution that depends on a temperature parameter $\tau$, but here we concentrate on the Bernoulli distribution case. It turns out that we now have a simple formula for the continuous relaxation $\tilde{\pi }^t$ of $\pi ^t$:¹

$$\begin{aligned} \begin{aligned} \tilde{\pi }^t = \frac{\exp \left( \frac{\log (\lambda ^t) + g_1}{\tau } \right) }{\exp \left( \frac{\log (\lambda ^t) + g_1}{\tau } \right) + \exp \left( \frac{\log (1-\lambda ^t) + g_2}{\tau } \right) }\\ \text{ with } g_1, g_2 \sim Gumbel(0,1) \end{aligned} \end{aligned}$$

(9)

In each iteration, we draw L samples ($\{\tilde{\pi }^t_l\}_{l=1}^L$) of $\pi ^t$ to calculate $E_{q(\pi ^t|\lambda ^t)}\left[ \log p(D^t|\pi ^t, \beta ^t) \right]$ as follows:

$$\begin{aligned} E_{q(\pi ^t|\lambda ^t)}\left[ \log p(D^t|\pi ^t, \beta ^t) \right] =\frac{1}{L}\sum _{l=1}^L \log p(D^t|\tilde{\pi }^t_l, \beta ^t) \end{aligned}$$

The previous studies (Jang et al., 2017; Kingma & Welling, 2014) showed that using the reparameterization trick with $L=1$ also achieves good performance in terms of both computation and quality. The objective function (8) can then be rewritten in the form of:

$$\begin{aligned} \begin{aligned} \{ \hat{\beta }^t, \hat{\lambda }^t, \hat{p}^t\} = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t, \lambda ^t, p^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + \log p(D^t|\tilde{\pi }^t, \beta ^t) - KL\left[ q(\pi ^t|\lambda ^t)||p(\pi ^t|p^t) \right] \right\} \end{aligned} \end{aligned}$$

(10)

Similar to the previous subsection, instead of directly optimizing $\log p(D^t|\tilde{\pi }^t, \beta ^t)$, we try to optimize the complete-data log likelihood $\int _{z^t} p(D^t, z^t|\tilde{\pi }^t, \beta ^t)$. We then rewrite (10) in the form of:

$$\begin{aligned} \begin{aligned} \{ \hat{\beta }^t, \hat{\phi ^t}, \hat{\lambda }^t, \hat{p}^t\}&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t, \phi ^t, \lambda ^t, p^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + E_{q(z^t|\phi ^t)}\left[ \log \frac{p(D^t, z^t|\tilde{\pi }^t, \beta ^t)}{q(z^t|\phi ^t)} \right] \right. \\&\quad \left. - KL\left[ q(\pi ^t|\lambda ^t)||p(\pi ^t|p^t) \right] \right\} \end{aligned} \end{aligned}$$

(11)

It is worth observing that the parts of objective functions w.r.t $\beta$ and $\phi$ in iDropout (5) and aiDropout (11) are in the same form. They are merely different in the random dropout variable $\pi$. While in iDropout $\pi$ is sampled from a Bernoulli distribution with a fixed drop rate, aiDropout provides a mechanism to autonomously learn drop rate for adapting to new data. In the special case that samples of $\pi$ in both iDropout and aiDropout are the same, aiDropout will degenerate to iDropout. Algorithm 2 briefly describes the learning process of aiDropout.

4 Case study

We will show the application of aiDropout to latent Dirichlet allocation (LDA) (Blei et al., 2003) for document analysis and Multinomial Naïve Bayes (NB) (Russell & Norvig, 2016) for document classification (see Appendix A for iDropout).

4.1 Case study 1: when LDA is the base model

LDA is one of the most popular unsupervised models and provides an effective and interpretable solution in a wide range of applications such as text mining, recommendation system, etc. Therefore, some recent studies considered LDA as a base model to develop learning methods in the streaming environment. We merely explore how aiDropout works on LDA.

Suppose that each mini-batch t consists of M documents and each document d contains $N_d$ words. LDA aims to learn hidden topics in a text dataset as well as the topic proportion of each document. Hyper-parameter $\alpha$ is the parameter of Dirichlet distribution for topic mixture $\theta$, the matrix $\tilde{\beta }$ of size $K \times V$ is the topic distribution over V words in the vocabulary.

The generative process for documents in each mini-batch $t^{th}$ is as follows:

• 1. Draw $\beta ^t: \beta ^t_k \sim \mathcal {N}(\beta ^{t-1}_k, \sigma ^2 I)$

• 2. Draw $\pi ^t: \pi ^t_{kj} \sim \text{ Bernoulli }(p^t_{kj})$

• 3. Calculate topic distribution $\tilde{\beta ^t}$:

  $$\begin{aligned} \tilde{\beta }^t_{kj} = \text{ softmax }(\beta ^t_k \odot \pi ^t_k)_j = \frac{\exp (\beta ^t_{kj}\pi ^t_{kj})}{\sum _{i=1}^V \exp (\beta ^t_{ki}\pi ^t_{ki})} \end{aligned}$$

• 4. For each document d in mini-batch t:

  • (a) Draw topic mixture: $\theta _d \sim \text{ Dirichlet }(\alpha )$

  • (b) For $n^{th}$ word in document d:

  • i Draw a topic index:$z_{dn} \sim \text{Multinomial }(\theta _d)$

  • 2 Draw a word: $w_{dn} \sim \text{ Multinomial }(\tilde{\beta }^t_{z_{dn}})$ word in document d:

Learning process: At each mini-batch t, we maximize $\log p({\beta ^t}|{\beta ^{t - 1}},{p^t},\alpha ,{D^t})$

$$\begin{aligned} \begin{aligned} \hat{\beta }^t&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}, p^t, \alpha , D^t) \right\} \\&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t, D^t|\beta ^{t-1}, p^t, \alpha ) \right\} \\&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + \log p(D^t|p^t, \beta ^t, \alpha ) \right\} \end{aligned} \end{aligned}$$

(12)

We have a lower bound on $\log p(D^t|p^t, \beta ^t, \alpha )$, which is the same as (7):

$$\begin{aligned} \begin{aligned}&\log p(D^t|p^t, \beta ^t, \alpha ) = \log \sum _{\pi ^t} p(D^t, \pi ^t|p^t, \beta ^t, \alpha ) = \log \sum _{\pi ^t} q(\pi ^t|\lambda ^t) \frac{p(D^t, \pi ^t|p^t, \beta ^t, \alpha )}{q(\pi ^t|\lambda ^t)}\\&\qquad \quad\quad\ge \sum _{\pi ^t} q(\pi ^t|\lambda ^t) \log \frac{p(D^t, \pi ^t|p^t, \beta ^t, \alpha )}{q(\pi ^t|\lambda ^t)} = \sum _{\pi ^t} q(\pi ^t|\lambda ^t) \log \frac{p(D^t|\pi ^t, \beta ^t, \alpha )p(\pi ^t|p^t)}{q(\pi ^t|\lambda ^t)}\\&\quad \qquad\quad= E_{q(\pi ^t|\lambda ^t)}\left[ \log p(D^t|\pi ^t, \beta ^t, \alpha ) \right] - KL\left[ q(\pi ^t|\lambda ^t)||p(\pi ^t|p^t) \right] \\&\qquad\quad\quad \simeq \log p(D^t|\tilde{\pi }^t, \beta ^t, \alpha ) - KL\left[ q(\pi ^t|\lambda ^t)||p(\pi ^t|p^t) \right] \end{aligned} \end{aligned}$$

(13)

As mentioned above, due to the difficulties in directly optimizing $p(D^t|\tilde{\pi }^t, \beta ^t, \alpha )$, inference for local variables $\theta$ and z can be done by using Mean-field variational inference as in the original paper (Blei et al., 2003). In particular, for each document d: $q(\theta _d, z_d|\gamma _d, \phi _d)=q(\theta _d|\gamma _d)\prod _{n \in [N_d]}q(z_{dn}|\phi _{dn})$ with the variational distributions: $q(\theta _d|\gamma _d) = Dirichlet(.|\gamma )$ and $q(z_{dn}|\phi _{dn})=Multinomial(.|\phi _{dn})$ where $\gamma _d$ and $\phi _d$ are variational parameters. According to Blei et al. (2003), these parameters for each document d are updated until convergence as follow:

$$\begin{aligned}&\gamma _{dk} \leftarrow \alpha _k + \sum _{n=1}^{N_d} \phi _{dnk} \text{ for } k=1,...,K \end{aligned}$$

(14)

$$\begin{aligned}&\phi _{dnk} \propto \exp (\mathbb {E}_q[\log \theta _{dk}] + \sum _{v=1}^V \mathbb {I}[w_{dn}=v]\log \tilde{\beta }_{kv}) \end{aligned}$$

(15)

where $[V] = \{1,...,V\}$, $\mathbb {I}[.]$ is an indicator function that equals 1 if the condition is true.

As the topics are independent, we consider the objective function with respect to $\beta _k^t$, $\lambda ^t_k$ and $p^t$:

$$\begin{aligned} \begin{aligned}&\{ \hat{\beta }_k^t, \hat{\phi }^t_k, \hat{\lambda }^t_k, \hat{p}^t_k\}\\&\quad = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t_k, \phi ^t_k, \lambda ^t_k, p^t_k} \left\{ \log p(\beta ^t_k|\beta ^{t-1}_k) + \sum _{d=1}^M \sum _{n=1}^{N_d} \log p(w_{dn}|z_{dn}, {\beta }^t_k, \tilde{\pi }^t_k) - KL[q(\pi ^t_k|\lambda ^t_k)||p(\pi ^t_k|p^t_k)] \right\} \\&\quad = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t_k, \phi ^t_k, \lambda ^t_k, p^t_k} \left\{ -\frac{1}{2\sigma ^2}\Vert \beta ^t_k - \beta ^{t-1}_k\Vert ^2_2 + \sum _{d=1}^M \sum _{n=1}^{N_d} \sum _{j=1}^V \phi _{dnk} \mathbb {I}[w_{dn}=j] \beta _{kj}^t \tilde{\pi }_{kj}^t \right. \\&\qquad \left. - \sum _{d=1}^M \sum _{n=1}^{N_d} \sum _{j=1}^V \phi _{dnk} \mathbb {I}[w_{dn}=j] \log (\sum _{i=1}^V \exp (\beta ^t_{ki}\tilde{\pi }^t_{ki})) - KL[q(\pi ^t_k|\lambda ^t_k)||p(\pi ^t_k|p^t_k)] \right\} \end{aligned} \end{aligned}$$

(16)

Algorithm 3 briefly describes the learning process of aiDropout for LDA.

4.2 Case study 2: when NB is the base model

NB is a popular supervised model for text classification. We will use NB as a base model to evaluate how our framework works in the streaming environment.

Suppose that each mini-batch consists of M documents, each document d contains $N_d$ words and belongs to a class $c_d \in \{1,2,...,C\}$. Each $c_d$ is generated by: $c_d \sim Multinomial(\alpha )$ in which $\alpha$ is a fixed symmetric vector, and finally $\beta$ of size $C \times V$ is the class distribution over V words in the vocabulary.

The generative process for each mini-batch t is as follows:

• 1. Draw $\beta ^t$: $\beta _c^t \sim N (\beta _c^{t-1}, \sigma ^2 I)$

• 2. Draw $\pi ^t$: $\pi ^t_{cj} \sim \text{ Bernoulli }(p^t_{cj})$

• 3. Calculate the class matrix: $\tilde{\beta }^t_{cj} = \text{ softmax }(\beta _c^t \odot \pi ^t_c)_j$

• 4. Each document d is drawn by:

  • (a) Choose the class label $c_d \sim \text{ Multinomial }(\alpha )$

  • (b) Draw nth word $w_{dn} \sim \text{ Multinominal }(\tilde{\beta }^t_{cd})$

Learning process:

At each mini-batch t, our goal is to maximize $\log p(\beta ^t|\beta ^{t-1}, p^t, c, D^t)$:

$$\begin{aligned} \begin{aligned} \hat{\beta }^t&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}, p^t, c, D^t) \right\} \\&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t, D^t|\beta ^{t-1}, p^t, c) \right\} \\&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + \log p(D^t|p^t, \beta ^t, c) \right\} \end{aligned} \end{aligned}$$

(17)

Same as (7), we have a lower bound on $\log p(D^t|p^t, \beta ^t, c)$:

$$\begin{aligned} \begin{aligned}&\log p(D^t|p^t, \beta ^t, c) \\&\quad = \log \sum _{\pi ^t} p(D^t, \pi ^t|p^t, \beta ^t, c) = \log \sum _{\pi ^t} q(\pi ^t|\lambda ^t) \frac{p(D^t, \pi ^t|p^t, \beta ^t, c)}{q(\pi ^t|\lambda ^t)}\\&\quad \ge \sum _{\pi ^t} q(\pi ^t|\lambda ^t) \log \frac{p(D^t, \pi ^t|p^t, \beta ^t, c)}{q(\pi ^t|\lambda ^t)} = \sum _{\pi ^t} q(\pi ^t|\lambda ^t) \log \frac{p(D^t|\pi ^t, \beta ^t, c)p(\pi ^t|p^t)}{q(\pi ^t|\lambda ^t)}\\&\quad = E_{q(\pi ^t|\lambda ^t)}\left[ \log p(D^t|\pi ^t, \beta ^t, c) \right] - KL\left[ q(\pi ^t|\lambda ^t)||p(\pi ^t|p^t) \right] \\&\quad \simeq \log p(D^t|\tilde{\pi }^t, \beta ^t, c) - KL\left[ q(\pi ^t|\lambda ^t)||p(\pi ^t|p^t) \right] \end{aligned} \end{aligned}$$

(18)

For each class c, the objective function with respect to $\beta ^t_c$ and $\lambda ^t_c$ is:

$$\begin{aligned} \begin{aligned}&\{\hat{\beta }^t_c, \hat{\lambda }^t_c, \hat{p}^t_c\} = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t_c, \lambda ^t_c, p^t_c} \left\{ \log p(\beta ^t_c|\beta ^{t-1}_c) + \left[ \sum _{d=1}^{D_c^t} \sum _{n=1}^{N_d} \log p(w_{dn} | c_d, \beta ^t_c, \tilde{\pi }^t_c)\right] \right. \\&\qquad \qquad \qquad \quad \left. - KL[q(\pi ^t_c|\lambda ^t_c)||p(\pi ^t_c|p^t_c)] \right\} \\&\qquad \qquad \qquad = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t_c, \lambda ^t_c, p^t_c} \left\{ -\frac{1}{2\sigma ^2}\Vert \beta ^t_c - \beta ^{t-1}_c\Vert ^2_2 + \sum _{d=1}^{D_c^t} \sum _{n=1}^{N_d} \sum _{j=1}^V \mathbb {I}[w_{dn}=j] \beta ^t_{cj} \tilde{\pi }^t_{cj} \right. \\&\qquad \qquad \qquad \quad \left. - N_c \log (\sum _{i=1}^V \exp (\beta _{ci}^t\tilde{\pi }^t_{cj})) - KL[q(\pi ^t_c|\lambda ^t_c)||p(\pi ^t_c|p^t_c)]\right\} \end{aligned} \end{aligned}$$

(19)

where $D_c^t$ includes all documents which belong to class c, $N_c$ is the total number of words in all documents belonging to class c. We use a gradient-based algorithm to maximize $F(\beta ^t_c, \lambda ^t_c, p^t_c)$ with respect to $\beta ^t_c, \lambda ^t_c, p^t_c$.

5 Discussions

In this section, we discuss some aspects of aiDropout. First, we analyse how existing frameworks and aiDropout deal with the stability-plasticity dilemma. Then, we present the role of Dropout in our framework and prove that aiDropout provides a data-dependent regularization.

5.1 The stability-plasticity dilemma

In this subsection, we investigate how different streaming learning frameworks trade off stability against plasticity in models similar to LDA,² i.e., how they balance between old and new information from data streams. In particular, SVB (Broderick et al., 2013) uses the variational parameter of the global variable $\beta ^t$ at mini-batch t, which we denote by $\lambda ^t$, as the parameter of the Dirichlet prior distribution at mini-batch $t+1$. In other words, for each $k \in \{1,\cdots ,K \}$, $\beta ^{t+1}_k$ has the prior distribution $Dir(\beta ^{t+1}_k | \lambda _k^t)$ (Dir is Dirichlet distribution). Then we have:

Theorem 1

In SVB: $\mathbb {E}[\beta _{kj}^{t+1}] = \beta _{kj}^t$ and $\text {Var}[\beta ^{t+1}_{kj}] \rightarrow 0$ as $t \rightarrow \infty$.

Proof

SVB (Broderick et al., 2013) proposes recursive updating of the variational distribution. For LDA (conjugate models, exponential family, i.i.d. data), the variational parameter $\lambda ^t$ of global variable $\beta ^t$ is updated by: $\lambda ^t = \lambda ^{t-1} + \tilde{\lambda }^t$, where $\lambda ^{t-1}$ is made available from the previous mini-batch and $\tilde{\lambda }^t$ is the learned information from the current mini-batch. In other words, $\lambda ^t$ is the addition of the learned information from all previous steps:

$$\begin{aligned} \lambda ^t = \tilde{\lambda }^t + \cdots + \tilde{\lambda }^1 + \lambda ^0 \end{aligned}$$

where:

$$\begin{aligned} \Vert \tilde{\lambda }^t \Vert _1&= \sum _{k=1}^K \sum _{j=1}^V \tilde{\lambda }^t_{kj} = \sum _{d \in D^t} \sum _{n=1}^{N_d} \sum _{k=1}^K \sum _{j=1}^V \phi _{dnk} \mathbb {I}[w_{dn} = j]\\&= \sum _{d \in D^t} \sum _{n=1}^{N_d} \sum _{k=1}^K \phi _{dnk} = \sum _{d \in D^t} N_d \ge 1 \end{aligned}$$

Therefore, $||\lambda ^t||_1 = \sum _{t=1}^T \sum _{d \in D^t} N_d \ge t$, which approaches infinity as t goes to infinity. When a new mini-batch $t+1$ arrives, $\lambda ^t$ will be used as the parameter of the prior: $p(\beta ^{t+1}_k | \lambda ^t_k) = Dir(.|\lambda ^t_k)$. This distribution has the expectation:

$$\begin{aligned} \mathbb {E}[\beta ^{t+1}_k] \propto \lambda ^t_k = \beta ^t_k \end{aligned}$$

and the variance:

$$\begin{aligned} \text {Var}[\beta ^{t+1}_{kj}] = \frac{\lambda ^t_{kj}(\sum _{i=1}^{V}\lambda ^t_{ki} - \lambda ^t_{kj})}{(\sum _{i=1}^{V}\lambda ^t_{ki})^2(\sum _{i=1}^{V}\lambda ^t_{ki} + 1)} \end{aligned}$$

which varies inversely with the size of $\lambda _k^t$. As $t \rightarrow \infty$, leading to $||\lambda ^t||_1 \rightarrow \infty$, we have $\text {Var}[\beta ^{t+1}_{kj}] \rightarrow 0$. $\square$

This problem is potentially present in SVB-PP (Masegosa et al., 2017), albeit $\lambda ^t$ takes longer to accumulate: $\lambda ^t = \rho \lambda ^{t-1} + (1 - \rho ) \eta + \tilde{\lambda }^t$, where $\rho$ is the forgetting factor $(0<\rho <1)$ and $\eta$ is the uninformative prior.

When this happens, SVB and SVB-PP expect the model at time $t+1$ to be nearly identical to the model at time t. This phenomenon essentially says that a model will evolve very slowly and have difficulties in learning new information, thus could not deal well with sudden changes in the environment.

aiDropout does not encounter this problem. In aiDropout, we have an easy mechanism to balance the information between old and new data. Indeed, to maximize the objective function $F(\beta ^t_k) = -\frac{1}{2\sigma ^2}||\beta ^t_k - \beta ^{t-1}_k||_2^2 + \log p(D^t|\tilde{\pi }^t_k, \beta ^t_k)$, we need to consider both components. While the first term encourages new model $\beta ^t$ to fluctuate around the previously learned $\beta ^{t-1}$, the latter allows model to accommodate information from new data $D^t$. In other words, aiDropout helps model to flexibly learn new information, while retaining relevant information from historical observations to maintain the stability.

The balancing ability of aiDropout is easily controlled by the variance $\sigma ^2$. The bigger $\sigma ^2$ is, the more we focus on learning new information, rather than keeping old information, and vice versa. This balance is unchanged throughout the learning process. Unlike aiDropout, SVB and SVB-PP cannot control this balance. Particularly, in LDA, SVB and SVB-PP become too rigid and unable to learn new information after receiving a large amount of data, due to the reason mentioned above.

5.2 The role of dropout in aiDropout

In streaming environments, the problem of noisy and sparse data is unavoidable. Specifically, learning from noisy data can potentially overfit models, while sparsity in data may not provide enough relevant information to make good predictions for unseen data, both leading to poor performance.

To overcome these challenges, we propose to utilize Dropout by omitting randomly a number of elements of the global variable $\beta ^t$ at each mini-batch t. Dropout in our framework has two main roles. Firstly, we theoretically prove that it plays as a data-dependent regularizer, which makes aiDropout more robust against overfitting. Moreover, in our framework, Dropout is used throughout the data stream, leading to a special effect, which is ensemble learning. Indeed, at each mini-batch in the training process, the use of Dropout is equivalent to sampling a single learner from a set of $2^{K \times V}$ possible learners. Then, by rescaling $\beta ^t$ with $\mathbb {E}[\pi ^t]$, $2^{K \times V}$ learners with shared parameters can be combined into a single learner to be used at test time. Therefore, methodically, we would like to remark that there is not much difference between the dropout technique in aiDropout and the original one used widely in deep learning. However, we also agree that there would be certain differences in terms of the ensembling efficiency. Concretely, in deep neural nets, the desirable effect of Dropout ensemble could be interpreted well via the functional behaviors (such as diversity, mutual explanation) of the predictive distribution. Whilst the similar effect in our method needs further investigation for better understanding.

The ability to prevent overfitting and the ensemble property make iDropout have better generalization on future data, which is specially important in streaming learning, because data streams can be non-stationary and have high uncertainty.

5.3 Dropout in aiDropout as adaptive data-dependent regularization

The learning process at each mini-batch in aiDropout for LDA and NB can be reduced to maximizing the objective function of the following form:

$$\begin{aligned} F&= -\frac{1}{2\sigma ^2}||\beta _k - \beta _k^{prev}||_2^2 + \sum _{j=1}^{V} u_{kj} \mathbb {E}_{q(\pi _k|\lambda _k)} \log \big (\text {softmax}(\beta _k \odot \pi _k)_j \big ) \nonumber \\&\qquad - KL[q(\pi _k|\lambda _k)||p(\pi _k|p_k)] \end{aligned}$$

(20)

where $\beta _k^{prev}$ is made available from the previous mini-batch, $\lambda _k$ is the drop rate that needs to be learned on the current mini-batch (we omit superscript t for simplicity) and $u_{kj}$ is defined as follows:

$$\begin{aligned} u_{kj} = \left\{ \begin{aligned}&\sum _{d=1}^{M} \sum _{n=1}^{N_d}\phi _{dnk} \mathbb {I}[w_{dn} = j] \text { in LDA } \\&\sum _{d \in D_c^t} \sum _{n=1}^{N_d} \mathbb {I}[w_{dn} = j] \text { in NB } \end{aligned} \right. \end{aligned}$$

Consider $x_1, \cdots , x_K$ as K-dimension one-hot vectors ($x_k$ has only kth element activated) and $\beta = [\beta _1 \beta _2 \cdots \beta _V]$ where $\beta _j$ is jth column of matrix $\beta$, then:

$$\begin{aligned} \text {softmax}(\beta _k)_j = \exp (s_{kj} - A(s_k)) \end{aligned}$$

with $s_{kj} = \beta _{j}^T x_k$ is a undropped score value and $A(s_k) = \log \sum _{i=1}^V \exp (s_{ki})$ is the log-partition function.

Assume $\pi _k$ is drawn from $q(\pi _k|\lambda _k)$ which is a Bernoulli distribution parameterized by $\lambda _k$, corresponding to the Inverted Dropout:

$$\begin{aligned} q(\pi _{ij} = {1}/{(1 - \lambda _k)} | \lambda _k) = 1 - \lambda _k, q(\pi _{ij} = 0 | \lambda _k) = \lambda _k \end{aligned}$$

then $\mathbb {E}_{q(\pi _k|\lambda _k)}[\pi _{kj}] = 1$, and:

$$\begin{aligned} \text {softmax}(\beta _k \odot \pi _k)_j = \exp (\tilde{s}_{kj} - A(\tilde{s}_k)) \end{aligned}$$

with $\tilde{s}_{kj} = (\beta _i \odot \pi _i)^T x_k$, $A(\tilde{s}_k) = \log \sum _{i=1}^V \exp (\tilde{s}_{ki})$. Using this notation, we can write F as:

$$\begin{aligned} F = -\frac{1}{2\sigma ^2}||\beta _k - \beta _k^{prev}||_2^2 + \sum _{j=1}^{V} u_{kj} \mathbb {E}_{q(\pi _k|\lambda _k)}[\tilde{s}_{kj} - A(\tilde{s}_k)] - KL[q(\pi _k|\lambda _k)||p(\pi _k|p_k)] \end{aligned}$$

Since $\mathbb {E}_{q(\pi _k|\lambda _k)}[\pi _{kj}] = 1$ so the dropout technique preserves mean, leading to $\mathbb {E}_{q(\pi _k|\lambda _k)}[\tilde{s}_{kj}] = s_{kj}$, we have:

$$\begin{aligned} \mathbb {E}_{q(\pi _k|\lambda _k)}[\tilde{s}_{kj} - A(\tilde{s}_k)]&= s_{kj} - A(s_k) - (\mathbb {E}_{q(\pi _k|\lambda _k)}[A(\tilde{s}_k)] - A(s_k)) \\&= \text {softmax}(\beta _k)_j - (\mathbb {E}_{q(\pi _k|\lambda _k)}[A(\tilde{s}_k)] - A(s_k)) \end{aligned}$$

Then we can write:

$$\begin{aligned} F =&-\frac{1}{2\sigma ^2}||\beta _k - \beta _k^{prev}||_2^2 + \sum _{j=1}^{V} u_{kj} \log \big (\text {softmax}(\beta _k)_j \big )\\&- (\mathbb {E}_{q(\pi _k|\lambda _k)}[A(\tilde{s}_k)] - A(s_k)) \sum _{j=1}^{V} u_{kj} - KL[q(\pi _k|\lambda _k)||p(\pi _k|p_k)] \end{aligned}$$

Since the log-partition function A(.) is convex, $(\mathbb {E}_{q(\pi _k|\lambda _k)}[A(\tilde{s}_k)] - A(s_k))$ is always positive by Jensen’s inequality and can therefore be interpreted as a regularizer. Indeed, applying second-order Taylor approximation to $A(\tilde{s}_k)$ around the undropped score vector $s_k$, we have means and covariances of the dropout features:

$$\begin{aligned} A(\tilde{s}_k) = A(s_k)&+ \nabla A(s_k)^T(\tilde{s}_k - s_k) + \frac{1}{2}(\tilde{s}_k - s_k)^T\nabla ^2 A(s_k)(\tilde{s}_k - s_k) \end{aligned}$$

then we obtain a following regularizer:

$$\begin{aligned}\mathbb {E}_{q(\pi _k|\lambda _k)}[A(\tilde{s}_k)] - A(s_k) &= \frac{1}{2}\mathbb {E}_{q(\pi _k|\lambda _k)}[(\tilde{s}_k - s_k)^T\nabla ^2A(s_k)(\tilde{s}_k - s_k)] \\& = \frac{1}{2}\text {Tr}[\nabla ^2 A(s_k) \text {Cov}_{q(\pi _k|\lambda _k)}(\tilde{s}_k)] = \frac{1}{2} \sum _{j=1}^{V} \mu _{kj}(1 - \mu _{kj})\text {Var}_{q(\pi _k|\lambda _k)}[\tilde{s}_{kj}] \\& = \frac{1}{2} \sum _{j=1}^{V} \mu _{kj}(1 - \mu _{kj}) \beta _j^T \text {Cov}_{q(\pi _k|\lambda _k)}(x_k)\beta _j \end{aligned}$$

where $\mu _{kj} = \text {softmax}(s_k)_j$ is the model probability, the variance $\mu _{kj}(1-\mu _{kj})$ measures model uncertainty, and

$$\begin{aligned} \beta _j^T \text {Cov}_{q(\pi _k|\lambda _k)}(x_k)\beta _j = \sum _{m=1}^{K} \frac{\lambda _k}{1-\lambda _k}x^2_{km}\beta _{mj}^2 = \frac{\lambda _k}{1-\lambda _k}\beta _{kj}^2 \end{aligned}$$

Hence, $\mathbb {E}_{q(\pi _k|\lambda _k)}[A(\tilde{s}_k)] - A(s_k) = \frac{\lambda _k}{2(1-\lambda _k)}\sum _{j=1}^{V}\mu _{kj}(1-\mu _{kj})\beta _{kj}^2$ has quadratic format w.r.t $\beta _k$. In other words, the effect of Dropout in aiDropout is equivalent to a L2-regularization $R(\beta )$:

$$\begin{aligned} R(\beta )&= (\mathbb {E}_{q(\pi _k|\lambda _k)}[A(\tilde{s}_k)] - A(s_k)) \sum _{j=1}^{V} u_{kj} \\&= \frac{\lambda _k}{2(1-\lambda _k)} \sum _{j=1}^{V}\bigg [\mu _{kj}(1-\mu _{kj})\sum _{j=1}^{V} u_{kj}\bigg ]\beta _{kj}^2. \end{aligned}$$

This is a theoretical interpretation on the ability of iDropout to reduce overfitting. Unlike other regularization techniques, each $\beta _{kj}$ in aiDropout has a different regularization parameter $\frac{\lambda _k}{2(1-\lambda _k)}\mu _{kj}(1 - \mu _{kj})\sum _{j=1}^{V}u_{kj}$, depending on the input data. This is interesting, since this data-dependent regularization allows each $\beta _{kj}$ to have its own search space to catch the geometric property of data. With this property, dropout in our method is more effective than other standard computationally inexpensive regularizers, such as weight decay, filter norm constraints and sparse activity regularization (Goodfellow et al., 2016).

6 Empirical evaluation

This section will present extensive experiments to evaluate how our methods (iDropout and aiDropout) and baselines deal with two challenges: Short and noisy texts and stability-plasticity dilemma. In terms of short and noisy texts, we use two popular scenarios: Evaluating on a hold-out test set and evaluating on consecutive arriving mini-batches. The former scenario (Broderick et al., 2013; McInerney et al., 2015) is often used to examine the performance of the methods in simulated streaming environments on datasets without time stamp. Meanwhile, the latter scenario (Masegosa et al., 2017, 2020) helps evaluate them on actual streaming environments. Regarding stability-plasticity dilemma, we investigate how the methods deal with concept drift and forgetting the knowledge learned from past data.

6.1 Baselines

We compare aiDropout³ to iDropout (Nguyen et al., 2019), SVB (Broderick et al., 2013), SVB-PP (Masegosa et al., 2017),⁴ PVB (McInerney et al., 2015). We select the best result of each method by using grid search. The range of each parameter is as follows:

• the forgetting factor $\rho \in \{0.5, 0.6, 0.7, 0.8, 0.9, 0.99 \}$ for SVB-PP.

• the population size $\nu \in \{10^3, 10^4, 10^5, 10^6, 5.10^3, 5.10^4, 5.10^5, 5.10^6 \}$ and dimming factor $\kappa \in \{0.5, 0.6, 0.7, 0.8, 0.9 \}$ for PVB.

• the variance $\sigma ^2 \in \{0.01, 0.1, 1, 10, 100 \}$ and the drop rate $dr \in \{0, 0.15, 0.25, 0.35 \}$ for iDropout.

• the variance $\sigma ^2 \in \{0.01, 0.1, 1, 10, 100 \}$, the hyperparameter of the Gumbel-Softmax distribution $\tau = 0.01$ for aiDropout.

Moreover, for iDropout and aiDropout, the gradient-based algorithm is Adagrad with learning rate 0.01, the maximum number of Adagrad iterations 100, and the number of iterations between the updating phases of local and global parameters in each mini-batch is set to 10.

Table 1 Six datasets without time stamp

6.2 Experiments on noisy and sparse data

To evaluate how the methods deal with noisy and sparse data, we conduct extensive experiments with both chronological and non-chronological datasets. While the two chronological datasets (The Irish Times and News Aggregator) have available published time for each document, the six non-chronological datasets do not have this information. On the non-chronological datasets, we follow the experimental scenarios of prior studies (Nguyen et al., 2021; Broderick et al., 2013; Duc et al., 2017; McInerney et al., 2015; Van et al., 2022) to create a sequence of mini-batches for training and a hold-out set for evaluating after having finished traininig each mini-batch. The experiments not only show how the methods deal with sparse and noisy data but also consider the stability of the methods when they are evaluated on the same hold-out test set. Meanwhile, we follow the experimental scenarios of recent studies (Masegosa et al., 2017, 2020; Van et al., 2022) on the two chronological datasets to examine how the methods work on actual noisy and sparse data streams.

6.2.1 Experiments on datasets without time stamp

Base model and datasets: In this subsection, we use LDA as our base model. As mentioned in Sect. 4, LDA, a popular Bayesian model, is widely applied to uncover hidden topics. We analyze how the methods deal with sparse and noisy data by using six non-chronological datasets, including two long text datasets (20Newsgroups,⁵ Grolier)⁶ and four short text ones (TagMyNews (TMN),⁷ TagMyNews-title (TMN-title), Yahoo-title, NYT-title⁸ with some statistics in Table 1.

Settings: To simulate streaming data, we randomly shuffle and then divide each dataset into a sequence of mini-batches with batchsize: 500 for Grolier, 20Newsgroups, TMN, TMN-title; 5000 for NYT-title, Yahoo-title. We set prior of topic mixture $\alpha = 0.01$; the number of topic $K = 50$ for Grolier, 20Newsgroups, TMN, TMN-title; $K = 100$ for NYT-title, Yahoo-title. We note that batchzise and the number of topics are selected based on the sizes of datasets. We can consider the stability of our methods (aiDropout and iDropout) compared to the others when they are evaluated on the same hold-out test set after having finished training each mini-batch. Moreover, we conduct experiments with different dropout rates $(dr \in \{0; 0.15; 0.25; 0.35\})$ for iDropout to show the sensitivity of iDropout w.r.t dropout rate.

Evaluation metric: Log Predictive Probability (LPP) (Hoffman et al., 2013) and Normalized Pointwise Mutual Information (NPMI) (Bouma, 2009) are used. While LPP measures the generalization of a model on unseen data, NPMI is used to examine the coherence and interpretability of the learned topics. LPP calculates the probabilities of a part of a test document given the remaining part and trained model’s parameters. NPMI is based on the co-occurrence of pairs of top words of learned topics. The details on the calculation of these two metrics are given in the Appendix B.

Experimental results:

Figure 2 shows the performance of all methods. The results of aiDropout roughly approximate that of iDropout and are better than the others. For short text datasets (NYT-title, Yahoo-title,TMN, and TMN-title), it is quite likely to encounter the unwanted properties of data such as noise and sparsity in these datasets. While noisy data may lead to overfitting, sparse data causes the model to make wrong predictions due to the lack of information. Thanks to the benefits of dropout, our methods can address this problem effectively. In contrast, the other methods do not have efficient ways to deal with this issue, hence give poor performance. The LPPs and NPMIs of baselines reduce significantly although more mini-batches arrive. It means that the baselines suffer from overfitting on short and noisy datasets. We also consider the performances of the methods on long (regular) text datasets (20Newsgropus and Grolier). It is obvious that the baselines do not suffer from decreasing both LPP and NPMI when more data comes. SVB and SVB-PP become too stable once received large enough data. This may explain why the results of these two methods are roughly unchanged. It can be seen that PVB does not encounter this problem and has a considerable evolution over time. Our proposed methods also overcome this issue and have superior results.

Fig. 2

Performance of the 5 methods on datasets without time stamp. LDA is the base model. Higher is better

Figure 3 shows the results of LPP measurement on aiDropout and iDropout with different drop rates($dr \in \{0, 0.15, 0.25, 0.35\}$). It can be seen that aiDropout with adaptive drop rate has different effects on different datasets. It is remarkable to see that with four short text datasets (NYT-title, Yahoo-title,TMN, and TMN-title) that have two typical properties in streaming data, i.e., noise and sparsity, the results of aiDropout outperform that of iDropout with most drop rates. This may be explained that while iDropout with fixed drop rate is not flexible in handling noisy and sparse data, aiDropout enables the drop rate to be automatically adapted along the change in data. However, with two long text datasets (20Newsgropus and Grolier), aiDropout seems not to work as well as itself with the short datasets. This results could be clarified that as training on these long datasets does not severely meet the problem of noise and sparsity, learning the drop rate does not give a significant improvement.

Fig. 3

Performance of aiDropout compared to iDropout with different drop rates. LDA is the base model. Higher is better

6.2.2 Experiments on datasets with time stamp

Base model and datasets: In this subsection, LDA is used as a base model for topic modeling and NB for classification. We will study how the methods work on actual data streams on two chronological datasets which are The Irish Times dataset⁹ and News Aggregator dataset.¹⁰ Particularly, The Irish Times corpus contains 1376099 data instances from 02/01/1996 to 31/12/2017 with 6 classes and its vocab size is 25328. News Aggregator dataset includes 422937 news stories between 10/03/2014 and 10/08/2014 with 4 classes and its vocab size is 25509.

Settings: When evaluating using LDA, we simply throw away labels and use $K = 100$ and $\alpha = 0.01$. We also divide the whole datasets into mini-batches in which each mini-batch corresponds to a month in The Irish Times and two consecutive days in News Aggregator. To find out how our proposed frameworks act in streaming environments compared with other methods, we use documents of the next mini-batch to evaluate the model at any mini-batch. Additionally, we also study on how sensitive iDropout is when dropout rate is tuned, particularly we set $dr \in \{0; 0.1; 0.3; 0.5\}$ with The Irish Times dataset and $dr \in \{0; 0.2; 0.4; 0.6; 0.8\}$ with News Aggregator dataset when NB is base model.

Evaluation metric: We use LPP to evaluate the learned topic model in LDA and accuracy to evaluate the classification performance in NB.

Fig. 4

Performance of the 5 methods on datasets with time stamp. LDA is the base model. Higher is better

Experimental results on LDA: The results are shown in Fig. 4. It is clear that our methods with dropout outperform the others. Comparing the results of aiDropout and iDropout on both of the two datasets, we see that while the performance of aiDropout on The Irish Times is much better than that of iDropout, the two frameworks give similar results on News Aggregator. This could be due to the small number of mini-batches, and the fairly large number of data points per mini-batch on News Aggregator, hence the aiDropout cannot enhance significantly compared to the one with fixed drop rate. It can also be easily seen that the methods with no dropout suffer from overfitting and decline in performance as learning from more data, especially SVB. In contrast, our proposed methods with dropout demonstrate the effectiveness of handling overfitting. This may be explained that because both two datasets are short-text and contain unwanted properties such as noise and sparsity, the use of dropout helps our methods reduce overfitting, and hence obtains better generalization.

Fig. 5

Performance of the 5 methods on datasets with time stamp. NB is the base model. Higher is better

Fig. 6

Performance of aiDropout compared to iDropout with different drop rates. NB is the base model. Higher is better

Experimental results on NB:

Figure 5 shows the performance of five methods on classfication task. In particular, the results of aiDropout are slightly better than that of iDropout. Compared to the others with no dropout, the performance of aiDropout with adaptive drop rate gets about 6–8% better than SVB, and about 3–4% better than SVB-PP and PVB on The Irish Times, about 5–6% better than SVB and SVB-PP, and about 1–2% better than PVB on News Aggregator. It is clear that dropout plays a crucial role in helping our framework work effectively in data streams. We also notice that about the 175th mini-batch on The Irish Times dataset, the results of all methods drop due to abnormal changes. Again, thanks to the benefits of dropout, our proposed methods do not fall too deeply and then recover quickly to keep leading on the successive mini-batches.

Figure 6 shows the accuracy for aiDropout and iDropout with different settings of drop rate ($dr \in \{0, 0.1, 0.3, 0.5 \}$ with The Irish Times, and $dr \in \{0.2, 0.4, 0.6, 0.8\}$ with News Aggregator). We observe that the performance of aiDropout is slightly higher than that of iDropout with the best drop rate setting (dr = 0.5 with The Irish Times, and dr = 0.2 with News Aggregator), and outperforms the others. Specifically, the datasets used in this experiment are short-text, and hence contain significant undesirable properties such as noise and sparsity. Our framework with adaptive drop rate tends to work more flexibly than the fixed drop rate based method when dealing with this problem. It can also be seen that there is not much difference between the performance of aiDropout and various settings of iDropout on News Aggregator compared to The Irish Times. It seems that when the number of mini-batches on News Aggregator is small and the number of data points per mini-batch is quite large, aiDropout and iDropout can obtain similar results.

6.3 Balancing stability and plasticity

In this subsection, we consider how the methods balance stability and plasticity when training on data streams. We design experimental scenarios with various kinds of concept drifts to evaluate the plasticity of the methods for adapting to new concepts. Meanwhile, we examine the forgetting phenomenon of the methods to evaluate their stability.

6.3.1 Evaluation on sudden concept drift

Fig. 7

Performance of the methods when facing with sudden concept drift on The Irish Times and News Aggregator datasets. LDA is the base model. Higher is better

The problem in which the underlying relationships in the data change suddenly is referred to as sudden concept drift (Gama et al., 2014; Krawczyk & Cano, 2018). This issue is very likely to be encountered in streaming data. We evaluate how well our frameworks and other methods deal with abrupt changes in data streams. In appendix C, we present how the methods face incremental and recurring concept drifts (Krawczyk & Cano, 2018).

Base model and settings: We use LDA with $K=100$ and $\alpha = 0.01$ as our base model and two datasets (News Aggregator and The Irish Times) for this experiment. Each dataset is split into mini-batches, each mini-batch contains 2000 documents of a particular class, and all mini-batches of the same class are placed adjacent to each other. Therefore, concept drift happens noticeably when data transfers from one class to another. After learning on each mini-batch, the model is evaluated by computing LPP on the next mini-batch.

Experimental results: The result is illustrated in Fig. 7. It is clear that after each drift point, SVB recovers slowly and gives poor performance when encountering concept drift. SVB-PP and PVB seem to adapt better to concept drift. While SVB-PP uses a forgetting factor which allows it to learn new information from new data, the variance of the variational posterior in PVB never decreases below a given threshold indirectly controlled by population size $\alpha$ that helps adapt to concept drift. iDropout gets better result compared to the mentioned methods. This may be easily explained that iDropout has the balance mechanism which enables it to learn new underlying distribution of data. In addition, thanks to the ability to reduce overfitting and the ensemble property of dropout, the fixed drop rate based method can obtain better generalization, and hence prevent the performance from falling too deeply when facing the concept drift problem. Finally, aiDropout outperforms the others significantly. This result may be due to the drop rate adaptation over time. Particularly, The Irish Times and News Aggregator datasets are short-text datasets that can contain undesirable properties, such as noise and sparsity. aiDropout enables the drop rate to be adaptively learned corresponding to the changes in arriving data, thereby it addresses the problem of noisy and sparse data in streaming data better than the method with a fixed drop rate.

Next, we examine the methods’ behaviors more thoroughly when dealing with concept drift. Following by Guzy and Woźniak (2020) and Shaker and Hüllermeier (2015), we evaluate the five methods in terms of the lowest LPP achieved in a drift area, the median LPP in each concept, and restoration time for each new concept. While the lowest LPP shows the performance of methods when a new concept has just appeared, the median LPP illustrates the ability to learn this new concept from all data. Meanwhile, restoration time shows the number of required mini-batches for a method to achieve back good performance after appearing a new concept. For each new concept, restoration time $T_R$ is calculated as follow:

$$\begin{aligned} T_R = \frac{t_2-t_1}{T} \end{aligned}$$

(21)

where $t_1$ is a mini-batch where the LPP drops below $95\%$ of the median LPP of an old concept, $t_2$ is a mini-batch where the LPP achieves $95\%$ of the mean LPP of the next concept, and T is the total number of mini-batches. We use again the available source code¹¹ from Guzy and Woźniak (2020) to compute the mentioned measures.

Table 2 shows the performance of the five methods in terms of the average of lowest LPP, median LPP, and restoration time on all times that concepts happen. In terms of the lowest LPP, both aiDropout and iDropout achieve significantly better results than PVB, SVB-PP, and SVB. It means that aiDropout and iDropout can work better than the remaining methods on data from a new concept without any training on this concept. After that, many mini-batches arrive, the LPPs of all methods increase considerably Fig. 7. Therefore, their median LPPs are noticeably higher than their lowest LPPs, respectively. Because aiDropout and iDropout have high uncertainty, they can learn new concepts well. Thus, their LPPs are higher than PVB, SVB-PP, SVB. Moreover, aiDropout uses adaptive droprate, and it obtains a better median LPP than iDropout. It is obvious that online Bayesian updating (such as SVB Broderick et al., 2013) often suffers from the phenomenon of overconfident posterior after receiving a large enough amount of data. Consequently, it cannot learn new concepts well. After the LPPs of SVB drop significantly (the lowest LPP is low) when concept drift happens, its median LPP does not increase significantly in comparison with the lowest LPP. SVB-PP and PVB alleviate this issue, however, they do not achieve good results as aiDropout and iDropout. Regarding restoration time, aiDropout achieves the smallest value among the five methods. It means that aiDropout requires the smallest number of mini-batches to work well on a new concept in comparison with the remaining methods. Meanwhile, iDropout restore more quickly than PVB, SVB-PP, and SVB on the News Aggregator dataset, but it needs more mini-batchs on the Irish Times dataset. It is acceptable when iDropout achieves significantly better median LPP than PVB, SVB-PP, and SVB.

Table 2 The lowest LPP, median LPP, and restoration time of the five methods when dealing with sudden concept drifts

6.3.2 Catastrophic forgetting phenomenon when training LDA on data streams

Fig. 8

Catastrophic forgetting phenomenon when training LDA on data streams. LPP is averagely calculated on hold-out test sets of past classes. Higher is better

In this subsection, we examine the stability of the methods in streaming environments. The methods often deal with the problem of forgetting knowledge acquired from past data, known as catastrophic forgetting phenomenon (Ahn et al., 2019; Ebrahimi et al., 2020; Kirkpatrick et al., 2017; Nguyen et al., 2018), when training on new data. This phenomenon is studied carefully in the continual learning field where a method must learn multiple tasks consecutively. We follow the experimental scenarios of continual learning to evaluate the catastrophic forgetting phenomenon of the methods. In detail, learning hidden topics in each class is considered as a task and tasks are learned consecutively as in the experimental scenarios of the sudden concept drift on News Aggregator and The Irish Times datasets. However, we create a hold-out test set (2000 short texts) for each class. The average LPP on the hold-out test sets of past classes is calculated after finishing training each class. The predictive ability of a method on past data shows how it deals with the forgetting problem.

Figure 8 presents the average LPP of the methods. It is obvious that forgetting phenomenon is unavoidable for artificial intelligence as well as human beings. The average LPPs of the methods decrease when training new tasks. Albeit both iDropout and aiDropout suffer from catastrophic forgetting, their average LPPs are superior to these of remaining methods. Because our methods learn each task well and outperform the others with significant magnitudes. Moreover, some studies (De Lange et al., 2021; Goodfellow et al., 2013) practically investigated dropout in continual learning and they showed that dropout can reduce the catastrophic forgetting phenomenon. Meanwhile, according to our theoretical analyses, SVB is the most stable, therefore, the average LLPs of SVB reduce the least on both of the two datasets. While SVB-PP and PVB deal better with concept drift than SVB, they forget previous tasks more considerably than SVB. These results demonstrate stability-plasticity dilemma that all the methods must face with.

7 Conclusion

In this paper, we aim to develop a framework which helps learn a wide range of Bayesian models on data streams. We focus on two popular challenges: Noisy and sparse data and stability-plasticity dilemma to build an effective streaming method. We propose aiDropout, a novel and straightforward framework, which is based on the transition model and adaptive dropout technique to address these challenges. The transition model creates a simple mechanism to balance knowledge learned from past data and current data. In spite of simplicity, aiDropout avoids being too stable to learn new concepts. Meanwhile, the adaptive dropout brings the properties of data-dependent regularization and ensemble learning to tackle the stability-plasticity dilemma as well as handle noisy and sparse data. The extensively experimental results shows that aiDropout prevents overfitting which prior methods suffer when training in noisy and sparse data. Although the performance of aiDropout decreases dramatically when new concepts happen, aiDropout is still significantly better than other methods. Then, the performance of aiDropout increases more quickly as well as significantly than those of other methods. Moreover, our framework achieves better performances than the baselines in facing catastrophic forgetting phenomenon.

In the future, we will focus on three topics to make aiDropout more effective and impactful. Firstly, our framework needs to manually tune the parameter of the transition model $\sigma$. Therefore, a solution to automatically learn this parameter will make aiDropout more practical in actual streaming environments. Secondly, in this paper, aiDropout is merely applied to the two Bayesian models: LDA and Multinomial naive Bayes for text mining. We will aim to exploit aiDropout for recommender systems that also deals with the noise and sparse rating matrix. Finally, this work only focuses on learning one task on data streams. In the next work, we will consider how our framework deals with multiple tasks in online continual learning.

Appendices

A iDropout for LDA and NB

1.1 A.1 When LDA is the base model

Learning process: Inference for local variables $\theta$ and z can be done as in aiDropout. We only consider the objective function with respect to $\beta _k^t$:

$$\begin{aligned} F(\beta ^t_k) =&\log p(\beta ^t_k | \beta ^{t-1}_k) + \sum _{d=1}^{M} \sum _{n=1}^{N_d} \log p(w_{dn} | z_{dn}, \tilde{\beta }^t) \nonumber \\ =&-\frac{1}{2\sigma ^2} ||\beta _k^t - \beta ^{t-1}_k||^2 + \sum _{d=1}^{M} \sum _{n, j=1}^{N_d, V} \phi _{dnk} \mathbb {I}[w_{dn} = j]\log \tilde{\beta }^t_{kj} \nonumber \\ =&-\frac{1}{2\sigma ^2} ||\beta _k^t {-}\beta ^t_{k-1}||^2 + \sum _{d=1}^{M} \sum _{n, j=1}^{N_d, V} \phi _{dnk} I[w_{dn} = j] \beta ^t_{kj}\pi ^t_{kj} \nonumber \\&-\sum _{d=1}^{M} \sum _{n, j=1}^{N_d, V} \phi _{dnk} I[w_{dn} = j] \log (\sum _{i=1}^{V} \exp (\beta ^t_{ki} \pi ^t_{ki})) \end{aligned}$$

(22)

The objective function F is guaranteed to be concave. In deed, $-\frac{1}{2\sigma ^2}||\beta _k^t - \beta ^{t-1}_k||^2$ and $\beta ^t_{kj}\pi ^t_{kj}$ are obviously concave with respect to $\beta ^t_k$, while the log-sum-exp is also a well-known convex function. Therefore, $F(\beta ^t_k)$ is concave with respect to $\beta ^t_k$, and we can find its maximum by applying gradient ascent on F. We sum up the learning algorithm of iDropout for LDA in Algorithm 4.

1.2 When NB is the base model

The generative process for each mini-batch t is as follows. Firstly, draw the global variable $\beta ^t$: $\beta ^t_c \sim \mathcal {N}(\beta ^{t-1}_c, \sigma ^2I)$ and calculate the class matrix: $\tilde{\beta }_{cj}^t = \text {softmax}(\beta _c^t \odot \pi _c^t)_j$. Each document d is drawn by first choosing the class label $c_d \sim Mult(\alpha )$ and then drawing nth word $w_{dn} \sim Mult(\tilde{\beta }^t_{c_d})$.

Learning process: For each class c, the objective function with respect to $\beta ^t_c$ is:

$$\begin{aligned} F(\beta ^t_c) =&\log p(\beta ^t_c | \beta ^{t-1}_c) + \sum _{d \in D_c^t} \sum _{n=1}^{N_d} \log p(w_{dn} | c_d, \tilde{\beta }^t)\\ =&-\frac{1}{2\sigma ^2}||\beta ^t_c - \beta ^{t-1}_c||_2^2 + \sum _{d \in D_c^t} \sum _{n=1}^{N_d} \sum _{j=1}^{V} \mathbb {I}[w_{dn} = j] \log \tilde{\beta }^t_{cj} \\ =&-\frac{1}{2\sigma ^2}||\beta ^t_c - \beta ^{t-1}_c||_2^2 + \sum _{d \in D_c^t} \sum _{n=1}^{N_d} \sum _{j=1}^{V} \mathbb {I}[w_{dn} = j]\beta ^t_{cj}\pi ^t_{cj} - N_c\log (\sum _{i \in [V]} \exp (\beta ^t_{ci} \pi ^t_{ci}) \big ) \end{aligned}$$

where $D^t_c$ includes all documents which belong to class c, $N_c$ is the total number of words in all documents belonging to class c. Learning for NB is very simple. At each mini-batch t, we use gradient ascent to maximize $F(\beta _c^t)$ with respect to $\beta _c^t$.

B Evaluation metrics for the unsupervised task

Log predictive probability (Hoffman et al., 2013): Predictive Probability measures the predictiveness and generalization of a model on new data. Assume that after learning from training data $D_{train}$, we obtain the model parameter $\beta$. For each document in testing $D_{test}$ with more than or equal to 5 words, we divide randomly into two disjoint parts $\mathbf {w_{obs}}$ and $\mathbf {w_{ho}}$ with a ratio of 80:20. We next do inference for $\mathbf {w_{obs}}$ to estimate $\theta ^{obs}$. Then, we approximate the predictive probability $\mathbf {w_{ho}}$ as:

$$\begin{aligned} p(\mathbf {w_{ho}} \mid \mathbf {w_{obs}}, \beta )&= \prod _{w \in \mathbf {w_{ho}}} p(w \mid \mathbf {w_{obs}}, \beta ) \\&\approx \prod _{w \in \mathbf {w_{ho}}} p(w \mid \theta ^{obs}, \beta ) \\&= \prod _{w \in \mathbf {w_{ho}}} \sum _{k=1}^K p(w \mid z=k, \beta )p(z=k\mid \theta ^{obs}) \\&= \prod _{w \in \mathbf {w_{ho}}} \sum _{k=1}^K {\theta ^{obs}_k\beta _{kw}} \end{aligned}$$

Then Log Predictive Probability of each document d is:

$$\begin{aligned} LPP_d = \frac{\log p(\mathbf {w_{ho}} \mid \mathbf {w_{obs}}, \beta )}{|\mathbf {w_{ho}}|} \end{aligned}$$

(23)

(with $|\mathbf {w_{ho}}|$ is the length of d in $\mathbf {w_{ho}}$) and on the whole testing $D_{test}$ is:

$$\begin{aligned} \text {Log Predictive Probability} = \frac{\sum _{d \in D_{test}} LPP_d}{|D_{test}|} \end{aligned}$$

(24)

Log Predictive Probability was averaged from 5 random splits, each was on 1000 documents.

Normalized Pointwise Mutual Information (Bouma, 2009): NPMI is the measure to help us see the coherence or semantic quality of individual topics. For each topic k, we pick a set $\mathbf {w^k} = \{w^k_1, w^k_2,..., w^k_t\}$, including t words with the highest probabilities in topic distribution $\beta _k$. NPMI of one topic k is computed as follows:

$$\begin{aligned}&\text {NPMI}(k, \mathbf {w^k}) = \frac{2}{t(t-1)} \sum _{i=2}^t\sum _{j=1}^{i-1}\frac{\log \frac{p(w^k_i, w^k_j)}{p(w^k_i)p(w^k_j)}}{-\log p(w^k_i, w^k_j)} \\&\quad \approx \frac{2}{t(t-1)} \sum _{i=2}^t\sum _{j=1}^{i-1}\frac{\log \frac{D(w^k_i, w^k_j) + 10^{-2}}{D} - \log \frac{D(w^k_i)D(w^k_j)}{D^2}}{-\log \frac{D(w^k_i, w^k_j) + 10^{-2}}{D}} \\&\quad = \frac{2}{t(t-1)} \sum _{i=2}^t\sum _{j=1}^{i-1} -1 + \frac{2\log D - \log D(w^k_i) - \log D(w^k_j)}{\log D - \log (D(w^k_i, w^k_j) + 10^{-2})} \end{aligned}$$

where D is the total number of documents, $D(w^k_i)$ is the number of docs containing $w^k_i$, $D(w^k_i, w^k_j)$ is the number of docs containing pair $(w^k_i, w^k_j)$.

Overall, NPMI of a model with all K topics is:

$$\begin{aligned} NPMI = \frac{1}{K} \sum _{k=1}^K NPMI(k, t) \end{aligned}$$

(25)

In the experiments, we choose $t=20$ for each topic.

C Evaluation on incremental and recurring concept drifts

Table 3 Data streams with incremental and recurring concept drifts on news aggregator

Fig. 9

Performance of the methods when facing with incremental concept drift on News Aggregator dataset. LDA is the base model. Higher is better

Fig. 10

Performance of the methods when facing with recurring concept drift on News Aggregator dataset. LDA is the base model. Higher is better

Table 4 The lowest LPP, median LPP and restoration time of the 5 methods when dealing with gradual and recurring concept drift on News Agrregator dataset

We conduct more experiments on News Aggregator dataset to investigate how our methods (iDropout and aiDropout) and the baselines deal with incremental and recurring concept drifts. We use LDA with $K=100$ and $\alpha = 0.01$ as our base model for these experiments. Each dataset is split into mini-batches, each mini-batch contains 2000 documents. Regarding incremental concept drift, we randomly shuffle data instances in each class and then divide them into mini-batches. We train LDA on the mini-batches of consecutive classes. At the change point between two classes, we add 5 mixed mini-batches which include data from both of the two classes. In terms of recurring concept drift, the mini-batches of each class are divided into three parts to simulate the recurring concept drift with three iterations. Table 3 shows mini-batch sequence in incremental and recurring concept drifts. After finishing training each mini-batch, we measure LPP on the next mini-batch to evaluate how the methods adapt to new concept drift.

Figures 9 and 10 illustrate the performance of the methods when dealing with the incremental and recurring concept drifts respectively. Overall, both iDropout and aiDropout achieve better performance than the baselines. Although their LPPs decrease dramatically when new concept drift happens, they adapt quickly to the new concept after a few next mini-batches. It is obvious that the decrease in the performances of all methods in the incremental concept drift is less than this in both the sudden and recurring concept drifts. In particular, aiDropout outperforms significantly iDropout in the recurring concept drift where several new concepts occur. This phenomenon can be because the adaptive mechanism helps learn dropout rate automatically to adapt to new data effectively. Moreover, Table 4 shows the lowest LPP, median LPP and restoration time of the 5 methods when dealing with gradual and recurring concept drift on News Agrregator dataset. Overall, the behaviours of the 5 methods on recurring and gradual concept drifts are similar to them on sudden one. Both aiDropout and iDropout drop LPP least when a new concept happens, then they restore most quickly to achieve better performance than the remaining methods.

D Discussion on computational and memory complexity

This section discusses the computational and memory complexity of iDropout and aiDropout. We make an intuitive comparison with the baselines (SVB, PVB, and SVB-PP) albeit it is difficult to theoretically analyze the computational and memory complexity of the methods for a general model. Then, we make an empirical comparison.

We consider a general model $B(\beta ,z,x)$ (as in Sect. 3) where $\beta$ is the global variable, $x= x_{1:M}$ is the set of observations, and $z=z_{1:M}$ is the set of hidden variables of observations. All methods often use variational inference for inferring local variable z. However, while SVB, PVB, SVB-PP aim to full Bayesian approximation for global variable $\beta$ based on variational inference, iDropout and aiDropout use the maximum a posterior (MAP) to learn a point estimate. The model is consecutively trained on collected mini-batches in a general learning scenario in a streaming environment. Let $\eta ^t$ and $\phi ^t$ be variational parameters of $\beta$ and z at mini-batch t respectively, $\gamma$ be the hyperparameter of prior distribution $p(\beta ^t|\gamma )$, and $\rho$ be a forgetting factor. When learning the model on a mini-batch $D^t$, the objective function of each method is re-written as bellow:

For SVB:¹²

$$\begin{aligned} \begin{aligned} \{ \hat{\eta }^t, \hat{\phi ^t}\}&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\eta ^t, \phi ^t}\left\{ E_{q(z^t|\phi ^t)}\left[ \log \frac{p(D^t, z^t| \beta ^t)}{q(z^t|\phi ^t)} \right] - KL\left[ q(\beta ^t|\eta ^t)||q(\beta ^t|\eta ^{t-1}) \right] \right\} \end{aligned} \end{aligned}$$

(26)

For PVB:

$$\begin{aligned} \begin{aligned} \{ \hat{\eta }^t, \hat{\phi ^t}\}&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\eta ^t, \phi ^t}\left\{ E_{q(z^t|\phi ^t)}\left[ \log \frac{p(D^t, z^t| \beta ^t)}{q(z^t|\phi ^t)} \right] - KL\left[ q(\beta ^t|\eta ^t)||p(\beta ^t|\gamma ) \right] \right\} \end{aligned} \end{aligned}$$

(27)

For SVB-PP:

$$\begin{aligned} \begin{aligned} \{ \hat{\eta }^t, \hat{\phi ^t}\}&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\eta ^t, \phi ^t}\left\{ E_{q(z^t|\phi ^t)}\left[ \log \frac{p(D^t, z^t| \beta ^t)}{q(z^t|\phi ^t)} \right] - KL\left[ q(\beta ^t|\eta ^t)||q(\beta ^t|\rho \eta ^{t-1} + (1-\rho )\gamma ) \right] \right\} \end{aligned} \end{aligned}$$

(28)

For iDropout:

$$\begin{aligned} \begin{aligned} \{ \hat{\beta }^t, \hat{\phi }^t\} = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t, \phi ^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + E_{q(z^t|\phi ^t)}\left[ \log \frac{p(D^t, z^t|\tilde{\beta }^t)}{q(z^t|\phi ^t)} \right] \right\} \end{aligned} \end{aligned}$$

(29)

where $\tilde{\beta }^t = f(\beta ^t \odot \pi ^t)$ and $\pi ^t$ is sampled from Bernoulli distribution with hyperparameter p.

For aiDropout:

$$\begin{aligned} \begin{aligned} \{ \hat{\beta }^t, \hat{\phi ^t}, \hat{\lambda }^t, \hat{p}^t\}&= \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{\beta ^t, \phi ^t, \lambda ^t, p^t}\left\{ \log p(\beta ^t|\beta ^{t-1}) + E_{q(z^t|\phi ^t)}\left[ \log \frac{p(D^t, z^t|\tilde{\beta }^t)}{q(z^t|\phi ^t)} \right] \right. \\&\quad \left. - KL\left[ q(\pi ^t|\lambda ^t)||p(\pi ^t|p^t) \right] \right\} \end{aligned} \end{aligned}$$

(30)

where $\tilde{\beta }^t = f(\beta ^t \odot \pi ^t)$ and $\pi ^t$ is sampled from variational distribution $q(\pi ^t|\lambda ^t)$.

We emphasize that the five methods have the same objective function w.r.t the variational parameter $\phi ^t$ of local variable z, the parameters related to the global variable make them different. We will focus on discussing their computational and memory complexity on global variables.

Regarding memory complexity, compared to the three baselines (SVB, PVB, and SVB-PP), both aiDropout and iDropout must use dropout matrix $\pi ^t$ and sample it in each iteration. Note that $\pi ^t$ has the same size as the global variable $\beta$. Moreover, because aiDropout approximates the true posterior of $\pi ^t$ by a variational distribution $q(\pi ^t|\lambda ^t)$ in order to create an adaptive droprate mechanism, it must store variational parameter $\lambda ^t$. In our work, the size of $\lambda ^t$ is set the same as $\pi ^t$. Therefore, iDropout and aiDropout must store more parameters than the baselines by once and twice the size of $\beta ^t$, respectively.

In terms of computational complexity, both aiDropout and iDropout are often more complex than the baselines. They use gradient-based optimizers that often require a large number of iterations to learn global parameters. Moreover, due to optimizing the dropout rate, aiDropout requires more computation than iDropout to do an iteration. Meanwhile, SVB, PVB, and SVB-PP achieve closed-form solutions when they apply for conjugate models (as in our case studies); therefore, they often run considerably faster than both iDropout and aiDropout in these cases. When working with non-conjugate models, iDropout can compare to the baselines. However, it is difficult to make a clear comparison because they learn different models when both iDropout and aiDropout change the prior distribution of $\beta$ compared to the baselines.

From the discussion above, it is evident that aiDropout trades off the quality of the learned model against computational and memory complexity. However, we consider a general learning scenario in a streaming environment where data is often collected in mini-batches based on the fixed mini-batch size or timestamp; then a model is trained on each mini-batch. Therefore, the velocity and volume of arriving mini-batches directly make the computational and memory complexity requirements for learning methods. iDropout and aiDropout are effective solutions when working on a streaming environment in which they can respond to time and memory requirements well.

To show the trade-off in aiDropout more obviously, we measure mini-batch’s average training time when using the five methods to learn LDA as in subsection 6.3.1 (Fig. 8) and NB as in 6.2.2 (Fig. 5). We use our server (64 cores CPU, 128G DDR) to train LDA and Google colab with free GPU Tesla K80 to train NB. Table 5 shows the results. aiDropout and iDropout are noticeably slower than the baselines in both LDA and NB. Because LDA and NB are conjugate models, the baselines obtain closed-form solutions. Meanwhile, both aiDropout and iDropout require large iterations (100 in our experiments) when conducting gradient-based algorithms.

Table 5 The average training time (second) of minibatches when using the five methods to learn LDA and NB