Skip to main content

Advertisement

SpringerLink
Log in

Spatial Landslide Hazard Prediction Using Rainfall Probability and a Logistic Regression Model

  • Published:
Mathematical Geosciences Aims and scope Submit manuscript

Abstract

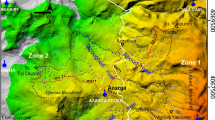
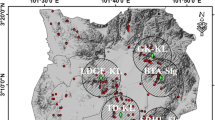
The aims of this study were to apply and validate a logistic regression model for landslide hazard, considering rainfall probability and using a geographic information system. The study focused on the Deokeokri and Karisanri areas of Inje, South Korea. We chose logistic regression for its mathematical rigor and its use of implementation in GIS software. Rainfall probability is analyzed for a quantitative prediction of rainfall changes in the study area. The rainfall probability was calculated using the Gumbel distribution. Then, the probabilities of landslides in the study area in target years (1, 3, 10, 50, and 100 years in the future) were calculated assuming that landslides are triggered by daily rainfall of 202 mm or 3-day cumulative rainfall of 449 mm. Landslide hazard maps were developed for the two study areas, and the logistic regression coefficients for one area were applied to the other area to validate the method. In Karisanri, all recorded landslides were used for validation. Validation results for the 202-mm daily precipitation threshold in Karisanri showed an average accuracy of 79.14 %, whereas those for the 449-mm 3-day cumulative precipitation threshold showed an average accuracy of 81.31 %. A combination of rainfall probability and logistic regression with a GIS is an effective method for analyzing the possibility of future landslides.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Bai S, Lü G, Wang J, Zhou P, Ding L (2010) GIS-based rare events logistic regression for landslide-susceptibility mapping of Lianyungang, China. Environ Earth Sci 62:139–149

    Article  Google Scholar 

  • Dai FC, Lee CF (2002) Landslide characteristics and slope instability modeling using GIS, Lantau Island, Hong Kong. Geomorphology 42:213–228

  • Dong JJ, Lee CT, Tung YH, Liu CN, Lin KP, Lee JF (2009) The role of the sediment budget in understanding debris flow susceptibility. Earth Surf Proc Land 34:1612–1624

    Article  Google Scholar 

  • Fell R, Corominas J, Bonnard C, Cascini L, Leroi E, William Z (2008) Guidelines for landslide susceptibility, hazard and risk zoning for land-use planning. Eng Geol 102:99–111

    Article  Google Scholar 

  • Fisher RA (1925) Statistical methods for research workers. Oliver & Boyd, Edinburgh

    Google Scholar 

  • Frattini P, Crosta G, Sosio R (2009) Approaches for defining thresholds and return periods for rainfall-triggered shallow landslides. Hydrol Proc 23:1444–1460

    Article  Google Scholar 

  • Guzzetti F, Carrarra A, Cardinali M, Reichenbach P (1999) Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 31:181–216

    Article  Google Scholar 

  • Hair JF, Anderson RE, Tatham RL, Black WC (1998) Multivariate data analysis, 5edn. Prentice-Hall, London

  • Henry DH, Roman K (2005) Generic probability distribution of rainfall in space: the bivariate model. J Hydrol 306:234–263

    Article  Google Scholar 

  • Hosmer DW, Lemeshow S (2000) Applied logistic regression, 2nd edn. Wiley, New York

  • Jaiswal P, van Westen CJ, Jetten V (2011) Quantitative estimation of landslide risk from rapid debris slides on natural slopes in the Nilgiri hills, India. Nat Hazards Earth Syst Sci 11:1723–1743

    Article  Google Scholar 

  • Lee S, Min K (2001) Statistical analysis of landslide susceptibility at Yongin, Korea. Environ Geol 40:1095–1113

    Article  Google Scholar 

  • Lee S, Ryu JH, Won JS, Park HJ (2004) Determination and application of the weights for landslide susceptibility mapping using an artificial neural network. Eng Geol 71:289–302

    Article  Google Scholar 

  • Lee S (2005) Application of logistic regression model and its validation for landslide susceptibility mapping using GIS and remote sensing data. Int J Remote Sens 26:1477–1491

    Article  Google Scholar 

  • Lee S, Pradhan B (2006) Probabilistic landslide hazards and risk mapping on Penang Island, Malaysia. J Earth Sys Sci 115:661–672

    Article  Google Scholar 

  • Lee S (2007) Comparison of landslide susceptibility maps generated through multiple logistic regression for three test areas in Korea. Earth Surf Proc Land 32:2133–2148

    Article  Google Scholar 

  • Marco B (2002) Accuracy of radar rainfall estimates for streamflow simulation. J Hydrol 267:26–39

    Article  Google Scholar 

  • Nandi A, Shakoor A (2010) A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses. Eng Geol 110:11–20

    Article  Google Scholar 

  • Nefeslioglu HA, Gokceoglu C, Sonmez H, Gorum T (2011) Medium-scale hazard mapping for shallow landslide initiation: the Buyukkoy catchment area (Cayeli Landslides, Rize, Turkey). doi:10.1007/s10346-011-0267-7

  • Oh HJ, Lee S, Chotikasathien W, Kim C, Kwon J (2009) Predictive landslide susceptibility mapping using spatial information in the Pechabun area of Thailand. Environ Geol 57:641–651

    Article  Google Scholar 

  • Oh HJ, Lee S (2010) Cross-validation of logistic regression model for landslide susceptibility mapping at Geneoung areas, Korea. Disaster Adv 3:44–55

    Google Scholar 

  • Ozdemir A (2009) Landslide susceptibility mapping of vicinity of Yaka Landslide (Gelendost, Turkey) using conditional probability approach in GIS. Environ Geol 57:1675–1686

    Article  Google Scholar 

  • Park NW (2010) Application of Dempster–Shafer theory of evidence to GIS-based landslide susceptibility analysis. Environ Earth Sci 62:367–376

    Article  Google Scholar 

  • Pieter C (2008) River flow prediction through rainfall-runoff modelling with a probability-distributed model (PDM) in Flanders, Belgium. Agr Water Manag 95:859–868

    Article  Google Scholar 

  • Pradhan B (2010) Manifestation of an advanced fuzzy logic model coupled with geo-information techniques to landslide susceptibility mapping and their comparison with logistic regression modelling. Environ Ecol Stat. doi:10.1007/s10651-010-0147-7

  • Pradhan B, Lee S (2010a) Delineation of landslide hazard areas on Penang Island, Malaysia, by using frequency ratio, logistic regression, and artificial neural network models. Environ Earth Sci 60:1037–1054

    Article  Google Scholar 

  • Pradhan B, Lee S (2010b) Regional landslide susceptibility analysis using back-propagation neural network model at Cameron Highland, Malaysia. Landslides 7:13–30

    Article  Google Scholar 

  • Regmi NR, Giardino JR, Vitek JD (2010) Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 115:172–187

    Article  Google Scholar 

  • Schaeben H (2014) A mathematical view of weights-of-evidence, conditional independence, and logistic regression in terms of Markov random fields. Math Geosci. doi:10.1007/s11004-013-9513-y

  • Schaeben H (2012) Comparison of mathematical methods of potential modeling. Math Geosci 44(1):101–129

    Article  Google Scholar 

  • Shou K, Chen Y, Liu H (2009) Hazard analysis of Li-shan landslide in Taiwan. Geomorphology 103:143–153

    Article  Google Scholar 

  • Tangestani MH (2009) A comparative study of Dempster–Shafer and fuzzy models for landslide susceptibility mapping using a GIS: an experience from Zagros Mountains, SW Iran. J Asian Earth Sci 35:66–73

    Article  Google Scholar 

  • Vahidnia MH, Alesheikh AA, Alimohammadi A, Hosseinali F (2009) Landslide hazard zonation using quantitative methods in GIS. Int J Civil Eng 7:176–189

    Google Scholar 

  • Virmani SM, Siva Kumar MVK, Reddy SJ (1982) Rainfall probability estimates for selected locations of semi-arid India. International Crops Research Institute for the Semi-Arid Tropics, Patancheru

  • Vogel RM, McMartin DE (1991) Probability plot goodness-of-fit and skewness estimation procedures for the Pearson type 3 distribution. Water Resour Res 27:3149–3158

    Article  Google Scholar 

  • Yalcin A (2008) GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): comparisons of results and confirmations. Catena 72:1–12

    Article  Google Scholar 

  • Yilmaz I (2009) A case study from Koyulhisar (Sivas-Turkey) for landslide susceptibility mapping by artificial neural networks. B Eng Geol Environ 68:297–306

    Article  Google Scholar 

  • Yilmaz I (2010) The effect of the sampling strategies on the landslide susceptibility mapping by conditional probability and artificial neural networks. Environ Earth Sci 60:505–519

    Article  Google Scholar 

Download references

Acknowledgments

This research was supported by the Basic Research Project of the Korea Institute of Geoscience and Mineral Resources (KIGAM) funded by the Ministry of Science, ICT & Future Planning, and the Development Project of Environmental Technology for Climate Change by the Korea Environmental Industry & Technology Institute.

Author information

Authors and Affiliations

  1. Geological Research Division, Korea Institute of Geoscience and Mineral Resources (KIGAM), 124, Gwahang-no, Yuseong-Gu, Daejeon, 305-350, South Korea

    Saro Lee

  2. Korea University of Science and Technology, 217 Gajeong-ro, Yuseong-gu, Daejeon, 305-350, Korea

    Saro Lee

  3. Department of Earth System Sciences, Yonsei University, 134 Shinchon-dong, Seoul, Korea

    Joong-Sun Won & Moung Jin Lee

  4. Korea Environment Institute, 290 Jinheungno, Eunpyeong-gu, Seoul, 122-706, Korea

    Seong Woo Jeon & Moung Jin Lee

  5. Department of Geoinformatics, University of Seoul, Siripdae-gil 13, Dongdaemun-gu, Seoul, 130-743 , Republic of Korea

    Inhye Park

Authors
  1. Saro Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Joong-Sun Won
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Seong Woo Jeon
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Inhye Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Moung Jin Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Moung Jin Lee.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lee, S., Won, JS., Jeon, S.W. et al. Spatial Landslide Hazard Prediction Using Rainfall Probability and a Logistic Regression Model. Math Geosci 47, 565–589 (2015). https://doi.org/10.1007/s11004-014-9560-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11004-014-9560-z

Keywords

Search

Navigation