1 Introduction

Understanding and quantifying spatial and temporal variability of precipitation in a watershed are crucial tasks for hydrological modelling, climate analysis and climate change predictions (Secci et al. 2021; Todaro et al. 2022a, b). Gaps in time series, which can be caused by many circumstances (e.g. sensor malfunction, measurement errors and faults in data acquisition from operators), are a common problem in hydrometeorological data sets, and ignoring missing data can produce error-affected analysis. Alternatively, the affected time series could be directly removed, but the stations under study may be highly relevant for certain hydrometeorological processes in the investigated area (Aguilera et al. 2020). For these reasons, it is fundamental to find efficient methods to estimate the missing values in order to obtain complete time series.

Gap-filling procedures are usually specific to the nature of the variable under study. Precipitation is one of the most difficult atmospheric variables to characterize, estimate and forecast, especially on a daily scale, because of its high spatio-temporal variability and the large number of interconnected variables involved (Portuguez-Maurtua et al. 2022). Several interpolation methods have been developed to estimate missing values in precipitation time series. The most popular and simplest deterministic techniques are the Thiessen polygon method (THI; Thiessen 1911) or its implementation known as natural neighbour (NN; Sibson 1981), the nearest neighbour (NNb; Brandsma and Buishand 1998) and the inverse distance weighting (IDW; U.S. National Weather Service 1972). THI consists of assigning the precipitation of the area of influence containing the unsampled location. The NN estimates values at the unsampled point by computing the weighted average of the available data of its natural neighbours, where the weights assigned to each neighbour are based on the area of overlap between their areas of interest and the area of interest of the unsampled location. The NNb, rather than calculating an average value based on a weighting criterion, simply determines the closest point and assumes its value. Otherwise, the IDW assigns a value calculated from the weighted average of the available data, where the weights depend on the distance between the locations of the unknown and known data. Another approach used is the linear regression method proposed by the Food and Agriculture Organization (FAO) of the United Nations (Allen et al. 1998). The FAO method fills the gaps in the rainfall time series using data collected on the gap time at available stations, which presents a high correlation coefficient with the one of interest. This is a common gap-filling method in climate analysis (D’Oria et al. 2019; Huang et al. 2020). Geostatistical modelling, which is based on the theory of regionalized variables, provides an option for the estimation of missing precipitation data. It is preferred to the above-mentioned deterministic techniques because it incorporates the spatial correlation of observations into data processing (Goovaerts 1997) and allows one to assess the estimation uncertainty. Kriging represents the most used geostatistical method for rainfall interpolation. Several authors (Tabios and Salas 1985; Bacchi and Kottegoda 1995; Campling et al. 2001; Bostan et al. 2012) have shown that it provides better results than traditional gap-filling methods (as the above-mentioned ones) due to the incorporation of a spatial continuity pattern in the predictions. Another advantage of geostatistics is that there are numerous possibilities to incorporate one or more secondary variables to improve the estimation accuracy of the primary attributes (i.e. the variable of interest). Cokriging and kriging with an external drift (KED) are part of the multivariate geostatistical methods. Due to the orographic effect of mountainous terrain, precipitation tends to be related to elevation (Hevesi et al. 1992); hence it is common to use the elevation, taken from the available digital elevation models (DEM), as secondary variable to improve rainfall estimation (Hevesi et al. 1992; Daly et al. 1994; Prudhomme and Reed 1999; Goovaerts 2000; Lloyd 2005; Jacquin and Soto-Sandoval 2013; Cheng et al. 2017). It has been demonstrated that using elevation as an auxiliary variable could significantly enhance rainfall estimation (Carrera-Hernández and Gaskin 2007; Adhikary et al. 2017).

Except for the Carrera-Hernández and Gaskin (2007) study, none of the above-cited articles has used geostatistical methods to estimate daily rainfall data. Only a few studies have discussed this methodological approach. Beek et al. (1992) applied kriging to interpolate precipitation data for only 4 days in 1984, which were selected to investigate the spatial variability of daily precipitation in North-Western Europe. Buytaert et al. (2006) analysed the spatio-temporal patterns of daily precipitation series in the south of Ecuador in mountainous terrains. THI and universal kriging (UK) were used to point out the difference in uncertainty assessment. Incorporating external trends improved the accuracy of both methods, even though UK estimation resulted closer to the true values than THI estimation. Carrera-Hernández and Gaskin 2007 compared five different kriging methods: ordinary kriging (OK), kriging with external drift (KED), block kriging with external drift (BKED), ordinary kriging in a local neighbourhood (OKl) and kriging with external drift in a local neighbourhood (KEDl). Elevation was considered the second variable in the external drift. Their work aimed to estimate three different daily climatological variables (rainfall and minimum and maximum temperature) for a period between June 1978 and June 1985 in a Mexican basin. The results showed that the integration of elevation improved the estimation of the daily events even when the variables show low correlation. Chen et al. (2010) focused on identifying an accurate interpolation method to produce gridded daily precipitation in China. Five interpolation methods were compared: ordinary nearest neighbour; local polynomial; radial basis function; IDW; and OK based on seasonal semi-variograms. OK and IWD were ranked highest in terms of interpolation quality. Ly et al. (2011) compared two deterministic algorithms (IDW and THI) and four geostatistical methods (OK, UK, KED and ordinary cokriging—OCK; the last two techniques utilized elevation as the secondary variable) using a 30-year data set in Ourthe and Ambleve catchments in Belgium. Seven semi-variogram models were fitted for daily samples of different density. In terms of residual mean square error, the study concluded that OK was considered the best and most robust method followed by IDW. The estimation was not improved by the OCK and KED methods.

Alternative techniques have been proposed as gap-filling methodologies and compared with the kriging-based method. Oriani et al. (2020) tested IDW, various models based on OK and two pattern-based approaches (K-nearest neighbour and a new algorithm called vector sampling) to find an automatic method that does not require a big computational effort. The authors considered five case studies with different complex terrain, climate regimes and sensitivity to the amount of data. The results turned out to be related to the level of complexity of the associated precipitation patterns. Aguilera et al. (2020) dealt with this problem by comparing three different methodologies (spatio-temporal kriging [STK], multiple imputations by chained equations through predictive mean matching [PMM], and the random forest [RF] machine learning algorithm). Their work focused on the estimation of missing precipitation data considering the percentage of gaps in the time series. The results show that STK and RF can both deal with extreme lack, whereas PMM requires larger observed sample sizes. STK led to the most reliable results but has large computational cost.

Few of the studies mentioned above have performed daily-scale estimation, and most of those have typically focused on short periods or a limited number of days. Furthermore, some studies have shown that for long periods of missing data, gap-filling procedures require a high computational time. Typically, using geostatistical modelling, a semi-variogram for the day under consideration is calculated, and then the precipitation at the desired location is estimated (Beek et al. 1992; Carrera-Hernández and Gaskin 2007; Ly et al. 2011). One of the main problems with daily-scale analysis is that the number of data could be insufficient for the evaluation of semi-variograms. Furthermore, it is necessary to compute as many semi-variograms as there are missing data days, which results in high computational demand in case of long time series analysis more prone to contain large amount of gaps. This study intends to find a suitable and computationally efficient method to fill in daily gaps in precipitation time series for a specific pilot site by comparing three different interpolation approaches, since no single estimation method can work well everywhere (Daly 2006). The work proposed herein aims to contribute to the advancement of gap-filling techniques and improve the accuracy of precipitation time series analysis while keeping reasonable computational cost. The proposed method presents an innovative approach based on the use of monthly average semi-variograms, which overcomes the problems just mentioned. All the available data over the entire time series are used to build the monthly semi-variogram. Moreover, only 12 monthly semi-variograms (i.e. one semi-variogram per month), rather than one semi-variogram for every day of the data set, are used. The proposed methodology also allows seasonal variability to be taken into account. Additionally, simple cokriging (SCK) is investigated to improve the results using elevation as the second variable. The Portuguese case study of the InTheMED project (Todaro et al. 2022a, b), located in the southern part of the country, is used to analyse and compare the geostatistical approaches and the FAO method. The efficacy of the methods is assessed by cross-validation processes and by comparing different performance metrics.

The remainder of this paper is organized as follows. After a description of the methods applied in Sect. 2, the study area and data analysis are presented in Sect. 3. Subsequently, results and a discussion are reported in Sect. 4. Finally, the conclusions are illustrated by examining the pros and cons of each method in Sect. 5.

2 Methods

The methodology adopted in this research includes a linear regression method (FAO) and two kriging-based geostatistical techniques (OK and SCK). This section provides a brief overview of the approaches used. The reader is referred to Goovaerts (1997) and Kitanidis (1997) for extensive reviews of geostatistical theory.

2.1 Linear Regression (FAO)

The linear regression approach (briefly referred as the FAO method) fills gaps using the data collected at the gap time in another consistent station. Given a data set Y at a certain station that has missing observations, its historical series is completed using observations from another data set X of a nearby homogeneous station with comparable characteristics. The estimation procedure operates by integrating the missing data using a regression equation that is fitted based on the values simultaneously observed at the two stations.

Computing the correlation coefficient between pairs of stations is a key part of the method. It makes it possible to highlight the intensity of similarity between stations, identifying the best-correlated ones. Pearson’s correlation coefficient r was used

$$ r = \frac{{{\text{Cov}}_{xy} }}{{\sigma_{x} \sigma_{y} }} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (x_{i} - \overline{x})\left( {y_{i} - \overline{y}} \right)}}{{\left( {\mathop \sum \nolimits_{i = 1}^{n} (x_{i} - \overline{x}} \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} (y_{i} - \overline{y})^{2} )^{1/2 } }}, $$
(1)

where \(\overline{x}\) and \(\overline{y}\) are the means of the two data sets computed from the concurrent observations, σx and σy are the standard deviations, \({\text{Cov}}_{xy} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (x_{i} \cdot y_{i} ) - n \cdot \overline{x} \cdot \overline{y}}}{n - 1}\) represents the covariance between the data sets X and Y at time i and n is the number of simultaneous observations of the two time series.

The approach is characterized by a regression of Y on X performed for the periods when the data from both data sets are present

$$ y_{i} = b + a \cdot x_{i} , $$
(2)

where a and b are empirical regression parameters, and \(a = \frac{{{\text{Cov}}_{xy} }}{{\sigma_{x}^{2} }} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (x_{i} - \overline{x})\left( {y_{i} - \overline{y}} \right)}}{{\mathop \sum \nolimits_{i = 1}^{n} (x_{i} - \overline{x})^{2} }}\).

The FAO method can be applied only if the following three constraints are respected:

  1. I.

    The station to be filled must have at least 70% of complete data.

  2. II.

    The square of Pearson’s correlation coefficient (r2) between the station having missing data and the twin station used to fill the gaps must be greater than or equal to 0.7.

  3. III.

    The regression coefficient (a) must be between 0.7 and 1.3.

When all three conditions are fulfilled, the regression equation (Eq. (2)) is used to estimate the missing data at the station of interest using the parameters a and b obtained from the best-correlated station.

2.2 Spatial Correlation Analysis

In geostatistics, the basic tool to account for the spatial distribution of natural phenomena is the semi-variogram, which is the function that describes how the variance of increments increases with distance. In the application example shown herein, instead of deriving a semi-variogram for every day of the time series (Beek et al. 1992; Carrera-Hernández and Gaskin 2007; Ly et al. 2011), an average monthly semi-variogram has been considered. This is computed by taking, at each monitoring station and for each month, the mean of the daily precipitation observed in the specific month of interest in all the years of the analysed period. The monthly averaged semi-variogram allows for a faster calculation by reducing the number of semi-variograms to 12 instead of one for each day of the missing period. Furthermore, it enables accounting for seasonal variations when performing data interpolation.

The determination of the semi-variograms can be summarized as follows:

  1. I.

    Compute the average daily precipitation of each month at each monitoring station over the entire time series.

  2. II.

    Compute the monthly experimental semi-variogram using data grouped by month from all available gauge stations

    $$ \gamma^{*} \left( {\mathbf{h}} \right) = \frac{1}{{2N\left( {\mathbf{h}} \right)}}\mathop \sum \limits_{j = 1}^{{N\left( {\mathbf{h}} \right)}} \left( {Z\left( {{\mathbf{u}}_{j} } \right) - Z\left( {{\mathbf{u}}_{j} + {\mathbf{h}}} \right)} \right)^{2} , $$
    (3)

    where N(h) is the number of pairs of locations separated by the vector h, and Z(uj) is the observed variable at location uj of the monitoring station j.

  3. III.

    Fit a theoretical semi-variogram model, γ(h), to the experimental variogram. Exponential, Gaussian and spherical (Table 1) are the most commonly used semi-variogram models for kriging applications in hydrology (Adhikary et al. 2017). These can be combined with a nugget model (Table 1).

  4. IV.

    To quantify the suitability of the theoretical semi-variogram models on the experimental model, the sum of the residual square (RSS) is provided

    $$ {\text{RSS}} = \mathop \sum \limits_{i = 1}^{Nc} \left[ {\gamma^{*} \left( {h_{i} } \right) - \gamma \left( {h_{i} } \right)} \right]^{2} , $$
    (4)

    where Nc is the number of intervals into which the data pairs are classified.

Table 1 Theoretical semi-variogram models. C0 is the nugget effect, θ is the sill value, l is the range and h is the distance between pairs of point
Full size table

To obtain the best-fitted model, the above procedure is repeated for different lag sizes, with the parameters adjusted according to the least-square methodology until the minimum of the RSS (Eq. (4)) is reached. The coefficients of this model can then be used for kriging estimation.

2.3 Ordinary Kriging

Ordinary kriging (OK) is the most widely used kriging method. It estimates a value at a point in a region, for which a semi-variogram is known, by using the neighbour observations of the estimation location (Goovaerts 1997). OK accounts for local mean fluctuations by restricting the domain of mean stationarity to the local neighbourhood. The OK estimation is given by

$$ \hat{Z}\left( {{\mathbf{u}}_{0} } \right) = \mathop \sum \limits_{i = 1}^{J} \lambda_{i} Z\left( {{\mathbf{u}}_{i} } \right)\quad {\text{with}}\quad \mathop \sum \limits_{i = 1}^{J} \lambda_{i} = 1, $$
(5)

where \(\hat{Z}\left( {{\mathbf{u}}_{0} } \right)\) is the estimated value at target location u0, λi are the kriging weights, and Z(ui) is the observed value at J monitoring stations.

OK also gives a measure of uncertainty attached to the results to signify the reliability of the estimation (Goovaerts 1997). This is done by calculating the estimation variance, which expresses the quality of the interpolation: high estimation variance means uncertain interpolation and low estimation variance indicates interpolation with smaller spatial uncertainty. It is estimated as follows

$$ \sigma_{{{\text{OK}}}}^{2} = E \left[ {\left( {\hat{Z}\left( {\mathbf{u}} \right) - Z\left( {\mathbf{u}} \right)} \right)^{2} } \right], $$
(6)

where E is the mathematical expectation.

The OK weights can be obtained by solving the system

$$ \left\{ {\begin{array}{*{20}l} {\sum\nolimits_{i = 1}^{J} {\lambda_{i} } \gamma_{ij} - \mu = \gamma_{i0} } \hfill \\ {\sum\nolimits_{i = 1}^{J} {\lambda_{i} } = 1} \hfill \\ \end{array} } \right.\quad {\text{for}}\quad j = 1, \ldots ,J, $$
(7)

where γij is the semi-variogram values between sampling locations ui and uj, γi0 are the semi-variogram values between sampling location ui and the target location u0, and μ is the Lagrange multiplier parameter. The unbiased estimate is guaranteed by the constraint of the sum of the weights to 1. The weights λi, obtained through the system (Eq. (7)) are inserted into Eq. (5) to make the estimation.

2.4 Simple Cokriging

Cokriging is a multivariate extension of kriging, which incorporates secondary information for improving the estimation of the primary variable. If the second variable is highly correlated with the primary variable, then incorporating it into the estimation process can lead to a reduction in prediction error variance compared to using kriging alone (Goovaerts 2000). Simple cokriging (SCK) assumes that the means of both the primary and secondary variables are known and constant within the study area. The method aims to estimate the primary variable as given by

$$ \hat{Z}_{1} \left( {{\mathbf{u}}_{0} } \right) = \left( {\mathop \sum \limits_{i = 1}^{J} \lambda_{1i} \left[ {Z_{1} \left( {{\mathbf{u}}_{i} } \right) - m_{1} } \right] + \mathop \sum \limits_{i = 1}^{K} \lambda_{2i} \left[ {Z_{2} \left( {{\mathbf{w}}_{i} } \right) - m_{2} } \right]} \right) + m_{1} , $$
(8)

where \(\hat{Z}_{1} \left( {{\mathbf{u}}_{0} } \right)\) is the estimated value of the primary variable at the target location u0, Z1(ui) are the observed values of the primary variable at locations ui, Z2(wi) are the observed values of the secondary variable at K locations wi, λ1i and λ2i are the weights of the first and second variables, and m1 and m2 are the stationary means of the primary and secondary variables, respectively.

The weights are obtained by solving the following system

$$ \left\{ {\begin{array}{*{20}l} {\sum\nolimits_{{i_{1} = 1}}^{J} {\gamma_{{z_{1} }} } \left( {{\mathbf{u}}_{{i_{1} }} - {\mathbf{u}}_{{j_{1} }} } \right)\lambda_{1i} + \sum\nolimits_{{i_{2} = 1}}^{K} {\gamma_{{z_{1} z_{2} }} } \left( {{\mathbf{w}}_{{i_{2} }} - {\mathbf{u}}_{{j_{1} }} } \right)\lambda_{2i} = \gamma_{{z_{1} }} \left( {{\mathbf{u}}_{{j_{1} }} - {\mathbf{u}}_{0} } \right)\quad {\text{for}}\quad j_{1} = 1, \ldots ,J} \hfill \\ {\sum\nolimits_{{i_{1} = 1}}^{J} {\gamma_{{z_{2} z_{1} }} } \left( {{\mathbf{u}}_{{i_{1} }} - {\mathbf{w}}_{{j_{2} }} } \right)\lambda_{1i} + \sum\nolimits_{{i_{2} = 1}}^{K} {\gamma_{{z_{2} }} } \left( {{\mathbf{w}}_{{i_{2} }} - {\mathbf{w}}_{{j_{2} }} } \right)\lambda_{2i} = \gamma_{{z_{1} z_{2} }} \left( {{\mathbf{w}}_{j2} - {\mathbf{u}}_{0} } \right)\quad {\text{for}}\quad j_{2} = 1, \ldots ,K} \hfill \\ \end{array} } \right., $$
(9)

where \(\gamma_{{z_{1} }}\) and \(\gamma_{{z_{2} }}\) are the theoretical semi-variograms of the first and second variable, respectively, and \(\gamma_{{z_{1} z_{2} }} = \gamma_{{z_{2} z_{1} }}\) are the theoretical cross-variograms between the two variables.

Unbiasedness is guaranteed by the subsequent equation whatever the cokriging weights

$$ E \left[ {\hat{Z}_{1} \left( {\mathbf{u}} \right) - Z_{1} \left( {\mathbf{u}} \right)} \right] = 0. $$
(10)

To make the prediction, the weights obtained through the system of equations (Eq. (9)) are entered into Eq. (8).

The first step of the method is to develop a suitable model for cross-continuity and dependency between the two variables involved. This positive correlation is known as cross-regionalization or coregionalization (Goovaerts 1997), and it can be computed using the cross-variogram or cross-covariogram. In the cokriging methods, the cross-variogram model between the primary and secondary variable is obtained by fitting an experimental cross-variogram

$$ \gamma_{{z_{1} z_{2} }}^{*} \left( {\mathbf{h}} \right) = \gamma_{{z_{2} z_{1} }}^{*} \left( {\mathbf{h}} \right) = \frac{1}{{2N\left( {\mathbf{h}} \right)}}\mathop \sum \limits_{j = 1}^{{N\left( {\mathbf{h}} \right)}} \left\{ {\left[ {Z_{1} \left( {{\mathbf{u}} + {\mathbf{h}}} \right) - Z_{1} \left( {\mathbf{u}} \right)} \right]\left[ {Z_{2} \left( {{\mathbf{u}} + {\mathbf{h}}} \right) - Z_{2} \left( {\mathbf{u}} \right)} \right]} \right\}, $$
(11)

where \(\gamma_{{z_{1} z_{2} }}^{*} \left( {\mathbf{h}} \right) = \gamma_{{z_{2} z_{1} }}^{*} \left( {\mathbf{h}} \right)\) are the experimental cross-variograms between the two variables.

The semi-variogram must satisfy the positive-definite condition (PDC). In a univariate context, the condition is met by choosing a semi-variogram or covariogram from the admissible models (Christakos 1984). In general, a linear combination of these models can be considered to ensure that the matrix of kriging coefficients is invertible and the variance positive (Matheron 1970). In multivariate geostatistics, and in this case, considering two variables, a cross-variogram and two semi-variograms are needed. To have a valid model that respects the PDC, the linear model of coregionalization (LMC; Journel and Huijbregts 1978) can be used. The use of a combination of permissible semi-variogram models, and each coregionalization matrix being positive semi-definite, are sufficient conditions for the so-called LMC to be allowable (Goovaerts 1999). The cross-variogram is used to model the spatial correlation between different variables at different locations. The shape of the cross-variogram is an important consideration in the LMC, as it can affect the accuracy of the model. In general, the shape of the cross-variogram should be the same for all variables included in the LMC (Stein 2012). This is because the LMC assumes that the variables are correlated with each other in a consistent manner across space, and a consistent cross-variogram shape helps ensure that this assumption is met. However, it is possible to use different cross-variogram shapes for different variables in the LMC. This can be useful when there is prior knowledge that the spatial correlation structure differs between variables. In such cases, a separate cross-variogram model can be fitted for each variable (Stein 2012). To make sure that the cross-variogram model is positive-definite, the Cauchy–Schwarz inequality must be fulfilled for all values of h

$$ \gamma_{{z_{1} z_{2} }}^{*} \left( {\mathbf{h}} \right) \le \left[ {\gamma_{{z_{1} }}^{*} \left( {\mathbf{h}} \right)\gamma_{{z_{2} }}^{*} \left( {\mathbf{h}} \right)} \right]^{\frac{1}{2}} , $$
(12)

where \(\gamma_{{z_{1} }}^{*}\) and \(\gamma_{{z_{2} }}^{*}\) are the experimental semi-variograms.

A simpler graphical test of the PDC was suggested by Hevesi et al. (1992) by graphing the proposed model with the PDC curve

$$ {\text{PDC}}\left( {\mathbf{h}} \right) = \left[ {\gamma_{{z_{1} }}^{*} \left( {\mathbf{h}} \right)\gamma_{{z_{2} }}^{*} \left( {\mathbf{h}} \right)} \right]^{\frac{1}{2}} . $$
(13)

The test is passed if the value of \(\gamma_{{z_{1} z_{2} }}^{*}\) does not exceed the value of PDC for all values of h, which also means that the cross-semi-variogram is under the PDC curve. The cokriging methods fit semi-variogram and cross-variogram models as a linear combination of the same set of basic models listed in Table 1. The same procedure applied for OK in the previous section is applied to SCK respecting the conditions of PDC as applied in the work of Adhikary et al. (2017).

Two situations can be distinguished based on the sampling density of primary and secondary variables (Goovaerts 1999). The first one is the equally sampled or isotopic case: all variables are recorded at every sampled location. The second one is the heterotopic case: the primary variable is under-sampled relative to the secondary variable. Measurements of the attribute of interest are usually supplemented by more abundant data on attributes related to secondary variables, which generally require less sampling effort. The second case is the recommended one.

3 Study Area and Data Analysis

The study area is one of the pilot sites investigated within the InTheMED PRIMA project. It involves the Portuguese portion of the Guadiana Hydrographic Basin. The Guadiana River basin is a cross-border basin located in Spain and Portugal. It drains a total area of 67,133 km2, of which 55,528 km2 lies within Spain and 11,611 km2 within Portugal. The Guadiana River has a length of 820 km. According to Todaro et al. (2022a, b), the average annual precipitation and temperature in the Portuguese region for the period of 1986–2005 were 545 mm and 16.1 °C, respectively. These findings are consistent with the study by Palop-Donat et al. (2020), which reported an average precipitation of 566 mm and an average temperature of 16.3 °C for the period of 1980/1981 to 2011/2012.

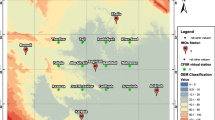
Daily precipitation data were collected from 96 rain gauges in the period 1970–2021. In this study, only the stations that present at least 70% of the data for a 30-year reference period (1976–2005) were analysed. This resulted in a total of 60 rain gauges being considered. Station elevations were extracted from a DEM (https://data.europa.eu/data). They range from 3 m above sea level (a.s.l.) to 499 m a.s.l. Table 2 summarizes the characteristics of the monitoring network (station ID, elevation and percentage of data available in the control period 1976–2005). Figure 1 shows the location of the rain gauges in the study area.

Table 2 Station ID, elevation, and available data percentage in the reference period
Full size table
Fig. 1
figure 1

Study area (UTM zone 29N-EPSG: 32629). Yellow dots are the location of the available precipitation stations, and the diamonds are the selected stations that fit FAO criteria (Sect. 2.1); DEM represented in colour scale

Full size image

3.1 Monitoring Station Selection

Since the FAO method is the most restrictive tested approach, the gap-filling approaches were tested only on the stations that satisfied the three conditions of the FAO method (see Sect. 2.1: I. data percentage ≥ 70%; II. r2 > 0.7; III. 0.7 ≤ a ≤ 1.3). This means that for a specific station, there exists a twin station that satisfies the three conditions. Table 3 summarizes for the 60 precipitation stations of the reference period whether the FAO criteria are met or not. Only 12 monitoring stations fulfilled the three constraints (in bold in Table 3 and represented by the diamonds in Fig. 1).

Table 3 FAO approach constraint verification for each monitoring station
Full size table

Table 4 lists the selected stations and the square of Pearson's correlation coefficient (r2) computed with the best-correlated one.

Table 4 Square of Pearson's coefficient (r2) between the selected monitoring stations and the best-correlated ones
Full size table

3.2 Semi-variogram Computation

The monthly means of the available daily rainfall collected at the monitoring stations in the reference period and elevations are considered as primary and secondary variables, respectively, for computing the semi-variograms and the cross-semi-variograms. In literature, the estimation of spatial anisotropy to model natural phenomena is a common point of discussion (e.g. Bernardi et al. 2018; Agou et al. 2019). A reliable determination of the existence and characteristics of anisotropy requires a large data set with sufficient variants in all possible directions. In many cases, including the present study, the available data are sparse or unevenly distributed, making it challenging to reliably perform anisotropy estimation. Therefore, spatial homogeneity is assumed, and anisotropy is neglected, as applied in the works of Goovaerts (2000) and Ly et al. (2011). For these reasons, in this work, omnidirectional semi-variograms are considered, which may be more reliable in case of limited or sparse data, as it simplifies the modelling process and reduces the risk of overfitting the data.

3.2.1 Precipitation

The semi-variogram of each month was defined by fitting the average daily precipitation of the 60 available rainfall stations for that specific month over the entire period. Isotropic semi-variograms were estimated by assuming identical spatial correlation in all directions. Under this assumption, the semi-variogram construction followed the procedure outlined in Sect. 2.2 using the models in Table 1. The monthly semi-variograms obtained are shown in Fig. 2.

Fig. 2
figure 2

Experimental and fitted semi-variogram models from the daily average rainfall of the 60 stations

Full size image

The adopted semi-variogram models fit the data satisfactorily. It was decided to estimate all 12 monthly semi-variograms using the parameters of a combined exponential and nugget semi-variogram model. The parameters of the adopted semi-variograms are listed in Table 1(S) in the supplementary material.

Figure 3 shows for each month the average daily rainfall computed over the reference period. It is noteworthy that the semi-variograms reflect the precipitation regime of the study area depicted in Fig. 1. In fact, autumn and winter months (from October to February) are the wettest months, and this is reflected in the high variability of the semi-variograms (i.e. higher spatial variability). In spring months (i.e. March, April and May), precipitation is lower than in winter everywhere, implying less variability in the semi-variograms. The summer months (from June to September) are the driest, involving semivariance tending toward zero.

Fig. 3
figure 3

Bar chart of the mean daily precipitation over 1976–2005 for each month in the whole study area

Full size image

3.2.2 Elevation

The experimental semi-variogram on the second variable was computed using approximately 180,000 elevation data extracted on a regular grid from the DEM. This was carried out in order to avoid the isotopic case, that is, the use of elevation data only in the location of the precipitation stations, and to represent more extensive spatial variability.

The same assumptions as for the precipitation semi-variograms were applied. The experimental semi-variogram on the elevation and the theoretical ones (Table 1) are shown in Fig. 4.

Fig. 4
figure 4

Experimental and fitted semi-variogram models for the elevation DEM

Full size image

To comply with the PDC conditions, the estimates using SCK were made using the parameters of the semi-variogram with an exponential model (parameters reported in Table 2(S)).

3.3 Cross-Variograms

The cokriging analysis requires the estimation of the semi-variogram and cross-variogram models for precipitation and elevation at the same time. Table 5 shows the correlation coefficients between the two variables.

Table 5 Average correlation coefficients between the primary variable (precipitation) and secondary variable (elevation) for each month
Full size table

According to Asli and Marcotte (1995), the use of secondary information is justified only for correlations greater than 0.4. Because the correlations between rainfall and elevation range from 0.4 to 0.77, it is considered worthwhile to carry out precipitation estimation by the SCK.

As for the precipitation, isotropic experimental cross-variograms were computed. Figure 5 shows the cross-variograms between precipitation and elevation for each month. To meet the PDC condition, the same model of precipitation was chosen for all the cross-variograms (parameters listed in Table 3(S)). The PDC curve based on Eq. (13) is also shown in Fig. 5 to graphically examine the criteria.

Fig. 5
figure 5

Experimental cross-variograms (black dots) with the fitted cross-variogram models (solid line) and positive-definite condition curve (dashed line) based on the rainfall and elevation data

Full size image

4 Results and Discussion

The performance of the proposed approaches was assessed for each of the 12 selected precipitation stations that fit the FAO criteria (Sect. 3.1; Table 4) for a chosen year, as follows:

  1. I.

    Removing the precipitation values of the selected year from the observation.

  2. II.

    Estimating the 365-day precipitation using the available data (highest correlated station for FAO method and 59 remaining station data for kriging-based approaches).

  3. III.

    Computation of the error statistics.

To test the methods, the year 1985 was chosen, since none of the 12 selected stations presented gaps in the time series.

The estimation through kriging-based approaches was carried out considering 60 rainfall stations and 110 elevation values as the primary and secondary variables, respectively. The number of elevation data points was reduced to 110 to limit the computational time. The mGstat tool implemented in MATLAB (Hansen 2022) was used for the application of the geostatistical methods. The computation time varied from 2 min for the OK to 2 h for the SCK for each precipitation station. The FAO method was implemented by a MATLAB (2022) code that takes a few seconds for the estimation of each station.

The goodness of the estimation of the three gap-filling methods (FAO, OK and SCK) was evaluated through a cross-validation process and a comparison of the error statistics. In addition, the monthly cumulative values derived from the daily interpolations (Fig. 6) were examined to provide further insight on how well each method performed.

Fig. 6
figure 6

Cumulative monthly rainfall for the year 1985 observed and estimated following the FAO, OK and SCK methods at 12 precipitation stations

Full size image

The performance evaluation was carried out computing the mean error (ME), the mean absolute error (MAE) and the root mean square error (RMSE). The ME is the average of all errors and quantifies the error in terms of underestimation if the result is negative, and overestimation if the result is positive. The MAE measures the magnitude of the errors.

The RMSE is a common accuracy performance measurement that is frequently used as a magnitude error evaluation. RMSE is never negative, and a value of 0 indicates a perfect fit with the data.

The metrics of the gap-filling methods used to estimate the daily and monthly cumulative precipitation in the year 1985 at the chosen stations are summarized in Tables 6 and 7, and are depicted in graphical form in Figs. 1(S) to 3(S) in the supplementary material.

Table 6 Evaluation metrics of the proposed methods for the estimation of the daily rainfall of the year 1985 at the 12 monitoring stations
Full size table
Table 7 Evaluation metrics of FAO, OK and SCK methods for the computation of the monthly cumulative rainfall of the year 1985 at the 12 monitoring stations
Full size table

The kriging-based methods (OK and SCK) performed better than the deterministic method (FAO) in the daily estimation of the precipitation in almost all cases. ME (Table 6; Fig. 1(S) above) indicates whether the variables are under- or overestimated. In terms of daily MAE (Table 6; Fig. 2(S) above), the SCK outperforms six out of 12 stations. OK provides the best estimates in three cases, despite being similar to SCK estimates. The FAO approach performs slightly better at three precipitation stations (POR046, POR062 and POR096). The RMSE analysis (Table 6; Fig. 3(S) above) shows that the kriging-based approaches provide better estimates than the FAO, except for POR046. Among the evaluated methods, POR057 displays the best daily statistics with MAE of 0.423 mm/day and RMSE of 1.186 mm/day for the OK method. In contrast, POR062 shows the poorest performance. Moreover, POR046 yields better results for the FAO method (MAE of 0.597 mm/day and RMSE of 1.919 mm/day) compared to the kriging-based approaches (MAE of 0.726 mm/day and RMSE of 2.095 mm/day for OK; MAE of 0.724 mm/day and RMSE of 2.094 mm/day for SCK); however, the station presents ME of −0.275 mm/day, which suggested an average underestimation of precipitation.

The actual cumulative monthly rainfall was compared with that obtained from daily estimations (Fig. 6), and subsequently, error statistics were calculated (Table 7; Figs. 1(S) to 3(S) bottom). This approach makes it possible to evaluate the accuracy of the daily estimates over an extended period and helps to identify any systematic errors present in the estimates. According to Table 7 and Fig. 2(S) bottom, kriging-based methods are comparable, although SCK showed better performance on MAE, outperforming the other methods at seven out of 12 stations, while OK performed better at three stations. The FAO approach yielded slightly better results in two precipitation stations (POR02 and POR096). In terms of RMSE (Table 7; Fig. 3(S) bottom), SCK achieved higher results in six out of 12 stations, with OK performing better in four stations and FAO resulting in the same precipitation stations as MAE.

The error metrics for daily and cumulative monthly precipitation can differ because they consider different aspects. Daily rainfall provides information on the amount of precipitation that falls on a specific day. Cumulative monthly precipitation data, on the other hand, provide information on the total amount of precipitation that falls in a given month. The differences in the error metrics reflect the fact that daily precipitation can exhibit high variability, while monthly precipitation is generally smoother and more consistent.

Considering all performance metrics (Tables 6 and 7; Figs. 1(S) to 3(S)), the results of the OK and SCK are comparable. Differences between estimates increase as secondary data become more numerous than primary data. On the downside, a large data set on elevation implies an extremely long time for the SCK estimation. Furthermore, there is no significant improvement in using the SCK even though the correlations between the two variables are good (Table 5).

The cross-validation values of observed and estimated daily rainfall for 1985 values for the 12 chosen stations are plotted in Fig. 7. The 45° line indicates a perfect fit between the observed and estimated values.

Fig. 7
figure 7

Cross-validation for the selected stations for the year 1985

Full size image

Taking into consideration daily estimation across methods, kriging-based estimates are weighted on spatially distributed observations at the same time (Eq. (5)), which implies that dry days are well identified, while localized intense rainfall events may be smoother than actual ones; the FAO method relies heavily on the best-correlated station, which means that all weather events (both dry and intense) are replicated across the regression line (Eq. (2)).

One of the advantages of the kriging-based approaches over the FAO method is that they can also provide the evaluation of the uncertainty associated with the estimation. Figure 8 shows an example of error variance estimation for January computed with OK (a) and SCK (b) and the difference between them (c). The OK variance was calculated based on information from the 60 precipitation stations. In contrast, in addition to the precipitation data, 110 elevation data points, including 60 elevation data points collected at monitoring stations and 50 elevation data points retrieved from the DEM on a regular grid with a side length of 15 km, were used for the SCK.

Fig. 8
figure 8

Error variance estimation of daily precipitation for January according to OK (a), SCK (b) and difference between OK and SCK variances (c). The cross represents the location of the rainfall data, and the circle shows the location of the elevation information (second variable in cokriging)

Full size image

The error variance is zero at the data positions and increases away from them. The hot spots in the OK variance map (Fig. 8a) denote the areas where the estimation becomes more uncertain, resulting in higher error variance, due to the lack of information in those areas. The use of the auxiliary information (SCK method) can help in reducing the estimation variance (Fig. 8b). By incorporating additional information from the secondary variable, SCK provides a more accurate estimate of the primary variable, especially in areas where there are no primary data points available. Figure 8c shows the difference between the error variances of OK and SCK. The areas where the difference is the greatest are the areas where the SCK method shows the greatest improvement over OK. These areas are likely to be where there are few primary data points available, and the SCK method incorporates additional information from secondary variables.

Overall, the results shown in Fig. 8 suggest that the use of SCK can lead to significant improvements in the accuracy of spatial interpolation, particularly in areas with limited primary data and where auxiliary information can be incorporated to improve the estimation. The SCK estimator is theoretically better because its error variance is always less than or equal to the error variance of kriging (Goovaerts 1997).

5 Conclusion

In this study, an alternative gap-filling approach using kriging-based methods (OK and SCK) is presented and compared with a determinist technique (FAO method). The case study involves estimating missing daily precipitation data at certain monitoring stations located in the Portuguese portion of the Guadiana River basin. The proposed approach involves fitting kriging and cokriging semi-variograms to the monthly averages of the daily rainfall data over the entire time series of each station. This results in the creation of 12 semi-variograms, one for each month.

According to the outcomes obtained, the geostatistical techniques (OK and SCK) outperformed the deterministic method (FAO).

Even though it is highly dependent on the constraints imposed, the FAO is the least computationally demanding method to use because it is based on a simple linear regression between two correlated stations. As long as the imposed restrictions are met, the FAO method can be a viable approach to perform gap filling. However, unlike geostatistical approaches, it does not account for spatial correlation and does not provide a measure of the uncertainty associated with the results.

On the other hand, geostatistical estimation requires a sufficient number of reliable observations to ensure the accuracy of the estimates and the computation of the semi-variograms, which govern the spatial variability. Cokriging is much more computationally demanding than kriging because semi-variograms (for each variable) and cross semi-variograms must be inferred and jointly modelled, resulting in a large cokriging system to be solved.

The use of monthly semi-variograms in kriging-based methods proposed in this study leads to satisfactory results and to a significant reduction of the computation time when compared to the standard kriging-based approach that involves computing variograms for each day. However, the disadvantage of using this procedure is that it may smooth the local extreme rainfall events. In fact, the monthly averaged semi-variograms may not accurately estimate the intensity and the extent of such events. With the FAO approach, on the other hand, the impact of extreme events depends on the correlation between the monitoring stations and available data. An extreme event is estimated in a monitoring station only if a highly correlated monitoring station, in which the extreme event is detected, exists.

Although SCK is expected to provide better results than OK, it did not significantly improve the estimates in this study. Although the monthly correlations between precipitation and elevations are above 0.4, the SCK shows slight improvements in estimation at both daily and monthly scales. In conclusion, OK provides a good balance of computational effort and estimation accuracy, and it is considered the best estimator for the area under study.

To speed up the cokriging process and take advantage of the availability of densely sampled secondary variable (i.e. high-resolution digital elevation models), colocated cokriging can be applied as a forthcoming development. It avoids instability caused by highly redundant secondary data; furthermore, it is faster, since it calls for a smaller cokriging system (Goovaerts 1997).

Future works will deal with the application of the proposed method to the temperature. In particular, the application of cokriging could be very promising due to the high dependency of temperature on the elevation.