Skip to main content
SpringerLink
Log in

Elastic inverted pendulum with backlash in suspension: stabilization problem

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

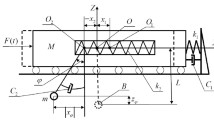
In this paper, we investigate the elastic inverted pendulum with hysteretic nonlinearity (a backlash) in the suspension point. Namely, the problems of stabilization and optimization of such a system are considered. The algorithm (based on the bionic model) which provides the effective procedure for finding of optimal parameters is presented and applied to considered system. The results of numerical simulations, namely the phase portraits and the dynamics of Lyapunov function, are also presented and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. Here it should be noted that although a lot of control algorithms are researched in the system control design, proportional-integral-derivative (PID) controller is the most widely used controller structure in the realization of a control system [36]. The advantages of PID controller, which have greatly contributed to its wide acceptance, are its simplicity and sufficient ability to solve many practical control problems.

  2. It should be noted that such an operator is considered on the monotonic inputs. On the piecewise monotonic inputs, this operator can be determined using the semigroup identity [19]

    $$\begin{aligned} \varGamma [X(t_{1}),L]Y(t)=\varGamma \left[ \varGamma [X_{0},L] Y(t_{1}),L\right] Y(t). \end{aligned}$$

    And then, using the special limit construction, such an operator can be redefined on the all continuous functions.

  3. In this paper, we use the following notations: \(a_{x}=\frac{\partial a}{\partial x}\), \(a_{t}=\frac{\partial a}{\partial t}\).

References

  1. Arinstein, A., Gitterman, M.: Inverted spring pendulum driven by a periodic force: linear versus nonlinear analysis. Eur. J. Phys. 29, 385–392 (2008)

    Article  Google Scholar 

  2. Arkhipova, I.M., Luongo, A.: Stabilization via parametric excitation of multi-dof statically unstable systems. Commun. Nonlinear Sci. Numer. Simul. 19, 3913–3926 (2014)

    Article  MathSciNet  Google Scholar 

  3. Arkhipova, I.M., Luongo, A., Seyranian, A.P.: Vibrational stabilization of the upright statically unstable position of a double pendulum. J. Sound Vib. 331, 457–469 (2012)

    Article  Google Scholar 

  4. Åström, K.J., Furuta, K.: Swinging up a pendulum by energy control. Automatica 36, 287–295 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bloch, A.M., Leonard, N.E., Marsden, J.E.: Controlled lagrangians and the stabilization of mechanical systems. I. The first matching theorem. IEEE Trans. Autom. Control 45, 2253–2270 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  6. Boubaker, O.: The inverted pendulum: a fundamental benchmark in control theory and robotics. In: International Conference on Education and e-Learning Innovations (ICEELI 2012), pp. 1–6 (2012)

  7. Butikov, E.I.: Subharmonic resonances of the parametrically driven pendulum. J. Phys. A Math. Theor. 35, 6209 (2002)

    Article  Google Scholar 

  8. Butikov, E.I.: An improved criterion for Kapitza’s pendulum stability. J. Phys. A Math. Theor. 44, 295,202 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  9. Butikov, E.I.: Oscillations of a simple pendulum with extremely large amplitudes. Eur. J. Phys. 33, 1555–1563 (2012)

    Article  MATH  Google Scholar 

  10. Chang, L.H., Lee, A.C.: Design of nonlinear controller for bi-axial inverted pendulum system. IET Control Theory Appl. 1, 979–986 (2007)

    Article  Google Scholar 

  11. Chaturvedi, N.A., McClamroch, N.H., Bernstein, D.S.: Stabilization of a 3D axially symmetric pendulum. Automatica 44, 2258–2265 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  12. Chernous’ko, F.L., Reshmin, S.A.: Time-optimal swing-up feedback control of a pendulum. Nonlinear Dynam. 47, 65–73 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  13. Dadfarnia, M., Jalili, N., Xian, B., Dawson, D.M.: A Lyapunov-based piezoelectric controller for flexible cartesian robot manipulators. J. Dyn. Syst. Meas. Control 126, 347–358 (2004)

    Article  Google Scholar 

  14. Dadios, E.P., Fernandez, P.S., Williams, D.J.: Genetic algorithm on line controller for the flexible inverted pendulum problem. J. Adv. Comput. Intell. Intell. Inform. 10, 155–160 (2006)

    Google Scholar 

  15. Huang, J., Ding, F., Fukuda, T., Matsuno, T.: Modeling and velocity control for a novel narrow vehicle based on mobile wheeled inverted pendulum. IEEE Trans. Control Syst. Technol. 21, 1607–1617 (2013)

    Article  Google Scholar 

  16. Kapitza, P.L.: Dynamic stability of a pendulum when its point of suspension vibrates. Soviet Phys. JETP 21, 588–592 (1951)

    Google Scholar 

  17. Kapitza, P.L.: Pendulum with a vibrating suspension. Usp. Fiz. Nauk 44, 7–15 (1951). (in Russian)

    Google Scholar 

  18. Kim, K.D., Kumar, P.: Real-time middleware for networked control systems and application to an unstable system. IEEE Trans. Control Syst. Technol. 21, 1898–1906 (2013)

    Article  Google Scholar 

  19. Krasnosel’skii, M.A., Pokrovskii, A.V.: Syst. Hysteresis. Springer, Berlin (1989)

    Book  Google Scholar 

  20. Kuwana, Y., Shimoyama, I., Sayama, Y., Miura, H.: Synthesis of pheromone-oriented emergent behavior of a silkworm moth. In: Intelligent Robots and Systems ’96, IROS 96, Proceedings of the 1996 IEEE/RSJ International Conference on 3,1722–1729 (1996)

  21. Li, G., Liu, X.: Dynamic characteristic prediction of inverted pendulum under the reduced-gravity space environments. Acta Astronaut. 67, 596–604 (2010)

    Article  Google Scholar 

  22. Lozano, R., Fantoni, I., Block, D.J.: Stabilization of the inverted pendulum around its homoclinic orbit. Syst. Control Lett. 40, 197–204 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  23. Luo, Z.H., Guo, B.Z.: Shear force feedback control of a single-link flexible robot with a revolute joint. IEEE Trans. Autom. Control 42, 53–65 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  24. Mason, P., Broucke, M., Piccoli, B.: Time optimal swing-up of the planar pendulum. IEEE Trans. Autom. Control 53, 1876–1886 (2008)

    Article  MathSciNet  Google Scholar 

  25. Mata, G.J., Pestana, E.: Effective hamiltonian and dynamic stability of the inverted pendulum. Eur. J. Phys. 25, 717 (2004)

    Article  MATH  Google Scholar 

  26. Mikheev, Y.V., Sobolev, V.A., Fridman, E.M.: Asymptotic analysis of digital control systems. Autom. Rem. Control 49, 1175–1180 (1988)

    MathSciNet  MATH  Google Scholar 

  27. Pierce-Shimomura, J.T., Morse, T.M., Lockery, S.R.: The fundamental role of pirouettes in Caenorhabditis elegans chemotaxis. J. Neurosci. 19, 9557–9569 (1999)

    Google Scholar 

  28. Reshmin, S.A., Chernous’ko, F.L.: A time-optimal control synthesis for a nonlinear pendulum. J. Comput. Syst. Sci. Int. 46, 9–18 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  29. Sazhin, S., Shakked, T., Katoshevski, D., Sobolev, V.: Particle grouping in oscillating flows. Eur. J. Mech. B Fluid. 27, 131–149 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. Semenov, M.E., Grachikov, D.V., Mishin, M.Y., Shevlyakova, D.V.: Stabilization and control models of systems with hysteresis nonlinearities. Eur. Res. 20, 523–528 (2012)

    Google Scholar 

  31. Semenov, M.E., Shevlyakova, D.V., Meleshenko, P.A.: Inverted pendulum under hysteretic control: stability zones and periodic solutions. Nonlinear Dyn. 75, 247–256 (2014)

    Article  MathSciNet  Google Scholar 

  32. Sieber, J., Krauskopf, B.: Complex balancing motions of an inverted pendulum subject to delayed feedback control. Phys. D 197, 332–345 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  33. Siuka, A., Schöberl, M.: Applications of energy based control methods for the inverted pendulum on a cart. Robot. Auton. Syst. 57, 1012–1017 (2009)

    Article  Google Scholar 

  34. Stephenson, A.: On an induced stability. Philos. Mag. 15, 233 (1908)

    Article  MATH  Google Scholar 

  35. Tang, J., Ren, G.: Modeling and simulation of a flexible inverted pendulum system. Tsinghua Sci. Technol. 14(Suppl. 2), 22–26 (2009)

    Article  MathSciNet  Google Scholar 

  36. Wang, J.J.: Simulation studies of inverted pendulum based on PID controllers. Simul. Model. Pract. Theory 19, 440–449 (2011)

    Article  Google Scholar 

  37. Xu, C., Yu, X.: Mathematical model of elastic inverted pendulum control system. Control Theory Technol. 2, 281–282 (2004)

    Article  Google Scholar 

  38. Yavin, Y.: Control of a rotary inverted pendulum. Appl. Math. Lett. 12, 131–134 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  39. Yue, J., Zhou, Z., Jiang, J., Liu, Y., Hu, D.: Balancing a simulated inverted pendulum through motor imagery: an EEG-based real-time control paradigm. Neurosci. Lett. 524, 95–100 (2012)

    Article  Google Scholar 

  40. Zhang, Y.X., Han, Z.J., Xu, G.Q.: Expansion of solution of an inverted pendulum system with time delay. Appl. Math. Comput. 217, 6476–6489 (2011)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This work is supported by the RFBR Grant 13-08-00532-a.

Author information

Author notes

  1. Mikhail E. Semenov, Andrey M. Solovyov & Peter A. Meleshenko

    Present address: Digital Technologies Department, Voronezh State University, Universitetskaya sq. 1, 394006, Voronezh, Russia

Authors and Affiliations

  1. Meteorology Department, Zhukovsky–Gagarin Air Force Academy, Starykh Bolshevikov St. 54 “A”, 394064, Voronezh, Russia

    Mikhail E. Semenov

  2. Mathematics Department, Voronezh State University of Architecture and Civil Engineering, XX-letiya Oktyabrya St. 84, 394006, Voronezh, Russia

    Mikhail E. Semenov

  3. The National University of Science and Technology MISiS, Makarenko 42, Staryi Oskol, Russia

    Mikhail E. Semenov

  4. Communication Department, Zhukovsky–Gagarin Air Force Academy, Starykh Bolshevikov St. 54 “A”, 394064, Voronezh, Russia

    Peter A. Meleshenko

Authors
  1. Mikhail E. Semenov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andrey M. Solovyov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Peter A. Meleshenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mikhail E. Semenov.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Semenov, M.E., Solovyov, A.M. & Meleshenko, P.A. Elastic inverted pendulum with backlash in suspension: stabilization problem. Nonlinear Dyn 82, 677–688 (2015). https://doi.org/10.1007/s11071-015-2186-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2186-y

Keywords

Search

Navigation