Collective dynamics of periodic nonlinear oscillators under simultaneous parametric and external excitations

Abstract

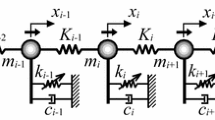
The collective dynamics of a periodic structure of coupled Duffing–Van Der Pol oscillators is investigated under simultaneous external and parametric excitations. An analytico-computational model based on a perturbation technique, combined with standing wave decomposition and the asymptotic numerical method is developed for a finite number of coupled oscillators. The frequency responses and the basins of attraction are analyzed for the case of small arrays, demonstrating the importance of the multi-mode solutions and the robustness of their attractors. This model can be exploited to design periodic structure-based smart systems with high performance, by taking advantage of the multi-modes induced by the collective dynamics.

Appendices

Appendix 1

Substituting Eq. (5) into the EOM term by term. Up to the order $\varepsilon ^{\frac{3}{2}}$, we obtain:

$$\begin{aligned}&(u_{n+1}-2u_{n}+u_{n-1})\\&\quad =\,-4\varepsilon ^{\frac{1}{2}} \sum _{m=1}^{N}\sin ^{2}\left( \frac{q_{m}}{2}\right) \sin (n q_{m})(A_{m}e^{i\omega _{m}t}+c.c.)\\&\qquad \quad +\,\varepsilon ^{\frac{3}{2}}(u_{n+1}^{(1)}-2u_{n}^{(1)}+u_{n-1}^{(1)}),\\&u_{n}^{3}\!=\!\frac{\varepsilon ^{\frac{3}{2}}}{4}\!\! \sum _{j,k,l}\{T^{(-j,k,l)}\!+\!T^{(j,-k,l)}\!+\!T^{(j,k,-l)}\!-\!T^{(j,k,l)}\}\\&\qquad \quad \times \, \{A_{j}A_{k}A_{l}e^{i(\omega _{j}+\omega _{k}+\omega _{l})t}\\&\qquad \quad +\,3A_{j}A_{k}A_{l}^{*}e^{i(\omega _{j}+\omega _{k}-\omega _{l})t}+c.c.\},\\&u_{n}^{2}\dot{u}_{n}= 4 \varepsilon ^{\frac{3}{2}}\sum _{j,k,l}\{T^{(-j,k,l)}\\&\qquad \quad +T^{(j,-k,l)}+ T^{(j,k,-l)}-T^{(j,k,l)}\}\\&\qquad \qquad \times \, (A_{j}e^{i\omega _{j}t}+c.c.)(A_{k}e^{i\omega _{k}t}+c.c.)\\&\qquad \qquad \times (i\omega _{l}A_{l}e^{i\omega _{l}t}+c.c.),\\&[(u_{n}-u_{n+1})^{3}+(u_{n}-u_{n-1})^{3}]\\&\quad =\, 4 \varepsilon ^{\frac{3}{2}}\sum _{j,k,l}\varPi _{j, k, l} \{ S^{(-j,k,l)}+S^{(j,-k,l)}\\&\quad \quad + S^{(j,k,-l)}+S^{(j,k,l)}\} \\&\quad \quad \times \, \{A_{j}A_{k}A_{l}e^{i(\omega _{j}+\omega _{k}+\omega _{l})t}\\&\quad \quad +3A_{j}A_{k}A_{l}^{*}e^{i(\omega _{j}+\omega _{k}-\omega _{l})t}+c.c.\},\\&[(u_{n}\!-\!u_{n+1})^{2}(\dot{u}_{n}\!-\!\dot{u}_{n+1})\!+\! (u_{n}\!-\!u_{n-1})^{2}(\dot{u}_{n}\!-\!\dot{u}_{n-1})]\\&\quad =\, \frac{\varepsilon ^{\frac{3}{2}}}{4} \sum _{j,k,l}\varPi _{j, k, l} \{ S^{(-j,k,l)}+S^{(j,-k,l)}\\&\qquad \quad +\, S^{(j,k,-l)}+S^{(j,k,l)}\} \\&\qquad \quad \times \, (A_{j}e^{i\omega _{j}t}\!+\!c.c.)(A_{k}e^{i\omega _{k}t}\!+\!c.c.)(i\omega _{l}A_{l}e^{i\omega _{l}t}\!+\!c.c.), \end{aligned}$$

with:

$$\begin{aligned}&T^{(j,k,l)}=\sin [n (sgn(j)q_{j}+sgn(k)q_{k}+sgn(l)q_{l})]\\&S^{(j,k,l)}\!=\!\sin \!\left[ \frac{sgn(j)q_{j}\!+\!sgn(k)q_{k}\!+\!sgn(l)q_{l}}{2}\right] T^{(j,k,l)}\\&\varPi _{j, k,l}=\sin \left( \frac{q_{j}}{2}\right) \sin \left( \frac{q_{k}}{2}\right) \sin \left( \frac{q_{l}}{2}\right) \end{aligned}$$

Appendix 2

The two delta functions, defined in terms of Kronecker deltas are:

$$\begin{aligned}&\varDelta _{jkl;m}^{(1)}\!=\! \delta _{-j+k+l,m}\!-\!\delta _{-j+k+l,m}\!-\!\delta _{-j+k+l,2(N+1)-m}\\&\quad +\,\delta _{j-k+l,m}-\delta _{j-k+l,m}-\delta _{j-k+l,2(N+1)-m} \\&\quad +\,\delta _{j+k-l,m}-\delta _{j+k-l,m}-\delta _{j+k-l,2(N+1)-m} \\&\quad -\,\delta _{j+k+l,m}+\delta _{j+k+l,2(N+1)-m}-\delta _{j+k+l,2(N+1)+m} \end{aligned}$$

and

$$\begin{aligned}&\varDelta _{jkl;m}^{(2)}\!=\!\delta _{-j+k+l,m}\!+\!\delta _{-j+k+l,m}\!+\!\delta _{-j+k+l,2(N+1)-m}\\&\quad +\,\delta _{j-k+l,m}+\delta _{j-k+l,m}-\delta _{j-k+l,2(N+1)-m} \\&\quad +\,\delta _{j+k-l,m}+\delta _{j+k-l,m}-\delta _{j+k-l,2(N+1)-m} \\&\quad +\,\delta _{j+k+l,m}-\delta _{j+k+l,2(N+1)-m}-\delta _{j+k+l,2(N+1)+m} \end{aligned}$$