Vehicle–bridge interaction analysis modeling derailment during earthquakes

Abstract

A realistic simulation of train derailment is crucial when assessing the safety of a train running over a bridge during earthquake excitation. This paper presents a seismic vehicle–bridge interaction analysis that simulates directly different wheel–rail contact states including flange contact, detachment, uplifting, wheel–rail climbing-up, recontact, and ultimately, derailment. The proposed model determines the contact point and the direction of the contact forces over practical nonlinear profiles of wheels and rails. It then classifies the wheel–rail contact, as double contact, single contact or double detachment, and tackles accordingly the kinematics. The modeling of the wheel–rail contact along the normal direction hinges upon the principles of nonsmooth dynamics and accounts for continuous contacts of finite duration, impacts (instantaneous duration) and transitions from continuous contacts to detachments. The modeling of the tangential contact forces follows the nonlinear creep theory. The results verify that well-known force-based metrics such as derailment factor and offload factor yield conservative estimations of train operational safety. The analysis stresses the key role of flange contact under a large contact angle that could lead to the detachment of the other wheel of the same wheelset, and underlines the importance of a more realistic train–bridge interaction modeling during earthquakes. For the examples examined, which involve a complete three-dimensional vehicle running on simply supported bridge units, derailment occurs when a wheel rolls over the rail head (wheel–rail climbing-up). The results unveil that both the amplitude and the frequency of the earthquakes are important to the safety of trains running over bridges.

Appendices

Appendix A

The diagonal mass matrix of a single vehicle is [26]:

$$\begin{aligned} {{\mathbf{M}}^V} = \hbox {diag}\left[ {\begin{array}{*{20}{c}} {{{\mathbf{M}}^c}}&{{{\mathbf{M}}^{t1}}}&{{{\mathbf{M}}^{t2}}}&{{{\mathbf{M}}^{w1}}}&{{{\mathbf{M}}^{w2}}}&{{{\mathbf{M}}^{w3}}}&{{{\mathbf{M}}^{w4}}} \end{array}} \right] \end{aligned}$$

(37)

Sub-matrices in  ${{\mathbf{M}}^V}$  are:

$$\begin{aligned} {{\mathbf{M}}^c}= & {} \hbox {diag}\left[ {\begin{array}{*{20}{c}} {{m_c}}&{{m_c}}&{{I_{cx}}}&{{I_{cy}}}&{{I_{cz}}} \end{array}} \right] , \end{aligned}$$

(38)

$$\begin{aligned} {{\mathbf{M}}^{t1}}= & {} {{\mathbf{M}}^{t2}} = \hbox {diag}\left[ {\begin{array}{*{20}{c}} {{m_t}}&{{m_t}}&{{I_{tx}}}&{{I_{ty}}}&{{I_{tz}}} \end{array}} \right] , \end{aligned}$$

(39)

and

$$\begin{aligned} {{\mathbf{M}}^{w1}}= & {} {{\mathbf{M}}^{w2}} = {{\mathbf{M}}^{w3}} = {{\mathbf{M}}^{w4}} \nonumber \\= & {} diag\left[ {\begin{array}{*{20}{c}} {{m_w}}&{{m_w}}&{{I_{wx}}}&{{I_{wz}}} \end{array}} \right] . \end{aligned}$$

(40)

The partitioned stiffness matrix is given as:

$$\begin{aligned} {{\mathbf{K}}^V} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{K}}{}^{cc}}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{{\mathrm{symm}}{\mathrm{.}}}\\ {{{\mathbf{K}}^{t1c}}}&{}{{{\mathbf{K}}^{t1t1}}}&{}{}&{}{}&{}{}&{}{}&{}{}\\ {{{\mathbf{K}}^{t2c}}}&{}{\mathbf{0}}&{}{{{\mathbf{K}}^{t2t2}}}&{}{}&{}{}&{}{}&{}{}\\ {\mathbf{0}}&{}{{{\mathbf{K}}^{w1t1}}}&{}{\mathbf{0}}&{}{{{\mathbf{K}}^{w1w1}}}&{}{}&{}{}&{}{}\\ {\mathbf{0}}&{}{{{\mathbf{K}}^{w2t1}}}&{}{\mathbf{0}}&{}{\mathbf{0}}&{}{{{\mathbf{K}}^{w2w2}}}&{}{}&{}{}\\ {\mathbf{0}}&{}{\mathbf{0}}&{}{{{\mathbf{K}}^{w3t2}}}&{}{\mathbf{0}}&{}{\mathbf{0}}&{}{{{\mathbf{K}}^{w3w3}}} &{}{}\\ {\mathbf{0}}&{}{\mathbf{0}}&{}{{{\mathbf{K}}^{w4t2}}}&{}{\mathbf{0}}&{}{\mathbf{0}}&{}{\mathbf{0}}&{}{{{\mathbf{K}}^{w4w4}}} \end{array}} \right] \end{aligned}$$

(41)

Table 3 The parameters and properties of the vehicle model of HSR trains [25]

The nonzero entries in the partitioned matrix are:

$$\begin{aligned} {{\mathbf{K}}^{cc}}= & {} \left[ {\begin{array}{*{20}{c}} {4{k_{y2}}}&{}{}&{}{}&{}{}&{}{{\mathrm{symm}}{\mathrm{.}}}\\ 0&{}{4{k_{z2}}}&{}{}&{}{}&{}{}\\ {4{h_1}{k_{y2}}}&{}0&{}a&{}{}&{}{}\\ 0&{}0&{}0&{}b&{}{}\\ 0&{}0&{}0&{}0&{}c \end{array}} \right] , \end{aligned}$$

(42)

$$\begin{aligned} {{\mathbf{K}}^{t1c}}= & {} \left[ {\begin{array}{*{20}{c}} { - 2{k_{y2}}}&{}0&{}{ - 2{h_1}{k_{y2}}}&{}0&{}{ - 2{d_2}{k_{y2}}}\\ 0&{}{ - 2{k_{z2}}}&{}0&{}{2{d_2}{k_{z2}}}&{}0\\ {2{h_2}{k_{y2}}}&{}0&{}d&{}0&{}{2{h_2}{d_2}{k_{y2}}}\\ 0&{}0&{}0&{}{2{h_1}{h_2}{k_{x2}}}&{}0\\ 0&{}0&{}0&{}0&{}{ - 2{b_2}^2{k_{x2}}} \end{array}} \right] , \nonumber \\ \end{aligned}$$

(43)

$$\begin{aligned} {{\mathbf{K}}^{t2c}}= & {} \left[ {\begin{array}{*{20}{c}} { - 2{k_{y2}}}&{}0&{}{ - 2{h_2}{k_{y2}}}&{}0&{}{2{d_2}{k_{y2}}}\\ 0&{}{ - 2{k_{z2}}}&{}0&{}{ - 2{d_2}{k_{z2}}}&{}0\\ {2{h_2}{k_{y2}}}&{}0&{}d&{}0&{}{ - 2{h_2}{d_2}{k_{y2}}}\\ 0&{}0&{}0&{}{2{h_1}{h_2}{k_{x2}}}&{}0\\ 0&{}0&{}0&{}0&{}{ - 2{b_2}^2{k_{x2}}} \end{array}} \right] , \nonumber \\ \end{aligned}$$

(44)

$$\begin{aligned} {{\mathbf{K}}^{t1t1}}= & {} {{\mathbf{K}}^{t2t2}} \nonumber \\= & {} \left[ {\begin{array}{*{20}{c}} {2{k_{y2}} + 4{k_{y1}}}&{}{}&{}{}&{}{}&{}{{\mathrm{symm}}.}\\ 0&{}{2{k_{z2}} + 4{k_{z1}}}&{}{}&{}{}&{}{}\\ {4{h_3}{k_{y1}} - 2{h_2}{k_{y2}}}&{}0&{}e&{}{}&{}{}\\ 0&{}0&{}0&{}f&{}{}\\ 0&{}0&{}0&{}0&{}g \end{array}} \right] , \nonumber \\ \end{aligned}$$

(45)

$$\begin{aligned} {{\mathbf{K}}^{w1t1}}= & {} {{\mathbf{K}}^{w3t2}} \nonumber \\= & {} \left[ {\begin{array}{*{20}{c}} { - 2{k_{y1}}}&{}0&{}{2{h_3}{k_{y1}}}&{}0&{}{ - 2{d_1}{k_{y1}}}\\ 0&{}{ - 2{k_{z1}}}&{}0&{}{2{d_1}{k_{z1}}}&{}0\\ 0&{}0&{}{ - 2{b_1}^2{k_{z1}}}&{}0&{}0\\ 0&{}0&{}0&{}0&{}{ - 2{b_1}^2{k_{x1}}} \end{array}} \right] , \nonumber \\ \end{aligned}$$

(46)

$$\begin{aligned} {{\mathbf{K}}^{w2t1}}= & {} {{\mathbf{K}}^{w4t2}} \nonumber \\= & {} \left[ {\begin{array}{*{20}{c}} { - 2{k_{y1}}}&{}0&{}{2{h_3}{k_{y1}}}&{}0&{}{2{d_1}{k_{y1}}}\\ 0&{}{ - 2{k_{z1}}}&{}0&{}{ - 2{d_1}{k_{z1}}}&{}0\\ 0&{}0&{}{ - 2{b_1}^2{k_{z1}}}&{}0&{}0\\ 0&{}0&{}0&{}0&{}{ - 2{b_1}^2{k_{x1}}} \end{array}} \right] , \nonumber \\ \end{aligned}$$

(47)

$$\begin{aligned} {{\mathbf{K}}^{w1w1}}= & {} {{\mathbf{K}}^{w2w2}} = {{\mathbf{K}}^{w3w3}} = {{\mathbf{K}}^{w4w4}}\nonumber \\= & {} diag\left[ {\begin{array}{*{20}{c}} {2{k_{y1}}}&{2{k_{z1}}}&{2{b_1}^2{k_{z1}}}&{2{b_1}^2{k_{x1}}} \end{array}} \right] \end{aligned}$$

(48)

where

$$\begin{aligned} \begin{aligned} a&= 4{h_1}^2{k_{y2}}\; + 4{b_2}^2{k_{z2}},b = 4{d_2}^2{k_{z2}} + 4{h_1}^2{k_{x2}},\\ c&= 4{d_2}^2{k_{y2}} + 4{b_2}^2{k_{x2}},d = - 2{b_2}^2{k_{z2}} + 2{h_1}{h_2}{k_{y2}},\\ e&= 2{b_2}^2{k_{z2}} + 2{h_2}^2{k_{y2}} + 4{b_1}^2{k_{z1}} + 4{h_3}^2{k_{y1}}\\ f&= 2{h_2}^2{k_{x2}} + 4{d_1}^2{k_{z1}} + 4{h_3}^2{k_{x1}},\\ g&= 4{b_1}^2{k_{x1}} + 4{d_1}^2{k_{y1}} + 2{b_2}^2{k_{x2}}. \end{aligned} \end{aligned}$$

(49)

Replacing  ‘k’  in the corresponding sub-stiffness matrix with  ‘c’, the damping matrix  ${{\mathbf{C}}^V}$  is identical in form with the stiffness matrix  ${{\mathbf{K}}^V}$  [26].

The contact direction matrices for the upper parts of the vehicle (car body and bogies) are zero. The nonzero normal contact direction matrix of a single wheelset in Eq. (9) is given as [29]:

$$\begin{aligned} {{\mathbf{W}}_N}^{wi} = \left[ {\begin{array}{*{20}{c}} {{\mathrm{c}}{\delta _L} \cdot {\mathrm{s}} {\phi ^{wi}} \cdot {\mathrm{s}} {\psi ^{wi}} + {\mathrm{s}}{\delta _L} \cdot {\mathrm{c}}{\phi ^{wi}} \cdot {\mathrm{s}} {\psi ^{wi}}}&{}{{\mathrm{c}}{\delta _R} \cdot {\mathrm{s}} {\phi ^{wi}} \cdot {\mathrm{s}} {\psi ^{wi}} - {\mathrm{s}}{\delta _R} \cdot {\mathrm{c}}{\phi ^{wi}} \cdot {\mathrm{s}} {\psi ^{wi}}}\\ { -\, {\mathrm{c}}{\delta _L} \cdot {\mathrm{s}}{\phi ^{wi}} \cdot {\mathrm{c}}{\psi ^{wi}} - {\mathrm{s}}{\delta _L} \cdot {\mathrm{c}}{\phi ^{wi}} \cdot {\mathrm{c}}{\psi ^{wi}}}&{}{ -\, {\mathrm{c}}{\delta _R} \cdot {\mathrm{s}}{\phi ^{wi}} \cdot {\mathrm{c}}{\psi ^{wi}} + {\mathrm{s}}{\delta _R} \cdot {\mathrm{c}}{\phi ^{wi}} \cdot {\mathrm{c}}{\psi ^{wi}}}\\ {{\mathrm{c}}{\delta _L} \cdot {\mathrm{c}}{\phi ^{wi}} - {\mathrm{s}}{\delta _L} \cdot {\mathrm{s}}{\phi ^{wi}}}&{}{{\mathrm{c}}{\delta _R} \cdot {\mathrm{c}}{\phi ^{wi}} - {\mathrm{s}}{\delta _R} \cdot {\mathrm{s}}{\phi ^{wi}}}\\ 0&{}0\\ { -\, {r_L} \cdot {\mathrm{s}}{\delta _L} + {l_{aL}} \cdot {\mathrm{c}}{\delta _L}}&{}{{r_R} \cdot {\mathrm{s}}{\delta _R} - {l_{aR}} \cdot {\mathrm{c}}{\delta _R}}\\ 0&{}0 \end{array}} \right] \end{aligned}$$

(50)

The nonzero contact direction matrix of a single wheelset  ${{\mathbf{W}}_T}^{wi}$  corresponding to the longitudinal and the lateral creep forces (${{\lambda _{Tx}}^i}$  and  ${{\lambda _{Ty}}^i}$) and the spin moment (${{\lambda _{Mz}}^i}$) is given as:

$$\begin{aligned} {{\mathbf{W}}_T}^{wi} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf{W}}_{Tx}}^{wi}}&{{{\mathbf{W}}_{Ty}}^{wi}}&{{{\mathbf{W}}_{Mz}}^{wi}} \end{array}} \right] \end{aligned}$$

(51)

with

$$\begin{aligned} {{\mathbf{W}}_{Tx}}^{wi}= & {} \left[ {\begin{array}{*{20}{c}} {{\mathrm{c}}{\psi ^{wi}}}&{}{{\mathrm{c}}{\psi ^{wi}}}\\ {{\mathrm{s}} {\psi ^{wi}}}&{}{{\mathrm{s}} {\psi ^{wi}}}\\ 0&{}0\\ { - {l_{aL}} \cdot {\mathrm{c}} {\phi ^{wi}} - {r_L} \cdot {\mathrm{s}}{\phi ^{wi}}}&{}{{l_{aR}} \cdot {\mathrm{c}} {\phi ^{wi}} - {r_R} \cdot {\mathrm{s}}{\phi ^{wi}}}\\ 0&{}0\\ { - {r_L}}&{}{ - {r_R}} \end{array}} \right] , \end{aligned}$$

(52)

$$\begin{aligned} {{\mathbf{W}}_{Ty}}^{wi}= & {} \left[ {\begin{array}{*{20}{c}} { - {\mathrm{c}}{\delta _L} \cdot {\mathrm{c}} {\phi ^{wi}} \cdot {\mathrm{s}} {\psi ^{wi}} + {\mathrm{s}}{\delta _L} \cdot {\mathrm{s}}{\phi ^{wi}} \cdot {\mathrm{s}} {\psi ^{wi}}}&{}{ - {\mathrm{c}}{\delta _R} \cdot {\mathrm{c}} {\phi ^{wi}} \cdot {\mathrm{s}} {\psi ^{wi}} - {\mathrm{s}}{\delta _R} \cdot {\mathrm{s}}{\phi ^{wi}} \cdot {\mathrm{s}} {\psi ^{wi}}}\\ {{\mathrm{c}}{\delta _L} \cdot {\mathrm{c}} {\phi ^{wi}} \cdot {\mathrm{c}}{\psi ^{wi}} - {\mathrm{s}}{\delta _L} \cdot {\mathrm{s}}{\phi ^{wi}} \cdot {\mathrm{c}}{\psi ^{wi}}}&{}{{\mathrm{c}}{\delta _R} \cdot {\mathrm{c}} {\phi ^{wi}} \cdot {\mathrm{c}}{\psi ^{wi}} + {\mathrm{s}}{\delta _R} \cdot {\mathrm{s}}{\phi ^{wi}} \cdot {\mathrm{c}}{\psi ^{wi}}}\\ {{\mathrm{c}}{\delta _L} \cdot {\mathrm{s}}{\phi ^{wi}} + {\mathrm{s}}{\delta _L} \cdot {\mathrm{c}}{\phi ^{wi}}}&{}{{\mathrm{c}}{\delta _R} \cdot {\mathrm{s}}{\phi ^{wi}} - {\mathrm{s}}{\delta _R} \cdot {\mathrm{c}}{\phi ^{wi}}}\\ 0&{}0\\ {{r_L} \cdot {\mathrm{c}}{\delta _L} + {l_{aL}} \cdot {\mathrm{s}}{\delta _L}}&{}{{r_R} \cdot {\mathrm{c}}{\delta _R} + {l_{aR}} \cdot {\mathrm{s}}{\delta _R}}\\ 0&{}0 \end{array}} \right] , \end{aligned}$$

(53)

and

$$\begin{aligned} {{\mathbf{W}}_{Mz}}^{wi} = \left[ {\begin{array}{*{20}{c}} 0&{}0\\ 0&{}0\\ 0&{}0\\ {{\mathrm{c}}{\delta _L} \cdot {\mathrm{c}} {\phi ^{wi}} - {\mathrm{s}}{\delta _L} \cdot {\mathrm{s}}{\phi ^{wi}}}&{}{{\mathrm{c}}{\delta _R} \cdot {\mathrm{c}} {\phi ^{wi}} + {\mathrm{s}}{\delta _R} \cdot {\mathrm{s}}{\phi ^{wi}}}\\ 0&{}0\\ { - {\mathrm{s}}{\delta _L}}&{}{{\mathrm{s}}{\delta _R}} \end{array}} \right] \end{aligned}$$

(54)

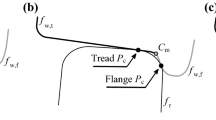
where the contact parameters  $\delta _L$  and  $\delta _R$  are the contact angles of the left  (L)  wheel and the right  (R)  wheel; $r_L$  and  $r_R$  are the actual rolling radii; and  $l_{aL}$  and  $l_{aR}$  are the half-contact width of the left and the right wheels (Fig. 5b). Abbreviations ‘s’ and ‘c’ denote the ‘sin’ and the ‘cos’ functions.

Table 3 lists the properties of the vehicle model [25]:

Table 4 Comparison of computational time between lookup tables and online contact search approach

Appendix B

See Table 4.