Dynamic analysis and performance evaluation of nonlinear inerter-based vibration isolators

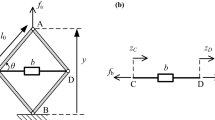
Abstract

This paper investigates a nonlinear inertance mechanism (NIM) for vibration mitigation and evaluates the performance of nonlinear vibration isolators employing such mechanism. The NIM comprises a pair of oblique inerters with one common hinged terminal and the other terminals fixed. The addition of the NIM to a linear spring-damper isolator and to nonlinear quasi-zero-stiffness (QZS) isolators is considered. The harmonic balance method is used to derive the steady-state frequency response relationship and force transmissibility of the isolators subjected to harmonic force excitations. Different performance indices associated with the dynamic displacement response and force transmissibility are employed to evaluate the performance of the resulting isolators. It is found that the frequency response curve of the inerter-based nonlinear isolation system with the NIM and a linear stiffness bends towards the low-frequency range, similar to the characteristics of the Duffing oscillator with softening stiffness. It is shown that the addition of NIM to a QZS isolator enhances vibration isolation performance by providing a wider frequency band of low amplitude response and force transmissibility. These findings provide a better understanding of the functionality of the NIM and assist in better designs of nonlinear passive vibration mitigation systems with inerters.

Appendix: Vibration power flow analysis

The non-dimensional power flow balance equations of the systems shown by Fig. 3d and c are obtained by multiplying by non-dimensional velocity $X'$ on both sides of the original governing equations (6a) and (6b):

$$\begin{aligned}&(1+\lambda )X''X'+2\zeta X'X'+XX'=X'F_e\cos {\varOmega \tau }, \end{aligned}$$

(41a)

$$\begin{aligned}&X''X'+2\zeta X'X'+H(X)X'+G(X,X',X'')X'\nonumber \\&\quad =X'F_e\cos {\varOmega \tau }, \end{aligned}$$

(41b)

Thus, for the vibration isolation systems shown in Fig. 3, the non-dimensional instantaneous time-averaged input power by the external excitation force and the dissipated power by the damper in the isolator are expressed by the products of the forces and the corresponding velocities:

$$\begin{aligned} p_\mathrm{in}&=X'F_e\cos {\varOmega \tau }, \end{aligned}$$

(42a)

$$\begin{aligned} p_{d}&=2\zeta X'X', \end{aligned}$$

(42b)

respectively. Interested readers may refer to ref. [18] for the basic concept and definition of vibration power flow as well as its application to dynamic analysis of linear and nonlinear vibration suppression systems as in Refs. [2, 19, 20, 22, 25, 26]. In the steady-state motion, the non-dimensional time-averaged input and dissipated powers over one period of the external excitation are

$$\begin{aligned} {\bar{p}}_\mathrm{in}(\varOmega )&=\frac{1}{T}\int _{\tau _0}^{\tau _0+T} X'F_e\cos {\varOmega \tau } \,\mathrm {d}\tau \approx -\frac{r\varOmega }{2}F_e \sin \phi , \end{aligned}$$

(43a)

$$\begin{aligned} {\bar{p}}_{d}(\varOmega )&=\frac{1}{T}\int _{\tau _0}^{\tau _0+T} 2\zeta X'X'\,\mathrm {d}\tau \approx \zeta r^2 \varOmega ^2, \end{aligned}$$

(43b)

respectively, where $\tau _0$ is the starting time while T is the averaging time, set to be a period of excitation, i.e. $T=2\pi /\varOmega$, and a first-order approximation of the velocity with $X'=-r\varOmega \sin (\varOmega \tau +\phi )$ was used for the inerter-based nonlinear isolation system shown in Fig. 3c. Note that based on Eqs. (16b) and (43a), the first-order approximation of the time-averaged input power into the system shown in Fig. 3c is

$$\begin{aligned} {\bar{p}}_\mathrm{in}(\varOmega )=\zeta r^2 \varOmega ^2. \end{aligned}$$

(44)

Note that it has been shown that Eq. (44) presents the exact analytical expression of the time-averaged input power into the inerter-based linear isolator [20]. Equations (43b) and (44) show that the first-order approximate expressions for the time-averaged input and dissipated powers are identical. This is due to the fact that over a cycle of steady-state periodic oscillation, there is no net change in potential and kinetic energies of the integrated nonlinear isolation system. Consequently, the vibration power input from the external excitation is all dissipated by damping.

The maximum kinetic energy of the excited system is widely used as a performance index of vibration control systems [19]. The non-dimensional maximum kinetic energy of the mass in the steady-state motion is

$$\begin{aligned} K_{\max }=\frac{1}{2}X'^2 \approx \frac{1}{2} r^2 \varOmega ^2. \end{aligned}$$

(45)

where a first-order approximation the steady-state velocity response was used for the inerter-based nonlinear isolator shown in Fig. 3. Note that a comparison of Eqs. (44) and (45) shows that

$$\begin{aligned} {\bar{p}}_\mathrm{in}=2\zeta K_{\max }. \end{aligned}$$

(46)

Equation (46) shows that for the system with a predetermined damping coefficient $\zeta$, the time-averaged input power is proportional to the maximum kinetic energy of the harmonically excited mass.

With reference to the frequency response relationship expressed by Eq. (17), the time-averaged input power and the maximum kinetic energy of the mass for the system shown in Fig. 3c can be rewritten as:

$$\begin{aligned}&{\bar{p}}_\mathrm{in}=\frac{\zeta \varOmega ^2 F_e^2}{(2\zeta \varOmega )^2+\Big (\alpha +\frac{3}{4}\beta r^2-\Big (1+\frac{\lambda }{2}r^2+\frac{\lambda }{4}r^4\Big )\varOmega ^2\Big )^2} \nonumber \\&\quad \le \frac{F_e^2}{4\zeta }, \end{aligned}$$

(47a)

$$\begin{aligned}&K_{\max }=\frac{\varOmega ^2 F_e^2}{2(2\zeta \varOmega )^2+2\Big (\alpha +\frac{3}{4}\beta r^2-\Big (1+\frac{\lambda }{2}r^2+\frac{\lambda }{4}r^4\Big )\varOmega ^2\Big )^2} \nonumber \\&\quad \le \frac{F_e^2}{8\zeta ^2}. \end{aligned}$$

(47b)

These equations show that there are upper limits for both the time-averaged input power and the maximum kinetic energy of the mass, respectively. The upper limits are only determined by the damping coefficient $\zeta$ and the excitation force amplitude $F_e$. These upper limits of the time-averaged power flow and the maximum kinetic energy of the mass may be reached when

$$\begin{aligned} \alpha +\frac{3\beta r^2}{4}-\left( 1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\right) \varOmega ^2=0. \end{aligned}$$

(48)

Recalling the backbone curve expression in Eq. (21) and frequency response relationship in (17), it is found that the upper limits of input power and kinetic energy of the mass are reached at the intersection point of the backbone curve and the displacement response curve.