Nonlinear dynamic response of sandwich plates with functionally graded auxetic 3D lattice core

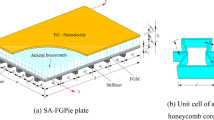
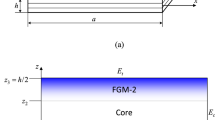
Abstract

This paper presents full-scale modeling and nonlinear dynamic analysis of sandwich plates with auxetic 3D lattice core, which is further designed to possess three functionally graded (FG) configurations through the plate thickness direction for the first time. The effective Poisson’s ratio (EPR) and fundamental frequencies of auxetic 3D lattice metamaterials are analyzed and verified by static and vibration tests using specimens fabricated by 3D printing. Considering the large deflection nonlinearity of sandwich plates and the accompanying changes in effective properties of lattice microstructures, full-scale FE modeling and nonlinear dynamic thermal–mechanical analysis are performed, with material properties assumed to be temperature dependent. Numerical results revealed that the auxetic core can significantly reduce the dynamic deflections, in comparison with its counterpart with positive EPR. Furthermore, FG configurations have distinct effects on the natural frequencies and dynamic deflection–time curves of sandwich plates, along with EPR–deflection curves in the large deflection region.

Appendix

The relative displacement along x₃-direction is twice that of endpoint A:

$$ \begin{aligned} \delta_{3} & = - 2 \cdot \left( {\delta_{3}^{\text{N}} + \delta_{3}^{\text{Q}} + \delta_{3}^{\text{M}} } \right) \\ & = - 2 \cdot \left[ {\frac{{b_{0} r^{2} }}{8EI}\frac{{\partial \left( {N^{2} } \right)}}{\partial P} + \left( {\frac{{b_{0}^{3} }}{24EI} + \frac{{5b_{0} r^{2} \left( {1 + \nu_{c} } \right)}}{18EI}} \right)\frac{{\partial \left( {Q^{2} } \right)}}{\partial P}} \right] \\ \end{aligned} $$

(A.1)

in which the minus sign is added to make this value negative because of the compressive loads, and

$$ \frac{{\partial \left( {N^{2} } \right)}}{\partial P} = 2P{\text{cos}}^{2} \alpha + 2T{\text{cos}}^{2} \alpha $$

(A.2a)

$$ \frac{{\partial \left( {Q^{2} } \right)}}{\partial P} = 2P{\text{sin}}^{2} \alpha - 2T\cos^{2} \alpha. $$

(A.2b)

To calculate the displacement along in-plane direction, two pairs of opposite forces are then applied as virtual additional loads. As illustrated in Fig. 1(d), the internal forces in the incline strut AC are now:

$$ \left\{ {\begin{array}{*{20}l} {N = P\cos \alpha + T\cos \alpha + F\sin \theta } \hfill \\ {Q = T(\begin{array}{*{20}c} 0 & { - 1} & 0 \\ \end{array} ) - T\cos \alpha (\begin{array}{*{20}c} {\sin \theta } & {{{ - a_{0} } \mathord{\left/ {\vphantom {{ - a_{0} } {2b_{0} }}} \right. \kern-0pt} {2b_{0} }}} & {{{ - H_u } \mathord{\left/ {\vphantom {{ - H_u } {2b_{0} }}} \right. \kern-0pt} {2b_{0} }}} \\ \end{array} )} \hfill \\ {\quad \,\,\,\, + P(\begin{array}{*{20}c} 0 & 0 & { - 1} \\ \end{array} ) - P\cos \alpha (\begin{array}{*{20}c} {\sin \theta } & {{{ - a_{0} } \mathord{\left/ {\vphantom {{ - a_{0} } {2b_{0} }}} \right. \kern-0pt} {2b_{0} }}} & {{{ - H_u } \mathord{\left/ {\vphantom {{ - H_u } {2b_{0} }}} \right. \kern-0pt} {2b_{0} }}} \\ \end{array} )} \hfill \\ {\quad \,\,\,\, + F(\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} ) - F\sin \theta (\begin{array}{*{20}c} {\sin \theta } & {{{ - a_{0} } \mathord{\left/ {\vphantom {{ - a_{0} } {2b_{0} }}} \right. \kern-0pt} {2b_{0} }}} & {{{ - H_u } \mathord{\left/ {\vphantom {{ - H_u } {2b_{0} }}} \right. \kern-0pt} {2b_{0} }}} \\ \end{array} )} \hfill \\ {M^{2} = \frac{{Q^{2} b_{0}^{2} }}{4}\left( {1 - \frac{2x}{{b_{0} }}} \right)^{2} } \hfill \\ \end{array} } \right.. $$

(A.3)

The relative displacement along in-plane direction is twice that of point C:

$$ \delta_{1} = 2 \cdot \left( {\Delta + \delta_{1}^{\text{N}} + \delta_{1}^{\text{Q}} + \delta_{1}^{\text{M}} } \right) $$

(A.4)

in which

$$ \delta_{1}^{\text{N}} = \left. {\frac{{b_{0} r^{2} }}{8EI}\frac{{\partial \left( {N^{2} } \right)}}{\partial F}} \right|_{F = 0} $$

(A.5a)

$$ \delta_{1}^{\text{Q}} = \frac{{5b_{0} r^{2} \left( {1 + \nu_c } \right)}}{18EI}\left. {\frac{{\partial \left( {Q^{2} } \right)}}{\partial F}} \right|_{F = 0} $$

(A.5b)

$$ \delta_{1}^{M} = \frac{{b_{0}^{3} }}{24EI}\left. {\frac{{\partial \left( {Q^{2} } \right)}}{\partial F}} \right|_{F = 0} $$

(A.5c)

and

$$ \left. {\frac{{\partial \left( {N^{2} } \right)}}{\partial F}} \right|_{F = 0} = 2\sin \theta \left( {P\cos \alpha + T\cos \alpha } \right) $$

(A.6a)

$$ \begin{aligned} \left. {\frac{{\partial \left( {Q^{2} } \right)}}{\partial F}} \right|_{F = 0} & = - 2\left( {\cos^{2} \theta } \right)\left[ {\left( {T + P} \right)\cos \alpha \sin \theta } \right] \\ & \quad + 2\left[ {\left( {\sin \theta } \right)\frac{{a_{0} }}{{2b_{0} }}} \right]\left[ { - T + \left( {T + P} \right)\cos \alpha \frac{{a_{0} }}{{2b_{0} }}} \right] \\ & \quad + 2\left[ {\left( {\sin \theta } \right)\frac{{H_u }}{{2b_{0} }}} \right]\left[ { - P + \left( {T + P} \right)\cos \alpha \frac{{H_u }}{{2b_{0} }}} \right]. \\ \end{aligned} $$

(A.6b)