Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: one-lump-multi-stripe and one-lump-multi-soliton types

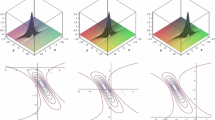
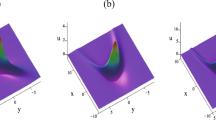
Abstract

Interaction solutions between lump and soliton are analytical exact solutions to nonlinear partial differential equations. The explicit expressions of the interaction solutions are of value for analysis of the interacting mechanism. We analyze the one-lump-multi-stripe and one-lump-multi-soliton solutions to nonlinear partial differential equations via Hirota bilinear forms. The one-lump-multi-stripe solutions are generated from the combined solution of quadratic functions and N exponential functions, while the one-lump-multi-soliton solutions from the combined solution of quadratic functions and N hyperbolic cosine functions. Within the context of the derivation of the lump solution and soliton solution, necessary and sufficient conditions are presented for the two types of interaction solutions, respectively, based on the combined solutions to the associated bilinear equations. Applications are made for a (2+1)-dimensional generalized KdV equation, the (2+1)-dimensional NNV system and the (2+1)-dimensional Ito equation.

Appendices

A

The lump solutions to the KPI equation [24] are given as

$$\begin{aligned} u=\frac{4(a_{1}^{2}+a_{5}^{2})f-8(a_{1}g+a_{5}h)^{2}}{f^{2}}, \end{aligned}$$

(A1)

where the functions f,  g and h are as follows:

$$\begin{aligned} f&=\Bigg (a_{1}x+a_{2}y+\frac{a_{1}a_{2}^{2}-a_{1}a_{6}^{2}+2a_{2}a_{5}a_{6}}{a_{1}^{2}+a_{5}^{2}}t+a_{4}\Bigg )^{2}+\Bigg (a_{5}x+a_{6}y+\frac{2a_{1}a_{2}a_{6}-a_{2}^{2}a_{5}+a_{5}a_{6}^{2}}{a_{1}^{2}+a_{5}^{2}}t+a_{8}\Bigg )^{2}\\&\quad +\frac{3(a_{1}^{2}+a_{5}^{2})^{3}}{(a_{1}a_{6}-a_{2}a_{5})^{2}}, \end{aligned}$$

$$\begin{aligned} g=a_{1}x+a_{2}y+\frac{a_{1}a_{2}^{2}-a_{1}a_{6}^{2}+2a_{2}a_{5}a_{6}}{a_{1}^{2}+a_{5}^{2}}t+a_{4},\nonumber \\ h=a_{5}x+a_{6}y+\frac{2a_{1}a_{2}a_{6}-a_{2}^{2}a_{5}+a_{5}a_{6}^{2}}{a_{1}^{2}+a_{5}^{2}}t+a_{8}. \end{aligned}$$

(A2)

Two classes of lump-stripe solutions to the KPI equation [39] are given as

$$\begin{aligned} u_{11}&=\frac{2(2a_{5}^{2}+a_{9}^{2}e^{l})}{f} -\frac{2(2a_{5}h+a_{9}e^{l})^{2}}{f^{2}}, \end{aligned}$$

(A3)

where

$$\begin{aligned} f&=\Bigg (\mu _{1}a_{5}a_{9}y+2\mu _{1}a_{6}a_{9}t+a_{4}\Bigg )^{2}+\Bigg (a_{5}x+a_{6}y-\frac{3a_{5}^{2}a_{9}^{2}-a_{6}^{2}}{a_{5}}t+a_{8}\Bigg )^{2}+e^{a_{9}x+\frac{a_{6}a_{9}}{a_{5}}y -\frac{a_{9}}{a_{5}^{2}}(a_{5}^{2}a_{9}^{2}-a_{6}^{2})t+a_{12}} +\frac{a_{5}^{2}}{a_{9}^{2}},\\ h&=a_{5}x+a_{6}y-\frac{3a_{5}^{2}a_{9}^{2}-a_{6}^{2}}{a_{5}}t+a_{8}, \end{aligned}$$

$$\begin{aligned}&l=a_{9}x+\frac{a_{6}a_{9}}{a_{5}}y -\frac{a_{9}(a_{5}^{2}a_{9}^{2}-a_{6}^{2})}{a_{5}^{2}}t+a_{12}, \end{aligned}$$

(A4)

and

$$\begin{aligned} u_{12}&=\frac{2\bigg [\frac{2}{3a_{9}^{4}}(a_{5}a_{10}-a_{6}a_{9})^{2}+2a_{5}^{2}+a_{9}^{2}e^{l}\bigg ]}{f}-\frac{2\bigg [\frac{2\mu _{2}}{a_{9}^{2}}(a_{5}a_{10}-a_{6}a_{9})g+2a_{5}h+a_{9}e^{l}\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(A5)

where

$$\begin{aligned} f&=\Bigg [\frac{\mu _{2}(a_{5}a_{10}-a_{6}a_{9})}{a_{9}^{2}}x +\frac{3a_{5}a_{9}^{4}+a_{5}a_{10}^{2}-a_{6}a_{9}a_{10}}{3\mu _{2}a_{9}^{3}}y +\frac{3a_{5}a_{9}^{4}a_{10}+3a_{6}a_{9}^{5}+a_{5}a_{10}^{3}-a_{6}a_{9}a_{10}^{2}}{3\mu _{2}a_{9}^{4}}t +a_{4}\Bigg ]^{2}\\&\quad +\Bigg [a_{5}x+a_{6}y -\frac{3a_{5}a_{9}^{4}+a_{5}a_{10}^{2}-2a_{6}a_{9}a_{10}}{a_{9}^{2}}t +a_{8}\Bigg ]^{2} +e^{a_{9}x+a_{10}y -\frac{a_{9}^{4}-a_{10}^{2}}{a_{9}}t+a_{12}}\\&\quad +\frac{3a_{5}^{2}a_{9}^{4}+a_{5}^{2}a_{10}^{2}-2a_{5}a_{6}a_{9}a_{10}+a_{6}^{2}a_{9}^{2}}{3a_{9}^{6}}, \end{aligned}$$

$$\begin{aligned} g&=\frac{\mu _{2}(a_{5}a_{10}-a_{6}a_{9})}{a_{9}^{2}}x +\frac{3a_{5}a_{9}^{4}+a_{5}a_{10}^{2}-a_{6}a_{9}a_{10}}{3\mu _{2}a_{9}^{3}}y+\frac{3a_{5}a_{9}^{4}a_{10}+3a_{6}a_{9}^{5}+a_{5}a_{10}^{3}-a_{6}a_{9}a_{10}^{2}}{3\mu _{2}a_{9}^{4}}t +a_{4},\nonumber \\ h&=a_{5}x+a_{6}y-\frac{3a_{5}a_{9}^{4}+a_{5}a_{10}^{2}-2a_{6}a_{9}a_{10}}{a_{9}^{2}}t +a_{8},\nonumber \\ l&=a_{9}x+a_{10}y -\frac{a_{9}^{4}-a_{10}^{2}}{a_{9}}t+a_{12}, \end{aligned}$$

(A6)

while the constants $\mu _{1}$ and $\mu _{2}$ are determined by $\mu _{1}^{2}-3=0$ and $3\mu _{2}^{2}-1=0$.

Two classes of lump-soliton solutions to the KPI equation [40] are given as

$$\begin{aligned} u_{21}&=\frac{2\bigg [2a_{1}^{2}+2a_{5}^{2}+\frac{a_{6}^{2}}{3a_{1}^{2}}\cosh (l)\bigg ]}{f}-\frac{2\bigg [2a_{1}g+2a_{5}h+\frac{\mu _{2}a_{6}}{a_{1}}\sinh (l)\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(A7)

where

$$\begin{aligned}&f=\Bigg (a_{1}x-\frac{a_{5}a_{6}}{a_{1}}y-\frac{a_{6}^{2}}{a_{1}}t+a_{4}\Bigg )^{2}+\Bigg (a_{5}x+a_{6}y-\frac{a_{5}a_{6}^{2}}{a_{1}^{2}}t+a_{8}\Bigg )^{2} +\cosh \Bigg (\frac{\mu _{2}a_{6}}{a_{1}}x-\frac{a_{6}^{3}}{9\mu _{2}a_{1}^{3}}t+a_{12}\Bigg )\nonumber \\&\qquad +\frac{36a_{1}^{8}+72a_{1}^{6}a_{5}^{2}+36a_{1}^{4}a_{5}^{4}+a_{6}^{4}}{12a_{1}^{2}a_{6}^{2}(a_{1}^{2}+a_{5}^{2})},\nonumber \\&g=a_{1}x-\frac{a_{5}a_{6}}{a_{1}}y-\frac{a_{6}^{2}}{a_{1}}t+a_{4},\nonumber \\&h=a_{5}x+a_{6}y-\frac{a_{5}a_{6}^{2}}{a_{1}^{2}}t+a_{8},\nonumber \\&l=\frac{\mu _{2}a_{6}}{a_{1}}x-\frac{a_{6}^{3}}{9\mu _{2}a_{1}^{3}}t+a_{12}, \end{aligned}$$

(A8)

and

$$\begin{aligned} u_{22}&=\frac{2\bigg [\frac{a_{7}^{2}}{2a_{9}^{4}}+a_{9}^{2}\cosh (l)\bigg ]}{f} \quad -\frac{2\bigg [-\frac{a_{7}h}{a_{9}^{2}}+a_{9}\sinh (l)\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(A9)

where

$$\begin{aligned}&f=\Bigg (\frac{\mu _{1}a_{7}}{2a_{9}}y-\mu _{1}a_{7}t+a_{4}\Bigg )^{2}+\Bigg (-\frac{a_{7}}{2a_{9}^{2}}x+\frac{a_{7}}{2a_{9}}y+a_{7}t+a_{8}\Bigg )^{2}+\cosh (a_{9}x-a_{9}^{2}y+a_{12}) +\frac{4a_{9}^{12}+a_{7}^{4}}{4a_{7}^{2}a_{9}^{6}},\nonumber \\&g=\frac{\mu _{1}a_{7}}{2a_{9}}y-\mu _{1}a_{7}t+a_{4},\nonumber \\&h=-\frac{a_{7}}{2a_{9}^{2}}x+\frac{a_{7}}{2a_{9}}y+a_{7}t+a_{8},\nonumber \\&l=a_{9}x-a_{9}^{2}y+a_{12}. \end{aligned}$$

(A10)

The lump-stripe solutions to the (2+1)-dimensional NNV system [41] are given as

$$\begin{aligned}&u=\frac{2(2a_{2}g+2a_{6}h+a_{10}e^{l})(2a_{1}g+2a_{5}h+a_{9}e^{l})}{f^{2}} -\frac{2(2a_{1}a_{2}+2a_{5}a_{6}+a_{9}a_{10}e^{l})}{f}+a_{0},\nonumber \\&v=\frac{2(2a_{1}g+2a_{5}h+a_{9}e^{l})^{2}}{f^{2}}-\frac{2(2a_{1}^{2}+2a_{5}^{2}+a_{9}^{2}e^{l})}{f}+\frac{\lambda _{3}}{3\lambda _{1}},\nonumber \\&w=\frac{2(2a_{2}g+2a_{6}h+a_{10}e^{l})^{2}}{f^{2}} -\frac{2(2a_{2}^{2}+2a_{6}^{2}+a_{10}^{2}e^{l})}{f} +\frac{\lambda _{4}}{3\lambda _{2}}, \end{aligned}$$

(A11)

where

$$\begin{aligned} f&=\Bigg [-\frac{a_{6}a_{9}}{a_{10}}x+\frac{a_{5}a_{10}}{a_{9}}y +\frac{3(\lambda _{2}a_{6}a_{10}^{2}-\lambda _{1}a_{5}a_{9}^{2})}{2}t+a_{4}\Bigg ]^{2}+\Bigg [a_{5}x+a_{6}y-\frac{3(\lambda _{1}a_{6}a_{9}^{4}+\lambda _{2}a_{5}a_{10}^{4})}{2a_{9}a_{10}}t+a_{8}\Bigg ]^{2}\nonumber \\&\quad +e^{a_{9}x+a_{10}y+\frac{\lambda _{1}a_{9}^{3}+\lambda _{2}a_{10}^{3}}{2}t+a_{12}},\nonumber \\ g&=-\frac{a_{6}a_{9}}{a_{10}}x+\frac{a_{5}a_{10}}{a_{9}}y +\frac{3(\lambda _{2}a_{6}a_{10}^{2}-\lambda _{1}a_{5}a_{9}^{2})}{2}t+a_{4},\nonumber \\ h&=a_{5}x+a_{6}y-\frac{3(\lambda _{1}a_{6}a_{9}^{4}+\lambda _{2}a_{5}a_{10}^{4})}{2a_{9}a_{10}}t+a_{8},\nonumber \\ l&=a_{9}x+a_{10}y+\frac{\lambda _{1}a_{9}^{3}+\lambda _{2}a_{10}^{3}}{2}t+a_{12}. \end{aligned}$$

(A12)

Associated with the test function

$$\begin{aligned} f=g^{2}+h^{2}+p+q+a_{9}, \end{aligned}$$

(A13)

with

$$\begin{aligned}&g=a_{1}x+a_{2}y+a_{3}t+a_{4},\nonumber \\&h=a_{5}x+a_{6}y+a_{7}t+a_{8},\nonumber \\&p=k_{0}e^{k_{1}x+k_{2}y+k_{3}t},\nonumber \\&q=n_{0}e^{-k_{1}x-k_{2}y-k_{3}t}, \end{aligned}$$

(A14)

where $a_{i}~(1\le i \le 9),~k_{j}~(0\le j \le 3)$ and $n_{0}$ are real constants, the lump-soliton solutions to the (2+1)-dimensional NNV system [41] are given as

$$\begin{aligned} u&=\frac{2(2a_{2}g+2a_{6}h+k_{2}p-k_{2}q) (2a_{1}g+2a_{5}h+k_{1}p-k_{1}q)}{f^{2}}-\frac{2(2a_{1}a_{2}+2a_{5}a_{6}+k_{1}k_{2}p+k_{1}k_{2}q)}{f} +a_{0},\nonumber \\ v&=\frac{2(2a_{1}g+2a_{5}h+k_{1}p-k_{1}q)^{2}}{f^{2}} -\frac{2(2a_{1}^{2}+2a_{5}^{2}+k_{1}^{2}p+k_{1}^{2}q)}{f}+\frac{\lambda _{3}}{3\lambda _{1}},\nonumber \\ w&=\frac{2(2a_{2}g+2a_{6}h+k_{2}p-k_{2}q)^{2}}{f^{2}} -\frac{2(2a_{2}^{2}+2a_{6}^{2}+k_{2}^{2}p+k_{2}^{2}q)}{f}+\frac{\lambda _{4}}{3\lambda _{2}}, \end{aligned}$$

(A15)

where

$$\begin{aligned}&f=\Bigg [\frac{a_{6}k_{1}}{k_{2}}x-\frac{a_{5}k_{2}}{k_{1}}y +\frac{3(\lambda _{1}a_{5}k_{1}^{2}-\lambda _{2}a_{6}k_{2}^{2})}{2}t+a_{4}\Bigg ]^{2} +\Bigg [a_{5}x+a_{6}y-\frac{3(\lambda _{1}a_{6}k_{1}^{4}+\lambda _{2}a_{5}k_{2}^{4})}{2k_{1}k_{2}}t+a_{8}\Bigg ]^{2}\nonumber \\&\qquad +k_{0}e^{k_{1}x+k_{2}y+\frac{\lambda _{1}k_{1}^{3}+\lambda _{2}k_{2}^{3}}{2}t} +n_{0}e^{-k_{1}x-k_{2}y-\frac{\lambda _{1}k_{1}^{3}+\lambda _{2}k_{2}^{3}}{2}t} +\frac{2k_{0}n_{0}k_{1}^{2}k_{2}^{2}}{a_{5}^{2}k_{2}^{2}+a_{6}k_{1}^{2}},\nonumber \\&g=\frac{a_{6}k_{1}}{k_{2}}x-\frac{a_{5}k_{2}}{k_{1}}y +\frac{3(\lambda _{1}a_{5}k_{1}^{2}-\lambda _{2}a_{6}k_{2}^{2})}{2}t+a_{4},\nonumber \\&h=a_{5}x+a_{6}y-\frac{3(\lambda _{1}a_{6}k_{1}^{4}+\lambda _{2}a_{5}k_{2}^{4})}{2k_{1}k_{2}}t+a_{8},\nonumber \\&p=k_{0}e^{k_{1}x+k_{2}y+\frac{\lambda _{1}k_{1}^{3}+\lambda _{2}k_{2}^{3}}{2}t},\nonumber \\&q=n_{0}e^{-k_{1}x-k_{2}y-\frac{\lambda _{1}k_{1}^{3}+\lambda _{2}k_{2}^{3}}{2}t}. \end{aligned}$$

(A16)

The lump-stripe solutions and lump-soliton solutions to the (2+1)-dimensional Ito equation [44, 45] are, respectively, given as

$$\begin{aligned} u&=\frac{2(2a_{1}^{2}+2a_{5}^{2}+a_{9}^{2}e^{l})}{f} -\frac{2(2a_{1}g+2a_{5}h+a_{9}e^{l})^{2}}{f^{2}}, \end{aligned}$$

(A17)

where

$$\begin{aligned} f=&\Bigg [a_{1}x+a_{2}y-(\alpha a_{2}+a_{1}\beta )t+a_{4}\Bigg ]^{2}+\Bigg [a_{5}x-\frac{\alpha a_{1}a_{2}+a_{1}^{2}\beta +a_{5}^{2}\beta }{\alpha a_{5}}y +a_{7}t+a_{8}\Bigg ]^{2}\nonumber \\&+e^{a_{9}x+\frac{a_{1}}{a_{5}}(\alpha a_{2}+a_{1}\beta )y+a_{12}} +a_{13},\nonumber \\ g=&a_{1}x+a_{2}y-(\alpha a_{2}+a_{1}\beta )t+a_{4},\nonumber \\ h=&a_{5}x-\frac{\alpha a_{1}a_{2}+a_{1}^{2}\beta +a_{5}^{2}\beta }{\alpha a_{5}}y+a_{7}t+a_{8},\nonumber \\ l=&a_{9}x+\frac{a_{1}(\alpha a_{2}+a_{1}\beta )}{a_{5}}y+a_{12}, \end{aligned}$$

(A18)

and

$$\begin{aligned} u&=\frac{2\bigg [\frac{2a_{5}^{2}a_{7}^{2}}{a_{3}^{2}}+2a_{5}^{2}+a_{9}^{2}\cosh (l)\bigg ]}{f}-\frac{2\bigg [-\frac{2a_{5}a_{7}}{a_{3}}g+2a_{5}h+a_{9}\sinh (l)\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(A19)

where

$$\begin{aligned} f=&\Bigg (-\frac{a_{5}a_{7}}{a_{3}}x-\frac{-a_{5}a_{7}\beta +a_{3}^{2}}{\alpha a_{3}}y+a_{3}t+a_{4}\Bigg )^{2}+\Bigg (a_{5}x-\frac{a_{5}\beta +a_{7}}{\alpha }y+a_{7}t+\frac{a_{4}a_{7}}{a_{3}}\Bigg )^{2}\nonumber \\&+\cosh \Bigg [a_{9}x-\frac{a_{9}(a_{9}^{2}+\beta )}{\alpha }y+a_{12}\Bigg ] +a_{13},\nonumber \\&g=-\frac{a_{5}a_{7}}{a_{3}}x -\frac{-a_{5}a_{7}\beta +a_{3}^{2}}{\alpha a_{3}}y+a_{3}t+a_{4},\nonumber \\&h=a_{5}x-\frac{a_{5}\beta +a_{7}}{\alpha }y+a_{7}t+\frac{a_{4}a_{7}}{a_{3}},\nonumber \\&l=a_{9}x-\frac{a_{9}(a_{9}^{2}+\beta )}{\alpha }y+a_{12}. \end{aligned}$$

(A20)

B

The proof of Theorem 1

Through direct computation by use of the following properties of the Hirota derivatives

$$\begin{aligned}&P(D_{x_{1}},D_{x_{2}},\ldots ,D_{x_{n}},D_{t}) e^{l_{i}}\cdot e^{l_{i}}=0,\\&P(D_{x_{1}},D_{x_{2}},\ldots ,D_{x_{n}},D_{t}) e^{l_{i}}\cdot e^{l_{j}}=P(a_{i1}-a_{j1},a_{i2}-a_{j2}, \ldots ,a_{i,n+1}-a_{j,n+1})e^{l_{i}+l_{j}}, \end{aligned}$$

it now follows from Eq. (11) to have

$$\begin{aligned}&0=P\Big (g^{2}+h^{2}+m+\sum \limits _{i=1}^{N}e^{l_{i}}\Big )\cdot \Big (g^{2}+h^{2}+m +\sum \limits _{i=1}^{N}e^{l_{i}}\Big )\\ =&P(g^{2}+h^{2}+m)\cdot (g^{2}+h^{2}+m) +2P(g^{2}+h^{2}+m)\cdot \Big (\sum \limits _{i=1}^{N}e^{l_{i}}\Big ) +P\Big (\sum \limits _{i=1}^{N}e^{l_{i}}\Big )\cdot \Big (\sum \limits _{i=1}^{N}e^{l_{i}}\Big )\\ =&P(g^{2}+h^{2}+m)\cdot (g^{2}+h^{2}+m)+2\sum \limits _{i=1}^{N}P(g^{2}+h^{2}+m)\cdot e^{l_{i}}+\sum \limits _{i=1}^{N}P (e^{l_{i}}\cdot e^{l_{i}})+2\sum \limits _{i\ne j}P (e^{l_{i}}\cdot e^{l_{j}})\\&\Leftrightarrow \left\{ \begin{aligned}&P(g^{2}+h^{2}+m)\cdot (g^{2}+h^{2}+m)=0,\\&\sum \limits _{i=1}^{N}P(g^{2}+h^{2}+m)\cdot e^{l_{i}}=0,\\&\sum \limits _{i\ne j}P(a_{i1}-a_{j1},a_{i2}-a_{j2}, \ldots ,a_{i,n+1}-a_{j,n+1})e^{l_{i}+l_{j}}=0, \end{aligned} \right. \\&\Leftrightarrow \left\{ \begin{aligned}&P(g^{2}+h^{2}+m)\cdot (g^{2}+h^{2}+m)=0,\\&P(g^{2}+h^{2}+m)\cdot e^{l_{i}}=0,~~i=1,2,\ldots ,N,\\&P(a_{i1}-a_{j1},a_{i2}-a_{j2}, \ldots ,a_{i,n+1}-a_{j,n+1})=0,~~i\ne j,~i,j=1,2,\ldots ,N. \end{aligned} \right. \end{aligned}$$

The proof is finished. $\square$

The proof of Theorem 2

Substituting the combined solution f in Eq. (20) into Eq. (11), we get

$$\begin{aligned} 0=&P\Big (g^{2}+h^{2}+m+\sum \limits _{i=1}^{N}\cosh {l_{i}}+c\Big )\cdot \Big (g^{2}+h^{2}+m +\sum \limits _{i=1}^{N}\cosh {l_{i}}+c\Big )\nonumber \\ =&P(g^{2}+h^{2}+m)\cdot (g^{2}+h^{2}+m)+2P(g^{2}+h^{2}+m)\cdot c+2P(g^{2}+h^{2}+m)\cdot \Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )\nonumber \\&+2P(g^{2}+h^{2}+m)\cdot \Big (\sum \limits _{i=1}^{N}\frac{e^{-l_{i}}}{2}\Big ) +2P\Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )\cdot c+2P\Big (\sum \limits _{i=1}^{N}\frac{e^{-l_{i}}}{2}\Big )\cdot c+P\Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )\cdot \Big (\sum \limits _{i=1}^{N} \frac{e^{l_{i}}}{2}\Big )\nonumber \\&\quad +P\Big (\sum \limits _{i=1}^{N}\frac{e^{-l_{i}}}{2}\Big )\cdot \Big (\sum \limits _{i=1}^{N} \frac{e^{-l_{i}}}{2}\Big )+2P\Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )\cdot \Big (\sum \limits _{i=1}^{N} \frac{e^{-l_{i}}}{2}\Big ). \end{aligned}$$

(B1)

In virtue of the following identities

$$\begin{aligned}&P\Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )\cdot \Big (\sum \limits _{i=1}^{N} \frac{e^{l_{i}}}{2}\Big ) =\sum \limits _{i\ne j}\frac{1}{4}P(a_{i1}-a_{j1},a_{i2}-a_{j2}, \ldots ,a_{i,n+1}-a_{j,n+1})e^{l_{i}+l_{j}},\nonumber \\&P\Big (\sum \limits _{i=1}^{N}\frac{e^{-l_{i}}}{2}\Big )\cdot \Big (\sum \limits _{i=1}^{N} \frac{e^{-l_{i}}}{2}\Big ) =\sum \limits _{i\ne j}\frac{1}{4}P(a_{j1}-a_{i1},a_{j2}-a_{i2}, \ldots ,a_{j,n+1}-a_{i,n+1})e^{-(l_{i}+l_{j})},\\&2P\Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )\cdot \Big (\sum \limits _{i=1}^{N} \frac{e^{-l_{i}}}{2}\Big )=\sum \limits _{i=1}^{N}\frac{1}{2}P(2a_{i1},2a_{i2}, \ldots ,2a_{i,n+1})+\sum \limits _{i\ne j}\frac{1}{2}P(a_{i1}+a_{j1},a_{i2}+a_{j2}, \ldots ,a_{i,n+1}+a_{j,n+1})e^{l_{i}-l_{j}}, \end{aligned}$$

we rewrite Eq. (B1) as

$$\begin{aligned} 0=&P(g^{2}+h^{2}+m)\cdot (g^{2}+h^{2}+m)+2P(g^{2}+h^{2}+m)\cdot c+2P(g^{2}+h^{2}+m)\cdot \Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )\\&+2P(g^{2}+h^{2}+m)\cdot \Big (\sum \limits _{i=1}^{N}\frac{e^{-l_{i}}}{2}\Big ) +2P\Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )\cdot c+2P\Big (\sum \limits _{i=1}^{N}\frac{e^{-l_{i}}}{2}\Big )\cdot c\\&+\sum \limits _{i\ne j}\frac{1}{4}P(a_{i1}-a_{j1},a_{i2}-a_{j2}, \ldots ,a_{i,n+1}-a_{j,n+1})e^{l_{i}+l_{j}}\\&+\sum \limits _{i\ne j}\frac{1}{4}P(a_{j1}-a_{i1},a_{j2}-a_{i2}, \ldots ,a_{j,n+1}-a_{i,n+1})e^{-(l_{i}+l_{j})}\\&+\sum \limits _{i=1}^{N}\frac{1}{2}P(2a_{i1},2a_{i2}, \ldots ,2a_{i,n+1})+\sum \limits _{i\ne j}\frac{1}{2}P(a_{i1}+a_{j1},a_{i2}+a_{j2}, \ldots ,a_{i,n+1}+a_{j,n+1})e^{l_{i}-l_{j}} \end{aligned}$$

$$\begin{aligned}&\Leftrightarrow \left\{ \begin{aligned}&P(g^{2}+h^{2}+m)\cdot (g^{2}+h^{2}+m)=0,\\&P(g^{2}+h^{2}+m)\cdot \Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )=0,\\&P(g^{2}+h^{2}+m)\cdot \Big (\sum \limits _{i=1}^{N}\frac{e^{-l_{i}}}{2}\Big )=0,\\&P\Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )\cdot c=0,\\&P\Big (\sum \limits _{i=1}^{N}\frac{e^{-l_{i}}}{2}\Big )\cdot c=0,\\&\sum \limits _{i\ne j}P(a_{i1}-a_{j1},a_{i2}-a_{j2}, \ldots ,a_{i,n+1}-a_{j,n+1})e^{l_{i}+l_{j}}=0,\\&\sum \limits _{i\ne j}P(a_{j1}-a_{i1},a_{j2}-a_{i2}, \ldots ,a_{j,n+1}-a_{i,n+1})e^{-(l_{i}+l_{j})}=0,\\&P(g^{2}+h^{2}+m)\cdot c+\sum \limits _{i=1}^{N}\frac{1}{4}P(2a_{i1},2a_{i2}, \ldots ,2a_{i,n+1})=0,\\&\sum \limits _{i\ne j}P(a_{i1}+a_{j1},a_{i2}+a_{j2}, \ldots ,a_{i,n+1}+a_{j,n+1})e^{l_{i}-l_{j}}=0. \end{aligned} \right. \end{aligned}$$

(B2)

Keeping in mind of the properties in Eqs. (12) and  (17), we hereby simplify Eqs. (B2) into

$$\begin{aligned} \quad \left\{ \begin{aligned}&P(g^{2}+h^{2}+m)\cdot (g^{2}+h^{2}+m)=0,\\&P(g^{2}+h^{2}+m)\cdot \Big (\sum \limits _{i=1}^{N}\frac{e^{l_{i}}}{2}\Big )=0,\\&\sum \limits _{i\ne j}P(a_{i1}-a_{j1},a_{i2}-a_{j2}, \ldots ,a_{i,n+1}-a_{j,n+1})e^{l_{i}+l_{j}}=0,\\&P(g^{2}+h^{2}+m)\cdot c+\sum \limits _{i=1}^{N}\frac{1}{4}P(2a_{i1},2a_{i2}, \ldots ,2a_{i,n+1})=0,\\&\sum \limits _{i\ne j}P(a_{i1}+a_{j1},a_{i2}+a_{j2}, \ldots ,a_{i,n+1}+a_{j,n+1})e^{l_{i}-l_{j}}=0, \end{aligned} \right. \end{aligned}$$

which are equivalent to

$$\begin{aligned} \left\{ \begin{aligned}&P(g^{2}+h^{2}+m)\cdot (g^{2}+h^{2}+m)=0,\\&P(g^{2}+h^{2}+m)\cdot e^{l_{i}}=0,~~i=1,2,\ldots ,N,\\&P(a_{i1}-a_{j1},a_{i2}-a_{j2}, \ldots ,a_{i,n+1}-a_{j,n+1})=0,~~i\ne j,~i,j=1,2,\ldots ,N,\\ {}&P(g^{2}+h^{2}+m)\cdot c+\sum \limits _{i=1}^{N}\frac{1}{4} P(2a_{i1},2a_{i2},\ldots ,2a_{i,n+1})=0,\\&P(a_{i1}+a_{j1},a_{i2}+a_{j2}, \ldots ,a_{i,n+1}+a_{j,n+1})=0,~~i\ne j,~i,j=1,2,\ldots ,N. \end{aligned} \right. \end{aligned}$$

The proof is finished. $\square$

C

The one-lump-multi-stripe solutions to the (2+1)-dimensional generalized KdV equation (26) are derived as

$$\begin{aligned} u&=\frac{2\bigg (2m_{11}^{2}+2m_{21}^{2}+\sum \limits _{i=1}^{N}a_{i1}^{2}e^{l_{i}}\bigg )}{f}-\frac{2\bigg (2m_{11}g+2m_{21}h+\sum \limits _{i=1}^{N}a_{i1}e^{l_{i}}\bigg )^{2}}{f^{2}}, \end{aligned}$$

(C1)

where

$$\begin{aligned} f&=\Bigg (m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y -m_{11}t+m_{14}\Bigg )^{2}+\Bigg (m_{21}x+m_{22}y-m_{21}t+m_{24}\Bigg )^{2}+m\nonumber \\&\quad +\sum \limits _{i=1}^{N}e^{a_{i1}x-a_{i1}y-(a_{i1}^{3}+a_{i1})t+a_{i4}},\nonumber \\ g&=m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y -m_{11}t+m_{14},\nonumber \\ h&=m_{21}x+m_{22}y-m_{21}t+m_{24},\nonumber \\ l_{i}&=a_{i1}x-a_{i1}y-(a_{i1}^{3}+a_{i1})t+a_{i4},~~i=1,2,\ldots ,N, \end{aligned}$$

(C2)

while $m_{11}m_{22}+\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}m_{21}\ne 0$, and $m>0$ is an arbitrary constant.

The one-lump-one-stripe solutions to the (2+1)-dimensional generalized KdV equation (26) are derived as

$$\begin{aligned} u&=\frac{2\bigg (2m_{11}^{2}+2m_{21}^{2}+a_{11}^{2}e^{l_{1}}\bigg )}{f}-\frac{2\bigg (2m_{11}g+2m_{21}h+a_{11}e^{l_{1}}\bigg )^{2}}{f^{2}}, \end{aligned}$$

(C3)

where

$$\begin{aligned}&f=\Bigg (m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y -m_{11}t+m_{14}\Bigg )^{2}+\Bigg (m_{21}x+m_{22}y-m_{21}t+m_{24}\Bigg )^{2}+m\nonumber \\&\qquad +e^{a_{11}x-a_{11}y-(a_{11}^{3}+a_{11})t+a_{14}},\nonumber \\&g=m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y -m_{11}t+m_{14},\nonumber \\&h=m_{21}x+m_{22}y-m_{21}t+m_{24},\nonumber \\&l_{1}=a_{11}x-a_{11}y-(a_{11}^{3}+a_{11})t+a_{14}. \end{aligned}$$

(C4)

The one-lump-two-stripe solutions to the (2+1)-dimensional generalized KdV equation (26) are derived as

$$\begin{aligned} u&=\frac{2\bigg (2m_{11}^{2}+2m_{21}^{2}+a_{11}^{2}e^{l_{1}}+a_{21}^{2}e^{l_{2}}\bigg )}{f}-\frac{2\bigg (2m_{11}g+2m_{21}h+a_{11}e^{l_{1}}+a_{21}e^{l_{2}}\bigg )^{2}}{f^{2}}, \end{aligned}$$

(C5)

where

$$\begin{aligned}&f=\Bigg (m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y -m_{11}t+m_{14}\Bigg )^{2}+\Bigg (m_{21}x+m_{22}y-m_{21}t+m_{24}\Bigg )^{2}+m\nonumber \\&\qquad +e^{a_{11}x-a_{11}y-(a_{11}^{3}+a_{11})t+a_{14}}+e^{a_{21}x-a_{21}y-(a_{21}^{3}+a_{21})t+a_{24}},\nonumber \\&g=m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y -m_{11}t+m_{14},\nonumber \\&h=m_{21}x+m_{22}y-m_{21}t+m_{24},\nonumber \\&l_{1}=a_{11}x-a_{11}y-(a_{11}^{3}+a_{11})t+a_{14},\nonumber \\&l_{2}=a_{21}x-a_{21}y-(a_{21}^{3}+a_{21})t+a_{24}. \end{aligned}$$

(C6)

The one-lump-three-stripe solutions to the (2+1)-dimensional generalized KdV equation (26) are derived as

$$\begin{aligned} u&=\frac{2\bigg (2m_{11}^{2}+2m_{21}^{2}+a_{11}^{2}e^{l_{1}}+a_{21}^{2}e^{l_{2}}+a_{31}^{2}e^{l_{3}}\bigg )}{f}-\frac{2\bigg (2m_{11}g+2m_{21}h+a_{11}e^{l_{1}}+a_{21}e^{l_{2}}+a_{31}e^{l_{3}}\bigg )^{2}}{f^{2}}, \end{aligned}$$

(C7)

where

$$\begin{aligned}&f=\Bigg (m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y -m_{11}t+m_{14}\Bigg )^{2}+\Bigg (m_{21}x+m_{22}y-m_{21}t+m_{24}\Bigg )^{2}+m\nonumber \\&\qquad +e^{a_{11}x-a_{11}y-(a_{11}^{3}+a_{11})t+a_{14}}+e^{a_{21}x-a_{21}y-(a_{21}^{3}+a_{21})t+a_{24}}+ e^{a_{31}x-a_{31}y-(a_{31}^{3}+a_{31})t+a_{34}},\nonumber \\&g=m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y -m_{11}t+m_{14},\nonumber \\&h=m_{21}x+m_{22}y-m_{21}t+m_{24},\nonumber \\&l_{1}=a_{11}x-a_{11}y-(a_{11}^{3}+a_{11})t+a_{14},\nonumber \\&l_{2}=a_{21}x-a_{21}y-(a_{21}^{3}+a_{21})t+a_{24},\nonumber \\&l_{3}=a_{31}x-a_{31}y-(a_{31}^{3}+a_{31})t+a_{34}. \end{aligned}$$

(C8)

The one-lump-multi-soliton solutions to the (2+1)-dimensional generalized KdV equation (26) are derived as

$$\begin{aligned} u&=\frac{2\bigg [2m_{11}^{2}+2m_{21}^{2}+\sum \limits _{i=1}^{N}a_{i1}^{2}\cosh (l_{i})\bigg ]}{f}-\frac{2\bigg [2m_{11}g+2m_{21}h+\sum \limits _{i=1}^{N}a_{i1}\sinh (l_{i})\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(C9)

where

$$\begin{aligned}&f=\Bigg (m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y-m_{11}t+m_{14}\Bigg )^{2} +\qquad \Bigg (m_{21}x+m_{22}y-m_{21}t+m_{24}\Bigg )^{2}+m\\&\qquad +\sum \limits _{i=1}^{N}\cosh [a_{i1}x-a_{i1}y-(a_{i1}^{3}+a_{i1})t+a_{i4}]+c, \end{aligned}$$

while g,  h and $l_{i}$ are as the same as these in Eq. (C2), and $m >0$ and $c>0$ are arbitrary constants. To guarantee that two vectors $(m_{11},m_{12})$ and $(m_{21},m_{22})$ in the (x, y)-plane are not parallel, the condition $m_{11}m_{22}+\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}m_{21}\ne 0$ needs to be satisfied.

The one-lump-one-soliton solutions to the (2+1)-dimensional generalized KdV equation (26) are derived as

$$\begin{aligned} u&=\frac{2\bigg [2m_{11}^{2}+2m_{21}^{2}+a_{11}^{2}\cosh (l_{1})\bigg ]}{f}-\frac{2\bigg [2m_{11}g+2m_{21}h+a_{11}\sinh (l_{1})\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(C10)

where

$$\begin{aligned} f=&\Bigg (m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y-m_{11}t+m_{14}\Bigg )^{2} +\Bigg (m_{21}x+m_{22}y-m_{21}t+m_{24}\Bigg )^{2}+m\\&+\cosh [a_{11}x-a_{11}y-(a_{11}^{3}+a_{11})t+a_{14}]+c, \end{aligned}$$

while g,  h and $l_{1}$ are as the same as these in Eq. (C4), and $m >0$ and $c>0$ are arbitrary constants.

The one-lump-two-soliton solutions to the (2+1)-dimensional generalized KdV equation (26) are derived as

$$\begin{aligned} u&=\frac{2\bigg [2m_{11}^{2}+2m_{21}^{2}+a_{11}^{2}\cosh (l_{1})+a_{21}^{2}\cosh (l_{2})\bigg ]}{f}-\frac{2\bigg [2m_{11}g+2m_{21}h+a_{11}\sinh (l_{1})+a_{21}\sinh (l_{2})\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(C11)

where

$$\begin{aligned} f=&\Bigg (m_{11}x-\frac{m_{11}^{2}+m_{21}^{2}+m_{21}m_{22}}{m_{11}}y-m_{11}t+m_{14}\Bigg )^{2} +\Bigg (m_{21}x+m_{22}y-m_{21}t+m_{24}\Bigg )^{2}+m\\&+\cosh [a_{11}x-a_{11}y-(a_{11}^{3}+a_{11})t+a_{14}]+\cosh [a_{21}x-a_{21}y-(a_{21}^{3}+a_{21})t+a_{24}]+c, \end{aligned}$$

while g,  h and $l_{1}$ are as the same as these in Eq. (C6), and $m >0$ and $c>0$ are arbitrary constants.

The one-lump-multi-stripe solutions to the NNV system (8) with $\lambda _{2}=0$ are derived as

$$\begin{aligned}&u=\frac{2\Big (-\frac{2m_{21}m_{22}g}{m_{12}}+2m_{21}h+ \sum \limits _{i=1}^{N}a_{i1}e^{l_{i}}\Big ) (2m_{12}g+2m_{22}h)}{f^{2}},\nonumber \\&v=\frac{2\bigg (-\frac{2m_{21}m_{22}}{m_{12}}g+2m_{21}h+ \sum \limits _{i=1}^{N}a_{i1}e^{l_{i}}\bigg )^{2}}{f^{2}}-\frac{2\bigg (\frac{2m_{21}^{2}m_{22}^{2}}{m_{12}^{2}}+ 2m_{21}^{2}+\sum \limits _{i=1}^{N}a_{i1}^{2}e^{l_{i}}\bigg )}{f}+v_0,\nonumber \\&w=\frac{2(2m_{12}g+2m_{22}h)^{2}}{f^{2}}-\frac{2(2m_{12}^{2}+2m_{22}^{2})}{f}+w_{0}, \end{aligned}$$

(C12)

where

$$\begin{aligned} f&=\Bigg (-\frac{m_{21}m_{22}}{m_{12}}x+m_{12}y-\frac{3\lambda _{1} v_{0}m_{21}m_{22}-\lambda _{3}m_{21}m_{22}+\lambda _{4}m_{12}^{2}}{m_{12}}t+m_{14}\Bigg )^{2}\nonumber \\&\quad +\Bigg (m_{21}x+m_{22}y+(3\lambda _{1} v_{0}m_{21}-\lambda _{3}m_{21}-\lambda _{4}m_{22})t+m_{24}\Bigg )^{2}+m+\sum \limits _{i=1}^{N} e^{a_{i1}x-(\lambda _{1} a_{i1}^{3}-3a_{i1}\lambda _{1} v_{0}+a_{i1}\lambda _{3})t+a_{i4}},\nonumber \\ g&=-\frac{m_{21}m_{22}}{m_{12}}x+m_{12}y-\frac{3\lambda _{1} v_{0}m_{21}m_{22}-\lambda _{3}m_{21}m_{22}+\lambda _{4}m_{12}^{2}}{m_{12}}t+m_{14},\nonumber \\ h&=m_{21}x+m_{22}y+(3\lambda _{1} v_{0}m_{21}-\lambda _{3}m_{21}-\lambda _{4}m_{22})t+m_{24},\nonumber \\ l_{i}&=a_{i1}x-(\lambda _{1} a_{i1}^{3}-3a_{i1}\lambda _{1} v_{0}+a_{i1}\lambda _{3})t+a_{i4},~~i=1,2,\ldots ,N, \end{aligned}$$

(C13)

while $-\frac{m_{21}m_{22}}{m_{12}}m_{22}-m_{12}m_{21}\ne 0$, and $m > 0,~v_{0}$ and $w_{0}$ are two arbitrary constants.

The one-lump-multi-soliton solutions to the NNV system (8) with $\lambda _{2}=0$ are derived as

$$\begin{aligned} u&=\frac{2\Big [-\frac{2m_{21}m_{22}g}{m_{12}}+2m_{21}h+ \sum \limits _{i=1}^{N}a_{i1}\sinh (l_{i})\Big ] (2m_{12}g+2m_{22}h)}{f^{2}},\nonumber \\ v&=\frac{2\Bigg [-\frac{2m_{21}m_{22}}{m_{12}}g+2m_{21}h+ \sum \limits _{i=1}^{N}a_{i1}\sinh (l_{i})\Bigg ]^{2}}{f^{2}}-\frac{2\bigg [\frac{2m_{21}^{2}m_{22}^{2}}{m_{12}^{2}}+ 2m_{21}^{2}+\sum \limits _{i=1}^{N}a_{i1}^{2}\cosh (l_{i})\Bigg ]}{f}+v_0,\nonumber \\ w&=\frac{2(2m_{12}g+2m_{22}h)^{2}}{f^{2}}-\frac{2(2m_{12}^{2}+2m_{22}^{2})}{f}+w_{0}, \end{aligned}$$

(C14)

where

$$\begin{aligned}&f=\Bigg (-\frac{m_{21}m_{22}}{m_{12}}x+m_{12}y-\frac{3\lambda _{1} v_{0}m_{21}m_{22}-\lambda _{3}m_{21}m_{22}+\lambda _{4}m_{12}^{2}}{m_{12}}t+m_{14}\Bigg )^{2}\nonumber \\&\qquad +\Bigg (m_{21}x+m_{22}y+(3\lambda _{1} v_{0}m_{21}-\lambda _{3}m_{21}-\lambda _{4}m_{22})t+m_{24}\Bigg )^{2} +m\nonumber \\&\qquad +\sum \limits _{i=1}^{N} \cosh [a_{i1}x-(\lambda _{1} a_{i1}^{3}-3a_{i1}\lambda _{1} v_{0}+a_{i1}\lambda _{3})t +a_{i4}] +c, \end{aligned}$$

(C15)

while g,  h and $l_{i}$ are as the same as these in Eq. (C13), $m > 0$, $c>0$, $v_{0}$ and $w_{0}$ are arbitrary constants. Moreover, the condition $-\frac{m_{21}m_{22}}{m_{12}}m_{22}-m_{12}m_{21}\ne 0$ needs to be satisfied.

For the parameters of Class 1, the one-lump-multi-stripe solutions to the (2+1)-dimensional Ito equation (9) can be expressed as

$$\begin{aligned} u_{11}&=\frac{2\bigg (2m_{11}^{2}+\sum \limits _{i=1}^{N}a_{i1}^{2}e^{l_{i}}\bigg )}{f} -\frac{2\bigg (2m_{11}g+\sum \limits _{i=1}^{N}a_{i1}e^{l_{i}}\bigg )^{2}}{f^{2}}, \end{aligned}$$

(C16)

where

$$\begin{aligned}&f=\Bigg (m_{11}x-\frac{\beta m_{11}}{\alpha }y+m_{14}\Bigg )^{2}+\Bigg (m_{22}y-\alpha m_{22}t\Bigg )^{2}+m+\sum \limits _{i=1}^{N} e^{a_{i1}x-\frac{a_{i1}}{\alpha }(a_{i1}^{2}+\beta )y+a_{i4}},\nonumber \\&g=m_{11}x-\frac{\beta m_{11}}{\alpha }y+m_{14},\nonumber \\&l_{i}=a_{i1}x-\frac{a_{i1}(a_{i1}^{2}+\beta )}{\alpha }y+a_{i4},~~i=1,2,\ldots ,N, \end{aligned}$$

(C17)

while $m_{11}m_{22}\ne 0$ and $m > 0$ is an arbitrary constant.

The parameters of Class 2 give rise to the one-lump-multi-stripe solutions to the (2+1)-dimensional Ito equation (9) as

$$\begin{aligned} u_{12}=&\frac{2\bigg [\frac{2m_{23}^{2}}{m_{13}^{2}\beta ^{2}}(\alpha m_{22}+m_{23})^{2}+\frac{2}{\beta ^{2}}(\alpha m_{22}+m_{23})^{2}+\sum \nolimits _{i=1}^{N}a_{i1}^{2}e^{l_{i}}\bigg ]}{f}\nonumber \\&-\frac{2\bigg [\frac{2m_{23}}{m_{13}\beta }(\alpha m_{22}+m_{23})h- \frac{2}{\beta }(\alpha m_{22}+m_{23})h+\sum \nolimits _{i=1}^{N}a_{i1}e^{l_{i}}\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(C18)

where

$$\begin{aligned}&f=\Bigg (\frac{(\alpha m_{22}+m_{23})m_{23}}{m_{13}\beta }x-\frac{\alpha m_{22}m_{23}+m_{13}^{2}+m_{23}^{2}}{\alpha m_{13}}y+m_{13}t+m_{14}\Bigg )^{2}\nonumber \\&\qquad +\Bigg (-\frac{\alpha m_{22}+m_{23}}{\beta }x+m_{22}y+m_{23}t+m_{24}\Bigg )^{2}+m +\sum \limits _{i=1}^{N} e^{a_{i1}x-\frac{a_{i1}}{\alpha }(a_{i1}^{2}+\beta )y+a_{i4}}\nonumber \\&g=\frac{(\alpha m_{22}+m_{23})m_{23}}{m_{13}\beta }x-\frac{\alpha m_{22}m_{23}+m_{13}^{2}+m_{23}^{2}}{\alpha m_{13}}y+m_{13}t+m_{14},\nonumber \\&h=-\frac{\alpha m_{22}+m_{23}}{\beta }x+m_{22}y+m_{23}t+m_{24},\nonumber \\&l_{i}=a_{i1}x-\frac{a_{i1}}{\alpha }(a_{i1}^{2}+\beta )y+a_{i4},~~i=1,2,\ldots ,N, \end{aligned}$$

(C19)

while $\frac{m_{23}(\alpha m_{22}+m_{23})}{m_{13}\beta }m_{22}-\frac{\alpha m_{22}m_{23}+m_{13}^{2}+m_{23}^{2}}{\alpha m_{13}}\frac{\alpha m_{22}+m_{23}}{\beta } \ne 0$ and $m > 0$ is an arbitrary constant.

For the parameters of Class 1, we have the one-lump-multi-soliton solutions to the (2+1)-dimensional Ito equation (9) as

$$\begin{aligned} u_{21}&=\frac{2\bigg [2m_{11}^{2}+\sum \limits _{i=1}^{N}a_{i1}^{2}\cosh (l_{i})\bigg ]}{f}-\frac{2\bigg [2m_{11}g+\sum \limits _{i=1}^{N}a_{i1}\sinh (l_{i})\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(C20)

where

$$\begin{aligned} f&=\Bigg (m_{11}x-\frac{\beta m_{11}}{\alpha }y+m_{14}\Bigg )^{2} +\Bigg (m_{22}y-\alpha m_{22}t\Bigg )^{2}+m +\sum \limits _{i=1}^{N} \cosh \Bigg (a_{i1}x-\frac{a_{i1}(a_{i1}^{2}+\beta )}{\alpha }y+a_{i4}\Bigg )+c, \end{aligned}$$

(C21)

while g and $l_{i}$ are as the same as these in Eq. (C17), and $m > 0$ and $c>0$ are arbitrary constants. The condition $m_{11}m_{22}\ne 0$ needs to be satisfied.

The parameters of Class 2 yield the one-lump-multi-soliton solutions to the (2+1)-dimensional Ito equation (9) as

$$\begin{aligned} u_{22}=&\frac{2\bigg [\frac{2m_{23}^{2}}{m_{13}^{2}\beta ^{2}}(\alpha m_{22}+m_{23})^{2}+\frac{2}{\beta ^{2}}(\alpha m_{22}+m_{23})^{2}+\sum \limits _{i=1}^{N}a_{i1}^{2}\cosh (l_{i})\bigg ]}{f}\nonumber \\&-\frac{2\bigg [\frac{2m_{23}}{m_{13}\beta }(\alpha m_{22}+m_{23})h- \frac{2}{\beta }(\alpha m_{22}+m_{23})h+\sum \limits _{i=1}^{N}a_{i1}\cosh (l_{i})\bigg ]^{2}}{f^{2}}, \end{aligned}$$

(C22)

where

$$\begin{aligned} f=&\Bigg (\frac{(\alpha m_{22}+m_{23})m_{23}}{m_{13}\beta }x -\frac{\alpha m_{22}m_{23}+m_{13}^{2}+m_{23}^{2}}{\alpha m_{13}}y+m_{13}t+m_{14}\Bigg )^{2}\nonumber \\&+\Bigg (-\frac{\alpha m_{22}+m_{23}}{\beta }x+m_{22}y+m_{23}t+m_{24}\Bigg )^{2}+m +\sum \limits _{i=1}^{N} \cosh \Bigg (a_{i1}x-\frac{a_{i1}}{\alpha }(a_{i1}^{2}+\beta )y+a_{i4}\Bigg )+c, \end{aligned}$$

(C23)

while g,  h and $l_{i}$ are as the same as these in Eq. (C19), $m > 0$ and $c>0$ are constants. The condition $\frac{m_{23}(\alpha m_{22}+m_{23})}{m_{13}\beta }m_{22}-\frac{\alpha m_{22}m_{23}+m_{13}^{2}+m_{23}^{2}}{\alpha m_{13}}\frac{\alpha m_{22}+m_{23}}{\beta } \ne 0$ needs to be satisfied.

D

One-lump-one-stripe solution parameters

$$\begin{aligned}&\left\{ \begin{aligned}&\lambda _{1}=1,~\lambda _{3}=2,~\lambda _{4}=1,~v_{0}=0,~ m_{12}=1,~m_{14}=2,~m_{21}=2,~m_{22}=1,~m_{24}=1,~m=2,\\&a_{11}=1,~a_{14}=1 \end{aligned} \right\} ; \end{aligned}$$

(D1)

One-lump-two-stripe solution parameters

$$\begin{aligned}&\left\{ \begin{aligned}&\lambda _{1}=1,~\lambda _{3}=2,~\lambda _{4}=1,~v_{0}=0,~ m_{12}=1,~m_{14}=2,~m_{21}=2,~m_{22}=1,~m_{24}=1,~m=2,\\&a_{11}=1,~a_{14}=1,~a_{21}=\frac{3}{2},~a_{24}=1 \end{aligned} \right\} ; \end{aligned}$$

(D2)

One-lump-three-stripe solution parameters

$$\begin{aligned}&\left\{ \begin{aligned}&\lambda _{1}=1,~\lambda _{3}=2,~\lambda _{4}=1,~v_{0}=0,~ m_{12}=1,~m_{14}=2,~m_{21}=2,~m_{22}=1,~m_{24}=1,~m=2,\\&a_{11}=1,~a_{14}=1,~a_{21}=2,~a_{24}=1,~ a_{31}=\frac{3}{2},~a_{34}=1 \end{aligned} \right\} ; \end{aligned}$$

(D3)