The variable separation solution, fractal and chaos in an extended coupled (2+1)-dimensional Burgers system

Abstract

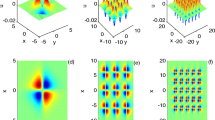
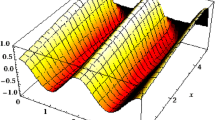
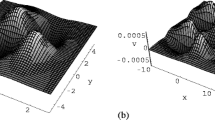
As one kind of Burgers-type equation, the extended coupled (2+1)-dimensional Burgers system is used to describe certain wave process in oceanography, acoustics or hydrodynamics. With the Riccati projective equation method and symbolic computation, the variable separation solution is derived. Due to the arbitrary functions in the variable separation solutions, the fractal and chaotic structures are studied based on the gradient function (say, U in the text). Some excitation properties of the solutions are analyzed and figures are plotted to show the shape and the structure.

Appendix I

In Eq. (1), we assume that

$$\begin{aligned} u=\psi ^{-\alpha }\sum \limits _{j=0}^{\infty }u_{j}\psi ^{j},~~v=\psi ^{-\beta }\sum \limits _{j=0}^{\infty }v_{j}\psi ^{j}, \end{aligned}$$

(42)

where $\alpha ,~\beta$ are positive integers and

$$\begin{aligned} \psi =\psi (x,y,t),~~u_{j}=u_{j}(x,y,t),~~v_{j}=v_{j}(x,y,t), \end{aligned}$$

(43)

are analytic functions of (x, y, t) near a singularity manifold $M=\{(x,y,t):\psi (x,y,t)=0\}$.

To balance the dominant terms, we assume the leading order singular behavior is in the form of

$$\begin{aligned} u\sim u_{0}\psi ^{-\alpha },~~v\sim v_{0}\psi ^{-\beta }, \end{aligned}$$

(44)

and obtain

$$\begin{aligned}&\alpha =1,~~\beta =1,\nonumber \\&u_{0}=\pm \frac{2\sqrt{BC}}{A}\psi _{x},~~v_{0}=\frac{2C}{A}\psi _{x}. \end{aligned}$$

(45)

We directly substitute

$$\begin{aligned}&u\sim \pm \frac{2\sqrt{BC}}{A}\psi _{x}\psi ^{-1}\nonumber \\&\qquad +\cdots +u_{j}\psi ^{j-1}+\cdots ,~~ v\sim \frac{2C}{A}\psi _{x}\psi ^{-1}\nonumber \\&\qquad +\cdots +v_{j}\psi ^{j-1}+\cdots , \end{aligned}$$

(46)

into Eq. (1), and make the determinant of the coefficients on $u_{j},~v_{j}$ in the lowest order system of Eq. (1) with respect to $\psi$ to zero, leading to

$$\begin{aligned} \left| \begin{matrix} 4\sqrt{BC}\psi _{x}^{2}-2\sqrt{BC}j\psi _{x}^{2} &{} ~~-2B\psi _{x}^{2}+3Bj\psi _{x}^{2}-Bj^{2}\psi _{x}^{2}\\ -9Cj\psi _{y}\psi _{x}^{2}+6Cj^{2}\psi _{y}\psi _{x}^{2}-Cj^{3}\psi _{y}\psi _{x}^{2} &{} ~~-6\sqrt{BC}\psi _{y}\psi _{x}^{2}+8\sqrt{BC}j\psi _{y}\psi _{x}^{2}-2\sqrt{BC}j^{2}\psi _{y}\psi _{x}^{2} \end{matrix}\right| =0 \end{aligned}$$

(47)

Solving Eq. (47) gives the resonance values as

$$\begin{aligned} j=-1, 1, 2, 3, 4. \end{aligned}$$

(48)

$j=-1$ corresponds to the arbitrary singular manifold. From the coefficients of $(\psi ^{-3},\psi ^{-3})$, $(\psi ^{-2},\psi ^{-2})$, $(\psi ^{-1},\psi ^{-1})$ and $(\psi ^{0},\psi ^{0})$, we can show that either $u_{1}$ or $v_{1}$, $u_{2}$ or $v_{2}$, $u_{3}$ or $v_{3}$ and $u_{4}$ or $v_{4}$ is arbitrary. Thus, we can conclude that Eq. (1) possesses the Painlevé property.