Skip to main content
SpringerLink
Log in

A new derivation of (2 + 1)-dimensional Schrödinger equation with separated real and imaginary parts of the dependent variable and its solitary wave solutions

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

In this work, we have derived a new \((2+1)\)-dimensional Schrödinger equation that contains separated real and imaginary parts of the dependent variable as follows

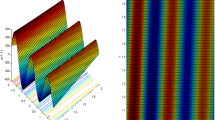
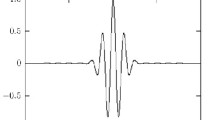
$$\begin{aligned}{} & {} iw_{tx}+\left( iw_{t}-w_{xx}+w|w|^2\right) _{y}\\{} & {} \qquad \,\, +2\left( w\left( \partial _{x}^{-1}\left( \Re (w)\Re (w)_{y}\right. \right. \right. \\{} & {} \qquad \left. \left. \left. +\Im (w)\Im (w)_{y}\right) \right) \right) _{x}=0. \end{aligned}$$

This nonintegrable equation has been extracted by adopting the recursion operator of the known Schrödinger equation. However, the resulting model has proven too complex to solve or explore the physical meaning of its solutions. Therefore, we have transferred it into a system of three equations, and then, we have applied the Lie symmetry technique to reduce the latter to a simpler equivalent system. As a result, many solitary wave solutions have been attained, including bright solitary wave, dipole, kink, breather, periodic, and their interactions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Ablowitz, M.J., Prinari, B., Trubatch, A.D.: Discrete and Continuous Nonlinear Schrödinger Systems. Cambridge University Press, Cambridge (2003). https://doi.org/10.1017/cbo9780511546709

  2. Akhmediev, N., Ankiewicz, A.: First-order exact solutions of the nonlinear Schrödinger equation in the normal-dispersion regime. Phys. Rev. A 47(4), 3213–3221 (1993). https://doi.org/10.1103/PhysRevA.47.3213

    Article  Google Scholar 

  3. Benoudina, N., Zhang, Y., Khalique, C.M.: Lie symmetry analysis, optimal system, new solitary wave solutions and conservation laws of the Pavlov equation. Commun. Nonlinear Sci. Numer. Simul. 94, 105560 (2021). https://doi.org/10.1016/j.cnsns.2020.105560

    Article  MathSciNet  MATH  Google Scholar 

  4. Benoudina, N., Zhang, Y., Khalique, C.M., Bessaad, N.: Novel hybrid solitary waves and shrunken-period solutions, solitary Moiré pattern and conserved vectors of the (4 + 1)-Fokas equation Nardjess. Int. J. Geom. Methods Mod. Phys. (2022). https://doi.org/10.1142/S021988782250195X

    Article  Google Scholar 

  5. Biswas, A., Triki, H., Zhou, Q., Moshokoa, S.P., Ullah, M.Z., Belic, M.: Cubic-quartic optical solitons in Kerr and power law media. Opt. (Stuttg) 144, 357–362 (2017). https://doi.org/10.1016/j.ijleo.2017.07.008

    Article  Google Scholar 

  6. Hermann, J., Schätzle, Z., Noé, F.: Deep-neural-network solution of the electronic Schrödinger equation. Nat. Chem. 12(10), 891–897 (2020). https://doi.org/10.1038/s41557-020-0544-y

    Article  Google Scholar 

  7. Hu, X., Li, Y., Chen, Y.: A direct algorithm of one-dimensional optimal system for the group invariant solutions. J. Math. Phys. 56(5), 053504 (2015). https://doi.org/10.1063/1.4921229

    Article  MathSciNet  MATH  Google Scholar 

  8. Hydon, P.: Symmetry Methods for Differential Equations. Cambridge University Press, New York (2000)

    Book  MATH  Google Scholar 

  9. Kragh, H.: Equation with the many fathers. The Klein–Gordon equation in 1926. Am. J. Phys. 52(11), 1024–1033 (1984). https://doi.org/10.1119/1.13782

  10. Krasil’ shchik, I.S., Kersten, P.H.M.: Symmetries and Recursion Operators for Classical and Supersymmetric Differential Equations, 1 edn. Springer, Dordrecht (2000). https://doi.org/10.1007/978-94-017-3196-6

  11. Kumar, R., Verma, R.S.: Dynamics of invariant solutions of mKdV-ZK arising in a homogeneous magnetised plasma. Nonlinear Dyn. 108(4), 4081–4092 (2022). https://doi.org/10.1007/s11071-022-07389-4

    Article  Google Scholar 

  12. Kumar, S., Dhiman, S.K., Baleanu, D., Osman, M.S., Wazwaz, A.M.: Lie symmetries, closed-form solutions, and various dynamical profiles of solitons for the variable coefficient (2+1)-dimensional KP equations. Symmetry (Basel) 14(3), 597 (2022). https://doi.org/10.3390/sym14030597

    Article  Google Scholar 

  13. Lenells, J., Fokas, A.S.: On a novel integrable generalization of the nonlinear Schrödinger equation. Nonlinearity 22(1), 11–27 (2009). https://doi.org/10.1088/0951-7715/22/1/002

    Article  MathSciNet  MATH  Google Scholar 

  14. Lewenstein, M., Ciappina, M.F., Pisanty, E., Rivera-Dean, J., Stammer, P., Lamprou, T., Tzallas, P.: Generation of optical Schrödinger cat states in intense laser-matter interactions. Nat. Phys. 17(10), 1104–1108 (2021). https://doi.org/10.1038/s41567-021-01317-w

    Article  Google Scholar 

  15. Liu, W., Zhang, Y., Luan, Z., Zhou, Q., Mirzazadeh, M., Ekici, M., Biswas, A.: Dromion-like soliton interactions for nonlinear Schrödinger equation with variable coefficients in inhomogeneous optical fibers. Nonlinear Dyn. 96(1), 729–736 (2019). https://doi.org/10.1007/s11071-019-04817-w

    Article  MATH  Google Scholar 

  16. Lou, S.: Higher-dimensional integrable models with a common recursion operator. Commun. Theor. Phys. 28(1), 41–50 (1997). https://doi.org/10.1088/0253-6102/28/1/41

    Article  MathSciNet  Google Scholar 

  17. Olver, P.: Applications of Lie Groups to Differential Equations. Springer, New York (1993)

    Book  MATH  Google Scholar 

  18. Schrödinger, E.: An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 28(6), 1049–1070 (1926). https://doi.org/10.1103/PhysRev.28.1049

    Article  Google Scholar 

  19. Triki, H., Biswas, A.: Sub pico-second chirped envelope solitons and conservation laws in monomode optical fibers for a new derivative nonlinear Schrödinger’s model. Opt. (Stuttg) 173, 235–241 (2018). https://doi.org/10.1016/j.ijleo.2018.08.026

    Article  Google Scholar 

  20. Wang, G.: A new (3 + 1)-dimensional Schrödinger equation: derivation, soliton solutions and conservation laws. Nonlinear Dyn. 104(2), 1595–1602 (2021). https://doi.org/10.1007/s11071-021-06359-6

    Article  Google Scholar 

  21. Wazwaz, A.M.: Painlevé analysis for a new integrable equation combining the modified Calogero-Bogoyavlenskii-Schiff (MCBS) equation with its negative-order form. Nonlinear Dyn. 91(2), 877–883 (2018). https://doi.org/10.1007/s11071-017-3916-0

    Article  MATH  Google Scholar 

  22. Wazwaz, A.M.: New (3 + 1) -dimensional Painlevé integrable fifth-order equation with third-order temporal dispersion. Nonlinear Dyn. 106(1), 891–897 (2021). https://doi.org/10.1007/s11071-021-06872-8

    Article  Google Scholar 

  23. Wazwaz, A.M., Abu Hammad, M., El-Tantawy, S.: Bright and dark optical solitons for (3 + 1)-dimensional hyperbolic nonlinear Schrödinger equation using a variety of distinct schemes. Opt. (Stuttg) 270(September), 170043 (2022). https://doi.org/10.1016/j.ijleo.2022.170043

    Article  Google Scholar 

  24. Wazwaz, A.M., Albalawi, W., El-Tantawy, S.A.: Optical envelope soliton solutions for coupled nonlinear Schrödinger equations applicable to high birefringence fibers. Opt. (Stuttg) 255(February), 168673 (2022). https://doi.org/10.1016/j.ijleo.2022.168673

    Article  Google Scholar 

  25. Wazwaz, A.M., El-Tantawy, S.A.: A new integrable (3+1)-dimensional KdV-like model with its multiple-soliton solutions. Nonlinear Dyn. 83(3), 1529–1534 (2016). https://doi.org/10.1007/s11071-015-2427-0

  26. Zhang, R.F., Li, M.C., Al-Mosharea, E., Zheng, F.C., Bilige, S.: Rogue waves, classical lump solutions and generalized lump solutions for Sawada-Kotera-like equation. Int. J. Mod. Phys. B 36(5), 1–11 (2022). https://doi.org/10.1142/S0217979222500448

    Article  Google Scholar 

  27. Zhang, R.F., Li, M.C., Gan, J.Y., Li, Q., Lan, Z.Z.: Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method. Chaos Solitons Fractals 154, 111692 (2022). https://doi.org/10.1016/j.chaos.2021.111692

    Article  MathSciNet  MATH  Google Scholar 

  28. Zhang, R.F., Li, M.C., Yin, H.M.: Rogue wave solutions and the bright and dark solitons of the (3+1)-dimensional Jimbo-Miwa equation. Nonlinear Dyn. 103(1), 1071–1079 (2021). https://doi.org/10.1007/s11071-020-06112-5

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 11371326215 and No. 11975145). We thank the reviewers and editor for their recommendations to improve this manuscript.

Author information

Authors and Affiliations

  1. Department of Mathematics, Zhejiang Normal University, Jinhua, 321004, People’s Republic of China

    Nardjess Benoudina & Yi Zhang

  2. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai, 200240, People’s Republic of China

    Nassim Bessaad

Authors
  1. Nardjess Benoudina
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nassim Bessaad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nardjess Benoudina.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Benoudina, N., Zhang, Y. & Bessaad, N. A new derivation of (2 + 1)-dimensional Schrödinger equation with separated real and imaginary parts of the dependent variable and its solitary wave solutions. Nonlinear Dyn 111, 6711–6726 (2023). https://doi.org/10.1007/s11071-022-08193-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-08193-w

Keywords

Search

Navigation