Skip to main content
SpringerLink
Log in

Competence effects for choices involving gains and losses

  • Published:
Journal of Risk and Uncertainty Aims and scope Submit manuscript

Abstract

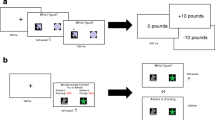
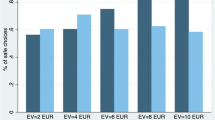
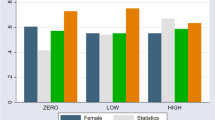
We investigate how choices for uncertain gain and loss prospects are affected by the decision maker’s perceived level of knowledge about the underlying domain of uncertainty. Specifically, we test whether Heath and Tversky’s (J Risk Uncertain 4:5–28, 1991) competence hypothesis extends from gains to losses. We predict that the commonly-observed preference for high knowledge over low knowledge prospects for gains reverses for losses. We employ an empirical setup in which participants make hypothetical choices between gain or loss prospects in which the outcome depends on whether a high or low knowledge event occurs. We infer decision weighting functions for high and low knowledge events from choices using a representative agent preference model. For gains, we replicate the results of Kilka and Weber (Manage Sci 47:1712–1726, 2001), finding that decision makers are more attracted to choices that they feel more knowledgeable about. However, for losses, we find limited support for our extension of the competence effect.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. Machina (2009) presented a four-color generalization of the Ellsberg Paradox that violates expected utility, as well as Choquet expected utility. Baillon et al. (forthcoming) showed that this counter-example violates most existing models of ambiguity as well.

  2. Wu and Gonzalez (1999) showed that the weighting function satisfies a stronger property for gains, concavity for low probability events and convexity for high probability events.

  3. Support theory allows nonadditive probability judgments, P(A ∪ A′) ≤ P(A) + P(A′). There are other hypotheses besides binary complementarity that follow from support theory, such as proportionality, product rule, and unpacking principle. However, binary complementarity is the only one that our design permits us to test.

  4. Full instructions and program code are available upon request.

  5. The same basic findings discussed below hold if we use different criteria to distinguish between low and high knowledge domains.

  6. We also computed Pearson statistics and found similar results.

  7. We also produced similar results using Prelec’s (1998) two-parameter function.

  8. We also performed an additional estimation, restricting the sample of the observations in which the reported knowledge difference exceeded 3, leaving us with 468 of 1,284 observation. This analysis produced qualitatively similar results (Gains: Δi ≈ 0.50, p < 0.001; Losses: Δi ≈ − 0.05, n.s.).

  9. We also compared expected utility to our more general model. The expected utility restriction was conducted by setting all parameters equal to 1. A likelihood ratio test strongly rejected the expected utility model for both gains and losses.

References

  • Abdellaoui, M. (2000). Parameter-free elicitation of utility and probability weighting functions. Management Science, 46, 1497–1512.

    Article  Google Scholar 

  • Abdellaoui, M., Vossmann, F., & Weber, M. (2005). Choice-based elicitation and decomposition of decision weights for gains and losses under uncertainty. Management Science, 51, 1384–1399.

    Article  Google Scholar 

  • Abdellaoui, M., Bleichrodt, H., & Paraschiv, C. (2007). Measuring loss aversion: A parameter-free approach. Management Science, 53, 1659–1674.

    Article  Google Scholar 

  • Ballinger, T. P., & Wilcox, N. T. (1997). Decisions, error and heterogeneity. Economic Journal, 106, 1090–1105.

    Article  Google Scholar 

  • Baillon, A., l’Haridon, O., & Placido, L. (forthcoming). Ambiguity Models and the Machina Paradox. American Economic Review.

  • Basili, M., Chateauneuf, A., & Fontini, F. (2005). Choices under ambiguity with familiar and unfamiliar outcomes. Theory and Decision, 58, 195–207.

    Article  Google Scholar 

  • Becker, S. W., & Brownson, F. O. (1964). What price ambiguity? Or the role of ambiguity in decision-making. Journal of Political Economy, 72, 62–73.

    Article  Google Scholar 

  • Bettman, J. R., Luce, M. F., & Payne, J. W. (1998). Constructive consumer choice processes. Journal of Consumer Research, 25, 187–217.

    Article  Google Scholar 

  • Birnbaum, M. H., & McIntosh, W. R. (1996). Violations of branch independence in choices between gambles. Organizational Behavior and Human Decision Processes, 67, 91–110.

    Article  Google Scholar 

  • Blavatskyy, P. (2007). Stochastic expected utility theory. Journal of Risk and Uncertainty, 34, 259–286.

    Article  Google Scholar 

  • Brenner, L. A., & Rottenstreich, Y. (1999). Focus, repacking, and the judgment of grouped hypotheses. Journal of Behavioral Decision Making, 12, 141–148.

    Article  Google Scholar 

  • Camerer, C. F., & Ho, T.-H. (1994). Violations of the betweenness axiom and nonlinearity in probability. Journal of Risk and Uncertainty, 8, 167–196.

    Article  Google Scholar 

  • Camerer, C. F., & Hogarth, R. (1999). The effects of financial incentives in experiments: A review and capital–labor–production framework. Journal of Risk and Uncertainty, 3, 7–42.

    Article  Google Scholar 

  • Camerer, C. F., & Weber, M. (1992). Recent developments in modeling preferences: Uncertainty and ambiguity. Journal of Risk and Uncertainty, 5, 325–370.

    Article  Google Scholar 

  • Choquet, G. (1954). Theory of capacities. Annales de l’Institut Fourier, 5, 131–295.

    Google Scholar 

  • Chow, C. C., & Sarin, R. K. (2001). Comparative ignorance and the Ellsberg paradox. Journal of Risk and Uncertainty, 2, 129–139.

    Article  Google Scholar 

  • Cohen, M., Jaffray, J.-Y., & Said, T. (1985). Individual behavior under risk and under uncertainty: An experimental study. Theory and Decision, 18, 203–228.

    Article  Google Scholar 

  • de Bruin, W. B., Fischhoff, B., Millstein, S. G., & Halpern-Felsher, B. L. (2000). Verbal and numerical expressions of probability: ‘It’s a fifty-fifty chance’. Organizational Behavior and Human Decision Processes, 81, 115–131.

    Article  Google Scholar 

  • Dickhaut, J., McCabe, K., Nagode, J. C., Rustichini, A., Smith, K., & Pardo, J. V. (2003). The impact of the certainty context on the process of choice. Proceedings of the National Academy of Sciences of the United States of America, 100, 3536–3541.

    Article  Google Scholar 

  • Einhorn, H. J., & Hogarth, R. M. (1986). Decision making under ambiguity. Journal of Business, 59, S225–S250.

    Article  Google Scholar 

  • Ellsberg, D. (1961). Risk, ambiguity and the Savage axioms. Quarterly Journal of Economics, 75, 643–669.

    Article  Google Scholar 

  • Etchart-Vincent, N. (2004). Is probability weighting sensitive to the magnitude of consequences? An experimental investigation on losses. Journal of Risk and Uncertainty, 3, 217–235.

    Article  Google Scholar 

  • Fischer, G. W., Carmon, Z., Ariely, D., & Zauberman, G. (1999). Goal-based construction of preferences: Task goals and the prominence effect. Management Science, 45, 1057–1075.

    Article  Google Scholar 

  • Fox, C. R., & Tversky, A. (1995). Ambiguity aversion and comparative ignorance. Quarterly Journal of Economics, 110, 585–603.

    Article  Google Scholar 

  • Fox, C. R., & Tversky, A. (1998). A belief-based account of decision under uncertainty. Management Science, 44, 879–895.

    Article  Google Scholar 

  • Fox, C. R., & See, K. E. (2003). Belief and preference in decision under uncertainty. In D. Hardman & L. Macchi (Eds.), Thinking: Psychological perspectives on reasoning, judgment and decision making (pp. 273–314). New York: Wiley.

    Chapter  Google Scholar 

  • Fox, C. R., & Weber, M. (2002). Ambiguity aversion, comparative ignorance and decision context. Organizational Behavior and Human Decision Processes, 88, 476–498.

    Article  Google Scholar 

  • Frisch, D., & Baron, J. (1988). Ambiguity and rationality. Journal of Behavioral Decision Making, 1, 149–157.

    Article  Google Scholar 

  • Gilboa, I. (1987). Expected utility with purely subjective nonadditive probabilities. Journal of Mathematical Economics, 16, 65–88.

    Article  Google Scholar 

  • Goldstein, W. M., & Einhorn, H. J. (1987). Expression theory and the preference reversal phenomena. Psychological Review, 94, 236–254.

    Article  Google Scholar 

  • Gonzalez, R., & Wu, G. (1999). On the shape of the probability weighting function. Cognitive Psychology, 38, 129–166.

    Article  Google Scholar 

  • Harless, D. W., & Camerer, C. F. (1994). The predictive utility of generalized expected utility theories. Econometrica, 62, 1251–1290.

    Article  Google Scholar 

  • Heath, C., & Tversky, A. (1991). Preference and belief: Ambiguity and competence in choice under uncertainty. Journal of Risk and Uncertainty, 4, 5–28.

    Article  Google Scholar 

  • Hertwig, R., & Ortmann, A. (2001). Experimental practices in economics: A methodological challenge for psychologists? Behavioral and Brain Sciences, 24, 383–403.

    Google Scholar 

  • Hey, J. D. (1995). Experimental investigations of errors in decision-making under risk. European Economic Review, 39, 633–640.

    Article  Google Scholar 

  • Hogarth, R. M., & Einhorn, H. J. (1990). Venture theory: A model of decision weights. Management Science, 36, 780–803.

    Article  Google Scholar 

  • Kahn, B. E., & Sarin, R. K. (1988). Modelling ambiguity in decisions under uncertainty. Journal of Consumer Research, 15, 265–272.

    Article  Google Scholar 

  • Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263–291.

    Article  Google Scholar 

  • Keynes, J. M. (1921). A treatise on probability. London: Macmillan.

    Google Scholar 

  • Kilka, M., & Weber, M. (2001). What determines the shape of the probability weighting function under uncertainty? Management Science, 47, 1712–1726.

    Article  Google Scholar 

  • Lattimore, P. K., Baker, J. K., & Witte, A. D. (1992). The influence of probability on risky choice: A parametric examination. Journal of Economic Behavior and Organization, 17, 377–400.

    Article  Google Scholar 

  • Loomes, G., & Sugden, R. (1998). Testing different stochastic specifications of risky choice. Economica, 65, 581–598.

    Article  Google Scholar 

  • Macchi, L., Osherson, D., & Krantz, D. M. (1999). A note on superadditive probability judgment. Psychological Review, 106, 210–214.

    Article  Google Scholar 

  • Machina, M. J. (2009). Risk, ambiguity, and the rank-dependence axioms. American Economic Review, 99, 385–392.

    Article  Google Scholar 

  • Maxwell, A. E. (1970). Comparing the classification of subjects by two independent judges. British Journal of Psychiatry, 116, 651–655.

    Article  Google Scholar 

  • Prelec, D. (1998). The probability weighting function. Econometrica, 66, 497–527.

    Article  Google Scholar 

  • Quiggin, J. (1982). A theory of anticipated utility. Journal of Economic Behavior and Organization, 3, 323–343.

    Article  Google Scholar 

  • Samanez-Larkin, G. R., Gibbs, S. E. B., Khanna, K., Nielsen, L., Carstensen, L. L., & Knutson, B. (2007). Anticipation of monetary gain but not loss in healthy older adults. Nature Neuroscience, 10, 787–791.

    Article  Google Scholar 

  • Savage, L. J. (1954). The foundations of statistics. New York: Wiley.

    Google Scholar 

  • Schmeidler, D. (1989). Subjective probability and expected utility without additivity. Econometrica, 57, 571–587.

    Article  Google Scholar 

  • See, K. E. (2009). Reactions to decisions with uncertain consequences: Reliance on perceived fairness versus predicted outcomes depends on knowledge. Journal of Personality and Social Psychology, 96, 104–118.

    Article  Google Scholar 

  • Stott, H. (2006). Cumulative prospect theory’s functional menagerie. Journal of Risk and Uncertainty, 32, 101–130.

    Article  Google Scholar 

  • Stuart, A. (1955). A test for homogeneity of the marginal distributions in a two-way classification. Biometrika, 42, 412–416.

    Google Scholar 

  • Taylor, K. A. (1995). Testing credit and blame attributions as explanation for choices under ambiguity. Organizational Behavior & Human Decision Processes, 64, 128–137.

    Article  Google Scholar 

  • Thaler, R., & Johnson, E. (1990). Gambling with the house money and trying to break even: The effects of prior outcomes on risky choice. Management Science, 36, 643–660.

    Article  Google Scholar 

  • Trautmann, S. T., Vieider, F. M., & Wakker, P. P. (2008). Causes of ambiguity aversion: Known versus unknown preferences. Journal of Risk and Uncertainty, 36, 225–243.

    Article  Google Scholar 

  • Tversky, A., & Fox, C. R. (1995). Weighing risk and uncertainty. Psychological Review, 102, 269–283.

    Article  Google Scholar 

  • Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323.

    Article  Google Scholar 

  • Tversky, A., & Koehler, D. J. (1994). Support theory: A nonextensional representation of subjective probabilities. Psychological Review, 101, 547–567.

    Article  Google Scholar 

  • Tversky, A., & Wakker, P. (1995). Risk attitudes and decision weights. Econometrica, 63, 1255–1280.

    Article  Google Scholar 

  • Wakker, P. P. (1990). Under stochastic dominance Choquet-expected utility and anticipated utility are identical. Theory and Decision, 29, 119–132.

    Article  Google Scholar 

  • Wakker, P. P. (2004). On the composition of risk preference and belief. Psychological Review, 111, 236–241.

    Article  Google Scholar 

  • Wilcox, N. T. (2008). Stochastic models for binary discrete choice under risk: A critical primer and econometric comparison. In J. C. Cox & G. W. Harrison (Eds.), Risk aversion in experiments; research in experimental economics (Vol. 12, pp. 197–292). Bingley: Emerald.

  • Wu, G., & Gonzalez, R. (1996). Curvature of the probability weighting function. Management Science, 42, 1676–1690.

    Article  Google Scholar 

  • Wu, G., & Gonzalez, R. (1999). Nonlinear decision weights in choice under uncertainty. Management Science, 45, 74–85.

    Article  Google Scholar 

  • Wu, G., & Markle, A. B. (2008). An empirical test of gain–loss separability in prospect theory. Management Science, 54, 1322–1335.

    Article  Google Scholar 

Download references

Acknowledgements

We thank Hugo Sonnenschein and Lars Hansen for their help and Peter Wakker for his useful comments. Special thanks goes to Heleno Pioner. José Guilherme de Lara Resende gratefully acknowledges financial support from the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Ministry of Education, Brasil, and from the Haddad fellowship, University of Chicago.

Author information

Authors and Affiliations

  1. Departamento de Economia—Campus Universitário Darcy Ribeiro, Universidade de Brasília, ICC Ala Norte Caixa Postal 04587, Brasília, DF, 70919-970, Brazil

    José Guilherme de Lara Resende

  2. Booth School of Business, University of Chicago, 5807 S. Woodlawn Avenue, Chicago, IL, 60637, USA

    George Wu

Authors
  1. José Guilherme de Lara Resende
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. George Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to George Wu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

de Lara Resende, J.G., Wu, G. Competence effects for choices involving gains and losses. J Risk Uncertain 40, 109–132 (2010). https://doi.org/10.1007/s11166-010-9089-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11166-010-9089-6

Keywords

JEL Classification

Search

Navigation