1 Introduction

Over the years, thermal convection in porous media has attracted the interest of many researchers because numerous applications in geological context and in many engineering fields such as geothermal energy utilization, thermal insulation technology, tube refrigerators, heat exchangers, oil reservoir modelling and many others (see, for instance, Capone et al. 2020a; Gentile and Straughan 2013, 2017; Tyvand and Noland 2020; Barletta 2019; Straughan 2008; Nield and Bejan 2017; Capone and De Luca 2017; Capone and Rionero 2016b; Capone and De Luca 2014a, 2012 and references therein)

In nature, many porous media, like for example sedimentary and metamorphic rocks, exhibit a strong anisotropic behaviour in both thermal and mechanical features. Moreover, anisotropy is a property of artificial porous materials, as well, for example materials used in chemical engineering. Because of the emerging utilization of fully anisotropic porous materials in many applications to real life, the majority of investigations on thermal convection in porous media dealt with anisotropic porous materials (Malashetty et al. 2005; Tyvand and Storesletten 2015; Storesletten 2004; Capone et al. 2010, 2012; Nield and Kuznetsov 2019; Kuznetsov et al. 2015; Capone and De Luca 2020; Capone and Rionero 2016a; Storesletten and Rees 1997; Govender and Vadasz 2007).

Furthermore, as far as thermal convection in porous media is concerned, there are many situations in which local thermal equilibrium assumption is not realistic and therefore the fluid temperature, \(T_f\), is supposed to be different from the solid skeleton temperature, \(T_s\). When the two temperatures are different the scheme is usually referred to as local thermal non-equilibrium scheme, namely LTNE. In LTNE scheme, it is assumed that fluid and solid phases communicate in such a way that heat exchanges better describe the physics of the problem. In the past as nowadays, a great attention to LTNE flows in porous media is given by many researchers, as shown in Capone and Gentile (2018), Capone et al. (2020a, b), Govender and Vadasz (2007), Straughan (2013), Barletta and Rees (2015), Kuznetsov et al. (2015), Celli et al. (2017), Franchi et al. (2018), Hema et al. (2020). This is due to the numerous applications to real-life situations, such as preserving food, cooling computer chips, nanofluids flows, biological tissues analysis and convection in stellar atmospheres.

In the present paper, we analyse the onset of convection in a fully anisotropic porous medium in LTNE scheme, allowing for the Corolis force. The study of flow in rotating porous medium is motivated by its numerous applications in real processes, like, for example, in physiological processes in human body subject to rotating trajectories; in engineering processes with rotating electronic devices, in magma flow in the Earth mantle close to the Earth crust and in chemical process industry (Vadasz 1998, 2002, 2016, 2019; Govender 2007; Capone et al. 2020a, b; Capone and De Luca 2014b).

The plan of the paper is the following. In Sect. 2, we introduce the mathematical model and the dimensionless evolution equations for perturbation fields to conduction solution in order to study the stability of the motionless state (conduction solution). Then, in Sect. 3, a detailed proof of principle of exchange of stabilities is performed and the critical Rayleigh number for the onset of (stationary) convection is determined, in a closed algebraic form. Section 4 deals with the nonlinear stability analysis of the conduction solution and we prove the coincidence between the linear instability threshold and the (global) nonlinear stability threshold of the conduction solution, with respect to the \(L^2-\)norm. Finally, in Sect. 5, numerical simulations concerning the influence of rotation and anisotropy on the stability/instability thresholds is analysed.

2 Mathematical Model

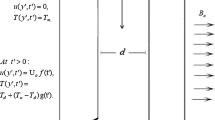
Let us consider a horizontal porous layer of depth d, filled by an incompressible, homogeneous fluid at rest. We assume that the medium is uniformly heated from below and uniformly rotating about the vertical axis z (upward vertical) with constant angular velocity \(\varOmega\). Let \(T_L\) be the temperature of the lower plane \(z=0\) and let \(T_U\) be the temperature of the upper plane \(z=d\). In the local thermal non-equilibrium scheme (LTNE), denoting by \(T_f\) and \(T_s\) the fluid temperature and the solid skeleton temperature, respectively, it turns out that

$$\begin{aligned} T_s=T_f=T_L \quad \text {on} \ z=0, \qquad T_s=T_f=T_U \quad \text {on} \ z=d \quad (T_L>T_U)\,. \end{aligned}$$
(1)

Moreover, we assume that the layer is anisotropic and we denote by \({\mathcal {K}}\) the permeability tensor, and let \({\mathcal {D}}_s\), \({\mathcal {D}}_f\) be the thermal conductivity tensors of solid phase and fluid phase, respectively. Assume that the principal axis (x, y, z) of the permeability tensor are the same as the ones of conductivity tensor, one obtains

$$\begin{aligned} \begin{aligned} {\mathcal {K}}&= K_z {\mathcal {K}}^{*} \qquad {\mathcal {K}}^{*} = \begin{pmatrix} \xi _1 &{} 0 &{} 0 \\ 0 &{} \xi _2 &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix} \qquad \xi _1 = \frac{K_x}{K_z} \quad \xi _2 = \frac{K_y}{K_z} \\ {\mathcal {D}}_s&= \kappa _z^s {\mathcal {D}}_s^{*} \qquad {\mathcal {D}}_s^{*} = \begin{pmatrix} \zeta _1 &{} 0 &{} 0 \\ 0 &{} \zeta _2 &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix} \qquad \zeta _1 = \frac{\kappa _x^s}{\kappa _z^s} \quad \zeta _2 = \frac{\kappa _y^s}{\kappa _z^s} \\ {\mathcal {D}}_f&= \kappa _z^f {\mathcal {D}}_f^{*} \qquad {\mathcal {D}}_f^{*} = \begin{pmatrix} \eta &{} 0 &{} 0 \\ 0 &{} \eta &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix} \qquad \eta = \frac{\kappa _h^f}{\kappa _z^f} \end{aligned} \end{aligned}$$
(2)

where, in particular, \(\eta\) is the thermal anisotropy parameter for the fluid phase.

The mathematical model, in the Oberbeck–Boussinesq approximation and accounting for the Coriolis force due to the uniform rotation of the layer about the vertical axis z is (Straughan 2015; Govender and Vadasz 2007; Capone and Gentile 2018; Capone et al. 2020a)

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} \mathbf{v } = \mu ^{-1}{\mathcal {K}} \Bigg [ -\nabla p + \rho _f g \alpha T_f \mathbf{k } - \dfrac{2 \varOmega \rho _f}{\varepsilon } \mathbf{k } \times \mathbf{v } \Bigg ] \\ &{} \nabla \cdot \mathbf{v } =0 \\ &{} \varepsilon (\rho c)_f T^f_{,t} + (\rho c)_f \mathbf{v } \cdot \nabla T_f = \varepsilon \nabla \cdot ({\mathcal {D}}^f \cdot \nabla T_f) + h(T_s - T_f) \\ &{} (1-\varepsilon )(\rho c)_s T^s_{,t} = (1-\varepsilon ) \nabla \cdot ({\mathcal {D}}^s \cdot \nabla T_s ) - h(T_s - T_f) \end{array}\right. } \end{aligned}$$
(3)

where \(\mathbf{v }\), p, \(T_s\) and \(T_f\) are (seepage) velocity, reduced pressure, solid phase temperature and fluid phase temperature, respectively; \(\mu\), \(\rho _f\), \(\rho _s\), g, \(\alpha\), \(\varOmega\), \(\varepsilon\), c, h are dynamic viscosity, fluid density, solid density, gravity acceleration, thermal expansion coefficient, angular velocity, porosity, specific heat and interaction coefficient, respectively.

To system (3), we append the following boundary conditions

$$\begin{aligned} \begin{aligned}&T_s = T_f = T_L \quad \text {on} \ z=0, \qquad T_s = T_f = T_U \quad \text {on} \ z=d, \\&\mathbf{v } \cdot \mathbf{n } = 0 \quad \text {on} \ z=0,d \end{aligned} \end{aligned}$$
(4)

being \(\mathbf{n }\) the unit outward normal to planes \(z=0,d\).

The system (3) admits the conduction solution \(m_0\):

$$\begin{aligned} m_0=\left\{ \bar{\mathbf{v }} = \mathbf{0 }\,, \quad \bar{T_s} = \bar{T_f} = -\beta z + T_L\,, \quad {\bar{p}} = -\rho _f g \alpha \beta \frac{z^2}{2} + \rho _f g \alpha T_L z\right\} \end{aligned}$$
(5)

where \(\beta =\dfrac{T_L-T_U}{d}(>0)\) is the adverse temperature gradient.

In order to study the stability of the steady solution (5), let us introduce the following perturbation fields

$$\begin{aligned} v_i = u_i + {\bar{v}}_i \qquad T_s = \phi + \bar{T_s} \qquad T_f = \theta + \bar{T_f} \qquad p = \pi + {\bar{p}} \end{aligned}$$
(6)

and the dimensionless quantities

$$\begin{aligned} x_i = {{\tilde{x}}}_i d, \quad t = {{\tilde{t}}} \dfrac{\varepsilon d}{U} , \quad \pi = {{\tilde{\pi }}} P, \quad u_i = {{\tilde{u}}}_i U, \quad \theta = {{\tilde{\theta }}} T^{\prime }, \quad \phi = {{\tilde{\phi }}} T^{\prime } \end{aligned}$$
(7)

where

$$\begin{aligned} U = \frac{\varepsilon \kappa _z^f}{(\rho c)_f d}\,, \qquad P = \frac{U \mu d}{K_z}\,, \qquad T^{\prime } = \beta d \sqrt{\frac{\kappa _z^f \varepsilon \mu }{\beta g \alpha K_z \rho _f^2 c_f d^2}}. \end{aligned}$$
(8)

The dimensionless equations for the perturbation fields, omitting all the tilde, are

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {K}}^{-1} \mathbf{u } = -\nabla \pi + R \theta \mathbf{k } - {\mathcal {T}} \mathbf{k } \times \mathbf{u }\\ \nabla \cdot \mathbf{u }=0\\ \theta _{,t} + \mathbf{u } \cdot \nabla \theta = R w + \eta \varDelta _1 \theta + \theta _{,zz} + H(\phi - \theta )\\ A \phi _{,t} - \zeta _1 \phi _{,xx} - \zeta _2 \phi _{,yy} - \phi _{,zz} + H \gamma (\phi - \theta ) = 0 \end{array}\right. } \end{aligned}$$
(9)

where \(\varDelta _1 = \partial _{,xx} + \partial _{,yy}\) and

$$\begin{aligned} \gamma= & {} \dfrac{\varepsilon \kappa _z^f}{(1-\varepsilon ) \kappa _z^s}\,, \qquad A= \dfrac{(\rho c)_s \kappa _z^f}{(\rho c)_f \kappa _z^s}\,, \qquad H=\dfrac{h d^2}{\varepsilon \kappa _z^f}\\ R^2= & {} \dfrac{K_z \rho ^2_f c_f d^2 \beta g \alpha }{\mu \varepsilon \kappa _z^f} \quad \text{ Rayleigh } \text{ number }\,, \quad {{{\mathcal {T}}}}=\dfrac{2 \varOmega \rho _f K_z}{\varepsilon \mu }\quad \text{ Taylor } \text{ number }. \end{aligned}$$

To system (9), we append the following initial conditions

$$\begin{aligned} {\mathbf {u}}({\mathbf {x}},0)={\mathbf {u}}_0({\mathbf {x}})\,,\quad \pi ({\mathbf {x}},0)=\pi _0({\mathbf {x}})\,,\quad \theta ({\mathbf {x}},0)=\theta _0({\mathbf {x}})\,,\quad \phi ({\mathbf {x}},0)=\phi _0({\mathbf {x}}) \end{aligned}$$
(10)

where \(\nabla \cdot {\mathbf {u}}_0=0\), and the following boundary conditions

$$\begin{aligned} w = \theta = \phi = 0 \qquad \text {on} \ z=0,1. \end{aligned}$$
(11)

We assume that perturbation fields are periodic in x and y directions of periods \(\dfrac{2\pi }{a_x}\) and \(\dfrac{2\pi }{a_y}\), respectively, and they belong to \(W^{2,2} (V), \, \forall t \in {\mathbb {R}}^+\)where \(V = \bigg [ 0, \dfrac{2\pi }{a_x} \bigg ] \times \bigg [ 0, \dfrac{2\pi }{a_y} \bigg ] \times [0, 1]\) is the periodicity cell. Then we denote by \((\cdot , \cdot )\) and \(\Vert \cdot \Vert\) the scalar product on the Hilbert space \(L^2(V)\), and the related norm, respectively.

3 Instability Analysis of \(m_0\)

In order to study the linear stability of \(m_0\), let us consider the linear version of (9), i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {K}}^{-1} \mathbf{u } = -\nabla \pi + R \theta \mathbf{k } - {\mathcal {T}} \mathbf{k } \times \mathbf{u }\\ \nabla \cdot \mathbf{u }=0\\ \theta _{,t} = R w + \eta \varDelta _1 \theta + \theta _{,zz} + H(\phi - \theta )\\ A \phi _{,t} - \zeta _1 \phi _{,xx} - \zeta _2 \phi _{,yy} - \phi _{,zz} + H \gamma (\phi - \theta ) = 0 \end{array}\right. } \end{aligned}$$
(12)

under the boundary conditions (11). Applying the curl to (12)\(_1\), one obtains

$$\begin{aligned} {\left\{ \begin{array}{ll} w_{,y} \xi _2 - v_{,z} = R \theta _{,y} \xi _2 + {\mathcal {T}} u_{,z} \xi _2\\ u_{,z} - w_{,x} \xi _1 = - R \theta _{,x} \xi _1 + {\mathcal {T}} v_{,z} \xi _1\\ v_{,x} \xi _1 - u_{,y} \xi _2 = {\mathcal {T}} \xi _1 \xi _2 w_{,z} \end{array}\right. } \end{aligned}$$
(13)

and deriving (13)\(_1\) by y, (13)\(_2\) by x and (13)\(_3\) by z, one gets

$$\begin{aligned} {\left\{ \begin{array}{ll} w_{,yy} \xi _2 - v_{,zy} = R \theta _{,yy} \xi _2 + {\mathcal {T}} u_{,zy} \xi _2\\ u_{,zx} - w_{,xx} \xi _1 = - R \theta _{,xx} \xi _1 + {\mathcal {T}} v_{,zx} \xi _1\\ v_{,xz} \xi _1 - u_{,yz} \xi _2 = {\mathcal {T}} \xi _1 \xi _2 w_{,zz}. \end{array}\right. } \end{aligned}$$
(14)

Subtracting (14)\(_2\) from (14)\(_1\) and then substituting the result in (14)\(_3\), it follows that

$$\begin{aligned} \xi _1 w_{,xx} + \xi _2 w_{,yy} + w_{,zz} = \xi _1 R \theta _{,xx} + \xi _2 R \theta _{,yy} - {\mathcal {T}}^2 \xi _1 \xi _2 w_{,zz}. \end{aligned}$$
(15)

Let us consider now the autonomous system

$$\begin{aligned} {\left\{ \begin{array}{ll} \xi _1 w_{,xx} + \xi _2 w_{,yy} + w_{,zz} + {\mathcal {T}}^2 \xi _1 \xi _2 w_{,zz} - \xi _1 R \theta _{,xx} - \xi _2 R \theta _{,yy} =0 \\ \theta _{,t} - R w - \eta \varDelta _1 \theta - \theta _{,zz} - H(\phi - \theta ) = 0\\ A \phi _{,t} - \zeta _1 \phi _{,xx} - \zeta _2 \phi _{,yy} - \phi _{,zz} + H \gamma (\phi - \theta ) =0 \end{array}\right. } \end{aligned}$$
(16)

and seek for solutions having the following time-dependence (Chandrasekhar 2013) \({\hat{\varphi }} (t,\mathbf{x }) = \varphi (\mathbf{x }) \ e^{\sigma t}, \, \forall {\hat{\varphi }} \in (w, \theta , \phi )\,,\, \sigma \in {\mathbb {C}}\), (16) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \xi _1 w_{,xx} + \xi _2 w_{,yy} + w_{,zz} + {\mathcal {T}}^2 \xi _1 \xi _2 w_{,zz} - \xi _1 R \theta _{,xx} - \xi _2 R \theta _{,yy} =0 \\ \sigma \theta - R w - \eta \varDelta _1 \theta - \theta _{,zz} - H(\phi - \theta ) = 0\\ A \sigma \phi - \zeta _1 \phi _{,xx} - \zeta _2 \phi _{,yy} - \phi _{,zz} + H \gamma (\phi - \theta ) =0. \end{array}\right. } \end{aligned}$$
(17)

Let us multiply (17)\(_1\) by \(w^{*}\), (17)\(_2\) once by \(\xi _1 \theta ^{*}_{,xx}\) and once by \(\xi _2 \theta ^{*}_{,yy}\), (17)\(_3\) once by \(\xi _1\phi ^{*}_{,xx}\) and once by \(\xi _2 \phi ^{*}_{,yy}\)where the asterisks denote the complex conjugate, accounting for the boundary conditions one obtains:

$$\begin{aligned} \begin{aligned}&\sigma \bigg [ \xi _1 \Vert \theta _{,x} \Vert ^2 + \xi _2 \Vert \theta _{,y} \Vert ^2 + \frac{A \xi _1}{\gamma } \Vert \phi _{,x} \Vert ^2 + \frac{A \xi _2}{\gamma } \Vert \phi _{,y} \Vert ^2 \bigg ] \\&\quad = - \xi _1 \Vert w_{,x} \Vert ^2 - \xi _2 \Vert w_{,y} \Vert ^2 - (1+{\mathcal {T}}^2 \xi _1 \xi _2) \Vert w_{,z} \Vert ^2 - \xi _1 R \bigg [ (\theta _{,xx} , w^{*} ) + ( w , \theta ^{*}_{,xx} ) \bigg ] \\&\qquad - \xi _2 R \bigg [ (\theta _{,yy} , w^{*} ) + ( w , \theta ^{*}_{,yy} ) \bigg ] - \xi _1 \eta \Vert \theta _{,xx} \Vert ^2 - \xi _1 \eta \Vert \theta _{,xy} \Vert ^2 - \xi _1 \Vert \theta _{,xz} \Vert ^2 \\&\qquad - H \xi _1 \bigg [ ( \phi _{,x x} , \theta ^{*}) + (\theta , \phi ^{*}_{,x x})\bigg ] - H \xi _1 \Vert \theta _{,x} \Vert ^2 - \xi _2 \eta \Vert \theta _{,xy} \Vert ^2 - \xi _2 \eta \Vert \theta _{,yy} \Vert ^2 \\&\qquad - \xi _2 \Vert \theta _{,y z} \Vert ^2 - H \xi _2 \bigg [(\phi _{,yy}, \theta ^{*}) + (\theta , \phi ^{*}_{,yy}) \bigg ] - H \xi _2 \Vert \theta _{,y} \Vert ^2 - \frac{\zeta _1 \xi _1}{\gamma } \Vert \phi _{,x x} \Vert ^2 \\&\qquad - \frac{\zeta _2 \xi _1}{\gamma } \Vert \phi _{,x y} \Vert ^2 - \frac{\xi _1}{\gamma } \Vert \phi _{,xz} \Vert ^2 - H \xi _1 \Vert \phi _{,x} \Vert ^2 - \frac{\zeta _1 \xi _2}{\gamma } \Vert \phi _{,xy} \Vert ^2 \\&\qquad - \frac{\zeta _2 \xi _2}{\gamma } \Vert \phi _{,yy} \Vert ^2 - \frac{\xi _2}{\gamma } \Vert \phi _{,y z} \Vert ^2 - H \xi _2 \Vert \phi _{,y} \Vert ^2 \end{aligned} \end{aligned}$$
(18)

and hence, since terms in (18) are real, then necessarily \(\sigma \in {\mathbb {R}}\). Therefore, the strong form of the principle of exchange of stabilities holds, i.e. convection can occur only through a steady motion.

In order to determine the critical Rayleigh number for the onset of convection, by virtue of the principle of exchange of stabilities, setting \(\sigma =0\) in (17), one obtains

$$\begin{aligned} {\left\{ \begin{array}{ll} \xi _1 w_{,xx} + \xi _2 w_{,yy} + w_{,zz} + {\mathcal {T}}^2 \xi _1 \xi _2 w_{,zz} = \xi _1 R \theta _{,xx} + \xi _2 R \theta _{,yy}\\ \eta \varDelta _1 \theta + \theta _{,zz} - H \theta = - R w - H \phi \\ \zeta _1 \phi _{,xx} + \zeta _2 \phi _{,yy} + \phi _{,zz} - H \gamma \phi = - H \gamma \theta . \end{array}\right. } \end{aligned}$$
(19)

Denoting

$$\begin{aligned} \begin{aligned}&{\mathcal {L}} \equiv \xi _1 \partial _{,xx} + \xi _2 \partial _{,yy} + \partial _{,zz} + {\mathcal {T}}^2 \xi _1 \xi _2 \partial _{,zz}\\&{\mathcal {L}}_1 \equiv \eta \varDelta _1 \theta + \partial _{,zz} - H\\&{\mathcal {L}}_2 \equiv \zeta _1 \partial _{,xx} + \zeta _2 \partial _{,yy} + \partial _{,zz} - H \gamma \end{aligned} \end{aligned}$$
(20)

(19) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {L}} w = \xi _1 R \theta _{,xx} + \xi _2 R \theta _{,yy}\\ {\mathcal {L}}_1 \theta = - R w - H \phi \\ {\mathcal {L}}_2 \phi = - H \gamma \theta . \end{array}\right. } \end{aligned}$$
(21)

Now, applying the operators \({\mathcal {L}}\) and \({\mathcal {L}}_2\) to (21)\(_2\) and substituting (21)\(_1\) and (21)\(_3\) in the resulting equation, one leads

$$\begin{aligned} {\mathcal {L}} {\mathcal {L}}_1 {\mathcal {L}}_2 \theta = - R^2 \xi _1 ({\mathcal {L}}_2 \theta )_{,xx} - R^2 \xi _2 ({\mathcal {L}}_2 \theta )_{,yy} + H^2 \gamma {\mathcal {L}} \theta . \end{aligned}$$
(22)

Splitting the operators \({\mathcal {L}}_1\) and \({\mathcal {L}}_2\), from (22) it follows that

$$\begin{aligned} \begin{aligned}&( \zeta _1 \partial _{,x x} +\zeta _2 \partial _{,y y} + \partial _{,z z} -H \gamma ) ( \eta \varDelta _1 + \partial _{,z z} ) {\mathcal {L}} \theta \\&\quad = ( \zeta _1 \partial _{,x x} +\zeta _2 \partial _{,y y} + \partial _{,z z} ) H {\mathcal {L}} \theta \\&\qquad - R^2 ( \xi _1 \partial _{,x x} + \xi _2 \partial _{,y y} ) ( \zeta _1 \partial _{,x x} +\zeta _2 \partial _{,y y} + \partial _{,z z} ) \theta \\&\qquad + R^2 ( \xi _1 \partial _{,x x} + \xi _2 \partial _{,y y} ) H \gamma \theta . \end{aligned} \end{aligned}$$
(23)

By virtue of the periodicity and of the boundary conditions (11)\(_2\), since the sequence \(\{\sin (n\pi z)\}_{n\in {\mathbb {N}}}\) is a complete orthogonal system for \(L^2([0,1])\), accounting for solutions of the form \(\theta =\varTheta _0\sin (n\pi z) e^{i(a_xx+a_yy)}\), (23) becomes

$$\begin{aligned} \begin{aligned}&( -\zeta _1 a_x^2 - \zeta _2 a_y^2 - n^2 \pi ^2 - H \gamma ) ( - \eta a_x^2 - \eta a_y^2 - n^2 \pi ^2 ) \\&( - \xi _1 a_x^2 - \xi _2 a_y^2 -n^2 \pi ^2 - {\mathcal {T}}^2 \xi _1 \xi _2 n^2 \pi ^2 ) \\&\quad = ( -\zeta _1 a_x^2 - \zeta _2 a_y^2 - n^2 \pi ^2 ) H ( - \xi _1 a_x^2 - \xi _2 a_y^2 -n^2 \pi ^2 - {\mathcal {T}}^2 \xi _1 \xi _2 n^2 \pi ^2 ) \\&\qquad - R^2 ( - \xi _1 a_x^2 - \xi _2 a_y^2) ( -\zeta _1 a_x^2 - \zeta _2 a_y^2 - n^2 \pi ^2 - H \gamma ). \end{aligned} \end{aligned}$$
(24)

Setting \(A^*=1+{{{\mathcal {T}}}}^2\xi _1\xi _2\) and

$$\begin{aligned} \begin{aligned} f(a^2_x, a^2_y, n^2)&= \frac{ \xi _1 a_x^2 + \xi _2 a_y^2 +n^2 \pi ^2 A^*}{\xi _1 a_x^2 + \xi _2 a_y^2}\\&\quad \cdot \left[ \eta a_x^2 + \eta a_y^2 + n^2 \pi ^2 + \frac{H(\zeta _1 a_x^2 + \zeta _2 a_y^2 + n^2 \pi ^2)}{\zeta _1 a_x^2 + \zeta _2 a_y^2 + n^2 \pi ^2 + H \gamma } \right] \,, \end{aligned} \end{aligned}$$
(25)

from (24) it follows that the critical Rayleigh number \(R_L\) for the onset of convection is given by

$$\begin{aligned} R_L=\displaystyle {\min _{(n^2,a_x^2,a_y^2)\in {\mathbb {N}}\times {\mathbb {R}}^+\times {\mathbb {R}}^+}}f(a_x^2, a_y^2, n^2) \end{aligned}$$
(26)

and since \(f(a_x^2, a_y^2, n^2)\) is strictly increasing with \(n^2\), this implies that the minimum is attained at \(n^2=1\). Hence,

$$\begin{aligned} R_L = \min _{(a_x^2 , a_y^2) \in {\mathbb {R}}^+ \times {\mathbb {R}}^+} f(a^2_x, a^2_y, 1). \end{aligned}$$
(27)

Remark 1

Define

$$\begin{aligned} R_0 = \frac{R_L}{\pi ^2} = \min _{({{\bar{x}}} , {{\bar{y}}}) \in {\mathbb {R}}^+ \times {\mathbb {R}}^+} f_1({{\bar{x}}},{{\bar{y}}}), \end{aligned}$$
(28)

where

$$\begin{aligned} \begin{aligned} f_1({{\bar{x}}},{{\bar{y}}})&= \frac{ \xi _1 {{\bar{x}}} + \xi _2 {{\bar{y}}} + A^{*} }{\xi _1 {{\bar{x}}} + \xi _2 {{\bar{y}}}} \bigg [ \eta {{\bar{x}}} + \eta {{\bar{y}}} + 1 + \frac{H_0 (\zeta _1{{\bar{x}}} + \zeta _2 {{\bar{y}}} + 1)}{\zeta _1 {{\bar{x}}} + \zeta _2 {{\bar{y}}} + 1 + H_0 \gamma } \bigg ]\\ {{\bar{x}}}&= \dfrac{a_x^2}{\pi ^2}, \qquad {{\bar{y}}} = \dfrac{a_y^2}{\pi ^2}, \qquad H_0 = \dfrac{H}{\pi ^2}\,. \end{aligned} \end{aligned}$$
(29)

Let us observe that:

  1. (i)

    In the case of horizontal isotropy, i.e. \(\xi _1 = \xi _2\) and \(\zeta _1 = \zeta _2\), the critical Rayleigh number \(R_0\) given by (28) coincides with that one obtained in Capone and Gentile (2018);

  2. (ii)

    In the absence of rotation \(({\mathcal {T}}^2=0)\) and if the porous medium is isotropic \((\xi _1=\xi _2=\zeta _1=\zeta _2=\eta =1)\), then the critical Rayleigh number \(R_0\) coincides with that one obtained in Banu and Rees (2002). Moreover, in the hypothesis of local thermal equilibrium \((H_0\rightarrow \infty )\), by simple calculations, the critical Rayleigh reverts to the classical Rayleigh number for the isotropic porous medium in the local thermal equilibrium (Govender and Vadasz 2007);

  3. (iii)

    The stabilizing effect of fluid thermal conductivity on the onset of convection is evident since the partial derivative of (29) with respect to \(\eta\) is strictly positive.

4 Nonlinear Stability

In order to study the nonlinear stability of the conduction solution \(m_0\), let us introduce the following Lyapunov functional

$$\begin{aligned} E(t) = \frac{\Vert \theta \Vert ^2}{2} + \frac{A \Vert \phi \Vert ^2}{2 \gamma } \end{aligned}$$
(30)

and define

$$\begin{aligned} \begin{aligned} D(t)&= \eta \Vert \nabla _1 \theta \Vert ^2 + \Vert \theta _{,z} \Vert ^2 + \frac{\zeta _1}{\gamma }\Vert \phi _{,x} \Vert ^2 \\&\quad +\frac{\zeta _2}{\gamma }\Vert \phi _{,y} \Vert ^2 + \frac{1}{\gamma }\Vert \phi _{,z} \Vert ^2 + H \Vert \theta - \phi \Vert ^2 \\ I(t)&= (\theta , w)\,. \end{aligned} \end{aligned}$$
(31)

Multiplying (9)\(_3\) by \(\theta\), (16)\(_3\) by \(\phi\), integrating over V and then adding the resulting equations, we find out

$$\begin{aligned} \frac{d E}{d t} = - D \bigg (1 - R\frac{ I}{D}\bigg )\,. \end{aligned}$$
(32)

In order to capture the influence of rotation on the nonlinear stability analysis of the conduction solution \(m_0\), we shall apply the differential constraint approach (Straughan 2006; Ouarzazi et al. 2017; Capone and Gentile 2018]. To this end, let us consider the following variational problem

$$\begin{aligned} \frac{1}{R_E} = \max _{{\mathcal {H}}^*} \frac{I}{D} \end{aligned}$$
(33)

with

$$\begin{aligned} \begin{aligned} {\mathcal {H}}^*&= \{ (w, \theta , \phi ) \ : \ w = \theta = \phi =0 \ \text {on} \ z=0,1; \ \text {periodic in} \ x \ \text {and} \ y \\&\qquad \text {directions, with period} \ \frac{2 \pi }{a_x}, \frac{2 \pi }{a_y} \ \text {respectively}; \ D< \infty ; \ \text {verifying} \ (16)_1 \} \end{aligned} \end{aligned}$$
(34)

the space of the kinematically admissible perturbations.

The variational problem (33) is equivalent to

$$\begin{aligned} \frac{1}{R_E} = \max _{{\mathcal {H}}} \frac{I + \int _V \lambda \ g \ dV}{D} \end{aligned}$$
(35)

where \(\lambda (\mathbf{x })\) is a Lagrange multiplier and

$$\begin{aligned} \begin{aligned} g(\mathbf{x })&= \xi _1 w_{,xx} + \xi _2 w_{,yy} + w_{,zz} + T^2 \xi _1 \xi _2 w_{,zz} - \xi _1 R \theta _{,xx} - \xi _2 R \theta _{,yy}\\ {\mathcal {H}}&= \{ (w, \theta , \phi ) \ : \ w = \theta = \phi =0 \ \text {on} \ z=0,1; \ \text {periodic in} \ x \ \text {and} \ y \\&\qquad \left. \text {directions, with period} \ \frac{2 \pi }{a_x}, \frac{2 \pi }{a_y} \ \text {respectively}; \ D< \infty \right\} . \end{aligned} \end{aligned}$$
(36)

By applying the Poincaré inequality in (31)\(_1\), it turns out that

$$\begin{aligned} D(t) \ge \pi ^2 a \Vert \theta \Vert ^2 + b \frac{\pi ^2}{\gamma }\Vert \phi \Vert ^2 \end{aligned}$$
(37)

where

$$\begin{aligned} a = \min \{ \eta , 1 \} \qquad b = \min \{ \zeta _1, \zeta _2, 1 \}. \end{aligned}$$
(38)

Then, from (32) by virtue of (37) , if \(R<R_E\) one obtains:

$$\begin{aligned} \dfrac{dE}{dt}\le \dfrac{\pi ^2 (R-R_E)c}{R_E} E \end{aligned}$$

where \(c\le \min \left\{ 2a, \dfrac{2b}{A}\right\}\). Hence, the condition \(R<R_E\) implies the nonlinear, global and exponential stability of \(m_0\), according to the following inequality

$$\begin{aligned} E(t)\le E(0)\, \text{ exp }\left[ \dfrac{\pi ^2(R-R_E)c}{R_E}\, t\right] \,. \end{aligned}$$
(39)

Remark 2

Multiplying (9)\(_1\) by \(\mathbf{u }\), integrating over V and applying the Cauchy–Schwarz inequality, it turns out that

$$\begin{aligned} {\delta }^{-1} \Vert \mathbf{u } \Vert ^2 \le \Vert \theta \Vert ^2 \end{aligned}$$
(40)

where \(\delta = \dfrac{R^2}{2}\max \{ \xi _1, \xi _2, 2 \}\). Therefore, the condition \(R <R_E\) implies the decay of \(\Vert \mathbf{u } \Vert\), as well.

In order to determine the critical Rayleigh number \(R_E\), we solve the variational problem (35). The Euler Lagrange equations are

$$\begin{aligned} {\left\{ \begin{array}{ll} \theta + \xi _1 \lambda _{,xx} + \xi _2 \lambda _{,yy} + \lambda _{,zz} + {\mathcal {T}}^2 \xi _1 \xi _2 \lambda _{,zz} = 0 \\ 2 [ \eta \varDelta _1 \theta + \theta _{,zz} - H(\theta - \phi ) ] = \xi _1 R^2 \lambda _{,xx} + \xi _2 R^2 \lambda _{,yy} - Rw\\ \zeta _1 \phi _{,xx} + \zeta _2 \phi _{,yy} + \phi _{,zz} + H \gamma (\theta - \phi ) =0 \\ \xi _1 w_{,xx} + \xi _2 w_{,yy} + w_{,zz} + {\mathcal {T}}^2 \xi _1 \xi _2 w_{,zz} = \xi _1 R \theta _{,xx} + \xi _2 R \theta _{,yy}. \end{array}\right. } \end{aligned}$$
(41)

By virtue of (20), (41) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {L}} {\mathcal {L}}_1 \theta = - H {\mathcal {L}} \phi - R {\mathcal {L}}w\\ {\mathcal {L}} w = \xi _1 R \theta _{,xx} + \xi _2 R \theta _{,yy}\\ {\mathcal {L}}_2 \phi = - H \gamma \theta . \\ \end{array}\right. } \end{aligned}$$
(42)

Applying \({\mathcal {L}}_2\) to (42)\(_1\) and substituting (42)\(_2\) and (42)\(_3\) in the resulting equation, one obtains (22) and therefore \(R_L=R_E\), i.e. the coincidence between the global nonlinear stability threshold and the linear instability threshold, implying the absence of subcritical instabilities. This is an optimal result since the condition \(R<R_E=R_L\) is a necessary and sufficient condition to guarantee the stability of \(m_0\).

5 Numerical Simulations

This section will deal with the solution of equation (28). It will be analysed the influence of parameters on the critical Rayleigh number. First of all, we would like to point out the behaviour of function \(f_1({{\bar{x}}},{{\bar{y}}})\) in (29). Fixed five parameters \((\xi _1, \xi _2, \zeta _1, \zeta _2, \eta )\) in \(f_1({{\bar{x}}},{{\bar{y}}})\), once the following transformation is adopted

$$\begin{aligned} (\xi _1, \xi _2, \zeta _1, \zeta _2, \eta ) \rightarrow (\xi _2, \xi _1, \zeta _2, \zeta _1, \eta ), \end{aligned}$$
(43)

values initially assumed by \({{\bar{x}}}\) are taken by \({{\bar{y}}}\) and vice versa. Moreover, function \(f_1({{\bar{x}}},0)\) will have the same graph as \(f_1(0,{{\bar{y}}})\). This behaviour is important because by applying the previous transformation, the same results obtained for \({{\bar{x}}}\) hold for \({{\bar{y}}}\) and vice versa.

Figure 1 shows the stabilizing effect of rotation on the onset of convection, which is an expected physical behaviour. Moreover, taking into account (29), one immediately proves that \(f_1({{\bar{x}}}, {{\bar{y}}})\) is an increasing function of \({{{\mathcal {T}}}}^2\). In numerical analysis, for the sake of simplicity, we confine ourselves in considering the case of isotropic porous medium, i.e. \(\xi _1 = \xi _2 = \zeta _1 = \zeta _2 = \eta =1\). However, analogous results are obtained when another set of these parameters is fixed.

Fig. 1
figure 1

Critical Rayleigh number as function of the scaled inter-phase heat transfer coefficient \(H_0\) for different values of Taylor number \({{{\mathcal {T}}}}\) with \(\xi _1 = \xi _2 = \zeta _1 = \zeta _2 = \eta =1\) and \(\gamma = 0.4\)

Full size image

Note that in Fig. 1 the critical Rayleigh number is taken as a function of the scaled inter-phase heat transfer coefficient \(H_0\). As Govender and Vadasz (2007) pointed out, since this quantity is not easily measured, we need to determine a range in which this parameter can vary. Starting from its definition \(H_0 = \dfrac{h^2 d}{\varepsilon \kappa _z^f \pi ^2}\), for reasonable combinations of these parameters, \(H_0\) is assumed to vary between 0.01 and \(10^6\). It is well known that rotation has a stabilizing effect on conduction. In particular, Fig. 1 shows that this effect of Taylor number is very pronounced for large values of \(H_0\), while it is less remarkable for \(H_0 \sim 10^{-1}\). We would like to remark that for large values of \(H_0\), each curve tends to become parallel to x axis. As shown in Govender and Vadasz (2007), this behaviour represents the region of local thermodynamic equilibrium and it will characterize the following images, as well.

Fig. 2
figure 2

Critical Rayleigh number as function of the scaled inter-phase heat transfer coefficient \(H_0\) for different values of \(\gamma\) with \(\xi _1=\zeta _1=0.1, \ \xi _2=\zeta _2=\eta =1\) and \({{{\mathcal {T}}}}^2=20\)

Full size image

In Fig. 2, the destabilizing effect of the parameter \(\gamma\) on the onset of convection is clear. For large values of \(H_0\), \(R_0\) is inversely proportional to \(\gamma\), while for small values of \(H_0\), the presence of \(\gamma\) is negligible. This kind of behaviour is evident in equation (28), and it is reported in Govender and Vadasz (2007), as well. Physically, if h is large, i.e. the heat exchange between the phases is high, increasing the fluid conductivity \(\kappa _z^f\) fosters the onset of convection.

Fig. 3
figure 3

Critical Rayleigh number as function of the scaled inter-phase heat transfer coefficient \(H_0\) for different values of \(\xi _1\) with \(\xi _2=\zeta _2=\eta =1, \ \zeta _1=0.1, \ \gamma = 0.4\) and \({{{\mathcal {T}}}}^2=20\)

Full size image
Fig. 4
figure 4

Critical Rayleigh number as function of \(\xi _1\) with \(\zeta _1=0.1, \ \zeta _2=\xi _2=\eta =1, \ {{{\mathcal {T}}}}^2=20, \ \gamma =0.4\), a \(H_0=100\), b \(H_0=0.01\)

Full size image

Figure 3 shows the behaviour of the critical Rayleigh number as a function of \(H_0\) for different values of \(\xi _1\). The behaviour for low values of \(H_0\) is similar to the one for large values. In particular, \(R_0\) increases up to a certain value either for \(H_0=0.01\) and \(H_0=10^6\). After this point, it starts decreasing toward a limit value. The asymptotic trend is highlighted in Figs 4a, b, where \(H_0=100\) and \(H_0=0.01\), respectively.

Table 1 Significant values of \(R_0\), \({{\bar{x}}}\) and \({{\bar{y}}}\) depending on \(\xi _1\), with \(\xi _2 = \eta = \zeta _2=1, \ \zeta _1=0.1\)
Full size table
Table 2 Significant values of \(R_0\), \({{\bar{x}}}\) and \({{\bar{y}}}\) depending on \(\xi _2\), with \(\xi _1 = \eta =\zeta _1=1, \ \zeta _2=0.1\)
Full size table

Furthermore, in Tables 1–2, some significant values of \(R_0\) are reported in order to show which is the critical anisotropy parameter beyond which \(R_0\) inverts its trend, both for \(H_0=100\) and \(H_0=0.01\). In addition, note that the moment in which \(R_0\) starts decreasing coincides with the one in which the periodicity cells change their nature. Firstly, when \(\xi _2\) is fixed and \(\xi _1\) is increasing, they are rolls aligned along x axis. Then they turn into rolls aligned along y axis. The opposite transition occurs when transformation (43) is adopted, as shown in Table 2. This phenomenon is physically admissible, as pointed out by Straughan (2019). Small values of \(\xi _1\) imply that the fluid struggles to move in the x direction therefore the motion has components along y and z axis. Whereas, greater values of \(\xi _1\) allow the fluid to move easier in x direction, favouring the creation of rolls along y axis.

Kvernvold and Tyvand (1979) found that the presence of anisotropic porous media yields a two-dimensional fluid motion. Convective cells are rolls aligned in x or y direction, depending on the ratios between anisotropy parameters. This fluid behaviour is preserved under the hypothesis of local thermal non-equilibrium.

Table 3 Significant values of \(R_0\), \({{\bar{x}}}\) and \({{\bar{y}}}\) depending on \(\xi _1\), with \(\xi _2=\eta =\zeta _1=1, \ \zeta _2=0.1\)
Full size table
Fig. 5
figure 5

Critical Rayleigh number as function of the scaled inter-phase heat transfer coefficient \(H_0\) for different values of \(\xi _1\) with \(\xi _2=\eta =\zeta _1=1, \ \zeta _2=0.1, \ \gamma = 0.4\) and \({{{\mathcal {T}}}}^2=20\)

Full size image

The behaviour of critical Rayleigh number for different values of \(\xi _1\) changes once the ratio \(\dfrac{\zeta _1}{\zeta _2}\) is inverted. However, Fig. 5 is similar to Fig. 3.

Increasing \(\xi _1\) makes \(R_0\) grow up to a certain value, beyond which it starts decreasing. Moreover, for small values of \(H_0\), inverting \(\zeta _1\) and \(\zeta _2\) affects neither the shape of periodicity cells, which are firstly still rolls aligned along x axis, nor the influence of \(\xi _1\) on \(R_0\). Table 3 shows what has been just pointed out.

Fig. 6
figure 6

Critical Rayleigh number as function of \(H_0\) for different values of \(\xi _1\) with \(\eta =1, \ \ {{{\mathcal {T}}}}^2=20, \ \gamma =0.4\) a \(\xi _2=\zeta _1=0.1, \ \zeta _2 = 1\), b \(\xi _2=\zeta _2=0.1, \ \zeta _1 = 1\)

Full size image

Now, we decided to fix a direction in which the fluid fails to move easily. So we assumed \(\xi _2=0.1\) and looked at the critical Rayleigh number as a function of \(\xi _1\). In Fig. 6a, b, the destabilizing effect of permeability is evident, for all \(H_0\), both for \(\zeta _1 < \zeta _2\) and \(\zeta _1 > \zeta _2\). Recalling the definition of Rayleigh number, this kind of behaviour is expected. Fixed the horizontal permeability parameters \(K_x\) and \(K_y\), decreasing values of vertical permeability \(K_z\) yield a decrease of Rayleigh number, in agreement with findings of Govender and Vadasz (2007) in the case of horizontal isotropy. Furthermore, increasing \(K_x\) will promote the horizontal motion, which increases the preferred cells width and reduces the critical Rayleigh number, as also proposed by Tyvand and Storesletten (1991).

Now, let us analyse how \(R_0\) varies with respect to the thermal anisotropy. Figure 7 shows clearly that \(\zeta _1\) has a stabilizing effect on conduction if \(H_0\) is large. A similar result is found by Govender and Vadasz (2007) in a simpler situation. Physically, increasing solid conductivity implies that the solid matrix absorbs heat from the fluid more easily. On the other hand, when \(H_0 \sim 10^{-1}\), the effect of \(\zeta _1\) is negligible.

Fig. 7
figure 7

Critical Rayleigh number as function of the scaled inter-phase heat transfer coefficient \(H_0\) for different values of \(\zeta _1\) with \(\xi _1=\eta =\zeta _2=1, \ \xi _2=0.8, \ \gamma = 0.4\) and \({{{\mathcal {T}}}}^2=20\)

Full size image

Tables 4a–b represent a focus on the influence of solid thermal conductivity on the onset of convection. They are obtained when \(H_0=100\), but however analogous results are valid for all large \(H_0\).

Note that the stabilizing effect of \(\zeta _1\) is evident up to a certain value, beyond which \(R_0\) is constant. This behaviour is direct consequence of the change of rolls direction. Once the fluid motion occurs on the plane yz, i.e. rolls are aligned along x axis, modifying \(\zeta _1\) does not produce any effect on the motion. Furthermore, inverting the ratio \(\dfrac{\xi _1}{\xi _2}\) does not modify the way \(\zeta _1\) affects \(R_0\), as shown in Table 4b.

Table 4 (a) Significant values of \(R_0\) as function of \(\zeta _1\) with \(\xi _1=\eta =\zeta _2=1, \ \xi _2=0.8, \ H_0=100\). (b) Significant values of \(R_0\) as function of \(\zeta _1\) with \(\xi _2=\eta =\zeta _2=1, \ \xi _1=0.8, \ H_0=100\)
Full size table
Fig. 8
figure 8

Critical Rayleigh number as function of the scaled inter-phase heat transfer coefficient \(H_0\) for different values of \(\eta\) with \(\xi _1=1.6, \ \xi _2=\zeta _1=\zeta _2=1, \ \gamma = 0.4\) and \({{{\mathcal {T}}}}^2=20\)

Full size image

In Fig. 8, the stabilizing effect of fluid thermal conductivity \(\eta\) is highlighted for any \(H_0\). This behaviour is expected since we have shown previously that increasing \(\kappa _z^f\) fosters the onset of convection. Moreover, looking at the definition of \(R_0\) in (28), it is evident that the critical Rayleigh number is directly proportional to \(\eta\).

6 Conclusions

A linear and nonlinear stability analysis of the conduction solution in a fluid saturating an anisotropic porous layer under the effect of rotation, in local thermal non-equilibrium, has been performed. In particular, the coincidence between the global nonlinear stability threshold and the linear instability threshold has been proved. This means that a necessary and sufficient condition for global nonlinear stability of conduction solution has been obtained. Moreover, we have shown that convection can occur only through a steady motion.

Given that the critical Rayleigh number is obtained in a closed form, we have performed a numerical analysis. We have shown that the increasing conductivity ratio \(\gamma\) has a destabilizing effect on conduction. Mechanical anisotropy \(\xi _i\) (\(i=1,2\)) has the same effect, for \(\xi _j\) small (\(j \ne i\)), while a slightly different behaviour is obtained when \(\xi _j\) is high. Then we have proved that increasing fluid and solid thermal conductivities delay the onset of convection, as well as rotation.

Moreover, the presence of anisotropy forces the fluid in a two-dimensional motion. Convective cells are rolls aligned in x or y direction, depending on the ratios between anisotropy parameters.