Introduction

Green energy, defined by Walker and Devine-Wright (2008), includes the energy produced sustainably from biomass and that produced by indefinitely regenerated sources, like hydropower, solar, and wind energies. With the awareness that coal, oil, and gas are the major causes of pollution and lead to environmental degradation, the green energy sectors have become vertical to the global economy in the past decade (Khurshid and Deng 2020). The growth of energy demand and the constraints of reduced carbon emissions will make it more challenging for the global economy to achieve green growth (Wang et al. 2020).

Compared with traditional fossil energy, the resource scale of green energy is 800 times that of the former. Therefore, the attributes of manufacturing are far greater than the attributes of resources, which will promote the manufacturing industry to better play its advantages in photovoltaic, wind power, lithium battery, and hydrogen energy industries. After generating economies of scale and technological iteration, energy costs will be further reduced, bringing more economical costs. Some research finds that with the carbon price rising, investments in green energy firms would be encouraged (Kumar et al. 2012). While carbon emission rights trading covers multiple high-emission and high-energy-consuming industries such as electricity, steel, heating, truth, and oil refining. Therefore, the carbon price affects the upgrading and transformation of these industries, which in turn affects the stock returns of listed companies in these industries. The carbon price is the major factor to be considered when a pollution-generating company implements green technology in operational decisions (Pan et al. 2021). It is also studied that carbon price could facilitate the adoption of carbon capture and storage technology and can effectively reduce coal-related greenhouse gas emissions (Jie et al. 2020).

Apart from affecting the technology improvement and the costs of the green energy companies, the carbon price affects the stock prices of green energy companies by affecting corporate earnings. When the carbon price is low, emission control companies generally tend to buy carbon emission rights, and green energy companies save a large number of carbon allowances available for sale due to the advantages of emission reduction technology and new energy technology. Carbon trading gains additional income, and the increase in income drives up corporate stock prices. When the price of carbon emission rights is high, companies turn to seek alternative energy sources or introduce emission reduction technologies and equipment to reduce carbon emissions and prevent excess emissions. It creates more market demand for green energy companies to sell new energy technologies, equipment, and services. Besides, it helps green energy companies increase their profits, which in turn drives the simultaneous rise of stock prices. In addition, the carbon market plays the role of resource allocation through carbon price signals and guides the flow of social capital to more environmentally friendly new energy companies, which will help reduce the financing costs of green energy companies and boost their market value and stock price growth. In short, green energy companies can benefit from the change of carbon price, and their stock prices are always positively affected by the price of the carbon price.

The contribution of this paper is as follows: (i) to our best knowledge, this is the first paper to analyze the correlation of the carbon price and the stock returns of different green energy industries; (ii) we apply some novel quantile approaches in this study to expand the previous literature in this field; (iii) it provides some feasibility suggestion for the investors in the carbon trading and green energies fields.

The remainder of this paper is as follows. Section 2 reviews the related literature. Section 3 introduces the main methodology utilized in this paper. Section 4 shows the dataset and some preliminary results based on the raw data. Section 5 illustrates the dynamics of the carbon price and stock returns of the green energy market from a quantile perspective. Section 6 concludes the paper.

Literature review

The relationship between the carbon price and stock markets has been widely discussed since carbon trading becomes the most cost-effective emission reduction tool to deal with climate change (see Moreno and Silva 2016; Fang et al. 2018; Reboredo and Ugolini 2018; Mejdoub and Ghorbel 2018; Pereira and Pereira 2019; Krokida et al. 2020; Wen et al. 2020a, b; Batten et al. 2020; Duan et al. 2021). Researches find that key energy prices, including coal, gas, oil, and electricity, explain 12% of carbon price variation (Batten et al. 2020). The establishment of China’s carbon emissions trading market and the opening of carbon prices promote the carbon premium in the stock returns of the listed companies that participate in carbon emission trading. Those companies always need higher carbon exposures (Wen et al. 2020a). Furthermore, Wen et al. (2020b) reveal an asymmetric relationship between the carbon price and stock returns in China. A rise in carbon price shows a higher spillover effect on the stock market than a decrease in the carbon price. Fang et al. (2018) find that in different countries, the correlation of carbon and stock returns are significantly multifractal.

This paper is related to two strands of literature. The first strand is the literature analyzing the correlation between the carbon price and the stock returns of green energy companies. Since the electricity sector is the main participant in the European Union Emissions Trading Scheme (EU-ETS), the carbon price has a strong interdependence with electricity stock returns (see Tian et al. 2016; Ji et al. 2019; Kanamura 2019; Keeley 2019; Zhu and Ancev 2020). Tian et al. (2016) find that the carbon price affects the volatility and magnitude of electricity stock returns. The volatility of electricity stock returns is significantly driven by carbon price volatility. Besides, the carbon-intensive electricity companies are vulnerable negatively affected by the carbon price, compared to the less carbon-intensive electricity companies. Ji et al. (2019) suggest that the carbon price impacts the stock return of electricity companies with varying degrees of spillover effects. Large electricity companies receive a higher but less stable spillover effect from the carbon price than the small ones. Zhu and Ancev (2020) investigate that the carbon price tends to raise the electricity prices, which enhances the expectation of the stock returns of the electricity companies. The metallurgical sector is another important participant in the EU-ETS. Moreno et al. (2017) find that carbon price affects the operation of a firm, which is contributed to the fluctuation of the stock returns.

The second strand relates to the methodology in analyzing the correlation of return series. The GARCH family method is the most popular one in analyzing the correlation of the energy market (see Balcilar et al. 2016; Jiang et al. 2019; Hung 2019; Muhammad et al. 2021; Meng et al. 2020;). Applying a Markov regime-switching dynamic correlation, Balcilar et al. (2016) generalized the autoregressive conditional heteroscedasticity (MS-DCC-GARCH) method to capture the time-varying risk spillover effect from the energy futures prices and carbon prices. With the employment of a two-regime threshold vector error correction with the DCC-GARCH model, Muhammad et al. (2021) analyze the nonlinear price transmission mechanisms from the crude oil price to the green energy stock returns. Another method that is widely utilized is the quantile regression approach (see Tan and Wang 2017; Zhu et al. 2018; Jiang et al. 2020; Duan et al. 2021). Zhu et al. (2018) use a panel quantile regression approach to investigate the affection of carbon price on the stock returns of European carbon-intensive industries. They conclude that the influences show heterogeneous and asymmetric character in different quantiles. Duan et al. (2021) apply the quantile-on-quantile (QQ) regression and the causality-in-quantiles approach to analyze the asymmetric and negative impacts of energy prices on carbon prices.

From the literature above, it can be summarized that the extant literature on the effect of the carbon price on the green energy market focuses on the electrical sector. However, given that many other green energy industry companies, such as the wind, solar industries, are contributing to the green development, it is virtual to investigate that to what extent they are affected by the carbon price. Motivated by this, we collect different kinds of indexes that reflect the stock returns of different green energy industries to investigate the dynamic correlation between the carbon price and the stock returns of green energy industries.

Research methodology

Quantile regression analysis

We first adopt the quantile regression modelFootnote 1 to get some basic results in measuring the dynamic effects of the carbon price on the stock returns of green energy sectors:

$$ {Q}_{\tau}\left({\mathrm{Com}}_t\right)={\mu}_{0,\tau }+\beta {\prime}_{1,\tau }{C}_t $$
(1)

where Ct is the carbon price at time t, Comt is the stock returns of the green energy sectors at time t. The coefficient β denotes the impact of the carbon price on green energies over quantiles. The advantage of the quantile regression model is that it does not need any distribution assumption but has an optimal solution. To be more specific, it takes a sample with the empirical distribution randomly: \( {\hat{F}}_y\left(\theta \right)=\frac{1}{n}\ne \left\{{y}_i\le \theta \right\} \).

Quantile-on-quantile approach

The quantile-on-quantile (QQ) model, proposed by Sim and Zhou (2015), has been widely applied in studies of economic activities (See Jiang et al. 2020; Naifar et al. 2020).

In this part, we introduce the main part of this approach to analyze the dynamic relationship of the carbon price and the stock returns in the green energy sectors. The QQ method, combining a nonparametric method to illustrate the dynamic structure over quantiles, is an expansion of the traditional quantile regression methods. Then, to test the effect of the carbon price on stock returns in green energy sectors, we begin our study from a regression equation with Taylor expansion (first-order) to decompose the quantile regression coefficient βθ(∙) that we are interested in:

$$ {\mathrm{Com}}_t\approx {\beta}^{\theta \prime}\left({C}^{\tau}\right)\left({C}_t-{C}^{\tau}\right)+{\mu}_t^{\theta } $$
(2)

where Ct is the carbon price at time t, Comt is the stock returns of the green energy sectors at time t. θ means the θth quantile, \( {\mu}_t^{\theta } \) is the quantile residue, and βθ′(Ct) is the partial derivative of βθ(Ct).

Following Mo et al. (2019), we solve a local optimization problem by replacing Ct and Cτ with the empirical counterpart and further the local linear regression’s estimates b0 and b1 are used to replace β0 and β1:

$$ {\min}_{b_0,{b}_1}{\sum}_i^n{\rho}_{\theta}\left[{\mathrm{Com}}_t-{b}_0-{b}_1\left({\hat{C}}_t-{\hat{C}}^{\tau}\right)K\left(\frac{F_n\left({\hat{C}}_t-\tau \right)}{h}\right)\right] $$
(3)

where ρθ(u) is the quantile loss function with ρθ(u) = u(θ − I(u < 0)), I is an indicator function, and K(∙) refers to a conventional kernel function. Following Sim and Zhou (2015), Sim (2016), and Shahbaz et al. (2018), the Gaussian kernel is introduced here to calculate the neighborhood of Cτ. Besides, the bandwidth parameterFootnote 2h = 0.05 is considered in this paper.

Quantile coherency approach

The quantile coherency approach proposed by Baruník and Kley (2019) is a novel method that can calculate the general dependence by quantiles of the joint distributions in different frequencies. In this paper, we use it to study the dependence between the carbon price and the stock returns of green energy sectors as frequencies and quantiles change.

Set the carbon price and the stock returns of green energy sectors be two stationary series as X = {xt} and Y = {yt}, respectively. Then, the dynamic dependence between X and Y can be defined as follows:

(4)

where −π ≪ ω ≪ π, τ ∈ [0, 1], ϜX, Y, ϜX, X, and ϜY, Y denote quantile cross-spectral and quantile spectral densities of processes {xt} and {yt}, respectively.

Hedging effects

To verify the results of the QC approach, we further introduce the hedging effects (HE) index (Basher and Sadorsky 2016), which is a measurement of the hedging effect. We first calculate the risk-adjusted performance of the hedged portfolio and the unhedged portfolio in each series. Set RH, t is the return on a hedged portfolio including carbon trading and stock in green energy sectors:

$$ {R}_{H,t}={R}_{S,t}-{\gamma}_t{R}_{C,t} $$
(5)

where γt means the hedge ratio, and RS, t and RC, t denote the stock return in green energy sectors and the carbon price at time t, respectively. Hence, given information with It − 1, the variance of the hedged portfolio conditional is

$$ \operatorname{var}\left({R}_{H,t}{I}_{t-1}\right)=\operatorname{var}\left({R}_{S,t}{I}_{t-1}\right)-2{\gamma}_t\operatorname{cov}\left({R}_{C,t},{R}_{S,t}{I}_{t-1}\right)+{\gamma}_t^2\operatorname{var}\left({R}_{C,t}{I}_{t-1}\right) $$
(6)

The optimal hedge ratios (OHRs) that minimize the conditional variance var(RH, tIt − 1) on the information set at time t − 1 is following Baillie and Myers (1991):

$$ {\gamma}_t^{\ast }{I}_{t-1}=\frac{\operatorname{cov}\left({R}_{S,t},{R}_{C,t}|{I}_{t-1}\right)}{\operatorname{var}\left({R}_{C,t}|{I}_{t-1}\right)} $$
(7)

Following Basher and Sadorsky (2016), we utilize a multivariate generalized orthogonal GARCH (GO-GARCH) model of Weide (2002) and assume a multivariate affine NIG distribution. As in the quantile cross-spectral approach, the mean equation also includes an auto-regressive (AR(2)) term and a constant. For example, a long position in the stock of green energy sector hedge with a short position in the carbon trading market can be calculated as follows:

$$ {\gamma}_t^{\ast}\mid {I}_{t-1}=\frac{h_{SC,t}}{h_{C,t}} $$
(8)

where hSC, t is the conditional covariance, and hC, t is the conditional variance of the carbon price. And the HE index is calculated as:

$$ \mathrm{HE}=\frac{{\operatorname{var}}_{\mathrm{unhedged}}-{\operatorname{var}}_{\mathrm{hedged}}}{{\operatorname{var}}_{\mathrm{unhedged}}} $$
(9)

Data and statistics

In this paper, we use the daily data spanning from 14 October 2013 to 30 December 2020 with 1568 observations to analyze the dynamic relationship between the carbon price on the stock return of the green energy market. The dataset includes two types of data. First, we adopt the emission certificates (EUA), which are determined by the EU emission trading system (ETS) as the carbon price. Second, we use the Wilder Hill Clean Energy Index (hereafter ECO), the S&P Global Clean Energy Index (hereafter S&P), European Renewable Energy Index (hereafter REIX), the Clean Energy Technology Index (hereafter TEC), World Solar Energy Index (hereafter SOLAR), and the Global Wind Energy Index (hereafter WIND) to represent the green energy market, including solar, photovoltaic, wind, and other renewable energyFootnote 3.

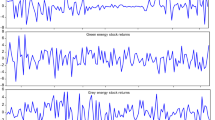
To show the fluctuations of all the indexes, we plot the time-paths of seven original data of stock returns of green energy firms in Fig. 1Footnote 4. ERIX, S&P, TECH, and WIND fluctuate smoothly before 2020 but rise rapidly after 2020, which underwent a two-year lag according to EUA. Besides, ECO and SOLAR turned out to decline before 2016, remain steady on a low level from 2016 to 2020, and increase after 2020.

Fig 1
figure 1

Time series plot of the carbon price and stock returns of green energy sectors

Full size image

The descriptive statistics for carbon price return and other green energies index returns are shown in Table 1. It can be seen that the mean of each series is positive, and the normality test suggests that all series do not follow a normal distribution. Besides, from the skewness, all the series are negative, which means that the carbon price always leads to a negative shock on the green energy markets. The ADF test implies that all the time series are stationary.

Table 1 Descriptive statistics
Full size table

Fig. 2 shows Pearson’s correlation matrix, which illustrates the varying degree of dependence between all the pairs. It can be noticed that the carbon price return has a positive correlation with all the series except ECO. Among the green energies, most of them have a strong dependence on each other, which means that these series can be integrated.

Fig. 2
figure 2

Pearson’s correlation matrix between carbon returns and stock returns in green energy sectors

Full size image

Empirical analysis

Quantile regression with rolling windows

In this part, we first utilize the conventional quantile regression with 7 quantiles to analyze the effects of the carbon market on the green energy markets. The quantile results are shown in Table 2. It is suggested that all pairs have significant explaining power except the EUA-ECO pair. Specifically, the effects of all pairs are positive at all quantiles except for 3 insignificant negative coefficients for the EUA-ECO pair at the quantile level of 0.25, 0.5, and 0.9, separately. The regression coefficient of the low quantile (10%) is bigger than the regression coefficient of the high quantile (90%), which indicates that the impact of the carbon price plummet is greater. EUA-ERIX shows a relatively strong co-movement, which is mainly because the REIX index is composed of the 10 largest and most liquid stocks in the green energy field.

Table 2 Quantile results for the carbon price on the stock return of green energy sector
Full size table

Though the results of the conventional quantile regression show a basic co-relationship of the series, it does not illustrate the dynamic co-movement of them. So, we then apply the rolling window quantile regression (Naifar et al. 2020) with #95 to further explain the varying effect of carbon price shock on the green energy markets over time. The results are shown in Fig. 3. We mainly discuss the effect of the carbon price on the green energy market in 10 quantiles and 90 quantiles.

Fig. 3
figure 3

Rolling-window quantile regression estimates of the impact of carbon returns on green energy indices return with windows=95. Notes: the blue line and the red line are the 10% and 90% quantile, separately. The black line is the fraction of the statistically significant coefficients across the quantiles

Full size image

From Fig. 3, it is easy to find the quantile regression coefficients differ with time. It also shows that the carbon price return is easier to shock the green energy market when some extreme events happen, like the COVID-19 that spread globally after 2020. Besides, it reveals that the most significant coefficients are in EUA- ERIX pair due to a high level of the dashed gray line. This is also consistent with the results shown in Table 2. As for all the pairs, after 2020, the variation of crude oil on S&P, TECH, WIND, and SOLAR is high according to the red line with a high quantile (90%). The blue line with a lower quantile (10%) turns out to be a lower level than the red line in all pairs.

Quantile-on-quantile results

In this part, we use the quantile-on-quantile method to analyze the varying effect of the carbon price returns on the green energy markets with results in Fig. 4. It can be seen that the effects change with quantiles and the effect shows heterogenetic and asymmetrical characters following Hammoudeh et al. (2014).

Fig. 4
figure 4

The QQ estimates for carbon returns on green energy indices returns. Notes: these results report the slope coefficient \( \hat{\beta_1}\left(\theta, \tau \right) \) in the z-axis with the quantiles (x-axis) of green energy indices returns (θ) and the quantiles (y-axis) of carbon returns (τ)

Full size image

As for the EUA-ERIX pair, the overall effects of the carbon price on the green energy stock return are mainly positive. At higher quantiles of the carbon and a lower quantile of the green energy, the effects turn negative. While in other major quantiles, it shows a positive effect. In addition, as the quantile of the green energy increases, the slope coefficient increases, as well. An obvious asymmetrical character can be summarized at a high quantile of carbon, higher quantile of ERIX. A similar asymmetrical property can be seen in the EUA-TECH pair. As for the EUA-ECO pair, the effects are evenly distributed between -0.5 and 0.5. the asymmetric property is not so obvious. Regarding the EUA-S&P pair, in most zones, the effects are average. But in a lower quantile of green energy, the carbon prices with different quantile have a different effect on the green energy. Regarding the EUA-WIND pair, the average effect is positive. But with carbon in higher quantile and green energy in lower quantile, the effect is negative. Besides, as the green energy is in high quantile, the effect shows an inverted U-shaped distribution. At the middle quantile of the carbon, the slope coefficient is the highest. An asymmetric character can be seen from this pair.

At last, following Shahzad et al. (2016) and Al-Yahyaee et al. (2019), we applied the quantile regression (QR) and the quantile-on-quantile (QQ) regression to test the validity of the QQ estimates. We get a similar result from the two methodsFootnote 5, which means the results are valid.

QC method results and hedging effects

To further analyze the different time-frequency (short, medium, and long) impact of the carbon price on the stock return of the green energies, we utilize the quantile coherency (QC) approach, in which the 0.1, 0.05, and 0.5 quantiles are involved, following Maghyereh and Abdoh (2020) and Jiang et al. (2020). The results are shown in Fig. 5. In actual investment activities, zero or negative terms in the QC matrix are signed as good choices which could reduce risks. Comparing the three time-frequency, the short-term one turns out to display the best hedging effect, which indicates that high-frequency trading in the carbon trading market and the green energy stock market can obtain a higher yield.

Fig. 5
figure 5

Quantile coherency (QC) matrices for carbon and green energy indices. Notes: above the diagonal line, we set non-significant values at the 5% significance level into zero. Red presents positive values, and blue presents negative values

Full size image

To be more specific, the short-term QC matrix shows that, at the lowest quantile (1%) of the carbon price and the highest quantile (50%) of the green energies, the carbon and green energy market show the best hedging effect with lots of zero and negative terms. It shows that all the green energies except SOLAR at a high quantile level can be good candidates for hedging the risk from the carbon trading market. At a higher quantile (5%) of the carbon price, all the green energies at a high quantile level show a good hedging effect on the carbon. While for the highest quantile (50%) of carbon and green energies, ERIX does not show a good hedging effect while others are a good choice. Similarly, the medium-term QC matrix illustrates that in each quantile horizon of the carbon price, ECO, S&P, and SOLAR at the high-frequency level are always good hedging tools. In the long-term, at the lowest quantile level of the carbon price, only WIND in the high quantile level is not fit for hedging. At a 5% level of carbon and 50% level of green energies, TECH is not a good choice for hedging. It is interesting that when the carbon is at a high level of 50%, ERIX and WIND at 5% level show good hedging effects. All the results verify that hedging strategies differ with quantiles, which is consistent with Selmi et al. (2018).

The QC results show lots of choices of hedging candidates in the short-term, fewer choices in the long-term, and the medium-term choices are the least. It indicates that it is more effective to hedge in the short term. What is interesting is that, when the carbon price is at the extreme quantile (bear market), more zero relationships are found between the carbon price and green energy. While the carbon price is at the middle quantile (normal market), hedging strategies are less. So when the carbon price experiences the bear market, investors can benefit from it.

We further investigate the hedging effect from the perspective of the time domain. Following the definition of the hedge ratios and hedging effect in Eqs. (8) and (9), we calculate the HE indexes and hedge ratios of the carbon and green energies. The results are shown in Fig. 6. Based on our sample data, we choose different rolling windows. In Fig. 6, (600, 30) means that the model is fitted by 30 observations with 600 one-period-ahead forecasts.

Fig. 6
figure 6

Hedging effects and hedge ratios for carbon and green energy indices. Notes: (600, 30) means that the model is fitted by 30 observations with 600 one-period-ahead forecasts

Full size image

Besides, we can obtain some revelations from Fig. 6(a). The ratio tells us how many units of carbon we should buy or sell when setting a portfolio of buying a green energy index. All the hedging ratios are positive, which indicates that a short position in the carbon trading market is beneficial for investors. For instance, as for the EUA-TECH and the EUA-ERIX pairs, the ratios are relatively higher and positive. The ratio coefficient of the EUA-TECH is 0.43, which means a portfolio with 100 units long position of TECH index and 43 units short position of the carbon can obtain a higher hedging benefit.

Fig. 6(b) shows the hedging effects. Except for the ERIX and ECO, the portfolios of the green energies have relatively higher hedging effects, which supports that the carbon trading market supplies an effective way to hedge risks from the stock market in green energy sectors. Besides, it also provides evidence that the hedging effects are heterogeneous since carbon is not a good choice to hedge risks from the ECO index and exhibits a weak hedge effect in ERIX. As the rolling windows change, the hedging effects vary, too.

Conclusions

This paper is aimed at analyzing the dynamic relationship of the carbon price on the stock returns in green energy sectors. By utilizing a series of quantile models, adopting a daily dataset span from 14 October 2013 to 30 December 2020, we investigate the dynamic correlation of the carbon and green energy stock returns in different quantiles and calculate the hedging effects, which supplies some indication for investors to optimize their portfolio.

Basically, by utilizing the rolling quantile regression model, we find that the coefficients change with time and are vulnerable to some special events, like the COVID-19 which spread quickly after 2020. Among the six green energy stock indexes, the ERIX shows a high co-movement with the carbon price, which is also confirmed by the results gained from the QQ model. By utilizing the QC model, we find that investors can benefit more in the short term to hedge between carbon trading and the green energy stock market. That means high-frequency trading in those two markets can earn a higher hedging effect. We further compute the hedging effects and hedge ratios of the carbon and green energy stock indexes from the perspective of the time domain. The results show that all the hedging ratios are positive. A portfolio with a long position of green energies and a short position of carbon can obtain a higher hedging benefit. It is also demonstrated that hedging effects are heterogenetic. So, as for investors, the hedging strategies should be adjusted in different backgrounds.