Skip to main content
SpringerLink
Log in

Energy convergence effect and jet phenomenon of shock-heavy spherical bubble interaction

  • Article
  • Fluid Dynamics
  • Published:
Science China Physics, Mechanics & Astronomy Aims and scope Submit manuscript

Abstract

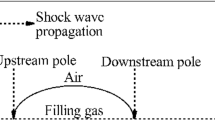
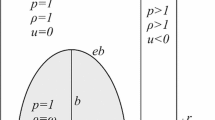
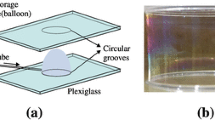
We present computational results on the evolution of the shock-accelerated heavy bubbles surrounded by nitrogen with the Atwood number A t = 0.497–0.677 and the emphasis is on the jet phenomenon caused by the shock focusing. The multi-fluid Eulerian equation is solved by a finite volume method based on MUSCL-Hancock approach. Based on the numerical schlieren and the distributions of density and pressure, it is found that there are three typical jet structures (outward jet, no jet, inward jet) for different combinations of gas mixture inside the bubble which determine the position of shock focusing relative to the downstream pole of the heavy bubble (upstream of the pole, at the pole, downstream the pole). Compared with the inward jet, the velocity of outward jet is obviously larger. As A t increases, the moment of jet formation is postponed, and the maximal values and magnifications of pressure and density increase distinctly. Therefore, the energy convergence effects are heavily enhanced with the increase of bubble gas density.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ma T, Patel P K, Izumi N, et al. Onset of hydrodynamic mix in high-velocity, highly compressed inertial confinement fusion implosions. Phys Rev Lett, 2013, 111: 085004

    Article  ADS  Google Scholar 

  2. Yang J, Kubota T, Zukoski E E, et al. Application of shock-induced mixing to supersonic combustion. AIAA J, 1993, 31: 854–862

  3. Jamaluddin A R, Ball G J, Leighton T J. Shock/bubble interaction near a rigid boundary in shock wave lithotripsy. In: Proceedings of the 24th International Symposium on Shock Waves. Jiang Z L, ed. Beijing: Springer, 2005. 1211–1216

    Google Scholar 

  4. Arnett W D, Bahcall J N, Kirshner R P, et al. Supernova 1987A. Annu Rev Astron Astrophys, 1989, 27: 629–700

    Article  ADS  Google Scholar 

  5. Rudinger G, Somers L M. Behavior of small regions of different gases carried in accelerated gas flows. J Fluid Mech, 1960, 7: 161–176

  6. Winkler K H, Chalmers J W, Hodson S W, et al. A numerical laboratory. Phys Today, 1987, 40: 28–37

  7. Picone J M, Boris J P. Vorticity generation by shock propagation through bubbles in a gas. J Fluid Mech, 1988, 189: 23–51

  8. Haas J F, Sturtevant B. Interaction of weak shock waves with cylindrical and spherical inhomogeneities. J Fluid Mech, 1987, 181: 41–76

    Article  ADS  Google Scholar 

  9. Niederhaus J H J, Greenough J A, Oakley J G, et al. A computational parameter study for the three-dimensional shock-bubble interaction. J Fluid Mech, 2008, 594: 85–124

    Article  ADS  MATH  Google Scholar 

  10. Ranjan D, Oakley J, Bonazz R. Shock-bubble interactions. Annu Rev Fluid Mech, 2011, 43: 117–140

    Article  ADS  Google Scholar 

  11. Zhai Z, Si T, Luo X, et al. On the evolution of spherical gas interfaces accelerated by a planar shock wave. Phys Fluids, 2011, 23: 084104

    Article  ADS  Google Scholar 

  12. Si T, Zhai Z, Luo X, et al. Experimental studies of reshocked spherical gas interfaces. Phys Fluids, 2012, 24: 054101

    Article  ADS  Google Scholar 

  13. Hawker N A, Ventikos Y. Interaction of a strong shockwave with a gas bubble in a liquid medium: A numerical study. J Fluid Mech, 2012, 701: 59–97

  14. Layes G, Metayer O L. Quantitative numerical and experimental studies of the shock accelerated heterogeneous bubbles motion. Phys Fluids, 2007, 19: 042105

    Article  ADS  Google Scholar 

  15. Zhai Z, Si T, Zou L, et al. Jet formation in shock-heavy gas bubble interaction. Acta Mech Sin, 2013, 29: 24–35

    Article  ADS  Google Scholar 

  16. Sun M, Takayama K. Conservative smoothing on an adaptive quadrilateral grid. J Comput Phys, 1999, 150: 143–180

  17. Luo X, Prast B, van Dongen M E H, et al. On phase transition in compressible flows: Modelling and validation. J Fluid Mech, 2006, 548: 403–430

  18. Zhai Z, Si T, Luo X, et al. Parametric study on the cylindrical converging shock waves generated based on shock dynamics theory. Phys Fluids, 2012, 24: 026101

    Article  ADS  Google Scholar 

  19. Wang M, Zhai Z, Si T, et al. Generation of polygonal gas interfaces by soap film for Richtmyer-Meshkov instability study. Exp Fluids, 2013, 54: 1427

    Article  Google Scholar 

  20. Zhai Z, Wang M, Si T, et al. On the interaction of a planar shock with a light polygonal interface. J Fluid Mech, 2014, 757: 800–816

  21. Fan M, Zhai Z, Si T, et al. Numerical study on the evolution of the shock-accelerated SF6 Interface: Influence of the interface shape. Sci China-Phys Mech Astron, 2012, 55: 284–296

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory for Shock Wave and Detonation Physics, Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang, 621900, China

    LiYong Zou, JinHong Liu, YanPing Wang & CangLi Liu

  2. Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences University of Cambridge, Cambridge, CB3 0WA, UK

    LiYong Zou

  3. Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei, 230026, China

    ZhiGang Zhai

Authors
  1. LiYong Zou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. ZhiGang Zhai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. JinHong Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. YanPing Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. CangLi Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to LiYong Zou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zou, L., Zhai, Z., Liu, J. et al. Energy convergence effect and jet phenomenon of shock-heavy spherical bubble interaction. Sci. China Phys. Mech. Astron. 58, 124703 (2015). https://doi.org/10.1007/s11433-015-5697-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11433-015-5697-0

Keywords

Search

Navigation