A rational hypoplastic constitutive equation for anisotropic granular materials incorporating the microstructure tensor

Abstract

A rational study has been made to describe the behavior of anisotropic granular materials by a hypoplastic constitutive equation. The concept of the microstructure tensor in describing the anisotropy has been implemented to develop a general form of a hypoplastic constitutive equation for anisotropic materials. Attempt was made to present all formulations in a rational way with no additional assumption. Both inherent and induced anisotropy have been studied and the evolution of the material internal structure has been rationally defined through an evolutionary function. Since all developments are primarily mathematical, no particular form of a constitutive equation has been assumed. Verifications by some available experimental data reveal the success of the proposed developments outlined in this study.

Appendices

Appendix 1: Equivalent limit state equations for hypoplastic anisotropic materials based on common yield criteria in classical plasticity theory

By making use of the scalar anisotropic parameter, η [41, 45, 48]:

$$\eta = 3\frac{{{\text{tr}}\left( {{\varvec{T}}^{2} {\mathbf{\mathfrak{F}}}} \right)}}{{{\text{tr}}\left( {{\varvec{T}}^{2} } \right)}} = 3\frac{{t_{im} t_{jn} {\mathfrak{F}}_{mn} }}{{t_{pq} t_{pq} }}$$

(43)

The following yield criteria for anisotropic granular materials and their equivalent limit state surfaces in hypoplasticity can be defined.

1.1 Anisotropic form of the Drucker and Prager [10] yield criterion

$$f\left( {I_{1} ,J_{2} } \right) = \sqrt {\left| {J_{2} } \right|} - \eta kI_{1} - \beta = 0$$

(44)

In this equation $I_{1} = {\text{tr}}{\varvec{T}}$ and $J_{2} = \frac{1}{2}\left[ {\left( {{\text{tr}}{\varvec{S}}} \right)^{2} - {\text{tr}}{\varvec{S}}^{2} } \right] = - \frac{1}{2}{\varvec{S}}{:}{\varvec{S}}$. Therefore:

$$f\left( {I_{1} ,J_{2} } \right) = \frac{1}{\sqrt 2 }\sqrt {{\varvec{S}}{:}{\varvec{S}}} - \eta k{\text{tr}}{\varvec{T}} - \beta = 0$$

(45)

$$f\left( {I_{1} ,J_{2} } \right) = {\varvec{S}}{:}{\varvec{S}} = 2\left( {\eta k{\text{tr}}{\varvec{T}} + \beta } \right)^{2} = 2\eta^{2} k^{2} \left( {{\text{tr}}{\varvec{T}}} \right)^{2} + 2\beta^{2} + 4\beta \eta k{\text{tr}}{\varvec{T}}$$

(46)

In case of sand with no cohesion, i.e., β = 0, we have:

$$f\left( {I_{1} ,J_{2} } \right) = {\varvec{S}}{:}{\varvec{S}} = 2\eta^{2} k^{2} \left( {{\text{tr}}{\varvec{T}}} \right)^{2}$$

(47)

$$f\left( {I_{1} ,J_{2} } \right) = \hat{\user2{S}}{:}\hat{\user2{S}} = 2\eta^{2} k^{2} = \alpha^{2}$$

(48)

which is identical to the previous one obtained by hypoplasticity.

1.2 Anisotropic form of the Matsuoka and Nakai [25] yield criterion

$$I_{1} I_{2} - \eta kI_{3} = 0$$

(49)

where

$$\hat{I}_{1} \hat{I}_{2} - \eta k\hat{I}_{3} = 0,\quad \hat{I}_{1} = \frac{{{\text{tr}}\left( {\varvec{T}} \right)}}{{{\text{tr}}\left( {\varvec{T}} \right)}} = 1,\quad \hat{I}_{2} = \frac{1}{2}\left[ {\left( {{\text{tr}}\hat{\user2{T}}} \right)^{2} - {\text{tr}}\left( {\hat{\user2{T}}^{2} } \right)} \right] = \eta k\det \hat{\user2{T}},\quad \hat{\user2{T}}{:}\hat{\user2{T}} = 1 - 2\eta k\det \hat{\user2{T}}$$

(50)

Therefore:

$${\varvec{T}}{:}{\varvec{T}} - \left( {{\text{tr}}{\varvec{T}}} \right)^{2} g\left( {\alpha^{2} } \right) = 0, \hat{\user2{T}}{:}\hat{\user2{T}} - g\left( {\alpha^{2} } \right) = 0$$

(51)

$$g\left( {\alpha^{2} } \right) = \alpha^{2} + \frac{1}{3} = 1 - 2\eta k\det \hat{\user2{T}}, \alpha^{2} = \frac{2}{3} - 2\eta k\det \hat{\user2{T}}$$

(52)

which gives the final form for α. The same proof can be provided for the Lade–Duncan yield criterion.

Appendix 2: Fabric tensor for special case of transversely isotropic materials

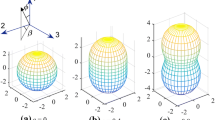
For transversely isotropic materials (Ω₂ = Ω₃), the fabric tensor (or the microstructure tensor), ${\mathbf{\mathfrak{F}}}$ (or equivalently, Ω) can be found as follows. Reminding that Ω is a traceless tensor, it can be fully prescribed by only one of its entries:

$$\Omega_{2} = \Omega_{3} ,\quad \Omega_{1} + \Omega_{2} + \Omega_{3} = 0,\quad \Omega_{2} = \Omega_{3} = - \Omega_{1} /2$$

(53)

If T and ${\mathbf{\mathfrak{F}}}$ (or Ω) are coaxial, i.e., possessing the same eigenvectors, then:

$$\eta = 3\frac{{{\text{tr}}\left( {{\varvec{T}}^{2} {\mathbf{\mathfrak{F}}}} \right)}}{{{\text{tr}}\left( {{\varvec{T}}^{2} } \right)}} = 3\frac{{t_{im} t_{in} {\mathfrak{F}}_{mn} }}{{t_{mn} t_{mn} }} = \frac{{t_{im} t_{in} \left( {\delta_{mn} + \Omega_{mn} } \right)}}{{t_{mn} t_{mn} }} = \frac{{t_{mn} t_{mn} + t_{im} t_{in} \Omega_{mn} }}{{t_{mn} t_{mn} }} = 1 + \frac{{t_{im} t_{in} \Omega_{mn} }}{{t_{mn} t_{mn} }}$$

(54)

Without loss of generality, we can assume that the global coordinates system is the same as the principal stress direction, i.e., θ = 90°. Therefore, three special cases can be inspected which are very useful in standard triaxial compression:

Case (i) β = 0 (bedding planes parallel to x₂–x₃ plane)

$$\eta = 1 + \frac{{\sigma_{1}^{2} \Omega_{1} + 2\sigma_{3}^{2} \Omega_{3} }}{{\sigma_{1}^{2} + 2\sigma_{3}^{2} }} = 1 + \frac{{\sigma_{1}^{2} - \sigma_{3}^{2} }}{{\sigma_{1}^{2} + 2\sigma_{3}^{2} }}\Omega_{1}$$

(55)

Case (ii) β = 90° (bedding planes parallel to x₁–x₂ plane)

$$\eta = 1 + \frac{{\sigma_{1}^{2} \Omega_{3} + \sigma_{3}^{2} \left( {\Omega_{1} + \Omega_{3} } \right)}}{{\sigma_{1}^{2} + 2\sigma_{3}^{2} }} = 1 - \frac{{\sigma_{1}^{2} - \sigma_{3}^{2} }}{{2\left( {\sigma_{1}^{2} + 2\sigma_{3}^{2} } \right)}}\Omega_{1}$$

(56)

Case (iii) β arbitrary

$${{\varvec{\Omega}}}^{{\prime }} = {\varvec{A}}^{{\text{T}}} {{\varvec{\Omega}}}{\varvec{A}},\quad \Omega_{mn}^{{\prime }} = a_{im} a_{jn} \Omega_{ij}$$

(57)

where a_ij are cosines of the subtended angles between x_i and $x_{j}^{\prime }$:

$$\begin{aligned} a_{11} & = \cos \beta ,\quad a_{22} = 1,\quad a_{33} = \cos \beta ,\quad a_{12} = a_{21} = 1, \\ a_{13} & = - a_{31} = - \sin \beta ,\quad a_{23} = a_{32} = 0 \\ \end{aligned}$$

(58a)

$$\begin{aligned} & \varvec{A} = \left( {\begin{array}{ccc} {\cos \beta } & 0 & { - \sin \beta } \\ 0 & 1 & 0 \\ { + \sin \beta } & 0 & {\cos \beta } \\ \end{array} } \right),~ \\ \\ & {\varvec{\Omega }}^{{\prime }} = \left( {\begin{array}{cc} {\Omega _{1} \cos ^{2} \beta + \Omega _{3} \sin ^{2} \beta } & 0 \\ 0 & {\Omega _{2} = \Omega _{3} } \\ {\left( { - \Omega _{1} + \Omega _{3} } \right)\sin \beta \cos \beta } & 0 \\ \end{array} } \right. \\ \\ & \quad\quad \quad \quad \left. \begin{array}{c} \left( - \Omega _{1} + \Omega _{3} \right)\sin \beta \cos \beta \\ 0 \\ \Omega _{1} \sin ^{2} \beta + \Omega _{3} \cos ^{2} \beta \\ \end{array} \right), \\ \end{aligned}$$

(58b)

Equivalently:

$${{\varvec{\Omega}}}^{{\prime }} = \left( {\begin{array}{*{20}c} {\Omega_{11}^{{\prime }} } & 0 & {\Omega_{13}^{{\prime }} } \\ {} & {\Omega_{22}^{{\prime }} } & 0 \\ {{\text{sym}}.} & {} & {\Omega_{33}^{{\prime }} } \\ \end{array} } \right),\quad \Omega_{11}^{{\prime }} + \Omega_{22}^{{\prime }} + \Omega_{33}^{{\prime }} = 0, \beta {:}\,{\text{given}},\,{\text{fixed}},\quad {\text{tr}}{{\varvec{\Omega}}}^{{\prime }} = 0$$

(59)

Therefore, having known β only one independent component of Ω is left to be found. Thus, by conducting at least two standard triaxial compression tests, a single paramer limit state function together with the fabric tensor, ${\mathbf{\mathfrak{F}}}$ (or equivalently, Ω) can be found.