Introduction

Plasmonic nanocomposites that consist of small noble metal particles embedded in metal oxides have attracted attention because they are expected to have many useful electronic and optical properties as a result of quantum size effects [1, 2]. These systems find useful applications in catalysis, photocatalysis, sensors, and novel optoelectronic devices [3,4,5]. Particularly, nanocomposites containing gold nanoparticle (AuNPs) embedded in a \({Al}_{2}{O}_{3}\) matrix have been studied over the past few years in several scientific and technological areas [6,7,8], due to their notable potential in the field of plasmonic sensing [9, 10]. These nanoplasmonic composites manifest Surface Plasmon Resonance (SPR) phenomenon [11], which enables their use in several sensing applications. Thanks to this SPR phenomenon, AuNPs possess the capability to focus a strong electromagnetic field at the nanoscale level. Light of a certain wavelength turns nanoparticles into efficient nanosources of heat [12]. Under lighting at their plasmon resonance wavelength, AuNPs can absorb incident light and transform into heat sources that can be remotely controlled by light. This feature is used in thermal therapy; indeed, when a nanoparticle is excited by a laser beam, a part of the energy from the light will be converted to heat and will be transferred to the surrounding medium [13]. The research field in which plasmonics and its applications are investigated is called thermoplasmonics. A very recent application of thermoplasmonics has been also employed in the battle against coronavirus outbreak. Some examples are mainly devoted to detecting the current pandemic (SARS-CoV-2), enabling a real-time and label-free detection of viral sequences [14, 15]. Other applications are aimed at realizing nano-based antimicrobial and antiviral formulations that are not only suitable for disinfecting air and surfaces but are also effective in reinforcing personal protective equipment such as facial respirators [16]. Other emerging applications of thermoplasmonics are also present in nonbiomedical field, such as the use of nanoparticles to improve light absorption in perovskite solar cells or to achieve high storage densities in optical data storage [17, 18]. In the most disparate fields, all these applications have given rise to the real need to monitor the heat induced by the photothermal effect at the nanoscale and the macroscale, generated by an ensemble of AuNPs. The detection of the temperature change in the proximity of the AuNP surface is a crucial application. One technique relies on the utilization of temperature-sensitive materials as media surrounding the AuNPs.

The SPR band characteristics such as position, amplitude, and width peak depend strongly on the geometric characteristics (size, shape, and concentration) of the nanoparticles, as well as on the dielectric properties (dielectric permittivity) of their surrounding medium [19]. Furthermore, the use of a solid support as an oxide matrix can influence the growth mechanisms of the nanoparticles during the nanoplasmonic composite preparation, thus affecting their size distribution [20]. In addition, it also allows to tune the position of the SPR band, shifting it to higher wavelengths as the refractive index of the surrounding medium increases [21]. To determine the optical and thermoplasmonic properties of the Au-\({Al}_{2}{O}_{3}\) nanocomposite, it is very important to know two main effective parameters, the dielectric constant (\({\varepsilon }_{eff}^{^{\prime}}\)) and dissipation factor \((\varepsilon^{''}_{eff})\). The dielectric constant of a material can be defined as the ratio of the absolute relative permittivity of the material to the electric permeability of free space (i.e., vacuum). The magnitude of \({\varepsilon }_{eff}^{^{\prime}}\) depends on the amount of mobile (polarizable) electrical charges and the degree of mobility of these charges in the material. In an alternating current (AC) field, the effective dielectric constant is represented as a complex quantity, \({\varepsilon }_{eff}^{*}\) and is the combination of a real component (dielectric constant \({\varepsilon }_{eff}^{^{\prime}}\)), and an imaginary component, called the dielectric loss \(\varepsilon^{''}_{eff}\). This complex dielectric permittivity can be defined by the following equation: \({\varepsilon }_{eff}^{*}={\varepsilon }_{eff}^{^{\prime}}+i\varepsilon^{''}_{eff}\). In order to simulate the dielectric behavior of heterostructures, several methods have been developed, mainly the finite difference method in the time domain (FDTD) [22], the discrete-dipole approximation (DDA) [23], and surface integral method [24]. On theoretical side, the effective medium theory (EMT) is a powerful way to handle the optical properties of the composite materials. Maxwell Garnett Theory (MGT) [25] constitutes a variant of EMT. However, this theory often claimed that a weak interaction between particles is a condition for the validity of MGT.

One of the greatest achievements in thermoplasmonics is related to the implementation of thermoplasmonic desalination using Ag and Au nanoparticles. This should be mentioned by the authors among the applications of thermoplasmonics [26,27,28,29,30,31]. Experimental works on Au surface plasmons should be discussed [32,33,34]. In previous work [35], plasmonic nanoantennas focus light below the diffraction limit, creating strong field enhancements, typically within a nanoscale junction.

In this paper, we used the FEM to determine the effective dielectric permittivity of plasmonic nanocomposites consisting of spherical AuNPs periodically distributed in \({Al}_{2}{O}_{3}\) matrix in the ultraviolet–visible-near infrared (UV–Vis-NIR) spectral range. Such a method allowed us to derive the electrical and optical parameters of the nanocomposites such as the refractive index \(n\), extinction coefficient \(\kappa\), absorption coefficient \({\mu }_{a}\), optical conductivity \(\sigma\), and enhancement electric field \({E}_{loc}\). The characteristics of the SPR are deduced from the absorption spectrum. After, the band gap energy is determined from the Tauc plots [36] for different concentrations of AuNPs in the Al2O3 matrix. The thermoplasmonic dissipation relative to the optical extinction corresponding to the identical AuNPs dispersed in the Al2O3 matrix is determined relative to an individual particle and relative to 1 g of particles.

The content of this manuscript is organized as follows: In “Theory and Method,” we summarize the context of the problem and we describe the essential to our computational procedure. In “Results and Discussion,” we present the obtained results using this method which focuses on the spectra of the various optical parameters of our system, as well as the band gap energy, the enhanced electric field, and the generated thermoplasmonic power at the SPR. Finally, the concluding remarks of the paper will be presented in “Conclusion.”

Theory and Method

Surface plasmon resonance (SPR) in metallic nanoparticles is the origin of many novel optical phenomena such as resonance light absorption and light scattering. The collective motion of free electrons on the metal surface oscillates like a simple dipole and consequently results in an intense polarized electric field. The polarized field is called local field because of its large intensity appearing near the particle surface and could be enhanced via coupling to the SPR what known by local field enhancement in metallic nanostructure.

The characterization of the optical, electrical, and thermal phenomena related to the SPR of AuNPs integrated in an electric matrix requires the calculation of the effective dielectric permittivity which is defined as the ratio of the average displacement field vector and the applied electric field; we may write this quantity as:

$$\overline E^2\varepsilon_{eff}=\frac1\Omega\int_\Omega\varepsilon\vert\triangle V\vert^2d\Omega$$
(1)

where \(\varepsilon\) is a spatially dependent permittivity, \(\overline{E }=\frac{1}{\Omega }\underset{\Omega }{\overset{}{\int }}{E}_{loc}d\Omega\) denotes a volume average field over a sample large compared with microscopic correlation lengths and depends on the applied potentials, \(\Omega\) is the volume of the medium, and \({E}_{loc}\) is the local electric field in the cell which is defined as:

$${E}_{loc}={E}_{0}+\frac{1}{3\upvarepsilon }P$$
(2)

where \({E}_{0}\) is the applied field and \(P\) is the material polarization. The complex effective permittivity will depend on the permittivity of each constituent in the mixture and their volume fractions, and eventually on the sizes, shapes, and distribution in space of the inclusions. In previous work [37], the optical properties of nanocomposites constituted of metallic particles dispersed in a dielectric matrix, among these, we cite the most popular, Maxwell Garnett Theory (MGT). This theory makes it possible to calculate the effective dielectric function of nanocomposite (inclusion-matrix), provided that the volume fraction of the nanoparticles is not very high, in order to neglect the interaction between inclusions.

The calculation of the effective dielectric constant of composite materials from the known properties of the pure, homogeneous components is an electrostatics problem which involves the resolution of Laplace’s Eq. (3) and taking into account boundary conditions defined on domains with given geometries.

$$\overrightarrow{\nabla }\left({\upvarepsilon }_{0}\upvarepsilon \left(\overrightarrow{\mathrm{r}}\right)\overrightarrow{\nabla }\mathrm{V}\left(\overrightarrow{\mathrm{r}}\right)\right)=0$$
(3)

where \(\varepsilon \left(\overrightarrow{r}\right)\), \(V\left(\overrightarrow{r}\right)\), and \({\upvarepsilon }_{0}=8.85.{10}^{-12}\mathrm{F}/\mathrm{m}\) are the local relative permittivity, potential distribution inside the material domain respectively with zero charge density and permittivity of the vacuum.

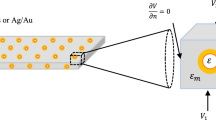
The solution of Laplace’s equation can be calculated by the FEM. We give here only some of the most important details of the studied model and the essential characteristics of this method that we used in this work. More details can be found elsewhere [38,39,40]. The nanocomposite studied here consists of an \({Al}_{2}{O}_{3}\) matrix in which the AuNPs are dispersed periodically. The resolution of the Laplace’s equation is therefore reduced to an elementary cell with periodic boundary conditions as shown in Fig. 1.

Fig. 1
figure 1

Illustration and boundary conditions related to a three-dimensional calculation cell of the AuNPs-Al2O3 composite

Full size image

The two components of nanocomposites \({Al}_{2}{O}_{3}\) and AuNPs are characterized by their dielectric permittivity which is a complex quantity. In this work, the real \({\varepsilon }_{1}(\omega )\) and imaginary \({\varepsilon }_{2}(\omega )\) parts of the permittivity of alumina \({Al}_{2}{O}_{3}\) are obtained in the UV–Vis-NIR frequency band from the tabulation published in the reference [41] using relations \({\varepsilon }_{1}\left(\omega \right)={n}^{2}-{\kappa }^{2}\) and \({\varepsilon }_{2}\left(\omega \right)=2n\kappa\), such that \(n\) and \(\kappa\) are the refractive index and the extinction coefficient, respectively. We used Drude’s two-point critical model in which the permittivity of an AuNPs is expressed as a function of the frequency of the incident electromagnetic wave to describe the permittivity of gold in a wide band of frequencies [42].

Implementation of the FEM consists in dividing the volume domain into tetrahedral finite elements and for each element, the calculation is carried out by interpolation of the potential \(V\) and its normal derivative \(\partial V/\partial n\) with the corresponding nodal values \(\mathrm{V}=\sum_{\mathrm{i}}{\uplambda }_{\mathrm{i}}{\mathrm{V}}_{\mathrm{i}}\) and \(\frac{\partial \mathrm{V}}{\partial \mathrm{n}}=\sum_{\mathrm{i}}{\uplambda }_{\mathrm{i}}\left(\frac{\partial {\mathrm{V}}_{\mathrm{i}}}{\partial \mathrm{n}}\right)\), where \({\lambda }_{i}\) denotes interpolating functions [43]. The field and potential distributions are obtained from the boundary conditions using the Galerkin method and solving the matrix equations resulting from the discretization procedure by standard numerical techniques, e.g., Gauss method [44]. After having calculated the potential and its normal derivative on each node of the mesh, the electrostatic energy \({\mathrm{W}}_{\mathrm{e}}^{\mathrm{k}}\) and losses \({\mathrm{P}}_{\mathrm{e}}^{\mathrm{k}}\) for each tetrahedral element are evaluated as:

$${\mathrm{W}}_{\mathrm{e}}^{\mathrm{k}}=\frac{{\upvarepsilon }_{0}}{2}{\iiint }_{{\mathrm{V}}_{\mathrm{k}}}{\upvarepsilon }_{\mathrm{k}}^{\mathrm{^{\prime}}}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)\left[{\left(\frac{\partial \mathrm{V}}{\partial \mathrm{x}}\right)}^{2}+{\left(\frac{\partial \mathrm{V}}{\partial \mathrm{y}}\right)}^{2}+{\left(\frac{\partial \mathrm{V}}{\partial \mathrm{z}}\right)}^{2}\right]{\mathrm{dV}}_{\mathrm{k}} ,$$
(4)
$${\mathrm{P}}_{\mathrm{e}}^{\mathrm{k}}=\frac{{\upvarepsilon }_{0}}{2}{\iiint }_{{\mathrm{V}}_{\mathrm{k}}}{\mathrm{\omega \varepsilon }}_{\mathrm{k}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)\left[{\left(\frac{\partial \mathrm{V}}{\partial \mathrm{x}}\right)}^{2}+{\left(\frac{\partial \mathrm{V}}{\partial \mathrm{y}}\right)}^{2}+{\left(\frac{\partial \mathrm{V}}{\partial \mathrm{z}}\right)}^{2}\right]{\mathrm{dV}}_{\mathrm{k}} .$$
(5)

where \({\varepsilon }_{k}\) and \({V}_{k}\) represent the permittivity and the volume of the \({k}^{\mathrm{th}}\) tetrahedron element, respectively. The total electrostatic energy and losses in the entire composite can be calculated by summation of all the elements. The composite material can be regarded as a capacitor that stores the electrostatic energy with losses when it is exposed to the electric field; these two quantities are evaluated macroscopically by:

$${W}_{e}=\frac{1}{2}{\upvarepsilon }_{\mathrm{eff}}^{\mathrm{^{\prime}}}\frac{S}{L}{\left({\mathrm{V}}_{2}-{\mathrm{V}}_{1}\right)}^{2}$$
(6)
$${\mathrm{P}}_{e}=\frac{1}{2}\upomega {\upvarepsilon }_{\mathrm{eff}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\frac{\mathrm{S}}{L}{\left({\mathrm{V}}_{2}-{\mathrm{V}}_{1}\right)}^{2}$$
(7)

where \(S\) is the area of each surface exposed to the electric field and \(d\) is distance between them. \({\varepsilon }_{eff}^{^{\prime}}\) and \(\varepsilon^{''}_{eff}\) are real and imaginary components of the effective dielectric function.

Results and Discussion

The linear response of a composite material to an electromagnetic wave is described by their dielectric function, which regulates exclusively the proliferation behavior of the radiation within the material. In this section, we present the optical properties of the AuNPs-\({Al}_{2}{O}_{3}\) nanocomposite obtained from the effective dielectric function, as a function of frequency, \({\varepsilon }_{eff}(\omega )={\varepsilon }_{1}(\omega )+ i{\varepsilon }_{2}(\omega )\). The imaginary part \({\varepsilon }_{2}(\omega )\) is directly interrelated to the absorption of the incident wave and it is interconnected to the electronic structure. \({\varepsilon }_{1}(\omega )\) and \({\varepsilon }_{2}(\omega )\) are determined from the relations (7) and (8), respectively. The mathematical expressions for refractive index, \((n)\), and extinction coefficient, \((\kappa )\), are derived from the real and imaginary of the dielectric function given by the expression [45]:

$$n={\left(\frac{\sqrt{{\varepsilon }_{1}^{2}+{\varepsilon }_{2}^{2}}+{\varepsilon }_{1}}{2}\right)}^\frac{1}{2}$$
(8)
$$\kappa ={\left(\frac{\sqrt{{\varepsilon }_{1}^{2}+{\varepsilon }_{2}^{2}}-{\varepsilon }_{1}}{2}\right)}^\frac{1}{2}$$
(9)

Figure 2a, b shows the estimated refractive index \(n\) and the extinction coefficient \(\kappa\) as a function of the wavelength of AuNPs-\({Al}_{2}{O}_{3}\) nanocomposite for different sizes of AuNPs in the UV–Vis-NIR frequency band. The refractive index determines the speed at which light passes through a medium while the extinction coefficient is a measure of the part of the beam lost as it passes through the medium. These curves show that the refractive and extinction indices obey strong changes in the vicinity of a typical wavelength noted \({\lambda }_{max}\) which corresponds to the SPR phenomenon. In other words, the refractive index varies between two extreme values; the difference between these two values increases when the size of the AuNPs increases. While the extinction coefficient takes a peak for \({\lambda }_{max}\), the amplitude of this peak increases when the size of the AuNPs increases which signifies the strong absorption of AuNPs at the SPR. Beyond the SPR, the two indices \(n\) and \(\kappa\) remain constant but their values depend on the size of the AuNPs. Figure 2a shows that for the wavelengths \(\lambda <{\lambda }_{max}\), \(n\) is constant and does not depend on the size its value which is estimated at \(n=1.76\) and for \(\lambda {>\lambda }_{max}\), the value of \(n\) increases when the size of the particles increases its value which varies from \(n=1.75\) to \(n=2.45\) when the radius of the AuNPs varies from \(r=5\) to \(r=30 nm\). Figure 2b shows that for \(\lambda <{\lambda }_{max}\), the extinction coefficient \(\kappa\) remains constant but its mean value depends on the size of the AuNPs; its estimated average value varies from \(\kappa =0.013\) to \(\kappa =0.47\) when the radius of the gold particles varies from \(r=5\) to \(r=30 nm\), while for \(\lambda {>\lambda }_{max}\), \(\kappa\) does not depend on the size; its estimated average value is \(\kappa =0.02\).

The absorption coefficient is an important parameter for optical property analysis. It indicates a measure in the intensity of electromagnetic radiation as it passes through any material. As light penetrates through any material, its intensity gets decreased; the absorption coefficient gives the measure of how much distance a beam of definite energy can penetrate into the material before it being absorbed. The absorption coefficient is calculated from the mathematical expression [46]:

$${\mu }_{a}=\frac{2\omega \kappa }{c}$$
(10)

where \(\omega ~\mathrm{and}\) \(c\) are the pulsation of the incident wave and speed of light in vacuum, respectively. The spectral distribution of the absorption coefficient of AuNPs-\({Al}_{2}{O}_{3}\) nanocomposite is shown in Fig. 3 for different sizes of AuNPs. The characteristics of the SPR are estimated by the absorption peak shown in the vicinity of \({\lambda }_{max}\); the SPR-peak position shifted from \({\lambda }_{max}=560 nm\) for \(r=5 nm\) to \({\lambda }_{max}=600 nm\) for \(r=30 nm\), while the width and the amplitude of the peak increase when the particle size increases. These curves also show that the average absorbance below the SPR band increases as a function of the size of the particles and it is negligible above the SPR band regardless of the particles size.

Fig. 2
figure 2

(a), (b) The spectra of refractive index (a) and extinction coefficient of AuNPs-\({Al}_{2}{O}_{3}\) nanocomposite for different sizes of gold nanoparticles

Full size image

The optical band gap, \({E}_{g}\), of the AuNPs-\({Al}_{2}{O}_{3}\) nanocomposites is estimated by the well-known relationship (Tauc equation), assuming a direct transition between the valence and conduction bands [47]:

$${\mu }_{a}h\nu =A{\left(h\nu -{E}_{g}\right)}^{1/2}$$
(11)

where \(A\) is the absorbance, \(h\) is the Plank constant, \({\mu }_{a}\) is the absorption coefficient, and \(\nu\) is the radiation frequency of the light wave (\(h\nu\) is the photon energy). Figure 4 shows the Tauc plot used to estimate the optical energy band gap of AuNPs-\({Al}_{2}{O}_{3}\) nanocomposite for different particle sizes. The values of the band gap are estimated by the conventional method of extrapolating the linear portion of the curve to \({{(\mu }_{a}h\nu )}^{2}=0\). The estimated band gaps are \({E}_{g}=5.34eV\) for Al2O3 without AuNPs and \({E}_{g}=5.37eV\), \({E}_{g}=5.44eV\), and \({E}_{g}=5.49eV\) when it is doped by AuNPs of size \(r=5 nm\), \(r=10 nm\), and \(r=15 nm\), respectively.

Fig. 3
figure 3

The spectrum of absorption coefficient of AuNPs-\({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\) nanocomposite for different sizes of gold nanoparticles

Full size image

When photon incident with energy greater than the band gap gets absorbed in a structure, bound electron–hole pair is generated. These pairs are free to move in the material; movement of these bound pair electrons causes the presence of optical conductivity. Optical conductivity is used for designing of optical detectors. Due to electronic charge neutrality, these do not contribute to the electrical conductivity [48]. Electrical conductivity is negligible for insulators or semiconductors but optical conductivity is always finite after the optical bandgap. To express the optical conductivity in the AuNPs-Al2O3 nanocomposite, consider the propagation of a plane wave in this material along the \(z\) direction. This wave can be described by the electric field \(\overrightarrow{E}={\overrightarrow{E}}_{0}{e}^{i\left(zk-\omega t\right)}\), where ω is the wave frequency and \(k=\frac{\omega n}{c}\) is its wave vector. A complex wave number can be expressed as \(\tilde{k }=\frac{\omega \tilde{n }}{c}\), where \(\tilde{n }\) is the complex refractive index \(\tilde{n }=n+i\kappa\). The electric field inside a conductor can be found by replacing \(k\) by \(\tilde{k }\). One can express Ohm’s law as \(\overrightarrow{J}=\sigma \left(\omega \right)\overrightarrow{E}\) and the electric displacement vector by \(\overrightarrow{D}={\varepsilon }_{eff}\overrightarrow{E}\), and hence one can express the effective dielectric constant in the form \({\varepsilon }_{eff}={\varepsilon }_{0}+\frac{i\sigma }{\omega }\). The electric conductivity \(\sigma\) is defined as:

$$\sigma =\frac{4\pi {\varepsilon }_{0}cn\kappa }{\lambda }$$
(12)

One can then define the optical conductivity, \({\sigma }_{p}=\frac{\sigma }{4\pi {\varepsilon }_{0}}\) as [49]:

$${\sigma }_{p}=\frac{{\mu }_{a}nc}{4\pi }$$
(13)

where \({\mu }_{a}\), \(n\), and \(c\) are the absorption coefficient, refractive index, and the velocity of light, respectively. Figure 5 shows the plots of the optical conductivity calculated from the relation (14) of the AuNPs-\({Al}_{2}{O}_{3}\) nanocomposite for different particle sizes. These curves show that the optical conductivity exhibits a maximum at the SPR band, which is non-zero in the near-UV region and negligible in the NIR band. The peak amplitude of the optical conductivity at the SPR increases when the size of the AuPNs increases, which shows that the number of electron–hole pairs created at the SPR is maximum.

Fig. 4
figure 4

Tauc plots to estimate the band gap energy of AuNPs-\({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\) nanocomposite for different volume fraction of gold nanoparticles

Full size image

In order to improve the application of local field enhancement in plasmonic nanocomposites, many efforts have been made to increase the enhancement factor and tune the resonance frequency. Previous reports indicate that both the intensity and resonance wavelength could be tailored by changing the particle shape, structure, and aggregation fashion. Because of plasmon hybridization, a giant localized field enhancement in the visible spectrum could be achieved in this nanostructure by resonance. It is known that the local field enhancement is dependent in the dielectric permittivity of environment [50]. Figure 6 shows the local field distribution of a nanocomposite AuNPs-\({Al}_{2}{O}_{3}\) in the UV–Vis-NIR frequency band for different values of the particle radius. These curves are obtained for an incident field amplitude fixed at \({E }_{0}=4V/m\), and for different particle sizes. It is seen that the peak local field enhancement is of the same position as that of the SPR. These results also show that the local field enhancement factor which is defined as the local field divided by the incident field \(g=\frac{{E}_{loc}}{{E}_{0}}\) is the same value (\(g=4.71)\) for a AuNPs of radius \(r<15 nm\), while when the radius increases from \(r=15\) to \(r=30 nm\), the \(g\) factor varies from \(g=4.71\) to \(g=6.95\).

Fig. 5
figure 5

The optical conductivity of AuNPs-\({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\) nanocomposite for different sizes of gold nanoparticles

Full size image
Fig. 6
figure 6

Evolution of the local electric field in the UV–Vis-NIR frequency band of AuNPs-\({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\) nanocomposite for different sizes of gold nanoparticles

Full size image
Fig. 7
figure 7

(a) Thermal power per particle of the AuNPs at the SPR as a function of the incident field intensity for different sizes of gold nanoparticles. (b) Thermal power per gram particle at the SPR as a function of the incident field intensity for different sizes of gold nanoparticles.

Full size image
Fig. 8
figure 8

(a), (b) Variation of the temperature in the AuNPs-Al2O3 nanocomposite induced by the SPR for two different cases, particle radius \(\mathrm{r}=20\mathrm{ nm}\) and incident field \({\mathrm{E}}_{0}=4\mathrm{ V}/\mathrm{m}\) (a) and \(\mathrm{r}=20\mathrm{ nm}\), \({\mathrm{E}}_{0}=2\mathrm{V}/\mathrm{m}\) (b).

Full size image

The SPR is an efficient way to confine energy into the extremely small volume of AuNPs, thus drastically enhancing both its absorption and scattering cross-sections [51]. While the scattering cross-section tells how much energy is reradiated by the AuNP in the form of light, the absorption cross-section specifies the portion of absorbed light that is re-emitted in the form of heat. Thus, absorption is what primarily matters in thermoplasmonics [52]. Taking advantage of this light-to-heat conversion provides access to an innovative way of studying and controlling heat-induced processes; it is necessary to take into account that the optical properties of the nano-objects under investigation are governed by a series of energy exchanges, each of them characterized by a typical time scale. If the frequency of the incident radiation matches the SPR band, a resonant coupling with the EM wave occurs, with a resulting excitation at the plasmon resonance; this triggering of phenomena appears as a collective, coherent, and dipolar oscillation of electrons of the conduction band. To restore the internal thermal equilibrium of these electrons, the energy is redistributed, through electron–electron collisions \((e-e)\), inside the quasi-free electronic gas. Subsequently, the hot carriers’ energy is redistributed with a relaxation process through the electron–phonon interaction \((e-ph)\). The last step takes into account the medium surrounding the AuNP, and the transfer of thermal energy to the interface, via phonon–phonon-collisions \((ph-ph)\). This last process leads to the cooling of the AuNP, which releases heat to the surrounding medium, causing its temperature to rise. Thus, the aforementioned \((e-ph)\) collision represents the damping mechanisms for the LSPR phenomenon in AuNPs, which results in heat generation via the Joule mechanism. To calculate the temperature in proximity to the AuNP surface, it is fundamental to determine the Joule effect’s heat.

The amount of Joule heat generated by each gold nanoparticle under SPR can be estimated by gold nanoparticles as conductors of constant cross section:

$${P}_{SPR}={I}^{2}.R=\sigma \left(\omega \right).\left[S.d.{\left|{E}_{loc}\right|}^{2}\right]$$
(14)

where \(\sigma \left(\omega \right)\), \({E}_{loc}^{2}, S\), and \(d\) are the Drude model conductivity of gold at the SPR frequency, magnitude of the enhancement electric field, cross-sectional area of the gold nanoparticle, and its diameter, respectively. Assuming efficient heat transfers from \(N\) nanoparticles to the surrounding \({Al}_{2}{O}_{3}\) medium, the volumetric SPR–induced heating rate \((dT/dt)\) of gold nanoparticles is shown in the following equation [53]:

$$\frac{dT}{dt}=\left[\frac{\sigma \left(\omega \right).\left[S.d.{\left|{E}_{loc}\right|}^{2}\right]}{V.{C}_{{Al}_{2}{O}_{3}}}\right]$$
(15)

where are the volume of the suspension and heat capacity of \({Al}_{2}{O}_{3}\) matrix, respectively. Figure 7a, b shows the evolution of the thermal power generated per particle (Fig. 7a) and per gram of particles (Fig. 7b) at the SPR frequency as a function of the incident field intensity for different size of AuNPs. These curves show that the thermoplasmonic power increases exponentially as a function of the incident field intensity for a fixed nanoparticle size. At the same time, the thermal power generated by individual particle increases as a function of the particle size for a fixed field intensity. Figure 7b shows that the evolution of the thermal power per gram of particle is approximately the same for small size of AuNPs \(r<15 nm\); however, for particles with a radius greater than \(15 nm\), this power increases when the particle size increases. Figure 8a, b shows the evolution of the temperature as a function of time in AuNPs-Al2O3 nanocomposite, which is due to the conversation of light energy into heat by the SPR phenomenon of AuNPs. These two figures are plotted for a fixed AuNP size (radius \(r=20 nm\)) and for two different values of the incident electric field intensity, \({E}_{0}=4 V/m\) (Fig. 8a) and \({E}_{0}=2 V/m\) (Fig. 8b). In these two cases, the temperature change is calculated for different volume fraction of AuNPs \(\phi\) in the nanocomposite which is defined as \(\phi =\frac{{V}_{P}}{{V}_{C}}\), where \({V}_{P}\) is the volume of the particles and \({V}_{C}\) is that of the nanocomposite. These curves show that at the SPR frequency, the temperature increases according to a linear function relative of times and to the volume concentration of the particles. These results show that the heat dissipation in the plasmonic nanocomposite AuNPs-\({Al}_{2}{O}_{3}\) at the SPR can considerably increase the temperature of the medium depending on the size and concentration of the particles and on the irradiation power. The behavior of AuNPs as heating nanosources when irradiated by visible light opens a new scenario for realizing fully optical components and biomedical applications.

Conclusion

In conclusion, the optical and thermoplasmonic properties of a nanocomposite constituted by a spherical AuNP integrated in an alumina \({Al}_{2}{O}_{3}\) matrix have been investigated using the FEM. The linear response of a composite material to an electromagnetic wave is described by their dielectric function, which regulates exclusively the proliferation behavior of the radiation within the material. In this work, the optical properties of the AuNPs-\({Al}_{2}{O}_{3}\) nanocomposite are determined from the effective dielectric function. This function depends on the size, shape, volume fraction of the NPs, and the intrinsic properties of the nanocomposite constituents, especially their dielectric permittivity. First, we calculated the optical parameters such as refractive index, extinction coefficient, absorption coefficient, and optical conductivity of the nanocomposite in the UV–Vis-NIR frequency band for different sizes of AuNPs. The SPR characteristics of gold nanoparticles are determined from the absorption spectra which show a peak at the wavelength \({\lambda }_{max}\) corresponding to the SPR phenomenon. In particular, the SPR-peak position is shifted from \({\lambda }_{max}=560\) to \({\lambda }_{max}=600 nm\) when the radius of the particles increases from \(r=5\) to \(r=30 nm\). The spectra of the refractive index and the extinction coefficient show that for the wavelengths \(\lambda <{\lambda }_{max}\) (before SPR), the extinction dominate is compared to the transmission in the nanocomposite AuNPs-\({Al}_{2}{O}_{3}\) while for \(\lambda >{\lambda }_{max}\) (after SPR), the transmittance dominate is compared to the extinction. Second, the band gap energy is determined from the absorption coefficient for different values of the volume fraction of AuNPs in the nanocomposite using the Tauc plots. The results show that the band gap energy increases from \({E}_{g}=5.34eV\) for alumina \({Al}_{2}{O}_{3}\) without AuNPs to \({E}_{g}=5.49eV\) for a volume fraction \(\phi =0.82\%\) of AuNPs. The electric field enhancement induced by the AuNPs at plasmonic resonance is also determined depending to the particle size; the results show that the enhancement factor increases from \(g=4.71\) to \(g=6.95\) when the radius of the AuNPs increases from \(r=5\) to \(30 nm\). Third, the generated thermal power by particles is calculated for different sizes, which allows to calculate the thermal power per gram of particles depending on the intensity of the incident electric field. The results show that the plasmonic thermal power is almost identical for small particles when the radius is less than \(r=15 nm\) and increases considerably when the size increases from \(r=15\) to \(30 nm\). For a fixed size and incident field amplitude, we represent the temperature evolution in the nanocomposites AuNPs-\({Al}_{2}{O}_{3}\) depending of time for different particle concentrations. These results show that a new light in optics and bio-photonics is offered by utilizing and applying the thermo-optical properties of AuNPs. Under suitable light illumination, AuNPs behave as nanosource of heating, opening a new scenario to realize all-optical components and biomedical applications. While metallic NPs have been for long mainly used for their optical properties, they have recently triggered much expectation for enhancing thermal-induced processes in areas such as medical therapy, imaging in biology, hydrodynamics, and chemistry. The understanding of the physics associated with heating of metal NPs is still a matter under active investigation, which allows to highlight the possibility of realizing a new generation of biomedical applications by exploiting the photothermal heating of AuNPs. Ranging from light-controlled drug-release to the ongoing battle against COVID-19, thermoplasmonic-based AuNPs represent a new weapon for realizing a new generation of medical devices.