1 Introduction

Tooth root apical resection is a procedure most commonly performed in case of chronic periodontitis and is the treatment of choice in many endodontic complications. It consists of root apex reduction together with surrounding periapical granulation tissue, cyst, endodontic materials.

Missing bone regeneration in the lumen of the bone defect is crucial for the bone healing process. Several treatment methods are helpful in bone restoration, such as guided tissue regeneration (GTR) or guided bone regeneration (GBR) [1, 2]. For this purpose, osseous materials and bone graft substitutes, barrier membranes, polypeptide growth factors and morphogenic bone proteins are used [3]. The visual inspection of a bone roughness could not be sufficient for proper image interpretation. On the other hand, the interpretation of bone regeneration range after xenogenic material application shows a significant increase in bone density. New computer-aided image processing methods of the texture analysis can show proper bone remodeling or lack of total material integration. Therefore, it is necessary to search for alternative methods of radiographic interpretation of the treatment results.

An objective and explicit characterization of image regions is one of the major problems to deal with when a computer-aided image analysis is carried out. The texture is one of the useful sources of information about the analyzed image regions [4]. The texture features, such as a set of numerical parameters, can characterized regions of interests (ROIs) defined in the organs under study. Each of the texture parameters describes other textural properties such as roughness, the local contrast or homogeneity. Until now, a lot of different methods for calculating texture parameters have been investigated. The proposed texture measures use statistical (the texture can be defined by the local statistical properties of pixel gray levels, e.g., histogram or methods based on second-order statistics [5,6,7]) or structural approaches (texture can be represented by primitives and a hierarchy of spatial arrangements of those primitives, e.g., mathematical morphology [8, 9]). Another possibility includes model-based approaches (e.g., fractals [10, 11] and Markov fields [12] or on Wold decomposition [13]) and transform methods (Fourier-based [14], Gabor-based [11, 15] or wavelets [11, 16]).

Recent studies have demonstrated that the fractal methods are considered appropriate for quantifying changes in bone structures. Ruttimann et al. [17] used fractal dimension (D) to investigate whether fractal dimension calculated on the basis of the radiographs of periodontal alveolar bone can be a diagnostic indicator in the case of osteoporosis. Six radiographs of premenopausal and postmenopausal women were taken to calculate fractal dimension. In the case of the older group (postmenopausal women), fractal dimension values were higher. Southard et al. [18] applied fractal dimension to analysis of changes in alveolar bone in the case of simulated osteoporosis. Strong correlation between calcium loss and decreasing fractal dimension was found. Torres et al. [19] used fractal dimension in the case of patients with bisphosphonate-associated osteonecrosis of the jaws (BP-ONJ). Fractal dimension values were higher for patients with BP-ONJ than for controls. Wagle et al. [20] used fractal analysis to quantify the complex morphology of PDL–bone interface. In our investigations [10, 21], fractal analysis was used in the case of the healing process after bone loss. During the healing process after bone loss, the surfaces of radiographic images became smooth.

The aim of the present study was to estimate fractal dimension on radiographic images using box-counting dimension and information dimension to determine the physical roughness.

2 Methods

The term fractal was coined by Mandelbrot to describe irregular objects found in nature. Fractal objects are characterized by: self-similarity, large degree of heterogeneity and lack of a well-defined scale [22, 23]. “Self-similarity” refers to the resemblance of small-scale structures of the fractal set to its large-scale structures.

One of the biggest advantages of fractal analysis is its capacity for describing the shapes of very complex objects. Nature is full of structures, which are so complex that their mathematical description is impossible in terms of Euclidean geometry. In such sets, there is often a basic structure which makes a whole figure by copying itself. The best example of such a structure is a tree, which grows from a small branch by ramification. The immense crown consists of many branches broadly distributed in space. They spread chaotically, but the large-scale structure is built by mimicking small-scale structure. Such objects are difficult for traditional geometrical estimation, but they can be easily described using fractal geometry. The vascular patterns created by angiogenesis are examples of such complex and irregular objects [17, 24].

Fractal dimension [24] is a kind of dimension, which enables the measurement of the complexity of the given object. The history of the fractal dimension began in the early twentieth century, when Hausdorff [25] published a method of calculating the fractal dimension in his scientific work. Hausdorff’s definition of attractor dimension was generalized by Besicovitch [26]. However, Hausdorff–Besicovitch’s dimension is too complicated for practical estimation.

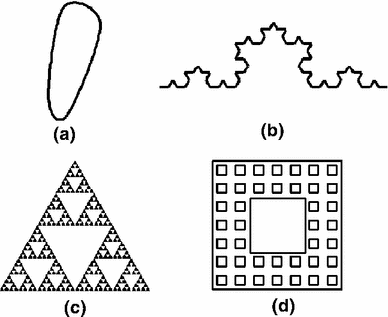
From the point of view of clinical application (i.e., the point of view of an ordinary physician), the interpretation of values of fractal dimension should be simple [18]. It is very interesting that visually similar patterns may have different fractal dimensions. This fact may be very important in medical diagnostic medical procedures. The differences between the values of D may give some new information which cannot be reflected using the conventional methods of radiological analysis. Figure 1 shows four figures (four patterns): a Euclidean shape, the Koch curve, the Sierpinski triangle and the Sierpinski carpet, with the fractal dimensions equaling 1.000, 1.262, 1.585 and 1.896, respectively. Fractal dimension is a measure of the complexity and irregularity of an object [19, 27,28,29].

Due to such difficulties, much easier to apply methods of calculating the fractal dimension were introduced. The most common and widespread methods of calculating fractal dimension value are based on calculating box-counting dimension, information dimension, mass dimension and ruler dimension.

Fig. 1
figure 1

Fractal dimension values of various figures: a Euclidean shape, fractal dimension \(D = 1.000\), b Koch curve, \(D = 1.262\), c Sierpinski triangle, \(D = 1.585\), d Sierpinski carpet, \(D = 1.896\)

Full size image

2.1 Box-counting dimension

The box-counting dimension (also called capacitive dimension) [22, 24, 30,31,32] is determined by the formula [30]:

$$\begin{aligned} D_{B}=\lim _{\delta \rightarrow 0}\frac{\log N(\delta )}{-\log (\delta )} \end{aligned}$$
(1)

where \(\delta \) is the length of one side of a square cell of the grid and \(N(\delta )\) is the number of square cells which contain elements of the study area.

In practice, while calculating the box-counting dimension on the basis of a two-dimensional image, the object must be covered with a square grid with a known length of the side of a mesh. Then, all the square cells of the grid, in which elements of the object are located, must be counted. Those two steps must be repeated for several decreasing values of the length of the side of the mesh. Calculated values must be presented on a fractal plot in logarithmic scale, where horizontal axis represents the length of the side of a cell and the vertical axis represents the number of mesh containing the elements of the object. Regression line can be marked on the basis of marked points. The value of the slope of the regression line is directly related to the box-counting dimension value [30]:

$$\begin{aligned} N(\delta )\approx \delta ^{-D_{B}} \end{aligned}$$
(2)

Due to simplicity of calculation, it is the most commonly used method of calculating fractal dimension in various types of research. Counting the value of the fractal dimension using “box-counting” can be applied both in the case of self-similar and not self-similar objects. The discussed method can also be used in any space, where three-dimensional object is covered with cubes, for example.

2.2 Information dimension

The method of calculating the information dimension [26, 31, 33, 34] is similar to the method of calculating the box-counting dimension. While calculating the box-counting dimension, all the square cells of the grid in which elements of the object are located must be counted—whether it is only one point or a large set of points—whereas the information dimension also considers the number of points lying within a given mesh. The information dimension value is given by the formula [31]:

$$\begin{aligned} D_{I}=\lim _{\delta \rightarrow 0}\frac{I(\delta )}{-\log (\delta )} \end{aligned}$$
(3)

where \(\delta \) is the length of one side of a square cell of the grid, and \(I(\delta )\) is an information entropy. A measure of information is determined by the formula [33]:

$$\begin{aligned} I(\delta )=\sum _{i=1}^{N(\delta )}P_{i}\log \frac{1}{P_{i}} \end{aligned}$$
(4)

where \(P_{i}\) is the probability of finding a point of the object in the mesh number i. This probability is given by the formula [26]:

$$\begin{aligned} P_{i}=\lim _{n\rightarrow \infty }\frac{N_{i}}{N} \end{aligned}$$
(5)

where \(N_{i}\) is the number of points in the mesh number i, and N is the total number of grid cells.

In practice, the method of calculating the information dimension on the basis of a two-dimensional image is similar to the method of calculating the box-counting dimension.

Calculated values can be presented on a fractal plot in logarithmic scale, where horizontal axis represents the length of the side of a cell and the vertical axis represents the information entropy. Regression line can be marked on the basis of marked points. The value of the slope of the regression line is directly related to the information dimension value:

$$\begin{aligned} I(\delta )\approx \delta ^{-D_{I}} \end{aligned}$$
(6)

Information dimension, similarly to box-counting dimension, can be used both for the analysis of two-dimensional objects and objects in other spaces, for example. In the case of three-dimensional objects, the square grid is replaced by cube grid.

3 Materials

Radiographic images used in the study come from Department of Oral Surgery in Bialystok (Medical University of Bialystok).

The research was carried out on a group of 20 patients aged from 18 to 53 years. All patients had the root cysts. Teeth roots and cysts were removed surgically. Bone losses in jawbone were filled up with xenogeneic material Geistlich Bio-Oss®[35] covered with membrane Geistlich Bio-Gide®[35] (method of guided bone regeneration was used). Geistlich Bio-Oss®is biocompatible xenogeneic granulated material, which is produced from beef bones and consists of cancellous bone granules (gradiation from 0.25 to 1 mm). Geistlich Bio-Gide®is resorbable membrane, which is produced from porcine collagen. In all cases, the bone regeneration proceeded in a proper way—there were no early or late postoperative complications.

A set of Kodak RVG 6100 with radiation beam collimator (\(90^{\circ }\) angle technique was applied) was used to take digital radiograms. The effective resolution of this device is >14 lp/mm. Exposure time equals 0.08 s.

Radiographic images used in the study were made before the surgery (11 images), directly after the surgery (8 images) and a year after the surgery (19 images). Radiographic images, which were taken before the surgery, were not included during calculation—only pictures taken directly after the surgery (8 radiographs) and the ones taken a year after the surgery (19 radiographs) were used.

4 Results

The areas of interest in the study were regions of xenotransplants used to fill jawbone losses. Square fields with a size of \(128\times 128\) pixels (Fig. 2) were separated from these areas. In the case of comparative analysis, best results are achieved if the test samples are cut from the same area (the area separated from radiographic image made directly after the surgery should be exactly the same place as the area separated from the digital radiography image made 1 year after the surgery) which is impossible in reality. The analyzed images of digital radiography are often moved or rotated due to high improbability of setting the radiovisiography sensor in the same position. To separate the areas of interest, CorelDRAW software was used, where roots canals centerlines were marked, regions of interest were rotated, etc.

Fig. 2
figure 2

Exemplary patient—digital radiography images with marked areas of interest: a directly after the surgery b a year after the surgery

Full size image

The next step was binarization of the areas of interest (Fig. 3). In the case of comparative analysis, it is important to binarize all images taken for study at the same threshold. For best results, optimal binarization thresholds were checked for all images. For this purpose, Otsu’s method [23] and MATLAB software were used. Binarization threshold values are in the range between 79 and 176. The mean value of threshold calculated from the determined range is 127.5.

Fig. 3
figure 3

Exemplary patient—areas of interest: a before binarization (from left: directly after the surgery and a year after the surgery), b after binarization (from left: directly after the surgery and a year after the surgery)

Full size image

The final step was calculating the fractal dimension of the areas of interest. BENOIT software [27], which enables fractal analysis, was used to calculate box-counting dimension and information dimension (Fig. 4). In this program, a rotating grid was used which allowed access to the minimum number of boxes which were occupied by the xenotransplants objects. BENOIT software allows users to deactivate groups of sequential points from the ends of the fractal plots. The deactivated points are not used to fit the line to the data. This operation improves the results by diminishing the standard deviation of the least-squares fitting.

Fig. 4
figure 4

Examples of fractal analysis of analyzed patterns. Upper left corner: image after binarization; upper right corner: log–log plot for box-counting method

Full size image

The results of fractal analysis of xenotransplants patterns are shown in Table 1.

Table 1 Mean value ± standard deviation of box-counting dimension and information dimension
Full size table

With the passage of time, box-counting dimension and information dimension values increase. The mean value of box-counting dimension (Table 1) calculated on the basis of radiographic images taken immediately after the operation equals \(1.04\pm 0.19\), while a year after the surgery it rose to \(1.63\pm 0.25\). Average increase in box-counting dimension value equals 0.6 (in the case of individual patients minimum increase equals 0.3 and maximum increase equals 1.0). Analogically (Table 1), mean values of information dimension were \(1.07\pm 0.24\) and \(1.65\pm 0.22\), respectively. Average increase in information dimension value equals 0.6 (in the case of individual patients minimum increase equals 0.1 and maximum increase equals 1.0).

Figures 5 and 6 show box-counting dimension and information dimension values in specified time for each patient. In all cases, differences between values of fractal dimension for individual patients and the mean values are slight (Figs. 7 and 8).

Fig. 5
figure 5

Box-counting dimension values for each patient calculated on the basis of radiographic images taken directly after the surgery and then 12 months later

Full size image
Fig. 6
figure 6

Information dimension values for each patient calculated on the basis of radiographic images taken directly after the surgery and then 12 months later

Full size image
Fig. 7
figure 7

Results of box-counting dimension for patients calculated on the basis of radiographic images taken directly after the surgery and then 12 months later

Full size image

Mann–Whitney test [36] was used for statistical analysis. This is a nonparametric test for two independent groups, based on the sum of ranks. In both cases, the significance of p value of the Mann–Whitney test (Table 1) is >0.05 (\(p<0.05\)). The results are significant from a statistical point of view. There are significant differences between the values calculated on the basis of radiograms taken directly after the surgery and a year after the surgery.

Scatterplot (Fig. 9) clearly shows the positive correlation between the information dimension and the box-counting dimension. The values of both dimensions increase with the passage of time. The coefficient of determination equals 0.97, which means that fitting points on the plot to a regression line is very good. The correlation coefficient between the values equals 0.98—there is very strong correlation between both dimensions.

The increase in fractal dimension means that the regions of xenotransplants become more complex as a result of bone tissue remodeling. Guided tissue regeneration biomaterial Geistlich Bio-Oss® applied, stimulates bone tissue formation and integrates with human tissues. After 1 year from the surgery, the areas of the xenotransplants have a different biological structure than directly after the surgery, which is noticeable during calculating fractal dimension and on the images of digital radiography.

Fig. 8
figure 8

Results of information dimension for patients calculated on the basis of radiographic images taken directly after the surgery and then 12 months later

Full size image
Fig. 9
figure 9

Scatterplot: information dimension—box-counting dimension

Full size image

5 Conclusion

Fractal geometry is a branch of science that is widely used in various fields of science, including medicine. A number of studies were carried out to confirm the usefulness of the fractal dimension as a diagnostic parameter. Fractal dimension values varied along the entire root length (from the apex to the cementoenamel junction). Two methods of calculating fractal dimension were presented in this study. Box-counting dimension and information dimension increase with the passage of time. This dependence between fractal dimension value and the passage of time can be used in medical diagnostics in the case of xenotransplants used to fill jawbone losses. Knowing that for normal regeneration of bone, the value of the fractal dimension equals 1.0 right after the surgery and 1.6 after a year after filling, we could use image segmentation to efficiently find fragments where this value differs from those acquired in the course of tests and quicken the diagnostics of irregularities in bone tissue regeneration.

In the future, the work on classification of the healing process in bone loss cases will be continued. The methods of extracting other texture parameters will be investigated.